Crystal growth and thermodynamic investigation of Bi₂M²⁺O₄ (M = Pd, Cu)

Abstract

Phase equilibria that are relevant for the growth of Bi₂MO₄ have been studied experimentally, and the ternary phase diagrams of Bi₂O₃–PdO₂–Pd and Bi₂O₃–Cu₂O–CuO and its isopleth section Bi₂O₃–CuO were redetermined. It is shown that every melting and crystallization process is always accompanied by a redox process at the phase boundary and that for both title compounds, the valence of the transition metal is lowered during melting. Vice versa, during crystal growth, O₂ must be transported through the melt to the phase boundary. Based on these new insights provided by our thermodynamic studies, Bi₂CuO₄ single crystals with a length of up to 7 cm and a diameter of 6 mm were grown by the OFZ technique to be used for investigations of magnetic, electronic and thermal transport properties. The grown crystals were characterized by powder X-ray diffraction, Laue, magnetization and specific heat measurements.

---

1 Introduction

Over the last decades, transition-metal (M) oxides containing MO₄ square-planar environments in their structure have attracted interest due to their fascinating structure based electronic and magnetic properties.^1,2 Compared to tetrahedral and octahedral coordination, the square planar geometry is rarely found in transition metal oxides because it is thermodynamically less stable.^1,3 However, MO₄ square planar coordination is typically encountered in d⁸ and d⁹ electron configurations, for example in Pd, Pt or Cu-based compositions, where it is favorable for electronic ground states.¹ The structure of Bi₂M²⁺O₄ (M = Pd, Cu) is composed of such MO₄ units forming staggered chains along the c-axis.²

In the past few decades, Bi₂CuO₄ has been extensively studied and has first come into the focus of the high temperature superconductivity community as a non-superconducting structural relative due to its shared CuO₄ motifs.⁴ Since then, it continues to be of fundamental interest as a low-dimensional S = 1/2 Heisenberg antiferromagnet exhibiting a plethora of intriguing phenomena including controversially discussed low-temperature anisotropic magnetic ground state properties that have been studied by bulk magnetization,² Raman,⁵ antiferromagnetic resonance⁶ or neutron scattering techniques,⁷ the observation of magnetically-induced ferroelectricity,⁸ and a recent prediction of the realization of a topologically non-trivial double-Dirac metal in Bi₂CuO₄ under pressure.⁹ In addition, Bi₂CuO₄ has recently been investigated as a photocathode material for photoelectrochemical water splitting^10,11 or even for gas-sensing applications.¹²

The isostructural system Bi₂PdO₄ has also recently attracted attention following experimental and theoretical work on the thermoelectric properties of similar oxide materials with square planar PdO₄ units.^13,14 Theoretical work by He et al.¹⁵ proposed favorable thermoelectric properties of Bi₂PdO₄ arising from a combination of its peculiar electronic band structure mainly related to the involved Pd²⁺ d_z² orbitals and a low lattice thermal conductivity. The latter has been ascribed to the presence of heavy Bi³⁺ ions in the crystal structure whose 6s² electron lone pairs are thought responsible for contributing to additional phonon scattering and anharmonic effects.

The tetragonal P4/ncc crystal structure of Bi₂MO₄, which is shown in Fig. 1, consists of square-planar MO₄ units and asymmetrically distorted BiO₆ octahedra.^15,16 The MO₄ units are stacked along the c-axis, forming tunnels along [001] and [110] with the BiO₆ octahedra.¹⁵

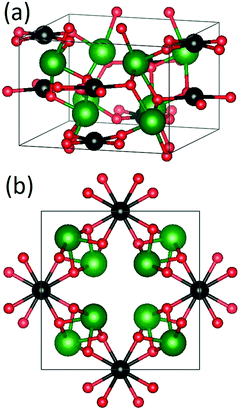Fig. 1 (a) 3D tetragonal crystal structure of Bi₂MO₄ and (b) projection along the c-axis (green = Bi, black = Cu/Pd, red = O) (drawn with VESTA³⁰).

In order to study magnetic, electronic or thermal transport properties in detail at a fundamental level, the use of large high quality single crystals (of either Bi₂CuO₄ or Bi₂PdO₄) is required. Knowledge of the thermodynamic processes and the relevant phase diagrams are essential for crystal growth.

Despite numerous studies on the crystal structure and low temperature magnetic properties of Bi₂CuO₄ in the past,^2,8,17–20 there is still no consensus on the Bi₂O₃–CuO phase diagram and thus the growth conditions required for large, centimeter-sized, high quality Bi₂CuO₄ single crystals. In the existing literature, the phase diagrams are very contradictory^21–29 and often the growth conditions are insufficiently detailed.

The phase diagram of Bi₂PdO₄ was proposed in 1979 by Kakhan et al.²² and apart from the work by Arpe and Müller-Buschbaum¹⁶ on that system discussing single crystal X-ray diffraction on tiny single crystal samples, to our knowledge no reports on crystal growth of larger single crystals, growth conditions or detailed thermodynamic investigation of Bi₂PdO₄ exist.

The present work therefore focuses on the thermodynamic investigations and the crystal growth of Bi₂M²⁺O₄ (M = Cu, Pd). Phase diagrams that are relevant for the growth of the title compounds are redetermined. We will show that pseudobinary systems of Bi₂O₃–CuO (–PdO) are insufficient to describe the growth process, rather Cu₂O (or Pd, respectively) has to be included for a satisfactory description of the experimental results. Redox processes that occur at the phase boundary during melting and crystallization of the Bi₂MO₄ phase were investigated. The grown crystals were characterized by powder X-ray diffraction (XRD), Laue, magnetization and specific heat measurements, demonstrating the excellent quality of the crystals synthesized in this work.

2 Experimental

2.1 Thermodynamics

Investigations on the pseudobinary Bi₂O₃–CuO and the ternary Bi₂O₃–Cu₂O–CuO phase diagrams are based on powder mixtures of the raw materials with concentrations between pure Bi₂O₃ (Sigma-Aldrich, 5N purity) and 80 mol% CuO (Alfa Aesar, 2N7 purity) in Bi₂O₃. Simultaneous thermogravimetric (TG) and differential thermal analysis (DTA) measurements (TG–DTA) were carried out with a Netzsch STA 409C on the powder mixtures placed in Al₂O₃ crucibles in air at heating and cooling rates of 10 K min⁻¹. In addition, a grown Bi₂CuO₄ single crystal was measured using a Netzsch STA 449 F3 with differential scanning calorimetry (DSC–TG) and the sample was placed in a platinum crucible with a lid. For this measurement, an oxygen-enriched atmosphere with flowing 66.7% O₂ + 33.3% Ar and heating and cooling rates of 5 K min⁻¹ were used.

The study of the thermodynamic properties of Bi₂PdO₄ was carried out on phase pure Bi₂PdO₄ powder obtained by the solid state reaction of a mixture in a stoichiometric ratio of Bi₂O₃ (Sigma-Aldrich, 5N purity) and PdO (Alfa Aesar, 3N purity), sintered three times for 24 h at 740 °C in air with intermediate grindings. Phase purity was confirmed by powder XRD under ambient conditions. TG–DTA measurements were carried out with a Netzsch STA 449 F3 in platinum crucibles at heating and cooling rates of 10 K min⁻¹. The gas flow was set using a mass flow controller to deliver atmospheres containing 10%, 20%, 80% and 100% O₂ in Ar, respectively. The phase composition was additionally studied by means of high temperature XRD measurements performed in air up to 1000 °C using a Bruker D8 Advance diffractometer with Cu-K_α radiation, equipped with a high temperature oven chamber (Anton Paar HTK 1200 N) and a LynxEye detector for rapid data acquisition.

2.2 Crystal growth

In preparation for the crystal growth, polycrystalline rods of Bi₂CuO₄ were prepared by mixing Bi₂O₃ and CuO powders in a 1 : 1 molar ratio followed by sintering in air for 24 h at 725 °C. After this first sintering step, the powder was ground in an agate mortar and sintered again for 24 h at 750 °C. XRD phase analysis confirmed that a single-phase, pure Bi₂CuO₄ phase resulted from this annealing process. The sintered material was then reground and compacted in cylindrical rubber balloons and pressed for three minutes at 2 kbar in a cold isostatic press (Engineered Pressure International NV, Belgium). To increase the rod density, the pressed rods were sintered again for 24 h at 750 °C. The final rods were on average about 11 cm long and 6 mm in diameter and had an estimated density of 85% of the theoretical value.

All growth experiments were carried out in an optical floating-zone (OFZ) furnace from Crystal System Corporation (type FZ-T-10000-H-VI-VPO) using polycrystalline feed and seed rods. The furnace consists of a four-mirror setup in which 300 W halogen lamps and a fused silica protection tube were used. For Bi₂CuO₄, an air flow of 0.3 l min⁻¹ was used as the growth atmosphere, and the Bi₂PdO₄ growth experiments were done in a flowing oxygen atmosphere (because the TG measurements in Fig. 5 revealed a significantly stronger tendency to lose oxygen for this compound). Seed and feed rods were rotated in opposite directions at 30 rpm and at 20 rpm, respectively. To ensure stable growth conditions without cracks, growth rates between 5 and 6 mm h⁻¹ were employed.

The grown crystals were characterized by XRD and Laue measurements. XRD data on crushed single crystal pieces mixed with a LaB₆ standard were used to determine the lattice parameters of the grown crystals. Magnetization measurements using a Magnetic Property Measurement System (MPMS by Quantum Design Inc.) were carried out between 1.9 K and 350 K on two single crystals with a mass of 40.79 mg and 19.0 mg with a magnetic field applied along the c or a axis, respectively, for comparison with previously published results and for confirmation of the crystal quality. Low temperature specific heat data between 2 and 100 K were collected in zero field with the standard adiabatic-relaxation technique using the heat capacity option of a Physical Property Measurement System (PPMS by Quantum Design Inc.) on a 7.95 mg sample.

The crystal growth of Bi₂PdO₄ in the OFZ was also attempted. For this, polycrystalline rods were prepared from a powder mixture of stoichiometric ratios of Bi₂O₃ and PdO that were sintered 2 times at 740 °C in air with intermediate grindings until a single-phase Bi₂PdO₄ powder was obtained. The feed and seed rods were then prepared analogously to those of Bi₂CuO₄ and underwent a final sintering step at 740 °C. The rods were 6 cm long and 6 mm in diameter. The density of the rods was estimated as 75% of the theoretical density, resulting in slightly less compact rods than those of Bi₂CuO₄.

3 Results and discussion

3.1 Thermodynamics

3.1.1 Bi₂CuO₄. In the past few decades, the system Bi–Cu–O has been investigated several times. Unfortunately, there are many contradictory phase diagrams for the Bi₂O₃–CuO system in the literature,^21–29 and in some references CuBi₄O₇ is additionally described as an existing phase.²¹ In many phase diagrams, the liquidus line is represented as a dashed line due to the reduction process of CuO, which makes it impossible to interpret the measured data clearly.

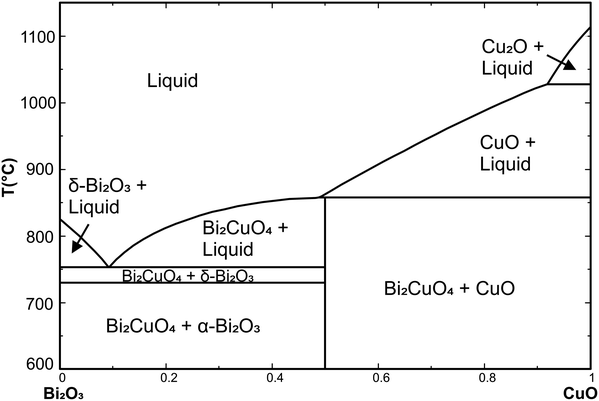
From our previous investigations on copper oxide compounds, it is known that copper oxide based melts always contain Cu⁺ and Cu²⁺.^31–34 Bi₂CuO₄ contains Cu²⁺ which is stabilized by low temperature T and high oxygen partial pressure p(O₂) which are the conditions where DTA with powder mixtures of Bi₂O₃ and CuO was performed. For powders with a CuO concentration of 0 ≤ x ≤ 0.5, two endothermal effects with constant onsets at T_t = 732 ± 5 °C and T_eut = 761 ± 5 °C were found, originating from the α–δ transition of Bi₂O₃ (ref. 35) and the eutectic of Bi₂O₃ with Bi₂CuO₄, respectively. The position of the liquidus could be derived from a bend in the DTA curve only for some samples.

Samples with x > 0.45 showed one clear endothermal effect around T_per = 851 ± 10 °C which could be attributed to the (almost, see below) peritectic melting of Bi₂CuO₄. However, the width of this DTA peak (ΔT ≈ 40 K) did not allow us to discriminate if this effect is really related to peritectic decomposition (like suggested by Hrovat and Kolar²³) or to congruent melting of Bi₂CuO₄ with another eutectic towards CuO which is just 5 K below the congruent melting point (like suggested by Kakhan et al.³⁶).

Despite this ambiguity, these preliminary results allowed successful OFZ growth experiments with 1 : 1 (molar) Bi₂O₃ : CuO rods. A small (24.66 mg) Bi₂CuO₄ single crystal that resulted from the growth experiments was investigated in more sensitive DSC–TG measurements in an atmosphere with a higher oxygen concentration to stabilize Cu²⁺. The results are shown in Fig. 2. During the first heating, the melting peak of the Bi₂CuO₄ compound appears at 855 °C and is connected with a mass loss of Δm/m = −0.41% in the associated TG curve. Bi³⁺ can be considered to be stable under the experimental conditions used here. Then, the experimental Δm/m can be attributed to a formal reaction Bi₂CuO₄ → Bi₂O₃ + CuO_0.86 + 0.07 O₂, because 0.07 O₂ corresponds to a mass loss of 0.41% (some Cu²⁺ is reduced to Cu⁺). One can assume that Cu²⁺ is stabilized in solid Bi₂CuO₄ and exists in equilibrium with Cu⁺ in the melt, with a composition that is close to the eutectic composition in the Cu₂O–CuO system.³⁷

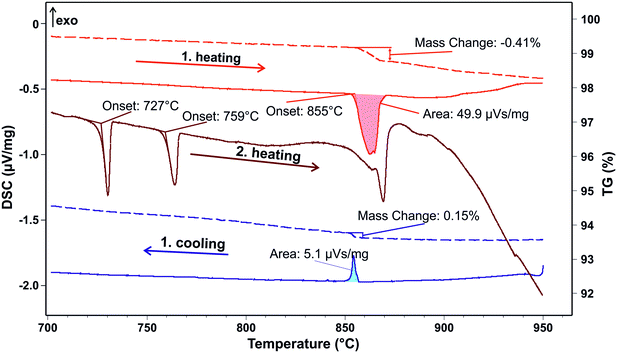Fig. 2 Bi₂CuO₄ single crystal TG–DSC measurement (1st and 2nd heating + 1st cooling at 5 K min⁻¹) in flowing 66.7% O₂ + 33.3% Ar. Solid lines: DSC, dashed lines: TG.

This reduction process CuO → Cu₂O continues with further heating, which means that overheating during a crystal growth experiment should be avoided. Experiments in a pure oxygen atmosphere are also not recommended because this increases the liquidus temperature (see Fig. 1 in ref. 37). During the cooling process, the sample gets partially reoxidized (Δm/m = +0.15%), connected with an additional small exothermal DTA peak. This is clearly not due to crystallization but results simply from the oxidation Cu₂O + 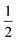O₂ → 2CuO with ΔH = −8122 J per gram O₂ (ref. 38) (the sensitivity calibration to convert the peak area of 5.1 μV s mg⁻¹ to that enthalpy increment in Fig. 2 was performed at T_f = 801 °C by melting NaCl). Crystallization of the sample occurs with strong supercooling below 700 °C, which is out of the scale of this figure.

Clear evidence for the incongruent nature of melting Bi₂CuO₄ is obtained from the second heating of the same sample, which is shown by the middle curve in Fig. 2. The additional peak at T_t = 727 °C results from the α–δ transition of Bi₂O₃ (ref. 35) and the eutectic of Bi₂O₃ with Bi₂CuO₄, as observed in the previous TG–DTA measurements with unreacted powders.

If Bi₂CuO₄ were to melt congruently, these two additional peaks would not appear in a second heating run. It should be noted, however, that Bi₂CuO₄ is also not melting simply peritectically, because this would imply the formation of a melt under the release of another solid phase (which would be CuO here). Here, however, the gas phase is inevitably involved in the melting process.

Data from FactSage³⁸ databases and from the literature^37,39,40 for Bi₂CuO₄ and the CuO_x–Bi₂O₃ melt were refined to describe the experimental data that are reported here, and an isopleth section CuO–Bi₂O₃ of the phase diagram was obtained (Fig. 3). The eutectic point was measured at around 7.5 mol% CuO and 761 °C, and is in good agreement with some literature data.^27–29

Fig. 3 Bi₂O₃–CuO isopleth section through the system Bi₂O₃–CuO–Cu₂O for p(O₂) = 0.21 bar.

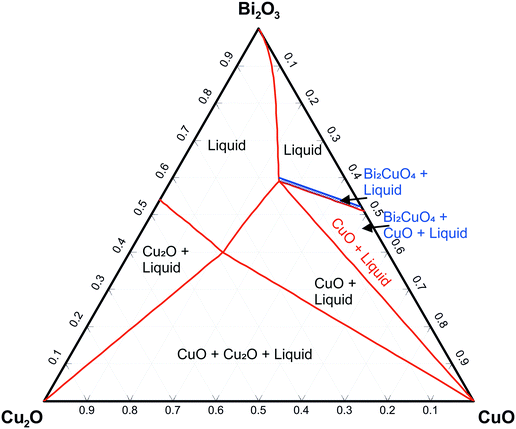
Fig. 4 shows the system as a concentration triangle of Bi₂O₃–Cu₂O–CuO at elevated temperatures in air. The red lines show an isothermal section above T_per = 857 °C. On the Bi₂O₃–CuO side of the phase diagram, only the crystallization phase field of CuO is visible. Immediately below the peritectic temperature of 856 °C, the Bi₂CuO₄ crystallization phase field begins to expand (the blue phase field in Fig. 4). This field begins slightly above the 0.5 composition of pure Bi₂CuO₄, which indicates the peritectic melting of this phase.

Fig. 4 Isothermal sections through the Bi₂O₃–Cu₂O–CuO system above (857 °C, red) and below (856 °C, blue) the peritectic temperature where Bi₂CuO₄ decomposes.

3.1.2 Bi₂PdO₄. So far, only scarce and contradictory thermodynamic data on the Bi₂O₃–PdO system can be found in the literature. Hrovat et al. reported that Bi₂PdO₄ melted incongruently at 845 °C with decomposition into the liquid phase and PdO, which in turn dissociates to elemental Pd and oxygen above 800 °C.⁴¹ In contrast, investigations by Kakhan et al. revealed congruent melting of Bi₂PdO₄ at 855 °C.²² They report 803 °C as the temperature of the dissociation of PdO to Pd metal and oxygen. The melting temperatures of Bi₂PdO₄ at around 850 °C are in good agreement with our TG–DTA measurement in an atmosphere containing 20% O₂, where the onset temperature of the melting peak was defined at 847.7 °C (Fig. 5).

Fig. 5 TG heating curves of Bi₂PdO₄ in five different atmospheres from 100% O₂ to 10% O₂ in Ar (O₂ concentration given as a parameter). For the measurements at 100% (blue) and 10% O₂ (red), DTA heating and TG cooling curves are shown additionally.

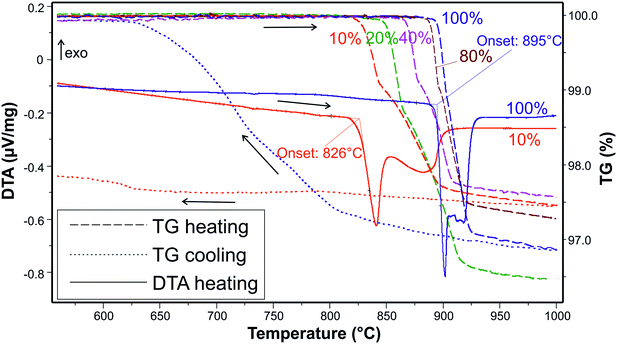
TG–DTA measurements in atmospheres containing between 10 and 100% oxygen revealed that the starting melting process (the onset of DTA curves) is always accompanied by a mass loss. Both effects shift to higher temperatures with increasing p(O₂). For example, at 10% O₂ (p(O₂) = 0.1 bar), the melting and immediate PdO reduction starts at 826 °C while at 100% O₂ the reaction starts at 895 °C (Fig. 5). The mass losses are only reversible under sufficiently high p(O₂), e.g. under pure O₂. Under low p(O₂), the sample mass never returns to the original value, as shown by the red dotted line in Fig. 5.

These observations can be discussed on the basis of the simplified predominance diagram of Bi–Pd–O₂ in Fig. 6 that was calculated with FactSage.³⁸ Unfortunately, the target phase Bi₂PdO₄ itself is not contained in the given databases. To enable its appearance in the diagram, its thermodynamic data were approximated by the sum of the constituents Bi₂O₃ and PdO (Hess' law), with an additional formation enthalpy of −20 kJ mol⁻¹. Another assumption had to be made regarding the molten phase (liq). For the calculation in Fig. 6, we assumed an ideal miscibility between Pd(liq) and Bi₂O₃(liq) because it is well accepted that palladium and silver behave similarly from the chemical point of view⁴² and bismuth oxide forms a eutectic with this metal, with a certain degree of miscibility between the liquid metal and oxide.⁴³

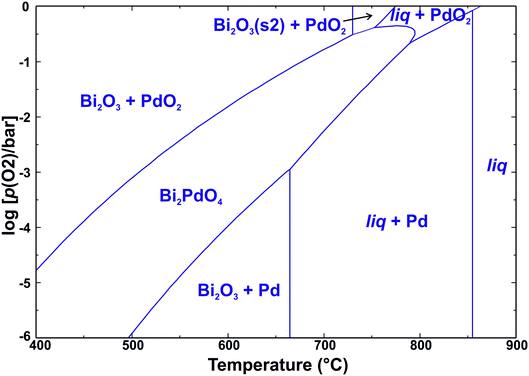Fig. 6 Phase stability in the system Bi–Pd–O₂. An enthalpy of 20 kJ mol⁻¹ was assumed for the reaction Bi₂O₃ + PdO → Bi₂PdO₄.

The diagram shows that under the given experimental conditions, bismuth always exists as Bi³⁺. Palladium, in contrast, can exist as Pd⁴⁺, Pd²⁺, or as metallic Pd⁰. The formation of Bi₂PdO₄ stabilizes the divalent Pd²⁺ and free PdO does not appear in the predominance diagram because it dissociates above 800 °C.⁴⁴ This also explains the observed mass loss during melting. A peritectic melting process Bi₂PdO₄ → PdO + liq would lead to a Bi₂O₃-rich melt under the release of solid PdO. In contrast, the melting observed here is described by the reaction Bi₂PdO₄ → Pd + 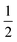O₂ + liq. This latter reaction cannot be reversed as easily as the first one because it requires the uptake of free oxygen from the atmosphere. Obviously, this is only possible in very oxygen rich atmospheres, but not for 10% O₂ in Ar as shown in Fig. 5 for the blue and red dotted lines, respectively. In particular, the loss of one oxygen atom per formula unit of Bi₂PdO₄via PdO → Pd + 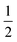O₂ would result in a theoretical mass loss of 2.7% which is in good agreement with the TG curves in Fig. 5.

The stability of the phases in the system Bi–Pd–O₂ as a function of the oxygen partial pressure and temperature can be qualitatively described in the predominance diagram as shown in Fig. 6. The vertical lines depict the different melting processes and the phase transition of Bi₂O₃ at 730 °C. In particular, the previously discussed melting of Bi₂PdO₄ corresponds to the phase boundary Bi₂PdO₄/liq + Pd.

High temperature XRD measurements revealed the presence of elemental Pd in the melt above 860 °C which does not dissolve even at higher temperatures. This elemental Pd makes the crystal growth method used in this work unsuitable, since Pd interferes in the melt zone. Alternative growth methods using a crucible could be advantageous for Bi₂PdO₄ but further research needs to be done on this.

For stable growth, it is crucial that the elemental Pd is reoxidized during crystallization. Our TG–DTA measurements showed that at least 80% O₂ in the atmosphere is necessary to achieve complete reoxidation.

Typical binary Bi₂O₃–PdO phase diagrams from the literature^41,22 must be used with caution because PdO is actually reduced, and is hence not a valid component of the system. Our TG–DTA measurements show that additional melting peaks in a second heating cycle occur even in 100% O₂ (not shown in Fig. 5), irrespective of Pd seemingly being reoxidized during the first cooling. These additional peaks can be assigned to the Bi₂O₃ phase transition and the eutectic line, which in turn implies the peritectic melting of the Bi₂PdO₄ phase. However, the melting of Bi₂PdO₄ can only be viewed correctly in the Bi–Pd–O ternary system, since the melting and crystallization are connected to redox processes. It should be noted that the ternary system depends strongly on the atmospheric conditions. A complete thermodynamic assessment of this ternary system, which would adjust Fig. 6 quantitatively to the experimental data, is beyond the scope of this paper.

3.2 Crystal growth

The growth of Bi₂CuO₄ single crystals was performed by taking into account the results of our above-described thermodynamic investigations. Even though Bi₂CuO₄ melts incongruently (Fig. 3), higher growth rates (up to 6 mm h⁻¹) than usually possible with incongruently melting compounds can be used. This is probably enabled by the strong tendency of the melt to supercooling, allowing crystal growth below the equilibrium melting temperature from a stoichiometric equimolar melt. XRD measurements of the initially crystallized material revealed that indeed not CuO_x but Bi₂CuO₄ is formed. The growth of Bi₂CuO₄ from a stoichiometric melt is supported because it melts only slightly peritectically. It should be noted that in some other systems even Czochralski crystal growth proved to be possible significantly below the equilibrium melting point. Kouta et al. demonstrated the growth of β-BaB₂O₄ (stable below 920 °C) from a stoichiometric melt that is in equilibrium with the high-temperature α-BaB₂O₄ at 1095 °C, 175 K above that of the α–β transition.⁴⁵

A growth rate of >5.5 mm h⁻¹ leads to a stable growth, and less cracks occur. So far, there are only a few publications on the crystal growth of Bi₂CuO₄ and in most works lower (typically 3 or 5 mm h⁻¹ (ref. 8, 46)) or higher (10 mm h⁻¹ (ref. 8, 46–48)) growth rates were used, which could be a reason for cracking. It is also described that a growth rate of 10 mm h⁻¹ improves the growth process because the low surface tension of the melt is problematic, but the crystal quality is lower.^8,46 In some experiments, excess CuO⁴⁶ or a pure oxygen atmosphere⁸ was used, which is, as described in our Thermodynamics section, not advantageous for the growth. The experiments in this work showed that the growth is most stable and crack-free crystals are obtained at a rate of 6 mm h⁻¹. When using polycrystalline seeds, however, the first grown 15–20 mm are always completely covered with cracks.

Although a growth rate of 6 mm h⁻¹ leads to crack-free growth, the CuO_x equilibrium in the melt cannot adjust fast enough. During the growth, CuO is removed from the melt, which leads to an increase in the Cu₂O/CuO ratio. This in turn leads to an increase in the liquidus temperature (see Fig. 1 in ref. 37). Therefore, the lamp power must be adjusted continuously, even if only in very small steps, during the growth experiments. The typical power of 300 W lamps during an experiment was, for example, between 30.80–31.67%.

Taking into account the thermodynamic investigations of this work and based on the chosen growth parameters and instrumental conditions, it was possible to grow Bi₂CuO₄ crystals with lengths of up to 7 cm and diameters of 6 mm (Fig. 7). The crystals show a rough surface in the later stages of the growth which is probably related to Cu₂O deposition. However, a clear proof of this assumption could not be provided by XRD and XRF measurements. Laue measurements along the crystal length show a constant orientation, which proves that the grown materials are single crystalline. The preferred growth direction of the crystals is along [120] (Fig. 7), but this is only the case in 3 of 4 grown crystals, and the cleavage is typically along (001), since the interatomic distances are larger in this direction, resulting in a weaker bond.¹⁸ The lattice parameters were refined using powder X-ray diffraction data on crushed single crystal pieces. It was found that Bi₂CuO₄ crystallizes in the tetragonal space group P4/ncc (130) with the lattice constants a = 8.501(1) Å and c = 5.818(4) Å, which are in good agreement with the crystal refinement by Yamada et al.¹⁸

Fig. 7 Bi₂CuO₄ single crystal with excess copper oxide on the surface in the later stages of the growth (top) and Laue measurement confirming the [120] growth direction (bottom).

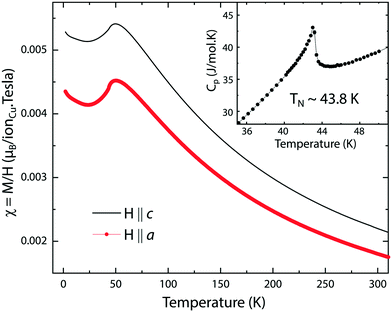
Magnetic susceptibility χ = M/H and specific heat data on the single crystal samples of Bi₂CuO₄ as a function of temperature are shown in Fig. 8. In agreement with earlier studies,^8,18,49,50 the temperature dependence of the susceptibility upon cooling is characterized by an increase of χ(T) leading to a broad hump with a maximum in χ(T) at ∼50 K, followed by an abrupt drop at around 43.8 K signaling the onset of the long-range antiferromagnetic order at that temperature (i.e. the Néel temperature, T_N), and by a further decrease before an upturn below about 25 K. The emergence of the long-range antiferromagnetic order at T_N ∼ 43.8 K is further corroborated by the sharp λ-like anomaly in the specific heat (Fig. 8 inset) obtained in zero field. The magnetic susceptibility is, also consistent with earlier reports,^8,18,50 anisotropic with a larger susceptibility along the c axis than along directions perpendicular to it, and it is highly field-dependent for applied fields of <1 T along the a axis below T_N (not shown here). Our magnetization and specific heat data therefore show that our Bi₂CuO₄ single crystals are of high crystalline quality.

Fig. 8 Temperature dependence of the magnetic susceptibility χ(T) in a magnetic field of 1 T applied along two perpendicular directions, along the c and a axes in Bi₂CuO₄, respectively. The inset shows the a-like specific heat anomaly associated with the antiferromagnetic ordering at T_N ∼ 43.8 K.

It was not possible to grow Bi₂PdO₄ crystals by the OFZ technique, because the elemental Pd prevents the formation of a melt zone (as discussed in the Thermodynamics section).

4 Summary and conclusions

Phase equilibria that are relevant for the growth of the title compounds were studied experimentally, and a semiquantitative description in terms of the ternary systems Bi₂O₃–CuO–Cu₂O or Bi₂O₃–PdO₂–Pd, respectively, was given. High-quality Bi₂CuO₄ single crystals with lengths of up to 7 cm and diameters of 6 mm were grown by the OFZ technique. Based on the results of the Laue, magnetization and specific heat measurements, we confirm the excellent quality of our grown samples. The growth of Bi₂PdO₄ by the OFZ technique is precluded, since the elemental Pd prevents the formation of a melt zone and other techniques such as the Czochralski method should be used for the growth of this material.

It could be shown that pseudobinary systems of Bi₂O₃–CuO (–PdO) are insufficient to describe the growth process, because every crystallization or melting process of the Bi₂M²⁺O₄ phase is accompanied by a redox process that can only be accounted for in the ternary systems. The melting processes of Bi₂CuO₄ and Bi₂PdO₄ are often called “peritectic”, which is not totally true: a peritectic reaction follows the scheme solid (1) → solid (2) + melt. In contrast, the melting/crystallization of the compounds in this study has the scheme Bi₂CuO₄ ⇄ CuO + (Bi₂O₃ + CuO_x) melt + O₂ or Bi₂PdO₄ ⇄ Pd + (Bi₂O₃ + Pd) melt + O₂ under the involvement of the gas phase. We recommend for this type of melting the term “exaperitectic” (greek: εξατμιση = to exhaust).

For both title compounds, the valence state of the transition metal is lowered during melting (Cu²⁺ → Cu²⁺ + Cu⁺ or Pd²⁺ → Pd⁰) under the release of free oxygen. Consequently, O₂ must be transported through the melt to the phase boundary during the crystal growth process to ensure the crystallization of high-quality stoichiometric Bi₂CuO₄ and Bi₂PdO₄. This is a process that limits the growth rate. When using a growth rate of 6 mm h⁻¹, as in the case of our Bi₂CuO₄ growth experiments, the CuO_x equilibrium in the melt cannot adjust fast enough, which leads to an increase of the liquidus temperature. During this growth process, the lamp power needs to be adjusted continuously. In the case of Bi₂PdO₄, other growth techniques are recommended, as the reoxidation of the elemental Pd needs more time and besides the formation of a melt zone is prevented.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The use of HZB's X-ray Corelab and the Corelab for Quantum Materials is acknowledged. We thank R. Gunder, K. Siemensmeyer and R. Feyerherm for technical support and N. Islam and K. Karmakar for helpful discussions on the OFZ setup. J.-E. Hoffmann is thanked for technical support with the TG–DTA setup.

References

1. M. A. Hayward, Inorg. Chem., 2019, 58, 11961–11970.
2. J. L. Garcia-Munoz, J. Rodriguez-Carvajal, F. Sapina, M. J. Sanchis, R. Ibanez and D. Beltran-Porter, J. Phys.: Condens. Matter, 1990, 2, 2205–2214.
3. S. Kanungo, B. Yan, P. Merz, C. Felser and M. Jansen, Angew. Chem., Int. Ed., 2015, 54, 1–5.
4. K. Yoshii, T. Fukuda, H. Akahama, J. Kano, T. Kambe and N. Ikeda, Phys. C, 2011, 471, 766–769.
5. Z. V. Popovic, G. Kliche, M. J. Konstantinovic and A. Revcolevschi, J. Phys.: Condens. Matter, 1992, 2, 10085–10092.
6. L. E. Svistov, V. A. Chubarenko, A. Y. Shapiro, A. V. Zalesskii and G. A. Petrakovskii, J. Exp. Theor. Phys., 1998, 86, 1228–1233.
7. B. Yuan, N. P. Butch, G. Xu and Y.-J. Kim, 2019, arXiv, 1907.07784, pp. 2406–2414.
8. L. Zhao, H. Guo, W. Schmidt, K. Nemkovski, M. Mostovoy and A. C. Komarek, Phys. Rev. B, 2017, 96, 054424.
9. D. Di Sante, P. Hausoel, A. Barone, J. M. Tomczak, G. Sangiovanni and R. Thomale, Phys. Rev. B, 2017, 96, 121106.
10. S. P. Berglund, F. F. Abdi, A. Bogdanoff, P. Chemseddine, D. Friedrich and R. van de Krol, Chem. Mater., 2016, 28, 4231–4242.
11. N. Xu, F. Li, L. Gao, H. Hu, Y. Hu, X. Long, J. Ma and J. Jin, ACS Sustainable Chem. Eng., 2018, 6, 7257–7264.
12. Y.-H. Choi, D.-H. Kim and S.-H. Hong, ACS Appl. Mater. Interfaces, 2018, 10, 14901–14913.
13. L. K. Lamontagne, G. Laurita, M. W. Gaultois, M. Knight, L. Ghadbeigi, T. D. Sparks, M. E. Gruner, R. Pentcheva, C. M. Brown and R. Seshadri, Chem. Mater., 2016, 28, 3367–3373.
14. T. C. Ozawa, T. Taniguchi, Y. Nagata, Y. Noro, T. Naka and A. Masushita, J. Alloys Compd., 2005, 388, 1–5.
15. J. He, S. Hao, Y. Xia, S. S. Naghavi, V. Ozolins and C. Wolverton, Chem. Mater., 2017, 29, 2529–2534.
16. R. Arpe and H. Müller-Buschbaum, Z. Naturforsch., 1976, 31b, 1708–1709.
17. J. P. Attfield, J. Phys.: Condens. Matter, 1989, 1, 7045.
18. K. Yamada, K. Takada, S. Hosoya, Y. Watanabe, Y. Endoh, N. Tomonaga, T. Suzuki, T. Ishigaki, T. Kamiyama, H. Asano and F. Izumi, J. Phys. Soc. Jpn., 1991, 60, 2406–2414.
19. K. Sreedhar, J. Phys. C: Solid State Phys., 1129, 21, 1129.
20. R. Troc, J. Janicki, I. Filatow, P. Fischer and A. Murasik, J. Phys.: Condens. Matter, 1990, 2, 6989–6998.
21. J. Cassedanne and C. P. Campelo, An. Acad. Bras. Cienc., 1966, 38, 35–38.
22. B. G. Kakhan, V. B. Lazarev and I. S. Shaplygin, Zh. Neorgan. Khim., 1979, 24, 1663–1668.
23. M. Hrovat and D. Kolar, J. Mater. Sci. Lett., 1984, 3, 659–662.
24. J. C. Boivin, D. J. Thomas and G. Tridot, C. R. Seances Acad. Sci., Ser. C, 1973, 276, 1105–1107.
25. Z. K. Huang, Y. X. Jia, J. X. Chen, P. L. Wang, R. F. Huang and D. S. Yan, Wuji Cailiao Xuebao, 1990, 5, 375–376.
26. M. P. Kulakov and D. Y. Lenchienko, Thermochim. Acta, 1991, 188, 129–133.
27. M. Nevriva, H. Kraus and D. Sedmidubsky, Thermochim. Acta, 1996, 282/283, 205–224.
28. J. Sestak, D. Sedmidubsky and G. K. Moiseev, J. Therm. Anal., 1997, 48, 1105–1122.
29. B. Hallstedt, D. Risold and L. J. Gauckler, J. Am. Ceram. Soc., 1996, 79, 353–358.
30. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
31. N. Wolff, D. Klimm and D. Siche, J. Solid State Chem., 2018, 258, 495–500.
32. N. Wolff, D. Klimm, S. Ganschow and D. Siche, Cryst. Res. Technol., 2019, 54, 1900036.
33. N. Wolff, PhD thesis, Technische Universität Berlin, Germany, 2019.
34. N. Wolff, T. Schwaigert, D. Siche, D. G. Schlom and D. Klimm, J. Cryst. Growth, 2020, 532, 125426.
35. F. Schröder, N. Bagdassarov, F. Ritter and L. Bayarjargal, Phase Transitions, 2010, 83, 311–325.
36. B. G. Kakhan, V. B. Lazarev and I. S. Shaplygin, Zh. Neorg. Khim., 1979, 24, 1663–1668.
37. L. Schramm, G. Behr, W. Löser and K. Wetzig, J. Phase Equilib. Diffus., 2005, 26, 605–612.
38. FactSage 7.3, GTT Technologies, Kaiserstr. 100, 52134 Herzogenrath, Germany, 2019, www.factsage.com.
39. A. Strejc, D. Sedmidubský, K. Růžička and J. Leitner, Thermochim. Acta, 2003, 402, 69–74.
40. V. M. Denisov, L. A. Irtyugo, L. T. Denisova, S. D. Kirik and L. G. Chumilina, Phys. Solid State, 2012, 54, 1943–1945.
41. M. Hrovat, S. Bernik and D. Kolar, J. Mater. Sci. Lett., 1988, 7, 637–638.
42. A. G. Massey, N. R. Thompson and B. F. G. Johnson, The Chemistry of Copper, Silver and Gold, Pergamon, 1973, p. 93.
43. J. Assal, B. Hallstedt and L. J. Gauckler, J. Am. Ceram. Soc., 1999, 82, 711–715.
44. G. Bayer and H. Wiedemann, Thermochim. Acta, 1975, 11, 79–88.
45. H. Kouta, Y. Kuwano, K. Ito and F. Marumo, J. Cryst. Growth, 1991, 114, 676–682.
46. B. D. White, W. M. Pätzold and J. J. Neumeier, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094439.
47. M. J. Konstantinovic, Z. V. Popovic, S. D. Devic, A. Revcolevschi and G. Dhalenne, J. Phys.: Condens. Matter, 1992, 4, 7913–7918.
48. G. Dhalenne, A. Revcolevschi, M. Ain, B. Hennion, G. Andre and G. Parette, Cryst. Prop. Prep., 1991, 36–38, 11–16.
49. M. Baran, Y. Gaidukov, N. Danilova, A. Inushkin, A. Jedrzejczak, Y. Koksharov, V. Nikiforov, A. Revcolevschi, R. Szymczak and H. Szymczak, J. Magn. Magn. Mater., 1999, 196–197, 532–533.
50. M. Herak, M. Miljak, G. Dhalenne and A. Revcolevschi, J. Phys.: Condens. Matter, 2009, 22, 026006.

---