DOI:
10.1039/D0CE00949K
(Highlight)
CrystEngComm, 2021,
23, 11-23
Dynamic force spectroscopy for quantifying single-molecule organo–mineral interactions
Received
2nd July 2020
, Accepted 16th November 2020
First published on 16th November 2020
Abstract
Organo–mineral interactions have long been the focus in the fields of biomineralization and geomineralization, since such interactions not only modulate the dynamics of crystal nucleation and growth but may also change crystal phases, morphologies, and structures. The utilization of an atomic force microscopy (AFM)-based dynamic force spectroscopy (DFS) technique makes it possible to quantify the single-molecule scale organo–mineral binding free energy (ΔGb) correlated with interfacial free energy (γ) and the nucleation energy barrier (ΔG). In this highlight, we briefly review theories of force spectroscopy (FS) and DFS, indicating that single-molecule force spectroscopy (SMFS) can be distinguished with the worm-like chain (WLC) model, and linear and nonlinear DFS data can be analyzed with the Bell–Evans and Friddle–Noy–De Yoreo models to derive noncovalent binding information through the introduction of detailed procedures for DFS experiments from AFM tip modification to FS collection. Moreover, we present some application cases of DFS in unraveling the mechanisms underlying organo-modified nucleation rates, nucleus critical sizes, and phase transformations as well as facet-dependent organo–mineral interactions. The use of an AFM-based DFS technique will improve the fundamental understanding of organo–mineral interactions that affect organo-modified crystal nucleation and growth in both biomineralization and geomineralization processes.
1. Introduction
Organo–mineral reactions control crystal mineralization and demineralization processes, including nucleation,1 growth,2 phase transformation,3 and dissolution.4 These complex reactions take place in both organisms5,6 and environments.7,8 In organisms, organo–mineral binding exhibits a close relationship with the formation of bone tissues,9 regeneration of enamel organs,10 and prevention of pathological crystallization.11 In natural environments, organo–mineral interactions regulate the weathering of soil minerals,12 bioavailability of nutrients,13 fate of contaminants,14 and biogeochemical cycling of elements.15 Organo–mineral binding mediates mineralization and demineralization through both kinetic and thermodynamic processes,16 which affects the nucleation17 and growth rate,18 facet stability,19 and crystal morphologies,20 irrespective of biotic and abiotic environments. Organic molecules are ubiquitous in all aqueous fluid environments and consequently they probably exert an influence on most aqueous fluid reactions in the earth.
Organic molecules bind to mineral surfaces and subsequently modify the interfacial free energy (γ) of the crystal–liquid in homogeneous nucleation or the crystal–liquid–substrate in heterogeneous nucleation. The interfacial free energy determines the energy barrier for crystal mineralization, thus, varying interfacial free energies among the system results in different nucleation rates and crystal morphologies.21–23 The effective γ components include the interfacial energies of the crystal–liquid (γCL), liquid–substrate (γLS), and crystal–substrate (γCS) interfaces. It is difficult to directly measure γ if the specific values are lacking.24,25 Bulk γCL measurements can be performed with the constant composition (CC) nucleation method by calculating the induction time (τ).26,27 In the presence of substrates, traditional γCL or γLS determination can be achieved by the contact angle (θ) method established by Owens, Wendt, Rabel, and Kaelble (OWRK).28–30 Using the OWRK method, the derived values of interfacial free energy between solid and air (γS–air) can be used as a proxy for γCL or γLS. However, the contact angle is not amenable to probing aqueous conditions for crystals with low surface area.31,32 In addition, data from these measurements at the bulk scale represent an average of all crystal faces, edges, and fracture surfaces, which lack facet specificity.33
With the rapid development of atomic force microscopy (AFM), in situ observations can be applied during crystal nucleation and growth at the nanoscale and even near-molecular scale and time sequences recorded.34–36 AFM-based interfacial free energy determination can be carried out through measuring the steady-state rate of heterogeneous nucleation37–39 and the critical size (the minimum size) of nuclei.40,41 During crystal surface growth, the step critical length and terrace width (step density) can be extracted as proxies for determining the step interfacial energy (γstep).42,43 In terms of an isotropic model, the mean value of γstep can be considered as a function of γCL.43 Furthermore, Hamm et al. demonstrated that nucleation barriers and binding free energies (ΔGb) are linearly related, which provides single-molecule insight into determining interfacial free energy.44
The rapid development of AFM-based force spectroscopy (FS) has made it possible to directly quantify ΔGb through analyzing the relationship between the rupture force (fr) and loading rate (rL) by the dynamic force spectroscopy (DFS) technique.45–48 AFM with both high positional accuracy and high force sensitivity allows for FS from the entropic force at the level of femtonewton (fN) to the rupture force of a covalent bond at the level of nanonewton (nN).49 The loading rates can be applied from several pN s−1 to a few nN s−1.50 The rupture forces are recorded at the moment of organo–mineral unbinding when the sample is retracted from the AFM tip. Prior to DFS, chemical force spectroscopy (CFS) has also been applied to probe organo–mineral interactions at a fixed pulling velocity.51–53 Due to the fact that any non-covalent bond will be broken at any level of pulling force if held for sufficient time, CFS is difficult or impossible to detect bond energy barriers that are in near-equilibrium assays.54 In contrast, DFS, which is based on the properties of time- and rL-dependent fr, can be applied to probe the complex relationship between the force, lifetime and energy landscape in single molecule–mineral interactions. Therefore, analyzing DFS data can estimate equilibrium rupture forces, transition rates from the binding to unbinding state, and widths of binding pockets at the single-molecule scale.55 In addition, the single-molecule investigation using DFS can also avoid interference from self-reactions among the molecules and provide insights into facet-dependent organo–mineral reactions, which can reveal thermodynamic mechanisms underlying phenomena occurring at larger length scales.56,57
Here, we aim to provide a brief review of theories, protocols, and applications of AFM-based DFS in studying single-molecule organo–mineral binding. This review starts with a brief assessment of the theories relating to single-molecule force spectroscopy (SMFS). The detailed procedures of the DFS technique are then presented, including AFM-tip modification and FS data collection. Several cases of DFS application in the study of organo-modified crystal nucleation and phase transformation are reviewed. Finally, a succinct conclusion is drawn and perspectives are provided, suggesting new possibilities for determining the energetic basis underlying organo-mediated crystal nucleation and growth during biomineralization and geomineralization.
2. Principle of DFS for binding energy determination
2.1 AFM-based force spectroscopy (FS)
AFM is a member of the scanning probe microscopy (SPM) family that can be used to monitor local interactions between a probe and sample surface.58 The essential components of AFM are a sharp tip mounted on a flexible cantilever, a piezoelectric scanner that moves the sample stage or the cantilever in x, y and z directions, and a sensitive optical deflection system which is composed of a laser, photodiode, and signal processing unit.59 As the tip scans the surface of the sample, changes in cantilever deflection (xc) due to attractive or repulsive forces between the tip and sample are recorded and converted to force signals according to Hooke's law (f = kcxc, where kc is the spring constant of the cantilever). In a typical AFM-based FS setup for studying organo–mineral binding, a mineral sample mounted on the scanner approaches towards and retracts from the AFM tip functionalized with probe molecules. The relative positions of the modified tip and sample with their corresponding force signals are schematically shown in Fig. 1. Positions from 1 to 2 are in the noncontact region (attractive van der Waals forces) and position 3 is in the contact region (repulsive forces) during the approach. When the force or distance, depending on the setup, approaches the setpoint, the sample starts to retract from the modified tip (position 4) and the rupture force for organo–mineral unbinding is determined at position 5 where the sample is separated from the modifying molecules on the tip. During the approach and detachment, force signals are recorded with the tip–sample separation and time, which can be converted into force versus distance (F–D) and force versus time (F–T) curves, respectively.
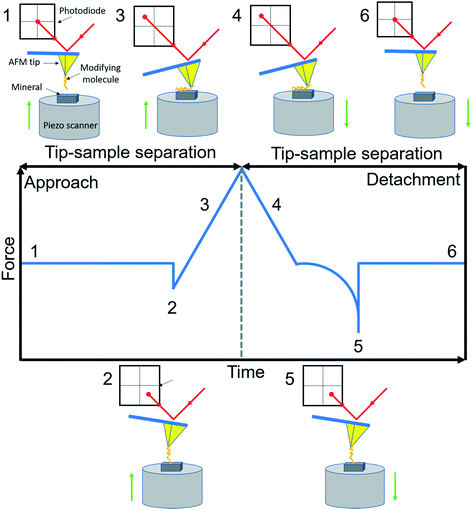 |
| | Fig. 1 A schematic diagram of AFM-based FS (AFM-Nanoscope V MultiMode VII, Bruker). A typical F–D curve with its corresponding F–T curve is recorded during the force measurement using a modified tip mounted on a soft cantilever. A laser beam hits the edge of the cantilever and is reflected onto a photodiode to amplify and record cantilever movements. Based on Hooke's law, the adhesion force between the modifying molecule and mineral substrate sample can be extracted when the sample is detached from the tip. Reactions of the modified tip and sample with their corresponding force signals are schematically shown at typical positions from 1 to 6. | |
2.2 Single molecular force spectroscopy (SMFS) identification
Based on F–D curves, we commonly observed three main types of interactions that include the tip–mineral, multiple molecule–mineral, and single molecule–mineral detachment. To quantify organo–mineral binding, the number of bonds of the molecule involved in the reaction needs to be known. The most straightforward way is to distinguish SMFS from collected FS data through fitting F–D curves using the worm-like chain (WLC) model.60–62 The WLC model properly depicts a complicated stretch of an organic molecule unbound from a mineral substrate surface and the relationship between the entropy force (fe) and the extension (xe, equal to the tip–surface separation) of the organic molecule can be described as:63| | 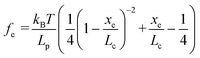 | (1) |
where kB is the Boltzmann constant (1.38064852 × 10−23 J K−1), T is the absolute temperature, Lp is the persistence length of the modifying molecule, and Lc is the contour length. The WLC model is a reasonable approximation for entropic elasticity with relatively smaller tensile forces. For larger tensile forces, enthalpy contributions will play an increasing role in stretching a molecule. In this case, a modified WLC (MWLC) model needs to be used for fitting F–D curves through the introduction of an extra term of elastic modulus (Φ) and is given by:64| | 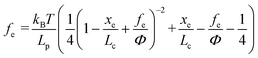 | (2) |
2.3 DFS interpretation
Force measurements conducted by AFM are usually restricted to the theories that connect the rupture forces to fundamental parameters of binding free energies. DFS is an experimental technique that provides the ability to characterize the energetic basis of organo–crystal reactions by assessing the binding strength, lifetime, and energy landscape.65 Evans et al. suggested a linear DFS (LDFS) technique to describe the relationship between the rupture force (fr) and loading rate (rL) as the Bell–Evans model:66,67| | 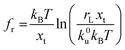 | (3a) |
| | 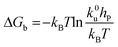 | (3b) |
where xt is the transition length (bond length) describing the spatial distance between the energy minima and the transition energy barrier, k0u is the intrinsic transition rate of the molecule–crystal complex from the binding to unbinding state, and hP is Planck's constant (Fig. 2). This model serves as the foundation for analyzing DFS data where a plot of frversus log(rL) derived from FS (including both F–D and F–T curves) is expected to form a straight line.
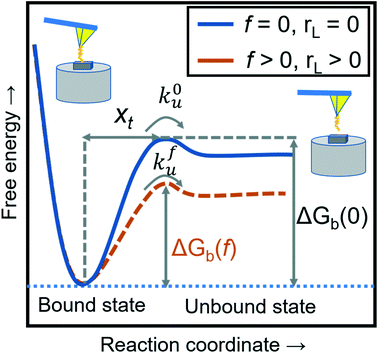 |
| | Fig. 2 A schematic diagram of the energy landscape, depending on external forces and loading rates. The blue solid line shows the dissociation between the modifying molecule and sample without an external force (loading rate) and the orange dashed line with an applied force (loading rate). The free energies of intermolecular dissociation with and without an applied external force depend on the dynamic parameters of xt, k0u, and kfu. | |
By applying Kramers' theory of diffusive barrier crossing to determine the kinetic and thermodynamic parameters,68 the Bell–vans Emodel can be further modified into the Dudko–Hummer–Szabo model with the expression:69
| | 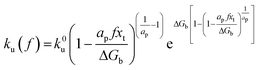 | (4a) |
| | 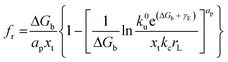 | (4b) |
where
ap is a power scaling factor (
ap =
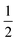
, 1,
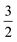
are for a cusp-like barrier, recovery of the Bell–Evans model, and linear-cubic barrier) and
γE is Euler's constant. Since more data of DFS show nonlinear trends focusing on inter- or intramolecular reactions,
70,71 to describe these nonlinear dynamic force spectroscopies (NLDFS), Friddle
et al. interpreted the widespread NLDFS with the Friddle–Noy–De Yoreo model:
65| | 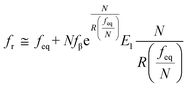 | (5a) |
| | 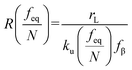 | (5b) |
where
feq is the equilibrium rupture force,
N is the number of bonds (
N = 1 for the single-molecule reaction),
fβ is the thermal force scale with an expression of
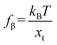
,
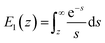
,
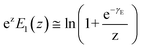
, and
ku(
f) is the transition rate given by an expression of
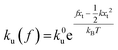
. According to
eqn (5), two primary regimes of DFS can be identified: an equilibrium regime when
rL approaches 0,
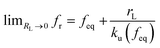
, and a kinetic regime in the fast loading rate,
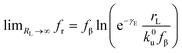
. If the assumption of strictly irreversible binding rupture in the standard analysis is abandoned, both kinetic and equilibrium properties can be described by three important parameters including
feq,
xt, and
k0u and Δ
Gb can be determined by:
65| | 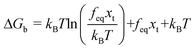 | (6) |
The condition required to observe NLDFS within the Friddle–Noy–De Yoreo model is that the loading rate needs to cover both near-equilibrium and kinetic regimes. The crossover point appears when R(feq) = 1 or rL = ku(feq)fβ for the single-molecule reactions. Using the extremes of experimentally derived values,72–74 the loading rates at the crossover position are estimated to encompass a range of 10−12–10−7 N s−1, that is, the lowest loading rates need to be set below 10−7 N s−1.
3. Protocols of DFS techniques
3.1 Tip modification and characterization
To quantify organo–mineral binding using FS, the tips need to be modified with the required probe molecules. The most popular approach is through the immobilization of an alkanethiol (HS–R–X, where X is the reactive group and R is the alkane)-based monolayer on the gold (Au)-coated tip (Fig. 3A1).75–77 The covalent adsorption of thiol-based monolayers on Au-coated tips can be considered as oxidative (S–H bond) addition to a gold surface, followed by reductive elimination of hydrogen:| | 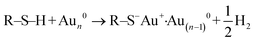 | (7) |
The utility of a thiol–gold coating is based on the following considerations: (1) gold is a relatively inert metal which can be cleaned simply without any contamination; (2) gold has a strong specific interaction with thiol and the homolytic bond strength of S–Au is known to be approximately 40 kcal mol−1, which contributes to a stable monolayer; (3) the density of the modified molecules can be well determined since the typical gold layer is 30–100 nm thick.78 When using this method, it will be better to deposit a 2–5 nm thick layer of titanium or chromium before coating gold onto the Si/Si3N4 tip to enhance the adhesion. In addition, protecting thiol from oxidation needs to be taken into consideration.
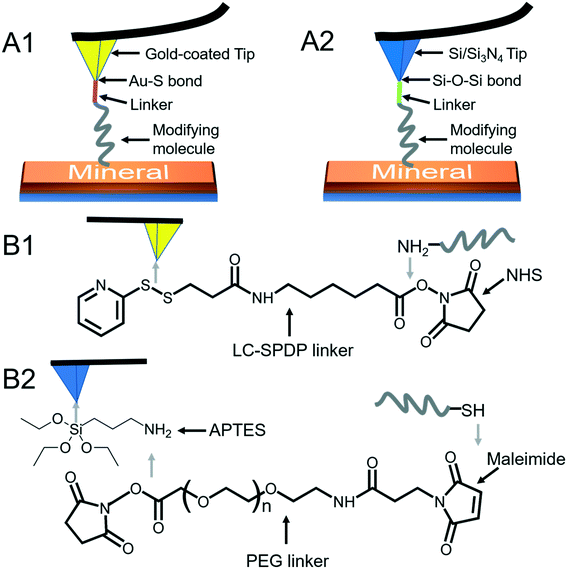 |
| | Fig. 3 Schematic diagrams of AFM tip modifications. (A1) A modifying molecule is covalently bound to an Au-coated tip with a linker through the Au–thiol bond. (A2) A modifying molecule is covalently bound to a Si/Si3N4 tip with a linker through the Si–O–Si bond. (B1) The LC-SPDP linker is used to bridge the probe molecule to an Au-coated tip through reacting with the amino group. (B2) The PEG linker bridges the probe molecule to an APTES-activated Si/Si3N4 tip through reacting with thiol. | |
Since the surface of most commercially available Si/Si3N4 tips carries a large number of silanol groups (SiOH), the second tip modification method is silanization to form organosilane layers via Si–O–Si covalent bonds using silanes (SiX3R) according to the following reaction (Fig. 3A2):79–81
| | | SiX3R + SiOH → SiOSiX2R + XH | (8) |
Prior to silanization, the surface of Si/Si
3N
4 tips still needs to be activated to generate more silanol groups. The activation can be done with removing organic contaminants using Piranha solution (a mixture of 3
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
7 (v/v) 30% H
2O
2 and 98% H
2SO
4), or 10% HNO
3, as well as by plasma treatment followed by washing with alkaline and acid solutions.
82–84 By reacting with 3-aminopropyl triethoxysilane (APTES), amino (NH
2)-terminated organosilane monolayers form on the surface of Si/Si
3N
4 tips and these amino-activated tips are widely used to anchor biomolecules for studying organo–mineral binding.
85
Most of the molecules of interest cannot be directly bound to Au-coated or Si/Si3N4 tips,86–88 and a heterobifunctional cross-linker is needed to bridge the probe molecule and activated tip (Fig. 3B). Moreover, the insertion of a linker increases the space allowing the probe molecule to freely react with a mineral surface and protects the molecule from being crushed during the tip hard contact with the sample (at positions 3 and 4 in Fig. 1). The soft or non-linear elasticity of the cross-linker may make it easier to distinguish a single molecule–mineral reaction as well.89 For Au-coated tips, long-chain succinimidyl 6-(3-[2-pyridyldithio]-propionamido)hexanoate (LC-SPDP) can be used since it bears a pyridyl disulfide to react with gold and an N-hydroxysuccinimide (NHS) ester forms a stable amide bond with amines (NH2) of biomolecules such as proteins and peptides (Fig. 3B1).90 For an NH2-activated Si/Si3N4 tip, polyethylene glycol (PEG) derivatives can be used as cross-linkers. The designed NHS–PEG–maleimide can be covalently bound to the amines via an NHS ester and reacted with a thiol-containing molecule via its end thiol-reactive group (Fig. 3B2).91
The modified tips need to be further characterized to determine the deflection sensitivity (sd) and spring constant. The deflection sensitivity describes the relationship between the position of the laser spot on the detector and z-piezo movement, which is usually calibrated by an optical lever technique.92 In brief, sd can be obtained from the slope (positions 3 to 4 in Fig. 1B) of a F–D curve acquired on a relatively harder (than the AFM tip) substrate based on the theory that the change of the laser beam position on the photodiode reflects the deformation of the AFM cantilever. We need to note that sd determination is the key step in spring constant calibration and force measurement. It will be better to calibrate sd values both before and after measurements. For cantilever spring constant determination, the Hutter–Bechhoefer method or thermal method is widely used.93,94 In brief, the spring constant can be derived from the power spectrum of thermal fluctuations of the cantilever when considering the cantilever as a simple harmonic oscillator.
3.2 FS collection
For homogeneous samples, we can directly collect FS data using the force-ramp mode.95 However, when the sample surface is heterogeneous after minerals have been deposited onto a substrate, we need to distinguish the organo–mineral from organo–substrate interactions prior to analyzing the collected FS data. It is possible to collect the surface topographies and mechanical properties (including adhesion force) simultaneously through the development of the force–volume (FV) mode.96 In the FV mode, the sample approaches the tip with a constant rate until a certain force (peak force), and then it is retracted and moves to the next position. However, the FV mode is a low-speed mode for mapping FS with a frequency range below 80 Hz and a relatively low image resolution ranging from 8 × 8 to 64 × 64 px2, that is, acquiring a relatively high-resolution image can take a few hours and this mode does not generate accurately precise images.97 To address these issues, a high-speed mode called the quantitative imaging (QI) mode has been developed by JPK Instruments (Bruker), which can process information more quickly than the FV mode when the tip moves laterally after being retracted to be positioned to the next point before approaching the surface again.98 The frequency in the QI mode can reach 100 Hz and the image resolution ranges from 8 × 8 to 512 × 512 px2. The highest-speed and highest-resolution mode is the PeakForce quantitative nanomechanical mapping (PF-QNM) mode.99 In the PF-QNM mode, the pathway of the z-piezo movement is modified, contributing to a faster scan. The frequency ranges from 250 to 500 Hz and the image resolution reaches 128 × 128 to 512 × 512 px2. In FV and QI modes, one FS is recorded for each pixel, allowing a single acquisition for both topography and mechanical properties. PF-QNM is the only mode that applies a good statistic of a number of FS for every pixel.99
4. Applications of DFS in studying organo–mineral interactions
4.1 Binding free energy and free energy barrier for organo-mediated nucleation
Derived binding free energy can be used for determining the nucleation energy barrier during crystal mineralization. Nucleation is the process where disordered atoms or molecules come together to form metastable embryos of a new phase (known as nuclei) in a crystallization medium.100–102 The free energy per molecule of the new phase is less than that of the solvated phase in the bulk. However, the surface molecules of the new phase are less well bound to their neighbors contributing to the greater free energy of the surface. This difference in free energy per molecule between the bulk and the surface is termed the interfacial free energy (or surface free energy). The interfacial free energy acts to destabilize the nucleus, thus, nucleation has to overcome an energy barrier (ΔG).103 According to classical nucleation theory (CNT), the energy barrier for nucleation of spherical particles can be described as:104,105| | 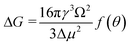 | (9a) |
| | 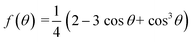 | (9c) |
where γ is the interfacial free energy, Ω is the volume per growth unit, Δμ is the chemical potential difference between the actual state and the equilibrium state, σ is the relative supersaturation (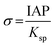 , IAP is the ion activity product and Ksp is the solubility product), f(θ) (0 ≤ f(θ) ≤ 1) is the interfacial correlation factor which describes the lowering of the nucleation barrier due to the presence of the substrates, and θ is the contact angle formed between the nucleated crystal and substrate. As shown in eqn (9a), the energy barrier for nucleation is proportional to γ3, thus, the energy barrier can be quantified by determining the interfacial free energy.
, IAP is the ion activity product and Ksp is the solubility product), f(θ) (0 ≤ f(θ) ≤ 1) is the interfacial correlation factor which describes the lowering of the nucleation barrier due to the presence of the substrates, and θ is the contact angle formed between the nucleated crystal and substrate. As shown in eqn (9a), the energy barrier for nucleation is proportional to γ3, thus, the energy barrier can be quantified by determining the interfacial free energy.
In a crystal–liquid–substrate system, the net surface free energy (γnet) is dependent on three factors which are the interfacial free energy of the liquid–crystal, substrate–crystal, and substrate–liquid with the expression:106
| | | γnet = γLC + h(γSC − γSL) | (10) |
where
h is the nucleus shape factor and always a positive term. However, it is still difficult to directly calculate the net surface free energy if specific values are lacking. In order to address this issue, Hamm
et al. provided a mechanistic explanation for organic template-directed nucleation by correlating heterogeneous nucleation energy barriers with binding free energies between the crystal and substrate.
44 The binding free energy for any given element of an area (
a) within the crystal–substrate contact area can be given by the difference between surface free energies of the liquid–crystal–substrate system in the crystal–substrate bound state and unbound state.
44 Therefore, Δ
Gb can be given by:
| | | ΔGb = a(γLC + γSL) − aγSC | (11) |
Combining
eqn (10) and
(11), it can be revealed that,
| | 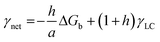 | (12) |
in which
γLC only depends on the interactions between the crystal and the liquid and remains constant. As a consequence, Δ
Gb should have a linear relationship with
γnet and an explicit relationship with the energy barrier to nucleation, that is, a higher binding free energy means a lower interfacial free energy as well as a lower energy barrier for nucleation.
4.2 Applications of DFS in studying organo-mediated nucleation rates
CNT states that the rate of formation of new nuclei on a substrate is determined by the energy barrier with an expression:107,108| | 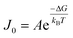 | (13a) |
| | 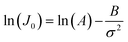 | (13b) |
| | 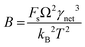 | (13c) |
where J0 is the heterogeneous nucleation rate (m−2 s−1) at steady state, A is the pre-exponential factor which is dependent on kinetic factors (including ion desolvation, attachment and detachment), and B (B ∝ ΔG) is the slope which is dependent on the nucleus shape factor (Fs) and γnet. With the bridge of ΔG, the DFS-experimentally derived ΔGb can be used to explain organo-mediated nucleation rates (combined with eqn (9a), (12), and (13a)). Based on this theory, the pathological biomineralization of stones modulated by osteopontin (OPN) has been investigated.109
Kidney stones may form with the heterogeneous nucleation of calcium phosphate (CaP) and calcium oxalate at the surface of renal papillae and the urinary space.110 OPN has been observed to inhibit the formation of kidney stones.111 In order to reveal the energetic mechanisms underlying OPN peptide segment-dependent inhibition of CaP heterogeneous nucleation, Li et al. first observed in situ the nucleation of CaP on a mimic lipid membrane surface (Fig. 4A).109 The heterogeneous nucleation rates in the presence of various OPN peptide segments show a linear relationship between ln(J0) and 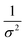 (Fig. 4B). The highest slope is acquired in the 93–106 peptide segment of OPN (Fig. 4B2), suggesting the highest energy barrier for CaP heterogeneous nucleation and the strongest inhibition for the CaP-induced stone formation. To further explain the observation, DFS was applied (Fig. 4C) and the experimentally derived binding free energy between various OPN peptide segments and CaP shows the greatest −ΔGb for the 93–106 peptide segment, corresponding to its greatest inhibitory effects. The interfacial free energy derived from the kinetics of CaP nucleation is linearly related to the binding free energy (Fig. 4D). Therefore, based on the relation
(Fig. 4B). The highest slope is acquired in the 93–106 peptide segment of OPN (Fig. 4B2), suggesting the highest energy barrier for CaP heterogeneous nucleation and the strongest inhibition for the CaP-induced stone formation. To further explain the observation, DFS was applied (Fig. 4C) and the experimentally derived binding free energy between various OPN peptide segments and CaP shows the greatest −ΔGb for the 93–106 peptide segment, corresponding to its greatest inhibitory effects. The interfacial free energy derived from the kinetics of CaP nucleation is linearly related to the binding free energy (Fig. 4D). Therefore, based on the relation 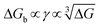 , DFS can be used for explaining mineral nucleation rates.
, DFS can be used for explaining mineral nucleation rates.
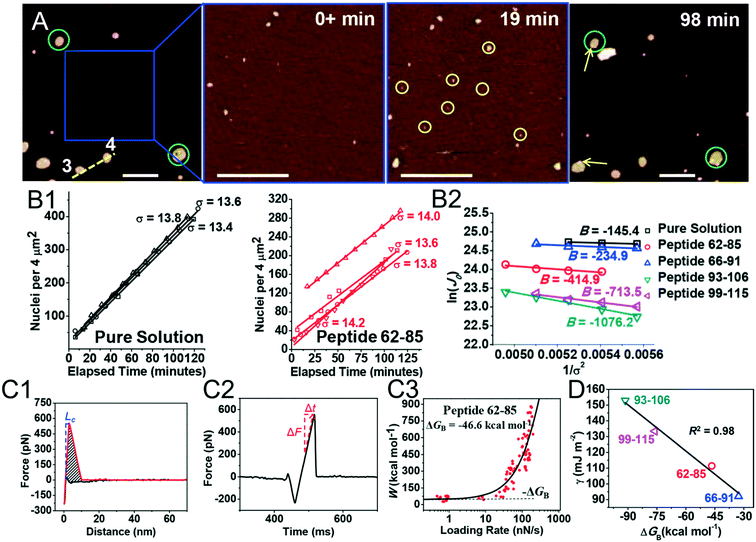 |
| | Fig. 4 DFS application in a study of organo-modified heterogeneous nucleation rates. (A) A representative AFM time sequence of CaP heterogeneous nucleation on membrane lipid rafts after the addition of a supersaturated solution with respect to HAP in the presence of 100 nM 93–106 peptide segment of OPN. Scale bars, 800 nm. (B) Nucleation rates. (B1) The number of CaP nuclei increases linearly with time at different supersaturations. (B2) The dependence of the nucleation rate on the supersaturation exhibits a linear relationship between ln(J0) and 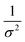 , showing additive-dependent slopes. (C) Binding free energy determinations for a single OPN peptide molecule adsorbing onto an HAP (100) surface. (C1) A representative F–D curve defines the energy dissipation (W). (C2) The corresponding F–T curve is used to calculate the loading rate. (C3) Loading rate-dependent dynamic works (W) of a single molecule OPN peptide–HAP are used to quantify the binding free energy. (D) A linear relationship (R2 = 0.98) between the experimentally derived interfacial free energy and measured binding free energy suggests that high interfacial energy correlates with strong peptide–HAP binding, that is, binding energy can be used to predict heterogeneous nucleation rates. Adapted with permission from ref. 109. Copyright 2017, American Chemical Society. , showing additive-dependent slopes. (C) Binding free energy determinations for a single OPN peptide molecule adsorbing onto an HAP (100) surface. (C1) A representative F–D curve defines the energy dissipation (W). (C2) The corresponding F–T curve is used to calculate the loading rate. (C3) Loading rate-dependent dynamic works (W) of a single molecule OPN peptide–HAP are used to quantify the binding free energy. (D) A linear relationship (R2 = 0.98) between the experimentally derived interfacial free energy and measured binding free energy suggests that high interfacial energy correlates with strong peptide–HAP binding, that is, binding energy can be used to predict heterogeneous nucleation rates. Adapted with permission from ref. 109. Copyright 2017, American Chemical Society. | |
4.3 Applications of DFS in studying organo-mediated critical sizes of nuclei
Nucleation in a supersaturated solution may not occur immediately unless the size of crystal nuclei exceeds a critical value (termed nucleus critical size, rC). The process for nuclei reaching critical sizes is the rate-limiting step for nucleation. According to CNT, the critical size is dependent on the interfacial free energy and supersaturation with an expression:16| | 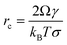 | (14) |
Due to the interfacial free energy having a linear relationship with the binding free energy, DFS can be applied to explain the organo-mediated nucleus critical size through analyzing the underlying energetics, for example, arsenate (As)-immobilization by natural organic matter (NOM).
Arsenate (As)-containing minerals have a close relationship with As release and As immobilization.112–114 Heterogeneous nucleation induced by NOM can dramatically lower the energy barrier for calcium arsenate (CaAs) formation and aid in immobilizing As.14,115,116 In order to investigate the rate-limiting step, we used in situ AFM to directly measure the critical size of CaAs nuclei on mica modified with various functional groups (COOH, OH, and NH2) found in NOM (Fig. 5A).41 The critical size ranks in a decreasing order NH2 > OH > COOH (Fig. 5A4). To further reveal the energetics of functional group-induced CaAs heterogeneous nucleation, AFM tips were modified with polymers with certain known functional groups via the silanization coating method (Fig. 5B1). To distinguish reactions between the modified tips and CaAs nuclei, the PF-QNM technique is then applied to simultaneously collect surface topographies (Fig. 5B2) and adhesion force distributions (Fig. 5B3). The extracted F–D (Fig. 5C1) and F–T (Fig. 5C2) curves were subsequently used for calculating rupture forces and loading rates, respectively. With fitting the Friddle–Noy–De Yoreo model (Fig. 5C3), the calculated −ΔGb on mica follows the trend NH2 < OH < COOH (Fig. 5C4), corresponding to the critical size of CaAs nuclei forming on modified mica.
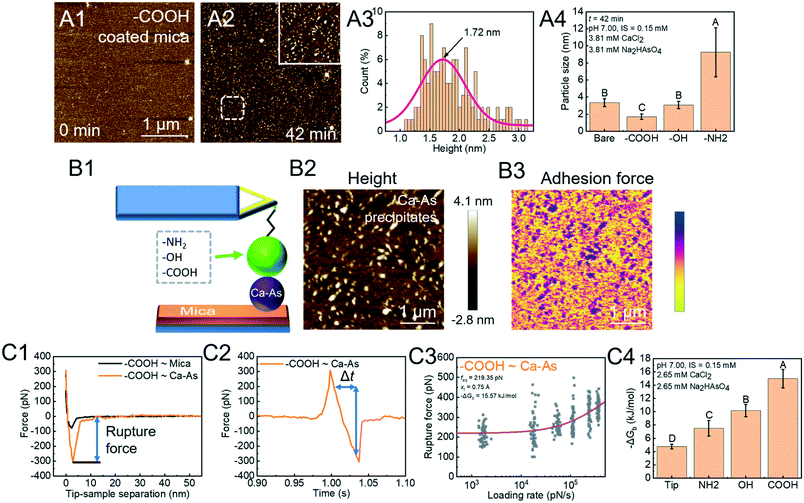 |
| | Fig. 5 DFS application in a study of organo-modified critical sizes of nuclei. (A1 and A2) Time sequences of AFM height images showing the formation of a CaAs nucleus. (A3) The particle height (a proxy for nucleus size) distribution of CaAs nuclei after 42 min of reaction. (A4) Heights of CaAs nuclei formed on various mica surfaces with different chemical functionalities after 42 min of reaction. (B) Protocols for obtaining FS using PF-QNM. (B1) Schematic of a DFS experimental system. Various polymers with different functional groups are covalently bonded to a Si3N4 tip through silanization coating. (B2) AFM height images of CaAs nuclei on mica and (B3) the corresponding adhesion-force distribution acquired with a COOH-modified tip are used to distinguish reactions between the modifying polymer and a CaAs nucleus from that between the polymer and a mica surface. (C) Binding free energy determination by the DFS technique. The (C1) F–D and (C2) F–T curves are used to extract the rupture force (fr) and loading rate (rL), respectively. (C3) The Friddle–Noy–De Yoreo model is fitted to the fr–rL curve to determine the binding free energy. (C4) Experimentally derived values for the binding free energy showing the strongest binding pair between COOH and a CaAs nucleus, which corresponds to (A4) the trends of nuclei size on various functional group-modified mica. The uppercase letters in A4 and C4 indicate significant difference at P < 0.01. Adapted with permission from ref. 41. Copyright 2020, Elsevier. | |
4.4 Applications of DFS in studying organo-mediated crystal phase transformation
Crystal phase transformation is expected as a key step in mineralization, which emphasizes the formation of transient phases (these may be amorphous) formed first prior to the final crystal.117 The free energy barrier of mineralization via crystal phase transformation is significantly lower than that through direct crystallization.118 The common CaP biomineral, hydroxyapatite (HAP), is suggested to be generated from amorphous calcium phosphate (ACP).119 However, the mechanisms underlying biomolecules mediating CaP phase transformations are unclear. To address this issue, Zhang et al. used DFS to reveal the mechanisms of phosphorylated/nonphosphorylated SSEEL peptides (the functional domain of amelotin) modulating the phase transformation of ACP–HAP.120
The phenomenon where a nonphosphorylated SSEEL peptide promotes ACP–HAP transition whereas the phosphorylated (p)S(p)SEEL stabilizes ACP was observed (Fig. 6A).120 In order to understand the above phenomenon, SSEEL or (p)S(p)SEEL peptides were covalently bound to Au-coated tips with the linker LC-SPDP (Fig. 6B1) to collect F–D curves (Fig. 6B2). The collected DFS data are analyzed with the Friddle–Noy–De Yoreo model (Fig. 6C). The experimentally derived (Fig. 6C1) equilibrium rupture force and binding free energy (Fig. 6C2 and C3) suggest that SSEEL prefers to react with ACP compared to (p)S(p)SEEL leading to ACP dissolution and ACP–HAP phase transformation by dissolution–reprecipitation.121
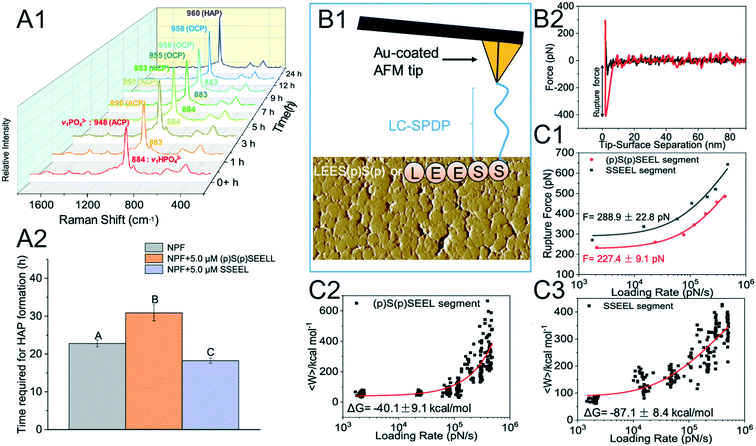 |
| | Fig. 6 DFS application in a study of an organo-modified crystal phase transformation. (A1, A2) The time required for the ACP–HAP transformation in a near-physiological fluid (NPF) without and with (p)S(p)SEEL is determined by (A1) Raman spectroscopy. Determination of the equilibrium rupture force and the binding free energy between an SSEEL or (p)S(p)SEEL peptide of AMTN and ACP by DFS. (B1) Schematic showing an SSEEL or (p)S(p)SEEL segment covalently bound to an Au-coated AFM tip. (B2) Representative F–D curve defining the force for the SSEEL peptide–ACP bond rupture at a pulling speed of 200 nm s−1. Analyzing FS-derived data with the Friddle–Noy–De Yoreo model for determining (C1) the equilibrium rupture force and (C2, C3) binding free energy. Experimentally derived binding free energy shows a stronger binding between an SSEEL peptide and ACP, which corresponds to the SSEEL peptide promoting ACP–HAP phase transition. Adapted with permission from ref. 120. Copyright 2020, American Chemical Society. | |
4.5 Applications of DFS in studying surface-dependent organo–mineral interactions
The anisotropic nature of most crystalline minerals (governed by the specific crystallographic form) contributes to facet-dependent interactions between organic molecules and mineral surfaces.122 Despite the importance of obtaining face-specific free energies of organo–mineral binding to understand biomineralization and geomineralization at the molecule scale, few techniques can be applied. Molecular modeling based on computational approaches may struggle with the complexities of organic molecules and inadequacies of calculating water potentials and background electrolyte effects, within a given time frame. In contrast, the SMFS-based DFS technique allows for measurements of a molecule binding to a specific surface. Using this technique, we reveal the mechanism of surface-dependent alginate–hematite interactions by directly measuring the binding energy between alginate and a specific surface of hematite (α-Fe2O3).123
Alginate is microbial-derived SOM and hematite mineral particles are ubiquitously present in soil systems.124,125 The adsorption of alginates onto the hematite surface reduces its surface potential (Fig. 7A and B). Based on this phenomenon, we quantify the reaction strength, showing an order of surface-specific attachment to amorphous FexOy > (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) > (11
0) > (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) > (0001) faces of hematite (Fig. 7C). In order to explain these facet-dependent reactions, an alginate molecule is modified onto a Si3N4 tip through silanization. The F–D curve is fitted with the WLC model to extract the single-molecule binding (Fig. 7D1). The rupture force and loading rate are calculated from F–D (Fig. 7D1) and F–T (Fig. 7D2) curves, respectively. Analyzed with the Friddle–Noy–De Yoreo model (Fig. 7D3), the derived binding free energies follow the order amorphous FexOy > the (10
0) > (0001) faces of hematite (Fig. 7C). In order to explain these facet-dependent reactions, an alginate molecule is modified onto a Si3N4 tip through silanization. The F–D curve is fitted with the WLC model to extract the single-molecule binding (Fig. 7D1). The rupture force and loading rate are calculated from F–D (Fig. 7D1) and F–T (Fig. 7D2) curves, respectively. Analyzed with the Friddle–Noy–De Yoreo model (Fig. 7D3), the derived binding free energies follow the order amorphous FexOy > the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) > (11
0) > (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) > (0001) faces of hematite, corresponding to Kelvin potential measurements (Fig. 7C).
0) > (0001) faces of hematite, corresponding to Kelvin potential measurements (Fig. 7C).
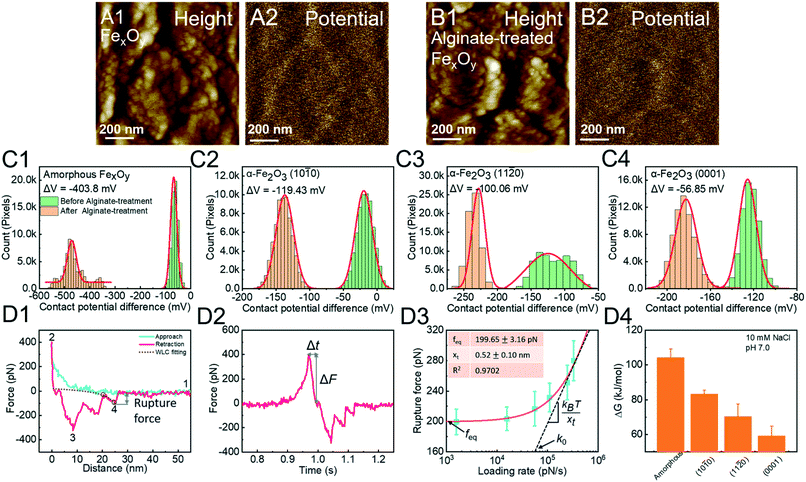 |
| | Fig. 7 DFS application in a study of surface/phase-dependent organo–mineral interactions. The decrease of the contact potential difference (CPD) between the tip and the iron oxide mineral surface is used to quantify alginate–mineral reactions. (A1) Representative height and corresponding (A2) CPD images of amorphous FexOy (A1 and A2) before and (B1 and B2) after reaction with alginate. The CPD distribution of (C1) amorphous FexOy and (C2) (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), (C3) (11 0), (C3) (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0), and (C4) (0001) faces of hematite shows that alginate adsorption follows the order amorphous FexOy > (10 0), and (C4) (0001) faces of hematite shows that alginate adsorption follows the order amorphous FexOy > (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) > (11 0) > (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) > (0001) faces. The red solid lines in (C1–4) represent Gauss fitting. (D1) A representative F–D curve shows the (1) noncontact, (2) contact, (3) multiple-molecule detachment, and (4) single-molecule detachment. The purple dashed line shows the WLC model fitting, suggesting that the last peak is the single-molecule unbinding and can be used for collecting the rupture force. (D2) A corresponding F–T curve is used to calculate the loading rate. (D3) A representative DFS measurement for an alginate molecule detached from the hematite (10 0) > (0001) faces. The red solid lines in (C1–4) represent Gauss fitting. (D1) A representative F–D curve shows the (1) noncontact, (2) contact, (3) multiple-molecule detachment, and (4) single-molecule detachment. The purple dashed line shows the WLC model fitting, suggesting that the last peak is the single-molecule unbinding and can be used for collecting the rupture force. (D2) A corresponding F–T curve is used to calculate the loading rate. (D3) A representative DFS measurement for an alginate molecule detached from the hematite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. The red solid line represents a fitting of the Friddle–Noy–De Yoreo model. (D4) Experimentally derived binding free energies show that alginate–amorphous FexOy/hematite interactions are strongly affected by crystal phases and exposed faces with the order amorphous FexOy > the (10 0) surface. The red solid line represents a fitting of the Friddle–Noy–De Yoreo model. (D4) Experimentally derived binding free energies show that alginate–amorphous FexOy/hematite interactions are strongly affected by crystal phases and exposed faces with the order amorphous FexOy > the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) > (11 0) > (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) > (0001) faces of hematite, which corresponds to the adsorption capacities of alginate determined by CPD in C1–4. Adapted with permission from ref. 123. Copyright 2020, Royal Society of Chemistry. 0) > (0001) faces of hematite, which corresponds to the adsorption capacities of alginate determined by CPD in C1–4. Adapted with permission from ref. 123. Copyright 2020, Royal Society of Chemistry. | |
5. Conclusion and perspectives
Organo–mineral interactions in both biomineralization and geomineralization processes control the crystal nucleation rate, nucleus size, growth orientation and structure. The development of the AFM-based DFS technique makes it possible to study organo–mineral binding at the single-molecule scale. The binding free energy between a single molecule and a specific surface of mineral as well as the organo-modified nucleation energy barrier can be derived from AFM-based DFS experiments. We first review basic theories of DFS for determining organo–mineral binding using AFM-based F–D and F–T curves. Then, detailed procedures of DFS are presented. Finally, four typical experimental cases of DFS are reviewed, specifically research related to crystal nucleation and phase transformation. However, further investigation of DFS issues and related studies are needed:
(1) Tip radius. The tip radius significantly affects the lateral resolution and a sharper tip will contribute to more precise data.126 During force measurements, a small tip radius probes a small surface area, providing high sensitivity to small force measurements.127 The tip radius needs to be determined prior to collecting FS data.
(2) Tip contamination. Tip contamination will lower the resolution of the AFM images and add to errors in the measurements. Because of tip contamination, the lifetime of functionalized tips will be shortened. How to avoid and identify the time limit of tip contamination needs to be addressed.
(3) DFS data analysis. One of the most limiting aspects of DFS is for complex molecules, that is, the technique is fully blind to the actual orientation and conformation of organic macromolecules, and often their number density and mutual and tertiary interactions that can influence the conformation/properties being measured. It is necessary to sort out the important information from the typically large amounts of scatter in the measured force data (Fig. 5C3, and 6C2 and C3). The scatter is large because it is never truly clear what exactly is going on between the tip and substrate. At present, measuring single molecules with known orientations and structures will be more suitable.
(4) Organo–organo and organo–mineral interactions. Since biomolecules selectively react with mineral surfaces, initially reacted biomolecules can serve as a new substrate for subsequent binding.128 This highlights both the organo–mineral and organo–organo–mineral binding.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (41977079, 41471245 and 41071208) and the Fundamental Research Funds for the Central Universities (2662017PY061).
References
- A. F. Wallace, J. J. DeYoreo and P. M. Dove, J. Am. Chem. Soc., 2009, 131, 5244–5250 CrossRef CAS.
- S. Elhadj, J. J. DeYoreo, J. R. Hoyer and P. M. Dove, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 19237–19242 CrossRef CAS.
- W. Jiang, X. Chu, B. Wang, H. Pan, X. Xu and R. Tang, J. Phys. Chem. B, 2009, 113, 10838–10844 CrossRef CAS.
- L. Qin, W. Zhang, J. Lu, A. G. Stack and L. Wang, Environ. Sci. Technol., 2013, 47, 13365–13374 CrossRef CAS.
- L. Addadi and S. Weiner, Phys. Scr., 2014, 89, 098003 CrossRef.
- P. U. Gilbert, S. M. Porter, C. Y. Sun, S. Xiao, B. M. Gibson, N. Shenkar and A. H. Knoll, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 17659–17665 CrossRef CAS.
- L. Wang, C. V. Putnis, H. E. King, J. Hövelmann, E. Ruiz-Agudo and A. Putnis, Environ. Sci. Technol., 2017, 51, 328–336 CrossRef CAS.
- L. Qin, L. Wang and B. Wang, ACS Sustainable Chem. Eng., 2017, 5, 3920–3928 CrossRef CAS.
- F. Barrère, C. A. van Blitterswijk and K. de Groot, Int. J. Nanomed., 2006, 1, 317 Search PubMed.
- M. D. Weir, L. C. Chow and H. H. Xu, J. Dent. Res., 2012, 91, 979–984 CrossRef CAS.
- J. D. Rimer, Z. An, Z. Zhu, M. H. Lee, D. S. Goldfarb, J. A. Wesson and M. D. Ward, Science, 2010, 330, 337–341 CrossRef CAS.
- J. Mejia, S. He, Y. Yang, M. Ginder-Vogel and E. E. Roden, Environ. Sci. Technol., 2018, 52, 13174–13183 CrossRef CAS.
- Z. Li, D. Liang, Q. Peng, Z. Cui, J. Huang and Z. Lin, Geoderma, 2017, 295, 69–79 CrossRef CAS.
- H. Zhai, L. Wang, J. Hövelmann, L. Qin, W. Zhang and C. V. Putnis, Environ. Sci. Technol., 2018, 53, 194–202 CrossRef.
- J. N. Quinton, G. Govers, K. Van Oost and R. D. Bardgett, Nat. Geosci., 2010, 3, 311–314 CrossRef CAS.
- J. J. De Yoreo and P. G. Vekilov, Rev. Mineral. Geochem., 2003, 54, 57–93 CrossRef CAS.
- S. A. Kulkarni, S. S. Kadam, H. Meekes, A. I. Stankiewicz and J. H. ter Horst, Cryst. Growth Des., 2013, 13, 2435–2440 CrossRef CAS.
- H. Zhai, L. Wang and C. V. Putnis, J. Phys. Chem. B, 2019, 123, 845–851 CrossRef CAS.
- H. Shindo and M. Kwak, Phys. Chem. Chem. Phys., 2005, 7, 691–696 RSC.
- J. J. De Yoreo and P. M. Dove, Science, 2004, 306, 1301–1302 CrossRef CAS.
- C. A. Orme, A. Noy, A. Wierzbicki, M. T. McBride, M. Grantham, H. H. Teng, P. M. Dove and J. J. DeYoreo, Nature, 2001, 411, 775–779 CrossRef CAS.
- C. Brandel and J. H. ter Horst, Faraday Discuss., 2015, 179, 199–214 RSC.
- N. Deng, A. G. Stack, J. Weber, B. Cao, J. J. De Yoreo and Y. Hu, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 13221–13226 CrossRef CAS.
- S. Naemura, Mol. Cryst. Liq. Cryst., 1981, 68, 183–198 CrossRef CAS.
- L. F. Mondolfo, Mater. Sci. Technol., 1989, 5, 118–122 CrossRef CAS.
- L. Wang, S. R. Qiu, W. Zachowicz, X. Guan, J. J. DeYoreo, G. H. Nancollas and J. R. Hoyer, Langmuir, 2006, 22, 7279–7285 CrossRef CAS.
- L. Wang, X. Guan, R. Tang, J. R. Hoyer, A. Wierzbicki, J. J. De Yoreo and G. H. Nancollas, J. Phys. Chem. B, 2008, 112, 9151–9157 CrossRef CAS.
- D. K. Owens and R. C. Wendt, J. Appl. Polym. Sci., 1969, 13, 1741–1747 CrossRef CAS.
- W. Rabel, Farbe und Lack, 1971, 77, 997–1006 CAS.
- D. H. Kaelble, J. Adhes., 1970, 2, 66–81 CrossRef CAS.
- D. W. Oxtoby, J. Phys.: Condens. Matter, 1992, 4, 7627 CrossRef.
- S. Giljean, M. Bigerelle, K. Anselme and H. Haidara, Appl. Surf. Sci., 2011, 257, 9631–9638 CrossRef CAS.
- H. Zhao, K. C. Park and K. Y. Law, Langmuir, 2012, 28, 14925–14934 CrossRef CAS.
- E. Ruiz-Agudo and C. V. Putnis, Mineral. Mag., 2012, 76, 227–253 CrossRef CAS.
- M. Li, L. Wang and C. V. Putnis, CrystEngComm, 2018, 20, 2886–2896 RSC.
- L. Wang and C. V. Putnis, Acc. Chem. Res., 2020, 53, 1196–1205 CrossRef.
- W. Fu, J. Vaughan and A. Gillespie, Chem. Eng. Sci., 2015, 126, 399–405 CrossRef CAS.
- Q. Li, A. Fernandez-Martinez, B. Lee, G. A. Waychunas and Y. S. Jun, Environ. Sci. Technol., 2014, 48, 5745–5753 CrossRef CAS.
- D. Kim, B. Lee, S. Thomopoulos and Y. S. Jun, Nat. Commun., 2018, 9, 1–9 CrossRef.
- H. Zhai, L. Wang, L. Qin, W. Zhang, C. V. Putnis and A. Putnis, Environ. Sci. Technol., 2018, 52, 3493–3502 CrossRef CAS.
- H. Zhai, R. Bernstein, O. Nir and L. Wang, J. Colloid Interface Sci., 2020, 575, 464–471 CrossRef CAS.
- S. Wu, H. Zhai, W. Zhang and L. Wang, Cryst. Growth Des., 2015, 15, 4490–4497 CrossRef CAS.
- R. Tang, M. Darragh, C. A. Orme, X. Guan, J. R. Hoyer and G. H. Nancollas, Angew. Chem., Int. Ed., 2005, 44, 3698–3702 CrossRef CAS.
- L. M. Hamm, A. G. Giuffre, N. Han, J. Tao, D. Wang, J. J. De Yoreo and P. M. Dove, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1304–1309 CrossRef CAS.
- T. J. Senden, Curr. Opin. Colloid Interface Sci., 2001, 6, 95–101 CrossRef CAS.
- K. C. Neuman and A. Nagy, Nat. Methods, 2008, 5, 491 CrossRef CAS.
- A. Noy and R. W. Friddle, Methods, 2013, 60, 142–150 CrossRef CAS.
- D. B. Haviland, Curr. Opin. Colloid Interface Sci., 2017, 27, 74–81 CrossRef CAS.
- T. Hugel and M. Seitz, Macromol.
Rapid Commun., 2001, 22, 989–1016 CrossRef CAS.
- O. Björnham and M. Andersson, Eur. Biophys. J., 2017, 46, 225–233 CrossRef.
- H. Li, B. Liu, X. Zhang, C. Gao, J. Shen and G. Zou, Langmuir, 1999, 15, 2120–2124 CrossRef CAS.
- T. Ito, D. Citterio, P. Bühlmann and Y. Umezawa, Langmuir, 1999, 15, 2788–2793 CrossRef CAS.
- S. K. Lower, C. J. Tadanier and M. F. Hochella Jr, Geochim. Cosmochim. Acta, 2000, 64, 3133–3139 CrossRef CAS.
- E. Evans, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 105–128 CrossRef CAS.
- C. K. Lee, Y. M. Wang, L. S. Huang and S. Lin, Micron, 2007, 38, 446–461 CrossRef CAS.
- F. Kienberger, A. Ebner, H. J. Gruber and P. Hinterdorfer, Acc. Chem. Res., 2006, 39, 29–36 CrossRef CAS.
- J. T. Bullerjahn, S. Sturm and K. Kroy, Nat. Commun., 2014, 5, 4463 CrossRef CAS.
- H. G. Hansma, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 14678–14680 CrossRef CAS.
- F. J. Giessibl, Rev. Mod. Phys., 2003, 75, 949 CrossRef CAS.
- W. Wang, K. A. Kistler, K. Sadeghipour and G. Baran, Phys. Lett. A, 2008, 372, 7007–7010 CrossRef CAS.
- J. Tao, K. C. Battle, H. Pan, E. A. Salter, Y. C. Chien, A. Wierzbicki and J. J. De Yoreo, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 326–331 CrossRef CAS.
- K. K. Sand, R. W. Friddle and J. J. DeYoreo, Sci. Rep., 2017, 7, 1–5 CrossRef CAS.
- C. Bustamante, J. F. Marko, E. D. Siggia and S. Smith, Science, 1994, 265, 1599–1600 CrossRef CAS.
- M. D. Wang, H. Yin, R. Landick, J. Gelles and S. M. Block, Biophys. J., 1997, 72, 1335 CrossRef CAS.
- R. W. Friddle, A. Noy and J. J. De Yoreo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 13573–13578 CrossRef CAS.
- R. Merkel, P. Nassoy, A. Leung, K. Ritchie and E. Evans, Nature, 1999, 397, 50–53 CrossRef CAS.
- E. Evans and K. Ritchie, Dynamic strength of molecular adhesion bonds, Biophys. J., 1997, 72, 1541–1555 CrossRef CAS.
- H. A. Kramers, Physica, 1940, 7, 284–304 CrossRef CAS.
- O. K. Dudko, G. Hummer and A. Szabo, Phys. Rev. Lett., 2006, 96, 108101 CrossRef.
- E. Sengupta, Y. Yan, X. Wang, K. Munechika and D. S. Ginger, ACS Nano, 2014, 8, 2625–2631 CrossRef CAS.
- D. Sluysmans, F. Devaux, C. J. Bruns, J. F. Stoddart and A. S. Duwez, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9362–9366 CrossRef CAS.
- H. Zhai, L. Qin, W. Zhang, C. V. Putnis and L. Wang, Environ. Sci. Technol., 2018, 52, 10472–10479 CrossRef CAS.
- X. Ge, L. Wang, W. Zhang and C. V. Putnis, Environ. Sci. Technol., 2020, 54, 207–215 CrossRef CAS.
- S. Jelavić, D. J. Tobler, T. Hassenkam, J. J. De Yoreo, S. L. S. Stipp and K. K. Sand, Chem. Commun., 2017, 53, 12700–12703 RSC.
- T. Han, J. M. Williams and T. P. Beebe Jr, Anal. Chim. Acta, 1995, 307, 365–376 CrossRef CAS.
- R. Barattin and N. Voyer, Chem. Commun., 2008, 1513–1532 RSC.
- R. Daza, L. Colchero, D. Corregidor, M. Elices, C. V. Guinea, F. J. Rojo and J. Pérez-Rigueiro, Appl. Surf. Sci., 2019, 484, 1141–1148 CrossRef CAS.
- H. J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152 CrossRef CAS.
- C. M. Yam, Z. Xiao, J. Gu, S. Boutet and C. Cai, J. Am. Chem. Soc., 2003, 125, 7498–7499 CrossRef CAS.
- J. E. Headrick and C. L. Berrie, Langmuir, 2004, 20, 4124–4131 CrossRef CAS.
- P. Hinterdorfer and Y. F. Dufrêne, Nat. Methods, 2006, 3, 347–355 CrossRef CAS.
- T. Ito, M. Namba, P. Bühlmann and Y. Umezawa, Langmuir, 1997, 13, 4323–4332 CrossRef CAS.
- G. Li, N. Xi and D. H. Wang, Nanomedicine, 2005, 1, 306–312 CrossRef CAS.
- C. Volcke, R. P. Gandhiraman, V. Gubala, C. Doyle, G. Fonder, P. A. Thiry, A. A. Cafolla, B. James and D. E. Williams, J. Colloid Interface Sci., 2010, 348, 322–328 CrossRef CAS.
- A. P. Limanskii, Biophysics, 2006, 51, 186–195 CrossRef.
- K. T. Sapra, P. M. Spoerri, A. Engel, D. Alsteens and D. J. Müller, Curr. Opin. Cell Biol., 2019, 57, 25–32 CrossRef CAS.
- M. R. Uhlig, C. A. Amo and R. Garcia, Nanoscale, 2018, 10, 17112–17116 RSC.
- S. Wu, M. Yu, M. Li, L. Wang, C. V. Putnis and A. Putnis, Cryst. Growth Des., 2017, 17, 2194–2202 CrossRef CAS.
- P. Hinterdorfer, F. Kienberger, A. Raab, H. J. Gruber, W. Baumgartner, G. Kada, C. Riener, S. Wielert-Badt, C. Borken and H. Schindler, Single Mol., 2000, 1, 99–103 CrossRef CAS.
- M. Bergkvist and N. C. Cady, Methods Mol. Biol., 2011, 751, 381–400 CrossRef CAS.
- H. A. Heus, E. M. Puchner, A. J. van Vugt-Jonker, J. L. Zimmermann and H. E. Gaub, Anal. Biochem., 2011, 414, 1–6 CrossRef CAS.
- M. Dukic, J. D. Adams and G. E. Fantner, Sci. Rep., 2015, 5, 16393 CrossRef CAS.
- J. L. Hutter and J. Bechhoefer, Rev. Sci. Instrum., 1993, 64, 1868–1873 CrossRef CAS.
- N. A. Burnham, X. Chen, C. S. Hodges, G. A. Matei, E. J. Thoreson, C. J. Roberts, M. C. Davies and S. J. B. Tendler, Nanotechnology, 2002, 14, 1 CrossRef.
- M. Schlierf, H. Li and J. M. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 7299–7304 CrossRef CAS.
- I. Medalsy, U. Hensen and D. J. Muller, Angew. Chem., Int. Ed., 2011, 50, 12103–12108 CrossRef CAS.
- G. Smolyakov, C. Formosa-Dague, C. Séverac, R. E. Duval and E. Dague, Micron, 2016, 85, 8–14 CrossRef CAS.
- L. Chopinet, C. Formosa, M. P. Rols, R. E. Duval and E. Dague, Micron, 2013, 48, 26–33 CrossRef CAS.
-
B. Pittenger, N. Erina and C. Su, Mechanical Property Mapping at the Nanoscale Using PeakForce QNM Scanning Probe Technique, in Nanomechanical Analysis of High Performance Materials: Solid Mechanics and Its Applications, Springer, 2014, vol. 203, pp. 31–51 Search PubMed.
- Y. G. Kuznetsov, A. J. Malkin and A. McPherson, J. Cryst. Growth, 1999, 196, 489–502 CrossRef CAS.
- K. Naka and Y. Chujo, Chem. Mater., 2001, 13, 3245–3259 CrossRef CAS.
- M. Li, L. Wang, W. Zhang, C. V. Putnis and A. Putnis, Cryst. Growth Des., 2016, 16, 4509–4518 CrossRef CAS.
- A. G. Walton, Science, 1965, 148, 601–607 CrossRef CAS.
- J. D. Gunton, J. Stat. Phys., 1999, 95, 903–923 CrossRef.
- X. Y. Liu and S. W. Lim, J. Am. Chem. Soc., 2003, 125, 888–895 CrossRef CAS.
- A. J. Giuffre, L. M. Hamm, N. Z. Han, J. J. De Yoreo and P. M. Dove, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9261–9266 CrossRef CAS.
- G. H. Nancollas and N. Purdie, Q. Rev., Chem. Soc., 1964, 18, 1–20 RSC.
-
A. A. Chernov, Nucleation and Epitaxy, in Modern Crystallography III, Springer, 1983, pp. 48–103 Search PubMed.
- M. Li, L. Wang and C. V. Putnis, J. Phys. Chem. B, 2017, 121, 5968–5976 CrossRef CAS.
- M. Parvinzadeh, M. Stir, M. Bourquin and J. Hulliger, Cryst. Growth Des., 2013, 13, 2166–2173 CrossRef.
- B. Kaleta, J. Inflammation Res., 2019, 68, 93–102 CrossRef CAS.
- A. H. Welch, D. B. Westjohn, D. R. Helsel and R. B. Wanty, Groundwater, 2000, 38, 589–604 CrossRef CAS.
- A. A. Duker, E. Carranza and M. Hale, Environ. Int., 2005, 31, 631–641 CrossRef CAS.
- F. Renard, C. V. Putnis, G. Montes-Hernandez, E. Ruiz-Agudo, J. Hovelmann and G. Sarret, Geochim. Cosmochim. Acta, 2015, 159, 61–79 CrossRef CAS.
- A. D. Redman, D. L. Macalady and D. Ahmann, Environ. Sci. Technol., 2002, 36, 2889–2896 CrossRef CAS.
- N. Mladenov, Y. Zheng, B. Simone, T. M. Bilinski, D. M. McKnight, D. Nemergut, K. A. Radloff, M. M. Rahman and K. M. Ahmed, Environ. Sci. Technol., 2015, 49, 10815–10824 CrossRef CAS.
- H. Pan, X. Y. Liu, R. Tang and H. Y. Xu, Chem. Commun., 2010, 46, 7415–7417 RSC.
- J. J. De Yoreo, P. U. Gilbert, N. A. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield and A. F. Wallace, Science, 2015, 349, aaa6760 CrossRef.
- L. Wang and G. H. Nancollas, Chem. Rev., 2008, 108, 4628–4669 CrossRef CAS.
- J. Zhang, L. Wang, W. Zhang and C. V. Putnis, Langmuir, 2020, 36, 2102–2109 CrossRef CAS.
- L. Wang and C. V. Putnis, Acc. Chem. Res., 2020, 53, 1196–1205 CrossRef.
- R. W. Friddle, K. Battle, V. Trubetskoy, J. Tao, E. A. Salter, J. Moradian-Oldak, J. J. De Yoreo and A. Wierzbicki, Angew. Chem., 2011, 123, 7683–7687 CrossRef.
- H. Zhai and L. Wang, Environ. Sci.: Nano, 2020, 7, 954–962 RSC.
- O. Orgad, Y. Oren, S. L. Walker and M. Herzberg, Biofouling, 2011, 27, 787–798 CrossRef CAS.
- G. A. Waychunas, C. S. Kim and J. F. Banfield, J. Nanopart. Res., 2005, 7, 409–433 CrossRef CAS.
- J. H. Hoh and P. K. Hansma, Trends Cell Biol., 1992, 2, 208–213 CrossRef CAS.
-
A. Ebner, L. Wildling and H. J. Gruber, Functionalization of AFM Tips and Supports for Molecular Recognition Force Spectroscopy and Recognition Imaging, in Atomic Force Microscopy, Humana Press, 2019, pp. 117–151 Search PubMed.
- H. Zhai, L. Wang and C. V. Putnis, Environ. Sci. Technol., 2019, 53, 11251–11259 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  ab,
Wenjun
Zhang
a,
Lijun
Wang
ab,
Wenjun
Zhang
a,
Lijun
Wang
 *a and
Christine V.
Putnis
cd
*a and
Christine V.
Putnis
cd
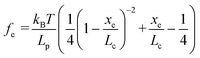
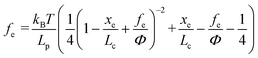
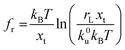
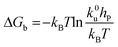
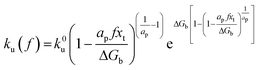
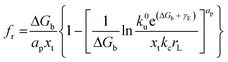
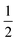 , 1,
, 1, 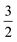 are for a cusp-like barrier, recovery of the Bell–Evans model, and linear-cubic barrier) and γE is Euler's constant. Since more data of DFS show nonlinear trends focusing on inter- or intramolecular reactions,70,71 to describe these nonlinear dynamic force spectroscopies (NLDFS), Friddle et al. interpreted the widespread NLDFS with the Friddle–Noy–De Yoreo model:65
are for a cusp-like barrier, recovery of the Bell–Evans model, and linear-cubic barrier) and γE is Euler's constant. Since more data of DFS show nonlinear trends focusing on inter- or intramolecular reactions,70,71 to describe these nonlinear dynamic force spectroscopies (NLDFS), Friddle et al. interpreted the widespread NLDFS with the Friddle–Noy–De Yoreo model:65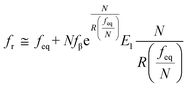
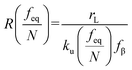
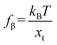 ,
, 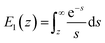 ,
, 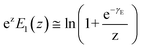 , and ku(f) is the transition rate given by an expression of
, and ku(f) is the transition rate given by an expression of 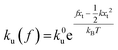 . According to eqn (5), two primary regimes of DFS can be identified: an equilibrium regime when rL approaches 0,
. According to eqn (5), two primary regimes of DFS can be identified: an equilibrium regime when rL approaches 0, 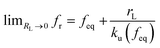 , and a kinetic regime in the fast loading rate,
, and a kinetic regime in the fast loading rate, 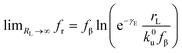 . If the assumption of strictly irreversible binding rupture in the standard analysis is abandoned, both kinetic and equilibrium properties can be described by three important parameters including feq, xt, and k0u and ΔGb can be determined by:65
. If the assumption of strictly irreversible binding rupture in the standard analysis is abandoned, both kinetic and equilibrium properties can be described by three important parameters including feq, xt, and k0u and ΔGb can be determined by:65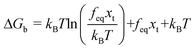
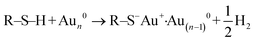
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (v/v) 30% H2O2 and 98% H2SO4), or 10% HNO3, as well as by plasma treatment followed by washing with alkaline and acid solutions.82–84 By reacting with 3-aminopropyl triethoxysilane (APTES), amino (NH2)-terminated organosilane monolayers form on the surface of Si/Si3N4 tips and these amino-activated tips are widely used to anchor biomolecules for studying organo–mineral binding.85
7 (v/v) 30% H2O2 and 98% H2SO4), or 10% HNO3, as well as by plasma treatment followed by washing with alkaline and acid solutions.82–84 By reacting with 3-aminopropyl triethoxysilane (APTES), amino (NH2)-terminated organosilane monolayers form on the surface of Si/Si3N4 tips and these amino-activated tips are widely used to anchor biomolecules for studying organo–mineral binding.85
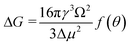
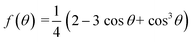
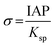 , IAP is the ion activity product and Ksp is the solubility product), f(θ) (0 ≤ f(θ) ≤ 1) is the interfacial correlation factor which describes the lowering of the nucleation barrier due to the presence of the substrates, and θ is the contact angle formed between the nucleated crystal and substrate. As shown in eqn (9a), the energy barrier for nucleation is proportional to γ3, thus, the energy barrier can be quantified by determining the interfacial free energy.
, IAP is the ion activity product and Ksp is the solubility product), f(θ) (0 ≤ f(θ) ≤ 1) is the interfacial correlation factor which describes the lowering of the nucleation barrier due to the presence of the substrates, and θ is the contact angle formed between the nucleated crystal and substrate. As shown in eqn (9a), the energy barrier for nucleation is proportional to γ3, thus, the energy barrier can be quantified by determining the interfacial free energy.
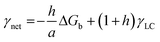
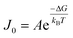
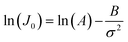
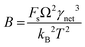
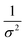 (Fig. 4B). The highest slope is acquired in the 93–106 peptide segment of OPN (Fig. 4B2), suggesting the highest energy barrier for CaP heterogeneous nucleation and the strongest inhibition for the CaP-induced stone formation. To further explain the observation, DFS was applied (Fig. 4C) and the experimentally derived binding free energy between various OPN peptide segments and CaP shows the greatest −ΔGb for the 93–106 peptide segment, corresponding to its greatest inhibitory effects. The interfacial free energy derived from the kinetics of CaP nucleation is linearly related to the binding free energy (Fig. 4D). Therefore, based on the relation
(Fig. 4B). The highest slope is acquired in the 93–106 peptide segment of OPN (Fig. 4B2), suggesting the highest energy barrier for CaP heterogeneous nucleation and the strongest inhibition for the CaP-induced stone formation. To further explain the observation, DFS was applied (Fig. 4C) and the experimentally derived binding free energy between various OPN peptide segments and CaP shows the greatest −ΔGb for the 93–106 peptide segment, corresponding to its greatest inhibitory effects. The interfacial free energy derived from the kinetics of CaP nucleation is linearly related to the binding free energy (Fig. 4D). Therefore, based on the relation 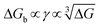 , DFS can be used for explaining mineral nucleation rates.
, DFS can be used for explaining mineral nucleation rates.
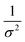 , showing additive-dependent slopes. (C) Binding free energy determinations for a single OPN peptide molecule adsorbing onto an HAP (100) surface. (C1) A representative F–D curve defines the energy dissipation (W). (C2) The corresponding F–T curve is used to calculate the loading rate. (C3) Loading rate-dependent dynamic works (W) of a single molecule OPN peptide–HAP are used to quantify the binding free energy. (D) A linear relationship (R2 = 0.98) between the experimentally derived interfacial free energy and measured binding free energy suggests that high interfacial energy correlates with strong peptide–HAP binding, that is, binding energy can be used to predict heterogeneous nucleation rates. Adapted with permission from ref. 109. Copyright 2017, American Chemical Society.
, showing additive-dependent slopes. (C) Binding free energy determinations for a single OPN peptide molecule adsorbing onto an HAP (100) surface. (C1) A representative F–D curve defines the energy dissipation (W). (C2) The corresponding F–T curve is used to calculate the loading rate. (C3) Loading rate-dependent dynamic works (W) of a single molecule OPN peptide–HAP are used to quantify the binding free energy. (D) A linear relationship (R2 = 0.98) between the experimentally derived interfacial free energy and measured binding free energy suggests that high interfacial energy correlates with strong peptide–HAP binding, that is, binding energy can be used to predict heterogeneous nucleation rates. Adapted with permission from ref. 109. Copyright 2017, American Chemical Society.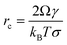


![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) > (11
0) > (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) > (0001) faces of hematite (Fig. 7C). In order to explain these facet-dependent reactions, an alginate molecule is modified onto a Si3N4 tip through silanization. The F–D curve is fitted with the WLC model to extract the single-molecule binding (Fig. 7D1). The rupture force and loading rate are calculated from F–D (Fig. 7D1) and F–T (Fig. 7D2) curves, respectively. Analyzed with the Friddle–Noy–De Yoreo model (Fig. 7D3), the derived binding free energies follow the order amorphous FexOy > the (10
0) > (0001) faces of hematite (Fig. 7C). In order to explain these facet-dependent reactions, an alginate molecule is modified onto a Si3N4 tip through silanization. The F–D curve is fitted with the WLC model to extract the single-molecule binding (Fig. 7D1). The rupture force and loading rate are calculated from F–D (Fig. 7D1) and F–T (Fig. 7D2) curves, respectively. Analyzed with the Friddle–Noy–De Yoreo model (Fig. 7D3), the derived binding free energies follow the order amorphous FexOy > the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) > (11
0) > (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) > (0001) faces of hematite, corresponding to Kelvin potential measurements (Fig. 7C).
0) > (0001) faces of hematite, corresponding to Kelvin potential measurements (Fig. 7C).
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), (C3) (11
0), (C3) (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0), and (C4) (0001) faces of hematite shows that alginate adsorption follows the order amorphous FexOy > (10
0), and (C4) (0001) faces of hematite shows that alginate adsorption follows the order amorphous FexOy > (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) > (11
0) > (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) > (0001) faces. The red solid lines in (C1–4) represent Gauss fitting. (D1) A representative F–D curve shows the (1) noncontact, (2) contact, (3) multiple-molecule detachment, and (4) single-molecule detachment. The purple dashed line shows the WLC model fitting, suggesting that the last peak is the single-molecule unbinding and can be used for collecting the rupture force. (D2) A corresponding F–T curve is used to calculate the loading rate. (D3) A representative DFS measurement for an alginate molecule detached from the hematite (10
0) > (0001) faces. The red solid lines in (C1–4) represent Gauss fitting. (D1) A representative F–D curve shows the (1) noncontact, (2) contact, (3) multiple-molecule detachment, and (4) single-molecule detachment. The purple dashed line shows the WLC model fitting, suggesting that the last peak is the single-molecule unbinding and can be used for collecting the rupture force. (D2) A corresponding F–T curve is used to calculate the loading rate. (D3) A representative DFS measurement for an alginate molecule detached from the hematite (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface. The red solid line represents a fitting of the Friddle–Noy–De Yoreo model. (D4) Experimentally derived binding free energies show that alginate–amorphous FexOy/hematite interactions are strongly affected by crystal phases and exposed faces with the order amorphous FexOy > the (10
0) surface. The red solid line represents a fitting of the Friddle–Noy–De Yoreo model. (D4) Experimentally derived binding free energies show that alginate–amorphous FexOy/hematite interactions are strongly affected by crystal phases and exposed faces with the order amorphous FexOy > the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) > (11
0) > (11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 0) > (0001) faces of hematite, which corresponds to the adsorption capacities of alginate determined by CPD in C1–4. Adapted with permission from ref. 123. Copyright 2020, Royal Society of Chemistry.
0) > (0001) faces of hematite, which corresponds to the adsorption capacities of alginate determined by CPD in C1–4. Adapted with permission from ref. 123. Copyright 2020, Royal Society of Chemistry.


