Photoacoustic measurement of localized optical dichroism in chiral crystals†
Gil
Otis‡
 a,
Matan
Benyamin‡
a,
Matan
Benyamin‡
 *b,
Yitzhak
Mastai
a and
Zeev
Zalevsky
b
*b,
Yitzhak
Mastai
a and
Zeev
Zalevsky
b
aDepartment of Chemistry and the Institute for Nanotechnology and Advanced Materials, Bar-Ilan University, Ramat Gan 5290002, Israel
bFaculty of Engineering and the Nanotechnology Center, Bar Ilan University, Ramat Gan 5290002, Israel
First published on 30th November 2021
Abstract
In this communication, we present a novel method to measure local optical dichroism (OD) in opaque crystal powder suspensions using photoacoustic (PA) effect. Our method is based upon the novel laser speckle contrast technique, in combination with a simple statistical approach, we were able to measure the OD of chiral crystals suspensions under completely random orientation.
Chirality is a fundamental property in nature describing the relationship between two objects that are non-superimposable mirror images.1,2 This property is especially important in the biological context as most of the important building blocks of life possess it, ranging from amino acids and sugars up to complex structures like proteins and polysaccharides.3,4 In the last two decades, tremendous efforts have been assigned into the study of chirality in solids as it became evidential that they play a leading role in explaining the phenomena of biochemical homochirality,5 in a paper, published by Prof. David Avnir in 2012,6 the abundance of natural chiral crystals was calculated and it was estimated that 30% of all organic and inorganic crystals are chiral. Therefore, studying the nature of chiral crystals is of immense value, however, analytical methods for the measurement and study of chirality in solid powders, especially in opaque powders, are very limited.
Throughout the years, many analytical methods were developed for the study of chirality in molecules especially for ones that are easily solvated, such as Optical rotatory dispersion(ORD),7 Circular dichroism (CD),8 vibrational circular dichroism (VCD),9 and Raman optical activity (ROA).10 Yet, these methods are not suitable for measurement in powders as they require the sample to be completely dissolved in liquid. Some analytical methods that can directly measure solid-state chirality did emerge such as low frequency (LF) Raman,11 polarized microscopy,12 electron paramagnetic resonance (EPR),13 and the leading of which: diffused reflection circular dichroism (DRCD),14 nonetheless, there is still a need to develop new methods to measure chirality in powders being that each of the above-mentioned methods has its limitations.
The photoacoustic effect (PA) is a term referring to the generation of mechanical vibration of an optically absorbing substance in response to a short-time optical pulse.15 PA enables to inspect materials’ optical properties by measuring an acoustical event and thus enjoying the relatively minimal scattering behavior of the acoustical wave, relative to the optical scattering.16,17 Since the mechanical wave is generated by a focused optical excitation before the beam continues to scatter, this enables to locally measure optical dichroism (OD) behavior of a material and minimize mixing of different OD behaviors from different regions in the sample.
Examples of chirality measurements using the photoacoustic effect in the literature mainly focused on measuring OD on chiral surfaces18,19 or in well-ordered chiral structures grown on top of surfaces such as nanowires or nano helixes.20,21
Herein, the method we have developed does not assume a predisposition regarding the orientation of the crystals and uses a statistical method to measure OD, therefore, enabling a simple approach for OD measurements in chiral powders, especially in organic chiral crystals (amino acids crystals e.g.) that tend to crystalize in diverse sizes and morphologies.22 In this work, a chiral crystal model system of Cobalt-doped L-Histidine polycrystalline powder was compared to a non-chiral system composed of gold nanoparticles as the reference for the experiment. We performed PA measurements for both systems and demonstrated the ability of our PA method to locally measure the optical dichroism of our chiral crystal model system.
Histidine polycrystalline powders were chosen to emphasize the advantage of our system in measuring opaque powders, the cobalt doping was used to improve the photoacoustic behavior of the powder as cobalt has very strong absorption in the IR region23,24 (which correlated with the excitation beam) and it is known to form stable complexes with the imidazole moiety of histidine.25 The crystals were synthesized using the well-known anti-solvent crystallization method.26 Briefly, a saturated solution of Co-His was prepared by dissolving 200 mg of L-His and 8.3 mg (5 mol%) of CoCl2 in 10 mL of double distilled water under mildly heating (50–60 °C) until the solution became clear. Next, the solution was left on to cool down to room temperature and then moved to the refrigerator (4 °C) for 1 hour of further cooling, afterwards, 90 mL of ethanol (also cooled to 4 °C) were added to the Co-His solution followed by the immediate formation of yellow/gold-colored crystals. The crystals were then collected using a Büchner funnel and washed several times with cold water and ethanol and finally, the polycrystalline powder was dried and taken to characterization. For the photoacoustic measurements, 5 mg of Co-doped L-His crystals were dispersed in 10 mL of ethanol.
The diffraction pattern of the crystals was measured using XRD and is shown in Fig. 1I, L-His naturally crystalizes as a mixture of two different polymorphs, one, an orthorhombic form with a space group of P 21 21 21, and the other, a monoclinic form with a space group of P 21.27 However, recent research had shown that in anti-solvent crystallization conditions L-His crystalizes only in the monoclinic form,28 in our case we also received only the monoclinic form of L-His confirmed by the presence of (0;1;2), (1;1;0) and (0;2;0) characteristic crystals planes of monoclinic L-His (CSD, CIF Nu.: 1206540). Next, the morphology and size distribution of the crystals was estimated by HR-SEM (Fig. 1II), it is evident from the image that the sample is very diverse and contains crystals in various sizes ranging from sizes as small as 0.5 mm and up to big crystals with sizes of 5 mm in length. As for the morphology, all of the crystals are monoclinic as mentioned earlier, and they form platelets in various shapes (Fig. 1II). This property, of diversity in shapes and sizes, is a very typical quality of polycrystalline powders, especially of ones from an organic source22,29 what eventually makes the chirality measurements very challenging in these samples.
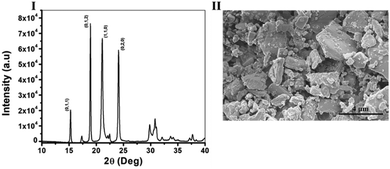 | ||
| Fig. 1 Characterization of photoacoustic chiral Co doped L-His crystals – (I). XRD spectra, and (II). HR-SEM images of monoclinic Co doped L-His crystals (space group: P 21). | ||
The measurements of location-specific chirality are based on the photoacoustic response of the chiral crystals. The amplitude of the photoacoustic response is linearly proportional to the crystals’ absorption coefficient.30 Therefore, chiral crystals will exhibit a difference in their photoacoustic amplitude in response to a left-handed or right-handed polarized excitation beam. We have excited the sample with left and right circular polarization consecutively and calculated the PA amplitude difference, if the crystals are chiral, we assume it would present a meaningful difference between the two excitations.
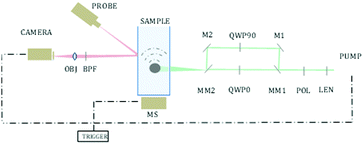
We demonstrate this idea, by creating a sample containing both chiral and non-chiral materials and scanning the different areas of the sample. This was performed by using an x–y motorized stage and scanning the sample, exciting a different area in each step. Excitation was performed using a 1047 nm pulsed laser (pulse width 0.5 ns, Lightwave Electronics). The excitation spot was focused to a size of 500 μm using a 75 mm lens (THORLABS). Each step of the motorized stage, used for raster scanning, was 500 μm as well, so there was no overlap between the pixels. The chiral crystals are free in a solution, and therefore have an unknown spatial orientation relative to the polarization direction. In addition, each focused excitation spot is rather large, and therefore excites more than one crystal at a time (the exact number varies due to the size variance, as seen in Fig. 1), creating an averaged response of multiple crystals in random orientations. This way, even chiral crystals may present no difference, on average, between excitation in two opposite polarization directions.
To address this issue of unknown orientation, we performed multiple repeated measurements for each pixel, allowing the crystals to freely rotate between the measurements. The underlying assumption was that at least in some of the measurements, if not all, the orientation of the crystals will be such that will generate a different response between the two polarization directions. Non-chiral crystals, however, should not present this kind of sensitivity to polarization even after multiple measurements, due to their symmetry. The number of repetitions per pixel was experimentally selected as described below, considering the system's speed of change between the polarization, and the system's ability to move between pixels with the rotating stage (0.5 [s] per pixel, 0.5 [s] per polarization).
Fast switching between polarizations was performed by redirecting the excitation beam to a different optical path each time using motorized mirrors. One path contained a quarter-wave plate, and the other path contained a quarter-wave plate rotated in 90 degrees, creating an oppositely polarized light, as described in Fig. 2.
For each excitation position(i,j) the measurement process was performed as follows:
(a) The area was excited with a pulsed excitation laser, set to a certain circular polarization. (b) The peak-to-peak amplitude of the acoustic response was measured using a non-contact setup thoroughly described by Benyamin.31 (c) Motorized mirrors are activated to change the light path to the oppositely polarizing path. Then (a and b) are repeated. (d) The difference between the amplitudes of the two polarizations was calculated:
| Dm = |Aleft − Aright| | (1) |
Steps (a–d) were repeated M times (m = 1,2⋯M), to eliminate the effect of the random orientation of the crystals. The final value pixel for excitation position (i,j) was taken as the difference between the 85th and the 15th percentile of D:
| Ci,j = percentile(D,85) − percentile(D,15) | (2) |
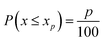 | (3) |
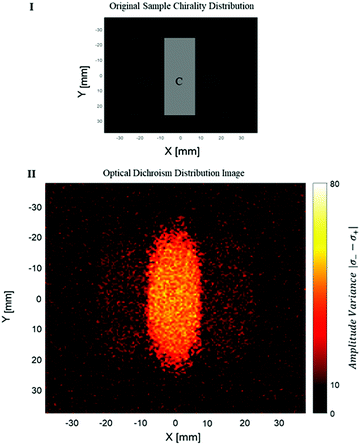
The measurement of the photoacoustic amplitude was performed in a non-contact technique based on laser speckle contrast, and is thoroughly described and detailed by Benyamin.31 The sample used in this experiment was made of wax gel (Mindset) – a relatively transparent and non-absorbing material, which is both solid and acts as a good acoustic medium. Inside the wax gel cube, three chambers were created, each of 15 × 50 × 20 mm. The middle chamber was filled with a solution with chiral crystals, whereas the outer right and left chambers were filled with standard non chiral gold nanoparticles (20 nm gold nanoparticles, NanoHybrid), which performed as the control group. A schematic description of the sample is described in Fig. 3I. Fig. 3II presents the optical dichroism image of the relative difference between the absorption of the two polarizations, excitation position.
It can be seen that a certain amount of dichroism was also detected in the area of the reference particles. However, the dichroism of the chiral crystals is noticeable with significance. Some amount of noise is present in the image. Some of the noise can be explained by a statistical deviation (the intensity of each pixel depends on the natural movement of the crystals during the measurement).
In conclusion, in this short paper, a new method for localized optical dichroism was presented. The method operates on solutions with an unknown orientation of the crystals, and its ability to differentiate between chiral and non-chiral materials with a photoacoustic response was shown in this manuscript. Common optical measurements of OD present rather limited spatial resolution. Although light can be focused onto a specific area in the sample; it will be naturally scattered and interact with other areas, contaminating the measurement and mixing different areas across the sample. Some purposed setups did manage to present spatially resolved OD measurements; however, those require either a nearly 2-dimensional sample, optical properties uniformity in one of the dimensions, or extremely complex setup and long acquisition time.32,33 In the work presented here, we have used the photoacoustic effect to measure the acoustic response originating mostly from the focused light, whereas the scattered light does not contribute significantly to the acoustic response. Thus, enabling us to detect chirality in a specific location onto which the excitation beam is focused, even in three-dimensional samples.
Although OD was already shown to be measured using PA effect,18 here we present a novel use in PA effect in several aspects. First, the measurement is done in a solution in which the crystals are scattered freely. Therefore, the orientation of the crystals, an extremely important property when measuring chirality, is unknown. The method shown here presents a means of overcoming the orientation ambiguity by taking a statistical approach and therefore can be applied with a simpler setup without prior knowledge or alignment process required to the crystals.
Moreover, the specific method used here to measure the photoacoustic amplitude requires no contact with the sample, significantly extending the possible applications of the method, to be used when contact with a transducer is undesired. The method is based on laser speckle contrast – a novel non-contact optical method presented by Benyamin.31 In addition to being remote, this method enables to focus not only on the excitation beam but also the probe, increasing the potential spatial resolution of the presented technique. Quantification of the potential resolution can be derived from ref. 34 and may reach 150 μm. Although the technique may be applied in its presented form, to locally measure dichroism, there are some improvements and analyses that can be performed in future work. First, the experiment described here includes a raster scan, which increased the duration of the experiment. However, the method applied by Benyamin34 can be simply applied here to avoid time-consuming raster scanning.
This technique is not sensitive to the enantiomer identity of the crystals, meaning it cannot identify if the sample contains the pure L or D crystals or a mixture of both of them, but only whether the sample exhibit chirality or not. This also means that this method is not suitable for measuring enantiomeric excess in crystal powders that is, since it measures the absolute difference between the polarizations statistically while the crystals move freely, so L and D crystals will behave similarly when averaging over time. Future work may include a means of separating the two modes, and therefore provide a close and more detailed analysis of the material's dichroism.
This research was partly supported by the Israel Science Foundation. (ISF, Grant No. 1549/17). The authors Gil Otis and Matan Benyamin would like to acknowledge the Bar Ilan president's scholarship for their support, and would also like to thank Denial Aias for her help with the DFT calculations.
Conflicts of interest
There are no conflicts to declare.Notes and references
- H. Flack, Acta Crystallogr., Sect. A: Found. Crystallogr., 2009, 65, 371–389 CrossRef CAS.
- J. Gal, Differentiation of enantiomers I, 2013, pp. 1–20 Search PubMed.
- L. D. Barron, Isr. J. Chem., 2021, 61(9–10), 517–529 CrossRef CAS.
- V. Percec and P. Leowanawat, Isr. J. Chem., 2011, 51, 1107–1117 CrossRef CAS.
- D. G. Blackmond, Cold Spring Harbor Perspect. Biol., 2010, 2, a002147 Search PubMed.
- C. Dryzun and D. Avnir, Chem. Commun., 2012, 48, 5874–5876 RSC.
- E. R. Simons, Spectroscopy in biochemistry, CRC Press, 2018, pp. 63–153 Search PubMed.
- G. Long, R. Sabatini, M. I. Saidaminov, G. Lakhwani, A. Rasmita, X. Liu, E. H. Sargent and W. Gao, Nat. Rev. Mater., 2020, 5, 423–439 CrossRef.
- P. J. Stephens, J. Phys. Chem., 1985, 89, 748–752 CrossRef CAS.
- L. D. Barron, L. Hecht, I. H. McColl and E. W. Blanch, Mol. Phys., 2004, 102, 731–744 CrossRef CAS.
- I. Nemtsov, Y. Mastai, Y. R. Tischler and H. Aviv, ChemPhysChem, 2018, 19, 3116–3121 CrossRef CAS.
- J. Han, J. You, X. Li, P. Duan and M. Liu, Adv. Mater., 2017, 29, 1606503 CrossRef.
- G. Otis, M. Nassir, M. Zutta, A. Saady, S. Ruthstein and Y. Mastai, Angew. Chem., Int. Ed., 2020, 59, 20924–20929 CrossRef CAS PubMed.
- I. Bilotti, P. Biscarini, E. Castiglioni, F. Ferranti and R. Kuroda, Chirality, 2002, 14, 750–756 CrossRef CAS PubMed.
- J. Xia, J. Yao and L. V. Wang, Electromagn. Waves, 2014, 147, 1 CrossRef.
- L. V. Wang and S. Hu, Science, 2012, 335, 1458–1462 CrossRef CAS PubMed.
- C. Li and L. V. Wang, Phys. Med. Biol., 2009, 54, R59 CrossRef CAS PubMed.
- E. Petronijević, G. Leahu, R. Li Voti, A. Belardini, C. Scian, N. Michieli, T. Cesca, G. Mattei and C. Sibilia, Appl. Phys. Lett., 2019, 114, 053101 CrossRef.
- E. Petronijevic, H. Ali, N. Zaric, A. Belardini, G. Leahu, T. Cesca, G. Mattei, L. Andreani and C. Sibilia, Opt. Quantum Electron., 2020, 52, 1–10 CrossRef.
- E. Petronijevic, G. Leahu, A. Belardini, M. Centini, R. L. Voti, T. Hakkarainen, E. Koivusalo, M. R. Piton, S. Suomalainen and M. Guina, Int. J. Thermophys., 2018, 39, 1–9 CrossRef.
- A. Belardini, M. Centini, G. Leahu, D. C. Hooper, R. L. Voti, E. Fazio, J. W. Haus, A. Sarangan, V. K. Valev and C. Sibilia, Sci. Rep., 2016, 6, 1–9 CrossRef.
- T. Tari, P. Szabó-Révész and Z. Aigner, Crystals, 2019, 9, 295 CrossRef CAS.
- A. Torreggiani, P. Taddei and G. Fini, Biopolymers, 2002, 67, 70–81 CrossRef CAS.
- D. M. Boghaei, E. Askarizadeh and A. Bezaatpour, Spectrochim. Acta, Part A, 2008, 69, 624–628 CrossRef PubMed.
- C. M. Yoshida, T. B. Freedman and T. M. Loehr, J. Am. Chem. Soc., 1975, 97, 1028–1032 CrossRef CAS PubMed.
- M. Konstantakou, D. Perganti, P. Falaras and T. Stergiopoulos, Crystals, 2017, 7, 291 CrossRef.
- R. Ravanfar and A. Abbaspourrad, ACS Appl. Mater. Interfaces, 2019, 11, 39376–39384 CrossRef CAS.
- G. D. Profio, A. Caridi, R. Caliandro, A. Guagliardi, E. Curcio and E. Drioli, Cryst. Growth Des., 2010, 10, 449–455 CrossRef.
- D. H. Dressler and Y. Mastai, Chirality, 2007, 19, 358–365 CrossRef CAS.
- I. G. Calasso, W. Craig and G. J. Diebold, Phys. Rev. Lett., 2001, 86, 3550 CrossRef CAS.
- M. Benyamin, H. Genish, R. Califa, A. Schwartz, Z. Zalevsky and N. Ozana, Opt. Lett., 2019, 44, 3110–3113 CrossRef CAS.
- T. Narushima and H. Okamoto, Sci. Rep., 2016, 6, 1–10 CrossRef.
- R. Hussain, T. Jávorfi and G. Siligardi, Front. Chem., 2021, 9 DOI:10.3389/fchem.2021.616928.
- M. Benyamin, H. Genish, R. Califa, N. Ozana, B. Lengenfelder, F. Klämpfl and Z. Zalevsky, OSA Continuum, 2021, 4, 1135–1142 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Materials, Experimental conditions, FTIR, DRUV, TGA, DSC, ICP, polarimetry, computational detailes, DFT calculations, algorithm 1: pseudocode for statistical photoacoustic measurement, statistical analysis conditions, and pixel value vs. the number of repetitions per pixel. See DOI: 10.1039/d1cc05961k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |