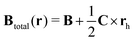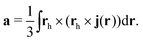DOI:
10.1039/D1CC03350F
(Feature Article)
Chem. Commun., 2021,
57, 12362-12378
Current density and molecular magnetic properties
Received
23rd June 2021
, Accepted 19th October 2021
First published on 19th October 2021
Abstract
We give an overview of the molecular response to an external magnetic field perturbing quantum mechanical systems. We present state-of-the-art methods for calculating magnetically-induced current-density susceptibilities. We discuss the essence and properties of current-density susceptibilities and how molecular magnetic properties can be calculated from them. We also review the theory of spin-current densities, how relativity affects current densities and magnetic properties. An overview of the magnetic ring-current criterion for aromaticity is given, which has implications on theoretical and experimental research. The recently reported theory of antiaromaticity and how molecular symmetry affects the magnetic response are discussed and applied to closed-shell paramagnetic molecules. The topology of magnetically induced current densities and its consequences for molecular magnetic properties are also presented with twisted and toroidal molecules as examples.

From left to right: Raphael J. F. Berger, Maria Dimitrova and Dage Sundholm
| Maria Dimitrova 24.12.1991, (middle) graduated in 2019 at the University of Helsinki with the grade Pass with Distinction. She was post-doctoral researcher at the Paris-Lodron University of Salzburg in 2021 and now at the University of Helsinki. Her scientific interests comprise quantum chemistry studies of molecular properties in magnetic fields. Raphael J. F. Berger 31.03.1973, (left) graduated in 2002 at the Technical University of Munich. He obtained the venia legendi in inorganic chemistry at the Paris-Lodron University of Salzburg in 2014. He is Adjunct Professor of Physcial Chemistry at the University of Helsinki since 2018. In 2016 he became Fellow of the Royal Society of Chemistry and was awarded the Hermann-Mark prize for his contribtions to gas-phase electron diffraction. His research interests include molecular gas-phase structure, relativistic effects in chemistry, molecular magnetic properties and the bio-inorganic chemistry of beryllium. Dage Sundholm 22.12.1957 (right) is a professor of theoretical and computational chemistry since 2009 at the University of Helsinki, where he graduated in 1985. His research interests comprise numerical electronic structure methods and studies of magnetically induced current densities. He calculates molecular optical properties of porphyrinoids, biochromophores and gold-containing molecules including rate constants for nonradiative transitions and quantum yields of luminescence. |
1 Introduction
Earth's magnetic field is too weak to detectably affect molecular properties. There are though other reasons why a proper understanding of the molecular magnetic response is essential in chemistry, since magnetic fields of dozens of tesla can be created on Earth. Such strong magnetic fields perturb the electronic structure of molecules and lead to splittings of energy levels that can be spectroscopically detected. The interaction of these magnetic fields are still weak as compared to electrostatic forces implying that the theoretical treatment of molecular magnetic interactions can be based on perturbation theory. NMR spectroscopy, which is unarguably the most prolific analytical method of chemical characterisation, is based on the magnetic response of electrons and nuclei in molecules. The probability current density, j(r), is the central physical quantity of the magnetic response of the electrons. It can be used for assessing molecular aromaticity, electron delocalisation and used for expressing and computing many molecular magnetic properties. Independently of the central role that j(r) is playing in theoretical magneto chemistry, the probability current density is an interesting quantum mechanical entity on its own rights. This is apparent, for example, in relativistic quantum mechanics, where the current density is a physically well-defined quantity.
This feature article will provide a short overview of the current state of the art of the theoretical description of current densities and molecular magnetic properties. By no means, can we claim to give an exhaustive overview of all branches of this field that is under active research.
2 Theoretical background
2.1 Quantum mechanical treatment of magnetic fields
The interactions between electrons and nuclei in atoms and molecules are described by the Hamiltonian operator containing kinetic-energy and potential-energy terms. Exposing atoms and molecules to a magnetic field gives rise to additional terms in the Hamiltonian.1–3 The kinetic energy comprises the linear momentum and the magnetic interaction. The canonical kinetic (mechanical) momentum operator, ![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1de.gif) , is introduced, which for an electron takes the form
, is introduced, which for an electron takes the form| | ![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e1de.gif) = −iħ∇ + eA, = −iħ∇ + eA, | (1) |
where i is the imaginary unit, ħ is the Dirac constant, ∇ is the vector differential operator, e is the electronic charge and A is the magnetic vector potential, the curl of which gives the magnetic flux, B, also known as the magnetic field strength,Eqn (2) suggests that the magnetic flux can be defined by any magnetic vector potential fulfillingwhere f is a continuous differentiable function with a vanishing curl.
The magnetic vector potential of a uniform magnetic field at point r can be given by
| | 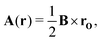 | (4) |
where
rO =
r −
O is the distance from
r to a gauge origin
O. In quantum chemistry, divergence-free vector potentials are used (∇·
A = 0) in order to reduce the number of terms in the Hamiltonian.
2.2 The Hamiltonian in the presence of a magnetic field
The Hamiltonian is derived by substituting the linear momentum operator in the field-free Hamiltonian, Ĥ(0), with the kinetic momentum operator in eqn (1), which yields terms of different powers of the magnetic vector potential,| | | Ĥ = Ĥ(0) + Ĥ(1)(A) + Ĥ(2)(A2). | (5) |
For closed-shell molecules, the first-order dependence on the magnetic field becomes| | 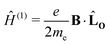 | (6) |
where me is the electron mass. The expression for the orbital angular momentum operator, ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) O, around O is
O, around O is| | ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) O = rO × p = −iħ(rO × ∇), O = rO × p = −iħ(rO × ∇), | (7) |
where p is the momentum operator. The expression for the first-order interaction between the spin angular momentum, Ŝ, and the magnetic field resembles the one for the orbital angular momentum,| | 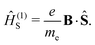 | (8) |
The terms Ĥ(1) and Ĥ(1)S can either increase or decrease the total energy. In contrast, the quadratic dependence on the magnetic field strength in Ĥ(2) can only increase the energy. It is given by| |  | (9) |
2.3 Gauge-origin transformations
The physical properties of a quantum mechanical system in a magnetic field are independent of the origin of the magnetic vector potential. Thus, the vector potential can be chosen arbitrarily. This is a fundamental property at the core of the standard model giving the freedom to choose any vector potential up to a scalar gauge function with a vanishing curl.4 When the magnetic vector potential in eqn (4) is used, one can freely choose the origin of the coordinate system, transform A(r) between different coordinate systems or equivalently, shifting the origin O of the A(r) potential, which can be seen by setting  in eqn (3).
in eqn (3).
The Hamiltonian is a Hermitian operator that remains gauge-invariant, meaning that it does not change as a consequence of gauge transformations, i.e., when shifting the gauge origin, O. However, the wave function acquires a complex exponential prefactor upon gauge transformations. When adding a scalar gauge function to the magnetic vector potential as in eqn (3), the change in the wave function is5
| | 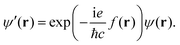 | (10) |
where
c is the speed of light. Hence for a given magnetic field there is no unique form of the magnetic vector potential,
Formally one deals with a type of symmetry which is sometimes called gauge symmetry, gauge freedom or, emphasising the arbitrariness of the functional expression, it is also called the gauge problem. The latter point of view becomes relevant in numerical computations where the choice of the gauge, though formally irrelevant, has a substantial, sometimes huge effects on the numerical accuracy of the results. The former point of view is important for theoretical considerations where one enjoys the freedom to choose the form of the vector potential that transforms the equations into convenient expressions.6
An alternative symmetric Coulomb (s.C.) gauge for a homogeneous magnetic field parallel to the z axis of the coordinate system can be constructed as
| |  | (12) |
fulfilling the ∇ ×
As.C. =
B and ∇·
As.C. = 0 conditions. The same holds for
| |  | (13) |
which is not of the symmetric Coulomb type and cannot be expressed as a single cross product. Magnetic vector potentials of the
As.C. type or gauge-including atomic orbitals (GIAO), also known as London orbitals,
7–10 have mainly been employed in quantum chemical calculations of molecular magnetic properties. Magnetic properties have though also been calculated with the Landau gauge.
11
GIAOs can be constructed to resemble the magnetic response of the wave function in eqn (10). They contain the magnetic vector potential, ABK, of the external magnetic field, B, with the gauge origin at nucleus K as an exponential prefactor to an ordinary basis function, χK(r),
| | | ωK(r, ABK) = exp(−ir·ABK(r))χK(r). | (14) |
Many studies have shown their importance in calculations of molecular magnetic properties,
7–10 since GIAOs consider the magnetic response to first order for any choice of the gauge origin leading to a rapid basis-set convergence as compared to calculations employing ordinary basis functions. The magnetic response of ordinary basis functions are correct only to zeroth order.
12
We also employ GIAOs in calculations of current-density susceptibilities with the gauge-including magnetically induced current method (GIMIC), as discussed in Section 2.9.
Since the magnetically induced current density JB, is a vector field, one can compute it using a different origin of the vector potential for every point in space. This scheme called the continuous set of gauge transformation (CSGT) was introduced by Keith and Bader,13 while Lazzeretti et al. called it the continuous transformation of the origin of the current density (CTOCD)14–16 approach. The gauge origin of the vector potential seems then to have the form of a function O(r). However, this is misleading since one cannot employ a single gauge transformation, since in general
| | 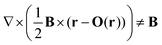 | (15) |
holds. Instead, it should be seen as using a continuous set of equations to be evaluated separately for each point in space. The first exploited CTOCD scheme was the so called CTOCD-diamagnetic-component-to-zero (CTOCD-DZ) approach, where each evaluation point is its own gauge origin,
The CTOCD-DZ approach was later called the ipsocentric method.
13–15,17,18
2.4 Current density
The continuity equation ensuring charge conservation can be derived using the hydrodynamical representation of the Schrödinger equation,19,20| | 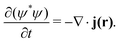 | (17) |
The probability current density or the current density, j(r), is then given by| | 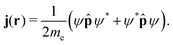 | (18) |
The current density is a subobservable, meaning that it is formally the expectation value of a quantum mechanical operator, and hence experimentally measurable if a suitable instrument were available.21 Multiplying j(r) by the electron charge yields the charge current density, J(r) = −ej(r). The electronic current density can be expressed as the expectation value of the anti-commutator of the kinetic momentum and the electron-density operator ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r),
(r),| | j(r′) = 〈Ψ|{![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1de.gif) , , ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r)}+|Ψ〉. (r)}+|Ψ〉. | (19) |
The electron-density operator is given by ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r) = δ(r − r′) with the Dirac delta function δ.
(r) = δ(r − r′) with the Dirac delta function δ.
The magnetically induced current density can be obtained to first order by expanding the wave function in series according to the Rayleigh–Schrödinger perturbation theory,22,23
| | | Ψ0 = Ψ(0)0 + Ψ(1)0 + …, | (20) |
where
Ψ(1)0 is the first-order magnetically perturbed wave function that can formally be obtained by introducing the angular momentum operator,
![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) O
O, as the perturbation,
| |  | (21) |
E(0)0 and
E(0)I in the denominator of
eqn (21) are the energies of the ground and the
Ith excited state, respectively, which are obtained in the absence of the external magnetic field.
The current-density expression can be obtained by inserting Ψ(1)0 in eqn (21) into eqn (20), which is then use in eqn (19). The quadratic and higher-order terms in B are omitted. The current density induced by a magnetic field can be formally separated into a diamagnetic term, JBdia, and a paramagnetic term, JBpara. However, this is a purely mathematical formality based on the fact that JBdia resembles the classical Larmor current density. Yet, only the sum of the Larmor and non-Larmor terms has a physical meaning.
| |  | (22) |
When an N-atomic molecule is exposed to an external magnetic field, the magnetic vector potential is
| | 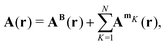 | (23) |
where
AB(
r) is the vector potential of the external magnetic field and
AmK(
r) is the vector potential of the nuclear magnetic dipole moment
mK of nucleus
K. To the first order, the magnetically perturbed wave function takes the form
| | | Ψ = Ψ0 + ΨB·B + ΨmK·mK + …, | (24) |
where
ΨB is the change in the wave function due to the external magnetic field and
ΨmK is the wave-function response due to the nuclear magnetic moment
mK.
2.5 Relativistic current density
The relativistic current density based on the solution of Dirac's time-independent relativistic wave equation is| | {cα·[−iħ∇ + A] + βmec2V}φ = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) φ, φ, | (25) |
where α and β are the standard Dirac matrices,24φ is the relativistic four-component wave function, and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) is the energy eigenvalue. The current density is then given bywhere cα is the relativistic velocity operator. Thus, j4c(r) can be interpreted as a velocity density discussed in Section 2.6.
is the energy eigenvalue. The current density is then given bywhere cα is the relativistic velocity operator. Thus, j4c(r) can be interpreted as a velocity density discussed in Section 2.6.
For many-electron systems, the expression for the relativistic current density can be recast in terms of the Gordon decomposition25,26 as
| |  | (27) |
where
φi are four-component Dirac orbitals and ℑ denotes imaginary part.

is the spin operator. An additional term accounting for the spin contribution to the exchange correlation potential appears at the Dirac–Kohn–Sham (DKS) level of theory.
27
2.6 The current density as a velocity density
Using atomic units but keeping the rest mass of the electron, me, (i.e. ħ = e = a0 = 1) eqn (18) yields the electron current density, j(r), which can be interpreted as the real part of the velocity density† originating from the velocity operator p/me,| | 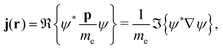 | (28) |
where ℜ and ℑ denote the real and imaginary part, respectively. This expression can be extended to the case of a non-vanishing external magnetic field by replacing the momentum operator, p, in eqn (28) with the mechanical momentum operator ![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) given by eqn (1), which is called minimal coupling. Substituting p →
given by eqn (1), which is called minimal coupling. Substituting p → ![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) = p + A yields
= p + A yields| |  | (29) |
which is equivalent to eqn (22). To consider the spin of the electron, we can follow the derivation by Dyall and Fægri24 and replace ![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1de.gif) with σ(σ·
with σ(σ·![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1de.gif) ) in eqn (29), where σ is a three-dimensional vector of the Pauli spin matrices.‡24 Replacing the one-component wave function, ψ, with the two-component Pauli spinors, φ, yields
) in eqn (29), where σ is a three-dimensional vector of the Pauli spin matrices.‡24 Replacing the one-component wave function, ψ, with the two-component Pauli spinors, φ, yields| | 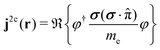 | (30) |
| |  | (31) |
which is identical to the expression for the current density derived by Landau from the Pauli–Schrödinger equation by variation of the differential of the Hamilton function.28 This expression cannot be derived from the Pauli–Schrödinger equation alone without considering the extremality condition of the Hamilton function.29 In four-component relativistic theory, the current density and its reformulation in terms of the Gordon decomposition25,26 is| |  | (33) |
The Gordon decomposition of the four-component relativistic current density eqn (33) is in the two-component limit equal to eqn (31).
2.7 Spin-current densities
The spin of the electron was introduced into the Schrödinger equation by Pauli to fit experimental observations.1,2 In the presence of an external magnetic field, the Schrödinger equation becomes a two-component equation, whose components are coupled by the external magnetic field.30–32 The spin of the electron is introduced in a natural way by using the relativistic Dirac equation or the Lévy–Leblond equation,3,33 which is a non-relativistic four-component equation with eigenenergies and eigenfunctions that are identical to the ones obtained by solving the Schrödinger equation.29 The spin-dependent term in the probability current is| |  | (34) |
An elegant way to introduce the spin into the current-density expression is to use the variation principle outlined, for example, in the textbook of Landau and Lifshitz28 that yields the spin-current density as a contribution to the charge current density without further assumptions.
Following an argument from Greiner34, this additional current-density term can be interpreted in analogy with classical electrodynamics as a magnetisation current density, JM, describing a magnetisation density M induced by the current density of a particle with charge q,
| | 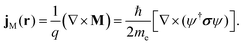 | (35) |
For electrons, M is obtained by multiplying the spin density ρspin = ψ†σψ with  , retaining its interpretation as the magnetisation density that arises from the spatial distribution of the spin which is the magnetic moment. The spin-current density appears then as an additional term to the total current density.29
, retaining its interpretation as the magnetisation density that arises from the spatial distribution of the spin which is the magnetic moment. The spin-current density appears then as an additional term to the total current density.29
As jspin(r) is divergence-free, it does not contribute to the charge-conservation equation in eqn (17). However, there are theoretical and experimental evidences that jspin(r) is a measurable component of the probability current density of spin-½ particles and not a mere virtual term that completes the magnetisation density with the spin contribution.29
2.8 Current-density susceptibility
The current density is a vector with its components in the three Cartesian directions. Expanding the current density in a Taylor series with respect to an external magnetic field results in the zero-field current density, j0(r), which vanishes for closed-shell quantum systems. The second term consists of the first derivative of JB(r), called the current-density susceptibility tensor, multiplied by the respective component of the magnetic field,| | 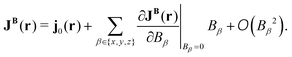 | (36) |
Higher-order terms can generally be omitted, since magnetic interactions under terrestrial conditions are weak in comparison to Coulomb forces. The current-density susceptibility tensor element in the α Cartesian direction for the magnetic field in the β Cartesian direction is| | 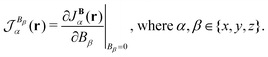 | (37) |
The current density scales almost linearly with the strength of the external magnetic field when field is weak. In stronger magnetic fields, non-linear effects become significant.31,35–39 The non-linearity is difficult to detect, since experimental chemical shifts are measured with respect to a reference, whose magnetic shielding constant also have a non-linear component at strong magnetic fields. Small deviations from linearity were recently found in measurements of 59Co NMR chemical shifts using a 28T NMR spectrometer.40
2.9 The gauge-including magnetically induced current method
An expression for the current-density susceptibility can be obtained by combining the expression for calculating nuclear magnetic shielding tensors using analytical derivative theory with the corresponding Biot-Savart expression.41–44 The final expression for calculating current-density susceptibilities contains the one-electron density matrix in the atomic-orbital (basis-function) basis, Dμν, and the magnetically perturbed one-electron density matrices, 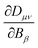 . Gauge-origin independence and a fast basis-set convergence are achieved by employing gauge-including atomic orbitals defined in eqn (14).
. Gauge-origin independence and a fast basis-set convergence are achieved by employing gauge-including atomic orbitals defined in eqn (14).
The tensor elements of the current-density susceptibility can be obtained as
| |  | (38) |
where
εαβδ is the Levi-Civita pseudotensor with
α,
β,
δ ∈ {
x,
y,
z}.
45 The actual interaction with the magnetic field is described by the operators
| |  | (39) |
and
| |  | (40) |
where
RK are the nuclear coordinates. The same singularity |
r −
RK|
−3 appearing in all terms of the current-density susceptibility expression cancel and can be omitted, even though the expression in
eqn (38) seems to depend on the gauge origin and the nuclear coordinates. The current-density susceptibility depends, though, implicitly on the nuclear positions. Equivalent expressions can be derived for the current-density susceptibility contributions of the spin-up and spin-down electrons of open-shell molecules.
42
2.10 Continuous transformation of the origin of the current density
The CTOCD method was introduced in 1993 primarily for improving the numerical accuracy of current-density calculations. In 2001 Steiner and Fowler discovered the symmetry rules for the diamagnetic and paramagnetic response using molecular-orbital (MO) based first-order perturbation theory and the CTOCD-DZ ansatz.46 They found that the paramagnetic response is determined by rotational occupied-virtual transition matrix elements,| | 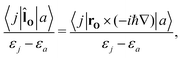 | (41) |
where |j〉 and |a〉 denote occupied and unoccupied orbitals, respectively, and εj and εa are their energies, ![[l with combining circumflex]](https://www.rsc.org/images/entities/b_char_006c_0302.gif) O is the one-particle angular momentum operator with respect to the origin, O. The diamagnetic response is determined by translational occupied-virtual transition matrix elements,
O is the one-particle angular momentum operator with respect to the origin, O. The diamagnetic response is determined by translational occupied-virtual transition matrix elements,| |  | (42) |
where p is the one-particle linear momentum operator. Similar expressions are obtained for the many-electron case, where |j〉 and |a〉 denote the ground and excited states, respectively. Hence, the selection rules for diamagnetic and paramagnetic contributions can be obtained using group theory. Virtual transitions from the ground state to excited states belonging to the same irreducible representations as infinitesimal rotations around the axis parallel to B yield paramagnetic contributions, whereas the diamagnetic contributions originate from dipole-allowed transitions perpendicular to B with the same irreducible representations as translations in the given point group. Using the momentum/position off-diagonal hypervirial theorem,47,48 the diamagnetic contribution can be shown to be equal to the diamagnetic term obtained with the common-gauge-origin (CGO) ansatz in the limit of complete basis set.
The CTOCD-DZ method is widely used due to its high numerical accuracy compared to other CTOCD ansätze. In particular, the zero-divergence condition is fulfilled with high accuracy for regions of small electron density already when employing relatively small basis sets. Variants of the CTODZ-DZ method such as shifting the gauge origin in core regions with high electron density closer to the nuclei (CTOCD-DZ2) have been proposed.49
CTOCD-paramagnetic-component-to-zero (CTOCD-PZ) is the antipodal ansatz, where the gauge-origin distribution O(r) is chosen such that the induced current density is given by
| |  | (43) |
where
ρ(
r) = |
Ψ(0)0|
2 is the electron density. The CTOCD-PZ implies that the paramagnetic current-density contributions originating from excited states vanish. The theoretically exact condition for the gauge-orgin distribution
O(
r) of the CTOCD-PZ ansatz in the complete basis set limit is
| |  | (44) |
where

is defined in
eqn (21).
A series of approaches closely related to CTOCD-DZ and CTOCD-PZ is implemented in the SYSMOIC package.50 Recently an origin-distribution scheme was proposed that leads to vanishing divergence of the diamagnetic current-density contribution, ∇·JBdia(r) = 0. The origin-distribution function is then of the form
| |  | (45) |
which can be used when
Φ(
r) is a well-behaved real scalar function.
51 The diamagnetic contribution to the current density,
| |  | (46) |
then inherits the topology of the origin-distribution function
Φ(
r).
§ In points
r0 where ∇
Φ(
r0) = 0 holds,
JBdia(
r) has stagnation points.
Φ(
r) functions that can be expressed as a function of the electron density are of particular interest, since a natural connection is then obtained between the topology of Bader-type bond critical points and stagnation points of the current density.
2.11 Spin-current-density susceptibility
The orbital contribution to the spin-current-density susceptibility can be calculated at non-relativistic levels of theory using the gauge-including magnetically induced current (GIMIC) method42 described in Section 2.9 or by using the continuous transformation of the origin of the current density (CTOCD-DZ) scheme described in Section 2.10.52 The spin-current-density susceptibility of the spin-up and spin-down electrons are obtained with the same expression as used for closed-shell molecules. For open-shell molecules, one needs density matrices of the spin-up (α) and spin-down (β) electrons that can be obtained in electronic structure calculations on open-shell molecules. The GIMIC method needs magnetically perturbed spin-density matrices that are obtained by performing a calculation of the orbital contribution to the NMR shieldings of open-shell molecule. The spin-current-density susceptibility is the difference between the current-density susceptibilities of the α and β electrons and the current-density susceptibility is the sum of the two.53 The spin-current density can be used in an integral expression for calculating the elements of the nuclear hyperfine coupling tensor and the density of hyperfine coupling, which is a function containing its spatial origin.52
2.12 Current-density susceptibility at relativistic levels
For closed-shell molecules, the largest purely relativistic contribution to the current density arises from a non-vanishing spin density, ρB,SOCspin, which is a second-order perturbation induced by the spin–orbit coupling (SOC) interaction in the presence of an external magnetic field.54 The spin–orbit coupling results in a contribution to the total current density via a spin-current-density-like term| |  | (48) |
where the second expression can be identified when comparing the expression to eqn (27).
Due to the SOC mechanism, ρB,SOCspin(r) is primarily located near the nuclei of heavy elements and less pronounced but still significant at the nuclei of lighter atoms that are directly bonded to heavy atoms. The latter case is especially pronounced when the bond is σ-dominated, since then a Fermi-contact coupling between heavy and light atoms can occur. This is the heavy atom-light atom (HALA) effect.55 The spin density at a covalently bonded hydrogen atom has the shape of an s orbital whose amplitude quickly decreases with the distance from the nucleus of the hydrogen atom leading to a spin-current density with a small but sharp vortex as for HgH2 shown in Fig. 1.
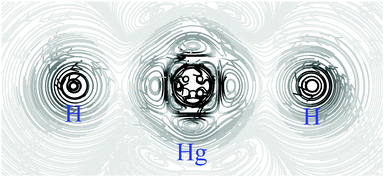 |
| | Fig. 1 Streamline representation of the magnetically induced spin-current density JspinB,SOC(r) in HgH2 in a plane containing the nuclei calculated at the four-component DKS level of theory. The external magnetic field is perpendicular to the inspection plane. A strongly located current density originating from ρB,SOCspin(r) with high curvature can be seen close to the Hg nucleus and at the hydrogen nuclei. | |
Magnetically induced current densities can be calculated at fully relativistic four-component (4C) density functional theory (DFT) levels of theory with the ReSpect54,56–59 and Dirac60–63 programs. The ReSpect program can be used in studies of closed-shell and open-shell systems. Perturbation-free current densities of open-shell systems as well as current densities induced by nuclear magnetic moments can be calculated and visualised with ReSpect.27 The two codes employ GIAOs in calculations of magnetic properties and magnetically induced current densities. In 4C-DFT calculations of magnetically induced current densities, restricted kinetically and magnetically balanced basis sets are used. These basis sets in combination with GIAOs ensure numerical stability and a rapid convergence of magnetic properties with respect to the size of the basis set.
2.13 Topology of the current-density field
Topology analysis of molecular electron densities that was introduced by Bader64–66 led to the development of the quantum theory of atoms in molecules (QTAIM),67 which is a means of partitioning the electron density, eρ(r), and molecular properties into chemically meaningful atomic domains. The current-density field can analogously be divided into atomic or chemically relevant domains. Such topology analyses provide valuable insights about the current-density distribution and the origin of molecular magnetic properties.
Dirac68 and later Hirschfelder et al.69–71 developed the theory of quantised vortices of the probability current-density flux around the nodal regions of complex wave functions, ψ = ψr + iψi. The vortices originate from wave interference and, hence, have no classical interpretation. The local velocity, v(r), of the probability current density, j(r), in eqn (18) is given by the flux divided by the probability density, ρ(r) = |ψ(r)|2,
| |  | (49) |
The local velocity can be integrated over a closed path, which is defined up to an integer multiplier,
i.e., it is quantised,
| |  | (50) |
where the circulation number
n is an integer,
L is a closed path, and
m is the mass of the particle. The circulation is the same for all loops of the same nodal regions of
ψ(
r).
The linear relation between the probability current density j(r) and the velocity v(r) allows investigations of the current-density field with methods developed for classical hydrodynamics studies.16,72,73 The velocity is given by
| |  | (51) |
which leads to
| |  | (52) |
where
τ is any coordinate along the trajectory. The time arrow gives the direction of
j(
r). The velocity vector field can be investigated numerically using the Runge–Kutta method in order to obtain the next step of the trajectory.
74,75 The result can be visualised as streamlines in three dimensions (3D) and the tropicity of the vortex can be determined from the circulation direction. Diatropic current-density vortices circulate in the classical direction, while the opposite direction defines a paratropic flow.
A magnetic field gives rise to an imaginary component of the wave function which depends linearly on the magnetic field strength. The intersections between the nodal surfaces of the real and imaginary parts of the wave function create axes or loops around which axial or toroidal vortices arise. Hirschfelder71 showed that axial vortices have an orbital angular-momentum dipole moment. When a nodal line forms a closed loop, a toroidal vortex arises, such that it flows concentrically around the nodal line. The angular-momentum dipole moment vanishes for toroidal vortices but instead they possess orbital angular-momentum quadrupole moments. Toroidal vortices can interact with the gradient of the magnetic field but not with homogeneous magnetic fields.71 Axial and toroidal vortices are the only kinds of vortices associated with one-particle wave functions.71 The analysis of the nodal lines of N-electron wave functions can either be done in a 3N-dimensional space, or in 3D after splitting the wave function into natural orbital components which, however, do not necessarily fulfill the continuity equation.76
The magnetically induced current density is a 3D vector field that can be analysed by evaluating its singular points. An expansion of the current density into a Taylor series at the singular point r0 shows that it is to first order related to the Jacobian matrix D(r) = [∇J(r)]r0, as
| | | Jα(r) ≈ Dβα(rβ − r0β). | (53) |
The singular points of the current-density field can be analysed using the Jacobian matrix that can be efficiently obtained by numerical differentiating the expression for the current-density susceptibility in eqn (38) or by differentiating it analytically. The number of non-zero eigenvalues of the D(r) tensor gives the rank of the singular point, r, while the difference between the number of eigenvalues with a positive and with a negative real part defines the signature of the singular point, s. Singular points of the current density are classified according to their Euler index (r, s),16,76–78 which is analogous to the topological treatment of the electronic density of molecules.67
An isolated singular point is a local maximum in two dimensions but a minimum in the third one. Such points are defined as (3, ±1), where the + and − sign correspond to a sink and a source, respectively. Points lying on stagnation lines are denoted by (2, 0), meaning that two of the eigenvalues of D(r) are of the same size but with opposite sign and the third eigenvalue is zero. When the three eigenvalues of the Jacobian vanish, the stagnation lines may split. The behaviour of the vector field around a stagnation line is characterised either by an index +1 when there is a vortical flux around the line, or by the index −1 when the singular point is a saddle point. The eigenvalues of D(r) are real for a saddle point and imaginary for a vortex. Streamline representations are shown in Fig. 2.
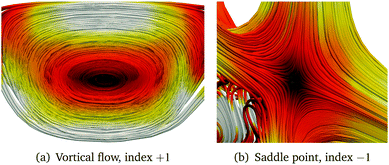 |
| | Fig. 2 Streamline representation of the magnetically induced current density around (2, 0) singular points. | |
Stagnation lines are open lines for axial vortices and they can branch into N new lines at critical points as long as the total index (±1) is conserved,76
| |  | (54) |
A streamline may not cross a reflection plane of the point-group symmetry.16 The properties of stagnation lines differ from those of the nodal lines of the wave function, since a stagnation line can be associated not only with a vortical flow but they can also form a set of saddle points.76
The set of asymptotic lines connecting two singular points forming a surface is called a separatrix, which serves as the boundary between the vortices of the current-density field. Separatices may never cross due to charge conservation. Plotting all the stagnation lines of the field gives its stagnation graph. Gomes proved that there is one and only one vortical line extending to infinity.76 It corresponds to a vortex that covers the whole molecule and vanishes far away from it. The global domain is associated with a dominating stagnation line parallel to the magnetic field. The main stagnation line can branch in the vicinity of the atoms where the electron density is large and may give rise to both vortical and saddle stagnation lines resulting in many smaller vortices inside the global current-density domain.
The stagnation graph of the molecule are useful since one can visually identify domains of the current density associated with chemical bonds, such as in Fig. 3, or with ring currents as shown in Fig. 4. One can also identify atomic vortices in the vicinity of the nuclei. In the centre of molecular rings there is typically a vortex as seen in blue in Fig. 5. In polycyclic molecules with fused rings, current-density pathways may trace the perimeter of some rings but avoid others, i.e., forming semilocal vortices. Heteroatoms often give rise to complicated and sometimes unpredictable current-density pathways.79 The current-density flux affects the nuclear magnetic shielding constants as discussed in Section 2.15.
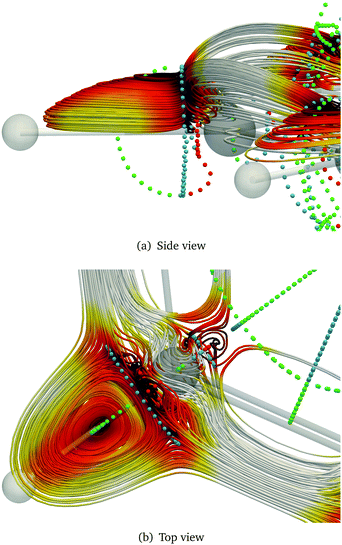 |
| | Fig. 3 Streamline representation of the magnetically induced current density and stagnation points in the vicinity of the C–H bond in benzene. Saddle points are drawn in blue, while green and red show the diatropic and the paratropic vortex points, respectively. | |
 |
| | Fig. 4 Streamline representation of the magnetically induced current density and stagnation points in benzene. Saddle points are drawn in blue, while green and red show the diatropic and the paratropic vortex points, respectively. | |
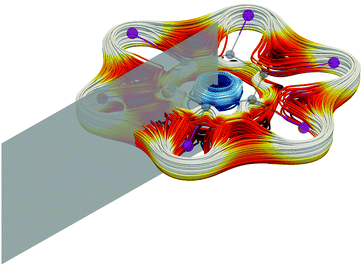 |
| | Fig. 5 The integration plane shown in gray for calculating the strength of the ring-current strengths of ring-shaped molecules, such as [C6I6]2+ here. The ring current is dominated by the diatropic contribution at the carbon ring and outside the iodine atoms. The paratropic ring current inside the ring is shown in blue.131 | |
By placing the magnetic field in the z direction, the negatively charged electrons flow in the clockwise direction when looking towards the negative z axis according to classical electrodynamics. However, the quantum-mechanical response of the molecular electron density to the magnetic field can also give rise to an induced current density in the counter-clockwise direction. Thus, the direction of the current-density flux inside a vortex is either clockwise or counter-clockwise for a given direction of the external magnetic field.
2.14 Magnetisability
The magnetic interaction energy can be expressed as the scalar product of the magnetically induced current density JB (r) with the vector potential AB(r) of the external magnetic field, B,16,80–86| |  | (55) |
The elements of the magnetic susceptibility tensor, χαβ with α, β ∈ {x, y, z}, are defined as the second derivative of EBB with respect to B,| | 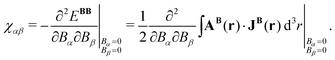 | (56) |
Magnetisabilities are generally calculated using analytic gradient theory, which is also known as response theory.10,87–89 Closed-shell molecules are, with a few exceptions, diamagnetic with a negative magnetisability,90–97 whereas molecules having a positive magnetisability are paramagnetic. In open-shell systems, paramagnetism is due to the spin of the unpaired electrons, whereas closed-shell paramagnetic molecules discussed in Section 2.18 are rare.
The second half of eqn (56) shows that the magnetisability can also be calculated by differentiating the magnetic interaction energy in eqn (55).16,80–87,98–101 The elements of the magnetisability tensor can then be expressed as
| |  | (57) |
where
ρχαβ(
r) is the magnetisability density given by
| |  | (58) |
where
εαδγ is the Levi-Civita symbol,
α,
β,
γ,
δ,
rδ ∈ {
x,
y,
z}. The integral expression renders numerical integration approaches feasible when the current-density susceptibility is available. The magnetisability density provides information about the spatial origin of the magnetisability, which is not possible when using analytic gradient theory. The magnetisability density is gauge dependent, since one can choose an arbitrary gauge origin in
eqn (4) due to the charge conservation of the current-density susceptibility,
102| |  | (59) |
However, the obvious and most likely the correct choice is
O = 0, because otherwise, for example, symmetry-related atoms would contribute differently to the magnetisability when the chosen gauge-origin of the magnetisability operator differs from zero. Since the current-density susceptibility can be obtained from calculations of nuclear magnetic shieldings, gauge-origin independent magnetisabilities are easily obtained using the integration approach.
86
Calculations of magnetic properties using functionals at the meta-generalised gradient approximation (mGGA) require extensions of the functional to ensure gauge-origin independence103,104 since in the presence of a magnetic field the ordinary kinetic density, τ ∝ |∇φ|2, depends the gauge origin (O).105,106 Recent benchmark calculations have shown that the widely used extension proposed by Maximoff and Scuseria leads to unphysical paramagnetic contributions to the NMR shielding constants of atoms.106,107 Such problems do not appear when using the extension proposed by Dobson,103 which is used when studying molecules in explicit magnetic fields at mGGA levels of theory36,38,108,109 and has also been used in some other applications.105,110,111 The unphysical effects are relatively small in calculations of NMR shielding constants using many mGGA functionals,106 whereas gradient-theory calculations of magnetisabilities lead to significant deviations from reference data.86,112 The magnetisabilities are more accurate when performing numerical integration using current-density susceptibilities obtained in magnetic shielding calculations.86,112
2.15 Nuclear shielding tensors
Atomic nuclei with non-zero spin give rise to a magnetic vector potential,  ,
,| | 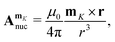 | (60) |
since they possess their own magnetic moment, mK. The combined magnetic vector potential of the external magnetic field and the magnetic moments of the nuclei becomes| |  | (61) |
where μ0 is the vacuum permeability, riO is the distance between the position of electron i, ri, and the gauge origin, the index K spans all nuclei, mK is the magnetic moment of nucleus K, and riK is the distance between electron i and nucleus K.
The external magnetic field interacts with the nuclear magnetic moments that experience a slightly weaker or stronger magnetic field than the external one due to the magnetically induced current density of the surrounding electrons which shields or deshields the nucleus. The local contribution to the effective magnetic field at the nucleus, Bloc, can be expressed using the Biot-Savart law as
| |  | (62) |
The local change in the external field can be combined into the shielding constant,
σK, for nucleus
K,
The isotropic shielding constant is the trace of the shielding tensor, which is a 3 × 3 tensor with elements for each pair of the three Cartesian directions,
α and
β, for each nucleus,
σKαβ. Nuclear shielding constants can be probed experimentally in nuclear magnetic resonance spectroscopy (NMR) by comparing the response of the nuclei of the investigated molecule to the nuclei of a standard. Even though the strength of the magnetically induced current density cannot be measured directly, NMR chemical shifts provide an indirect means of evaluating them experimentally.
The molecular energy associated with the magnetic interaction between a nuclear magnetic moment and the external magnetic field can be expressed via the magnetic vector potential and the current density as
| |  | (64) |
The nuclear magnetic shielding is the mixed second derivative of
EmKB with respect to the
mK and
B,
| |  | (65) |
where
α,
β ∈ {
x,
y,
z}. Alternatively, the shielding tensor can be obtained from the Biot-Savart expression, which is the second part of
eqn (65).
14,16,80,81,85,113,114 The expression for the magnetic shielding tensor elements then becomes
| | 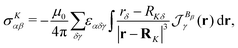 | (66) |
where

is the magnetically-induced current-density susceptibility,
α,
β,
γ,
δ ∈ {
x,
y,
z},
εαδγ is the Levi-Civita symbol, |
r −
RK| is the distance from nucleus
K.
The integrand in eqn (66) is a scalar function known as the nuclear magnetic shielding density80,81,115 whose spatial distribution provides detailed information about the origin of the elements of the nuclear magnetic shielding tensor.114,116–122 Positive and negative contributions to the magnetic shielding density yield the spatial origin of the shielding and deshielding contributions, respectively. They provide a rigorous physical basis for interpreting nuclear magnetic resonance (NMR) chemical shifts. Visualisation of the shielding density, σ(r), showed that it is not the tropicity but the relative direction of the current-density susceptibility with respect to the nuclear magnetic moment vector individually at each point that determines the magnetic shielding or deshielding of the nucleus.114
Information about spatial contributions to the magnetisability and magnetic shielding densities of the individual canonical orbitals can be obtained without any orbital-localisation scheme.16,46,115,117–125 The total magnetisability and nuclear magnetic shielding tensor of a given molecule are independent of the partitioning of the current-density susceptibility into orbital contributions, whereas the individual orbital contributions depend on the chosen orbital representation as also when using local-orbital approaches such as the canonical-molecular-orbital nuclear-chemical-shielding (CMO-NCS) method.126
2.16 Ring-current susceptibilities as an aromaticity index
Ring-shaped molecules sustaining a non-zero net ring current when exposed to an external magnetic field perpendicular to the ring are aromatic or antiaromatic depending on the direction of the ring current. Aromatic molecular rings sustain a net diatropic ring current, that is, a ring current in the classical direction, whereas antiaromatic molecules sustain a net ring current in the non-classical (paratropic) direction.130 Ring currents can be detected indirectly by measuring 1H NMR chemical shifts or the anisotropy of the magnetic susceptibility,7,127–129 which are important experimental indicators for aromaticity. Computationally, the aromatic character can be assessed by calculating the magnetically induced ring-current susceptibility.
The degree of aromaticity and the aromatic pathways can be obtained by integrating the current-density flux through a plane parallel to the magnetic field direction and perpendicular to the molecular ring. One of the vertical edges of the plane lies along the axis of the current-density vortex and crosses a selected chemical bond. The other vertical edge of the plane extends far out where the current density vanishes. Likewise, the horizontal edges of the plane extend until the current density vanishes above and below the molecule, as shown in Fig. 5. The strength of the current-density flux passing through the plane, I, is obtained by numerical integration,41
| |  | (67) |
The tensor elements of the current-density susceptibility,  , in eqn (67) are contracted with the three components of a specified direction of the external magnetic field, Bβ, normalised to one. The vector
, in eqn (67) are contracted with the three components of a specified direction of the external magnetic field, Bβ, normalised to one. The vector ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) is the normal of the integration plane. The SI unit for the current-density susceptibility is nA T−1 m−2. The integration yields the strength of ring-current susceptibilities in nA T−1.
is the normal of the integration plane. The SI unit for the current-density susceptibility is nA T−1 m−2. The integration yields the strength of ring-current susceptibilities in nA T−1.
The exact position where the integration plane crosses the bond is not important because the ring-current susceptibility strength should be the same for all points along the bond due to charge conservation. Small deviations may appear due to the use of finite basis sets, i.e., charge is not fully conserved. Larger uncertainties are introduced for asymmetric molecular rings where the vortex axis of the current-density susceptibility is not always vertical but shifted from the geometrical centre and bent with respect to the normal vector of the ring. Inaccuracies becomes more prominent when passing through atoms as the core orbitals sustain a larger current density.
The sign of the current-density susceptibility passing through the integration plane can be used for assigning its tropicity. By convention, diatropic current density is assigned as positive and paratropic current density gets a negative sign. However, since tropicity is a global property, this assignment must be considered with care, because the simple sign approach cannot distinguish between diatropic current densities and returning paratropic current densities and vice versa.
The assignment of diatropic and paratropic ring-current susceptibilities of polycyclic molecules is difficult, since the flux of the diatropic and returning paratropic ring currents through the plane can be superimposed.132,133 To resolve this problem, one has to identify diatropic and paratropic current-density fluxes and investigate them separately. Even though the tropicity can be unambiguously determined by following the trajectories of the current-density susceptibility, a thorough visual inspection also provides a clear notion about the tropicity of the current density.
Calculations have shown that the strength of the ring-current susceptibility of small aromatic molecules correlates with the stabilisation energy due to electron delocalisation in the conjugated chemical bonds.134–136 The correlation between the strength of the ring-current susceptibility and the aromatic stabilisation energy suggests that the ring-current criterion can be used for determining the degree of aromaticity of molecular rings. There is a similar correlation between the strength of the current-density vortex of hydrogen bonds and the strength of the hydrogen bond.137
Calculations of ring-current susceptibilities support Hückel's π-electron counting rule which states that molecular rings with (4n + 2) π electrons are aromatic and that antiaromatic molecules have 4n π electrons.138–141 The aromaticity concept has been extended to molecules with open shells and excited states,38,42,142–145 as well as to non-planar molecules.44,131,146–166
The net ring-current susceptibility of non-aromatic molecules vanishes, since they sustain diatropic and paratropic ring currents of the same strength. For example, in 1,4-cyclohexadiene, the current density is diatropic outside the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. The paratropic current density inside the ring is of about the same strength. The current density passing the CH moieties is paratropic inside the ring and diatropic on the outside of the carbon atom. Calculation of the diatropic and paratropic contributions to the ring-current susceptibility reveals that there is a current-density vortex at the centre of the C
C bond. The paratropic current density inside the ring is of about the same strength. The current density passing the CH moieties is paratropic inside the ring and diatropic on the outside of the carbon atom. Calculation of the diatropic and paratropic contributions to the ring-current susceptibility reveals that there is a current-density vortex at the centre of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond.167
C bond.167
2.17 Antiaromaticity
Antiaromaticity, defined as the co-existence of a paratropic ring current, symmetry breaking or structural distortion, and a small Fermi gap168,169 can be understood in terms of a general underlying symmetry principle as pointed out by Berger and Viel:170 Molecules belonging to certain point groups with a (near-)degenerate wave function, sustain a magnetically induced paratropic ring current and have the possibility of a (pseudo-)Jahn–Teller distortion. More specifically, let G be a point group among Cn, Cnv, Cnd, Dn, Dnv, Dnd, S2(n−1) with n > 2 but not belonging to the tetrahedral, T*, octahedral, O* and icosahedral, I*, point groups. Any symmetry-induced two-fold degeneracies (in G) are then necessarily connected with the irreducible representation of the angular momentum operator, ![[l with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006c_0302.gif) z, around the main symmetry axis, which is unique for these point groups. If the wave function is degenerate, having irreducible representations of e type (the only occurring type of degeneracy in these point groups), the paramagneticity and the symmetry-induced (first-order) Jahn–Teller distortions Q, occur together, which Berger and Viel called the Symmetry Principle of Antiaromaticity (SPA).170
z, around the main symmetry axis, which is unique for these point groups. If the wave function is degenerate, having irreducible representations of e type (the only occurring type of degeneracy in these point groups), the paramagneticity and the symmetry-induced (first-order) Jahn–Teller distortions Q, occur together, which Berger and Viel called the Symmetry Principle of Antiaromaticity (SPA).170
The SPA can also be applied to closed-shell states that are non-degenerate but nearly two-fold-degenerate. The magnetically induced paratropic ring current then appears together with a symmetry-induced (second-order) pseudo Jahn–Teller distortion, Q. A schematic representation in terms of energy level diagrams for both cases is given in Fig. 6.
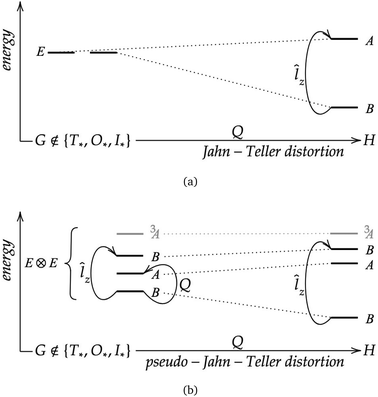 |
| | Fig. 6 Schematic representation of the symmetry principle of antiaromaticity (SPA), (a) a first-order case and (b) a second-order case occurring in closed-shell species. G and H are the symmetry point groups of the molecule, where H is a subgroup of G, and Q a mode of structural distortion or a vibrational normal mode. | |
Such near-degenerate electronic states are typically the ground state of antiaromatic molecules. For example, calculations on cyclobutadiene at the multiconfiguration self-consistent field (MC-SCF) level of theory in the D4h point group171 showed that the electronic 1B1g ground state (S0) and the close lying 1B2g state (S2) are paramagnetically coupled in the presence of a magnetic field. The angular momentum operator parallel to the main symmetry axis belongs to the a2g irreducible representation. Since the product of the irreducible representations of the two states comprises the irreducible representation of the angular momentum operator (b2g ⊗ b1g = a2g), the corresponding transition matrix element of the angular momentum operator does not vanish, implying that a magnetically induced paratropic ring current is expected. A second-order Jahn–Teller effect along a distortional or vibrational normal mode Q of the b1g irreducible representation also leads to a distorted structure belonging to the D2h point group because the b1g mode couples the 1B1g ground state with the close-lying 1A1g state (S1).
The spatial symmetries of the three singlet states (S0, S1, S2) and the first triplet T1 (3A2g) state are related as they span a two-dimensional subspace of the Eg irreducible representation of the D4h point group via A1g ⊕ A2g ⊕ B1g ⊕ B2g = Eg ⊗ Eg. After the structural distortion, the degenerate representation splits but the paramagnetic response remains symmetry allowed as seen by applying branching representation theory.
This example can be verified using a simple model of two electrons in two orbitals based on MC-SCF calculations. However, the principle is independent of any orbital frameworks and can be generalised using the natural-orbital degeneracy of the wave function. The present IUPAC definition of aromaticity and antiaromaticity, going back to Minkin168,169 is in agreement with the SPA, but it is not explicitly taken into account.
Hückel-antiaromatic molecules have often a broken 4- or 8-fold symmetry. The irreducible representations of the ground state and the lowest excited state or even the irreducible representations of the highest-occupied molecular orbital (HOMO) and the lowest-unoccupied molecular orbital (LUMO) are related via a 90° rotation around the highest symmetry axis of the point group. Antiaromatic molecules become stable with respect to a (second-order) pseudo-Jahn–Teller distortion by exerting this distortion and thereby breaking the point-group symmetry of the ring. Too large distortions result in a weaker paramagnetic response, since the rotational relation between the ground and the excited state or in many cases between the HOMO and LUMO is weakened leading to a wider energy gap and a smaller angular momentum transition integral. Consequently, antiaromaticity can be observed only when there is a balance between the two effects (distortion for stability and symmetry relation for paramagneticity). Berger and Viel suggested that antiaromaticity can be defined via the SPA as the presence of such a balance.170
2.18 Closed-shell paramagnetic molecules
The magnetisability can be written as a sum-over-state expression where it is formally divided into gauge-dependent negative diamagnetic (χdia) and paramagnetic (χpara) contributions.16,97,101,172,173 The magnetisability is then given by| |  | (68) |
The first term in eqn (68) is the diamagnetic contribution, which is always negative and depends only on the ground-state wave function. The second term is the paramagnetic contribution, which can be positive or negative depending on the direction of the flux of the magnetically induced current density susceptibility. Paratropic current densities result in positive contributions to the magnetisability. The diamagnetic contribution generally dominates, leading to a negative total magnetisability that scales nearly linearly with the size of the molecule, which is known as Pascal's rule.174 Ring-shaped molecules with a strong paratropic ring current whose radius is large may have a large positive contribution to the magnetisability leading to an overall positive magnetisability and paramagnetism.90–94,96,97,175,176
Calculations on antiaromatic porphyrinoids showed that they are closed-shell paramagnetic molecules when the strength of the paratropic ring-current susceptibility exceeds about −20 nA T−1.97 The same condition holds for molecules consisting of several fused porphyrin rings. The paratropic current density must be large as in strongly antiromatic molecules in order to yield a paramagnetic contribution to the magnetisability that is larger in absolute value than the diamagnetic contribution, which increases nearly linearly with the number of atoms.174 Furthermore, the external magnetic field induces ring currents only when it has a vector component perpendicular to the ring, whereas experimental magnetisabilities, which are obtained as the trace of the magnetisability tensor, have contributions for all directions of the external magnetic field. Alternatively, significant positive paramagnetic contributions to the magnetisability can be obtained for ring-shaped molecules with a large radius such as expanded porphyrins and porphyrin nanowheels, when they sustain a paratropic ring-current susceptibility in the presence of an external magnetic field.96,97
2.19 Twisted molecules
Calculations at the Hückel level of theory suggest that singly Möbius-twisted conjugated molecular rings with 4n π electrons are aromatic closed-shell molecules.146 Singly twisted molecular rings with (4n + 2) π electrons are analogously expected to be antiaromatic. The Hückel Hamiltonian for arbitrary number of half-twists shows that the aromaticity and antiaromaticity rules can be extended to molecules with multiple twists around the molecular ring.177 Details about the aromatic character of twisted molecules can be determined by performing calculations at DFT and ab initio levels of theory.147,148,178
Twisted molecular rings are characterised by their linking number, Lk, consisting of twist, Tw, and writhe, Wr. The twist is a local property of the molecular skeleton that is obtained by integrating all the local rotation angles around the ring. The writhe is the deformation of the molecule as a whole in 3D. It tells how deformation of the ring can reduce the local twisting. Lk and Wr are non-local properties which can be obtained by a double path integration around the ring.148,179–182 For a closed loop, it holds that Lk = Tw + Wr. A singly twisted molecular ring has an Lk value of ±1π, where π is often omitted for simplicity. The trans-C40H40 structures in Fig. 7(a and b) are constructed using Lk = 0 and Tw = −Wr where Tw = 0 and Tw = 1.5, respectively. The Lk value can be positive or negative. Molecular rings with the same absolute value of Lk have the same structure but their chirality differs. Molecular rings with odd Lk values are one-sided, whereas those with even Lk values including zero have two sides. For all rings with even Lk values, the aromatic character follows Hückel's (4n + 2) π-electron counting rule, and with 4n π electrons, the ring is antiaromatic.141,183 The opposite rules hold for all rings with odd Lk values.
The external magnetic field in the calculations of the magnetically induced ring current in the trans-C40H40 structures was set to be perpendicular to the maximum projection of the molecular ring, as the induced flux of JB is expected to be strongest in that orientation. The calculations showed that the largest ring current is obtained for rings with Tw = Lk and Wr = 0,162 even though rings with the smallest Tw value are expected to have the largest π-electron delocalisation.148 Molecular rings with large Wr values have, though, a small projection area perpendicularly to any orientation of the external magnetic field, leading to a weaker ring current. When the magnetic field is perpendicular to the trans-C40H40 ring in Fig. 7(b), it does not sustain any ring current due to the conflicting situation of the ring currents of the two loops, whereas with the magnetic field oriented from above in Fig. 7(b), the elliptical cross section of the ring is much smaller than in Fig. 7(a).162
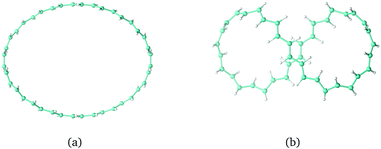 |
| | Fig. 7 The C40H40trans-annulene with Lk = 0 and (a) Tw = −Wr = 0 and (b) Tw = −Wr = 1.5. | |
The aromaticity rules of twisted molecules also hold for more complicated molecules like expanded porphyrinoids.184–190 Singly twisted hexaphyrins were shown to be aromatic, formally with 4n π electrons, and antiaromatic with (4n + 2) π electrons.184,191 Analogously, doubly twisted hexaphyrins obey the ordinary Hückel rule for aromaticity and antiaromaticity.158,184,191–193 The general aromaticity rules for closed-shell molecular rings state that evenly twisted molecular ring are aromatic when they have 4n + 2 π electrons and antiaromatic when the number of π electrons is 4n. For oddly twisted closed-shell molecular rings, the opposite aromaticity rules holds. For open-shell molecules in the triplet state, the aromaticity rules are again reversed.143
2.20 Toroidal molecules
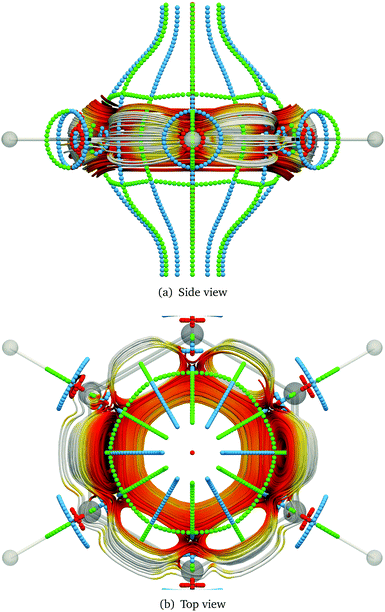
Toroidal molecules are a topological object with one hole. Thus, according to Euler's law they have genus 1.164,194,195 A torus can be described by two radii, the big radius, RT, of the hole in the middle of the torus, and the small radius, rT, of the cross-section of the torus. A toroidal molecule can be constructed formally by twisting a carbon nanotube (CNT), so that its two ends meet,196–198 or the molecular structure can be more sparse.164,199,200 In some cases, the molecular structure of toroidal molecules is helical, leading to chirality, since the helix can be left- or right-handed.
An external magnetic field along the main axis of a chiral toroidal molecule may induce a current density that has a flux component along the ring of the tube (characterised by RT) and another component around the small radius of the tube, leading to an induced magnetic field inside the tube of the torus without a north and a south pole. Due to the helical structure of molecule, the current density around the tube flows in opposite directions for the two enantiomers, leading to opposite directions of the induced magnetic field along the centerline of the tube. The corresponding anapole moment (toroidal dipole moment) also points in opposite directions along the symmetry axis.199–209
The difference in the magnetically induced current densities and the induced magnetic fields can also affect the properties of the two enantiomers in different ways when they are exposed to magnetic fields. For example, in a non-uniform magnetic field, the magnetically induced anapole moment can lead to an energy difference between the two enantiomers.209 For a non-uniform external magnetic field, the magnetic contribution to the molecular energy as a function of the magnetic field strength and the spatial changes in the strength of the magnetic field is
| |  | (69) |
where
B is a uniform contribution to the magnetic field,
C = ∇ ×
BNU is the curl of the non-uniform contribution to the magnetic field,
a is the anapole moment,
χ is the magnetisability (magnetic susceptibility) tensor,
![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif)
is the mixed anapole susceptibility tensor, and
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif)
is the anapole susceptibility tensor.
209 The magnetic dipole moment,
μO, at the gauge origin
O is obtained from the probability current density,
j(r), as
| |  | (70) |
where
rO =
r −
O. The non-uniform magnetic field can be parameterised as
209| |  | (71) |
where
b is a 3 × 3 tensor whose elements contain the magnetic field gradients,
rh =
r −
h is the spatial position relative to the reference point
h. By setting the symmetric part of
b to zero,
Btotal(
r) and the corresponding vector potential can be written as
| | 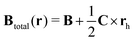 | (72) |
and
| |  | (73) |
The magnetic field given in
eqn (72) is the curl of the vector potential in
eqn (73).
The current density expression for the anapole moment at the reference point h is209
| | 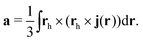 | (74) |
Alternative expressions for calculating the anapole moment can be found in ref.
204 and
206. This is still a rather unexplored research area where the topology of toroidal and chiral molecules might lead to unusual properties and even cause energy differences between enantiomers when the molecules are exposed to non-uniform magnetic fields.
3 Conclusions and outlook
The magnetically induced current density is the fingerprint of the molecular magnetic response. It is as fundamental as the electron density, providing contributions to magnetic properties such as nuclear magnetic resonance (NMR) shieldings, magnetisabilities etc. Numerical integration of magnetic property densities in atomic domains yields the atomic contributions to these properties. Spatial contributions from individual canonical orbitals to magnetic properties can also be obtained by scrutinising orbital magnetic property densities. The approach can be extended to spin-current densities, enabling similar studies of electronic paramagnetic resonance (EPR) spectroscopy parameters and other spin-current-density dependent molecular properties. Spatial contributions to spin–orbit coupling effects in heavy-element compounds can be obtained by performing current-density calculations at relativistic levels of theory. The numerical integration approach also opens the avenue towards calculations of novel magnetic properties that are difficult to compute using analytic gradient theory.
The degree of molecular aromaticity, the ring-current pathways and the extent of electron delocalisation can be determined by integrating the strength of the magnetically induced current-density susceptibility passing selected chemical bonds. Qualitative information about the current-density flux can be obtained using advanced methods of visualisation of current densities and magnetic property densities. Additional information about the current-density flux can be obtained by separating diatropic and paratropic current densities and analysing them separately. The tropicity of the current density in each point in space can be identified only by following the closed loops of the flux, i.e., streamlines.
Calculation and interpretation of magnetically induced current densities is an active research field with lots of new possibilities to obtain information about molecular magnetic properties and to understand the molecular behaviour in the presence of magnetic fields. Qualitative information can be obtained from the topology of the current density. Group-theoretical considerations provide suggestions about the origin of the diamagnetic and the paramagnetic response in symmetric molecules. An exact qualitative and an approximate quantitative relation between the topology of the electron density and the topology of the magnetically induced current density might exist and is being investigated. The symmetry principle of antiaromaticity might be generalised to aromatic compounds and extended to a fully relativistic treatment.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work has been supported by the Academy of Finland through project number 314821, by the Magnus Ehrnrooth Foundation, the Finnish Cultural Foundation, the Swedish Cultural Foundation in Finland and by the DFG (German Research Foundation) in the Priority Program SPP1807 “Control of LD in molecular chemistry”, BE4632/2-2. We acknowledge computational resources from the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533) and the CSC – IT Center for Science, Finland. The authors thank Dr Stanislav Komorovsky (Slovak Academy of Sciences/Bratislava) for discussions.
Notes and references
- E. Schrödinger, Ann. Phys., 1926, 384, 361–376 CrossRef.
- W. Pauli, Z. Phys., 1927, 43, 601–623 CrossRef CAS.
- P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1927, 114, 243–265 CAS.
- J. D. Jackson and L. B. Okun, Rev. Mod. Phys., 2001, 73, 663–680 CrossRef CAS.
- V. Fock, Z. Phys., 1926, 39, 226–232 CrossRef.
-
T. Tao, https://terrytao.wordpress.com/2008/09/27/what-is-a-gauge/, 2008, accessed: 2021-06-19.
- F. London, J. Phys. Rad., 1937, 8, 397–409 CrossRef CAS.
- R. Ditchfield, Mol. Phys., 1974, 27, 789–807 CrossRef CAS.
- D. B. Chesnut and C. K. Foley, Chem. Phys. Lett., 1985, 118, 316–321 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- M. B. Ferraro, T. E. Herr, P. Lazzeretti, M. Malagoli and R. Zanasi, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 6272–6281 CrossRef CAS PubMed.
- M. Pecul and K. Ruud, Adv. Quantum Chem., 2005, 50, 185–212 CrossRef CAS.
- T. A. Keith and R. F. W. Bader, J. Chem. Phys., 1993, 99, 3669–3682 CrossRef CAS.
- P. Lazzeretti, M. Malagoli and R. Zanasi, Chem. Phys. Lett., 1994, 220, 299–304 CrossRef CAS.
- S. Coriani, P. Lazzeretti, M. Malagoli and R. Zanasi, Theor. Chim. Acta, 1994, 89, 181–192 CrossRef CAS.
- P. Lazzeretti, Prog. Nucl. Magn. Reson. Spectrosc., 2000, 36, 1–88 CrossRef CAS.
- E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2001, 105, 9553–9562 CrossRef CAS.
- A. Soncini and P. Fowler, Chem. Phys. Lett., 2004, 396, 174–181 CrossRef CAS.
- E. Schrödinger, Ann. Phys., 1926, 386, 109–139 CrossRef.
- E. Madelung, Z. Phys., 1927, 40, 322–326 CrossRef.
- J. O. Hirschfelder, J. Chem. Phys., 1978, 68, 5151–5162 CrossRef CAS.
-
J. W. S. B. Rayleigh, The theory of sound, Macmillan, 1896, vol. 2, pp. 115–118 Search PubMed.
- E. Schrödinger, Ann. Phys., 1926, 385, 437–490 CrossRef.
-
K. G. Dyall and K. Faegri Jr., Introduction to relativistic quantum chemistry, Oxford University Press, Oxford, 2007 Search PubMed.
- W. Gordon, Z. Phys., 1928, 50, 630–632 CrossRef CAS.
- R. Szmytkowski, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 65, 032112 CrossRef.
- S. Komorovsky, K. Jakubowska, P. Świder, M. Repisky and M. Jaszuński, J. Phys. Chem. A, 2020, 124, 5157–5169 CrossRef CAS PubMed.
-
L. D. Landau and L. M. Lifshitz, Quantum Mechanics Non-Relativistic Theory, Butterworth-Heinemann, 3rd edn, 1981, vol. 3 Search PubMed.
- J. M. Wilkes, Eur. J. Phys., 2020, 41, 035402 CrossRef.
- E. I. Tellgren, A. Laestadius, T. Helgaker, S. Kvaal and A. M. Teale, J. Chem. Phys., 2018, 148, 024101 CrossRef PubMed.
- S. Stopkowicz, J. Gauss, K. K. Lange, E. I. Tellgren and T. Helgaker, J. Chem. Phys., 2015, 143, 074110 CrossRef PubMed.
- T. J. P. Irons, J. Zemen and A. M. Teale, J. Chem. Theory Comput., 2017, 13, 3636–3649 CrossRef CAS PubMed.
- J.-M. Lévy-Leblond, Commun. Math. Phys., 1967, 6, 286–311 CrossRef.
-
W. Greiner, Quantum Mechanics, Springer Berlin Heidelberg, 2001 Search PubMed.
- K. K. Lange, E. I. Tellgren, M. R. Hoffmann and T. Helgaker, Science, 2012, 337, 327–331 CrossRef CAS PubMed.
- S. Reimann, U. Ekström, S. Stopkowicz, A. M. Teale, A. Borgoo and T. Helgaker, Phys. Chem. Chem. Phys., 2015, 17, 18834–18842 RSC.
- R. D. Reynolds and T. Shiozaki, Phys. Chem. Chem. Phys., 2015, 17, 14280–14283 RSC.
- T. J. P. Irons, L. Spence, G. David, B. T. Speake, T. Helgaker and A. M. Teale, J. Phys. Chem. A, 2020, 124, 1321–1333 CrossRef CAS PubMed.
- S. Lehtola, M. Dimitrova and D. Sundholm, Mol. Phys., 2020, 114, e1597989 CrossRef.
- A. M. Kantola, P. Lantto, I. Heinmaa, J. Vaara and J. Jokisaari, Phys. Chem. Chem. Phys., 2020, 22, 8485–8490 RSC.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- S. Taubert, D. Sundholm and J. Jusélius, J. Chem. Phys., 2011, 134, 054123 CrossRef PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678 CAS.
- A. A. Evett, Am. J. Phys., 1966, 34, 503–507 CrossRef.
- E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2001, 105, 9553–9562 CrossRef CAS.
- P. Lazzeretti, J. Chem. Phys., 2020, 153, 214108 CrossRef CAS PubMed.
- C. A. Coulson, Q. J. Math, 1965, 16, 279–287 CrossRef.
- P. Fowler, R. Zanasi, B. Cadioli and E. Steiner, Chem. Phys. Lett., 1996, 251, 132–140 CrossRef CAS.
- G. Monaco, F. F. Summa and R. Zanasi, J. Chem. Inf. Model., 2021, 61, 270–283 CrossRef CAS PubMed.
- R. J. F. Berger, G. Monaco and R. Zanasi, J. Chem. Phys., 2020, 152, 194101 CrossRef CAS PubMed.
- A. Soncini, J. Chem. Theory Comput., 2007, 3, 2243–2257 CrossRef CAS PubMed.
- S. Taubert, V. R. I. Kaila and D. Sundholm, Int. J. Quantum Chem., 2011, 111, 848–857 CrossRef CAS.
- R. J. F. Berger, M. Repisky and S. Komorovsky, Chem. Commun., 2015, 51, 13961–13963 RSC.
- M. Kaupp, O. L. Malkina, V. G. Malkin and P. Pyykkö, Chem. – Eur. J., 1998, 4, 118–126 CrossRef CAS.
- M. Repisky, S. Komorovsky, M. Kadek, L. Konecny, U. Ekström, E. Malkin, M. Kaupp, K. Ruud, O. L. Malkina and V. G. Malkin, J. Chem. Phys., 2020, 152, 184101 CrossRef CAS PubMed.
- J. Vícha, S. Komorovsky, M. Repisky, R. Marek and M. Straka, J. Chem. Theory Comput., 2018, 14, 3025–3039 CrossRef PubMed.
- S. Komorovsky, M. Repisky, K. Ruud, O. L. Malkina and V. G. Malkin, J. Phys. Chem. A, 2013, 117, 14209–14219 CrossRef CAS PubMed.
- S. Komorovsky, M. Repisky, O. L. Malkina and V. G. Malkin, J. Chem. Phys., 2010, 132, 154101 CrossRef PubMed.
- T. Saue, R. Bast, A. S. P. Gomes, H. J. A. Jensen, L. Visscher, I. A. Aucar, R. Di Remigio, K. G. Dyall, E. Eliav, E. Fasshauer, T. Fleig, L. Halbert, E. D. Hedegård, B. Helmich-Paris, M. Iliaš, C. R. Jacob, S. Knecht, J. K. Laerdahl, M. L. Vidal, M. K. Nayak, M. Olejniczak, J. M. H. Olsen, M. Pernpointner, B. Senjean, A. Shee, A. Sunaga and J. N. P. van Stralen, J. Chem. Phys., 2020, 152, 204104 CrossRef CAS PubMed.
- M. Iliaš, T. Saue, T. Enevoldsen and H. J. A. Jensen, J. Chem. Phys., 2009, 131, 124119 CrossRef PubMed.
- R. Bast, J. Jusélius and T. Saue, Chem. Phys., 2009, 356, 187–194 CrossRef CAS.
- D. Sulzer, M. Olejniczak, R. Bast and T. Saue, Phys. Chem. Chem. Phys., 2011, 13, 20682–20689 RSC.
- R. F. W. Bader, S. G. Anderson and A. J. Duke, J. Am. Chem. Soc., 1979, 101, 1389–1395 CrossRef CAS.
- R. F. W. Bader, T. T. Nguyen-Dang and Y. Tal, J. Chem. Phys., 1979, 70, 4316–4329 CrossRef CAS.
- R. F. W. Bader, J. Chem. Phys., 1980, 73, 2871–2883 CrossRef CAS.
-
R. F. W. Bader, Atoms in molecules: a quantum theory, Clarendon Press, Oxford, 1990 Search PubMed.
- P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1931, 133, 60–72 Search PubMed.
- J. O. Hirschfelder, C. J. Goebel and L. W. Bruch, J. Chem. Phys., 1974, 61, 5456–5459 CrossRef CAS.
- J. O. Hirschfelder, A. C. Christoph and W. E. Palke, J. Chem. Phys., 1974, 61, 5435–5455 CrossRef CAS.
- J. O. Hirschfelder, J. Chem. Phys., 1977, 67, 5477–5483 CrossRef CAS.
- K. Collard and G. G. Hall, Int. J. Quantum Chem., 1977, 12, 623–637 CrossRef CAS.
- P. Lazzeretti, Phys. Chem. Chem. Phys., 2016, 18, 11765–11771 RSC.
- C. Runge, Math. Ann., 1895, 46, 167–178 CrossRef.
- W. Kutta, Z. Math. Phys., 1901, 46, 435–453 Search PubMed.
- J. A. N. F. Gomes, J. Chem. Phys., 1983, 78, 4585–4591 CrossRef CAS.
- T. A. Keith and R. F. Bader, Chem. Phys. Lett., 1993, 210, 223–231 CrossRef CAS.
- P. Lazzeretti, Rend. Lincei, Sci. Fis. Nat., 2019, 30, 515–535 CrossRef.
- M. Dimitrova, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2017, 19, 20213–20223 RSC.
- C. J. Jameson and A. D. Buckingham, J. Phys. Chem., 1979, 83, 3366–3371 CrossRef CAS.
- C. J. Jameson and A. D. Buckingham, J. Chem. Phys., 1980, 73, 5684–5692 CrossRef CAS.
- R. W. F. Bader and T. A. Keith, Int. J. Quant. Chem., 1996, 60, 373–379 CrossRef CAS.
- P. W. Fowler, E. Steiner, B. Cadioli and R. Zanasi, J. Phys. Chem. A, 1998, 102, 7297–7302 CrossRef CAS.
- M. Iliaš, H. J. A. Jensen, R. Bast and T. Saue, Mol. Phys., 2013, 111, 1373–1381 CrossRef.
- P. Lazzeretti, J. Chem. Phys., 2018, 148, 134109 CrossRef PubMed.
- S. Lehtola, M. Dimitrova, H. Fliegl and D. Sundholm, J. Chem. Theory Comput., 2021, 17, 1457–1468 CrossRef CAS PubMed.
- K. Ruud, T. Helgaker, K. L. Bak, P. Jørgensen and H. J. A. Jensen, J. Chem. Phys., 1993, 99, 3847–3859 CrossRef CAS.
- J. Olsen and P. Jørgensen, J. Chem. Phys., 1985, 82, 3235–3264 CrossRef CAS.
-
T. Helgaker, in European Summer School in Quantum Chemistry, ed. B. O. Roos and P.-O. Widmark, Lund Universitet, 2000, vol. 2, pp. 431–469 Search PubMed.
- R. M. Stevens and W. N. Lipscomb, J. Chem. Phys., 1965, 42, 3666–3669 CrossRef CAS.
- R. A. Hegstrom and W. N. Lipscomb, Rev. Mod. Phys., 1968, 40, 354–358 CrossRef CAS.
- S. P. A. Sauer, T. Enevoldsen and J. Oddershede, J. Chem. Phys., 1993, 98, 9748–9757 CrossRef CAS.
- K. Ruud, T. Helgaker, K. L. Bak, P. Jørgensen and J. Olsen, Chem. Phys., 1995, 195, 157–169 CrossRef CAS.
- S. Pelloni, P. Lazzeretti and R. Zanasi, J. Phys. Chem. A, 2009, 113, 14465–14479 CrossRef CAS PubMed.
- E. I. Tellgren, T. Helgaker and A. Soncini, Phys. Chem. Chem. Phys., 2009, 11, 5489 RSC.
- M. D. Peeks, T. D. Claridge and H. L. Anderson, Nature, 2017, 541, 200–203 CrossRef CAS PubMed.
- R. R. Valiev, G. V. Baryshnikov, R. T. Nasibullin, D. Sundholm and H. Ågren, J. Phys. Chem. C, 2020, 124, 21027–21035 CrossRef CAS.
- K. Ruud, T. Helgaker, R. Kobayashi, P. Jørgensen, K. L. Bak and H. J. A. Jensen, J. Chem. Phys., 1994, 100, 8178–8185 CrossRef CAS.
- K. Ruud, T. Helgaker and P. Jørgensen, J. Chem. Phys., 1997, 107, 10599–10606 CrossRef CAS.
- S. Loibl and M. Schütz, J. Chem. Phys., 2014, 141, 024108 CrossRef PubMed.
- T. Helgaker, S. Coriani, P. Jørgensen, K. Kristensen, J. Olsen and K. Ruud, Chem. Rev., 2012, 112, 543–631 CrossRef CAS PubMed.
- H. Sambe, J. Chem. Phys., 1973, 59, 555 CrossRef CAS.
- J. F. Dobson, J. Chem. Phys., 1993, 98, 8870–8872 CrossRef CAS.
- S. N. Maximoff and G. E. Scuseria, Chem. Phys. Lett., 2004, 390, 408–412 CrossRef CAS.
- J. E. Bates and F. Furche, J. Chem. Phys., 2012, 137, 164105 CrossRef PubMed.
- C. J. Schattenberg and M. Kaupp, J. Chem. Theory Comput., 2021, 17, 1469–1479 CrossRef CAS PubMed.
- C. Holzer, Y. J. Franzke and M. Kehry, J. Chem. Theory Comput., 2021, 17, 2928–2947 CrossRef CAS PubMed.
- E. Sagvolden, U. Ekström and E. I. Tellgren, Mol. Phys., 2013, 111, 1295–1302 CrossRef CAS.
- S. Sen and E. I. Tellgren, J. Chem. Phys., 2018, 149, 144109 CrossRef PubMed.
- A. D. Becke, Can. J. Chem., 1996, 74, 995–997 CrossRef CAS.
- J. Tao, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 205107 CrossRef.
- S. Lehtola, M. Dimitrova, H. Fliegl and D. Sundholm, J. Chem. Theory Comput., 2021, 17, 4629–4631 CrossRef CAS PubMed.
- R. McWeeny, J. Chem. Sci., 1986, 96, 263–273 CrossRef.
- R. K. Jinger, H. Fliegl, R. Bast, M. Dimitrova, S. Lehtola and D. Sundholm, J. Phys. Chem. A, 2021, 125, 1778–1786 CrossRef CAS PubMed.
- R. M. Stevens, R. M. Pitzer and W. N. Lipscomb, J. Chem. Phys., 1963, 38, 550–560 CrossRef CAS.
- E. Steiner and P. W. Fowler, Phys. Chem. Chem. Phys., 2004, 6, 261–272 RSC.
- S. Pelloni, A. Ligabue and P. Lazzeretti, Org. Lett., 2004, 6, 4451–4454 CrossRef CAS PubMed.
- M. B. Ferraro, P. Lazzeretti, R. G. Viglione and R. Zanasi, Chem. Phys. Lett., 2004, 390, 268–271 CrossRef CAS.
- A. Soncini, P. Fowler, P. Lazzeretti and R. Zanasi, Chem. Phys. Lett., 2005, 401, 164–169 CrossRef CAS.
- M. B. Ferraro, F. Faglioni, A. Ligabue, S. Pelloni and P. Lazzeretti, Magn. Reson. Chem., 2005, 43, 316–320 CrossRef CAS PubMed.
- G. Acke, S. Van Damme, R. W. A. Havenith and P. Bultinck, J. Comput. Chem., 2018, 39, 511–519 CrossRef CAS PubMed.
- G. Acke, S. Van Damme, R. W. A. Havenith and P. Bultinck, Phys. Chem. Chem. Phys., 2019, 21, 3145–3153 RSC.
- P. Lazzeretti, E. Rossi and R. Zanasi, J. Chem. Phys., 1982, 77, 3129–3139 CrossRef CAS.
- P. Lazzeretti, M. Malagoli and R. Zanasi, THEOCHEM, 1991, 234, 127–145 CrossRef.
- F. F. Summa, G. Monaco, L. T. Scott and R. Zanasi, J. Phys. Chem. Lett., 2020, 11, 7489–7494 CrossRef CAS PubMed.
- J. A. Bohmann, F. Weinhold and T. C. Farrar, J. Chem. Phys., 1997, 107, 1173–1184 CrossRef CAS.
- L. Pauling, J. Chem. Phys., 1936, 4, 673–677 CrossRef CAS.
- K. Lonsdale, Proc. R. Soc. London, Ser. A, 1937, 159, 149–161 CAS.
- J. M. Pochan and W. H. Flygare, J. Am. Chem. Soc., 1969, 91, 5928–5929 CrossRef CAS.
- J. A. N. F. Gomes and R. B. Mallion, Chem. Rev., 2001, 101, 1349–1384 CrossRef CAS PubMed.
- M. Rauhalahti, A. Muñoz-Castro and D. Sundholm, Phys. Chem. Chem. Phys., 2016, 18, 18880–18886 RSC.
- D. Sundholm, R. J. F. Berger and H. Fliegl, Phys. Chem. Chem. Phys., 2016, 18, 15934–15942 RSC.
-
M. Dimitrova and D. Sundholm, in Aromaticity: Modern Computational Methods and Applications, ed. I. Fernández López, Elsevier, 2021, ch. 5, pp. 155–194 DOI:10.1016/C2019-0-04193-3, http://arxiv.org/abs/2105.04902.
- C. Kumar, H. Fliegl and D. Sundholm, J. Phys. Chem. A, 2017, 121, 7282–7289 CrossRef CAS PubMed.
- G. Monaco and R. Zanasi, Phys. Chem. Chem. Phys., 2019, 21, 11564–11568 RSC.
- S. G. Patra and N. Mandal, Int. J. Quantum Chem., 2020, 120, e26152 CrossRef CAS.
- H. Fliegl, O. Lehtonen, D. Sundholm and V. R. I. Kaila, Phys. Chem. Chem. Phys., 2011, 13, 434–437 RSC.
- E. Hückel, Z. Phys., 1931, 70, 204–286 CrossRef.
- E. Hückel, Z. Phys., 1932, 76, 628–648 CrossRef.
- R. Breslow, Chem. Eng. News, 1965, 43, 90–100 CrossRef CAS.
- R. Breslow, Acc. Chem. Res., 1973, 6, 393–398 CrossRef CAS.
- N. C. Baird, J. Am. Chem. Soc., 1972, 94, 4941–4948 CrossRef CAS.
- M. Rosenberg, C. Dahlstrand, K. Kilså and H. Ottosson, Chem. Rev., 2014, 114, 5379–5425 CrossRef CAS PubMed.
- R. R. Valiev, A. K. Drozdova, P. V. Petunin, P. S. Postnikov, M. E. Trusova, V. N. Cherepanov and D. Sundholm, New J. Chem., 2018, 42, 19987–19994 RSC.
- V. Vijay, M. Madhu, R. Ramakrishnan, A. Benny and M. Hariharan, Chem. Commun., 2020, 56, 225–228 RSC.
- E. Heilbronner, Tetrahedron Lett., 1964, 5, 1923–1928 CrossRef.
- R. Herges, Chem. Rev., 2006, 106, 4820–4842 CrossRef CAS PubMed.
- S. M. Rappaport and H. S. Rzepa, J. Am. Chem. Soc., 2008, 130, 7613–7619 CrossRef CAS PubMed.
- A. Hirsch, Z. Chen and H. Jiao, Angew. Chem., Int. Ed., 2000, 39, 3915–3917 CrossRef CAS PubMed.
- M. Bühl and A. Hirsch, Chem. Rev., 2001, 101, 1153–1183 CrossRef PubMed.
- R. B. King, Chem. Rev., 2001, 101, 1119–1152 CrossRef CAS PubMed.
- Z. Chen and R. B. King, Chem. Rev., 2005, 105, 3613–3642 CrossRef CAS PubMed.
- M. P. Johansson, J. Jusélius and D. Sundholm, Angew. Chem., Int. Ed., 2005, 44, 1843–1846 CrossRef CAS PubMed.
- S. Taubert, D. Sundholm and F. Pichierri, J. Org. Chem., 2009, 74, 6495–6502 CrossRef CAS PubMed.
- M. P. Johansson, J. Phys. Chem. C, 2009, 113, 524–530 CrossRef CAS.
- S. Taubert, D. Sundholm and F. Pichierri, J. Org. Chem., 2010, 75, 5867–5874 CrossRef CAS PubMed.
- H. Fliegl, D. Sundholm, S. Taubert and F. Pichierri, J. Phys. Chem. A, 2010, 114, 7153–7161 CrossRef CAS PubMed.
- H. Fliegl, D. Sundholm and F. Pichierri, Phys. Chem. Chem. Phys., 2011, 13, 20659–20665 RSC.
- D. Sundholm, Phys. Chem. Chem. Phys., 2013, 15, 9025 RSC.
- R. Nozawa, H. Tanaka, W.-Y. Cha, Y. Hong, I. Hisaki, S. Shimizu, J.-Y. Shin, T. Kowalczyk, S. Irle, D. Kim and H. Shinokubo, Nat. Commun., 2016, 7, 13620 CrossRef CAS PubMed.
- R. R. Valiev, H. Fliegl and D. Sundholm, Phys. Chem. Chem. Phys., 2018, 20, 17705–17713 RSC.
- L. N. Wirz, M. Dimitrova, H. Fliegl and D. Sundholm, J. Phys. Chem. Lett., 2018, 9, 1627–1632 CrossRef CAS PubMed.
- R. Nozawa, J. Kim, J. Oh, A. Lamping, Y. Wang, S. Shimizu, I. Hisaki, T. Kowalczyk, H. Fliegl, D. Kim and H. Shinokubo, Nat. Commun., 2019, 10, 3576 CrossRef PubMed.
- K. Reiter, F. Weigend, L. N. Wirz, M. Dimitrova and D. Sundholm, J. Phys. Chem. C, 2019, 123, 15354–15365 CrossRef CAS.
- Y. Ni, T. Y. Gopalakrishna, H. Phan, T. Kim, T. S. Herng, Y. Han, T. Tao, J. Ding, D. Kim and J. Wu, Nat. Chem., 2020, 12, 242–248 CrossRef CAS PubMed.
- I. Benkyi, O. Staszewska-Krajewska, D. T. Gryko, M. Jaszuński, A. Stanger and D. Sundholm, J. Phys. Chem. A, 2020, 124, 695–703 CrossRef CAS PubMed.
- H. Fliegl, D. Sundholm, S. Taubert, J. Jusélius and W. Klopper, J. Phys. Chem. A, 2009, 113, 8668–8676 CrossRef CAS PubMed.
- IUPAC, Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”). Compiled by, A. D. McNaught and A. Wilkinson, Blackwell Scientific Publications, Oxford, 1997, Online version (2019) created by S. J. Chalk, ISBN 0-9678550-9-8, https://doi.org/10.1351/goldbook.
- V. I. Minkin, Pure Appl. Chem., 2009, 71, 1919–1981 Search PubMed.
- R. J. F. Berger and A. Viel, Z. Naturforsch., 2020, 75, 327–339 CrossRef CAS.
- K. Nakamura, Y. Osamura and S. Iwata, Chem. Phys., 1989, 136, 67–77 CrossRef CAS.
-
J. Van Vleck, The Theory of Electric and Magnetic Susceptibilities, Clarendon Press, 1932 Search PubMed.
- C. T. Corcoran and J. O. Hirschfelder, J. Chem. Phys., 1980, 72, 1524–1528 CrossRef CAS.
- P. Pascal, Ann. Chim. Phys., 1910, 19, 5–70 CAS.
- R. R. Valiev, H. Fliegl and D. Sundholm, Chem. Commun., 2017, 53, 9866–9869 RSC.
- R. R. Valiev, G. V. Baryshnikov and D. Sundholm, Phys. Chem. Chem. Phys., 2018, 20, 30239–30246 RSC.
- P. W. Fowler and H. S. Rzepa, Phys. Chem. Chem. Phys., 2006, 8, 1775–1777 RSC.
- H. S. Rzepa, Chem. Rev., 2005, 105, 3697–3715 CrossRef CAS PubMed.
- G. Călugăreanu, Czech. Math. J., 1961, 11, 588–625 Search PubMed.
- W. F. Pohl, Indiana Univ. Math. J., 1968, 17, 975–985 CrossRef.
- J. H. White, Am. J. Math., 1969, 91, 693–728 CrossRef.
- F. B. Fuller, Proc. Natl. Acad. Sci. U. S. A., 1971, 68, 815–819 CrossRef CAS PubMed.
-
E. Hückel, Grundzüge der Theorie ungesättigter und aromatischer Verbindungen, Verlag Chemie, 1938, pp. 77–85 Search PubMed.
- S. Shimizu, N. Aratani and A. Osuka, Chem. – Eur. J., 2006, 12, 4909–4918 CrossRef CAS PubMed.
- M. Stepień, L. Latos-Grażyński, N. Sprutta, P. Chwalisz and L. Szterenberg, Angew. Chem., Int. Ed., 2007, 46, 7869–7873 CrossRef PubMed.
- S. Saito, J. Y. Shin, J. M. Lim, K. S. Kim, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2008, 47, 9657–9660 CrossRef CAS PubMed.
- H. S. Rzepa, Org. Lett., 2008, 10, 949–952 CrossRef CAS PubMed.
- N. Jux, Angew. Chem., Int. Ed., 2008, 47, 2543–2546 CrossRef CAS PubMed.
- Z. S. Yoon, A. Osuka and D. Kim, Nat. Chem., 2009, 1, 113–122 CrossRef CAS PubMed.
- J. M. Lim, J.-Y. Shin, Y. Tanaka, S. Saito, A. Osuka and D. Kim, J. Am. Chem. Soc., 2010, 132, 3105–3114 CrossRef CAS PubMed.
- Y. Tanaka, S. Saito, S. Mori, N. Aratani, H. Shinokubo, N. Shibata, Y. Higuchi, Z. S. Yoon, K. S. Kim, S. B. Noh, J. K. Park, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2008, 47, 681–684 CrossRef CAS PubMed.
- J. Sankar, S. Mori, S. Saito, H. Rath, M. Suzuki, Y. Inokuma, H. Shinokubo, K. S. Kim, Z. S. Yoon, J. Y. Shin, J. M. Lim, Y. Matsuzaki, O. Matsushita, A. Muranaka, N. Kobayashi, D. Kim and A. Osuka, J. Am. Chem. Soc., 2008, 130, 13568–13579 CrossRef CAS PubMed.
- T. Higashino, J. M. Lim, T. Miura, S. Saito, J.-Y. Shin, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2010, 49, 1–6 CrossRef PubMed.
- H. Terrones and A. L. Mackay, Carbon, 1992, 30, 1251–1260 CrossRef CAS.
- P. Schwerdtfeger, L. N. Wirz and J. Avery, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 96–145 CAS.
- A. Sarkar, H. Kroto and M. Endo, Carbon, 1995, 33, 51–55 CrossRef CAS.
- M. Terrones, W. K. Hsu, J. P. Hare, H. W. Kroto, H. Terrones, D. R. M. Walton, J. Klinowski and A. L. Mackay, Philos. Trans. R. Soc., A, 1996, 354, 2025–2054 CrossRef CAS.
- J. Liu, H. Dai, J. H. Hafner, D. T. Colbert, R. E. Smalley, S. T. Jans and C. Dekker, Nature, 1997, 385, 780–781 CrossRef CAS.
- A. Ceulemans, L. F. Chibotaru and P. W. Fowler, Phys. Rev. Lett., 1998, 80, 1861–1864 CrossRef CAS.
- R. J. F. Berger, Z. Naturforsch. B, 2012, 67, 1127–1131 CrossRef CAS.
- Y. B. Zel'dovich, J. Exp. Theor. Phys. (U.S.S.R.), 1957, 33, 1531–1533 Search PubMed.
- Y. B. Zel'dovich, Sov. Phys. JETP, 1958, 6, 1148–1155 Search PubMed.
- I. B. Khriplovich and M. E. Pospelov, Z. Phys., 1990, 17, 81–84 CAS.
- C. G. Gray, G. Karl and V. A. Novikov, Am. J. Phys., 2010, 78, 936–948 CrossRef.
- E. I. Tellgren and H. Fliegl, J. Chem. Phys., 2013, 139, 164118 CrossRef PubMed.
- S. Pelloni, P. Lazzeretti, G. Monaco and R. Zanasi, Rend. Fis. Acc. Lincei, 2011, 22, 105–112 CrossRef.
- P. F. Provasi, G. I. Pagola, M. B. Ferraro, S. Pelloni and P. Lazzeretti, J. Phys. Chem. A, 2014, 118, 6333–6342 CrossRef CAS PubMed.
- V. Savinov, N. Papasimakis, D. P. Tsai and N. I. Zheludev, Commun. Phys., 2019, 2, 69 CrossRef.
- S. Sen and E. I. Tellgren, J. Chem. Theory Comput., 2021, 17, 1480–1496 CrossRef CAS PubMed.
Footnotes |
| † This velocity density should not be confused with the local velocity (see Section 2.13), nor with the classical or quasi-classical velocity density v defined viavρ = j with the electron density ρ. |
| ‡ Dyall and Fægri started the derivation from the classical Hamiltonian by replacing
and obtained the Pauli–Schrödinger Hamiltonian after quantisation. The same expression up to a factor of 3I2 is obtained by substituting ![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1de.gif) → σ(σ· → σ(σ·![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1de.gif) ). I2 is the two-dimensional identity matrix.24 ). I2 is the two-dimensional identity matrix.24 |
§ The original work51 contains a flaw in the derivation of the functional form of JBdia(r), which led to a formulation equivalent to
which is only a necessary but not a sufficient condition for the correct functional form (eqn (46)). This error has consequences for one of the main results of the study. The correct conclusion is that there is no inherent connection between the topologies of the unperturbed electron density and any divergence-free diamagnetic current contribution, arising from the zero-divergence constraint. An erratum is under preparation. |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Maria
Dimitrova
*a,
Maria
Dimitrova
 ab and
Raphael J. F.
Berger
ab and
Raphael J. F.
Berger
 b
b
![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1de.gif) , is introduced, which for an electron takes the form
, is introduced, which for an electron takes the form![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e1de.gif) = −iħ∇ + eA,
= −iħ∇ + eA,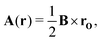
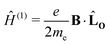
![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) O, around O is
O, around O is![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) O = rO × p = −iħ(rO × ∇),
O = rO × p = −iħ(rO × ∇),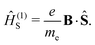

 in eqn (3).
in eqn (3).
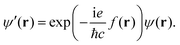


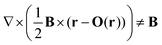
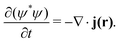
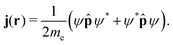
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r),
(r),![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1de.gif) ,
, ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r)}+|Ψ〉.
(r)}+|Ψ〉.![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r) = δ(r − r′) with the Dirac delta function δ.
(r) = δ(r − r′) with the Dirac delta function δ.
![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) O, as the perturbation,
O, as the perturbation,

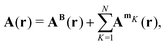
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) φ,
φ,![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) is the energy eigenvalue. The current density is then given by
is the energy eigenvalue. The current density is then given by
 is the spin operator. An additional term accounting for the spin contribution to the exchange correlation potential appears at the Dirac–Kohn–Sham (DKS) level of theory.27
is the spin operator. An additional term accounting for the spin contribution to the exchange correlation potential appears at the Dirac–Kohn–Sham (DKS) level of theory.27
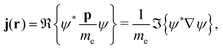
![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) given by eqn (1), which is called minimal coupling. Substituting p →
given by eqn (1), which is called minimal coupling. Substituting p → ![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1de.gif) = p + A yields
= p + A yields
![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1de.gif) with σ(σ·
with σ(σ·![[small pi, Greek, circumflex]](https://www.rsc.org/images/entities/char_e1de.gif) ) in eqn (29), where σ is a three-dimensional vector of the Pauli spin matrices.‡24 Replacing the one-component wave function, ψ, with the two-component Pauli spinors, φ, yields
) in eqn (29), where σ is a three-dimensional vector of the Pauli spin matrices.‡24 Replacing the one-component wave function, ψ, with the two-component Pauli spinors, φ, yields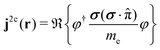



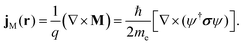
 , retaining its interpretation as the magnetisation density that arises from the spatial distribution of the spin which is the magnetic moment. The spin-current density appears then as an additional term to the total current density.29
, retaining its interpretation as the magnetisation density that arises from the spatial distribution of the spin which is the magnetic moment. The spin-current density appears then as an additional term to the total current density.29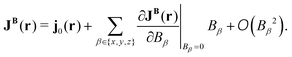
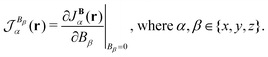
 . Gauge-origin independence and a fast basis-set convergence are achieved by employing gauge-including atomic orbitals defined in eqn (14).
. Gauge-origin independence and a fast basis-set convergence are achieved by employing gauge-including atomic orbitals defined in eqn (14).



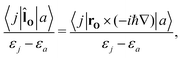
![[l with combining circumflex]](https://www.rsc.org/images/entities/b_char_006c_0302.gif) O is the one-particle angular momentum operator with respect to the origin, O. The diamagnetic response is determined by translational occupied-virtual transition matrix elements,
O is the one-particle angular momentum operator with respect to the origin, O. The diamagnetic response is determined by translational occupied-virtual transition matrix elements,


 is defined in eqn (21).
is defined in eqn (21).











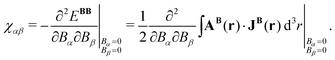



 ,
,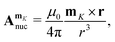




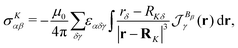
 is the magnetically-induced current-density susceptibility, α, β, γ, δ ∈ {x, y, z}, εαδγ is the Levi-Civita symbol, |r − RK| is the distance from nucleus K.
is the magnetically-induced current-density susceptibility, α, β, γ, δ ∈ {x, y, z}, εαδγ is the Levi-Civita symbol, |r − RK| is the distance from nucleus K.

 , in eqn (67) are contracted with the three components of a specified direction of the external magnetic field, Bβ, normalised to one. The vector
, in eqn (67) are contracted with the three components of a specified direction of the external magnetic field, Bβ, normalised to one. The vector ![[n with combining circumflex]](https://www.rsc.org/images/entities/b_char_006e_0302.gif) is the normal of the integration plane. The SI unit for the current-density susceptibility is nA T−1 m−2. The integration yields the strength of ring-current susceptibilities in nA T−1.
is the normal of the integration plane. The SI unit for the current-density susceptibility is nA T−1 m−2. The integration yields the strength of ring-current susceptibilities in nA T−1.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. The paratropic current density inside the ring is of about the same strength. The current density passing the CH moieties is paratropic inside the ring and diatropic on the outside of the carbon atom. Calculation of the diatropic and paratropic contributions to the ring-current susceptibility reveals that there is a current-density vortex at the centre of the C
C bond. The paratropic current density inside the ring is of about the same strength. The current density passing the CH moieties is paratropic inside the ring and diatropic on the outside of the carbon atom. Calculation of the diatropic and paratropic contributions to the ring-current susceptibility reveals that there is a current-density vortex at the centre of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond.167
C bond.167![[l with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006c_0302.gif) z, around the main symmetry axis, which is unique for these point groups. If the wave function is degenerate, having irreducible representations of e type (the only occurring type of degeneracy in these point groups), the paramagneticity and the symmetry-induced (first-order) Jahn–Teller distortions Q, occur together, which Berger and Viel called the Symmetry Principle of Antiaromaticity (SPA).170
z, around the main symmetry axis, which is unique for these point groups. If the wave function is degenerate, having irreducible representations of e type (the only occurring type of degeneracy in these point groups), the paramagneticity and the symmetry-induced (first-order) Jahn–Teller distortions Q, occur together, which Berger and Viel called the Symmetry Principle of Antiaromaticity (SPA).170


![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) is the mixed anapole susceptibility tensor, and
is the mixed anapole susceptibility tensor, and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) is the anapole susceptibility tensor.209 The magnetic dipole moment, μO, at the gauge origin O is obtained from the probability current density, j(r), as
is the anapole susceptibility tensor.209 The magnetic dipole moment, μO, at the gauge origin O is obtained from the probability current density, j(r), as