BiMnPO₅ with ferromagnetic Mn²⁺–(μ-O)₂–Mn²⁺ units: a model for magnetic exchange in edge-linked Mn²⁺O₆ octahedra

Abstract

Magnetic interactions within Mn–(μ-O)₂–Mn pairs are crucial to the function of some essential enzymes and catalysts, but their nature is unclear. Neutron diffraction reveals that similar units in BiMnPO₅ show ferromagnetic coupling which has been rationalized by density functional theory modelling and calculations of magnetic exchange energies. The results are important to many solid state and biological systems.

---

Magnetic Mn–O–Mn interactions play an important role in solid state, organometallic and biological chemistry. Perovskite related LaMnO₃ derivatives show a giant magneto-resistance (GMR) effect and AMnO₃ (A = Bi, Y) show multiferroic properties, which are fundamentally important for the new generation of integrated electronics.¹ The interaction is also crucial to the production of oxygen by the manganese containing enzyme photosystem II (PSII), hence the beginning of life on earth.² PSII has therefore initiated much research on itself³ and the synthesis of organometallic biomimetic catalysts with multinuclear Mn–O–Mn cores as the active sites for splitting H₂O.⁴

The properties of manganese oxides and complexes, especially magnetic, electric or catalytic, are related to local structures, oxidation states and spin states of the ions. For example, the functional Mn₄CaO₅ core for photosynthesis in PSII involves spin-dependent states and it is postulated that separate high- and low-spin states control the formation of the active high-spin state.⁵ Such spin states are controlled by direct Mn–Mn interactions or superexchange via bridging oxygen ligands. The nature of exchange interactions of 3d metal ions can often be explained by the Goodenough–Kanamori–Anderson (GKA) rules;⁶e.g. for Mn(II) (d⁵), the direct exchange involves overlap of half-filled d orbitals and is therefore always antiferromagnetic (AFM), whereas the exchange through the bridging O is strongly dependent on the Mn–O–Mn bridging angle θ. The simplest superexchange is ferromagnetic (FM) and occurs from the accidental orthogonality of 2p orbitals on the O bridges which is a maximum at θ = 90°. As a result, the overall exchange depends on local structure, and predictions are hindered by the existence of more complex exchange mechanisms.

Some enzyme research suffers significantly from the complexity of Mn–O–Mn magnetic interactions. Simple Mn–(μ-O)₂–Mn pairs are found in enzymes (e.g. arginase, catalase, and Ribonucleotide Reductase (RNR)), which are found in most living organisms including humans.⁷ Various studies on these and their biomimetic counterparts have greatly enhanced our understanding of their structure and function.⁸ Magnetically, binuclear Mn(II, II) pairs generally show AFM coupling to give an S = 0 unit, but some synthetic analogues with various ligands show FM behaviour.⁹ Complementary experimental and theoretical studies have probed the exchange mechanisms within the pairs but no reliable roadmap exists to allow reliable predictions.^9h

Our studies of materials containing MnO chains with FM interactions drew our attention to the current lack of appropriate signposts to the resultant magnetic order. Although Mn²⁺ is not widespread in solid oxides, we became aware that BiMnPO₅ contains Mn₂²⁺O₁₀ pairs formed by edge-shared MnO₆ octahedra,¹⁰ which therefore closely resemble the units in the biological systems. Given that the Mn–O–Mn angle (100.9°) is sufficiently greater than 90° to weaken the FM superexchange, time-of-flight (TOF) neutron powder diffraction (NPD) surprisingly revealed that the Mn ions within each Mn₂O₁₀ pair have FM coupling. Here, the NPD results are reported alongside density functional theory (DFT) calculations (with a hybrid functional) for a model molecule Mn₂O₂(H₂O)₈; importantly, we propose a phenomenological mechanism to explain this observation and suggest that it could enhance understanding of Mn–Mn interactions in other oxides and also biological systems.

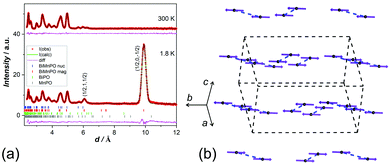
NPD data from a sample of BiMnPO₅ (details in ESI†) at 300 K were used for Rietveld refinement¹¹ and indicated impurities of ∼18 wt% of Bi_2.76O₂[PO_3.64][PO_3.5]¹² and ∼8 wt% of β′-Mn₃(PO₄)₂.¹³ § Because of the magnetic properties of the latter, magnetic characterization of the primary phase required the unique phase-specific abilities of neutron diffraction. All three phases were therefore included in the refinements, which included data from three discrete detector banks with average 2θ positions of 145°, 35° and 14°. Table 1 lists the refined parameters and Fig. 1(a) shows the structure containing Mn₂O₁₀ pairs linked by PO₄ groups; each pair is formed from two identical MnO₆ octahedra, edge-linked by O4 (Fig. 1(b)). The mid-point between the two Mn²⁺ ions in each pair is an inversion centre so the ions are linked by symmetric short/long bonds of a = 2.192 Å, b = 2.263 Å, with angles of θ₁ = θ₂ = 100.9°; the Mn–Mn separation is 3.435 Å. The symmetry and structural parameters are important for the computational considerations (vide infra).

Table 1 Structural parameters of BiMnPO₅ from NPD data at ambient temperature

Atoms	x/a	y/b	z/c	U iso/Å^2
Space group: P21/n, a = 7.43229 (8), b = 11.3559 (1), c = 5.35785 (5) Å, β = 109.189(1)° with χ^2 = 0.93.
Bi	0.18688(6)	0.09468(4)	0.11839(8)	0.00686(9)
Mn	0.809(2)	0.09219(9)	0.3685(2)	0.0049(2)
P	0.0168(1)	0.35033(6)	0.2125(1)	0.0058(1)
O1	0.16341(9)	0.42087(4)	0.4332(1)	0.0093(1)
O2	0.9869(1)	0.22847(6)	0.3163(1)	0.0131(2)
O3	0.83079(9)	0.41908(7)	0.1083(1)	0.0119(1)
O4	0.9855(1)	0.02294(4)	0.7530(1)	0.0072(1)
O5	0.0947(1)	0.32697(6)	0.9830(2)	0.0130(2)

---

Fig. 1 (a) The structure of BiMnPO₅ and (b) structural details for the Mn₂O₁₀ units. Spheres represent Bi (green), Mn (black), P (orange), O (red); Mn–Mn interactions are blue dotted lines.

Fig. 2(a) shows a very strong (1/2, 0, −1/2) magnetic peak at 1.8 K, which critically shows that the high-spin Mn²⁺ ions have FM coupling within each pair; AFM coupling between the pairs gives an enlarged unit cell. The magnetic moments, 4.46(2) μ_B at 1.8 K, are aligned with the unique b-axis; the order is shown in Fig. 2(b) with further information provided in Table 2 and ESI,† especially Fig. S1 and S2 (ESI†). The magnetic unit cell (symmetry P_a2₁/c) is derived from the standard setting (P2₁/c) of P2₁/n that is reported for BiMnPO₅.¹⁰ As previously indicated, most Mn–(μ-O)₂–Mn interactions are AFM, but NPD definitively shows that in BiMnPO₅ they are FM. There are no reports of clear FM coupling in similar pairs in the solid state, although MnV₂O₆ has infinite FM chains of edge-linked MnO₆ octahedra.¹⁴ In order to rationalize the magnetic order, we have modelled the Mn₂O₁₀ pair in BiMnPO₅ with the hypothetical molecule Mn₂O₂(H₂O)₈, shown in Fig. 3(a), using CRYSTAL 17 code with a hybrid functional (details in ESI†).¹⁵ Although a similar approach has been employed previously,¹⁶ in this case the geometry was constrained: all Mn–O bonds were held equal at approximately the average length in BiMnPO₅, and for this ideal model only the Mn–Mn separation was varied (and hence the correlated Mn–O4–Mn angle in Fig. 1(b)) to examine the effect of direct magnetic exchange on the final ordered state.

Fig. 2 (a) Fitted NPD patterns from BiMnPO₅ collected at 300 K and 1.8 K in the 2θ = 14° detector bank. The 300 K data are offset by ∼40 units for clarity; (b) magnetic order with reference to the nuclear unit cell (P2₁/n) showing moments aligned along ±[010] with FM coupling within the Mn–Mn pairs; FM layers perpendicular to [10−1] are AFM to adjacent layers and enlarge the unit cell.

Table 2 Structural parameters of BiMnPO₅ from NPD data at 1.8 K

Atoms	x/a	y/b	z/c	U iso/Å^2
Space group: P21/n, a = 7.4456(1), b = 11.3408(2), c = 5.3532(1) Å, β = 109.250(1)° with χ^2 = 1.19; wRp = 0.0160 (35° detector), 0.0062 (145° detector), 0.0206 (14° detector). Magnetic model: magnetic space group Pa21/c with transformation matrix to give a′ = 10.5060(2), b′ = 11.3408(2), c′ = 7.6034(1) Å, β = 109.588(1)°. Moment along [010] with μ = 4.46(2) μB on Mn at (0.9707, 0.9088, 0.1605) and μ = −4.46(2) μB on Mn at (0.4707, 0.9088, 0.6605).
Bi	0.18567(1)	0.09554(7)	0.1197(1)	0.0021(2)
Mn	0.8102(2)	0.0912(2)	0.3688(3)	0.00032(3)
P	0.0189(2)	0.3496(1)	0.2103(2)	0.0030(2)
O1	0.1633(1)	0.4220(1)	0.4330(2)	0.0034(2)
O2	0.9887(2)	0.22688(8)	0.3131(2)	0.0053(2)
O3	0.8305(1)	0.4179(1)	0.1075(2)	0.0036(2)
O4	0.9850(2)	0.02305(9)	0.7524(2)	0.0031(2)
O5	0.0938(2)	0.32842(9)	0.9778(2)	0.0054(2)

---

Fig. 3 (a) The Mn₂O₂(H₂O)₈ molecule (Mn black, O red, H blue) used to model the exchange energies for Mn₂O₁₀ pairs in BiMnPO₅; (b) the calculated overall exchange, J, against Mn–O–Mn angle and Mn–Mn distance.

The calculations revealed that the Mn–Mn exchange changes from AFM at smaller Mn–Mn separations to FM with a maximum FM exchange J at 3.4 Å (102°), and a trend to return to AFM at Mn–Mn >3.7 Å (115°), Fig. 3(b). More importantly, it predicts that at the experimental Mn–Mn separation of 3.435 Å in BiMnPO₅, the Mn₂O₁₀ pair is almost optimal for FM coupling. In addition, the crossover from FM to AFM exchange at low separation occurs at 3.19 Å (93°). This result is highly significant since GKA rules cannot indicate the dominant exchange in this region because the conflicting AFM (direct exchange) and FM (superexchange) interactions are both optimized. Our calculations are supported by data for organic complexes as well as solid state materials, which suggest that more than 75% of Mn–(μ-O)₂–Mn units are AFM. Indeed, our results are consistent with MnV₂O₆¹⁴ and MnSb₂O₄,¹⁷ which both contain chains of edge-linked MnO₆ octahedra where the intra-chain magnetic exchange is dominant. Whereas MnV₂O₆ (Mn–Mn = 3.53 Å, Mn–O–Mn = 105°) is FM, MnSb₂O₄ (Mn–Mn = 3.00 Å, Mn–O–Mn = 89°) is AFM. It is also interesting to note that the FM exchange in the binuclear Mn²⁺–(μ-N)₂–Mn²⁺ units in [Mn(terpy)(N₃)₂]¹⁸ with Mn–Mn 3.53 Å and Mn–N–Mn = 104.6° is also consistent with the results for the O-bridged units.

In order to rationalize these calculations, we have quantified the significant exchange pathways including the empirical model proposed by Kahn for the case of strict orthogonality.¹⁹ These interactions are given in Fig. S3 (ESI†). In the special case of Mn–(μ-O)₂–Mn with 90° Mn–O–Mn links, strict orthogonality can be fulfilled by appropriate orbital ordering (Fig. S3, ESI,† case III), as observed in O₃Cu–(μ-O)₂–VO₃,²⁰ inducing FM coupling. Following the proposal by Khomskii et al.,²¹ we considered the main contributions for the cases shown in Fig. S3 (ESI†) using typical parameters (all/eV):

U_dd = 4.5, U_pp = 2, Δ = 3, t_pdσ = 0.9, t_pdπ = 0.48 and t_dd = 0.33, J^d_H = 0.9, J^p_H = 1.2 (1)

The three major contributions are from the direct exchange (d_xy−xy, case I), Mn–O–Mn 180° superexchange (d_x²–y²–O2p–d_x²−y², case II) and Kahn's strict orthogonality (d_x²−y²–O2p–d_xy, case III) which have components J_dd = −24.2 meV, J^θ_S = −25.3 meV and J^σπ_K = 7.2 meV, respectively. Cases IV, V, and VI have only minor contributions which tend to cancel each other out. If we further assume rigid Mn–O bonds and consider the relations and J^θ_S = J⁹⁰_S sin² θ + J¹⁸⁰_S cos² θ (D is the Mn–Mn pair distance) previously proposed,²² the total magnetic exchange, as a function of bond angle θ is:

For these parameters, the overall empirical exchange interaction as a function of Mn–Mn distance (and the dependent Mn–O–Mn angle) is shown in Fig. 3(b); the general trend agrees not only with the DFT calculations but also, and more importantly, with the experimental observations.

The empirical model predicts that Mn–(μ-O)₂–Mn pairs with bond angles close to 90° will be subject to strongly AFM exchange rather than FM, which can be attributed to rapidly increasing d⁵–d⁵ direct AFM interactions caused by a shortening of the Mn–Mn distance with reduction in bond angle. At higher bond angles, the expansion in Mn–Mn separation reduces the direct orbital overlap (∝ D⁻⁵) and enhances the significance of the FM interactions via the strict orthogonality case III. At much higher bond angles, the 180° AFM superexchange (case II) eventually dominates and Fig. 3(b) shows that FM behaviour is predicted when:

3.287 Å (θ = 97.3°) < D < 3.645 Å (θ = 112.7°) (3)

An incomplete survey of literature reporting magnetic characterization of Mn–(μ-O)₂–Mn pairs shows that the Mn–Mn coupling constants (J^θ) generally comply with the above predictions. In recent compilations of dinuclear complexes,^9h,23 rare examples of FM pairs are reported, but no satisfactory explanations are provided. Since previous theoretical calculations for different models have always predicted AFM order, the present study provides an impetus to find new structures with FM pairs and hence develop our understanding of their functionality in biological materials. An extension of our theoretical investigation on the Mn₂O₂(H₂O)₈ model with asymmetric bonding geometries at the Mn₂O₂ core shows that Kahn's case III mechanism for FM exchange can tolerate different Mn–O bond lengths for a given bridging O, as long as a center of symmetry exists between the Mn ions (as is the case for BiMnPO₅). To a lesser extent, different bond angles (θ₁ and θ₂ in Fig. 1(b)), are also acceptable but this necessarily destroys the inversion center. α-MnMoO₄ contains unusual FM clusters of four edge-linked Mn²⁺O₆ octahedra, but the symmetry does not allow direct comparison with the results presented here and another mechanism may also be involved.²⁴ These structural modifications can explain the examples of AFM coupling which violate the general indications of eqn (3). An interesting test for our model is KMnBP₂O₇(OH)₂ which has centrosymmetric Mn–(μ-O)₂–Mn units with Mn–Mn = 3.34 Å and Mn–O–Mn = 98.9°.²⁵ The low temperature magnetic order is AFM but becomes FM in a field of 7 T. It is suggested that the individual Mn₂ pairs are internally AFM but our modelling suggests the alternative description in which FM Mn₂ units experience weak external exchange which allows full FM behaviour at 7 T. Low temperature NPD data would be needed to confirm the magnetic structure.

To conclude, the most significant aspect of the structure of BiMnPO₅ is the presence of Mn–(μ-O)₂–Mn pairs, which also occur in various enzymes and biomimetic catalysts. It is unusual that the magnetic interaction within the dimanganese(II, II) pair is ferromagnetic, whereas the pairs are antiferromagnetic coupled through Mn–O–P–O–Mn type super–super-exchange. DFT calculations for a model Mn₂O₂(H₂O)₈ molecule suggest that Mn–(μ-O)₂–Mn pairs can be FM only within a certain range of bond lengths and angles. This treatment, however, applies only to highly symmetric units and AFM is dominant where distortions occur. Nevertheless, calculations of the energies of the various exchange pathways provides a rationalization of the observed magnetic behaviour and can be extended to biological and biomimetic systems.

The present work was supported by the National Natural Science Foundation of China (No. 51772304) and the UK EPSRC (GR/R45871/01). The authors thank the Science and Technology Facilities Council (STFC) for the provision of neutron facilities. The experimental work and manuscript writing was conducted by all authors and the interpretation of results by R. K. L. and C. G.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. (a) S. Jin, T. H. Tiefel, M. McCormack, R. A. Fastnacht, R. Ramesh and L. H. Chen, Science, 1994, 264, 413–415; (b) W. Eerenstein, N. D. Mathur and J. F. Scott, Nature, 2006, 442, 759–765.
2. (a) M. Suga, F. Akita, K. Hirata, G. Ueno, H. Murakami, Y. Nakajima, T. Shimizu, K. Yamashita, M. Yamamoto, H. Ago and J.-R. Shen, Nature, 2015, 517, 99–103; (b) G. C. Dismukes, V. V. Klimov, S. V. Baranov, Yu. N Kozlov, J. DasGupta and A. Tyryshkin, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 2170–2175; (c) U. F. Lingappa, D. R. Monteverde, J. S. Magyar, J. Selverstone, V. Woodward and W. Fischer, Free Radical Biol. Med., 2019, 140, 113–125.
3. (a) S. Petrie, R. Terrett, R. Stranger and R. J. Pace, ChemPhysChem, 2000, 21, 785–801; (b) I. L. McConnell, V. M. Grigoryants, C. P. Scholes, W. K. Myers, P.-Y. Chen, J. W. Whittaker and G. W. Brudvig, J. Am. Chem. Soc., 2012, 134, 1504–1512.
4. (a) W. Ruttinger and G. C. Dismukes, Chem. Rev., 1997, 97, 1–24; (b) M. Wiechen, H.-M. Berends and P. Kurz, Dalton Trans., 2012, 41, 21–31; (c) S. Ye, C. M. Ding, M. Y. Liu, A. Q. Wang, Q. G. Huang and C. Li, Adv. Mater., 2019, 31, 1902069; (d) M. M. Najafpour, I. Zaharieva, Z. Zand, S. M. Hosseini, M. Kouzmanova, M. Hołynska, I. Tranca, A. W. Larkum, J.-R. Shen and S. I. Allakhverdiev, Coord. Chem. Rev., 2020, 409, 213183.
5. V. Krewald, M. Retegan, F. Neese, W. Lubitz, D. A. Pantazis and N. Cox, Inorg. Chem., 2016, 55, 488–501.
6. (a) J. B. Goodenough, Phys. Rev., 1955, 100, 564–573; (b) J. B. Goodenough, Magnetism and the Chemical Bond, John Wiley & Sons, New York, 1963; (c) J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98; (d) P. W. Anderson, Phys. Rev., 1959, 115, 2–13.
7. (a) L. D. Costanzo, G. Sabio, A. Mora, P. C. Rodriguez, A. C. Ochoa, F. Centeno and D. W. Christianson, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13058–13063; (b) S. V. Antonyuk, V. R. Melik-Adamyan, A. N. Popov, V. S. Lamzin, P. D. Hempstead, P. M. Harrison, P. J. Artymyuk and V. V. Barynin, Crystallogr. Rep., 2000, 45, 105–116; (c) A. K. Boal, J. A. Cotruvo Jr. and J. Stubbe, Science, 2010, 329, 1526–1530.
8. G. C. Dismukes, Chem. Rev., 1996, 96, 2909–2926.
9. (a) S. L. Lambert and D. N. Hendrickson, Inorg. Chem., 1979, 18, 2683–2686; (b) M. Wesolek, D. Meyer, J. A. Osborn, A. D. Cian, J. Fischer, A. Derory, P. Legoll and M. Drillon, Angew. Chem., Int. Ed. Engl., 1994, 33, 1592–1594; (c) S. V. Khangulov, P. J. Pessiki, V. V. Barynin, D. E. Ash and G. C. Dismukes, Biochemistry, 1995, 34, 2015–2025; (d) A. Gelasco, M. L. Kirk, J. W. Kampf and V. L. Pecoraro, Inorg. Chem., 1997, 36, 1829–1837; (e) S. Koizumi, M. Nihei and H. Oshio, Chem. Lett., 2004, 33, 896–897; (f) Y. Z. Tang, X. S. Wang, T. Zhou and R. G. Xiong, Cryst. Growth Des., 2006, 6, 11–13; (g) D. K. Cao, J. Xiao, J. W. Tong, Y. Z. Li and L. M. Zheng, Inorg. Chem., 2007, 46, 428–436; (h) E. Ruiz, Comprehensive Inorganic Chemistry II, Elsevier Ltd, 2013, pp. 501–546.
10. (a) X. Xun, S. Uma and A. W. Sleight, J. Alloys Compd., 2002, 338, 51–53; (b) S. Chowki, R. Kumar, N. Mohapatra and A. V. Mahajan, J. Phys.: Condens. Matter, 2016, 28, 486002.
11. (a) A. C. Larson and R. B. Von Dreele, General Structure Analysis System (GSAS), Los Alamos National Laboratory Report LAUR, 2004, pp. 86–748; (b) B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213.
12. O. A. Gurbanova, E. L. Belokoneva, O. V. Dimitrova and V. S. Kuazhkovskaya, Russ. J. Inorg. Chem., 2002, 47, 954–958.
13. B. El-Bali, A. Boukhari, R. Glaum, M. Gerk and K. Maass, Z. Anorg. Allg. Chem., 2000, 626, 2557–2562.
14. S. A. Kimber and J. P. Attfield, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 064406.
15. (a) R. Dovesi, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. Bush, P. D’Arco, Y. Noel, M. Rerat, P. Carbonniere, M. Causa, S. Salustro, V. Lacivita, B. Kirtman, A. M. Ferrari, F. S. Gentile, J. Baima, M. Ferrero, R. Demichelis and M. D. La Pierre, J. Chem. Phys., 2020, 152, 204111; (b) M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451–459; (c) K. Yamaguchi, H. Fukui and T. Fueno, Chem. Lett., 1986, 625–628.
16. (a) M. Mitani, Y. Wakamatsu, T. Katsurada and Y. Yoshioka, J. Phys. Chem. A, 2006, 110, 13895–13914; (b) S. B. Liu, L. Perera and L. G. Pedersen, Mol. Phys., 2007, 105, 2893–2898.
17. J. Cumby, B. P. de Laune and C. Greaves, J. Mater. Chem. C, 2016, 4, 201–208.
18. E. Ruiz, J. Cano, S. Alvarez and P. Almeny, J. Am. Chem. Soc., 1998, 120, 11122–11129.
19. O. Kahn, Angew. Chem., Int. Ed. Engl., 1985, 24, 834–850.
20. O. Kahn, J. Galy, Y. Journaux, J. Jaud and I. Morgenstern-Badarau, J. Am. Chem. Soc., 1982, 104, 2165–2176.
21. S. V. Streltsov and D. I. Khomskii, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 064405.
22. K. Motida and S. Miyahara, J. Phys. Soc. Jpn., 1970, 28, 1188–1196.
23. V. Gomez, M. Corbella, M. Font-Bardia and T. Calvet, Dalton Trans., 2010, 39, 11664–11674.
24. J. P. Attfield, J. Phys.: Condens. Matter, 1990, 2, 6999–7007.
25. G. Wang, M. Valldor, C. Lorbeer and A.-V. Mudring, Eur. J. Inorg. Chem., 2012, 3032–3038.

---

Footnotes

† Electronic supplementary information (ESI) available: Synthetic details; methods (NPD and computation); Fig. S1 (NPD plots at 300 K and 2 K), Fig. S2 (details of magnetic structure), Fig. S3 (magnetic exchange pathways). See DOI: 10.1039/d1cc02595c

‡ The manuscript was written through contributions of all authors.

§ Normalized NPD datasets are available from: Greaves, Colin; Li, Rukang (2020), “BiMnPO₅”, Mendeley Data, VI, DOI: 10.17632/93m5634wv9.1. For raw data, use DOI: 10.5286/ISIS.E.RB15094-3 for 1.8 K; replace 3 with 6 for ambient data.

---