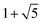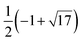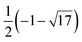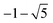Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exactly solvable 1D model explains the low-energy vibrational level structure of protonated methane†
Jonathan I.
Rawlinson
 *a,
Csaba
Fábri
*a,
Csaba
Fábri
 bc and
Attila G.
Császár
bc and
Attila G.
Császár
 bc
bc
aSchool of Mathematics, University of Bristol, Bristol, UK. E-mail: jonathanianrawlinson@gmail.com
bLaboratory of Molecular Structure and Dynamics, Institute of Chemistry, ELTE Eötvös Loránd University, Pázmány Péter sétány 1/A, Budapest H-1117, Hungary
cMTA-ELTE Complex Chemical Systems Research Group, P.O. Box 32, Budapest 112 H-1518, Hungary
First published on 12th April 2021
Abstract
A new one-dimensional model is proposed for the low-energy vibrational quantum dynamics of CH5+ based on the motion of an effective particle confined to a 60-vertex graph Γ60 with a single edge length parameter. Within this model, the quantum states of CH5+ are obtained in analytic form and are related to combinatorial properties of Γ60. The bipartite structure of Γ60 gives a simple explanation for curious symmetries observed in numerically exact variational calculations on CH5+.
Protonated methane, CH5+, also called methonium, is considered to be the prototype of pentacoordinated nonclassical carbonium ions.1–3 The curious carbonium cations yielded an extremely rich chemistry and a Nobel prize to their discoverer, George Olah.4 Nevertheless, these are not the only sources of fame for carbonium ions and in particular for CH5+. Over the last two decades,5 the internal motion of CH5+ has been posing a formidable challenge to high-resolution spectroscopists.5–15 The most outstanding issue is that the observed spectra of CH5+ remain exceptionally complex even when they are observed at temperatures of a few K,9,13 due to the quasistructural nature16 of this molecular ion.
As to the utilization of quantum chemistry to solve the experimental puzzle, through huge numerical efforts accurate rovibrational energy levels and eigenstates have been made available for CH5+ in recent years.7,12,14 These studies have revealed close-lying clusters in the rovibrational energy levels, with fascinating symmetry characteristics. These features have defied explanation by conventional means, motivating the development of novel models for CH5+. The most important models put forward so far are as follows: (a) particle-on-a-sphere (POS),17–23 (b) five-dimensional (5D) rotor (superrotor),24–26 and (c) quantum graph.15,27 So far, the quantum-graph model seems to have resulted in the most satisfactory explanation of the low-energy quantum dynamics of CH5+, including both vibrations15 and rotations.27
Quantum graphs have a long history in chemistry and physics, dating back to Linus Pauling's description of electrons in organic molecules in the 1930s.28 They have only recently been introduced to the study of nuclear dynamics, where they have proved useful in high-resolution spectroscopy15,27 and also in explaining α-cluster dynamics in nuclear physics.29,30 Quantum graphs31 are metric graphs, that is each of their edges possesses a length. In the context of rovibrational dynamics of molecules, each vertex of the graph represents a version32 of an equilibrium structure. Depending on the nuclear permutation-inversion symmetry32 of the molecule of a given composition, even if the molecule has a single minimum on a given potential energy surface it may possess a large number of versions. The vertices defined by the versions are connected by edges which represent collective internal motions converting different versions into each other. Once a quantum graph is set up, one constructs the one-dimensional (1D) Schrödinger equation for an effective particle confined to the graph and solves it to determine the energy levels and eigenstates (ESI†). In this way, the complex multidimensional rovibrational quantum dynamics of a polyatomic molecule is mapped onto the effective motion of a 1D particle confined to a much simpler space.
In the case of CH5+, the equilibrium structure, the only one found on its ground electronic state, is composed of a H2 unit sitting on top of a CH3+ tripod, an arrangement with Cs point-group symmetry. The five protons can be rearranged in 5! = 120 ways, generating 120 symmetry-equivalent versions. These versions become the 120 vertices of a quantum graph Γ120.15 There are two types of motion interconverting the 120 versions, equivalent to scrambling the H atoms of CH5+: the internal rotation of the H2 unit by 60° (both clockwise and counterclockwise), and the flip motion that exchanges a pair of protons between the H2 and CH3+ units. The barriers to these motions on the potential energy hypersurface of CH5+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33 are known to be relatively low. It is plausible that the low-energy dynamics is dominated by motion along these particular paths, so that motions other than the internal rotation and flip motions can be disregarded. Thus, one can take these motions to correspond to the edges of Γ120. As one flip edge and two internal rotation edges are connected to each vertex of Γ120, each vertex has a degree of three (Γ120 is a 3-regular graph). Due to the nature of the underlying internal motions, the 120 internal rotation and 60 flip edges are assigned effective lengths Lrot and Lflip, respectively.
33 are known to be relatively low. It is plausible that the low-energy dynamics is dominated by motion along these particular paths, so that motions other than the internal rotation and flip motions can be disregarded. Thus, one can take these motions to correspond to the edges of Γ120. As one flip edge and two internal rotation edges are connected to each vertex of Γ120, each vertex has a degree of three (Γ120 is a 3-regular graph). Due to the nature of the underlying internal motions, the 120 internal rotation and 60 flip edges are assigned effective lengths Lrot and Lflip, respectively.
As shown before,15,27 the quantum graph Γ120 reproduces the low-energy rovibrational energy levels of CH5+, as well as of CD5+, remarkably well when optimized values are used for Lfip and Lrot (ESI†). For instance, the Γ120 model perfectly reproduces the curious block structure (states occuring in groups of 15 and 30, see Table 1) of the vibrational eigenstates of CH5+, first noted in a variational study of Wang and Carrington12 and later confirmed in ref. 14. As seen in Table 1, rovibrational eigenstates of CH5+ are labelled by irreducible representations (irreps) of the molecular symmetry (MS) group32S5* = S5 × {E,E*}, generated by S5 permutations of the five protons together with spatial inversion E* (E denotes the identity operation).
| Block 1 | Block 2 |
|---|---|
| 0–60 cm−1 (15,15) | 110–200 cm−1 (15,15) |
| A 1 + ⊕ G1+ ⊕ H1+ ⊕ H2+⊕ | G 1 + ⊕ H1+ ⊕ I+ ⊕ |
| G 2 − ⊕ H2− ⊕ I− | A 2 − ⊕ G2− ⊕ H1− ⊕ H2− |
Beyond the existence of blocks, in Table 1 one can notice other clear symmetry relations for the first 60 quantum states. A comparison of the group-theoretic relation
| (A1+ ⊕ G1+ ⊕ H1+ ⊕ H2+) ⊗ A2− ≃ A2− ⊕ G2− ⊕ H2− ⊕ H1− | (1) |
| (G2− ⊕ H2− ⊕ I−) ⊗ A2− ≃ G1+ ⊕ H1+ ⊕ I+, | (2) |
Let us start our journey toward the simplest model with the quantum graph Γ120. We recall two important characteristics of our original study.15 First, we neglect the potential energy along the edges of Γ120, since the barriers to the internal rotation and flip motions are small (about 30 cm−1 and 300 cm−1, respectively33). Second, we fix the effective edge lengths Lflip and Lrot. In ref. 15 this was done by an optimization procedure to give the best fit to either 7D or 12D reference data. In both cases the optimized Lflip was much smaller than the optimized Lrot, with the ratio Lflip/Lrot = 1.0/61.2 in the 7D case.
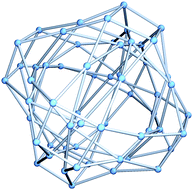
Our new model is based on the following idea: the ratio Lflip/Lrot is so small that it is tempting to imagine shrinking the flip edges to zero length, identifying the two vertices at the endpoints of each flip edge to give a single vertex. Setting Lflip = 0 has a negligible effect on the accuracy of the fit, at least at low energies. At the same time, this approximation gives a huge simplification: the number of vertices is halved and we get a new quantum graph, Γ60, with only the internal rotation edges remaining. It is reasonable to identify each new vertex with the midpoint of the (now contracted) flip edge, which is a C2v-symmetric transition state, as illustrated in Fig. 1. Γ60 represents 60 symmetry-equivalent versions of this configuration. We propose that the most important characteristics of the low-energy vibrational quantum states of CH5+ can be understood in terms of a 1D, potential-free motion between these versions corresponding to the vertices of the quantum graph Γ60. Note that each vertex is connected to precisely four other vertices, as shown also in Fig. 1, giving rise to the 4-regular (quartic) quantum graph Γ60, illustrated in Fig. 2.
There is an alternative way of rationalizing the above contraction procedure. At the energies we are interested in, one can show that the Γ120 wave functions for the energy eigenstates are approximately constant along the flip edges. In this limit, the boundary conditions of Γ120 become equivalent to those of Γ60 (ESI†). Either way, Γ60 only retains edges corresponding to the internal rotation. Our simplified model therefore has the feature of explaining the low-energy dynamics solely in terms of the internal rotation motion without the flip motion, with the constant wave function argument allowing for backstage full exchange of the protons. This model is thus set up in clear violation of the claim of the authors of ref. 34, namely that “the combination of the two [internal motions] enables large-amplitude motion and thus full scrambling … whereas partial scrambling leads to the well-known small-amplitude motion only”.
We now seek the quantum states corresponding to motion on the Γ60 graph. The eigenenergies are found by solving the time-independent Schrödinger equation for a freeeffective particle moving along the edges, with the so-called Neumann boundary conditions31 imposed on the eigenstates. These conditions are that the wave function should be continuous everywhere, with zero total momentum flux out of each vertex. As we have already pointed out, Γ60 is a 4-regular graph with all edges having a common length l = Lrot. Perhaps surprisingly, these properties imply that the structure of the quantum energy levels can be determined entirely from combinatorial properties of the graph.
More precisely, given a wave function ψ defined on the graph Γ60 and obeying the time-independent Schrödinger equation along each edge,
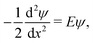 | (3) |
 | (4) |
 is an eigenvalue of the adjacency matrix A for the graph Γ60, with v in the corresponding eigenspace. A is simply a matrix whose elements indicate whether given pairs of vertices are connected by an edge or not:
is an eigenvalue of the adjacency matrix A for the graph Γ60, with v in the corresponding eigenspace. A is simply a matrix whose elements indicate whether given pairs of vertices are connected by an edge or not: | (5) |
Eqn (4) therefore relates the quantum spectrum (the eigenvalues of the Hamiltonian) to the so-called combinatorial spectrum (the eigenvalues of the adjacency matrix). The combinatorial spectrum is a concept already utilized in molecular spectroscopy,36 and only depends on the connectivity of the graph as encoded in A.
To find the combinatorial spectrum of Γ60, we look for roots of the characteristic polynomial χA(λ) = det(λI − A) associated with the adjacency matrix A. An explicit expression for A is easily derived by considering paths of the form illustrated in Fig. 1. In the end, we obtain
| χA(λ) = (λ4 − 9λ2 + 16)5(λ4 − 12λ2 + 16)4(λ2 − 1)11(λ2 − 16), | (6) |
We pause here to note the striking similarity between Tables 1 and 2. First, note that the combinatorial spectrum splits into positive λ and negative λ, with each corresponding to a total eigenspace dimension of 30. Moreover, the eigenspaces associated with positive λ transform in precisely the same irreps as Block 1 of Table 1, while those associated with negative λ transform precisely like Block 2. Thus, purely combinatorial properties of the quantum graph Γ60 have captured the block structure of the lowest vibrational states of CH5+. Even more interestingly, we have an explanation for the curious relationship between Block 1 states and Block 2 states: this corresponds to a λ → −λ symmetry of the combinatorial spectrum (see Table 2), under which the S5* irreps are related by multiplication with A2−. The symmetry of the combinatorial spectrum under λ → −λ is a simple consequence35 of the fact that the quantum graph Γ60 is bipartite: the set of vertices V can be divided into two disjoint and independent sets A and B such that every edge connects a vertex in A to one in B. The sets A and B are related by odd permutations of the protons (ESI†).
Eqn (4) relates the combinatorial spectrum to the quantum spectrum, as illustrated in Fig. 3. We can see the consequences of the λ → −λ symmetry for the quantum energy levels: each state in Block 1 comes with a partner in Block 2, with their corresponding values of  being related by reflection in the line
being related by reflection in the line 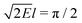 . In particular, the dimensionless ratios
. In particular, the dimensionless ratios
 | (7) |
 | ||
| Fig. 3 Illustration of the block structure and the symmetry properties of the spectrum of the quantum graph Γ60. Black dots indicate energies of the quantum states. | ||
In this paper we have drastically simplified the quantum graph model of the low-energy rovibrational quantum dynamics of CH5+ by reducing the original 120-vertex quantum graph to a 60-vertex graph, Γ60. Γ60 was constructed by shrinking the edges corresponding to the flip internal motion that exchanges a pair of protons between the H2 and CH3+ units of the equilibrium structure of CH5+. Thus, at first sight we neglect one of the two important large-amplitude internal motions characterizing the exchange dynamics (scrambling) of the H atoms of CH5+. This allows us to obtain the quantum states of Γ60 in analytic form, with the structure of the energy levels depending only on combinatorial properties. The eigenvalues of this simple 1D, potential-free model are in excellent agreement with the energies of the first 60 vibrational states determined by sophisticated variational nuclear-motion computations utilizing a potential energy hypersurface. Furthermore, the bipartite structure of Γ60 gives a natural explanation for symmetries in the vibrational energy-level structure of CH5+, again in perfect agreement with the results of variational nuclear-dynamics computations. Note that neither the variational computations7,12,14 nor the quantum-graph models15,27 yield only the Pauli-allowed states of CH5+ (states with A2±, G2±, and H2± symmetry have non-zero spin-statistical weights), so our discussion focused on all possible states; the non-existing states can be filtered out a posteriori.
The work of JIR was supported by the EPSRC grant CHAMPS EP/P021123/1. The work performed in Budapest received support from NKFIH (grant no. K119658) and from the ELTE Institutional Excellence Program (TKP2020-IKA-05) financed by the Hungarian Ministry of Human Capacities.
Conflicts of interest
There are no conflicts to declare.Notes and references
- G. A. Olah and R. H. Schlosberg, J. Am. Chem. Soc., 1968, 90, 2726–2727 CrossRef CAS.
- G. A. Olah, G. Klopman and R. H. Schlosberg, J. Am. Chem. Soc., 1969, 91, 3261–3268 CrossRef CAS.
- G. A. Olah, Carbocations and Electrophilic Reactions, VCH-Wiley Publishers, Weinheim, 1974 Search PubMed.
- G. A. Olah, My Search for Carbocations and Their Role in Chemistry, 1994, pp. 149–176 Search PubMed.
- E. T. White, J. Tang and T. Oka, Science, 1999, 284, 135–137 CrossRef CAS PubMed.
- O. Asvany, P. Padma Kumar, B. Redlich, I. Hegemann, S. Schlemmer and D. Marx, Science, 2005, 309, 1219–1222 CrossRef CAS PubMed.
- X.-G. Wang and T. Carrington Jr., J. Chem. Phys., 2008, 129, 234102 CrossRef PubMed.
- S. D. Ivanov, O. Asvany, A. Witt, E. Hugo, G. Mathias, B. Redlich, D. Marx and S. Schlemmer, Nat. Chem., 2010, 2, 298–302 CrossRef CAS PubMed.
- O. Asvany, K. M. T. Yamada, S. Brünken, A. Potapov and S. Schlemmer, Science, 2015, 347, 1346–1349 CrossRef CAS PubMed.
- R. Wodraszka and U. Manthe, J. Phys. Chem. Lett., 2015, 6, 4229–4232 CrossRef CAS PubMed.
- H. Schmiedt, S. Schlemmer and P. Jensen, J. Chem. Phys., 2015, 143, 154302 CrossRef PubMed.
- X.-G. Wang and T. Carrington, J. Chem. Phys., 2016, 144, 204304 CrossRef PubMed.
- S. Brackertz, S. Schlemmer and O. Asvany, J. Mol. Spectrosc., 2017, 342, 73–82 CrossRef CAS.
- C. Fábri, M. Quack and A. G. Császár, J. Chem. Phys., 2017, 147, 134101 CrossRef PubMed.
- C. Fábri and A. G. Császár, Phys. Chem. Chem. Phys., 2018, 20, 16913–16917 RSC.
- A. G. Császár, C. Fábri and J. Sarka, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1432 Search PubMed.
- G. A. Natanson, G. S. Ezra, G. Delgado-Barrio and R. S. Berry, J. Chem. Phys., 1984, 81, 3400–3406 CrossRef CAS.
- G. A. Natanson, G. S. Ezra, G. Delgado-Barrio and R. S. Berry, J. Chem. Phys., 1986, 84, 2035–2044 CrossRef CAS.
- D. M. Leitner, G. A. Natanson, R. Berry, P. Villarreal and G. Delgado-Barrio, Comput. Phys. Commun., 1988, 51, 207–216 CrossRef CAS.
- J. E. Hunter, D. M. Leitner, G. A. Natanson and R. Berry, Chem. Phys. Lett., 1988, 144, 145–148 CrossRef CAS.
- M. P. Deskevich and D. J. Nesbitt, J. Chem. Phys., 2005, 123, 084304 CrossRef PubMed.
- M. P. Deskevich, A. B. McCoy, J. M. Hutson and D. J. Nesbitt, J. Chem. Phys., 2008, 128, 094306 CrossRef PubMed.
- F. Uhl, L. Walewski, H. Forbert and D. Marx, J. Chem. Phys., 2014, 141, 104110 CrossRef PubMed.
- H. Schmiedt, P. Jensen and S. Schlemmer, Phys. Rev. Lett., 2016, 117, 223002 CrossRef PubMed.
- H. Schmiedt, P. Jensen and S. Schlemmer, Chem. Phys. Lett., 2017, 672, 34–46 CrossRef CAS.
- H. Schmiedt, P. Jensen and S. Schlemmer, J. Mol. Spectrosc., 2017, 342, 132–137 CrossRef CAS.
- J. I. Rawlinson, J. Chem. Phys., 2019, 151, 164303 CrossRef CAS PubMed.
- L. Pauling, J. Chem. Phys., 1936, 4, 673–677 CrossRef CAS.
- J. I. Rawlinson, Nucl. Phys. A, 2018, 975, 122–135 CrossRef CAS.
- J. I. Rawlinson, PhD thesis, University of Cambridge, 2020.
- G. Berkolaiko and P. Kuchment, Introduction to Quantum Graphs, American Mathematical Society, 2013, vol. 186 Search PubMed.
- P. R. Bunker and P. Jensen, Molecular symmetry and spectroscopy, NRC Research Press, Ottawa, 2006 Search PubMed.
- P. R. Schreiner, S.-J. Kim, H. F. Schaefer III and P. von Ragué Schleyer, J. Chem. Phys., 1993, 99, 3716–3720 CrossRef CAS.
- A. Witt, S. D. Ivanov and D. Marx, Phys. Rev. Lett., 2013, 110, 083003 CrossRef PubMed.
- N. Biggs, Algebraic Graph Theory, Cambridge University Press, 1993 Search PubMed.
- P. Árendás, T. Furtenbacher and A. G. Császár, J. Math. Chem., 2016, 54, 806–822 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Mathematical derivations and proofs relevant for the paper, technical details and vibrational energy levels of CH5+. See DOI: 10.1039/d1cc01214b |
| This journal is © The Royal Society of Chemistry 2021 |