Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Exploring AdaBoost and Random Forests machine learning approaches for infrared pathology on unbalanced data sets†‡
Jiayi
Tang
 ,
Alex
Henderson
,
Alex
Henderson
 * and
Peter
Gardner
* and
Peter
Gardner

Department of Chemical Engineering and Analytical Science, Manchester Institute of Biotechnology, The University of Manchester, 131 Princess Street, Manchester, M1 7DN, UK. E-mail: alex.henderson@manchester.ac.uk
First published on 18th May 2021
Abstract
The use of infrared spectroscopy to augment decision-making in histopathology is a promising direction for the diagnosis of many disease types. Hyperspectral images of healthy and diseased tissue, generated by infrared spectroscopy, are used to build chemometric models that can provide objective metrics of disease state. It is important to build robust and stable models to provide confidence to the end user. The data used to develop such models can have a variety of characteristics which can pose problems to many model-building approaches. Here we have compared the performance of two machine learning algorithms – AdaBoost and Random Forests – on a variety of non-uniform data sets. Using samples of breast cancer tissue, we devised a range of training data capable of describing the problem space. Models were constructed from these training sets and their characteristics compared. In terms of separating infrared spectra of cancerous epithelium tissue from normal-associated tissue on the tissue microarray, both AdaBoost and Random Forests algorithms were shown to give excellent classification performance (over 95% accuracy) in this study. AdaBoost models were more robust when datasets with large imbalance were provided. The outcomes of this work are a measure of classification accuracy as a function of training data available, and a clear recommendation for choice of machine learning approach.
Introduction
Infrared pathology
In recent years there has been increasing interest in augmenting conventional pathology, utilising light microscopy of stained tissue, with automated, label-free methodologies. At the forefront of these methods is infrared spectroscopy.Research has shown that infrared spectroscopy, hyperspectral imaging, coupled with machine learning, can be used to distinguish cancerous and normal samples and, in some cases, the type of cancer and histological grade can also be distinguished. This methodology has been applied to a wide range of tissue types including prostate,1–4 lung,5,6 colon,7–10 bladder11 and breast.12–19
These hyperspectral images can be composed of many thousands of pixels, each of which contains a full infrared spectrum of the sample under observation. Given that most human tissue is composed of essentially the same chemical species, advanced chemometric methods are required to classify the composite tissue types present; in particular, those that exhibit diseased characteristics. When attempting to develop a chemometric model, care must be taken to ensure its stability under different performance conditions. Typically, exemplar tissue samples will be examined by a trained pathologist and analysed using infrared spectroscopy. The pathologist will indicate regions of interest, while the spectroscopist identifies these regions in the data, before submitting them to the model-building process. The tissue under examination can have varying degrees of cell type, both in terms of naturally occurring diversity and those cells modified by the disease under investigation. Therefore, the data collected can have a variety of composition which presents an additional problem in the model-building process. In this paper we explore the influence of this composition using two machine learning algorithms.
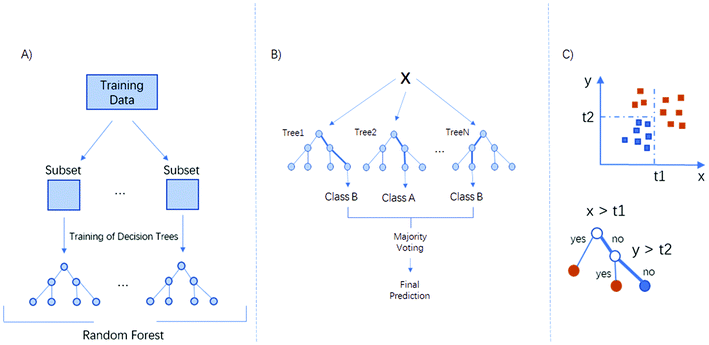
Machine learning
Machine learning (ML) is a branch of artificial intelligence. It allows a computer to learn from data and to improve decision making with experience. ML refines a model that can be used to predict outcomes of inquiry, based on previous learning. There are two types of machine learning: supervised and unsupervised. For supervised learning, a labelled set of input–output pairs is provided to the algorithm which then learns a model which can reproduce this mapping.20 Unsupervised learning can be described as knowledge discovery. Here, the objective is to find hidden patterns in data.20 There are no defined answers, as there is no specific existing pattern to find.20,21In the field of spectroscopy, a number of studies have combined FTIR hyperspectral imaging data with the Random Forests™ classification algorithm. Leslie et al. applied it on lymph node histopathology in 2015,22 Mittal et al. used Random Forests on a four-class classification for digital breast histopathology17 and simultaneous cancer and tumour microenvironment detection.23 Pilling et al. also showed that for biopsy tissue mounted on glass substrates, Random Forests could give classification accuracies over 95%.4
Adaboost is considered more effective at handling an unbalanced dataset than Random Forests, since the minority class, which is much more likely to be misclassified, can be given higher weighting in subsequent iterations, and can improve the performance of weak learners regardless of whether training data is balanced or unbalanced.30
Unbalanced data
In the real world, it is highly unlikely that there will be the same number of spectra of each class in any training data set, without specific pre-processing to that effect. Biased results can be produced if directly applying classification to these data.31,32 Studies, using a number of different approaches, have been conducted in various fields, to reduce the influence of unbalanced data sets in model predictions.30,33–35In terms of clinically related studies, data encountered for classification is often unbalanced. In the case of cancer biopsy samples, the class of interest, possibly dysplastic or cancerous epithelial cells, may be small compared with the total number of cells within the tissue sample which may consist of predominately stroma. Therefore, application of hyperspectral image analysis, where the pixels are arranged in a grid pattern, will result in the number of spectra from each cell type (class) being unequal.36
If a classification model is established to separate epithelium cells from stroma, a very unbalanced dataset will be obtained, which is inherently biased. When the number of samples in one class (majority) largely exceeds the number of samples in the other (minority), data mining algorithms tend to favour the majority class. The minority class, which is frequently the class of interest (positive class), can have poor classification accuracy due to the biased model. Therefore, techniques are required to ensure that a model can efficiently identify minority classes.
Different methods, for example weighting, can be employed to alleviate bias. Here, we explore re-sampling methods.37 There are two commonly used re-sampling methods: under-sampling and over-sampling. The class distribution can be balanced by either duplicating selected members of the minority class (over-sampling), or removing selected examples from the majority class (under-sampling).36 Under-sampling and over-sampling can be performed in different ways.30 Random under-sampling balances two classes by randomly removing data from the majority class to match the number of samples in the minority class. Random over-sampling replicates samples in the minority class until the number of samples matches that of the majority class.
In this work we compare the classification accuracy of models developed using two machine learning techniques—AdaBoost and Random Forests—to data from infrared spectroscopic analysis of human breast tissue biopsies, where that data has unbalanced class structure, and also when under- and over-sampling strategies have been employed to mitigate this.
Methodology
The sample
A formalin fixed, paraffin embedded, breast tissue microarray (TMA) – ID BR20832 – was used for this study (US Biomax, Rockville, MD, USA). The human tissue was collected under approved HIPPA protocols and approved for commercial product development. The TMA contained 15 pathologically indicated non-malignant cores and 192 malignant cores: in total 207 breast tissue biopsy cores, each 1 mm in diameter. Each core was biopsied from a different patient. A 5 μm thick section was floated onto a standard histology glass slide and stained using haematoxylin and eosin (H&E). An adjacent section of the same thickness was floated onto a BaF2 slide for infrared spectroscopic analysis. This IR sample was not dewaxed, reducing the likelihood of inducing chemical changes during deparaffinization, and decreasing spectral Mie scattering due to the closer refractive index values between paraffin and sample.38Fifty cores were selected from the TMA, which included forty cores with stage II breast cancer and ten normal-associated breast tissue cores: histological normal tissue adjacent to the tumor (NAT) from non-malignant cores.39
Data acquisition
FTIR scans were obtained in transmission mode using an Agilent Cary 670-IR spectrometer fitted with a liquid nitrogen-cooled 128 × 128 focal plane array (FPA), mercury cadmium telluride (MCT) detector. An Agilent Cary 620-IR imaging microscope, with a ×15 Cassegrain objective, was coupled to the spectrometer. The instrument produced a resultant field-of-view of 704 × 704 μm, with a corresponding pixel size of 5.5 μm.The FTIR instrument is fitted with a sealable enclosure, surrounding the sample stage and optics, through which dry air is continuously delivered. The relative humidity within this chamber was reduced to zero percent prior to any data acquisition. This has the benefit of removing any water vapour that might be otherwise present in the optical path and subsequently recorded as part of the sample's spectrum. Before imaging, background scans were taken from a region, selected to be clean and paraffin free, in the form of a single FPA tile with 128 co-added scans at a spectral resolution of 5 cm−1. For tissue analysis, 96 co-added sample scans were measured. Chemical images of each core were acquired as a 2 × 2 mosaic; each mosaic taking approximately 15 minutes to collect. Interferograms were processed using Happ–Genzel apodisation with two levels of zero filling and a spectral range of 900 to 3800 cm−1.
Data pre-processing
All data were pre-processed using MATLAB® R2017a (The MathWorks Inc., Natick, MA, USA). Infrared spectra for each biopsy core were extracted from the mosaic as a 256 × 256 × 1478 hypercube, where each hypercube consisted of 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 spectra, each with 1478 data points.
536 spectra, each with 1478 data points.
FTIR chemical images of each of the breast tissue cores were generated and compared to the H&E stained sections. Fig. 3 shows examples of both H&E stained and infrared hyperspectral images of a cancerous core, and a core containing normal associated tissue. Examples of the manually annotated regions, from which spectra were extracted, are indicated on the infrared images. Regions of epithelium were identified according to World Health Organisation (WHO) documentation: WHO Classification of Tumours in the Breast.40
Principal components-based noise reduction was used to improve the signal-to-noise ratio of raw spectra from each annotated area; the first 80 principal components being retained. Spectra were quality tested to remove data obtained from areas with little or no tissue, based on the intensity of the amide I band; spectra having absorbance between 0.1 and 2 being retained. Spectral regions describing the absorption bands of paraffin wax were removed with spectral ranges 1000 to 1319 cm−1, 1481 to 1769 cm−1, and 2986 to 3569 cm−1 being retained for further processing. Each spectrum was then converted to its first derivative using the Savitzky–Golay algorithm, based on a fourth order polynomial, with a window size of 19 data points. Further spectral ranges were then deleted from the derivatized data to remove the end regions, which can be influenced by the derivatization process, to leave a data set comprising the spectral ranges: 1019–1300, 1500–1750 and 3005–3550 cm−1. No spectral normalisation was performed since all tissue samples were part of the same tissue microarray, and thus have the same thickness.
Training and test sets
The data was separated into two collections: training data and independent test data. The training data contained 32 cancerous and 8 normal-associated cores, 40 in total, while the independent test data contained 8 cancerous and 2 normal-associated cores, 10 in total. Each core originated from a different patient. To eliminate the effect of different size of annotation areas contributing differently to each other in the model, the same number of pixels (327) were randomly selected from each core to match with the minimum number of pixels in the 40 cores, and maximising the use of different cores from different patients. | ||
| Fig. 4 Schematic showing the process involved in generating training sets A, with equal overall size, but an imbalance in composition. All spectra are unique. | ||
 | ||
| Fig. 5 Schematic showing the process used to generate training sets B, with equal class size, but different total number of unique spectra. | ||
1. Determine the difference in the size between the majority class and minority class. Replicate each of the spectra in the minority class enough times to match this difference. Append the replicates to the minority class.
2. Randomly select spectra from the minority class until the total equals the size of the majority class. This is sampling with replacement.
3. Determine the difference in size between the majority class and minority class. Randomly select spectra from the minority class enough times to match this difference. Append the replicates to the minority class.
4. Perform an interpolation of one or more spectra in the minority class, and append these to that class, to increase the number of spectra available.
The first approach allows for an (almost) equal number of each minority spectrum to be present in the over-sampled training data. The fully random nature of the second approach means that not all spectra in the original minority class may be included in the over-sampled set. There will be no guarantee of the degree of duplication of each minority class spectrum. The possibility that any of the original minority may be missing in the outcome means information is being lost. The third approach is a modification of the second. Here the entire minority class is included in the outcome, with the remainder being topped up randomly. No information is lost. The fourth approach does not duplicate spectra exactly; rather it creates interpolated versions of minority class spectra. This is expanded upon in the paper by Blagus and Lusa41 where they describe their Synthetic Minority Oversampling Technique (SMOTE) method.
In this study we used approach number three. This has the advantage of ensuring each member of the minority class is represented in the training set. Starting in the same manner as for training sets A and B, we randomly selected 2500 spectra of cancerous tissue and 2500 spectra of normal-associated tissue. These two sets of spectra were combined to form a balanced training set with 5000 spectra. The generation of the cancerous epithelium component of the training sets followed the same pattern as training sets A: For each set an additional 500 spectra were randomly selected from the pool of annotated spectra. To generate the subsequent NAT part of each training set, 500 spectra were removed from the first set, producing 2000 spectra. From these 2000 were randomly selected 1000 spectra which were appended to the 2000 to create a NAT training set of 3000 spectra. The 3000 cancerous spectra and 3000 NAT spectra were combined to produce a balanced training set of 6000 spectra.
Further training sets were generated in a similar manner. The cancerous component was topped up using previously unselected spectra from the overall pool. The NAT component was first reduced in number by deleting 500. Then, the difference in size between the cancerous component and NAT component was calculated. The requisite number of spectra (this difference) was then randomly selected from the current, depleted NAT component. In this way, the heavily unbalanced classes, for example 4500 versus 500, had their NAT component topped up by sampling 4000 times from the pool that only contained 500 spectra (Fig. 6). This has the effect of creating a large degree of duplication in the NAT class, with no control over the distribution of that sampling. Indeed, the same spectrum could be added 4000 times (Table 3).
Results
The AdaBoost algorithm was employed to construct models from the various training sets developed above. The same data were then used to construct models using the Random Forests algorithm for comparison. All models were tested using the same independent test data set. In all cases each experiment was repeated five times to assess variability.AdaBoost results
The AdaBoost.M1 algorithm, from the Statistics and Machine Learning Toolbox within MATLAB, was selected. AdaBoost.M1 is appropriate since only a two-class problem is considered here. 500 iterations were applied with a learning rate (to train an ensemble using shrinkage) equal to 1.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 to 90
50 to 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
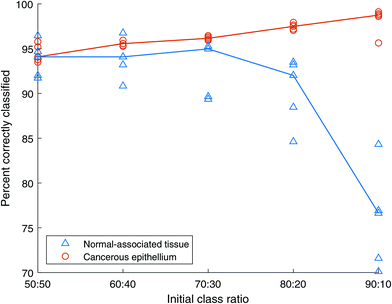
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10, cancer to normal-associated spectra respectively. AdaBoost models were constructed from these data, tested using the independent test set, and the results are shown in Fig. 7. The median accuracy of each of the five repeats is also indicated on the plot, with the median being selected as a robust statistic in the presence of outliers.
10, cancer to normal-associated spectra respectively. AdaBoost models were constructed from these data, tested using the independent test set, and the results are shown in Fig. 7. The median accuracy of each of the five repeats is also indicated on the plot, with the median being selected as a robust statistic in the presence of outliers.
Both cancer and NAT spectra are classified with over 95% accuracy for the initial case of balanced classes containing 2500 spectra each. As the class imbalance grows the accuracy of the NAT class decreases while that of the cancer class grows until they cross between the 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 and 90
20 and 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 ratios, corresponding to 4000
10 ratios, corresponding to 4000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1000 and 4500
1000 and 4500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500, cancer
500, cancer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NAT spectra respectively. Even at this final, large imbalance the classification accuracies are still over 94%. This indicates that the AdaBoost method is robust to class imbalance.
NAT spectra respectively. Even at this final, large imbalance the classification accuracies are still over 94%. This indicates that the AdaBoost method is robust to class imbalance.
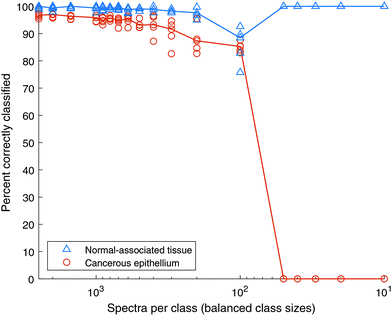
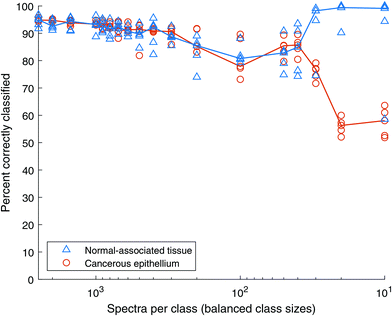
Fig. 8 shows the classification accuracy of each data set. The classification accuracy of the normal-associated spectra is approximately 99% with 2500 spectra of each class and remains very high even when reduced to 500 spectra each. Conversely, the classification rate of cancerous spectra drops from ∼96% to ∼86% as the total number of spectra drop. This experiment was extended, reducing the numbers of spectra in each class much further. The results are shown in Fig. 9. When the number of spectra in each class is reduced below 100, the classification rate of cancer spectra drops to zero and that of normal-associated tissue rises to 100%. In both these cases, the classification rate of normal-associated tissue remains high, while that of cancer spectra falls, until the model fails completely. It appears that the normal-associated tissue spectra are being correctly classified, but some of the cancer spectra are also being classified as normal-associated. As the number of spectra decreases, this reaches a critical point where all spectra are classed as normal-associated and therefore all cancer spectra are misclassified.
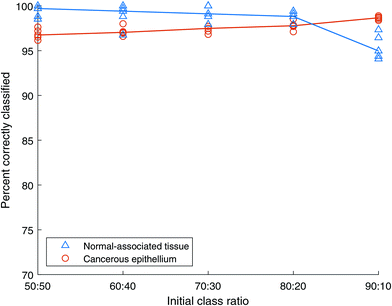
Using Training sets C above, we duplicated normal-associated spectra to match the number of cancer spectra, for different initial class sizes. AdaBoost models were then constructed from these training sets and tested using the independent test set. The results are shown in Fig. 10. Here the x-axis shows the initial class ratio, prior to over-sampling. Each training set becomes balanced, but the number of spectra also increases. For example, for a scenario with an initial ratio of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, the training set comprises 2500 of each class giving a total of 5000 spectra. Contrast this with an initial ratio of 90
50, the training set comprises 2500 of each class giving a total of 5000 spectra. Contrast this with an initial ratio of 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 which, following the oversampling exercise results in 9000 spectra.
10 which, following the oversampling exercise results in 9000 spectra.
The outcome here is similar to that produced by the unbalanced Training sets A, shown in Fig. 7, where the classification accuracy of the NAT class decreased slightly with increasing class imbalance, with the accuracy of the cancerous class increasing slightly. When the class sizes are balanced (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50) the normal-associated spectra show a classification rate of ∼99%, and the cancerous spectra, a rate of ∼96%. As the class imbalance grows, spectra in the minority class are randomly duplicated to ensure the numbers are the same in each class. The difference between this and under-sampling is that all the data from the majority class are unique, while those from the minority class will contain duplicates. However, under-sampling reduces the total number of spectra to twice the number in the minority class, while over-sampling increases the total number to twice that of the majority class. Therefore, in this case the 90
50) the normal-associated spectra show a classification rate of ∼99%, and the cancerous spectra, a rate of ∼96%. As the class imbalance grows, spectra in the minority class are randomly duplicated to ensure the numbers are the same in each class. The difference between this and under-sampling is that all the data from the majority class are unique, while those from the minority class will contain duplicates. However, under-sampling reduces the total number of spectra to twice the number in the minority class, while over-sampling increases the total number to twice that of the majority class. Therefore, in this case the 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 training set contains 4500 unique cancer spectra, but only 500 unique NAT spectra, the additional 4000 NAT spectra being randomly selected duplicates.
10 training set contains 4500 unique cancer spectra, but only 500 unique NAT spectra, the additional 4000 NAT spectra being randomly selected duplicates.
Random Forests results
Previous studies have employed the Random Forests algorithm to explore classification of cancerous and normal-associated tissues. For comparison purposes, we took the same test and training sets, generated above, and constructed a range of models using the Random Forests approach. The performance and outcomes were then assessed.The Random Forests algorithm incorporated into the MATLAB Statistics and Machine Learning Toolbox was used (fitcensemble.m, with the appropriate parameters). 500 trees were used to train the classifier. The minimum node size to split was left at the default value of one.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 training data set, containing 2500 spectra of cancerous tissue and 2500 spectra of normal-associated tissue, indicates a similar classification accuracy of approximately 94% for each class type, with the cancer spectra showing a slightly smaller standard deviation. As the total number of spectra in these balanced training sets decreases to 1000, the classification of normal-associated tissue improves, while that of cancerous tissue decreases. The standard deviation of classification rate for the cancer spectra also increases. This could be due to the limited number of spectra in the highly under-sampled cases leading the algorithm to construct overfitted models.
50 training data set, containing 2500 spectra of cancerous tissue and 2500 spectra of normal-associated tissue, indicates a similar classification accuracy of approximately 94% for each class type, with the cancer spectra showing a slightly smaller standard deviation. As the total number of spectra in these balanced training sets decreases to 1000, the classification of normal-associated tissue improves, while that of cancerous tissue decreases. The standard deviation of classification rate for the cancer spectra also increases. This could be due to the limited number of spectra in the highly under-sampled cases leading the algorithm to construct overfitted models.
When the total number of spectra is further reduced, the Random Forests classifier retains a level of performance over 70% until there are only 50 spectra of each class in the training data, as shown in Fig. 13. Note that in contrast to AdaBoost, the model does not fail completely. However, with the NAT spectra indicating approximately 100% accuracy, the cancer spectra fall to ∼50%, which is the equivalent of random chance in a two-class model.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 is reached, whereupon the majority cancer class accuracy increases, and the minority normal-associated class falls. Again, as seen with AdaBoost, the over-sampled data behaves in a similar fashion to the unbalanced data shown in Fig. 11.
30 is reached, whereupon the majority cancer class accuracy increases, and the minority normal-associated class falls. Again, as seen with AdaBoost, the over-sampled data behaves in a similar fashion to the unbalanced data shown in Fig. 11.
Discussion
The first observation is that with 2000 or more spectra, we can correctly classify over 90% of the spectra, regardless of the sampling method, or algorithm employed. This indicates that infrared spectroscopy is a useful tool for the detection of cancerous tissue, in the presence of normal-associated tissue, in breast cancer diagnosis.The models constructed from unbalanced data using AdaBoost showed good consistency across a wide range of class imbalance. Therefore, this study would suggest that there is no need to perform re-sampling of data, prior to analysis, when using this algorithm; with the proviso that sufficient training examples are available.
Under-sampling involves the removal of data from the majority class, which is likely to have the effect of constructing a less accurate model as the total number of spectra decreases. This can be seen in Fig. 8 and 9 for AdaBoost, and Fig. 12 and 13 for Random Forests. Limited training data prevents the derived models from learning the breadth of variability required to correctly predict the test data, and therefore any previously unseen data in operation.
Both AdaBoost and Random Forests showed similar trends in classification accuracy when comparing unbalanced data with its over-sampled version. With increased imbalance there is a large duplication of examples in the minority class. Therefore, although there appear to be sufficient spectra in the minority class, its variability is low. When the algorithm attempts to learn from these data it is presented with a majority class containing wide variability, capable of capturing the entire space of that tissue type, but a minority class with insufficient variability relating to its tissue type. The model overfits the minority class which then performs poorly when attempting to predict a range of test data. This could explain the difference in standard deviation of the cancer (majority) and NAT (minority) repeated examples, at 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 initial class ratio, in Fig. 10 and 14.
10 initial class ratio, in Fig. 10 and 14.
Over-sampling also increases the total number of spectra that the algorithms must manage, due to the replication of spectra in the minority class, thereby increasing the compute resource and analysis time required.
Comparison between AdaBoost and Random Forests approaches
When comparing AdaBoost with Random Forests, it is clear from Fig. 7 and 11 that AdaBoost is the more robust method when presented with unbalanced data. However, both algorithms require over 100 spectra of each class to perform with greater than 80% classification accuracy. With modern infrared imaging instrumentation this level of data is easily acquired, but the tissue samples must contain sufficient cancer cells in the sampled region to develop a useful model.AdaBoost is an iterative algorithm and so both the model building exercise, and unseen data prediction, are linear. Random Forests generates many decision trees, each independent. Therefore, Random Forests is amenable to parallel processing on modern computer processors, thus speeding up both model building and predictive analysis.
Conclusions
Both AdaBoost and Random Forests algorithms have been shown to give excellent classification performance, on the order of 95% accuracy, in separating infrared spectra of cancerous epithelium tissue from normal-associated tissue on the tissue microarray used in this study. Further work is required to determine whether this is a typical result when assessing model transfer across samples, instruments, and laboratories.AdaBoost is shown to be a robust algorithm in the presence of data of unbalanced composition, out-performing Random Forests at larger degrees of imbalance.
Given the stability of the AdaBoost algorithm on unbalanced data we suggest that the re-sampling approaches discussed in this paper may not be required.
Author contributions
Jiayi Tang: conceptualisation, data curation (lead), formal analysis (lead), investigation (lead), methodology (lead), software (lead), validation (lead), visualisation, writing the original draft (lead), review & editing. Alex Henderson: data curation, formal analysis, software, validation, review & editing. Peter Gardner: conceptualisation, project administration (lead), resources (lead), supervision (lead), visualisation, review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Daniela Kurfürstová of the Palacký University Olomouc, Czech Republic, for helpful discussion relating to cancer pathology. We also thank the Williamson Trust for generous support towards the purchase of the benchtop FTIR microscope used in this study.References
- D. C. Fernandez, R. Bhargava, S. M. Hewitt and I. W. Levin, Nat. Biotechnol., 2005, 23, 469–474 CrossRef CAS PubMed.
- E. Gazi, M. Baker, J. Dwyer, N. P. Lockyer, P. Gardner, J. H. Shanks, R. S. Reeve, C. A. Hart, N. W. Clarke and M. D. Brown, Eur. Urol., 2006, 50, 750–761 CrossRef PubMed.
- M. J. Baker, E. Gazi, M. D. Brown, J. H. Shanks, N. W. Clarke and P. Gardner, J. Biophotonics, 2009, 2, 104–113 CrossRef CAS PubMed.
- M. J. Pilling, A. Henderson, J. H. Shanks, M. D. Brown, N. W. Clarke and P. Gardner, Analyst, 2017, 142, 1258–1268 RSC.
- F. Großerueschkamp, A. Kallenbach-Thieltges, T. Behrens, T. Brüning, M. Altmayer, G. Stamatis, D. Theegarten and K. Gerwert, Analyst, 2015, 140, 2114–2120 RSC.
- X. Mu, M. Kon, A. Ergin, S. Remiszewski, A. Akalin, C. M. Thompson and M. Diem, Analyst, 2015, 140, 2449–2464 RSC.
- A. Kallenbach-Thieltges, F. Großerüschkamp, A. Mosig, M. Diem, A. Tannapfel and K. Gerwert, J. Biophotonics, 2013, 6, 88–100 CrossRef PubMed.
- N. Kröger-Lui, N. Gretz, K. Haase, B. Kränzlin, S. Neudecker, A. Pucci, A. Regenscheit, A. Schönhals and W. Petrich, Analyst, 2015, 140, 2086–2092 RSC.
- C. L. Song, M. Z. Vardaki, R. D. Goldin and S. G. Kazarian, Anal. Bioanal. Chem., 2019, 411, 6969–6981 CrossRef CAS PubMed.
- C. Kuepper, F. Großerueschkamp, A. Kallenbach-Thieltges, A. Mosig, A. Tannapfel and K. Gerwert, Faraday Discuss., 2016, 187, 105–118 RSC.
- C. Hughes, J. Iqbal-Wahid, M. Brown, J. H. Shanks, A. Eustace, H. Denley, P. J. Hoskin, C. West, N. W. Clarke and P. Gardner, J. Biophotonics, 2013, 6, 73–87 CrossRef CAS PubMed.
- M. Sattlecker, N. Stone and C. Bessant, TrAC, Trends Anal. Chem., 2014, 59, 17–25 CrossRef CAS.
- N. I. R. Yassin, S. Omran, E. M. F. El Houby and H. Allam, Comput Methods Programs Biomed, 2018, 156, 25–45 CrossRef PubMed.
- H. Fabian, N. A. N. Thi, M. Eiden, P. Lasch, J. Schmitt and D. Naumann, Biochim. Biophys. Acta, Biomembr., 2006, 1758, 874–882 CrossRef CAS.
- D. M. Mayerich, M. Walsh, A. Kadjacsy-Balla, S. Mittal and R. Bhargava, in Progress in Biomedical Optics and Imaging - Proceedings of SPIE, ed. M. N. Gurcan and A. Madabhushi, 2014, p. 904107 Search PubMed.
- P. Bassan, M. J. Weida, J. Rowlette and P. Gardner, Analyst, 2014, 139, 3856–3859 RSC.
- S. Mittal, T. P. Wrobel, L. S. Leslie, A. Kadjacsy-Balla and R. Bhargava, in Medical Imaging 2016: Digital Pathology, ed. M. N. Gurcan and A. Madabhushi, 2016, p. 979118 Search PubMed.
- J. Tang, D. Kurfürstová and P. Gardner, Clin. Spectrosc., 2021, 3, 100008 CrossRef.
- S. Mittal, C. Stoean, A. Kajdacsy-Balla and R. Bhargava, Front. Bioeng. Biotechnol., 2019, 7, 246 CrossRef PubMed.
- J. Bell, Machine Learning: Hands-On for Developers and Technical Professionals, John Wiley & Sons, Inc, Indianapolis, IN, USA, 2014 Search PubMed.
- K. P. Murphy, Machine Learning a Probabilistic Perspective, MIT Press, Cambridge, Massachusetts, Illustrate., 2012 Search PubMed.
- L. S. Leslie, T. P. Wrobel, D. Mayerich, S. Bindra, R. Emmadi and R. Bhargava, PLoS One, 2015, 10, e0127238 CrossRef.
- S. Mittal, K. Yeh, L. S. Leslie, S. Kenkel, A. Kajdacsy-Balla and R. Bhargava, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E5651–E5660 CrossRef CAS.
- T. G. Dietterich, in First International Workshop, MCS 2000 Cagliari, Italy, June 21–23, 2000 Proceedings, 2000, vol. 1857, pp. 1–15.
- A. Cutler, D. R. Cutler and J. R. Stevens, in Ensemble Machine Learning, Springer US, Boston, MA, 2012, pp. 157–175 Search PubMed.
- Y. Freund and R. E. Schapire, in Proceedings of the 13th International Conference on Machine Learning, Morgan Kaufmann Publishers, Burlington, Massachusetts, California, 1996, pp. 208–219 Search PubMed.
- Y. Freund, in Proceedings of the twelfth annual conference on Computational learning theory - COLT ‘99, ACM Press, New York, New York, USA, 1999, pp. 102–113 Search PubMed.
- R. E. Schapire, in Empirical Inference, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 37–52 Search PubMed.
- A. J. Ferreira and M. A. T. Figueiredo, in Ensemble Machine Learning, Springer US, Boston, MA, 2012, pp. 35–85 Search PubMed.
- C. Seiffert, T. M. Khoshgoftaar, J. Van Hulse and A. Napolitano, IEEE Trans. Syst., Man, Cybern. A, Syst. Humans, 2010, 40, 185–197 Search PubMed.
- N. Japkowicz, in AAAI Workshop on Learning from Imbalanced Data Sets, 2000, pp. 10–15 Search PubMed.
- E. El-shafeiy and A. Abohany, in Advances in Intelligent Systems and Computing, Springer, 2020, vol. 1153 AISC, pp. 81–91 Search PubMed.
- A. Ali, S. M. Shamsuddin and A. L. Ralescu, Int. J. Adv. Soft Comput. Appl., 2015, 7, 176–204 Search PubMed.
- H. He and E. A. Garcia, IEEE Trans. Knowl. Data Eng., 2009, 21, 1263–1284 Search PubMed.
- P. Branco, L. Torgo and R. P. Ribeiro, ACM Comput. Surv., 2016, 49, 1–50 CrossRef.
- M. M. Rahman and D. N. Davis, Int. J. Mach. Learn. Comput., 2013, 224–228 CrossRef.
- G. M. Weiss, ACM SIGKDD Explor. Newsl., 2004, 6, 7–19 CrossRef.
- F. Lyng, E. Gazi and P. Gardner, in RSC Analytical Spectroscopy Series, ed. D. Moss, Royal Society of Chemistry, Cambridge, 2010, pp. 147–191 Search PubMed.
- D. Aran, R. Camarda, J. Odegaard, H. Paik, B. Oskotsky, G. Krings, A. Goga, M. Sirota and A. J. Butte, Nat. Commun., 2017, 8, 1077 CrossRef.
- S. R. Lakhani, International Agency for Research on Cancer and World Health Organization, in WHO Classification of Tumours of the Breast, International Agency for Research on Cancer, Lyon, France, 4th edn, 2012 Search PubMed.
- R. Blagus and L. Lusa, BMC Bioinformatics, 2013, 14, 106 CrossRef PubMed.
Footnotes |
| † Data and source code availability: Processed data and MATLAB source code: https://doi.org/10.5281/zenodo.4730312. Raw data in Agilent IR mosaic file format: https://doi.org/10.5281/zenodo.4986399 |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/d0an02155e |
| This journal is © The Royal Society of Chemistry 2021 |