Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Enabling autonomous scanning probe microscopy imaging of single molecules with deep learning†
Javier
Sotres
 *ab,
Hannah
Boyd
ab and
Juan F.
Gonzalez-Martinez
ab
*ab,
Hannah
Boyd
ab and
Juan F.
Gonzalez-Martinez
ab
aDepartment of Biomedical Science, Faculty of Health and Society, Malmö University, 20506 Malmö, Sweden
bBiofilms-Research Center for Biointerfaces, Malmö University, 20506 Malmö, Sweden. E-mail: javier.sotres@mau.se
First published on 16th April 2021
Abstract
Scanning probe microscopies allow investigating surfaces at the nanoscale, in real space and with unparalleled signal-to-noise ratio. However, these microscopies are not used as much as it would be expected considering their potential. The main limitations preventing a broader use are the need of experienced users, the difficulty in data analysis and the time-consuming nature of experiments that require continuous user supervision. In this work, we addressed the latter and developed an algorithm that controlled the operation of an Atomic Force Microscope (AFM) that, without the need of user intervention, allowed acquiring multiple high-resolution images of different molecules. We used DNA on mica as a model sample to test our control algorithm, which made use of two deep learning techniques that so far have not been used for real time SPM automation. One was an object detector, YOLOv3, which provided the location of molecules in the captured images. The second was a Siamese network that could identify the same molecule in different images. This allowed both performing a series of images on selected molecules while incrementing the resolution, as well as keeping track of molecules already imaged at high resolution, avoiding loops where the same molecule would be imaged an unlimited number of times. Overall, our implementation of deep learning techniques brings SPM a step closer to full autonomous operation.
Introduction
The development of Scanning Probe Microscopies (SPM), especially Scanning Tunneling Microscopy (STM)1 and Atomic Force Microscopy (AFM),2 constituted a revolution on our understanding of the nanoworld. Since then, these techniques have not only been used to visualize a wide variety of samples from the μm-scale down to the single molecule and atom resolution,3–5 they have also been used for sample manipulation and for performing a variety of spectroscopies providing information on e.g., chemical identity, mechanical, electrical, electrochemical and magnetic properties.6–9 However, despite the possibilities that they offer, several bottlenecks are preventing broader use of SPMs. One of the major barriers to SPM use is the need for highly trained users to perform time-consuming experiments and to analyze and correctly interpret results that are often susceptible to artifacts.Recently, Machine Learning (ML) techniques have started to be applied to solve these challenges. So far, most of the works combining SPM and ML have focused on data analysis. For instance, algorithms like Random Forests and Gradient Boosting Trees were used to detect bladder cancer from images of cells collected from urine.10 A feed-forward neural network was used to discover electronic correlations in voltage-dependent STM data of doped copper oxide samples.11 Several works have also used SPM images to determine the quality of the probe, mostly by using Convolutional Neural Networks (CNN).12–14 CNNs were also used to identify different patterns in AFM images of adsorbed nanoparticles15 and to identify and even resolve the configuration of adsorbed organic molecules.16 The classification of AFM force curves has also been addressed by using algorithms such as Independent Component Analysis (ICA) and Supported Vector Machines (SVM),17 feed-forward neural networks18 and Extra Trees Regressors.19 Advanced CNNs architectures have also proved useful. Examples are the use of the Very Deep Super Resolution (VDSR) network to enhance the resolution of AFM images20 and the use of object detection networks like YOLO to locate nanowires in AFM images.21 In the latter, the authors also used bidirectional long short-term memory (LSTM) networks to determine the posture of the located nanowires.
ML methods have also been applied to the automation of SPM operation, although to a lower extent than to data analysis. Supported Vector Machines (SVMs) were used to detect, in real operation time, domain walls of ferroelectric materials, allowing zooming on them for performing switching spectroscopy piezo-response force microscopy (SS-PFM).22 In another work,14 an automatic routine was developed for tip conditioning based on indentation where the feedback on the success of the conditioning event relied on a CNN analysis of the image that provided the tip quality. Automatic control of the scanning speed and feedback controls by means of Gaussian Process Models has also been reported.23 Long term autonomous operation was reported for low-temperature STM imaging of adsorbed magnesium phthalocyanine (MgPc) molecules.24 The acquisition algorithm implemented ML methods at two steps. In one, acquired images were evaluated with a CNN classifier for determining the quality of the tip. In case the quality of the tip was classified as bad, the algorithm made use of Reinforcement Learning (RL) to choose between a list of actions commonly used for probe conditioning. After each conditioning step, the scanned area was imaged again, subsequently analyzed by the CNN and the RL agent rewarded accordingly. Leinen and co-workers25 also showed that it was possible to use RL to find optimal SPM tip trajectories for effectively lifting single molecules from perylenetetracarboxylic dianhydride (PTCDA) layers.
From the above discussion, it is clear that in recent years the application of ML methods are boosting SPM research, a trend shared by many other microscopies.26–30 In this work, we continued this research direction with the specific aim of advancing towards autonomous SPM operation. Specifically, we report on the use of state-of-the-art object detection and one-shot-learning deep learning models for the fully autonomous AFM imaging of single molecules, using DNA molecules on mica surfaces as a model sample. At present, high resolution SPM imaging on single molecules is a tedious process where the SPM operator starts by scanning large areas, identifies possible suitable molecules and performs a series of zoom steps (in order to avoid losing the molecule due to lateral drift) until the molecule is imaged with enough resolution. Then, the user zooms out and repeats the process multiple times ensuring that zooming is not performed on molecules visualized previously. Here, we demonstrate a deep learning-based algorithm that automates this process.
Results and discussion
Detection of single DNA molecules in AFM images
When an AFM user aims to obtain high-resolution images of single nm-sized structures, the first step is typically to scan large areas, identify suitable candidates and subsequently perform incremental zooms on a chosen structure. While straightforward for humans, object detection i.e., the location in an image of instances of predefined categories, has been one of the most challenging problems in computer vision. Extensive reviews on this topic are available.31,32 Here, we briefly discuss the main developments that motivated our use of the YOLOv3 network for detecting DNA molecules. The pipeline of traditional approaches to object detection i.e., those used before the deep learning area, was divided into three stages: region selection, feature extraction and classification. Scanning a whole image with a multi-scale sliding window was a common but computationally expensive approach for region selection. For extracting features from the scanned windows, SIFT,33 HOG34 and Haar-like35 algorithms were common choices. The main drawback of these algorithms was their limitations for describing different object categories. For classifying the category of the detected object, algorithms like Supported Vector Machines (SVM),36 Adaboost37 and Deformable Part-based Model (DPM)38 could then be used. However, the vast increase in computing power at gradually lower costs that has occurred recently, changed this field completely. Especially, the possibility to efficiently use Convolutional Neural Networks (CNNs).39,40 While the first works on CNNs focused on their use for object/image classification, shortly after they were also applied to object detection. Already in 2014, the R-CNN detector was published.41 It was characterized by the use of a CNN to extract features within the pipeline detailed above, that could then be classified e.g., with SVMs. In a latter development, Fast R-CNN,42 the output of the CNN for extracting features was fed into a pooling layer that down-samples feature maps with different sizes into a fixed-size vector. This vector bifurcates into two outputs characterized by fully connected layers with different activations for classification and location. While faster than R-CNN, Fast R-CNN still required proposing a set of candidate regions along with each input image. This model was further improved by the Faster R-CNN architecture,43 where a CNN is used for the region proposal step. However, Faster R-CNN is still characterized by a two-stage object detection architecture. While very precise, two-stage detection models are still time-consuming and limited for use in embedded systems where real-time computing constraints are an issue e.g., real-time AFM imaging. With the goal of achieving higher speed and simplicity, one-stage object detectors were developed. These are end-to-end single (deep) neural networks that provide the category along with the coordinates that bound detected objects directly from an input image. While several approaches exist,44,45 YOLO (You Only Look Once)46 and its later implementations47,48 have become widely used for applications where inference speed is critical. Briefly, YOLO networks split the input image into a grid of cells, where each cell is responsible for predicting a bounding box for an object, if the center of the bounding box falls within it. Each grid cell predicts the coordinates for a number of bounding boxes, the confidence that each box bounds an object as well as the prediction for the object class. In this work we used the YOLOv3 network,48 for which a detailed description is provided in the Experimental section. YOLOv3 improved YOLO in several aspects. Of specific relevance for our choice was its ability to detect objects from similar categories at different scales, while still offering an excellent trade-off between detection accuracy and computational speed.The performance of object detection models is typically characterized in terms of their precision–recall curve and by the area under this curve i.e., the average precision (AP). Precision is defined as the number of true positives divided by the total number of objects detected by the model (sum of true and false positives). Recall is defined as the number of true positives divided by the total number of ground-truths (sum of true positives and false negatives). For calculating precision–recall scores we used a similar metric as the PASCAL VOC challenge.49 Specifically, we calculated precision and recall values while varying the confidence score and fixing a threshold of 0.5 for the Intersection over Union (IoU, the area of the intersection divided by the area of the union of a predicted bounding box and a ground-truth box). A detected bounding box was considered a true positive if its confidence score was higher than the confidence threshold and the IoU with a ground-truth box was higher than the IoU threshold (0.5). If either of these two conditions was not satisfied, the detected bounding box was considered a false positive. In case multiple predictions corresponded to the same ground-truth, only the one with the highest confidence score counted as a true positive, while others were considered false positives. It is not needed to explicitly calculate the number of false negatives for estimating the recall, as the total number of ground truths is enough. The precision–recall curve calculated by applying our YOLOv3 model to the test dataset of AFM images of DNA molecules is shown in Fig. 1a.
The area under the precision–recall curve (precision–recall AUC) for our YOLOv3 model was 0.91, which is a reasonable value considering that a perfect detector would be characterized by a precision–recall AUC of 1. The precision–recall curve also allows estimation of the confidence threshold required for a balanced tradeoff between both quantities. A common approach is to use the threshold that maximizes the weighted harmonic mean of precision and recall, Fβ-score,50
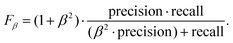 | (1) |
The weight β determines the relative importance of recall with respect to precision. For this work, we were especially interested in minimizing the number of false positives but still detecting most of the imaged molecules. Therefore, we chose β = 0.5 and determined from the precision–recall curve the confidence threshold that maximized F0.5. This point, highlighted in Fig. 1a, was obtained for a threshold of 0.38 and corresponded to a precision of 0.97 and a recall of 0.91. The performance of the detector is exemplified in Fig. 1b–d. These are images from our test dataset where the DNA bounding boxes predicted by our detector are over-imposed. It can be seen that the model successfully detects DNA molecules at different scales. Fig. 1c also shows how the model can discriminate between DNA molecules and contamination. Finally, Fig. 1d exemplifies the ability of the model to differentiate between close molecules.
Siamese networks for identifying DNA molecules
Obtaining consistent and reliable information of single nm-sized structures from AFM images typically requires collecting a large quantity of high-resolution images. In a common experiment, the AFM user starts by scanning a large area, identifies a suitable structure and zooms on it. Typically, zooming needs to be performed gradually, as a drastic zoom might result in losing the identified structure because of e.g., lateral drift. After each zoom, the user recognizes the structure of interest in the new image and zooms again. Once an image with high-enough resolution of the identified structure is acquired, the user zooms out, identifies a structure not visualized before and starts again the procedure. Thus, identifying the same structure in two or more scans is a typical aspect of AFM workflow (and almost of any other microscopy). In this work, we automated this aspect without the need of human interaction/supervision.Similarly to object detection, identification is a problem that has received significant attention from the computer vision community. Traditional similarity-based evaluation metrics like Structural Similarity Index (SSIM)51 are highly sensitive to geometric and scale distortions and, therefore, not an optimal choice for AFM images. Here, we used instead a deep learning approach. In the context of deep learning, identification typically falls within the problem of one-shot-learning i.e., categorizing new classes (for which the algorithm was not trained for) given only one example of each new class. This is exactly the problem we faced i.e., the need to identify a structure/molecule for which we only had one previous image (or very few at the best). In this regard, impressive results52,53 were achieved with Siamese Networks where deep CNN architectures and metric learning were combined. Siamese Networks consist of two symmetrical neural (embedding) networks, both sharing the same weights and architecture. Each of the embedding networks encode one of the inputs/images to be compared, xi, in a nth-dimensional embedding, f(xi) (often normalized for training stability). The two embedding networks are then joined and compared using a similarity metric. The goal is that similar input images e.g., those depicting the same DNA molecule, result in close embeddings whereas dissimilar images e.g., those depicting different DNA molecules, result in far apart embeddings.
Several loss functions can be used for training Siamese networks. One option is to treat the problem as a binary classification problem.52,54 In this approach, a sigmoid activation function is used to map a distance metric calculated from the encodings of two input images onto the interval [0 (same class), 1 (different class)] and then use a cross entropy loss function to train the network. Another option is to use the contrastive loss.55 If xi and xj are two input images, f(xi) and f(xj) are their corresponding embeddings, Dij is the distance metric between them and yij is the binary label for the input images (1 if the images correspond to a genuine pair and 0 otherwise), the contrastive loss is defined as:
| lc(i, j) = yijDij2 + (1 − yij)max(0, α − Dij)2 | (2) |
| lt(i, j) = max(0, Dap2 − Dan2 + α) | (3) |
Sampling images from the training dataset is a challenge when training with the triplet loss. One issue is that as the dataset gets larger, the possible number of triplets grows cubically. Thus, working with the entire possible number of triplets is impractical. Another issue is that networks trained with the triplet loss quickly learn to correctly map most trivial triplets, resulting in hard triplets i.e., positive pairs with far apart embeddings or negative pairs with close embeddings, barely contributing to the training. On the other hand, sampling only the hardest triplets leads to bad local minima early on when training.53 Thus, for a Siamese network to learn using a triplet loss is important to sample semi-hard triplets i.e., triplets that are hard, but not too hard to learn. Many different approaches have been proposed for this goal.53,56 In this work, we used online-mining of semi-hard triplets.53 For each batch, we randomly selected B anchors, each corresponding to different molecules, and we computed the same number, B, of triplets. For many of the input classes/molecules, the training dataset only contained two instances (even though in some cases this number could go up to five). Thus, images for completing the positive pairs were chosen randomly. For completing the negative pairs, we calculated the embeddings of the B inputs as well as those from a (higher) number of randomly selected images using the embedding network with updated weights. Then, we selected B/2 random negatives, and B/2 hard-negatives corresponding to those with the smallest Dij distance with the anchor. In order to prevent overfitting, during training the triplets were augmented before feeding them to the network (ESI S1†).
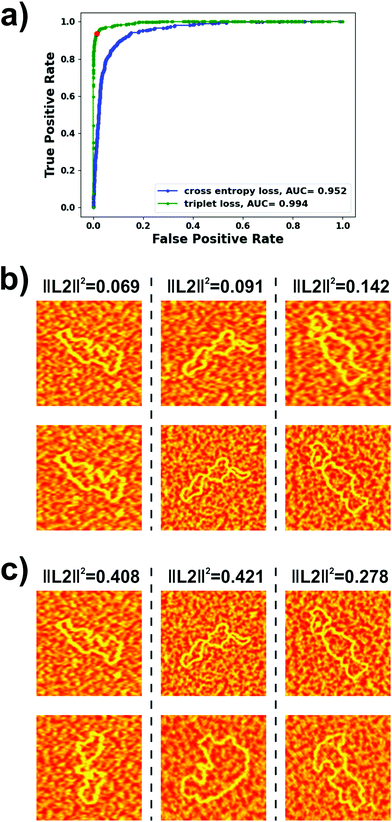
For identifying DNA molecules from AFM images, we experimented with diverse architectures for the embedding networks and trained them both with binary cross-entropy and triplet losses. The ROC curve and, more specifically, the area under this curve (AUC), for our test dataset was used as the metric for evaluating model performance. We obtained our best results using a modified VGG-16 architecture57 for the embedding network (details are provided in the Experimental section). As a similarity metric, we used the squared L2 norm between the outputs of the embedding networks. The ROC curves obtained on the test dataset with this architecture trained using both loss functions are shown in Fig. 2a. It can be seen that the model trained with the triplet loss (AUC = 0.994) clearly outperformed that trained with the binary cross-entropy loss (AUC = 0.952) and, therefore, was the one implemented in our autonomous AFM operation algorithm. The ROC curve also allows estimation of an optimal threshold for the metric used for verifying the identity of the molecules i.e., the squared L2 norm. An optimal classifier would be characterized by a false positive rate of 0 and a true positive rate of 1 i.e., all positives correctly classified and no negatives incorrectly classified. Thus, we chose to work with the threshold originating at the point in the ROC curve closest to the (0, 1) point. This squared L2 norm value was 0.255, which corresponded to a true positive rate of 0.935 and a false positive rate of 0.015.
Autonomous AFM imaging of single molecules
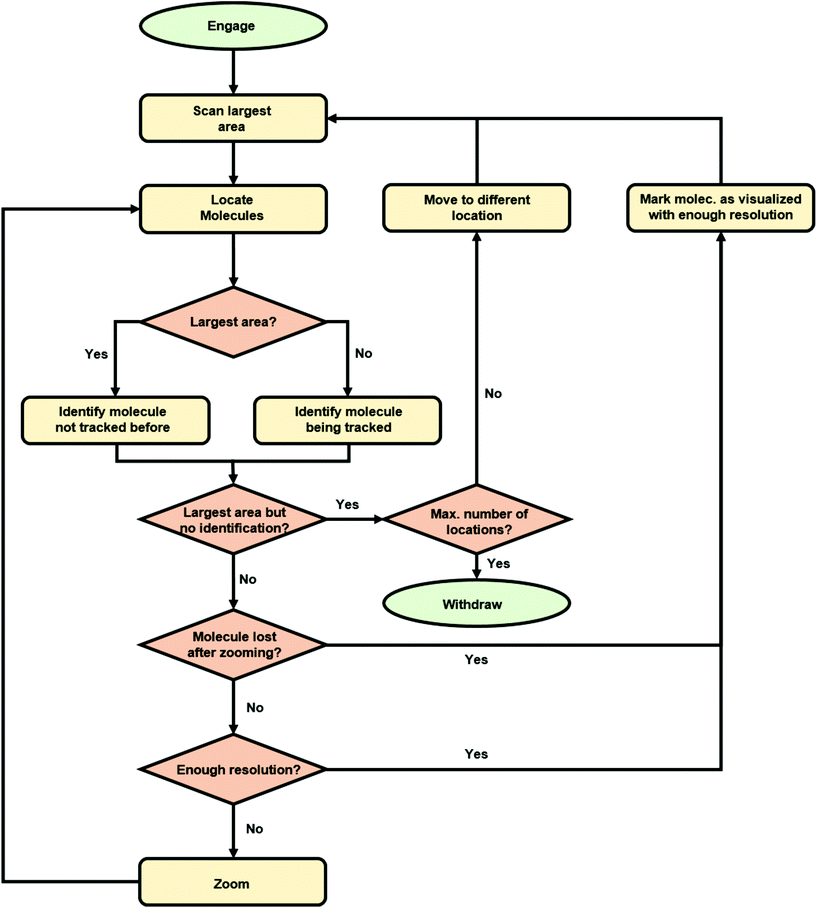
We implemented the described deep learning models i.e., YOLOv3 and Siamese network trained with a triplet loss, within an algorithm for the autonomous imaging of single DNA molecules. Before running an experiment with this algorithm, the user needs to provide scanning parameters, mainly the scan rate, set point and feedback parameters. The user also needs to provide additional information: the maximum and minimum areas to be scanned and the number of regions of the sample to be explored. Once these parameters are provided, the user only needs to run the algorithm that autonomously controls the AFM. The complete algorithm flowchart is shown in Fig. 3.Briefly, the algorithm starts by engaging the sample until the user-defined set point (vertical deflection, amplitude, etc. depending on the AFM operation mode) is reached. Then, it continues by scanning an area of the sample equal to the user-defined maximum scan area (5 μm in the presented experiments). When finished, the resulting topography image is analyzed with our YOLOv3 model, which provides the bounding boxes for the detected DNA molecules. At this stage, the algorithm selects the molecule closest to the image center (Fig. 4a) and crops a squared-area centered on the molecule and with a size 1.2 times that of the larger side of the molecule bounding box. This cropped image is stored and used later on for identifying the molecule in future images. Subsequently, the AFM zooms on the selected molecule, setting the new scan area to half its previous value. When the new scan finishes, YOLOv3 is used again for detecting DNA molecules on it. The squared-area centered on the detected molecules are again cropped from the new topography image. The molecule where zooming was performed is identified by comparing the previous image with the new cropped images using our Siamese network model (Fig. 4b). This allows zooming again on the same molecule (Fig. 4c). This process continues until the scan area is smaller than the user-defined minimum area (in this work, 1.5 times the larger side of the identified molecule bounding box, Fig. 4d). At this stage, the scan area is set back to its maximum value (Fig. 4e). A similar workflow is then continuously repeated with, however, a difference. Each new molecule identified as a suitable candidate is always compared with molecules previously imaged at high resolution using our Siamese network model. This prevents zooming on the same molecule several times. If after a maximum-area scan, no suitable molecules are detected (no molecules present, or all of them already imaged at high resolution), the algorithm moves the AFM cantilever to a new sample location and the whole process starts again.
The whole imaging process described above continues until a user-defined condition is reached e.g., all molecules within a user-defined number of locations across the sample being imaged at high resolution. When testing the algorithm to image DNA molecules, we were able to autonomously run the AFM for several days (no user intervention other than setting scanning parameters in the beginning of the experiment), obtaining a number of high-resolution images of single DNA molecules (Fig. 5) limited only by the number of molecules present in the sample.
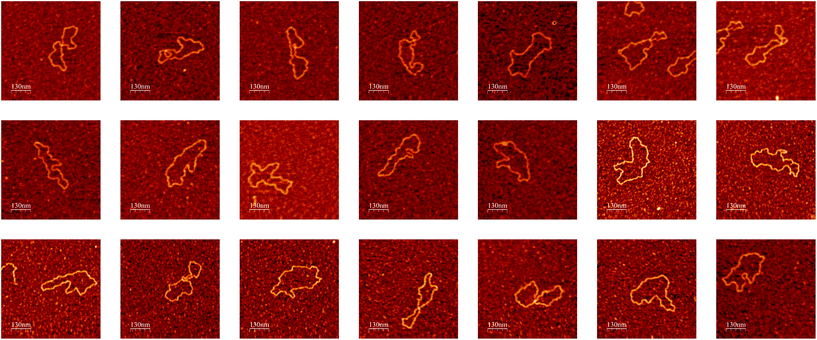 | ||
| Fig. 5 Examples of high-resolution AFM images of single DNA molecules obtained during a single experiment by the autonomous AFM imaging algorithm without user intervention. Color height scale 1 nm. Images were rendered with the WSxM software.58 | ||
Conclusions
We developed an algorithm for the autonomous operation of SPMs that allows, without the need of human intervention, the acquisition of high-resolution images of single molecules. The major novelty of our contribution relies on the use by the operation algorithm of state-of-the-art deep learning techniques: object detectors and Siamese networks. The object detector, YOLOv3, allowed locating molecules in the acquired images. In turn, Siamese networks allowed identifying particular molecules in different images. The latter allowed acquiring series of images of the same molecule while incrementing the lateral resolution. At the same time, it also allowed keeping track of already imaged molecules and, therefore, avoiding loops where the same molecule would be imaged an unlimited number of times. We used DNA on mica as a model sample to test our SPM control algorithm. The algorithm could autonomously run the SPM for several days, providing multiple high-resolution DNA molecules, the number only being limited by the number of molecules available within the SPM scanner range.Overall, this work brings SPM a step closer to full autonomous operation. Specifically, the proposed implementation would be highly useful in time-consuming studies where a statistically large number of single molecule images need to be acquired. Examples would include SPM imaging of single nucleic acids to determine their intrinsic curvature,59 and how this is affected e.g., by their sequence60 and environmental parameters.61 Within nucleic acids research, our approach would also facilitate studies e.g., on radiation-induced damage62 and on the mapping of protein-binding sites.63 Our algorithm could also be trained with other type of molecules e.g., with viruses for facilitating visualization of their different adsorption configurations.64
One of the main limitations for implementing supervised learning algorithms, like those used in this work, is the need for big amounts of data to train models. Traditionally, the SPM community has not shared with other computer vision related disciplines the tendency to open source data. This is a significant handicap for the development of supervised learning models for SPM, as researchers working on model development need to collect data as well. Moreover, the shortage of data also implies a lack of reference datasets to compare models. Nevertheless, the community already acknowledges this problem, and initiatives like SPMImages (https://spmportal.quasarsr.com/spmportal/index) that offers storage, curation and access to SPM images, and the JARVIS-STM website (https://jarvis.nist.gov/jarvisstm,65), where a database of STM images obtained using density functional theory is available, will definitely help in this challenge. Following this trend, we made all data used to train and test our models available at the repository of this work: https://git.io/JtP98. Another critical step towards intelligent SPMs will be a broader implementation of unsupervised learning approaches. An example where these would be of use is the visualization of samples for which prior knowledge of their topography is not available. In this regard, unsupervised object detection models for location of foreground objects66 are promising approaches. Another aspect that limits SPM use by a broader community is the need, in many cases, of experienced users for setting appropriate operational parameters (e.g., set point, feedback, gains, angles, etc.). This aspect could greatly benefit from e.g., reinforcement learning (RL) algorithms, which perform actions based on a current state and a reward. Recent studies have already shown the potential of RL in SPM automation.24,25 The availability of error signals in SPM e.g., the deviation of the signal on which feedback is performed with respect to the operation set point, should further facilitate their implementation. For instance, following an approach where the actions would be the variation of the scanning parameters and the reward the minimization of the error signal.
Experimental
Sample preparation
Plasmid DNA from E. coli RRI (D3404, Sigma-Aldrich, St Louis, MO) was purchased and used without further purification. Freshly cleaved mica sheets (71850-01, Electron Microscopy Sciences, Hatfield, PA) were used as substrates. For DNA sample preparation, mica sheets were coated with poly-lysine (PL) (P4832-50ML, Sigma-Aldrich, St Louis, MO) by pipetting 10 mL of the stock PL solution. After incubation for ∼30 s, the surface was rinsed with UHQ water (processed in an Elgastat UHQ II apparatus, Elga Ltd, High Wycombe, Bucks, England) and dried in a nitrogen stream, to ensure that only strongly adsorbed PL molecules remained on the surface. Afterwards, the surface was incubated in a DNA water solution for 1 min at a concentration of 1 mg mL−1, subsequently rinsed with water and finally dried with N2.Atomic force microscopy (AFM)
A commercial Atomic Force Microscope (AFM) setup (MultiMode 8 SPM with a NanoScope V control unit, Bruker AXS, Santa Barbara CA) was employed for imaging DNA molecules. Images were acquired by operating the AFM both in the Tapping mode and in the PeakForce Tapping mode. For imaging in the Tapping mode, cantilevers with a nominal resonance frequency between 320 and 364 kHz were used (RTESP7, Veeco Probes, Camarillo, CA). For imaging in the PeakForce Tapping mode, we used instead rectangular silicon nitride cantilevers with a nominal normal spring constant of 0.1 N m−1 (OMLC-RC800PSA, Olympus, Japan).Object detection model: YOLOv3
We used the YOLOv3 network48 to detect the positions of single DNA molecules in AFM topography images. YOLO networks are object detectors that use a single pass to detect the potential regions (bounding boxes) in the image where certain objects are present and to classify those regions into object classes. Specific details on the YOLOv3 network are provided in the original publication.48 Briefly, YOLOv3 structure includes a backbone network and a detection network. The backbone or feature extractor is the Darknet 53 network,67 which includes 52 convolutional layers and Resnet short cut connections to avoid the disappearance of gradients. The feature maps at three different scales are output to three different branches of the detection network. The detection network is characterized by a feature pyramid network (FPN),68 where the feature maps in a lower branch are concatenated with the ones in its next branch by up sampling. This FPN topology is critical for the ability of YOLOv3 to detect objects from the same class at different sizes. Finally, the outputs of the FPN are connected to a regression section to carry out predictions. Specifically, YOLOv3 makes different predictions for each detected object. These are the bounding box coordinates (x and y), its width (w) and height (h), the objectness score (p(o), which gives the confidence that the box contains one of the target objects using logistic regression) and the class scores for all Ci object categories (p(Ci|o), obtained using independent logistic classifiers i.e., YOLOv3 allows multi-label classification). The total confidence score for each class is thus the product of the objectness and the class score. The output of the network then goes through Non-Max Suppression (NMS) and a confidence threshold to give the final predictions. This last stage avoids multiple bounding boxes for the detected objects.In order to train YOLOv3, we used an initial set of 247 AFM images of adsorbed DNA molecules obtained by operating both in the Tapping and PeakForce Tapping modes. Lateral sizes ranged from 5 μm to 250 nm. Resolutions ranged from 1024 × 1024 points to 256 × 256 points. The training set was further augmented by random cropping of large size images, resulting in a total of 1348 images for training. For testing, we used a set of 90 images with similar lateral sizes and resolutions as those in the training set. No augmentation was applied to images in the test set. Bounding boxes for the DNA molecules in both the training and test sets were annotated using the labelImg software (https://git.io/JLXFr). Overall, the training and test sets contained 4250 and 652 molecules/bounding boxes respectively. Before feeding AFM images to YOLOv3, we applied a 3rd order flatten filter to the images that were subsequently stretched normalized with cutoffs of 2 times the standard deviation of their height histogram. The original structure of YOLOv3 requires 3-channel images and the pixel size should be an integer multiple of 32. Thus, the flattened and normalized 1-channel AFM height images were converted to 3-channels by replicating the height value in all 3 channels and subsequently re-scaling them to a 416 × 416 × 3 size. The same pre-processing steps were used for inference. For training, we fine-tuned a pre-trained model, darknet53.conv.74, available in ref. 67 on our training set of labelled images. For this, we used a batch size of 64, subdivisions of 16, maximum number of batches of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, momentum of 0.9 and a weight decay of 0.0005. We adopted a multistep learning rate policy with a base learning rate of 0.001, a step value of [400
000, momentum of 0.9 and a weight decay of 0.0005. We adopted a multistep learning rate policy with a base learning rate of 0.001, a step value of [400![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 450
000, 450![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000] and learning rate scales of [0.1, 0.1].
000] and learning rate scales of [0.1, 0.1].
Identification models: Siamese networks
The dataset for training and testing Siamese Networks was created from AFM topography images where the same sample location was scanned between 2 and 6 times. Lateral size and pixel resolution values for these images were similar to those of the images used for training our YOLOv3 model. Our YOLOv3 model was then used to automatically crop individual molecules from these images. This process resulted in a total of 1827 images of 692 different molecules. This was divided into a training set, with 1536 images of 598 different molecules, and a test set with 291 images of 94 different molecules. For the embedding network we used a modified VGG-16 network.57 In our case, the input size of the VGG network was modified to 96 × 96 × 3 and only contained one fully connected layer of size 4096 after the convolutional/max pool layers. Weights were randomly initiated. Siamese networks models were trained both with binary cross-entropy and triplet losses. For the reported models, we used the Adam optimization with an initial learning rate of 6 × 10−5, a 1st momentum of 0.9 and a 2nd momentum of 0.999. For the reported models, we also used a learning rate decay of 2.5 × 10−4. For Siamese networks trained with a binary cross-entropy loss, the architecture calculated the L1 distance between the feature vectors resulting from each of the embedding networks and used sigmoid activation to map this distance onto the interval [0, 1]. In this case, online-mined random pairs of images were used to train the network. For Siamese networks trained with a triplet loss, the final fully connected layers of each of the embedding networks were L2-normalized before estimating the distance between their outputs. In this case, online mining of semi-hard triplets was used to train the networks53 using a margin value of 0.2. In all cases, ROC curves for the test dataset were used to evaluate model performance.Communication between the AFM and the autonomous imaging algorithm
The AFM was controlled by the proprietary software Nanoscope (Bruker AXS, Santa Barbara CA). This software provides Open Architecture control through the Component Object Model (COM) from Microsoft. After being registered as a server, a set of instructions are available for custom applications. We used the Nanoscript feature (Bruker AXS, Santa Barbara CA) that allows sending instructions to this COM server through a customer programmed COM client. This was done by means of a custom Python routine, which could also analyze acquired images with the developed deep learning models and use the results from this analysis to send appropriate instructions to the Nanoscope COM server.Computer architectures
Deep learning models (detection and identification) were trained and validated on a system with the following characteristics: Intel® Core™ I9 7980XE (18 cores, 36 threads) CPU, 64 GB of DDR4 RAM and a GPU NVIDIA 2080 RTX Ti 11 GB GDDR6 (4352 computation cores). Models were always trained using the GPU. However, for inference i.e., for evaluating images with the models in real time during AFM operation, the AFM control computer itself was used. This computer was equipped with an Intel® Core™ I7 4790S (4 cores, 8 threads) CPU and 32 GB of DDR4 RAM both to control the AFM (by communicating with the Nanoscope COM server) and to evaluate the images with the deep learning models.Data and code availability
The code, models, and images to train and validate these models, used in the manuscript are available at https://git.io/JtP98.Author contributions
J.S.: Conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, software, writing – original draft, writing – review & editing; H.B.: Investigation, writing – review & editing; J.F.G.M.: Conceptualization, investigation, methodology, software, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Swedish Research Council (Grant No. 2016-06950) and the Gustaf Th. Ohlsson Foundation for financial support.References
- G. Binnig, H. Rohrer, C. Gerber and E. Weibel, Phys. Rev. Lett., 1983, 50, 120–123 CrossRef CAS.
- G. Binnig, C. F. Quate and C. Gerber, Phys. Rev. Lett., 1986, 56, 930–933 CrossRef PubMed.
- R. Pawlak, J. G. Vilhena, A. Hinaut, T. Meier, T. Glatzel, A. Baratoff, E. Gnecco, R. Pérez and E. Meyer, Nat. Commun., 2019, 10, 685 CrossRef CAS PubMed.
- Y. M. Efremov, A. X. Cartagena-Rivera, A. I. M. Athamneh, D. M. Suter and A. Raman, Nat. Protoc., 2018, 13, 2200–2216 CrossRef CAS PubMed.
- F. Moreno-Herrero, M. de Jager, N. H. Dekker, R. Kanaar, C. Wyman and C. Dekker, Nature, 2005, 437, 440–443 CrossRef CAS PubMed.
- V. V. Dremov, S. Y. Grebenchuk, A. G. Shishkin, D. S. Baranov, R. A. Hovhannisyan, O. V. Skryabina, N. Lebedev, I. A. Golovchanskiy, V. I. Chichkov, C. Brun, T. Cren, V. M. Krasnov, A. A. Golubov, D. Roditchev and V. S. Stolyarov, Nat. Commun., 2019, 10, 4009 CrossRef PubMed.
- P. Hapala, M. Švec, O. Stetsovych, N. J. van der Heijden, M. Ondráček, J. van der Lit, P. Mutombo, I. Swart and P. Jelínek, Nat. Commun., 2016, 7, 11560 CrossRef CAS PubMed.
- D. J. Müller and A. Engel, Nat. Protoc., 2007, 2, 2191–2197 CrossRef PubMed.
- Y. Sugimoto, P. Pou, M. Abe, P. Jelinek, R. Pérez, S. Morita and Ó. Custance, Nature, 2007, 446, 64–67 CrossRef CAS PubMed.
- I. Sokolov, M. E. Dokukin, V. Kalaparthi, M. Miljkovic, A. Wang, J. D. Seigne, P. Grivas and E. Demidenko, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 12920–12925 CrossRef CAS PubMed.
- Y. Zhang, A. Mesaros, K. Fujita, S. D. Edkins, M. H. Hamidian, K. Ch'ng, H. Eisaki, S. Uchida, J. C. S. Davis, E. Khatami and E.-A. Kim, Nature, 2019, 570, 484–490 CrossRef CAS PubMed.
- O. Gordon, P. D'Hondt, L. Knijff, S. E. Freeney, F. Junqueira, P. Moriarty and I. Swart, Rev. Sci. Instrum., 2019, 90, 103704 CrossRef.
- O. M. Gordon, F. L. Q. Junqueira and P. J. Moriarty, Mach. Learn.: Sci. Technol., 2020, 1, 015001 CrossRef.
- M. Rashidi and R. A. Wolkow, ACS Nano, 2018, 12, 5185–5189 CrossRef CAS PubMed.
- O. M. Gordon, J. E. A. Hodgkinson, S. M. Farley, E. L. Hunsicker and P. J. Moriarty, Nano Lett., 2020, 20, 7688–7693 CrossRef CAS PubMed.
- B. Alldritt, P. Hapala, N. Oinonen, F. Urtev, O. Krejci, F. Federici Canova, J. Kannala, F. Schulz, P. Liljeroth and A. S. Foster, Sci. Adv., 2020, 6, eaay6913 CrossRef CAS PubMed.
- F. Zhou, W. Wang, M. Li and L. Liu, Force curve classification using independent component analysis and support vector machine, 9th IEEE International Conference on Nano/Molecular Medicine & Engineering (NANOMED), 2015 Search PubMed.
- E. Minelli, G. Ciasca, T. E. Sassun, M. Antonelli, V. Palmieri, M. Papi, G. Maulucci, A. Santoro, F. Giangaspero, R. Delfini, G. Campi and M. De Spirito, Appl. Phys. Lett., 2017, 111, 143701 CrossRef.
- P. Müller, S. Abuhattum, S. Möllmert, E. Ulbricht, A. V. Taubenberger and J. Guck, BMC Bioinf., 2019, 20, 465 CrossRef PubMed.
- Y. Liu, Q. Sun, W. Lu, H. Wang, Y. Sun, Z. Wang, X. Lu and K. Zeng, Adv. Theory Simul., 2019, 2, 1800137 CrossRef.
- H. Bai and S. Wu, Microsc. Microanal., 2020, 1–11 Search PubMed.
- B. Huang, Z. Li and J. Li, Nanoscale, 2018, 10, 21320–21326 RSC.
- Y. Liu, C. Huang, H. Chen and L. Fu, An On-line Variable Speed Scanning Method with Machine Learning Based Feedforward Control for Atomic Force Microscopy, 12th Asian Control Conference (ASCC), 2019 Search PubMed.
- A. Krull, P. Hirsch, C. Rother, A. Schiffrin and C. Krull, Commun. Phys., 2020, 3, 54 CrossRef.
- P. Leinen, M. Esders, K. T. Schütt, C. Wagner, K.-R. Müller and F. S. Tautz, Sci. Adv., 2020, 6, eabb6987 CrossRef CAS PubMed.
- J. M. Ede and R. Beanland, Sci. Rep., 2020, 10, 8332 CrossRef CAS PubMed.
- A. Esteva, B. Kuprel, R. A. Novoa, J. Ko, S. M. Swetter, H. M. Blau and S. Thrun, Nature, 2017, 542, 115–118 CrossRef CAS PubMed.
- L. Waller and L. Tian, Nature, 2015, 523, 416–417 CrossRef CAS PubMed.
- H. Wang, Y. Rivenson, Y. Jin, Z. Wei, R. Gao, H. Günaydın, L. A. Bentolila, C. Kural and A. Ozcan, Nat. Methods, 2019, 16, 103–110 CrossRef CAS PubMed.
- M. Ziatdinov, O. Dyck, A. Maksov, X. Li, X. Sang, K. Xiao, R. R. Unocic, R. Vasudevan, S. Jesse and S. V. Kalinin, ACS Nano, 2017, 11, 12742–12752 CrossRef CAS PubMed.
- Y. Xiao, Z. Tian, J. Yu, Y. Zhang, S. Liu, S. Du and X. Lan, Multimed. Tools Appl., 2020, 79, 23729–23791 CrossRef.
- Z. Zhao, P. Zheng, S. Xu and X. Wu, IEEE Trans. Neural Netw. Learn. Syst., 2019, 30, 3212–3232 Search PubMed.
- D. G. Lowe, Int. J. Comput. Vis., 2004, 60, 91–110 CrossRef.
- N. Dalal and B. Triggs, Histograms of oriented gradients for human detection, IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), 2005 Search PubMed.
- R. Lienhart and J. Maydt, An extended set of Haar-like features for rapid object detection, International Conference on Image Processing, 2002 Search PubMed.
- C. Cortes and V. Vapnik, Mach. Learn., 1995, 20, 273–297 Search PubMed.
- P. Viola and M. Jones, Rapid object detection using a boosted cascade of simple features, IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), 2001 Search PubMed.
- P. F. Felzenszwalb, R. B. Girshick, D. McAllester and D. Ramanan, IEEE Trans. Pattern Anal. Mach. Intell., 2010, 32, 1627–1645 Search PubMed.
- A. Krizhevsky, I. Sutskever and G. E. Hinton, Commun. ACM, 2017, 60, 84–90 CrossRef.
- Y. Lecun, L. Bottou, Y. Bengio and P. Haffner, Proc. IEEE, 1998, 86, 2278–2324 CrossRef.
- R. Girshick, J. Donahue, T. Darrell and J. Malik, IEEE Trans. Pattern Anal. Mach. Intell., 2016, 38, 142–158 Search PubMed.
- R. Girshick, Fast R-CNN, IEEE International Conference on Computer Vision (ICCV), 2015 Search PubMed.
- S. Ren, K. He, R. Girshick and J. Sun, IEEE Trans. Pattern Anal. Mach. Intell., 2017, 39, 1137–1149 Search PubMed.
- T.-Y. Lin, P. Goyal, R. Girshick, K. He and P. Dollar, Focal loss for dense object detection, IEEE International Conference on Computer Vision (ICCV), 2017 Search PubMed.
- W. Liu, D. Anguelov, D. Erhan, C. Szegedy, S. Reed, C.-Y. Fu and A. C. Berg, SSD: Single Shot MultiBox Detector, Cham, 2016 Search PubMed.
- J. Redmon, S. Divvala, R. Girshick and A. Farhadi, You Only Look Once: Unified, Real-Time Object Detection, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016 Search PubMed.
- J. Redmon and A. Farhadi, YOLO9000: Better, Faster, Stronger, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017 Search PubMed.
- J. Redmon and A. Farhadi, http://arxiv.org/abs/1804.02767, 2018.
- M. Everingham, L. Van Gool, C. K. I. Williams, J. Winn and A. Zisserman, Int. J. Comput. Vis., 2010, 88, 303–338 CrossRef.
- C. J. van Rijsbergen, Information Retrieval, Butterworth-Heinemann, London, GB, Boston, MA, 1979 Search PubMed.
- Z. Wang, A. C. Bovik, H. R. Sheikh and E. P. Simoncelli, IEEE Trans. Image Process., 2004, 13, 600–612 CrossRef PubMed.
- Y. Taigman, M. Yang, M. Ranzato and L. Wolf, Deepface: closing the gap to human-level performance in face verification, IEEE Conference on Computer Vision and Pattern Recognition CVPR, 2014 Search PubMed.
- F. Schroff, D. Kalenichenko and J. Philbin, Facenet: A unified embedding for face recognition and clustering, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015 Search PubMed.
- G. Koch, R. Zemel and R. Salakhutdinov, Siamese neural networks for one-shot image recognition, ICML Deep Learning Workshop, vol. 2, 2015 Search PubMed.
- R. Hadsell, S. Chopra and Y. LeCun, Dimensionality Reduction by Learning an Invariant Mapping, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2006 Search PubMed.
- A. Hermans, L. Beyer and B. Leibe, 2017, arXiv preprint, arXiv:1703.07737.
- K. Simonyan and A. Zisserman, Very Deep Convolutional Networks for Large-Scale Image Recognition, International Conference on Learning Representations, 2015 Search PubMed.
- I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 013705 CrossRef CAS PubMed.
- J. Moukhtar, E. Fontaine, C. Faivre-Moskalenko and A. Arneodo, Phys. Rev. Lett., 2007, 98, 178101 CrossRef CAS PubMed.
- A. Marin-Gonzalez, C. Aicart-Ramos, M. Marin-Baquero, A. Martín-González, M. Suomalainen, A. Kannan, J. G. Vilhena, U. F. Greber, F. Moreno-Herrero and R. Pérez, Nucleic Acids Res., 2020, 48, 12917–12928 CrossRef CAS PubMed.
- D. Pastré, O. Piétrement, S. Fusil, F. Landousy, J. Jeusset, M. O. David, L. Hamon, E. Le Cam and A. Zozime, Biophys. J., 2003, 85, 2507–2518 CrossRef.
- C. Ke, Y. Jiang, P. A. Mieczkowski, G. G. Muramoto, J. P. Chute and P. E. Marszalek, Small, 2008, 4, 288–294 CrossRef CAS PubMed.
- F. Moreno-Herrero, P. Herrero, J. Colchero, A. M. Baró and F. Moreno, Biochem. Biophys. Res. Commun., 2001, 280, 151–157 CrossRef CAS PubMed.
- C. Carrasco, A. Carreira, I. A. T. Schaap, P. A. Serena, J. Gómez-Herrero, M. G. Mateu and P. J. de Pablo, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 13706–13711 CrossRef CAS PubMed.
- K. Choudhary, K. F. Garrity, C. Camp, S. V. Kalinin, R. Vasudevan, M. Ziatdinov and F. Tavazza, Sci. Data, 2021, 8, 57 CrossRef PubMed.
- I. Croitoru, S. Bogolin and M. Leordeanu, Unsupervised Learning from Video to Detect Foreground Objects in Single Images, IEEE International Conference on Computer Vision (ICCV), 2017 Search PubMed.
- R. Joseph, https://pjreddie.com/darknet/, 2016.
- T.-Y. Lin, P. Dollar, R. Girshick, K. He, B. Hariharan and S. Belongie, Feature pyramid networks for object detection, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr01109j |
| This journal is © The Royal Society of Chemistry 2021 |