Open Access Article
Open Access ArticleWide-angle X-ray scattering and molecular dynamics simulations of supercooled protein hydration water†
Maddalena
Bin
 a,
Rafat
Yousif
a,
Sharon
Berkowicz
a,
Rafat
Yousif
a,
Sharon
Berkowicz
 a,
Sudipta
Das
a,
Daniel
Schlesinger
a,
Sudipta
Das
a,
Daniel
Schlesinger
 b and
Fivos
Perakis
b and
Fivos
Perakis
 *a
*a
aDepartment of Physics, AlbaNova University Center, Stockholm University, 106 91 Stockholm, Sweden. E-mail: f.perakis@fysik.su.se
bDepartment of Environmental Science & Bolin Centre for Climate Research, Stockholm University, 106 91 Stockholm, Sweden
First published on 12th July 2021
Abstract
Understanding the mechanism responsible for the protein low-temperature crossover observed at T ≈ 220 K can help us improve current cryopreservation technologies. This crossover is associated with changes in the dynamics of the system, such as in the mean-squared displacement, whereas experimental evidence of structural changes is sparse. Here we investigate hydrated lysozyme proteins by using a combination of wide-angle X-ray scattering and molecular dynamics (MD) simulations. Experimentally we suppress crystallization by accurate control of the protein hydration level, which allows access to temperatures down to T = 175 K. The experimental data indicate that the scattering intensity peak at Q = 1.54 Å−1, attributed to interatomic distances, exhibits temperature-dependent changes upon cooling. In the MD simulations it is possible to decompose the water and protein contributions and we observe that, while the protein component is nearly temperature independent, the hydration water peak shifts in a fashion similar to that of bulk water. The observed trends are analysed by using the water–water and water-protein radial distribution functions, which indicate changes in the local probability density of hydration water.
1 Introduction
Understanding protein structure and dynamics under cryogenic conditions can help accelerate the development of vitrification techniques used in medical applications. This is a key step in the cryostorage of cells used in cancer research1 and in the cryopreservation of microorganisms, such as viruses and bacteria.2,3 Improving vitrification of protein solutions is linked to understanding the physics of supercooling, i.e. cooling solutions well below their freezing point. The properties of water at the protein hydration layer play an important role in supercooling and influence protein function and stability. The hydration level h, defined as the ratio of water over protein mass h = mwater/mprotein, is often used to quantify the hydration of the system.4–6 It was indicated that for proteins with hydration level below h = 0.2, biological activity is diminished, while for those between h = 0.2 and h = 0.5 the activity is enhanced and the functionality is restored.7,8It was previously observed that hydrated proteins undergo a low-temperature crossover,4,5,9–18 also called protein dynamic transition, which occurs at temperature T ≈ 220 K. Below the transition temperature, proteins exhibit reduced conformational flexibility and impaired biological function. To date, different views have been proposed to explain the origin of the low-temperature crossover. One hypothesis associates the transition with the intrinsic temperature dependence of the protein dynamics, which shows a crossover from a harmonic to an anharmonic regime.10 A second hypothesis, instead, proposes that the hydration water is responsible for the observed low-temperature crossover. It is hypothesized that hydration water exhibits a fragile-to-strong transition19 at T ≈ 220 K as indicated by quasi-elastic neutron scattering experiments.4 It has also been proposed that the coupling between protein and solvent deactivates the protein functionality upon cooling below T ≈ 200 K due to the arrest of the collective α-relaxation process occurring at this temperature in hydration water.20 Alternatively, it has been suggested that the transition reflects changes in the hydration water structure associated with the hypothesized low- and high-density liquid (LDL and HDL) phases of water.21,22 In this scenario, the observed crossover reflects the transition from an HDL dominated environment to an LDL dominated one, which occurs while crossing the Widom line. The term Widom line refers to the locus of correlation length maxima in the pressure–temperature plane emanating from the hypothesized liquid–liquid critical point.23 This hypothesis has received additional support, as the Widom line has been observed experimentally in bulk water.24
Here we investigate structural changes in hydrated lysozyme proteins from room temperature down to cryogenic conditions by combining wide-angle X-ray scattering (WAXS) and molecular dynamics (MD) simulations. The experimental scattering intensity exhibits temperature-dependent changes that originate from correlations between water and protein atoms. The MD simulations reproduce well the peak attributed to interatomic length scales and allows to decompose the protein and water contributions. We observe that, while the protein component is nearly temperature-independent, the hydration water peak shifts in a fashion similar to that observed in bulk water. The observed trends are attributed to changes in the local probability density of hydration water, which is quantified by the radial distribution function.
2 Methods
2.1 Experimental methods
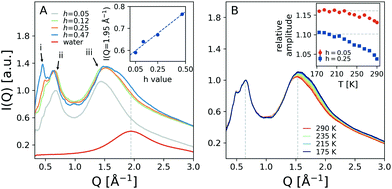
The lysozyme protein used was lyophilized powder from chicken egg white purchased from Sigma–Aldrich (L6876). The powder was grinded with a mortar to reduce the particle size, and used without further purification or drying process. The hydration level estimated was h = 0.05 by means of thermo-gravimetric analysis (TGA, see ESI† 1.1). Lysozyme powder was hydrated by exposing it to water vapor in a closed hydration chamber, controlling the humidity and the exposure time to reach the desired hydration value. Fig. 1A shows the scattering intensity of lysozyme powder samples with different hydration levels, h = 0.25 ± 0.01 (left) and h = 0.47 ± 0.04 (right) measured at T = 235 K. In the case of h = 0.47 crystallization is observed, which is indicated by the presence of Bragg peaks corresponding to crystalline ice (see ESI† 1.2). At the lower hydration level h = 0.25 crystallization is suppressed by confining water in the protein matrix. For more details on the experimental methods and data analysis, see ESI† 1.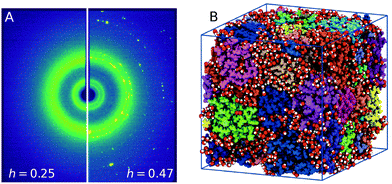 | ||
| Fig. 1 (A) Experimental X-ray scattering patterns of hydrated lysozyme at T = 235 K for different hydration levels, h = 0.25 (left panel) and h = 0.47 (right panel). Freezing is evident for higher hydration levels by the presence of Bragg peaks. (B) A frame from the MD trajectory depicting the 32 proteins (color-coded) used and the water molecules (red – oxygens, white – hydrogens) corresponding to hydration level of h = 0.23. The picture was generated with VMD.30 | ||
2.2 Simulation methods
We performed MD simulations using GROMACS 2019.4 with GPU acceleration support.25 The OPLS-AA force field26 was used for the protein and the TIP4P-EW model for water,27 a combination which was successfully implemented previously and was shown to reproduce the protein low-temperature crossover.28,29 We used 32 proteins (PDB file: 1AKI) for the model and for each protein 8 Cl− counterions were used to neutralise the system. The protein powder model was constructed based on previous methodology,6,16 by starting from a protein crystal lattice consisting of 32 proteins. The proteins were hydrated by introducing a water layer of a given thickness in order to reach the desired hydration values. A water layer of thickness 0.23 nm yielded a hydration value h = 0.23, corresponding to ≈170 water molecules per protein. The resulting triclinic box size was ≈89 Å × 86 Å × 103 Å and the total number of atoms was 84′756, including 5′445 water molecules. A snapshot of the simulation is shown in Fig. 1B, where the different colors indicate the separate proteins and water molecules. The simulation of bulk TIP4P-EW water was performed using an identical protocol and matching box size, containing 24'200 water molecules.The system was initially equilibrated at T = 300 K for 10 ns in the NVT ensemble, using a 2 fs time step. In addition, we performed equilibration in the NPT ensemble for 10 ns using the Berendsen barostat31 followed by additional longer NPT equilibration for temperatures ranging from T = 180 K to T = 300 K with 10 K steps and P = 1 atm using the Parrinello–Rahman barostat.32 The density as a function of the equilibration time is shown in the ESI† 2.1. Production runs were performed for 100 ns using the Parrinello–Rahman barostat for all temperatures. The X-ray scattering intensity calculations were performed based on Cromer-Mann method33–35 (see ESI† 2.2).
3 Results
3.1 Experimental results
Fig. 2A shows the temperature dependence of the angularly integrated scattering intensity of hydrated lysozyme with variable hydration levels, ranging from h = 0.05 to h = 0.47. The peak at lower momentum transfer exhibits two sub-peaks at Q = 0.50 Å−1 and Q = 0.65 Å−1, labeled as i and ii, which arise due to the protein packing arrangements and secondary structures36 and are enhanced with increasing hydration level. Moreover, the peak at Q = 1.54 Å−1, labeled iii, relates to the interatomic distances and contains contributions from both protein and water molecules.36 The scattering intensity of bulk water, shown for comparison, exhibits a peak centered near Q = 1.95 Å−1, marked by a vertical line. At this momentum transfer, the scattering intensity of peak iii of hydrated lysozyme is shown in the inset as a function of the hydration level. We observe a monotonic increase of the scattering intensity as the hydration level increases, which is consistent with the larger number of water molecules in the sample.The scattering intensities of samples with hydration level h = 0.25 are plotted in Fig. 2B for temperatures ranging from T = 175 K to T = 290 K (colored lines). In the inset of Fig. 2B the relative scattering intensities of peaks ii and iii are shown as a function of temperature (blue squares). Here we used the ratio between peak iii over peak ii, marked in Fig. 2B by vertical lines, since the absolute intensity of the peaks depends on experimental factors, such as the protein packing fraction and sample thickness. The relative amplitude exhibits a rapid change upon cooling and the data suggest a slope change below ≈220 K. We note here that a similar trend is also observed to a lesser extent in hydrated proteins with h = 0.05, shown as red circles. This observation indicates that the observed temperature dependence is sensitive to the amount of water in the sample. A similar trend is observed for the peak Q-position, which shifts towards increasing momentum transfer upon cooling (ESI† 1.5).
3.2 MD simulations results
In addition, we performed MD simulations, as described in the methods section and ESI† 1.2. The simulated scattering intensity with h = 0.23 is shown in Fig. 3A (circles) for the temperatures T = 290, 220, 180 K. The overall line shape matches that of the experiment (solid lines) with the two peaks at Q = 0.65 Å−1 and Q = 1.54 Å−1. The region below Q = 0.5 Å−1 exhibits an increase of the scattering intensity, which is attributed to possible voids and finite size effects in the simulations, as indicated in Fig. 3C. Such void effects can also influence the experimental data, although they mainly affect the lower momentum transfer region Q < 0.1 Å−1 due to the density difference at the protein–air interface of lysozyme powders.36 However we are able to reproduce the peak related to interatomic distances, which contains contributions from both water and protein molecules and according to the experiment exhibits the more significant temperature dependence. | ||
| Fig. 3 Molecular dynamics simulation results: (A) a comparison between the experimental (solid lines) and simulated (circles) scattering intensity at the temperatures indicated. (B) The total simulated scattering intensity (black line) is decomposed to the components arising from the protein (blue) and water (red) molecules, calculated by selecting the corresponding sub-assemblies, as indicated in panel (C). The scattering intensity of water has been scaled by a factor 4 in order to facilitate comparison. The pictures were generated with VMD.30 | ||
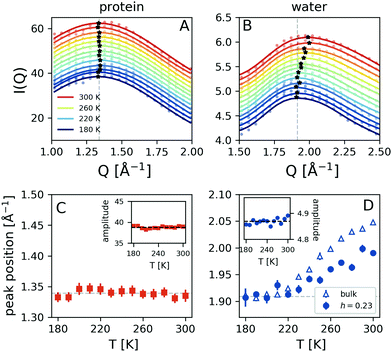
In order to decompose the possible contributions to the I(q), we calculated separately the scattering intensity by selecting in the simulation either only the water molecules or the protein molecules, as shown in Fig. 3C. The resulting contributions (red for water and blue for proteins) are depicted in Fig. 3B along with that of the total scattering intensity simulated from the complete system (black). Note that the scattering intensity of water has been scaled by a factor 4 in order to facilitate comparison. The results indicate that the protein scattering intensity gives a peak at Q = 1.35 Å−1 whereas the water exhibits a peak at Q ≈ 2 Å−1.
The temperature dependence of the simulated scattering intensity from the protein and water molecules is shown in Fig. 4A and B. This comparison reveals that the peak position arising from the protein molecules does not show any temperature dependence, whereas the peak arising from water shifts to lower momentum transfer upon cooling (panels C and D). The data indicate that there is a crossover occurring at T ≈ 220 K, as indicated by the dashed line. Here the data obtained from simulated bulk water are also depicted, which exhibits a similar trend. The corresponding amplitudes of the protein and hydration water components do not exhibit significant temperature-dependence, as indicated in the insets of panels Fig. 4C and D. The observed temperature dependence is consistent with the experimental trends shown in Fig. 2B. As the water peak shifts to lower Q upon cooling it contributes with increased intensity to the high momentum transfer of iii peak, which effectively shifts its resulting maximum to higher Q. At the same time, the difference in momentum transfer between the water and protein peak positions is reduced upon cooling, which can explain the amplitude increase of peak iii. The overall signal contains additional contributions due to the protein–water correlations, which we analyse by calculating the radial distribution function g(r).
3.3 Radial distribution functions
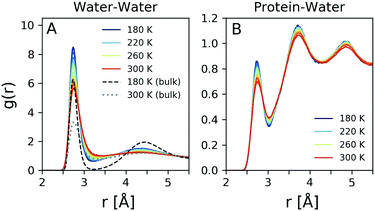
The radial distribution function g(r) is related by Fourier transform to the scattering intensity I(q), after applying the appropriate treatment to obtain the structure factor.37 Thus, it is in principle possible to obtain the total g(r) experimentally, although the Fourier transform makes the result sensitive to the high momentum transfer measured.37 In order to obtain reliable results one needs to utilise high photon energy X-ray diffraction, which allows to capture the structure factor to high momentum transfer. Here the g(r) is calculated directly from the MD simulation and reflects the changes observed in Fig. 4D. The oxygen–oxygen g(r) of hydration water was computed at temperatures from 180 K to 300 K and is shown in Fig. 5A for h = 0.23 (solid lines) compared to that of simulated bulk water for T = 180 K (dashed line) and T = 300 K (dotted line). The peak positions of bulk water agree closely with previous experimental values.37–41Here we observe significant changes in both the first and second coordination shell upon cooling, with the lineshape becoming more narrow and the amplitudes increasing. The fact that the amplitude of the first peak is significantly enhanced in hydration water indicates an increased number of first neighbor water–water distances due to the confinement. The second peak in the g(r) corresponds to the second coordination shell and correlates to the tetrahedral distance,42 which becomes more pronounced upon cooling. This trend is similar to the temperature dependence of bulk water, although in the case of hydration water the second coordination shell exhibits less pronounced changes. In addition, the region between the two coordination shells, referred to as the interstitial region, is gradually depleted upon cooling. Again here, this depletion is more pronounced for bulk water (black dashed line). The observation that the second peak amplitude is less pronounced in hydration water in comparison to the bulk, in combination with the reduced changes in the interstitial region, indicates that hydration water is on average less tetrahedral than bulk water, as suggested previously.43,44
It was shown previously that one can obtain information about the local density of water by analysis of the protein-water radial distribution function.45 Here, we adapt a similar approach by estimating the protein–water radial distribution function, depicted in Fig. 5B. This quantity refers to the distribution of distances of water from protein atoms, excluding hydrogen atoms. The first coordination shell is located in a similar position with that of the oxygen–oxygen radial distribution function, shown in Fig. 5A, although the amplitude is reduced. The second and third coordination shells are more narrow and well defined than in the case of the oxygen–oxygen radial distribution function. This is consistent with previous simulations, where it was shown that the protein–water radial distribution function can change significantly between hydrated and non-hydrated protein sites.46 Interestingly here the second and third coordination shells are better defined than in the case of the oxygen–oxygen radial distribution function, indicating the influence of the protein on the local hydration water coordination.
4 Conclusions
Experimentally, we investigated lysozyme powders with a variable hydration level and utilised the appropriate hydration value (h = 0.25) that allows us to suppress crystallization. The scattering intensity exhibits two main contributions: the low-Q peaks are attributed to length scales associated with the protein packing arrangements and secondary structures, whereas the high-Q peak is attributed to interatomic distances.36 We mainly observed temperature-dependent changes in the relative amplitude and peak position of the latter.The MD simulations reproduce well the scattering peak associated with interatomic distances and allows to decompose the protein and water contribution to the scattering intensity. The protein component appears to be independent of temperature, whereas the water peak exhibits a shift upon decreasing temperature, similar to that of bulk water. The difference between the water and protein peak positions is reduced upon cooling, which can explain the experimentally observed trends. Previous experiments in deeply supercooled water indicate that a similar shift towards lower momentum transfer is indicated upon cooling.24 Here we observe that the water peak shift is diminished below 220 K, in both hydration and bulk water.
The structure of hydration water is further examined by use of the radial distribution function g(r). The oxygen–oxygen g(r) indicates that the hydration water is, on average, less tetrahedral than bulk water, presumably due to the influence from the protein matrix44 and resembles bulk water at elevated pressures.43 Upon cooling the relative amount of tetrahedral coordination increases, as indicated by changes in the second coordination shell. The trend observed in the local probability density is consistent with the crossover occurring from an HDL-like to an LDL-like local environment, in agreement with previous MD simulations of the hydration water around lysozyme in solution, where it was observed that the tetrahedrality parameter exhibits a crossover at a similar temperature range.22 One should note here that the local hydrogen bond environment of bulk water can be different from the confined water, a fact indicated by the suppression of freezing due to confinement.47,48 The protein–water radial distribution function g(r) indicates that the proteins influence strongly the coordination of hydration water, which results in pronounced second and third coordination shells.
There is evidence that the dynamical properties of hydration water, such as the diffusion coefficient, also exhibit an abrupt change in this same temperature range.4,17,28 This observation has led to the proposal that a fragile-to-strong transition occurs in water,4 which has been recently interpreted as a transition between HDL and LDL liquids.49,50 From this perspective, it would be interesting to investigate the translational dynamics of protein hydration water by using state-of-the-art coherent X-ray scattering techniques, such as X-ray photon correlation spectroscopy.51
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
We would like to thank Petra Björk for help with the development of the sample preparation protocol, Giovanni Marco Saladino for the TGA measurements, as well as Gaia Camisasca and Katrin Amann-Winkel for useful discussions and comments on the manuscript. We acknowledge financial support by the Swedish National Research Council (Vetenskapsrådet) under Grant No. 2019-05542 and within the Röntgen-Ångström Cluster Grant No. 2019-06075. This research is part of the MaxWater initiative of the Max-Planck Society. The simulations were performed using resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre (NSC) and the High-Performance Computing Centre North (HPC2N) with project numbers 2020/5-28, 2020/9-36 and 2020/10-20.References
- G. M. Fahy, D. R. MacFarlane, C. A. Angell and H. T. Meryman, Cryobiology, 1984, 21, 407–426 CrossRef CAS PubMed.
- Z. Hubálek, Cryobiology, 2003, 46, 205–229 CrossRef.
- P. Brüggeller and E. Mayer, Nature, 1980, 288, 569–571 CrossRef.
- S.-H. Chen, L. Liu, E. Fratini, P. Baglioni, A. Faraone and E. Mamontov, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 9012–9016 CrossRef CAS PubMed.
- J. H. Roh, J. E. Curtis, S. Azzam, V. N. Novikov, I. Peral, Z. Chowdhuri, R. B. Gregory and A. P. Sokolov, Biophys. J., 2006, 91, 2573–2588 CrossRef CAS PubMed.
- M. Tarek and D. J. Tobias, Biophys. J., 2000, 79, 3244–3257 CrossRef CAS PubMed.
- J. A. Rupley and G. Careri, Adv. Protein Chem., 1991, 41, 37–172 CrossRef CAS PubMed.
- C. L. Brooks, M. Karplus and B. M. Pettitt, Proteins: A Theoretical Perspective of Dynamics, Structure and Thermodynamics, in Advances in Chemical Physics, John Wiley & Sons, New York, 1988, vol. 71 Search PubMed.
- F. Parak and E. W. Knapp, Proc. Natl. Acad. Sci. U. S. A., 1984, 81, 7088–7092 CrossRef CAS PubMed.
- W. Doster, S. Cusack and W. Petry, Nature, 1989, 337, 754–756 CrossRef CAS PubMed.
- B. F. Rasmussen, A. M. Stock, D. Ringe and G. A. Petsko, Nature, 1992, 357, 423–424 CrossRef CAS PubMed.
- D. Vitkup, D. Ringe, G. A. Petsko and M. Karplus, Nat. Struct. Biol., 2000, 7, 34–38 CrossRef CAS PubMed.
- D. Ringe and G. A. Petsko, Biophys. Chem., 2003, 105, 667–680 CrossRef CAS PubMed.
- F. Mallamace, M. Broccio, C. Corsaro, A. Faraone, U. Wanderlingh, L. Liu, C.-Y. Mou and S. H. Chen, J. Chem. Phys., 2006, 124, 161102 CrossRef CAS PubMed.
- S. Pawlus, S. Khodadadi and A. P. Sokolov, Phys. Rev. Lett., 2008, 100, 108103 CrossRef CAS PubMed.
- M. Tarek and D. J. Tobias, Phys. Rev. Lett., 2002, 88, 138101 CrossRef CAS PubMed.
- G. Camisasca, M. De Marzio, D. Corradini and P. Gallo, J. Chem. Phys., 2016, 145, 044503 CrossRef CAS PubMed.
- S. Magazù, F. Migliardo and A. Benedetto, J. Phys. Chem. B, 2011, 115, 7736–7743 CrossRef PubMed.
- P. G. Debenedetti, Nature, 2001, 410, 259–267 CrossRef CAS PubMed.
- J. Swenson, H. Jansson and R. Bergman, Phys. Rev. Lett., 2006, 96, 247802 CrossRef PubMed.
- P. H. Poole, F. Sciortino, U. Essmann and H. E. Stanley, Nature, 1992, 360, 324–328 CrossRef CAS.
- P. Kumar, Z. Yan, L. Xu, M. G. Mazza, S. V. Buldyrev, S.-H. Chen, S. Sastry and H. E. Stanley, Phys. Rev. Lett., 2006, 97, 177802 CrossRef PubMed.
- L. Xu, P. Kumar, S. V. Buldyrev, S.-H. Chen, P. H. Poole, F. Sciortino and H. E. Stanley, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 16558–16562 CrossRef CAS PubMed.
- K. H. Kim, A. Späh, H. Pathak, F. Perakis, D. Mariedahl, K. Amann-Winkel, J. A. Sellberg, J. H. Lee, S. Kim, J. Park, K. H. Nam, T. Katayama and A. Nilsson, Science, 2017, 358, 1589–1593 CrossRef CAS PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1-2, 19–25 CrossRef.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- H. W. Horn, W. C. Swope and J. W. Pitera, J. Chem. Phys., 2005, 123, 194504 CrossRef PubMed.
- M. Lagi, P. Baglioni and S.-H. Chen, Phys. Rev. Lett., 2009, 103, 108102 CrossRef PubMed.
- M. Lagi, X. Chu, C. Kim, F. Mallamace, P. Baglioni and S.-H. Chen, J. Phys. Chem. B, 2008, 112, 1571–1575 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- D. T. Cromer and J. B. Mann, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1968, 24, 321–324 CrossRef CAS.
- H. T. Nguyen, S. A. Pabit, S. P. Meisburger, L. Pollack and D. A. Case, J. Chem. Phys., 2014, 141, 22D508 CrossRef PubMed.
- S. Park, J. P. Bardhan, B. Roux and L. Makowski, J. Chem. Phys., 2009, 130, 134114 CrossRef PubMed.
- T. Phan-Xuan, E. Bogdanova, A. Millqvist Fureby, J. Fransson, A. E. Terry and V. Kocherbitov, Mol. Pharmaceutics, 2020, 17, 3246–3258 CrossRef CAS PubMed.
- L. B. Skinner, C. Huang, D. Schlesinger, L. G. M. Pettersson, A. Nilsson and C. J. Benmore, J. Chem. Phys., 2013, 138, 074506 CrossRef PubMed.
- A. K. Soper, Chem. Phys., 2000, 258, 121–137 CrossRef CAS.
- A. H. Narten and H. A. Levy, J. Chem. Phys., 1971, 55, 2263–2269 CrossRef CAS.
- A. H. Narten, W. E. Thiessen and L. Blum, Science, 1982, 217, 1033–1034 CrossRef CAS PubMed.
- K. Amann-Winkel, M.-C. Bellissent-Funel, L. E. Bove, T. Loerting, A. Nilsson, A. Paciaroni, D. Schlesinger and L. Skinner, Chem. Rev., 2016, 116, 7570–7589 CrossRef CAS PubMed.
- J. A. Sellberg, C. Huang, T. A. McQueen, N. D. Loh, H. Laksmono, D. Schlesinger, R. G. Sierra, D. Nordlund, C. Y. Hampton, D. Starodub, D. P. DePonte, M. Beye, C. Chen, A. V. Martin, A. Barty, K. T. Wikfeldt, T. M. Weiss, C. Caronna, J. Feldkamp, L. B. Skinner, M. M. Seibert, M. Messerschmidt, G. J. Williams, S. Boutet, L. G. M. Pettersson, M. J. Bogan and A. Nilsson, Nature, 2014, 510, 381–384 CrossRef CAS PubMed.
- D. Russo, A. Laloni, A. Filabozzi and M. Heyden, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 11410–11415 CrossRef CAS PubMed.
- F. Merzel and J. C. Smith, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5378–5383 CrossRef CAS PubMed.
- J. N. Dahanayake and K. R. Mitchell-Koch, Phys. Chem. Chem. Phys., 2018, 20, 14765–14777 RSC.
- G. Camisasca, A. Iorio, M. De Marzio and P. Gallo, J. Mol. Liq., 2018, 268, 903–910 CrossRef CAS.
- A. Faraone, L. Liu, C.-Y. Mou, C.-W. Yen and S.-H. Chen, J. Chem. Phys., 2004, 121, 10843–10846 CrossRef CAS PubMed.
- S. Cerveny, F. Mallamace, J. Swenson, M. Vogel and L. Xu, Chem. Rev., 2016, 116, 7608–7625 CrossRef CAS PubMed.
- R. Shi, J. Russo and H. Tanaka, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9444–9449 CrossRef CAS PubMed.
- N. J. Hestand and J. L. Skinner, J. Chem. Phys., 2018, 149, 140901 CrossRef PubMed.
- F. Perakis and C. Gutt, Phys. Chem. Chem. Phys., 2020, 22, 19443–19453 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1cp02126e |
| This journal is © the Owner Societies 2021 |