Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Voltage hysteresis during lithiation/delithiation of graphite associated with meta-stable carbon stackings†
Michael Peter
Mercer‡
 *abc,
Chao
Peng‡
*abc,
Chao
Peng‡
 cd,
Cindy
Soares
cd,
Cindy
Soares
 a,
Harry Ernst
Hoster
a,
Harry Ernst
Hoster
 abc and
Denis
Kramer
abc and
Denis
Kramer
 cde
cde
aDepartment of Chemistry, Lancaster University, Bailrigg, Lancaster LA1 4YB, UK. E-mail: m.mercer1@lancaster.ac.uk
bALISTORE European Research Institute, CNRS FR 3104, Hub de l'Energie, Rue Baudelocque, Amiens, 80039, France
cThe Faraday Institution, Quad One, Harwell Science and Innovation Campus, Didcot, UK
dSchool of Engineering, University of Southampton, Southampton, SO17 1BJ, UK
eFaculty of Mechanical Engineering, Helmut-Schmidt University, Holstenhofweg 85, 22043 Hamburg, Germany
First published on 27th November 2020
Abstract
Cell voltage is a fundamental quantity used to monitor and control Li-ion batteries. The open circuit voltage (OCV) is of particular interest as it is believed to be a thermodynamic quantity, free of kinetic effects and history and, therefore, “simple” to interpret. Here we show that the OCV characteristics of graphite show hysteresis between charge and discharge that do not solely originate from Li dynamics and that the OCV is in fact history dependent. Combining first-principles calculations with temperature-controlled electrochemical measurements, we identify a residual hysteresis that persists even at elevated temperatures of greater than 50 °C due to differences in the phase succession between charge and discharge. Experimental entropy profiling, as well as energies and volume changes determined from first-principles calculations, suggest that the residual hysteresis is associated with different host lattice stackings of carbon and is related to Li disorder across planes in stage II configurations.
1 Introduction
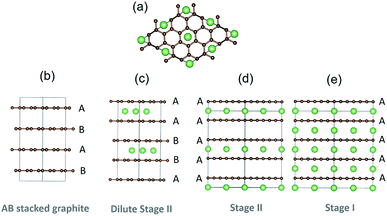
Graphite is ubiquitous as the primary anode material in lithium-ion batteries and has been the subject of extensive research, because of its high capacity, long cycle life, low operating voltage and high safety. Lithium (de)intercalation in graphite proceeds through a variety of stages, denoted “stage n”, where n is the number of graphene layers between each lithium-filled layer.1–4 The stages adopt different stackings in the carbon host lattice, as shown in Fig. 1. The nomenclature introduced elsewhere5 denotes the carbon stacking and Li occupancies: periodic carbon layer stackings along the [001] axis are designated by uppercase letters separated by Greek lowercase letters if Li is intercalated between planes. For instance, pristine graphite (x = 0) is AB stacked, while fully lithiated stage I LiC6 (x = 1) adopts AαAαAα stacking.3,6,7 Here α denotes a lithium filled layer and x is the fraction of Li in LixC6 (0 ≤ x ≤ 1).Table 1 summarises the current consensus on the stages formed during lithiation and delithiation of graphite, as obtained from in situ electrochemical X-ray diffraction (XRD) and neutron diffraction,1,2,7–12 spectroscopic measurements13,14 and X-ray ex situ analysis of compounds obtained by heat treatment.3
| Stage | Stacking | x in LixC6 |
|---|---|---|
| Stage I | AαAα | x = 1 (LiC6) |
| Stage II | AαAAαA | x = 0.5 (LiC12) |
| Dilute stage II (IID) | AαABβB | x ≈ 0.33 (LiC18) |
| Stage III | AαAB/AαABAαAC | x ≈ 0.22 (LiC27) |
| Stage IV | Unknown | x ≈ 0.17 (LiC36) |
| Dilute stage I (ID) | AB | x ≈ 0.083 (LiC72) |
| Graphite | AB | x = 0 |
In the higher stages III and IV proposed based on electrochemical and XRD measurements,1,2 the host lattice stacking is still either hypothetical or disputed. Diffraction and electrochemical dQ/dV features from these stages showed a complex temperature dependence.1,18 The associated XRD peaks are broader, indicating less long range order, so those stages are less important for interpreting the electrochemical behaviour than those indicated in Fig. 1.
The measured open circuit voltage (OCV) is sometimes erroneously considered equivalent to the equilibrium potential. However, the OCV refers to the measured voltage without any external current and so can drift with time. It is usually assumed that given sufficient time, the OCV will relax to the equilibrium potential, but meta-stable states can occur that show no variation over experimental time scales of hours or even days.19,20 The true equilibrium potential is a thermodynamic quantity and is not history dependent.21 A hysteresis between lithiation and delithiation of the measureable OCV is observed even for Li/graphite half cells,1,2,7,12,22–25 suggesting that the measured full cell OCV is not a simple function of the thermodynamic ground state. In control-oriented models for Battery Management Systems (BMS), small errors in OCV measurement can lead to large state of charge determination errors. It is possible to model OCV hysteresis empirically to account for these errors.26 The lack of a one-to-one relationship between the OCV and the state of charge could lead to incorrect battery management and control decisions, leading to degradation and safety issues.
There is a clear need to better comprehend the measured OCV hysteresis in graphite7,12,23,24 and therefore the OCV of nearly all commercial Li-ion cells. Larger hysteresis in graphitic anodes is associated with greater turbostratic disorder or a random deviation from ideal AB stacking.22,27 Hysteresis has also been observed in other carbon anodes such as hydrogen-containing carbons,28 mesoporous carbon microbeads29 and in cathode materials such as lithium iron phosphate (LFP),19 excess lithium layered cathodes,30,31 CoP conversion materials32 and proposed Na-ion intercalation hosts.33 The cited works suggest an influence of electrode nanosizing and host lattice disorder on the measured voltage hysteresis. Therefore, an improved understanding of the hysteresis mechanisms in graphite could also inform a better understanding of the origins of hysteresis in other intercalation and conversion materials.
To clarify the role of kinetics of lithiation/delithiation, versus a true path dependency on the OCV hysteresis in graphite, extending the measurement relaxation time indefinitely is unfeasible. Alternatively, the temperature can be varied to separate processes by activation energy. Surprisingly, the temperature-dependence of the OCV over a wider range than near room temperature (i.e., 20–30 °C) hasn't attracted much attention yet. Varying the temperature under OCV relaxation conditions also allows the entropic and enthalpic origins of the OCV hysteresis to be separated.23,30 First-principles calculations, such as the cluster expansions of different stage I and stage II compounds performed by Persson et al.,34 can also provide insights into the phase behaviour and kinetics of the staging phenomena. However, Persson et al. did not explicitly consider the rearrangement of the carbon layers during transitions between stages, motivating an extension of current understanding through a combined experimental/theoretical approach.
We hypothesise that the experimentally observed OCV hysteresis between lithiation and delithiation in slow continuous galvanostatic measurements and in galvanostatic intermittant titration technique (GITT) experiments originates from different carbon stacking pathways during lithiation versus delithiation.6,11,35,36In situ XRD suggests stage I and stage II coexistence for x ≥ 0.5 within an AAAA stacked host lattice in both cycling directions.8,9 Previous in situ measurements have failed to fully resolve the host lattice configurations for lithium filling x < 0.5.8,9,12,37 Therefore, a combination of carefully designed experiments and ab initio calculations is used to substantiate this interpretation.
The paper is structured as follows. The measureable OCV is thoroughly characterised through GITT experiments in both cycling directions and as a function of temperature. From the temperature dependence of the OCV, we show that energetic and entropic contributions to the OCV differ depending on cycle direction. Supported by first-principles total energy calculations, the energetic contribution is attributed to carbon stacking differences, with AA-type stackings persisting for x < 0.5 during delithiation. The measured entropic differences, on the other hand, originate from an increased amount of Li in formally empty layers during delithiation resulting in additional configurational entropy.
The existence of meta-stable carbon stackings suggests a significant activation energy for carbon layer shifts, which climbing-image nudged elastic band (CI-NEB) calculations show to not exist in perfectly ordered stage II configurations at 0 K. Rather, we propose that the levels of residual Li occupying formally empty layers alters the energy landscape of carbon stackings, resulting in the persistence of meta-stable AA-type stackings for x < 0.5 during delithiation. Further evidence of a different stacking behaviour is provided by comparing previously reported experimental graphite volume changes dependent on cycling direction with expected trends from Density Functional Theory (DFT) calculations.
2 Methods
2.1 Electrode and cell preparation
Carbon working electrodes were prepared by a mixture of graphite powder (particle size <20 μm, synthetic, Sigma-Aldrich), Super P carbon and polyvinylidene fluoride (PVDF) in N-methyl-2-pyrrolidone (NMP) in a mass ratio of 93![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, respectively. The slurry was then cast onto copper foil using a doctor blade, dried and calendared to approximately 80–90 μm thickness to make the working electrode.
2, respectively. The slurry was then cast onto copper foil using a doctor blade, dried and calendared to approximately 80–90 μm thickness to make the working electrode.
Stainless steel CR2032 coin cells were used for all measurements. Cells were prepared in an Argon-filled glovebox ([H2O] < 0.1 ppm, [O2] < 0.1 ppm) with Celgard separator and a 1 M LiPF6 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 wt/wt mixture of ethyl carbonate (EC) and dimethyl carbonate (DMC) electrolyte. Working electrodes of 12 mm diameter were punched out the film using a disc cutter. An oversized 16 mm Li foil was used as counter and reference electrode to mitigate effects from inhomogeneous lithiation. All voltages are, consequently, reported with respect to metallic Li. Experimental measurements were performed using aluminium heat exchangers, in direct thermal contact with the coin cells, which were connected to a Julabo F12 refrigerated – heating circulator, allowing direct control over the cell temperatures. This setup enabled more rapid thermal equilibration of the cells than would be possible using a climate chamber. Temperature was monitored by type-J thermocouples in direct contact with the heat exchangers. A Keysight 34972A data acquisition system with multiplexer unit was used for high resolution (22 bit) voltage and temperature measurements, assisting post processing of entropy profile data. Cell current and voltage was controlled by a BaSyTec CTS cycler. A software interface between the data acquisition unit and the battery cycler allowed real time measurement of temperature, current and voltage to the required resolution. Data points were recorded every 1 s. Further details of the setup can be found in earlier publications.38–40
1 wt/wt mixture of ethyl carbonate (EC) and dimethyl carbonate (DMC) electrolyte. Working electrodes of 12 mm diameter were punched out the film using a disc cutter. An oversized 16 mm Li foil was used as counter and reference electrode to mitigate effects from inhomogeneous lithiation. All voltages are, consequently, reported with respect to metallic Li. Experimental measurements were performed using aluminium heat exchangers, in direct thermal contact with the coin cells, which were connected to a Julabo F12 refrigerated – heating circulator, allowing direct control over the cell temperatures. This setup enabled more rapid thermal equilibration of the cells than would be possible using a climate chamber. Temperature was monitored by type-J thermocouples in direct contact with the heat exchangers. A Keysight 34972A data acquisition system with multiplexer unit was used for high resolution (22 bit) voltage and temperature measurements, assisting post processing of entropy profile data. Cell current and voltage was controlled by a BaSyTec CTS cycler. A software interface between the data acquisition unit and the battery cycler allowed real time measurement of temperature, current and voltage to the required resolution. Data points were recorded every 1 s. Further details of the setup can be found in earlier publications.38–40
All freshly assembled cells were subjected to a formation protocol before use: three full galvanostatic charge–discharge cycles were performed at a rate of 37.2 mA g−1 (determined from the active material mass of graphite) corresponding to a C/10 rate. These cycles were performed between voltage limits of 0.050 and 1.500 V, at a controlled temperature of 25 °C. Similar procedures have been used elsewhere39,41 and are intended to ensure stable solid electrolyte interphase (SEI) formation and representative cycling performance before performing the slower characterisation techniques described in the next sections.
2.2 Constant current/constant voltage protocols
All continuous galvanostatic, GITT and entropy profiling measurements described subsequently were preceded by a constant current/constant voltage (dis)charging protocol, designated “CCCV (dis)charge”, to ensure a consistent starting lithiation state for each experiment. A CCCV charge consists of galvanostatic delithiation at C/20 (18.6 mA g−1) up to 1.5 V, followed by at least 2 hours of polarisation at 1.5 V. A CCCV discharge starts with galvanostatic lithiation at C/25 (14.88 mA g−1) down to 0.005 V, followed by at least 2 hours of polarisation at 0.005 V. The low C-rate here was designed to mitigate the risk of lithium plating so close to 0 V, while allowing lithiation as close as possible to the ideal LiC6 structure (x = 1).2.3 Determination of thermodynamic profiles
Relevant thermodynamic variables are defined here to ensure consistency between experimental and DFT results in the following sections and to ensure those results are compared on equivalent energy and lithium concentration scales.It is well known that the equilibrium cell voltage, ϕ(x) and chemical potential of intercalated Li, μ(x) are related as
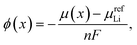 | (1) |
| ϕ(x) = −μ(x). | (2) |
The intercalated Li chemical potential is defined by
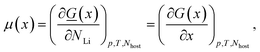 | (3) |
![[G with combining low line]](https://www.rsc.org/images/entities/i_char_0047_0332.gif) = the absolute (i.e. extensive) Gibbs free energy, p = pressure, T = the absolute temperature, Nhost and NLi are respectively the number of carbon and lithium atoms in the system. As there is one Li atom per LiC6 formula unit, with x expressing the fraction of lithium in LixC6 (0 ≤ x ≤ 1), i.e. x = NLi/(6Nhost). G is the Gibbs free energy per formula unit of 6C. The subscripts p, T and Nhost will be implicitly assumed constant from now on and dropped for simplicity.
= the absolute (i.e. extensive) Gibbs free energy, p = pressure, T = the absolute temperature, Nhost and NLi are respectively the number of carbon and lithium atoms in the system. As there is one Li atom per LiC6 formula unit, with x expressing the fraction of lithium in LixC6 (0 ≤ x ≤ 1), i.e. x = NLi/(6Nhost). G is the Gibbs free energy per formula unit of 6C. The subscripts p, T and Nhost will be implicitly assumed constant from now on and dropped for simplicity.
Likewise it is well known that
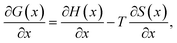 | (4) |
Assuming that the OCV, EOCV, measured at the end of the relaxation period for each x value corresponds to ϕ(x), we can use eqn (2)–(4) to get ∂G/∂x = −EOCV. Then, taking the derivative of the OCV with respect to T and using the chain rule, we obtain
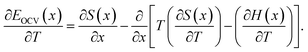 | (5) |
However,
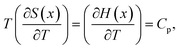 | (6) |
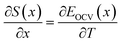 | (7) |
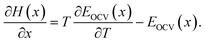 | (8) |
Due to the choice of units of eV per formula unit for the potentials H(x) and TS(x), i.e. as in the conversion between eqn (1) and (2), the usual factors of F have been omitted. All of the terms in eqn (7) and (8) are measurable using methods described in Section 2.4.
2.4 Entropy profiling and open circuit voltage measurement
We used similar methods as in our previous work to obtain entropy profiles under lithiation conditions.38–40 The method is akin to GITT, comprising alternating steps under galvanostatic control followed by relaxation under open circuit conditions, but in addition the temperature is varied during the relaxation period and entropy is calculated from the gradient of OCV with temperature. Measurements comprised iterative steps of galvanostatic (dis)charge at C/25 followed by a total of 80 minutes of relaxation time.All entropy profiling measurements were preceded by a constant current/constant voltage (dis)charging protocol, designated “CCCV (dis)charge”, to ensure a consistent starting lithiation state for each experiment. A CCCV charge consisted of galvanostatic delithiation at C/20 (18.6 mA g−1) up to 1.5 V, followed by at least 2 hours of polarisation at 1.5 V. A CCCV discharge started with galvanostatic lithiation at C/25 (14.88 mA g−1) down to 0.005 V, followed by at least 2 hours of polarisation at 0.005 V. The low C-rate here was designed to mitigate the risk of lithium plating so close to 0 V, while allowing lithiation as close as possible to the ideal LiC6 structure (x = 1).
Entropy profiling in lithiation mode was performed in an iterative procedure, where the current and temperature were changed dynamically as outlined in Table 2. The central temperature, Tc was varied as indicated in the results section. Entropy measurements comprising iterative steps of galvanostatic discharge were initiated by performing a “CCCV charge” step at T = Tc + 3 °C. Each iteration was repeated until the cell voltage was less than 0.005 V, mirroring the cutoff voltage of the CCCV discharge procedure. State of charge, x, was obtained from normalising the change of capacity from each galvanostatic step in Table 2 to the total change of capacity obtained during the entire experiment.
| Step | Time (min) | Temperature T (°C) | Applied T at Tc = 25 °C |
|---|---|---|---|
| Discharge (C/25) | 20 | T c + 3 | 28 |
| OC at T1 | 20 | T c + 3 | 28 |
| OC at T2 | 20 | T c | 25 |
| OC at T3 | 20 | T c − 3 | 22 |
| OC at T1 | 20 | T c + 3 | 28 |
We also performed a set of measurements where profiles were initiated from a “CCCV discharge” at T = Tc + 3 °C, and the graphite electrode was delithiated stepwise at C/25. These experiments were cut off once the cell voltage reached a value greater than 1.5 V. The temperature program in Table 2 was also used here, except that step 1 was a charge rather than a discharge.
The target variable from the temperature program shown in Table 2 is the slope of the open circuit voltage (EOCV) with respect to temperature, i.e. (∂EOCV/∂T), at constant x, as shown in Section 2.3. We applied the OCV background subtraction methods developed in our previous work38 to subtract the time-dependent voltage drift and avoid excessive measurement times for each x value.
2.5 Extracting configurational entropy
The experimental p.m. entropy profiles from Section 3.2 can be further analysed to obtain the configurational entropy, Sconfig, of lithium in graphite. The total entropy naturally is a sum of configurational, vibrational and electronic components.42–44The electronic entropy contribution,42–44 which should not vary much with x, can be neglected. However, Reynier et al. showed the vibrational entropy, Svib, of Li in graphite to be significant.42 Previous experimental45 and theoretical46 investigations also showed differences in the vibrational modes of Li in the different Li–graphite stages. Fortunately, Svib can be estimated by approximating the phonon spectrum with a single Debye temperature for each vibrational mode42,47,48 (cf. the ESI† for details). By taking the raw partial molar entropy data as shown in Fig. 3b and subtracting the vibrational entropy component obtained for each x value, the partial molar configurational entropy, ∂Sconfig/∂x, can be obtained, as shown in Fig. S4.† Then by integration
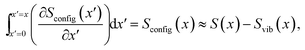 | (9) |
we obtain Sconfig(x). The integration constant is Sconfig(x = 0) = 0, because there can be no Li disorder in pure graphite.
2.6 Computational methods
Spin-polarized Density-Functional-Theory (DFT) calculations were performed using the Vienna Ab Initio Simulation Package (VASP).49–52 The Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation was used throughout.53 The projector-augmented wave method was used to represent the core electrons.54 The valence electronic states were expanded in plane-wave basis sets with cutoff energies of 450 eV. Periodic boundary conditions were applied in all three dimensions. The force convergence criterion in structural optimization was set to be 0.03 eV Å−1. A k-mesh of (12 × 12 × 7) was used for AαB and AαA stacked hosts and a (11 × 11 × 3) k-mesh for AαABβB stacked hosts. The DFT-D2 method was employed to account for van der Waals interactions,55 which faithfully describes the key stage formations such as the stage-II and stage-I formations in this work.The cluster expansion method, implemented within the Alloy Theoretic Automated Toolkit (ATAT),56,57 was used to efficiently sample low energy Li configurations within the respective carbon stackings. The energy of a configuration was calculated within density-functional-theory using VASP. In lithiated graphite, the stackings of AαBα, AαABβB and AαAα were used as the parent lattices to sample configurations with prototype structures shown in Fig. S1.† The cluster expansions of AA, AABB and AB stackings were well converged after sampling 87, 126 and 58 different Li ordering configurations, respectively. For each cluster expansion, the configurational degrees of freedom included only Li sites, i.e. we froze carbon stacking degrees of freedom (while allowing the lattice constant to relax) and confined calculations to a small number of experimentally confirmed stackings, representing the Li–graphite stages shown in Fig. 1 (more details of the cluster expansion are available in the ESI†).
Consistent reference energies across hosts, AB-stacked carbon (x = 0) and AA-stacked LiC6 (x = 1), were used for all cluster expansions. The formation energy, Ef was thus determined by
| Ef = E(LixC6) − (1 − x)E(C6) − xE(LiC6), | (10) |
The climbing-image nudged elastic band (CI-NEB) method was used to search for the transition states (TSs) of the structure transformation, with three images considered between the initial and final states.58,59
3 Results
3.1 Open circuit voltage (OCV) variation with cycle direction and temperature
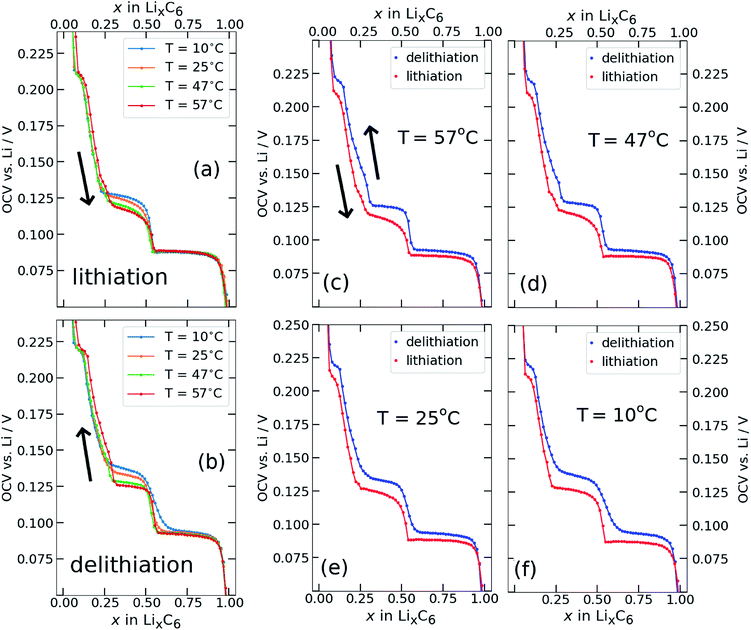
Open circuit voltage (OCV) results from Li/graphite coin cells, as obtained with the GITT variant described in Section 2.4 are shown in Fig. 2. The lithium content x was calculated by normalising the cumulative charge passed after each galvanostatic iteration to the total charge passed during the entire experiment. The OCV measured at the end of each relaxation period is plotted against Li content x (x = Li concentration in LixC6) for lithiation (Fig. 2a) and delithiation (Fig. 2b) at different temperatures T. The same results are plotted in Fig. 2c–f at fixed temperatures, with lithiation and delithiation overlaid.The electrochemical OCV behaviour at T = 25 ± 5 °C, has been well characterised elsewhere1,2,8,9,13,14,22,23,60 and our results are in good agreement. Briefly: a stage I solid solution occurs for x > 0.85. The interval 0.5 ≤ x ≤ 0.85 is ascribed to stage I and stage II coexistence,1,2,8,9,11,14,37 with the flat voltage response typical for a two-phase equilibrium. The observed step at x = 0.5 is attributed to a transition from an ordered stage II to a disordered stage IID.39,42,44,61,62 The voltage behaviour for 0.3 ≤ x ≤ 0.5 is ascribed to stage II and dilute stage II coexistence.1,3,11 Dilute higher order stages III and IV,1,2 approximating the behaviour of a solid solution, give rise to the observed behaviour for x < 0.3. However, the lowest voltage plateau at x ≈ 0.05 is associated with changes in the electronic behaviour of graphite in a dilute stage I structure,12,39,63 validated by the Knight shift observed from operando nuclear magnetic resonance (NMR) measurements.64
Most of the lithiation profile (Fig. 2a) is rather insensitive to temperature changes. In particular, the plateau at about 0.085 V in the interval 0.5 < x < 1.0, shows negligible variation with temperature, as expected for a first order phase transition. Likewise, there is no significant change of the measured OCV with temperature for x < 0.25. However, the interval 0.25 < x < 0.5 shows a systematic decrease in cell voltage with increasing cell temperature. Delithiation profiles, shown in Fig. 2b, display a more complex temperature dependence than the lithiation profiles. However, both data sets show a decrease in cell voltage with increasing temperature. We return to this point in Section 3.2.
The step at about x = 0.5 remains well defined above room temperature, and the change in OCV with temperature reflects the same trend as observed for lithiation: a decrease in OCV only in the interval 0.25 < x < 0.5. At and below room temperature, however, the profiles are sensitive to temperature over a broader range of x. In particular, the feature at x = 0.5 becomes much broader and extends further to higher lithium content.
Fig. 2c–f show that a hysteresis of the measured OCV between lithiation and delithiation is observed at all investigated temperatures. The hysteresis is smallest in the composition range 0.5 < x < 1.0, where the two curves appear to converge towards the same value of OCV with an increase in temperature. The voltage separation between lithiation and delithiation is lowest at the highest temperature, Fig. 2c, between 0.5 < x < 1, and then increases with lower temperatures.
The most important result for the subsequent analysis is that the hysteresis between lithiation and delithiation remains pronounced even at T = 57 °C for 0.05 < x < 0.5. For these compositions, a plateau is observed during delithiation that appears more clearly resolved at higher temperatures and broadens out at lower temperatures. A plateau is also observed during lithiation (Fig. 2f) in the same composition interval that appears most defined at the lowest temperature and loses definition with an increase in temperature.
3.2 Dependence of entropy and enthalpy profiles on cycle direction
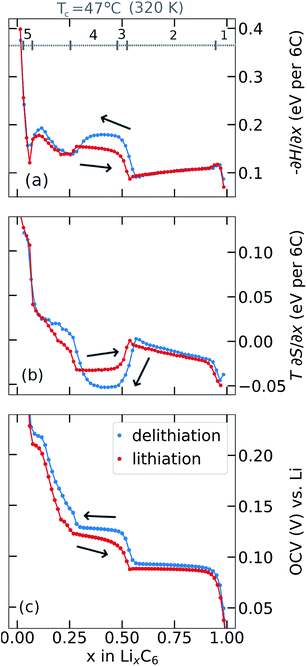
Partial molar (p.m.) entropy and enthalpy profiles, acquired using the procedure described in Section 2.4 are presented in Fig. 3a and b. Results were obtained by modifying the cell temperature during the OCV relaxation period for each x value and determining partial molar (p.m.) enthalpy (Fig. 3a) and p.m. entropy (Fig. 3b) by eqn (8) and (7), respectively. The corresponding OCV profiles at the end of the relaxation periods are shown in Fig. 3c. Results are shown in Fig. 3 such that addition of the upper two curves gives −∂G/∂x (i.e. the OCV) in the lower curve.Results obtained during lithiation, shown in Fig. 3a and b, are in good agreement with those obtained elsewhere by Reynier and Yazami,7,42,44 Thomas and Newman,65 and us.39 Key features of the lithiation profiles, labelled from right to left as 1–5 in Fig. 3a, are commonly interpreted according to the phase succession already discussed: (1) stage I solid solution; (2) stage I and stage II coexistence; (3) a transition from ordered stage II structure at x = 0.5 to a disordered dilute stage II for x < 0.5;7,39,42,44 (4) stage II – dilute stage II coexistence; (5) a dilute feature at low Li occupation39 that shows a p.m. entropy response approximating a solid solution and appears to have a distinct origin from a phase transition.39 Further interpretation of the entropy profile features is in the ESI, Fig. S4.†
There is a pronounced difference in entropy responses between lithiation and delithiation for x < 0.5 as previously observed by Allart et al.23 The negative p.m. entropy value in this interval, for both cycling directions, is also consistent with the observed decrease in OCV with increasing cell temperature, as shown in Fig. 2a and b. The voltage of the lithiation and delithiation curves decreases with temperature by a comparable order of magnitude, and so the OCV hysteresis magnitude does not appear to change significantly with temperature. Additionally, there is a difference between the enthalpy profiles obtained from the two cycling directions, Fig. 3a, suggesting there is both an entropy and an enthalpy component to the hysteresis over a wide range of composition 0.1 < x < 0.5.
Feature 4 in Fig. 3a shows a local maximum in the p.m. enthalpy, −∂H/∂x, in both cycling directions. The maximum, located between x = 0.3 and x = 0.5, is more pronounced in the delithiation direction than for lithiation. This trend is in agreement with the variation in the OCV response, Fig. 3c. The p.m. entropy response, Fig. 3b shows the opposite trend in this interval. The difference between the measured OCV in each cycling direction arises mostly from the p.m. enthalpy term, with partial cancellation due to the T∂S/∂x term. The net hysteresis in the OCV resulting from the enthalpy and entropy terms in this compostion range is approximately 10 mV, in agreement with the values shown in Fig. 3c.
3.3 Low temperature ground states from DFT
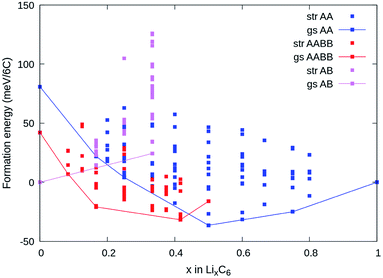
Fig. 4a shows the computed formation energies (Ef) of all sampled configurations as a function of Li content. Ef was determined by eqn (10). To be consistent with the derived experimental quantities, normalised in eV per formula unit, the Ef values are likewise normalised by 6NC, where NC is the number of carbon atoms in the unit cell. The energy landscape within the AA stacking host is shown in blue, the AABB host in red, and the AB host in pink. Thermodynamic ground-states within each host are connected by lines, giving convex hulls for each host. The overall thermodynamic ground-states result from a convex hull construction over all data points (not shown). We find several low energy orderings within the AABB and AA hosts that compete for overall thermodynamic stability.The results are consistent with the experimentally observed stacking sequences as a function of x. The AA-stacked stages I and II are favoured for x ≥ 0.5; AABB stacking (dilute stage II) is favoured over AB or AA stackings at intermediate x, and AB-stacked graphite is the ground-state for x → 0. It is also possible to draw a common tangent between the respective convex hulls for AABB and AA stackings (indicated by the red dashed line in Fig. 5a) reflecting the two-phase coexistence of dilute stage II and stage II compounds. Finally, a similar common tangent construction would be possible between AB and AABB stackings that does not reflect experimentally confirmed two-phase equilibria at low concentrations, which we attribute to us not considering the stage III and stage IV compounds.
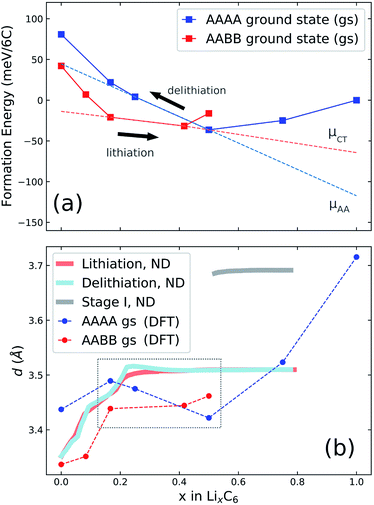 | ||
| Fig. 5 (a) Illustration of possible cycling pathways along the ground state (gs) free energy curves presented in Fig. 4a. The slope of the red dashed line designates a chemical potential, μCT, which we propose is followed during lithiation. During delithiation, the AAAA-stacked structure persists as lithium is extracted from the host lattice, corresponding to chemical potential μAA. (b) Results obtained from neutron diffraction (ND) data. The average interlayer carbon distance, d, is shown as a function of lithium concentration x. Reprinted (adapted) with permission from Fig. 1 of ref. 12. Copyright 2020 American Chemical Society. d values obtained from the AAAA and AABB-stacked DFT ground states from the present work are overlaid for comparison. | ||
3.4 Thermodynamics of carbon stacking and cycle direction
Our experimental results have shown that the p.m. enthalpy depends on cycling direction in the range 0.25 < x < 0.5, which we propose is due to graphite retaining AAAA stacking during delithiation well below x = 0.5 and only transitioning to the thermodynamically favoured AABB stacking (and/or AB) at much lower Li content. In the lithiation direction, on the other hand, the structure closely follows the AABB ground state configuration for approximately 0.17 < x < 0.5. Stacking transitions then occur during the two phase coexistence interval between the AABB and AAAA hosts. For x ≥ 0.5, we expect the same AAAA carbon stacking in both cycling directions for 0.5 ≤ x ≤ 1.The scheme is visualised in Fig. 5a. This shows the computed convex hulls for the AAAA and AABB-stacked systems. The dashed lines indicate the slope of the formation energy with respect to the Li concentration, x in the concentration range of interest. This slope is a chemical potential for lithium intercalation, μ, by eqn (3). However, because DFT calculations probe the ground state energy, the presented formation energies exclude partial molar entropy and thus are more precisely related to the partial molar enthalpy.
Regardless, the scheme in Fig. 5a suggests a more negative chemical potential if the structure follows an AAAA-stacked configuration during delithiation for x < 0.5 than given by the AABB to AAAA two-phase coexistence interval expected during lithiation. By eqn (2), this translates into a more negative partial molar enthalpy, and therefore more positive OCV, during delithiation than during lithiation, which is exactly the trend observed experimentally as compared in Table 3, although the ab initio results predict a slightly stronger effect than experimentally observed.
| Transition at x < 0.5 | μ (DFT) (eV per 6C) | ∂H/∂x (experiment) (eV per 6C) |
|---|---|---|
| Lithiation (L) | −0.056 | −0.150 |
| Delithiation (D) | −0.162 | −0.179 |
| Difference (L–D) | 0.106 | 0.029 |
The quantitative enthalpy difference between theory and experiment could be because of (i) systematic errors from the van-der-Waals correction to the exchange-correlation functional used in the DFT calculations and (ii) to the fact that we are comparing 0 K calculations to 320 K experiments. The experimental value could also be different due to deviations from ideal carbon stacking (turbostratic disorder), additional effects from interplanar Li sites, as analysed quantitatively later, or other types of structural defects.
The scheme is consistent with experimentally determined neutron diffraction (ND) studies of the average interlayer carbon spacing, d.8,9,12 Those studies suggest asymmetry in the formation of stage IID during lithiation and delithiation. We compare the results of in-operando neutron diffraction from the recent paper of Didier et al.12 to the average interlayer carbon spacing, d, of the ground state structures calculated by DFT. d values were obtained by visualising the ground state unit cells within VESTA66 and determining the most intense peak from simulated powder XRD patterns. The resultant d values are overlaid with the neutron diffraction data from ref. 12 in Fig. 5b. The region of interest is higlighted in the dashed grey box.
Results in the stage I region, and also for stages greater than I, suggest that DFT systematically underestimates the interlayer carbon spacing compared with experiment. Systematic differences between predicted and experimental d values were found previously from DFT,46 but it is nonetheless instructive to compare the trends between theory and experiment. In the interval 0.17 < x < 0.41, there is a slight gradual increase in d predicted as a function of x, while d is predicted to remain almost constant over the same concentration range in the AABB host. The same decrease of d is seen in the experimental profiles obtained from delithiation but absent in the opposite direction. We take this as further evidence that the lattices remains in an AAAA-stacked configuration as x decreases below 0.5 during delithiation.
The result in Fig. 5a is used to compute voltage profiles. The tangent between each point along the graph represents a chemical potential, and so, by eqn (2) and (3), corresponds to the cell voltage at a given x. Results are shown in Fig. 6a and b.
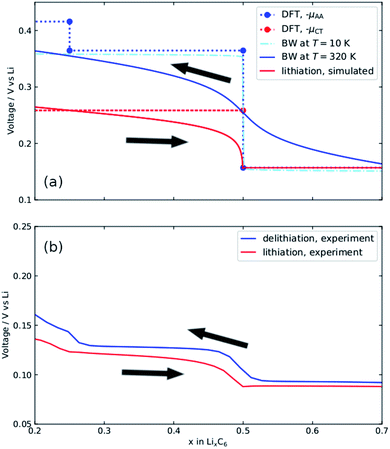 | ||
| Fig. 6 (a) Voltage profile obtained from Fig. 5a by following the common tangent of the AAAA stacking profile (μAA) and the common tangent indicated μCT between AAAA and AABB stackings. Bragg–Williams solutions at T = 10 K and T = 320 K are shown. The T = 320 K solution represents the simulated delithiation profile. Lithiation profiles are simulated as described in the text. Simulated profiles (solid lines in (a)) can be compared with the corresponding experimental profiles (b). | ||
The dotted lines in Fig. 6a represent the voltage profiles extracted from the DFT data. The chemical potential of metallic Li determined from DFT was used as a reference. These profiles provide the enthalpy contributions to the voltage. The entropic contributions, needed to model the experimental voltage profiles at T = 320 K (shown in Fig. 6b) were estimated as follows. Two-phase coexistence was experimentally observed for x > 0.5 and this voltage plateau showed negligible temperature variation. The experimental voltage profiles for lithiation for x < 0.5 resemble those of an ideal solid solution over half the lattice sites, with dS/dx described by eqn (S7).† The plateau −μCT, denoted by the red dotted line, describes the cell voltage, E(x,T), at T = 0 K. The cell voltage at T = 320 K is given by E(x,T) = −μCT + TdS/dx. The shapes of the simulated and experimental OCV curves in this interval are in good agreement.
As for delithiation, we consider the voltage profile for AA-stacking, denoted by the blue dotted line in Fig. 6a. Previous work39 showed that the voltage profile can be approximated by a Bragg–Williams (BW) model in which the largest term is a repulsion between Li atoms in adjacent layers, Δ. The step amplitude between the two blue points at x = 0.5 from DFT, i.e. the difference between the voltage plateau for x > 0.5 and the one for 0.25 < x < 0.5, was used to determine Δ. A value of Δ = 103 meV, representing exactly half the amplitude of the DFT voltage step, was input into the BW model at T = 10 K. This profile closely matches the DFT voltage profile. The delithiation profile at T = 320 K can therefore be approximated by the BW model.
The validity of the configurational entropy corrections will be assessed by performing further analysis in Section 3.6.
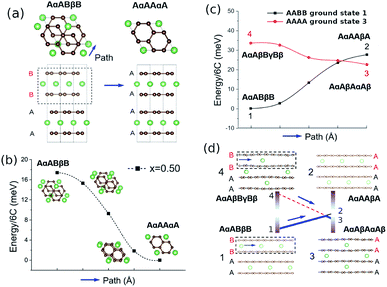
3.5 Energetic barriers for stacking shifts
The existence of meta-stable AAAA-stacked carbon during delithiation would suggest activation barriers for transitioning between AABB and AAAA stackings at intermediate Li concentrations. Otherwise, AAAA configurations would not be meta-stable and spontaneously convert to AABB as soon as x is small enough to thermodynamically favour AABB stacking. Based on the ground state structures found from the cluster expansion, activation energies for transitions between different carbon stackings were evaluated through the climbing image nudged elastic band (CI-NEB) method.58,59 In the CI-NEB calculations, a motif in the unit cell was translated along a path, as represented in Fig. 7.We found no relevant activation energy barriers for carbon layers shifting between AABB and AAAA stacking or AB and AA stacking. A result is shown at a select concentration of x = 0.5 in Fig. 7b. A full analysis over a range of x values can be found in Fig. S2 and S3 in the ESI.† There always exists a smooth, monotonous path connecting the ground-state stacking to possible alternative carbon stackings without a transition state. Therefore, energetic barriers to translate between different carbon stackings alone do not explain the hysteresis effect.
Fig. 7b indicates that AαAAαA stacking is energetically favourable at x = 0.5, consistent with the ground states from the cluster expansion (Fig. 4). These ground states exclude thermal excitations, which could transfer a small fraction of lithium to the interplanar sites. Indeed, our cluster expansion within the AAAA host suggests interplanar Li is energetically competitive within this stacking at x = 0.17 (points 2 and 3 in Fig. 7c and d. Fig. 7d, structure 3 shows that the AAAA ground state involves Li occupying interplanar sites, while structure 1, the AABB ground state and the overall lowest energy structure, shows Li occupying only every alternate plane, because of the unfavourable Li site environment between AB sheets.
Fig. 7c shows CI-NEB energy profiles obtained at x = 0.17, considering translations of the highlighted motifs in Fig. 7d along the indicated path.
The absence of lithium in the interlayer of structure 1 leads to a different qualitative energy change when the carbon layers transition from AABB to AAAA stacking (path 1 → 2 – uphill), than when the layers transition with lithium present in the interlayer (4 → 3 – downhill). The computed energetic difference between 3 and 2, the two different lithium arrangements within AAAA stacking, is very small (approximately 5 meV per 6C) and so is the average interlayer carbon distance, d (3: d = 3.46 Å, 2: d = 3.49 Å).
Plausibly, the presence of interlayer Li sites in AAAA stackings is an important factor determining the directional dependence of the layer transitions and, therefore, the hysteresis observed in OCV below x = 0.5. AAAA stackings could be stabilised by residual interlayer Li that is more likely to be present during delithiation than during lithiation, which could be a contributing factor to the observed hysteresis at intermediate concentrations x < 0.5 even without classical activation barriers for carbon layer shifts or considering possible barriers from overcoming interface energies.
In support of these statements, the proportion of these interlayer Li sites is assessed quantitatively in the next section.
3.6 Interplanar site occupation
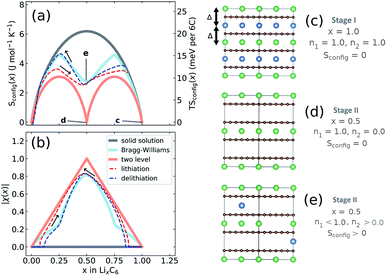
We performed further analysis the experimental entropy profiles from Section 2.3. The configurational entropy, Sconfig, contains additional information regarding the interplanar Li site occupation. Sconfig can be extracted from the profiles shown in Fig. 3b using the methods described in Section 2.5.Results for Sconfig as a function of x are shown in Fig. 8a, which was obtained by applying eqn (9) to the experimental result for ∂S/∂x obtained at T = 320 K, i.e.Fig. 3b. The total capacity of the Li/graphite cells was consistently found to be below the theoretical one of 372 mA h g−1. Therefore, we multiplied x by a correction factor so that value of Sconfig at maximum lithiation matched the dashed solid solution line corresponding to a stage I solid solution.
The Li occupation in each alternate layer can be considered in sublattices n1 and n2 for a given x, with representative examples shown in Fig. 8c–e, such that x = (n1 + n2)/2. Solid lines in Fig. 8a and b indicate three hypothetical cases. The salmon pink line denotes sequential filling of Li into two well-separated energy levels. This case, with Sconfig(x) described in eqn (S6) and (S8),† results in each alternate plane between the carbon sheets being filled randomly with Li up to x = 0.5; only then the next layer fills above x = 0.5. The dark grey line shows the result for an ideal solid solution, eqn (S4)† if Li were to fill all available sites at random, i.e. n1 = n2 for all x. The blue solid line is the solution to a Bragg–Williams model39 (introduced earlier in Section 3.4) assuming only nearest neighbour repulsive pairwise lithium interactions between planes of Δ = 75 meV and no in-plane interactions. The value Δ = 75 meV is quantitatively different from the value of Δ = 103 meV determined from the DFT analysis, but results in the same qualitative two-peak entropy behaviour inferred from experimental data. The model produces a behaviour in Sconfig(x) intermediate between the solid solution and sequential two level filling. At x = 1, there is a net repulsion on each Li atom of 2Δ, as represented in Fig. 8c. At x = 0.5, this model results in one of the sublattices being preferentially filled, as represented schematically in Fig. 8e. In contrast, a perfect stage II structure as predicted by sequential two level filling (Fig. 8d) would result in Sconfig(0.5) = 0.
Experimental results for lithiation and delithiation, shown as dashed lines, feature two peaks, with a local minimum centred at x ≈ 0.5. Both curves show a very similar value of TSconfig ≈ 10 meV per 6C at T = 320 K, indicating nearly the same lattice configuration at x = 0.5.
It is beneficial to construct a “staging order parameter”, χ(x) = n1 − n2, to quantify the interlayer Li disorder,67 which is plotted in Fig. 8b. Formally, χ(x) takes values between −1 and +1 but only the absolute value is meaningful here. If |χ(x)| = 1, then only one layer is filled with Li, representing maximal staging order. If χ(x) = 0, both layers are occupied with equal probability, disorder is maximal and no staging is observed. The required occupations of interplanar sites, n1 and n2 were obtained from Sconfig(x), using eqn (S10)† and applying a numerical procedure detailed in the ESI.†
As suggested by the previous results, the trend in order parameter |χ(x)| is very similar between lithiation and delithiation for x ≥ 0.5. At x = 0.5 both curves show nearly identical order parameters to the Bragg–Williams solution of |χ(x)| ≈ 0.8. However, there is a pronounced difference in the trend in |χ(x)| values for x < 0.5. The |χ(x)| value for delithiation is always greater than the value obtained during lithiation, indicating that greater configurational order is obtained during lithiation. In fact the experimental delithiation result closely resembles the Bragg–Williams model, while |χ(x)| values obtained for lithiation for x < 0.5 are only marginally higher than expected for sequential two level filling.
The staging order parameter trends for x < 0.5 are consistent with the carbon layer transitions and energetic trends predicted from DFT. During lithiation only half of the layers are filled with lithium in an AABB-stacked configuration, consistent with two level filling. The energy level difference can be attributed to the different Li environment between AA and AB sheets. During delithiation, alternate layers are preferentially emptied by Li due to repulsive interactions in an AAAA-stacked host, but the Li repulsion is insufficient to prevent some Li staging disorder, which we propose delays the transition to AABB-stacking. This result provides further support for the statement from DFT regarding the importance of interplanar sites to the observed hysteresis effect. It additionally provides insight into the origins of the hysteresis in OCV arising from the partial molar entropy term.
3.7 Kinetic origins of hysteresis
So far, we have not addressed the kinetic origin that could result in a metastable AA-stacking during delithiation. It is considered difficult for lithium to transition between carbon layers. Previous measurements of highly-oriented pyrolytic graphite (HOPG) estimate an intralayer diffusion coefficient on the order 10−6 to 10−7 cm2 s−1, compared with 10−11 to 10−12 cm2 s−1 across the grain boundaries.68 Interlayer lithium diffusion barriers on the order 1–10 eV have been calculated from first-principles,68–70 indicating that diffusion across ideal carbon planes does not occur, and that defects such as grain boundaries must be involved. The metastable AA stacking could be retained during delithiation due to the presence of interlayer Li, which is prohibitively difficult to transfer between the carbon layers at grain boundaries and then finally extract. The timescale for conversion to the structure corresponding to the equilibrium cell voltage (i.e. ϕ(x) in eqn (2)) appears not to be experimentally accessible during delithiation, resulting in a different measured OCV value in each cycling direction. The measurable OCV must therefore be considered a distinct quantity from ϕ(x).4 Conclusions
A residual hysteresis is observed in the measured open circuit voltage (OCV) during lithiation and delithiation in graphite. The hysteresis is not reduced even at temperatures T > 50 °C. Energetic and entropic components to the hysteresis were measured. Energetic differences and volume changes from first-principles calculations suggest the system remains in metastable AAAA carbon stacking configurations during delithiation. More interlayer Li disorder during delithiation was determined from measurements, as expected for Li in AAAA-stacked configurations. No relevant energetic barriers for transitioning between formal ground state stages were found from DFT. Instead, the interlayer Li sites in stage II configurations contribute to the hysteresis effect. In combination with the enthalpy difference in each cycling direction, this entropy difference results in a net higher OCV during delithiation. Increasing the temperature does not cause the lithiation and delithiation OCV curves to converge to the same values, since a temperature rise would increase the proportion of occupied sites in the interlayer.The work has implications for control of Li-ion batteries. The open circuit voltage is often considered equivalent to the equilibrium potential at each state of charge, i.e. lithiation fraction in graphite. However, the present results reveal that the cycling direction must also be taken into account under any practical temperature or relaxation time. Models of the OCV used to determine the state of charge in battery management systems (BMS) should take history dependence into account. Due to differences in the d-spacing with cycle direction, in situ pressure or stress measurements might be beneficial to augment BMS models.37,71
The entropy behaviour dependent on cycling direction of other materials that are known to show hysteresis should also be explored. As an example, lithium iron phosphate (LFP) particles have shown greater spatial heterogeneity during delithiation than during lithiation.72 The strategies are also relevant to understanding stacking sequence related changes in layered Li and Na-ion intercalation hosts due to lattice invariant shear.73,74
Conflicts of interest
There are no conflicts to declare.Acknowledgements
MPM, CP, HEH and DK thank the Faraday Institution (https://faraday.ac.uk/; EP/S003053/1), grant number FIRG003, for funding. CS thanks the EPSRC for PhD funding. We thank Richard Fields from University of Manchester Graphene Engineering Innovation Centre for providing the coatings used in the electrochemical measurements, and Miriam Ferrer-Huerta from the Department of Chemistry at Lancaster University for assistance in the experimental set up. Special thanks to David Howey from the University of Oxford for discussions on the use of the OCV in battery control models.Notes and references
- J. R. Dahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 9170–9177 CrossRef CAS PubMed.
- T. Ohzuku, J. Electrochem. Soc., 1993, 140, 2490 CrossRef CAS.
- S. Konar, U. Häusserman and G. Svensson, Chem. Mater., 2015, 27, 2566–2575 CrossRef CAS.
- D. Guerard and A. Herold, Carbon, 1975, 13, 337–345 CrossRef CAS.
- K. C. Woo, W. A. Kamitakahara, D. P. DiVincenzo, D. S. Robinson, H. Mertwoy, J. W. Milliken and J. E. Fischer, Phys. Rev. Lett., 1983, 50, 182–185 CrossRef CAS.
- H. He, C. Huang, C.-W. Luo, J.-J. Liu and Z.-S. Chao, Electrochim. Acta, 2013, 92, 148–152 CrossRef CAS.
- R. Yazami and Y. Reynier, J. Power Sources, 2006, 153, 312–318 CrossRef CAS.
- A. Senyshyn, O. Dolotko, M. J. Muhlbauer, K. Nikolowski, H. Fuess and H. Ehrenberg, J. Electrochem. Soc., 2013, 160, A3198–A3205 CrossRef CAS.
- S. Taminato, M. Yonemura, S. Shiotani, T. Kamiyama, S. Torii, M. Nagao, Y. Ishikawa, K. Mori, T. Fukunaga, Y. Onodera, T. Naka, M. Morishima, Y. Ukyo, D. S. Adipranoto, H. Arai, Y. Uchimoto, Z. Ogumi, K. Suzuki, M. Hirayama and R. Kanno, Sci. Rep., 2016, 6, 28843 CrossRef CAS PubMed.
- N. A. Cañas, P. Einsiedel, O. T. Freitag, C. Heim, M. Steinhauer, D.-W. Park and K. A. Friedrich, Carbon, 2017, 116, 255–263 CrossRef.
- D. Billaud, F. Henry, M. Lelaurain and P. Willmann, J. Phys. Chem. Solids, 1996, 57, 775–781 CrossRef CAS.
- C. Didier, W. K. Pang, Z. Guo, S. Schmid and V. K. Peterson, Chem. Mater., 2020, 32, 2518–2531 CrossRef CAS.
- V. A. Sethuraman, L. J. Hardwick, V. Srinivasan and R. Kostecki, J. Power Sources, 2010, 195, 3655–3660 CrossRef CAS.
- C. Sole, N. E. Drewett and L. J. Hardwick, Faraday Discuss., 2014, 172, 223–237 RSC.
- P. Trucano and R. Chen, Nature, 1975, 258, 136–137 CrossRef CAS.
- H. Okamoto, Bull. Alloy Phase Diagrams, 1989, 10, 69–72 CrossRef CAS.
- D. Billaud and F. Henry, Solid State Commun., 2002, 124, 299–304 CrossRef CAS.
- M. Levi, C. Wang, D. Aurbach and Z. Chvoj, J. Electroanal. Chem., 2004, 562, 187–203 CrossRef CAS.
- H. Liu, F. C. Strobridge, O. J. Borkiewicz, K. M. Wiaderek, K. W. Chapman, P. J. Chupas and C. P. Grey, Science, 2014, 344, 1252817 CrossRef.
- Y. Orikasa, T. Maeda, Y. Koyama, H. Murayama, K. Fukuda, H. Tanida, H. Arai, E. Matsubara, Y. Uchimoto and Z. Ogumi, J. Am. Chem. Soc., 2013, 135, 5497–5500 CrossRef CAS PubMed.
- A. Van der Ven, Z. Deng, S. Banerjee and S. P. Ong, Chem. Rev., 2020, 120, 6977–7019 CrossRef CAS PubMed.
- T. Zheng, J. N. Reimers and J. R. Dahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 734–741 CrossRef CAS PubMed.
- D. Allart, M. Montaru and H. Gualous, J. Electrochem. Soc., 2018, 165, A380–A387 CrossRef CAS.
- K. G. Gallagher, D. W. Dees, A. N. Jansen, D. P. Abraham and S.-H. Kang, J. Electrochem. Soc., 2012, 159, A2029–A2037 CrossRef CAS.
- F. Grimsmann, T. Gerbert, F. Brauchle, A. Gruhle, J. Parisi and M. Knipper, J. Energy Storage, 2018, 15, 17–22 CrossRef.
- G. L. Plett, J. Power Sources, 2004, 134, 262–276 CrossRef CAS.
- T. Zheng and J. R. Dahn, Synth. Met., 1995, 73, 1–7 CrossRef CAS.
- T. Zheng, W. R. McKinnon and J. R. Dahn, J. Electrochem. Soc., 1996, 143, 2137–2145 CrossRef CAS.
- M. Inaba, M. Fujikawa, T. Abe and Z. Ogumi, J. Electrochem. Soc., 2000, 147, 4008–4012 CrossRef CAS.
- G. Assat, S. L. Glazier, C. Delacourt and J.-M. Tarascon, Nat. Energy, 2019, 4, 647–656 CrossRef CAS.
- S. G. Rinaldo, K. G. Gallagher, B. R. Long, J. R. Croy, M. Bettge, D. P. Abraham, J. Bareño and D. W. Dees, J. Electrochem. Soc., 2015, 162, A897–A904 CrossRef CAS.
- R. Khatib, A.-L. Dalverny, M. Saubanère, M. Gaberscek and M.-L. Doublet, J. Phys. Chem. C, 2013, 117, 837–849 CrossRef CAS.
- U. Maitra, R. A. House, J. W. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Jin, M. A. Perez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Lu, D. E. McNally, A. V. Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Nat. Chem., 2018, 10, 288–295 CrossRef CAS PubMed.
- K. Persson, Y. Hinuma, Y. S. Meng, A. Van der Ven and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 125416 CrossRef.
- M. Drüe, M. Seyring and M. Rettenmayr, J. Power Sources, 2017, 353, 58–66 CrossRef.
- A. Funabiki, J. Electrochem. Soc., 1999, 146, 2443 CrossRef CAS.
- S. Schweidler, L. de Biasi, A. Schiele, P. Hartmann, T. Brezesinski and J. Janek, J. Phys. Chem. C, 2018, 122, 8829–8835 CrossRef CAS.
- P. J. Osswald, M. del Rosario, J. Garche, A. Jossen and H. E. Hoster, Electrochim. Acta, 2015, 177, 270–276 CrossRef CAS.
- M. P. Mercer, M. Otero, M. Ferrer-Huerta, A. Sigal, D. E. Barraco, H. E. Hoster and E. P. Leiva, Electrochim. Acta, 2019, 324, 134774 CrossRef CAS.
- S. Schlueter, R. Genieser, D. Richards, H. E. Hoster and M. P. Mercer, Phys. Chem. Chem. Phys., 2018, 20, 21417–21429 RSC.
- B. K. Antonopoulos, C. Stock, F. Maglia and H. E. Hoster, Electrochim. Acta, 2018, 269, 331–339 CrossRef CAS.
- Y. Reynier, R. Yazami and B. Fultz, J. Power Sources, 2003, 119–121, 850–855 CrossRef CAS.
- Y. Reynier, J. Graetz, T. Swan-Wood, P. Rez, R. Yazami and B. Fultz, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 174304 CrossRef.
- Y. F. Reynier, R. Yazami and B. Fultz, J. Electrochem. Soc., 2004, 151, A422–A426 CrossRef CAS.
- A. Schirmer, J. E. Fischer, P. Heitjans, H. J. Kim, A. Magerl, D. Vaknin and H. Zabel, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1994, 244, 299–305 CrossRef CAS.
- E. Hazrati, G. A. de Wijs and G. Brocks, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155448 CrossRef.
- R. Moreh, N. Shnieg and H. Zabel, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 1311–1317 CrossRef CAS PubMed.
- M. M. Beg and M. Nielsen, Phys. Rev. B: Solid State, 1976, 14, 4266–4273 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- A. van de Walle, M. D. Asta and G. Ceder, Calphad, 2002, 26, 539–553 CrossRef CAS.
- A. van de Walle, Calphad, 2009, 33, 266–278 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- E. Markevich, M. D. Levi and D. Aurbach, J. Electrochem. Soc., 2005, 152, A778 CrossRef CAS.
- J. S. Filhol, C. Combelles, R. Yazami and M. L. Doublet, J. Phys. Chem. C, 2008, 112, 3982–3988 CrossRef CAS.
- E. M. Gavilán Arriazu, B. A. López de Mishima, O. A. Oviedo, E. P. M. Leiva and O. A. Pinto, Phys. Chem. Chem. Phys., 2017, 19, 23138–23145 RSC.
- J. R. Dahn, J. N. Reimers, A. K. Sleigh and T. Tiedje, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 3773–3777 CrossRef CAS PubMed.
- J. L. Lorie Lopez, P. J. Grandinetti and A. C. Co, J. Mater. Chem. A, 2018, 6, 231–243 RSC.
- K. E. Thomas and J. Newman, J. Power Sources, 2003, 119–121, 844–849 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- A. R. Natarajan, J. C. Thomas, B. Puchala and A. Van der Ven, Phys. Rev. B, 2017, 96, 134204 CrossRef.
- K. Persson, V. A. Sethuraman, L. J. Hardwick, Y. Hinuma, Y. S. Meng, A. Van der Ven, V. Srinivasan, R. Kostecki and G. Ceder, J. Phys. Chem. Lett., 2010, 1, 1176–1180 CrossRef CAS.
- S. Thinius, M. M. Islam, P. Heitjans and T. Bredow, J. Phys. Chem. C, 2014, 118, 2273–2280 CrossRef CAS.
- E. M. Gavilán-Arriazu, M. P. Mercer, O. A. Pinto, O. A. Oviedo, D. E. Barraco, H. E. Hoster and E. P. M. Leiva, J. Electrochem. Soc., 2020, 167, 013533 CrossRef.
- F. Grimsmann, F. Brauchle, T. Gerbert, A. Gruhle, M. Knipper and J. Parisi, J. Energy Storage, 2017, 12, 132–137 CrossRef.
- J. Lim, Y. Li, D. H. Alsem, H. So, S. C. Lee, P. Bai, D. A. Cogswell, X. Liu, N. Jin, Y.-s. Yu, N. J. Salmon, D. A. Shapiro, M. Z. Bazant, T. Tyliszczak and W. C. Chueh, Science, 2016, 353, 566–571 CrossRef CAS PubMed.
- M. D. Radin, J. Alvarado, Y. S. Meng and A. Van der Ven, Nano Lett., 2017, 17, 7789–7795 CrossRef CAS PubMed.
- J. Vinckevičiūtė, M. D. Radin and A. Van der Ven, Chem. Mater., 2016, 28, 8640–8650 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta10403e |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |