Open Access Article
Open Access ArticleModelling of heterogeneous ion transport in conducting polymer supercapacitors†
Musbaudeen O.
Bamgbopa
 abc,
Dagmawi
Belaineh
abc,
Dagmawi
Belaineh
 ad,
Desalegn A.
Mengistie
ad,
Desalegn A.
Mengistie
 ae,
Jesper
Edberg
ae,
Jesper
Edberg
 d,
Isak
Engquist
d,
Isak
Engquist
 ab,
Magnus
Berggren
*ab and
Klas
Tybrandt
ab,
Magnus
Berggren
*ab and
Klas
Tybrandt
 *ab
*ab
aLaboratory of Organic Electronics, Department of Science and Technology, Linköping University, 60174 Norrköping, Sweden. E-mail: klas.tybrandt@liu.se; magnus.berggren@liu.se
bWallenberg Wood Science Center, Linköping University, 60174 Norrköping, Sweden
cResearch & Development Center, Dubai Electricity and Water Authority (DEWA), P.O. Box 564, Dubai, United Arab Emirates
dRISE Research Institutes of Sweden, Bio- and Organic Electronics, Bredgatan 33, SE-602 21, Norrköping, Sweden
eMaterials Engineering Department, California Polytechnic State University, San Luis Obispo, CA 93407, USA
First published on 14th December 2020
Abstract
The ongoing electrification of many energy systems has created a large demand for low-cost and scalable electrical energy storage solutions. Conducting polymer supercapacitors have received significant attention for this purpose due to the abundance of their constituent materials. Although there exists a large body of experimental work on conducting polymer supercapacitors, a detailed understanding of the mixed electronic–ionic transport processes within these devices and the included materials, is still lacking. Modelling, in combination with experimental data, is a powerful tool to facilitate a detailed understanding of the transport processes within the materials and devices. However, to date, there has been a shortage of physical models which account for the non-ideal capacitances typically found in conducting polymer-based supercapacitors. Here, we report a novel model which reproduces experimental data and provides insights into the cyclic voltammograms, galvanostatic charge–discharge curves, self-discharge characteristics, and impedance spectroscopy results of supercapacitors based on the conducting polymer poly(3,4-ethylenedioxythiophene):poly(styrene sulfonate) (PEDOT:PSS) and cellulose nanofibrils. We find that the non-ideal capacitive characteristics of the supercapacitors can be reproduced by the incorporation of heterogeneous ion transport features within the electrodes, comprising low ion diffusivity regions. The difference in charging rates of the high and low ion diffusivity regions accounts for the experimentally observed trends in cyclic voltammograms and self-discharge characteristics. The developed model demonstrates how complex transport processes, which govern the specifications of organic energy devices, can be analysed beyond the scope of conventional equivalent circuit models. It also provides an insight into how various transport and polarization processes are manifested in real measurement data and thus defines the limiting processes of conducting polymer energy storage devices.
Introduction
Scalable energy storage technology is one of the prime challenges of modern scientific research, driven by the need to transition our society to renewable/sustainable energy sources. Batteries and supercapacitors are examples of electrochemical energy storage systems that have been investigated for both large-scale stationary and small-sized mobile applications. Recently, a class of electrochemical supercapacitors (SCs) based on conducting polymers (CPs) has gained much attention in the research community owing to the abundance of the constituent materials, outstanding mixed ion–electron conductivity and high volumetric capacitance values.1,2 Due to its remarkable cycling stability and high mixed conductivity, the organic conjugated polymer poly(3,4-ethylenedioxythiophene):poly(styrene sulfonate) (PEDOT:PSS) has been investigated in many SC settings: as freestanding3,4 films, mixed with different forms of carbon/cellulose5,6 to promote high surface area, and in combination with redox molecules/biopolymers7–11 for higher energy density. However, achieving high energy density with good cycling stability in PEDOT:PSS-based SCs is limited as most of the previous studies utilize aqueous electrolytes. In aqueous electrolytes, the open circuit potential of the supercapacitor is restricted by the electrochemical window of water, with both coulombic efficiency and cycling stability potentially hindered by accompanying side reactions. The use of non-aqueous electrolytes, such as those including organic solvents or ionic liquids, presents lower ionic conductivity than the aqueous kinds, although they generally provide wider electrochemical windows. A few recent studies12–14 have investigated conjugated polymer supercapacitors based on ionic liquids, some mixed with small quantities of water,15,16 to maximize the benefits of PEDOT:PSS with respect to coulombic efficiency and cycling stability.For further design and development of conducting polymer supercapacitors (CPSCs), a fundamental understanding of the charge–discharge processes within the SC is crucial. This requires knowledge about both the morphology and electrochemical aspects of the material. The structure and morphology of PEDOT:PSS films have been investigated in countless previous studies.17–19 Rivnay et al.18 showed that the organizational structure of the PEDOT:PSS film on a substrate consists of a PEDOT-rich phase and a PSS-rich phase whose relative sizes in the film can be modulated to some extent. By controlling the phase separation, different electronic and ionic transport characteristics of the films were achieved.18 The organization of the PEDOT- and PSS-rich phases can be further controlled by incorporating additional materials that dictate the 3D organisation at different length scales. Composite electrodes made of PEDOT:PSS and cellulose nanofibrils (CNFs) show a different material organization with the PEDOT:PSS phases coated onto the cellulose nanofibrils.20 The electrical and electrochemical characteristics of PEDOT:PSS films in aqueous electrolytes have been studied for various pHs,21–23 with good cycling stability within reasonable potentials in acidic media.24 Regarding stability, one must also account for the possibility of the two-electron oxygen reduction reaction (ORR) that produces hydrogen peroxide,25 which is an undesirable side-reaction that may occur at negative potentials.
Theoretical modelling is essential to provide a deeper understanding of the experimental results. Most work in the literature makes use of equivalent circuit and transmission line models for macro-scale performance characterization.26,27 However, species and charge balance/transport-based models28,29 are valuable links to further and more precisely understand charge transfer dynamics at the molecular scale. Constants adopted in equivalent circuits30,31 and in transmission line32 models oftentimes lack attributable physical meanings and there is thus a need to connect physics to device parameters. Early developed models describing charge storage in CPs33 are typically based on the assumption that the capacitive charging results from redox-like reactions. These approaches fail to capture the charge dynamics of conductive polymers given that the ionic and electronic phases are not evaluated separately, as they are distinct in reality. Such phase separation is especially the case when organic mixed ionic electronic conductors, like PEDOT:PSS, are involved. In our recent work,17,24,34 we overcame this limitation by coupling the Fermi level in the semiconductor to the electric double layer established between the electronic and ionic phases of the CP. Based on this approach, we were able to quantitatively reproduce the charge dynamics of PEDOT:PSS-based electrodes. There exists plenty of experimental work on CPSCs from a design point of view (targeting higher power and energy densities) and several models have also been developed to describe organic mixed ionic electronic conductors theoretically. However, so far, the two approaches have not been combined to provide a better understanding of the voltammetry response and charge storage performance of CPSCs.
Here we apply multiphysics modelling in conjunction with experimental measurements to analyse and describe the characteristics and performance of a CPSC. The SC assembly is made of PEDOT:PSS – cellulose nanofibril composite electrodes separated by an ionic liquid (1-ethyl-3-methylimidazolium ethyl sulfate, EMIMES) soaked membrane. The theoretical model is based on our previous work24,34 but is further developed to account for all aspects of the studied CPSC. We find that the SC characteristics cannot be reproduced by a homogeneous model but instead require the incorporation of two phases with different ionic diffusivities. This heterogeneous model reproduces the cyclic voltammograms and galvanostatic charge–discharge characteristics of the SC. Next, we applied the model to the self-discharge of the SC and are now able to identify two phases in the discharge process: a fast phase which arises due to the equilibration of concentration gradients within the electrodes that arise from the charging, and a slow phase which can be attributed to ORR side reactions. Further, we generate impedance spectroscopy data from the model and analyse it in terms of equivalent circuits. We find that the heterogeneous transport in the model gives rise to constant phase element behaviour, which often is observed for CP electrodes. Finally, based on our model we investigate how the performance of the CPSC can be optimized with respect to various design parameters.
Experimental
Electrode preparation and cell assembly
The CNF + PEDOT:PSS electrodes were prepared following a recipe similar to the one reported by Malti et al.6 In short, poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate) (PEDOT:PSS, Clevios PH1000, 1–1.2 wt% dispersion), CNFs (carboxymethylated cellulose, degree of substitution 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12, 0.1 wt% aqueous dispersion), glycerol and DMSO were mixed in a ratio of (1
12, 0.1 wt% aqueous dispersion), glycerol and DMSO were mixed in a ratio of (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.9
4.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.7
7.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
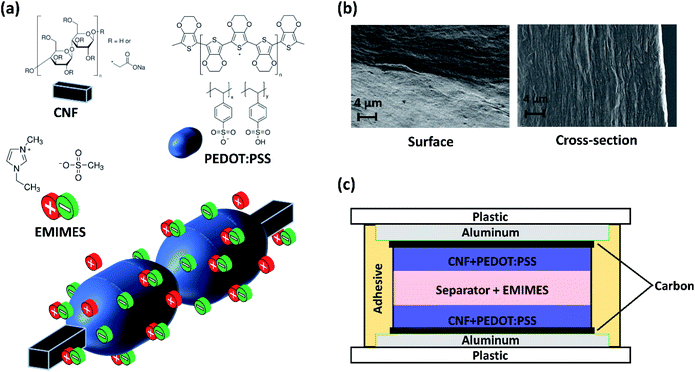
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54.5) and homogenized for 5 minutes with an ultra-Turrax® shear force mixer. The resulting dispersed solution was placed in a Petri dish and then baked in an oven for ca. 16 h at 60 °C to remove the excess solvents. Electrodes produced according to this procedure reach ca. 40 μm in thickness and appear flexible. The 1-ethyl-3-methylimidazolium ethyl sulfate electrolyte (EMIMES, ≥ 95%) was obtained from Sigma Aldrich. The chemical structures of PEDOT:PSS, CNFs and EMIMES are shown in Fig. 1a. The surface and cross-sectional images of the electrodes are shown in Fig. 1b.
54.5) and homogenized for 5 minutes with an ultra-Turrax® shear force mixer. The resulting dispersed solution was placed in a Petri dish and then baked in an oven for ca. 16 h at 60 °C to remove the excess solvents. Electrodes produced according to this procedure reach ca. 40 μm in thickness and appear flexible. The 1-ethyl-3-methylimidazolium ethyl sulfate electrolyte (EMIMES, ≥ 95%) was obtained from Sigma Aldrich. The chemical structures of PEDOT:PSS, CNFs and EMIMES are shown in Fig. 1a. The surface and cross-sectional images of the electrodes are shown in Fig. 1b.
For the supercapacitor assembly in Fig. 1c, a PET/aluminium/carbon current collector assembly was used. The patterned aluminium collectors on PET foil were provided by the company DP Patterning AB (dry-phase patterned). The carbon layer was screen printed on top of aluminium using an EKRA E2 semi-automatic screen and stencil printer. Two CNF + PEDOT:PSS electrodes were placed in direct contact with two separate aluminium/carbon platforms, subsequently sandwiching a fabric separator soaked in the EMIMES electrolyte. The arrangement was then laminated using double-sided tape to prepare a symmetrical supercapacitor as shown in Fig. 1c. For the ‘poor’ sealing test, ca. 15% of the double-sided tape was removed from the periphery so that the supercapacitor is not completely sealed from the outside environment.
Characterization
Potentiostatic and galvanostatic characterization was performed using a Keithley 2612B SourceMeter. Cyclic voltammetry (CV) was performed within 0 to 0.6 V at a 10 mV s−1 scan rate, unless otherwise stated. Galvanostatic measurements were performed by applying a gravimetric current density of 100, 350 or 700 mA g−1 of the active mass content (PEDOT mass), depending on the test case, to charge the supercapacitor up to selected upper vertex potential and subsequently discharging to 0 V. Self-discharge measurements were performed on an Ivium OctoStat200 potentiostat controlled using Ivium Soft software. Self-discharge measurements were performed by charging the device to the selected upper vertex potential and then letting it self-discharge for 5000 seconds by applying no current while monitoring the potential.The surface of the electrode was imaged using a Zeiss Sigma 500 Gemini Field Emission Scanning Electron Microscope (SEM). For the cross-sectional SEM images, the samples were frozen in liquid N2 and broken by holding with tweezers at opposite ends. The freshly fractured cross-section was then imaged by SEM. Both images are presented in Fig. 1b.
Mathematical model
COMSOL Multiphysics version 5.4 was used for model implementation and simulation. The modified Nernst–Planck–Poisson equations were setup by a combination of the electrostatics, transport of species and general mathematics modules. The nominal mapped mesh of the 2D models had about 40 elements in the horizontal direction. In the vertical direction, the model included finer meshing at both electrode-separator domain interfaces. The electrode domains comprised 100 vertical elements distributed according to a geometrical sequence with an element length ratio of 0.001 between the electrode-separator side and the current collector side. The separator was divided into two domains where each comprised 100 vertical elements distributed according to a geometrical sequence with an element length ratio of 0.0001 between the electrode-separator side and the middle of the separator. The galvanostatic tests were simulated using the events module, while the modelling fitting parameters were obtained by parametric sweeping. One CV cycle simulation was run before continuing to simulate the self-discharge tests as these tests were run in tandem during the experiments. Electrochemical impedance spectroscopy (EIS) spectra were simulated in COMSOL using small signal (frequency) analysis, with a 0 V static applied potential and a 10 mV sinusoidal wave, while the obtained Nyquist plots were fitted to equivalent circuits using EIS Spectrum Analyser software.Results and discussion
Supercapacitor operation
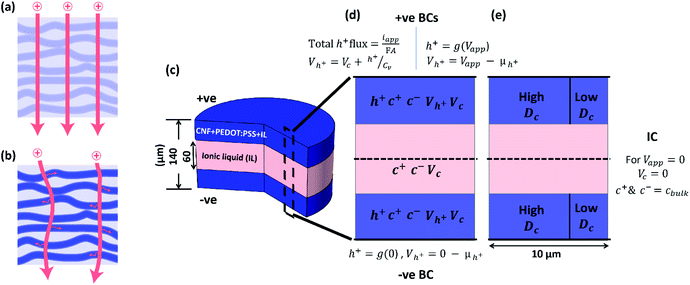
SCs based on CNF + PEDOT:PSS composite electrodes (Fig. 1b) and the EMIMES electrolyte were developed. The cell assembly is shown in Fig. 1c, comprising aluminium–carbon current collectors, CNF + PEDOT:PSS electrodes and a separator soaked in EMIMES. The aluminium layer provides lateral charge transport in the current collector, while the carbon layer prevents corrosion and promotes adhesion of the electrode. The electrodes were approximately 40 μm thick and the separator was around 60 μm thick. The cell was assembled from two half cells and sealed with an acrylic adhesive. The principle of operation of the supercapacitor is based on the charging characteristics of the PEDOT:PSS in the prevailing electrolyte environment, as PEDOT:PSS is the main electroactive electrode component. In CNF + PEDOT:PSS electrodes, previous work20 has shown that PEDOT:PSS is organized in π–π stacking forming beadlike structures of variable diameters around the CNF strands (Fig. 1a). The charge carriers (holes) in the PEDOT phase are initially electrostatically stabilized by the adjacent negative fixed charges in the PSS. The opportunity of charging/discharging ((de)doping) the PEDOT is then presented in an electrolyte environment.17 In the pure EMIMES electrolyte, the original counter ions to PSS are essentially immobile. Thus, during (dis)charging, excess PSS− ions or holes are subsequently compensated by dissociated EMIM+ or ES− ions, respectively (Fig. 1a). As previously reported,18 the PEDOT:PSS phase segregates when processed into films, yielding two phases with different ionic diffusivities. This aspect has not been considered in previous models but might affect the charging behaviour of electrodes. To adequately reproduce the observed non-ideal voltammetry/charging behaviour of the developed supercapacitors, we consider two modelling approaches: a homogeneous model (Fig. 2a) with constant diffusivities throughout the electrodes and a heterogeneous model (Fig. 2b) based on a two-phase system with one phase having significantly lower ionic diffusivity. Based on the study by Rivnay et al.,18 the phase segregation is expected to occur throughout the whole electrode, with low diffusivity domains distributed within a high diffusivity phase. From a transport perspective, this structure is very similar to arranging high and low diffusivity domains in parallel along the depth direction of the electrodes. Such a simplified geometry has been employed here for the heterogeneous model.Mathematical model
The homogeneous model representation of the SC is shown in Fig. 2d, with uniform ion diffusivity within the electrode domains. The relevant quantities within respective domains are given in Fig. 2d, including concentration of holes (h+), EMIM+ (c+), ES− (c−), hole potential (Vh+) and electrolyte potential (Vc). The heterogeneous model includes two regions of different ion diffusivity within the electrode domains (Fig. 2e). The models are based on modified Nernst–Planck–Poisson equations to describe the transport of the present species along with both hole and ion electrostatics,34 which together describe the charging characteristics of the CNF + PEDOT:PSS electrodes for both the homogeneous and heterogeneous representations. Given the cylindrical shape of the cell, the homogeneous model (Fig. 2d) can be represented by a 1D implementation; however, the more complicated heterogeneous model (Fig. 2e) requires a 2D implementation. Therefore, a 10 μm wide 2D portion of the cell was chosen as the computational domain (Fig. 2e).The hole transport and accumulation within the PEDOT phase is described by
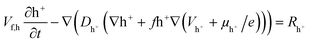 | (1) |
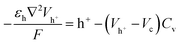 | (2) |
Assuming a Gaussian density of states in PEDOT:24
μh+ = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(h+) + eB ln(h+) + eB | (3) |
Since the self-ionization of pure EMIMES is around 65%,35 we set the free EMIM+ and ES− concentrations to 3.15 M in the electrolyte.36 Ionic transport is described by
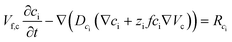 | (4) |
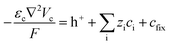 | (5) |
The boundary conditions for the 2D model are shown in Fig. 2d. During voltammetry, the negative boundary is grounded, while the magnitude of the electric potential across the cell Vapp is applied at the positive boundary, thereby defining Vh+ at both boundaries. With known PEDOT:PSS film charge characteristics via energy balance at the terminals,24 h+ at both positive and negative boundaries is given by the solution to the non-linear function g(Vapp) in eqn (6). Under galvanostatic test conditions, the same ground condition applies at the negative boundary, while the total hole flux is defined by the applied current iapp at the positive boundary.
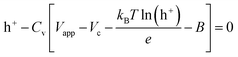 | (6) |
Eqn (6) mathematically takes the form of Euler's version of the Lambert W function, which is herein solved numerically – as with the other equations defining our model.
At the horizontal centre line of the modelling domain in Fig. 2d and e, the depicted initial conditions (IC) apply for Vapp = 0 to establish an initial mass/charge balance within the system. These conditions are then removed for subsequent transient simulations of galvanostatic or voltammetric tests. All other values of applied constants and parameters in eqn (1) through (6) not stated are supplied in ESI Table 1.†
Homogeneous vs. heterogeneous supercapacitor model
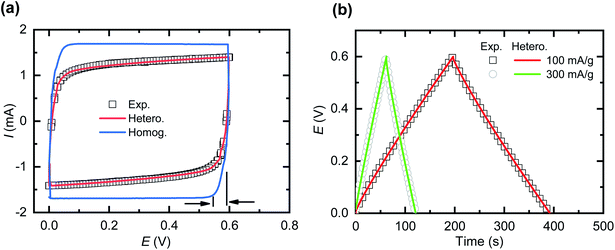
The experimental results of both cyclic voltammetry (CV) and galvanostatic charge–discharge provide the opportunity to qualitatively and quantitatively compare and validate the models. From our experience with CNF + PEDOT:PSS composite electrodes, we establish the validation within a reasonable potential range of 0.6 V. For the models, we apply the defined experimental geometries, known experimental test conditions and parameters from the literature. The only fitting parameters of the models were the effective diffusivities (Dci) of both cations and anions within the electrode domains. Dci in the separator domain is known from experimental measurements of the bulk electrolyte and is subsequently adjusted according to separator porosity.For an ideal capacitor, one expects that the shape of the lower right and upper left of the CV curve is indicative of prevalent ion mass transport limitations. For the homogeneous model, we based the fit of Dci in the electrodes on the horizontal deviation of the lower right part of the CV curve from the vertex potential (Fig. 3a). Although the total charge storage capacity of the active material (PEDOT:PSS) of the supercapacitor is known,24,34 the homogeneous model predicts a CV curve significantly different from the experimental results, suggesting that some processes have not been properly captured by the homogeneous model. In further attempts to fit the experimental data (see ESI Fig. S1†), increasing Dci in the electrodes for the homogeneous model leads to a CV curve appearing more box-like, while further reduction of Dci makes the CV curve excessively oval. The experimental CV curve indicates a non-ideal capacitor behaviour, where previous studies that apply equivalent circuit models31,37 commonly include this as a leakage resistance residing in parallel to the capacitance, oftentimes without any proper physical motivation. The physical explanation of this phenomenon is one of the main points of the present study as far as conducting polymer based SCs are concerned.
Next, we investigated if the heterogeneous model could capture the non-ideal capacitive behaviour of the measured SCs. The fitting parameters of the heterogeneous model were the relative sizes of the high and low Dci domains, and the actual Dci values in the low Dci region. The Dci value for the high Dci domain was adopted from the homogeneous model given that it reproduced horizontal deviation of the lower right part of the CV curve as mentioned (Fig. 3a). The fitting of the heterogeneous model to the experimental data (see ESI Fig. S1†) indicates that the low Dci domains occupy approximately 27% of the total electrode volume, with Dci values being only 0.005% of that of the high Dci region. The heterogeneous model closely reproduces both the experimental CV curve and the galvanostatic charge–discharge curve (Fig. 3b), indicating that the heterogeneous model captures the transport processes within the supercapacitor significantly better than the homogeneous model.
The assumption of regions of varying diffusivities is backed up by experimental observations. It has been known for a long time that films of PEDOT:PSS tend to phase segregate into PEDOT-rich and PSS-rich regions. More recently, Rivnay et al.18 quantified the composition of the segregated phases in the nano and meso-scale structure of PEDOT:PSS films. They showed that the relative sizes of either domain could be modified by the amount of ethylene glycol applied in electrode preparation. In moving front experiments, leading and lagging fronts were observed, which were attributed to different ionic diffusivities within the two phases. Regarding the CNF + PEDOT:PSS composite, a previous study20 has shown that PEDOT:PSS aggregates in bead-like structures with an average diameter of 13 nm around the CNFs (3–5 nm in diameter). This in turn dictates the electrode morphology observed in Fig. 1b, thereby potentially being a second source of inhomogeneity for the electrodes. The non-ideal CV behaviour is also expected to be more prominent in our system, in comparison to previous studies conducted using aqueous electrolytes, due to less swelling occurring in our case. The exact geometry and dimensions of the low-diffusivity regions within the electrodes are unknown. However, the model is rather insensitive to these factors since a longer distance can be compensated by a higher diffusivity when fitting the model parameters to the data. Thus, prior knowledge of the electrode morphology is needed to obtain absolute values of the diffusivities from the model.
Self-discharge analysis
Self-discharge is an important issue for SCs as it in part sets the limitation on their charge storage capability over extended periods of times. Experimental self-discharge tests of our SC indicate two different discharge processes: one faster (t < ∼1000 s) and one slower (t > ∼1000 s). In Fig. 4 the results of experimental self-discharge tests are compared to three different models. The homogeneous model manages to reproduce the charging behaviour and the iR drop but fails to account for any of the discharge processes. The heterogeneous model successfully captures both the iR drop and the fast self-discharge process (until about 1000 s in Fig. 4a) but fails to account for the slower self-discharge process. Based on discussions in previous studies38–41 and a re-evaluation of our experimental setup, two candidate processes for the further self-discharge after ∼1000 s in Fig. 4a were identified: direct electron transfer between both electrodes through the separator or additional faradaic electron transfer reactions occurring within the cell. As there was no cell compression and the separator has very high electron resistance, the first process seems unlikely here. Electrochemical over-oxidation is a known degradation mechanism for PEDOT:PSS electrodes,42 but it occurs above +0.8 V vs. Ag/AgCl, which is outside the range of operation in this work. A more probable explanation would be the two-electron oxygen reduction reaction (ORR) producing hydrogen peroxide, a phenomenon which has been demonstrated for PEDOT:PSS electrodes at cathodic potentials in previous studies.25 As the ionic liquid was not completely dried and the cells were assembled and tested under ambient conditions, a certain small amount of water and oxygen is expected to have been trapped within the cell volume. To indicate if oxygen is responsible for the slow discharge process, self-discharge tests of a typical cell assembly (with proper sealing) were compared to tests of a poorly sealed assembly. The self-discharge rate is higher for the poorly sealed cell (Fig. 4b), especially at higher voltages. This indicated that the presence and influx of oxygen is responsible for the slow discharge process through the ORR at the anode. During this reaction, the electrode loses electrons (holes are generated) and the charge stored within the cell is thus lost over time.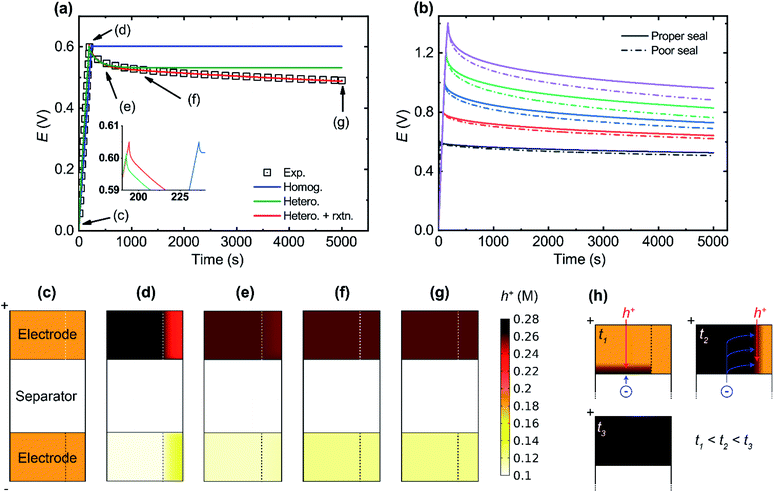 | ||
| Fig. 4 Modelling of self-discharge. (a) Experimental self-discharge test compared to three different models: the homogeneous model (Homog.), the heterogeneous model (Hetero.) and the heterogeneous model with the ORR reaction (Hetero. + rxtn.). The data points for panels c–g are labelled. (b) Self-discharge tests at increasing cut-off potentials (0.6, 0.8, 1, 1.2 and 1.4 V) with properly/poorly sealed cells. (c–g) Simulated hole concentration (in mol dm−3) within electrodes at critical points during self-discharge. Positive electrode on top and negative below as depicted in Fig. 2. (h) Schematic of how the doping within the electrode changes with time as a voltage is applied. The doping change occurs first in the high ionic diffusivity domain, followed by the low diffusivity domain. Charging at 100 mA g−1 and 350 mA g−1 for (a) and (b), respectively, until the cut-off potential, and then open circuit potential was monitored for 5000 seconds. Modelling domains of (c) to (g) are not to scale for better visualization, and the actual domain length and height are 10 and 140 μm, respectively. | ||
To account for the slow self-discharge process, the ORR was included in the heterogeneous model (using the same fitted Dci parameters) by the addition of a Rh+ term in eqn (1). Considering the potential dependent ORR reaction in eqn (7), Rh+ is approximated using eqn (8).
| O2 + 2H+ + 2e− → H2O2 | (7) |
Rh+ = −k0cO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(αO2f × 0.5(Vapp − E0)) exp(αO2f × 0.5(Vapp − E0)) | (8) |
In eqn (8), k0 is the rate constant, αO2 is the transfer coefficient and E0 is the reaction potential. k0 becomes another model fitting parameter when we assume αO2 to be equal to 0.5 (standard value, no information available for the reaction on this electrode) and cO2 being the initial oxygen concentration of the cell electrolyte. These values of αO2 and cO2 are only reasonable design assumptions as they were not directly measured in situ. Protons are available for the ORR from the PSS phase of the electrodes. The ORR starts around −0.2 V vs. Ag/AgCl for PEDOT:PSS;25 since both electrodes in our SC are at an initial potential around 0 V vs. Ag/AgCl, E0 is taken as 0.4 V on the assumption of even potential biases in both electrodes during the experiment. For diligence, an additional transport equation (eqn (4)) is then included for O2.
By including the ORR in the heterogeneous model, the experimental self-discharge results are adequately reproduced. The plot lines for both the experimental results and the heterogeneous model including the ORR (rxtn.) are superimposed and included in Fig. 4a. By studying the marked points in Fig. 4a, we can comprehensively describe the electrode processes during charging and self-discharge as follows: Fig. 4c: at the start of charging, the positive and negative electrodes are at equilibrium with respect to a homogeneous doping level (hole concentration), potential and ionic concentrations. Fig. 4d: at the end of charging to the cut-off potential, the positive electrode is oxidized while the negative electrode is reduced, as expected. The low diffusivity domains within both electrodes (to the right) lag in the charging due to the slow ionic transport. Fig. 4e and f: after charging reaches the cut-off, the doping levels equilibrate within the electrodes. The redistributions within the electrodes are caused by internal driving forces (difference in doping levels), resulting in the initial fast self-discharge process. Fig. 4e shows the doping distribution halfway through the redistribution process. Fig. 4f: once the redistribution process is completed, re-oxidation of the negative electrode from the ORR continues to slowly decrease the cell potential until the end of the tests at 5000 s. The concentration profiles for c+ and c− during the self-discharge process are given in ESI Fig. S2† and the hole concentrations along the horizontal centrelines through both electrodes are plotted in ESI Fig. S3.† We can conclude that the self-discharge in this family of supercapacitors is initially dominated by a fast ion redistribution process. The slower faradaic self-discharge runs as a parallel process but is only noticeable after the initial self-discharge has occurred. The speed and severity of the faradaic process are cell/electrode potential dependent. It is interesting to note that due to the relatively slower ORR considered herein, there is no significant difference in the CV curve at a 10 mV s−1 scan rate for the heterogeneous model with or without the inclusion of eqn (8). CV curves at lower scan rates of 5 mV s−1, 2 mV s−1 and 1 mV s−1 with or without the inclusion of eqn (8) (see ESI Fig. S4†) also show no significant difference. The influence of eqn (8) is, however, prominent at low frequency in Nyquist plots of simulated EIS spectra using the developed heterogeneous model (ESI Fig. S4†). This observation re-emphasizes the limitation of using only CV curves in describing prevalent charge and mass transport in supercapacitors. A schematic of the doping process within the electrode is provided in Fig. 4h. The faradaic discharge rate can likely be significantly reduced by preventing the dissolution of oxygen in the cell during the fabrication process; however this is not possible with our current process in ambient air.
Comparison to equivalent circuit modelling
Equivalent circuit fitting is a widely adopted method for analysing the processes within SCs; thus it is of interest to compare this method to our developed modelling approach. In equivalent circuit modelling, the non-ideal behaviour of SCs and batteries (given that both have mixed diffusion and kinetics limitations) is often represented by constant phase elements,43–45 whose resultant capacitance is time-scale (or frequency) dependent. Several different equivalent circuits were evaluated for fitting of the generated EIS spectra. Given the two apparent time constants within the system, it is not surprising that two constant phase elements are needed to fit the EIS data generated by our model (Fig. 5). By adjusting the relative diffusivity of the domains in the heterogeneous model, the model transitions from the homogeneous state (Dmod = 1) to the final heterogeneous state (Dmod = 5 × 10−5). The corresponding fitting parameters of the equivalent model are given in Table 1. As expected, the equivalent series resistance (Rs) is unaffected by the presence of Dci inhomogeneity, as it reflects the ionic resistance across the separator. As the Dci inhomogeneity is introduced, not only are CPE1 and CPE2 varied, but the parallel resistance, R1, is also adapting to CPE1. R1 and R2 are often described as charge transfer resistances in equivalent circuit analysis. This highlights a problematic feature in equivalent circuit analysis, as we know from our model results that R1 is only slightly influenced by the presence of the ORR (considering the comparison of EIS spectra with or without inclusion of eqn (8) in ESI Fig. S4†). The spectra are still defined by both R1 and R2, even though the DC potential of the EIS is 0 V, while the ORR reaction potential is 0.4 V (with respect to the applied potential). Therefore, these resistances need to be de-convoluted before direct physical meanings could be attributed to the respective system specific constants. We can conclude that in our case, R1 is defined by the ionic transport resistance within the electrode. The classical interpretation of R1 as charge transfer resistance is therefore invalid in this particular case. One should also note that the constant phase elements alone cannot account for the inhomogeneous transport and charging within the model, and the parallel resistors are necessary to obtain decent fits. Altogether these highlight the challenges associated with equivalent circuit analysis of complex systems and the benefits of modelling comprising clearly defined physical quantities and processes, like the species and charge balance/transport model of this work. ESI Fig. S5† shows how the model can fit the experimental EIS data well over a wide range of frequencies.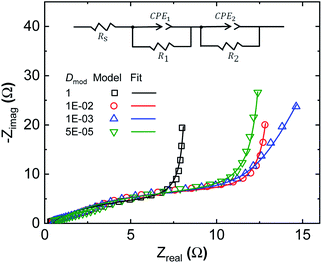 | ||
| Fig. 5 Equivalent circuit fit to modelled EIS spectra for various degrees of Dci inhomogeneity. Dci in the low Dci region (∼27% of the electrode domain seen in Fig. 2e) is reduced by the factor Dmod. | ||
| a D mod is the ratio of ion diffusivity in the low Dci domain to that in the high Dci domain. b The homogeneous model has a Dmod value of 1. Equivalent CPE impedance is defined as 1/Q(jw)n. | ||||
|---|---|---|---|---|
| Parameter | ||||
| D mod | 1b | 1 × 10−2 | 1 × 10−3 | 5 × 10−5b |
| R s (Ω) | 0.5 | |||
| R 1 (Ω) | 7.9 | 13.0 | 11.7 | 12.5 |
| R 2 (kΩ) | 20.0 | |||
| CPE1, Q (S(−n)) | 0.038 | 0.025 | 0.023 | 0.023 |
| n 1 | 0.83 | 0.80 | 0.80 | 0.76 |
| CPE2, Q (S(−n)) | 0.169 | 0.169 | 0.125 | 0.123 |
| n 2 | 1.00 | 1.00 | 0.92 | 1.00 |
Influence of cell design on performance
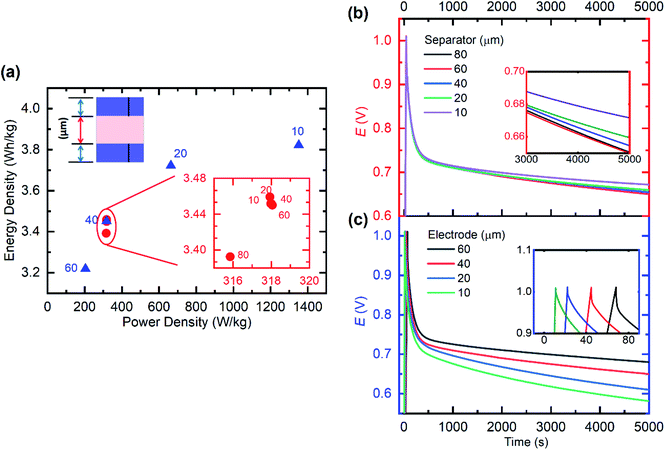
Based on our established heterogeneous model including the ORR, we then investigated how the cell design (electrode and separator thickness) influences the SC device performance. We select energy and power density (at discharge) as well as self-discharge dynamics as performance parameters here. A cut-off potential of 1.0 V is used for the investigations herein, given the need to maximize both discharge energy and power density, while also reducing the severity of the ORR during self-discharge as much as possible. Beyond a 1.4 V cut-off voltage, the negative electrode becomes fully de-doped (hole concentration approaches zero). Experimentally, this is observed as stalling/inconsistency of discharge capacity (consequent coulombic efficiency reduction) beyond a 1.4 V cut-off in the charge–discharge results (ESI Fig. S6†). The electrode thickness will directly scale versus the total amount of PEDOT in the electrode. Consequently, at cell assembly, the total amount of ions is affected. Also, by keeping the separator properties (porosity and Dci) constant, variation in separator thickness only affects the total amount of the electrolyte, e.g. ions/species present in the cell.Energy and power density show almost no dependence on separator thickness (Fig. 6a), indicating that the ion transport within the electrodes is the limiting factor for the cell. In the self-discharge tests in Fig. 6b, the inference that different mechanisms dominate different regions of the self-discharge is reiterated. For constant electrode thickness, the self-discharge up to about 1000 s (ion redistribution dominated) is similar for the different separator thicknesses. In the second phase, the total amount of oxygen within the system dominates (via the ORR) the self-discharge process until 5000 s (see the inset of Fig. 6b), as a higher separator thickness leads to more oxygen present in the system. For non-perfectly encapsulated cells, as more oxygen finds its way into the device system, a larger cell volume due to increased separator thickness allows for more accumulation of oxygen than thinner separators. In the absence of such a parasitic faradaic reaction, one expects a flatter self-discharge curve after ∼1000 s (towards that seen for ‘hetero.’ in Fig. 4a), which may be achieved by electrolyte drying and an oxygen/water-free packaging environment. If additional oxygen does not diffuse into the system long-term, the initial oxygen will eventually be consumed with less self-discharge as a result.
Both power and energy density improve with decreasing electrode thickness (Fig. 6a), with power density showing a greater improvement due to the reduced series resistance (seen as a lower ohmic drop in Fig. 6c). The self-discharge test results in Fig. 6c show two critical effects as electrodes become thinner. Firstly, the ion redistribution-induced self-discharge is more severe for the thin electrodes. A possible explanation is that the charging time is lower for thin electrodes, thereby leaving the low diffusivity region further away from equilibrium after charging, leading to more substantial discharge. Secondly, the faradaic self-discharge is also more severe for thin electrodes, as relatively more oxygen is stored within the separator, which eventually diffuses into the electrodes. We previously mentioned that the arrangement of both low and high Dci regions in reality is not exactly as arranged in Fig. 2e. However, our various simulations provide the foundation for analysing and understanding the influence on performance of various experimental structural arrangements within composite electrodes. In the previous sections, we've described a homogeneous model, which is characterized by homogeneous ion diffusivity within the electrode and absence of any faradaic parasitic reactions. This ideal performance represents an upper performance limit to target given any selected cell design specifications.
Conclusions
Conducting polymer supercapacitors often show non-ideal capacitive characteristics which are hard to analyse in detail by conventional methods like equivalent circuit modelling. Part of the challenge lies in the mixed and coupled electronic and ionic transport within the system. Herein we have developed a novel multiphysics model based on the Nernst–Planck–Poisson equations to analyse the characteristics of fabricated PEDOT:PSS-CNF-IL supercapacitors. We find that a homogeneous transport model, where diffusivities are constant throughout the electrodes, cannot reproduce the non-ideal capacitive behaviour of the CPSC. A previous experimental study by Rivnay et al.18 indicated the presence of inhomogeneous ion transport within PEDOT:PSS thin films. By incorporating electrode domains of low ion diffusivity, we developed a novel heterogeneous model for CPSCs which reproduces the experimentally observed CV curves. We proceeded with analysing the self-discharge of the CPSCs and found two regimes, one faster (<500 s) and one slower (>500 s). The faster discharge process can be understood from the model as an equilibration process between high and low ion diffusivity domains. By incorporating the faradaic oxygen reduction reaction into the model, the slower discharge reaction could also be reproduced accurately. Next, we analysed the impedance spectrum output of the model with conventional equivalent circuit analysis with the aim of establishing a link between the two methods. However, although the equivalent circuit fits well, its elements cannot be directly associated with transport phenomena within the model. Contrarily, changes in charge transfer resistances, which typically represent chemical reactions within equivalent circuit models, were found to be associated to the inhomogeneous ion transport within the model, highlighting the potential pitfalls of equivalent circuit analysis of such complex systems. Finally, we used the developed model to predict the performance of various CPSC device configurations and found that the electrode thickness has the largest effect on both power density and self-discharge. Altogether, we have demonstrated how a novel modelling approach based on heterogeneous ion transport can facilitate the understanding of conducting polymer energy devices. We believe that this represents an important finding for the modelling and understanding of CP energy storage devices in particular, and for organic mixed electron ion conductors in general.Conflicts of interest
A spin-out company, LIGNA Energy AB, has recently been established that aims to commercialize electrical energy storage technology in part based on forest-based biopolymers. The results from this work may be of importance for the work and development of that company. LIGNA Energy is in part owned by Linköping University (LiU Invest), RISE and researchers (e.g. Isak Engquist, Magnus Berggren, and Jesper Edberg) of LiU and RISE.Acknowledgements
The authors recognize the assistance from Ms Rayan Ali Mohamed Elsayed with the EIS equivalent circuit fitting. This work was financially supported by the Knut and Alice Wallenberg Foundation, Linköping University and industry through the Wallenberg Wood Science Centre and Wallenberg Scholar, the Swedish Government Strategic Research Area in Materials Science on Advanced Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009-00971), and the Swedish Foundation for Strategic Research.References
- M. Mastragostino, C. Arbizzani and F. Soavi, Solid State Ionics, 2002, 148, 493–498 CrossRef CAS.
- G. A. Snook, P. Kao and A. S. Best, J. Power Sources, 2011, 196, 1–12 CrossRef CAS.
- X. Li, C. Zhou, L. Shen, W. Zhou, J. Xu, C. Luo, J. Hou, R. Tan and F. Jiang, Int. J. Electrochem. Sci., 2019, 14, 4632–4642 CrossRef CAS.
- J. Song, G. Ma, F. Qin, L. Hu, B. Luo, T. Liu, X. Yin, Z. Su, Z. Zeng, Y. Jiang, G. Wang and Z. Li, Polymers, 2020, 12, 450 CrossRef CAS.
- S. Khasim, A. Pasha, N. Badi, M. Lakshmi and Y. Kumar Mishra, RSC Adv., 2020, 10, 10526–10539 RSC.
- A. Malti, J. Edberg, H. Granberg, Z. U. Khan, J. W. Andreasen, X. Liu, D. Zhao, H. Zhang, Y. Yao, J. W. Brill, I. Engquist, M. Fahlman, L. Wågberg, X. Crispin and M. Berggren, Adv. Sci., 2016, 3, 1500305 CrossRef.
- Q. Li, M. Horn, Y. Wang, J. MacLeod, N. Motta and J. Liu, Materials, 2019, 12, 703 CrossRef CAS.
- F. N. Ajjan, N. Casado, T. Rębiś, A. Elfwing, N. Solin, D. Mecerreyes and O. Inganäs, J. Mater. Chem. A, 2016, 4, 1838–1847 RSC.
- J. Edberg, R. Brooke, H. Granberg, I. Engquist and M. Berggren, Adv. Sustainable Syst., 2019, 3, 1900050 CrossRef.
- T. Rębiś and G. Milczarek, Electrochim. Acta, 2016, 204, 108–117 CrossRef.
- X. Gao, L. Zu, X. Cai, C. Li, H. Lian, Y. Liu, X. Wang and X. Cui, Nanomaterials, 2018, 8, 335 CrossRef.
- D. Aradilla, S. Sadki and G. Bidan, Synth. Met., 2019, 247, 131–143 CrossRef CAS.
- K. Ma, C. Zhang, C. E. Woodward and X. Wang, Electrochim. Acta, 2018, 289, 29–38 CrossRef CAS.
- R. A. Perera Jayawickramage and J. P. Ferraris, Nanotechnology, 2019, 30, 155402 CrossRef.
- Y. Zhang, R. Ye, D. Henkensmeier, R. Hempelmann and R. Chen, Electrochim. Acta, 2018, 263, 47–52 CrossRef CAS.
- T. Schoetz, M. Kurniawan, M. Stich, R. Peipmann, I. Efimov, A. Ispas, A. Bund, C. P. de Leon and M. Ueda, J. Mater. Chem. A, 2018, 6, 17787–17799 RSC.
- A. V. Volkov, K. Wijeratne, E. Mitraka, U. Ail, D. Zhao, K. Tybrandt, J. W. Andreasen, M. Berggren, X. Crispin and I. V. Zozoulenko, Adv. Funct. Mater., 2017, 27, 1700329 CrossRef.
- J. Rivnay, S. Inal, B. A. Collins, M. Sessolo, E. Stavrinidou, X. Strakosas, C. Tassone, D. M. Delongchamp and G. G. Malliaras, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- U. Lang, E. Müller, N. Naujoks and J. Dual, Adv. Funct. Mater., 2009, 19, 1215–1220 CrossRef CAS.
- D. Belaineh, J. W. Andreasen, J. Palisaitis, A. Malti, K. Håkansson, L. Wågberg, X. Crispin, I. Engquist and M. Berggren, ACS Appl. Polym. Mater., 2019, 1(9), 2342–2351 CrossRef CAS.
- Z. Tang, S. T. Donohoe, J. M. Robinson, P. A. Chiarelli and H.-L. Wang, Polymer, 2005, 46, 9043–9052 CrossRef CAS.
- T.-C. Tsai, H.-C. Chang, C.-H. Chen, Y.-C. Huang and W.-T. Whang, Org. Electron., 2014, 15, 641–645 CrossRef CAS.
- A. Cho, S. Kim, S. Kim, W. Cho, C. Park, F. S. Kim and J. H. Kim, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 1530–1536 CrossRef CAS.
- K. Tybrandt, I. V. Zozoulenko and M. Berggren, Sci. Adv., 2017, 3, eaao3659 CrossRef.
- E. Mitraka, M. Gryszel, M. Vagin, M. J. Jafari, A. Singh, M. Warczak, M. Mitrakas, M. Berggren, T. Ederth, I. Zozoulenko, X. Crispin and E. D. Głowacki, Adv. Sustainable Syst., 2019, 3, 1800110 CrossRef.
- C. Pean, B. Rotenberg, P. Simon and M. Salanne, J. Power Sources, 2016, 326, 680–685 CrossRef CAS.
- N. Devillers, S. Jemei, M.-C. Péra, D. Bienaimé and F. Gustin, J. Power Sources, 2014, 246, 596–608 CrossRef CAS.
- C. Hao, X. Wang, Y. Yin and Z. You, J. Electron. Mater., 2016, 45, 515–526 CrossRef CAS.
- Y. Wang, C. Zhang, X. Qiao, A. N. Mansour and X. Zhou, J. Power Sources, 2019, 423, 18–25 CrossRef CAS.
- B. Wang, C. Wang, Q. Hu, L. Zhang and Z. Wang, J. Energy Storage, 2020, 30, 101473 CrossRef.
- S. Fletcher, V. J. Black and I. Kirkpatrick, J. Solid State Electrochem., 2014, 18, 1377–1387 CrossRef CAS.
- F. Barzegar, L. Zhang, A. Bello, N. Manyala and X. Xia, J. Mater. Chem. A, 2018, 6, 17481–17487 RSC.
- T. Yeu, T. V. Nguyen and R. E. White, J. Electrochem. Soc., 1988, 135, 1971–1976 CrossRef CAS.
- M. O. Bamgbopa, J. Edberg, I. Engquist, M. Berggren and K. Tybrandt, J. Mater. Chem. A, 2019, 7, 23973–23980 RSC.
- Y. Mao and K. Damodaran, Chem. Phys., 2014, 440, 87–93 CrossRef CAS.
- H. Tokuda, S. Tsuzuki, M. A. B. H. Susan, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 19593–19600 CrossRef CAS.
- M. Ates, Prog. Org. Coat., 2011, 71, 1–10 CrossRef CAS.
- B. W. Ricketts and C. Ton-That, J. Power Sources, 2000, 89, 64–69 CrossRef CAS.
- Q. Zhang, J. Rong, D. Ma and B. Wei, Energy Environ. Sci., 2011, 4, 2152–2159 RSC.
- M. Xia, J. Nie, Z. Zhang, X. Lu and Z. L. Wang, Nano Energy, 2018, 47, 43–50 CrossRef CAS.
- Z. Wang, X. Chu, Z. Xu, H. Su, C. Yan, F. Liu, B. Gu, H. Huang, D. Xiong, H. Zhang, W. Deng, H. Zhang and W. Yang, J. Mater. Chem. A, 2019, 7, 8633–8640 RSC.
- P. Tehrani, A. Kanciurzewska, X. Crispin, N. Robinson, M. Fahlman and M. Berggren, Solid State Ionics, 2007, 177, 3521–3527 CrossRef CAS.
- I. Mustafa, M. O. Bamgbopa, E. Alraeesi, Y. Shao-Horn, H. Sun and S. Almheiri, J. Electrochem. Soc., 2017, 164, A3673–A3683 CrossRef CAS.
- M. O. Bamgbopa and S. Almheiri, J. Power Sources, 2017, 342, 371–381 CrossRef CAS.
- O. Gharbi, M. T. T. Tran, B. Tribollet, M. Turmine and V. Vivier, Electrochim. Acta, 2020, 343, 136109 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta09429c |
| This journal is © The Royal Society of Chemistry 2021 |