The effect of sub-surface strontium depletion on oxygen diffusion in La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ

Abstract

The immediate surface and sub-surface composition of heat treated La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ samples was measured by ion beam analysis and compared to oxygen transport properties over the same depth scale. Consistent with the literature, strontium segregation was observed for samples that received thermal treatments with the formation of an Sr–O based monolayer at the surface. Just below this, a sub-surface strontium depletion region over a depth scale of approximately 2–15 nm was seen. In this sub-surface region, a depletion of lanthanum was also observed. Oxygen transport properties were measured using isotopic labelling techniques and showed that, despite large changes in composition, the transport properties remain largely unchanged. Because strontium diffusion is slow in the bulk and grain boundaries only account for 0.03% of the material (due to large grains), it is suggested that 2D defects (such as dislocations and twins) can act as fast diffusion pathways for the strontium to account for the Sr depletion region observed below the surface.

---

1. Introduction

In the drive to lower operating temperatures in solid oxide fuel cells (SOFC), mixed ionic–electronic conducting (MIEC) materials have been utilised as cathode materials due to their excellent properties for the reduction and incorporation of oxygen. Although the oxygen reduction reaction (ORR) at the gas–solid interface is not fully understood, it is clear that understanding the outermost surface microstructure and composition is vital. Unfortunately, degradation of the solid–gas interface is a common observation amongst promising perovskite-based (ABO₃) MIEC materials such as La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ.^1–3

1.1. Strontium segregation

The predominant mechanism of MIEC cathode surface degradation is the formation of passivating secondary phases. These phases often have very low electronic and ionic conductivities and as such reduce the electrode's ‘active area’ by preventing the reduction and incorporation of oxygen. Secondary phase formation can occur as a result of a reaction between the MIEC surface and common gas phase components and impurities.^4,5 However, in addition to this, the surface of many perovskite-based MIECs appear to be inherently unstable as a result of aliovalent substitution.^6–8

Aliovalent substitution of the A-site in perovskite-based MIECs is used to introduce oxygen vacancies into the structure.⁹ However, an undesirable side-effect of this is the segregation of A-site substituents towards the surface. Due to the prevalence of strontium as an A-site substituent this is commonly referred to as ‘strontium segregation’,¹⁰ however, other substituent atoms with varying atomic sizes and formal charges also invoke segregation effects.¹¹ The degree of strontium segregation depends on several external factors (such as temperature, oxygen partial pressure, strain and electric field), but is also driven by elastic and electrostatic forces arising from aliovalent substitution.

Elastic contributions commonly result from size differences between the lattice atom and substituent atom. Any size mis-match will lead to lattice strain, which the system attempts to reduce by segregating substituent atoms towards interfaces (such as grain boundaries) and the surface.¹² The degree to which elastic forces influence segregation depends upon the magnitude of the mis-match and whether the substituent atom is larger or smaller than the lattice site.¹¹ In some perovskites (such as LSCF), the B site also receives aliovalent substitution in order to stabilise a particular crystal structure and tailor the thermal expansion coefficient (TEC).¹³ B-Site substitution is likely to alter elastic contributions by changing unit cell volume, however, this has not yet been fully investigated.

In general, the electrostatic driving force for segregation arises from the system's need to neutralise charged surfaces. Charged surfaces commonly occur in perovskite-based MIECs due to the presence of excess oxygen vacancies at the surface¹¹ and polar surfaces resulting from charged AO and BO₂ stacking planes (where the formal charge of the A and B site cation is 3+).¹⁴ Oxygen vacancies , with an effective charge of 2+, result in a positively charged surface, causing the negatively charged A-site substituent (Sr_La′) to be attracted towards the surface. The termination layer (AO or BO₂) will also influence the overall surface charge. Recent studies using Low Energy Ion Scattering (LEIS) suggest the outermost surface of 3 : 3 perovskites are AO terminated,^15,16 suggesting further positive surface charge. However, it should be noted that it is very difficult to produce a segregation-free surface (especially on a sintered ceramic sample),¹⁷ therefore, it is difficult to determine if these results actually indicate AO termination or simply an already segregated surface.

It is clear that both elastic and electrostatic effects influence the degree of segregation in an MIEC, however, it is not easy to decouple their effects. Koo et al. showed marked improvements in surface stability by increasing unit cell volume to more readily accommodate A-site substituents in the bulk whilst minimising lattice strain.¹⁸ Whereas, Tsvetkov et al. substituted surface B-site atoms to reduce the surface oxygen vacancy concentration, minimising electrostatic effects from a charged surface.¹⁹ Segregation is a complex process that is highly dependent upon the composition of the MIEC, making it difficult to generalise and predict the mechanisms of segregation. As such, the exact mechanisms of segregation in LSCF have not yet been fully elucidated, however, it is clear that strontium segregation and secondary phase growth is prevalent at intermediate temperature SOFC (IT-SOFC) operating temperatures.²⁰

To summarise the literature, it has been observed that: (1) segregated strontium first forms a Sr–O monolayer at the surface, which, given sufficient time at elevated temperatures, will eventually cover the whole surface of the material,^15,21 (2) secondary phases grow preferentially on microstructural defects such as grain boundaries and twin boundaries,^22–24 (3) Sr-based particles form, comprised of a strontium oxide (SrO) core with a ‘capping’ layer surrounding the core,²⁵ the composition of which is dependent upon the gas atmosphere present during the anneal, (5) particle growth rate is observed to vary with gas composition²² and (6) the onset of particle growth begins within minutes at temperatures around 1000 °C.^20,22 It is not yet clear how monolayer growth transitions into particle formation, however, it is assumed that once the concentration of strontium at the surface exceeds its solubility limit then phase separation will occur. Diffusion of strontium across the grain surface has been observed,²⁶ however, no direct evidence has linked surface diffusion to particle growth.

If the surface was completely passivated, cell performance would drop significantly, however, long term studies over several thousands of hours do not show such performance losses.²⁷ It is clear that passivation of the surface through secondary phase formation is a significant over-simplification of MIEC degradation as a whole.

1.2. The sub-surface

Although the outermost surface is the point at which the ORR occurs, the surface composition is dependent upon the structure of the immediate sub-surface. With segregation increasing the concentration of a particular cation and secondary phase growth causing depletion of constituents of the material, the surface and sub-surface composition is highly dynamic. For many materials a significant deviation in composition is usually accompanied by a crystallographic change and, as a result, modification of its physio-chemical properties. Currently, the literature indicates Sr-substituted MIECs have highly segregated surfaces after thermal anneals, however, there is conflicting evidence over the state of the sub-surface. Many reports show enhance strontium concentrations over approximately the first 6–20 nm of the material,^16,28–31 however, strontium deficiency has also been observed over the same depth scale.^25,32 Additionally, no correlation has been made between the changes in immediate sub-surface composition and oxygen exchange/transport properties in MIECs.

This correlation has been made in the fluorite-structured material Yttria-stabilised Zirconia (YSZ).^33,34 Surface impurities and segregation effects have been observed to alter the oxygen transport properties over the same depth scale. Fig. 1(a) shows schematically how surface impurities and yttria segregation in YSZ results in the formation of a series of distinct layers across the first 6 nm of the sub-surface. Experiments using labelled gases and mass spectrometry, such as Isotopic Exchange Depth Profiling (IEDP),³⁵ were used to measure the surface exchange coefficient and self-diffusivity in these materials over these layers. As shown in Fig. 1(b), the secondary phases in YSZ causes a significant inhibition to the diffusion of oxygen across this region as indicated by an ∼40% drop in measured isotopic fraction (IF) from the surface.

Fig. 1 Showing (a) a schematic of the fluorite-structured YSZ as a result of impurities and segregation effects and (b) an ¹⁸O tracer diffusion profile in YSZ measured using low energy ion scattering (LEIS). Schematics recreated from de Ridder et al.³³

When sintered as a single phase, perovskite-based MIEC materials have also been reported to have impurity free surfaces even after thermal anneals.¹⁵ Interestingly, in composite MIEC/fluorite electrode designs, the fluorite phase was observed to be ‘cleaner’ (reduced impurity concentration) as compared to analogous single phase fluorite systems.³⁶ This is believed to be as a result of the perovskite ‘absorbing’ these surface impurities. The perovskite structure has the ability to accommodate a wide range of ions with different charges and atomic radii without affecting the bulk crystal significantly,³⁷ suggesting that compositional changes may also be able to be accommodated.

It is widely assumed that segregation effects exacerbate the degradation of MIEC electrode materials, however, the link between the sub-surface chemistry and exchange/transport properties is not well documented. In this study, the effect of sub-surface compositional changes have been correlated to the self-diffusivity (D) of segregated La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ. Medium energy ion scattering (MEIS) was performed to measure sub-surface chemical distribution and low energy ion scattering (LEIS) spectra were taken of the outermost surface. LEIS depth profiles were also performed in order to corroborate the profiles measured by MEIS, however, direct correlation was not possible due to complex preferential sputtering and depth calibration issues mentioned later.

2. Experimental

2.1. Sample preparation

Pellet fabrication. Samples of bulk La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ pellets were fabricated from commercially available Sigma Aldrich powder (lot MKBT7480V). Green pellets were made by uniaxially pressing the powder into 10 mm diameter discs under 2 tonnes of pressure, followed by an isostatic press under 250 MPa of pressure. Green pellets were then sintered at 1250 °C for 8 hours using heating and cooling rates of 300 °C h⁻¹ to produce pellets with >97% relative density. The sintered pellets were then sequentially ground and polished using P320, P500, P800, P1200 and P2400 grade SiC paper and 6 μm, 3 μm, 1 μm and 1/4 μm water based diamond suspensions. A representative micrograph of the polished surface may be seen in Fig. 2(a).

Fig. 2 (a) A representative secondary electron micrograph of the an as-polished LSCF sample prior to heat treatment and (b) a representative micrograph of the same sample after annealing in dry oxygen.

Heat treatments. Four samples were analysed in this study. One ‘reference’ pellet received no heat treatments after the polishing step. Another was exchanged in accordance with the isotopic exchange process³⁵ with a 8 hour pre-anneal step followed by a 1 hour exchange at 800 °C. The other two pellets were annealed for 8 hours, one in 99.999% pure O₂ and the other in ambient air. A summary of each sample's heat treatment may be seen in Table 1 and a representative microstructure after dry oxygen annealing can be seen in Fig. 2(b).

Table 1 Sample heat treatment summary

Sample	Relative density (%)	Anneal atmosphere	Anneal/exchange temperature (°C)	Anneal time (hours)	Exchange time (hours)
As-polished	98.6	—	—	—	—
O2 annealed	98.1	99.999% pure O2	800	8	—
Exchanged	98.7	99.999 pure O2 followed by dry ^18O2	800	8	1
Air annealed	98.3	Ambient air	800	8	—

---

2.2. Analysis techniques

Multiple ion-beam analysis techniques were used to analyse the sub-surface: MEIS, LEIS depth profiling and secondary ion mass spectrometry (SIMS). Sub-surface cation ratios were measured using MEIS and LEIS depth profiles. Each sample was analysed identically, except the exchanged sample, which received an additional LEIS and SIMS analysis in order to measure the oxygen tracer diffusion profile.

Medium energy ion scattering. MEIS analysis was performed at the MEIS facility in the Ion Beam Centre at the University of Huddersfield. A primary beam of 100 keV He⁺ ions was scattered through 125° using an angle of incidence of 55° off normal. MEIS spectra were simulated using an IGOR^© graphics package based depth profiling analysis program.³⁸ Best fit depth profiles for each metallic component were found whereas the oxygen profile was assumed to be constant at 60%.

Low energy ion scattering. LEIS depth profiles were performed using an IoN-ToF QTAC 100 LEIS. Cation profiles were measured using a 5 keV Ne⁺ primary analysis beam at normal incidence to the sample and a 0.5 keV Ar⁺ sputter beam at 60° to the sample normal. The analysis raster area was 1000 × 1000 μm² with a beam current of ∼5 nA and sputter raster area of 1500 × 1500 μm² with a beam current of ∼100 nA. 5 rounds of analysis were performed to improve measurement statistics which applied a dose density of 1.8 × 10¹³ atoms per cm². This value, slightly above the static limit,³⁹ was chosen to provide a balance between data quality and surface sensitivity. However, given that the multiple sequential analysis and sputter steps are required for a depth profile, the dose of the analysis beam becomes inconsequential after the first sputter step. Depth profiles were very shallow, and as a result it was not possible to measure crater depths accurately. Sputter rates were estimated based upon the total dose density of the analysis and sputter beam (see ESI† for the calculation).

For the exchanged sample, a separate analysis was performed using a 3 keV He⁺ primary beam to measure the isotopic fraction of ¹⁶O and ¹⁸O. The same 0.5 keV Ar⁺ sputter beam settings were used in order to ensure the same depth scale was measured. It should be noted that LEIS sensitivity for ¹⁸O is approximately 18% greater than ¹⁶O and was scaled appropriately.⁴⁰

Secondary ion mass spectrometry. SIMS was performed on the exchanged sample in order to measure the oxygen tracer diffusion profile. Negative ions were measured using a 25 keV Bi⁺ beam. Burst alignment mode was used in order to prevent detector saturation.⁴¹ A 1 keV Cs⁺ sputter beam was used to depth profile as ceasiated surfaces enhance the ionisation of oxygen.⁴²

In order to measure the surface/near-surface isotopic fraction in the exchanged sample, a short depth profile was taken as described above. However, in order to measure the full, several hundred microns long, diffusion profile the ‘linescan’ method was employed.⁴³ Oxygen self-diffusivity (D) and surface exchange coefficient (k) were found using linear regression fitting using Crank's solution to the diffusion equation in a semi-infinite medium.⁴⁴

3. Results

MEIS, LEIS and SIMS analyses were performed subsequently on each of the samples. Fresh areas were chosen for each analysis to ensure a fresh surface was analysed each time. In order to perform a linescan measurement the sample is required to be sectioned and re-polished. This was only done after all the surface measurements were completed.

3.1. Medium energy ion scattering

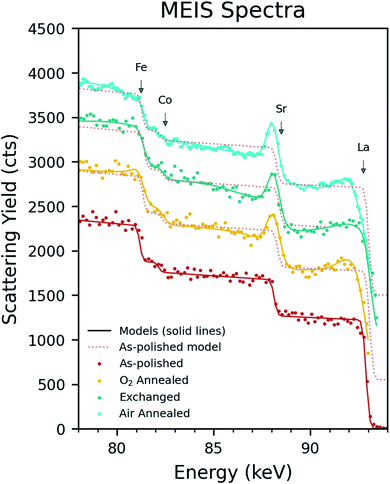
MEIS spectra were collected for each sample and an IGOR^© graphics package based simulation model was used to fit and derive cation fractional depth profiles. Fig. 3 shows the spectra together with the best fit simulated model for each sample. In the simulation, a depth dependent initial fraction for each element is assumed. At each specific depth, each element will contribute a backscattering yield that corresponds to a different part of the energy spectrum. This relationship is simulated and compared to the MEIS data. The difference is minimised and the best fit between the simulation and experiment yields the fractional elemental depth profiles, the results of which are shown in Fig. 4. A criterium for the best fit is based on the Chi squared test which for these simulations gave reduced values chi squared values between 0.90 and 0.97, on average 0.95.

Fig. 3 MEIS spectra for each sample (scatter plots) with the relevant model (solid line) overlaid across the data. The annealed samples' spectra have been offset for clarity. The as-polished model has also been overlaid across the annealed samples to enable direct comparison between an ‘un-segregated’ state and annealed state. The surface scattering edges have been indicated for the metallic elements in LSCF.

Fig. 4 MEIS ‘depth profiles’ derived from fitting the full set of spectra, showing cation distribution as a function of depth from the surface for: (a) the ‘as-polished’, (b) O₂ annealed, (c) exchanged and (d) air annealed samples.

As can be seen in Fig. 4, the ‘as-polished’ sample appears nominally stoichiometric across the whole depth range. This is an important observation in that it indicates that the screening and neutralisation ion scattering yield corrections as implemented in the IGOR simulation program appear to be correct. However, there are clear deviations from stoichiometry within each of the annealed samples. In these samples strontium segregation is observed at the immediate surface, however, the concentration of strontium drops rapidly over the first nm, followed immediately by a ‘depletion region’ over the subsequent ∼1–15 nm as the strontium concentration drops below stoichiometry. In the first nm, the lanthanum concentration is approximately the inverse of the strontium (showing a severe depletion as strontium has segregated to the surface), however, unusually, a depletion region is also observed further into the material in all samples. Small increases in the cobalt were observed over the first 2–6 nm, however, iron showed no clear trend between each sample. A comparison of the each element is shown in Fig. 5 to directly show the sub-surface differences between samples.

Fig. 5 Showing a direct comparison of the measured atomic fraction of (a) lanthanum, (b) strontium, (c) cobalt and (d) iron for each sample using MEIS.

The largest depletion region is seen in the air annealed sample, however, in the exchanged sample the depletion region is also large. Notably, it is significantly larger than the O₂ annealed sample despite only receiving one additional hour of annealing. We believe this is due to microstructural variation between samples rather than an effect of the additional anneal time.

3.2. Low energy ion scattering

LEIS depth profiles were also taken for each sample by alternating LEIS analysis and sputter steps. As shown in Fig. 6(a), neon spectra were background corrected, then Gaussian peaks used to fit each element. The integrated peak values were divided by the total peak counts (referred to as ‘surface cation fraction’) to provide an approximate quantification of each element, but it must be noted that these are liable to error because of different elemental sensitivities and the onset of preferential sputtering. Fig. 6(b) shows how cation signals change as a function of depth to build the full depth profiles as shown in Fig. 7.

Fig. 6 Showing (a) a typical neon spectra of LSCF with the raw data, background component (dotted line), element fit components and fit residual (red), and (b) two ‘partial’ spectra 5 sputter steps apart, clearly showing the change in cation ratio at different depths.

Fig. 7 LEIS depth profiles showing cation distribution (normalised to total counts) as a function of depth from the surface for: (a) the ‘as-polished’, (b) O₂ annealed, (c) exchanged and (d) air annealed samples.

Fig. 7 shows the sub-surface trends as measured by LEIS. Many similarities exist between the plots, whereby the only major differences are observed over the first 1–2 nm. In this region, the strontium signal is enhanced, with the other cations dropping as a result. Greater segregation is observed in the exchanged and air annealed sample, suggesting that, in line with the literature, more strontium has segregated to the surface due to a longer anneal time and the presence of humidity respectively.^22,45 After the first 2 nm, lanthanum appears depleted, iron appears enhanced and subtle enhancements of cobalt are observed over ∼2 nm. This result suggests there is a strontium deficient region, however, because the depth profiles for each sample appear very similar (unlike the MEIS data shown in Fig. 5), it is likely that, over this depth scale, sputtering equilibrium has not yet been established and significant preferential sputtering effects are observed. Therefore, without any meaningful correction, LEIS data over this region is susceptible to large errors. See Niania et al.⁴⁶ for further discussion.

3.3. Oxygen exchange

In order to assess oxygen self-diffusivity, three measurements were made: SIMS and LEIS depth profiles to measure the surface isotopic fraction and SIMS linescan to measure the whole diffusion profile. The linescan profile is shown in Fig. 8(a), with the first 30 nm measured using LEIS and SIMS depth profiles shown in the inset.

Fig. 8 Showing (a) the full diffusion profile of the ‘exchanged’ sample measured using the SIMS linescan method. The inset shows the surface isotopic fraction as measured using SIMS and LEIS. The oxygen self-diffusivity was found to be 2 × 10⁻⁸ cm² s⁻¹ and surface exchange coefficient, 3.6 × 10⁻⁶ cm s⁻¹. (b) The sub-surface cation distribution of the exchanged sample overlaid with the isotopic fraction as measured by SIMS. The fitting of the initial downturn is also shown. (c) Isotopic fraction as measured by SIMS depth compared with the total A (La + Sr) and B (Co + Fe) site fraction.

Due to the high self-diffusivity of La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ at 800 °C, the tracer diffusion length from the exchange was predicted to be several hundred microns. The sample was sectioned in order to perform a linescan measurement. Depth profiling to this depth would introduce very large errors as a result of crater roughness and also take a significant amount of time. It should, however, be noted that the first few micrometers of linescan data are often unreliable. Edge curvature can alter secondary ion intensity,^43,47 resulting in inconsistent isotopic fraction measurements after single shot correction.⁴⁸ This is evident by the significant drop-off in isotopic fraction over the first 5–10 μm of the diffusion profile in Fig. 8(a) and should be ignored during the fitting process. However, ignoring this data gives rise to potential errors in the measurement of the surface isotopic fraction. As a result, it was required to measure the surface concentration using a depth profile prior to sectioning for linescan measurement. This is shown in the inset of Fig. 8(a). Using SIMS the surface isotopic fraction was found to be very low, however, over approximately 2–3 nm this rose to 62% ± 1% where it remained constant for the next 25 nm. This was further corroborated by a LEIS depth profile using helium as the primary ion, also shown in the inset of Fig. 8(a). Despite the increased noise, a similar trend is observed, where initially the surface isotopic fraction was very low, rising sharply to approximately 65% ± 10%.

After fitting the remaining portion of the curve, the oxygen self-diffusivity was found to be 2 × 10⁻⁸ cm² s⁻¹ and surface exchange coefficient 3.6 × 10⁻⁶ cm s⁻¹. From these values, the fitting curve could be extrapolated to x = 0 in order to estimated the surface isotopic fraction. This was found to approximately 61%, showing good agreement with the experimentally measured values.

The isotopic fraction was then compared to the sub-surface cation distribution as measured by MEIS. Fig. 8(b) shows the isotopic fraction (as measured by SIMS) compared to each cation distribution across the same depth scale. The isotopic fraction shows a significant downturn seen by both SIMS and LEIS in the first couple of nanometers. A simulated fit of the surface downturn is overlaid across the isotopic fraction. This was fit using a diffusivity of 1 × 10⁻²¹ cm² s⁻¹, surface exchange coefficient of 5 × 10⁻¹⁴ cm s⁻¹ and a time value of 1 209 600 s (2 weeks). Fig. 8(c) shows and the total A (La + Sr) and B (Co + Fe) site fractions as compared to the isotopic fraction as measured by SIMS. As mentioned previously, the sub-surface shows a strong A-site deficiency, however, the oxygen transport properties appear broadly unaffected by the changes in stoichiometry. A very slightly increase in isotopic fraction over this regions is observed (indicating a small drop in diffusivity), however, the difference is too low to ascribe any relation to the depletion region.

4. Discussion

The overall structure of the gas–solid interface (or ‘outermost’ surface), is defined by sub-surface chemistry, crystal structure and microstructure. As has been discussed in the introduction, previous work on fluorite-structured electrolyte materials has shown that the surface exchange rate and diffusivity of the material can be altered significantly as a result of sub-surface compositional changes. In order to correlate sub-surface chemistry with the surface exchange and diffusivity of the MIEC electrode material, LSCF, the cation distribution and isotopic fraction were measured over the same depth scale.

4.1. Cation distribution

The oxygen reduction reaction is known to occur at oxygen vacancies at the immediate surface,^19,49–54 however, for materials such as LSCF, the oxygen vacancy concentration is determined by the temperature, the A/B cation ratio and the p(O₂) of the anneal atmosphere. If the material remains stoichiometric, the defect concentration should remain constant, therefore the transport properties should also remain constant. Conversely, changes in stoichiometry will correspond with changes in transport properties. As can be seen from the MEIS data in Fig. 4, the cation distribution over the first 20 nm of the sub-surface of the samples that received thermal anneals is not stoichiometric. Fig. 9(a) shows a sub-surface schematic of the results presented in this work. The following regions were observed: (1) the immediate surface almost completely covered by a Sr–O monolayer as shown by the LEIS results, (2) the first 1–2 nm of the sub-surface being highly strontium-rich and (3) followed by a region approximately 10–20 nm in length which was deficient in both lanthanum and strontium (A-site deficient). The Sr–O monolayer is consistent with the literature, however, this result confirms that the LSCF sub-surface is A-site deficient. Both lanthanum and strontium signals are approximately 30–40% smaller than stoichiometry, suggesting that the sub-surface composition in this region is approximately (La_0.6Sr_0.4)_0.6Co_0.2Fe_0.8O_3−δ. It should be noted that, the analysis area of both the LEIS and MEIS measurement was very large (approximately 1 mm), as such results are an averaged representation of the whole complex microstructure.

Fig. 9 Showing (a) schematic of the sub-surface using results from this work showing the Sr–O monolayer, Sr-rich region and A-site deficient region and (b) schematic of showing potential fast diffusion pathways including grain boundaries and 2D defect systems.

4.2. Oxygen transport

The measured diffusion profile for the oxygen is consistent with behaviour previously noted for this LSCF material. The values of D and k obtained at 800 °C from the linescan fitting are close to those reported by Benson.⁵⁵ The oxygen diffusivity is also broadly unaffected by the change in stoichiometry reported by the MEIS as shown in Fig. 8. The sub-surface isotopic profile is almost flat, as expected for such a long diffusion profile, and shows none of the strong sub-surface changes found for YSZ as reported by De Ridder et al.³³ A slight increase in oxygen isotopic fraction across the observed A-site depletion region, indicating a slight decrease in self-diffusivity over this region, however, the overall change is very low. This implies that the high mobility of oxygen and oxygen vacancy concentration is maintained over the region of the stoichiometric changes. Fig. 8(c) indicates that the depletion region is A-site deficient. A-Site deficient LSCF has been shown to have enhanced transport properties through the introduction of additional oxygen vacancies.^56,57 However, deliberate A-site deficiency tends to be 5–20%, not the 30–40% as observed here (although our result were only measured across a depth of only a few (10–20) unit cells), as the stability of these materials is generally dependant upon a narrow range of the A : B site ratio.⁵⁸ The sub-surface of other perovskite materials have been shown to decompose into the Ruddleston–Popper type layered perovskite and spinel phases as a result of changing stoichiometry.^59,60 However, at this time, it is unclear whether the sub-surface of LSCF underwent a phase change from the observed A-site deficiency.

One important feature of both the LEIS and SIMS oxygen isotopic fraction depth profiles is also noted. The surface isotopic fraction is very low (around 0.1 as determined by LEIS). Generally, this would suggest a low surface exchange value, however, the diffusion profile is seen to rise quickly to an approximately constant value of 0.62 after 1–2 nm. This strongly suggests that the downturn is introduced after the exchange step, as the concentration within the bulk should never rise above the surface concentration without lateral contributions (or ‘uphill’ diffusion). Whilst it's not possible to directly decouple the relationship between a segregated surface and the surface exchange coefficient (as a reference segregation-free surface is very difficult to achieve),¹⁷ it would appear that the segregated surface remains relatively active over the course of this experiment.

A short surface downturn has been observed previously, and Tellez et al. suggests that it is “limited by physics of the sputtering process itself” as sputtered ions are released from the first few atomic layers.^36,61 However, it is unclear why this would dramatically reduce the isotopic fraction. Given the strong correlation between the SIMS (purely sputtering) and LEIS (scattering after sputtering), we suspect the observed ‘downturn’ to be real and not totally a measurement artefact. Two possible causes of this downturn are discussed below.

Firstly, it is known that strontium particle growth is affected by the composition of the gas atmosphere,²² therefore, it is possible that the Sr–O monolayer (and particle capping layers) reacted with H₂¹⁶O and C¹⁶O₂ in the atmosphere during equipment transfer. The result of this would be dilution of the isotopic fraction by room temperature ‘back-exchange’ of the tracer out of the material.⁶² This would have the effect of diluting the isotopic fraction of ¹⁸O at the outermost layers when measuring in depth profile mode, as observed in Fig. 8. By extrapolating tracer diffusivity data for LSCF in dry oxygen,⁵⁵ the tracer diffusion co-efficient at room temperature can be estimated to be on the order of 10⁻²⁴ cm² s⁻¹. Although the exact amount of time the exchanged sample was exposed to ambient lab air was not recorded, this can be estimated to be on the order several weeks. Simulating diffusion curves using the room temperature diffusivity value and a time value of two weeks (t = 1 209 600 s) resulted in a substantial underestimation of the effect. As shown in Fig. 8(b), by using a diffusivity of 1 × 10⁻²¹ cm s⁻¹ it became possible to fit the downturn using a time value of 2 weeks. Although the fit is not particularly good, this result suggests that it is possible for the cause of the downturn to be oxygen back exchange despite possible errors in the extrapolated value used to estimate room temperature diffusivity.

The second effect that could contribute to the surface downturn is the atomic mixing of the adsorbed/reacted ¹⁶O surface layer, due to the sputter beam. For example, for the LEIS depth profiling, the projected range for the 0.5 keV argon sputter beam is 1 nm as calculated by SRIM.⁶³ This is the correct order of magnitude to contribute to this very shallow initial rise in isotopic fraction. It should be possible, by careful variation of the analytical conditions and control of the atmospheric exposure of the samples, to determine the relative importance of these two effects. However, this was not the main theme of these investigations and will be explored at a later date. At the moment, we cannot distinguish sufficiently between these possibilities but strongly suspect it is a combination of both atomic mixing during sputtering and a small amount of back-exchange during sample transfer that gives rise to initial lowering of the surface isotopic fraction.

4.3. Strontium diffusion and segregation

Strontium segregation has predominantly been reported as a steady increase from bulk stoichiometry to near 100% coverage at the surface,^16,29 although some reports observe sub-surface strontium depletion.^25,32 This work confirms the presence of this sub-surface strontium depletion region, however, it also opens the question as to which pathway the strontium (and the lanthanum) is able to diffuse through the material. Kubicek et al. showed that, in Pulse Laser Deposited (PLD) La_0.6Sr_0.4CoO_3−δ thin films, at 720 °C the strontium self-diffusion coefficient (D_g) is on the order of 10⁻¹⁸ cm² s⁻¹ and strontium self-diffusion coefficient in a grain boundary (D_gb) was on the order of 10⁻¹⁵ cm² s⁻¹.⁶⁴ It should be noted that these films displayed a strong columnar microstructure which is very different to the large grained ceramic materials used here. Assuming strontium in LSCF exhibits similar diffusivities, by performing a simple diffusion length calculation () for an 8 hour anneal (the same time as in these experiments), the diffusion length within bulk material is estimated to be 2 nm. This could account for the near surface distribution, however, a 10–15 nm depletion region could not exist if the bulk was the primary pathway for cation diffusion.

For many related perovskite materials, grain boundaries appear to be the predominant fast diffusion pathways.^65–68 However, by performing the same calculation using LSC's grain boundary diffusivity, we see that the diffusion length is approximately 85 nm. This length is large enough to account for the depth of the observed depletion region, however, for both LEIS and MEIS, detected ions (scattered or secondary) are integrated over a large area of the ceramic surface and include many elements of the microstructure. As a result, the measured spectra are proportional to the quantity of observable surface features, grains and grain boundaries in the analysed area. LSCF, sintered using the conditions in this work, produces an average grain size of approximately 2.5 μm. This means that, for all techniques used in this investigation, we have averaged over 10 s of thousands of grains and their grain boundaries. This appears to be a large number of boundaries and hence their influence should be noticeable, but an investigation of the relative proportions of the grain boundary contributions is instructive. Assuming these grains are square and the grain boundary width is 1 nm, grain boundary material only accounts for approximately 0.03% of the total surface area. If grain body material immediately neighbouring a grain boundary is A-site deficient and has a width of (2 nm), the depletion region as a result of grain boundaries still only accounts for 0.4% of the total surface area. As a result, the intensity of the signal originating from A-site deficient region close to the grain boundaries is very small compared to that originating from the grain interior (assuming no special ion–solid interactions at the grain boundaries). Therefore, it also unlikely that grain boundaries alone can account for the observed depletion region.

Under the assumption that neither the grain nor grain boundaries are the origin of the observed strontium depletion region, something else must be aiding cation diffusion. Extended defects such as dislocations and twin boundaries have been postulated to act as fast diffusion pathways in the perovskite related high T_c superconducting material YBa₂Cu₃O₇,⁶⁹ but also in single crystal CaTiO₃ which does not have any grain boundaries.⁷⁰

Dislocation networks and twins are also present in LSCF.^23,71 Strontium segregation and particle growth rate have been shown to be influenced by both compressive and tensile strains,⁷² suggesting that a strained superstructure can act as a fast pathway for strontium. Using high-temperature environmental scanning electron microscopy (HT-ESEM) and electron back-scattered diffraction (EBSD), the nucleation sites for Sr–O based particles appear to coincide with twin boundaries in the middle of grains at particular orientations.²² This would suggest that the twins act as heterogenous nucleation sites, however, may also indicate they can act as fast diffusion pathways as shown schematically in Fig. 9(b). Vullum et al. has shown that between 90–100% of the material volume in LSCF contains a ‘twin-like’ super-structure, which would provide ample pathways to account for the observed depletion region.⁷³ The lateral resolution of the ion-beam techniques used in this work was unfortunately insufficient to directly determine if such individual 2D defects were responsible for enhanced diffusion.

If the presence of long range defects is the origin of the fast diffusion of the Sr cations (and by comparison, the La cations), then this would produce a different apparent diffusivity for the bulk of the material, somewhat larger than reported by Kubicek et al.⁶⁴ However, the grain size in the two experiments are markedly different. In our experiments, the grains are large enough to accommodate a significant number of twins with twin domains of a few 100 nm (as shown previously by Niania et al. and Huang et al.)^22,23 and dislocation. Whereas in the case of the thin films produced by PLD, columnar grains with a width between 30 and 60 nm appear too small for these super-structures to exist. However, 2D defects has been observed in similar, PLD grown, epitaxial films of La_0.6Sr_0.4CoO_3−δ on YSZ,⁷⁴ suggesting that the superstructure may exist regardless.

5. Conclusion

The surface and sub-surface composition of MIECs is of utmost importance in facilitating the oxygen reduction reaction, an important component of the overall performance limitations for IT-SOFCs. In this work the surface and sub-surface cation composition of La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ was investigated and directly related to oxygen transport properties using oxygen isotopic labelling. In agreement with the literature, strontium segregation was observed in all samples that underwent a thermal anneal, however, contrary to many previous observations, both lanthanum and strontium depletion was observed in the sub-surface region of ∼10–15 nm. A-Site deficient LSCF is known to have enhance transport properties, however, the deliberate A-site deficiency is not usually as severe as seen in this work. Interestingly, despite large changes in A-site cation composition, oxygen transport properties remained largely unchanged in this compositionally altered region. This is believed to be due to the perovskite structure's ability to accommodate a very wide range of non-stoichiometry.

In LSCF, strontium diffusion in the bulk is slow. Any strontium depletion region would be much shallower than observed if bulk diffusion was the primary diffusion pathway. Grain boundary diffusion is fast enough to account for the depth of the depletion region, however, due to the large grain size of the ceramic pellets, the amount of grain boundary material at the surface (and thus probed by the ion beams) was very low at approximately 0.03%. Thus, any depleted regions caused by fast paths at grain boundaries can only account for very little of the observed cation distributions from the MEIS analysis. It is suggested that these 2D planar defects such as dislocation networks and twins can also act as fast diffusion pathways for strontium, leading to a much more widespread depletion layer within the grains.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the support of Solid Oxide Interfaces for Faster Ion Transport (SOIFIT) JSPS/EPSRC (EP/P026478/1) Core-to-Core Program (Advanced Research Networks). Additionally, the financial support from the UK National Ion Beam Centre (under grant number NS/A000059/1) for the MEIS analysis in this work is gratefully acknowledged.

References

1. J. A. Lane, S. J. Benson, D. Waller and J. A. Kilner, Solid State Ionics, 1999, 121, 201–208.
2. S. J. Skinner, Fuel Cells Bull., 2001, 4, 6–12.
3. X. Chen, Y. Zhen, J. Li and S. P. Jiang, Int. J. Hydrogen Energy, 2010, 35, 2477–2485.
4. E. Bucher, C. Gspan, F. Hofer and W. Sitte, Solid State Ionics, 2013, 230, 7–11.
5. E. Bucher, C. Gspan, F. Hofer and W. Sitte, Solid State Ionics, 2013, 238, 15–23.
6. A. K. Huber, M. Falk, M. Rohnke, B. Luerßen and L. Gregoratti, et al. , Phys. Chem. Chem. Phys., 2012, 14, 751–758.
7. M. Kubicek, A. Limbeck, T. Frömling, H. Hutter and J. Fleig, J. Electrochem. Soc., 2011, 158, B727.
8. D. Lee, Y. L. Lee, W. T. Hong, M. D. Biegalski and D. Morgan, et al. , J. Mater. Chem. A, 2015, 3, 2144–2157.
9. L. W. Tai, M. M. Nasrallah, H. U. Anderson, D. M. Sparlin and S. R. Sehlin, Solid State Ionics, 1995, 76, 273–283.
10. J. Y. Koo, H. Kwon, M. Ahn, M. Choi and J.-W. Son, et al. , ACS Appl. Mater. Interfaces, 2018, 10, 8057–8065.
11. W. Lee, J. W. Han, Y. Chen, Z. Cai and B. Yildiz, J. Am. Chem. Soc., 2013, 135, 7909–7925.
12. H. Kwon, W. Lee and J. W. Han, RSC Adv., 2016, 6, 69782–69789.
13. L. W. Tai, Solid State Ionics, 1995, 76, 259–271.
14. W. A. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–5.
15. J. Druce, T. Ishihara and J. Kilner, Solid State Ionics, 2014, 262, 893–896.
16. G. M. Rupp, H. Téllez, J. Druce, A. Limbeck and T. Ishihara, et al. , J. Mater. Chem. A, 2015, 3, 22759–22769.
17. M. Siebenhofer, T. M. Huber, G. Friedbacher, W. Artner and J. Fleig, et al. , J. Mater. Chem. A, 2020, 8, 7968–7979.
18. B. Koo, K. Kim, J. K. Kim, H. Kwon and J. W. Han, et al. , Joule, 2018, 2, 1476–1499.
19. N. Tsvetkov, Q. Lu, L. Sun, E. J. Crumlin and B. Yildiz, Nat. Mater., 2016, 15, 1010–1016.
20. D. Oh, D. Gostovic and E. D. Wachsman, J. Mater. Res., 2012, 27, 1992–1999.
21. K. C. Chang, B. Ingram, J. Ilavsky, S. Lee and P. Fuoss, et al , Solid State Ionics, 2017, 311, 118–126.
22. M. Niania, R. Podor, T. B. Britton, C. Li and S. J. Cooper, et al , J. Mater. Chem. A, 2018, 6, 14120–14135.
23. B. X. Huang, R. W. Steinbrech and J. Malzbender, Solid State Ionics, 2012, 228, 32–36.
24. F. Pişkin, R. Bliem and B. Yildiz, J. Mater. Chem. A, 2018, 6, 14136–14145.
25. Y. Yu, K. F. Ludwig, J. C. Woicik, S. Gopalan and U. B. Pal, et al , ACS Appl. Mater. Interfaces, 2016, 8, 26704–26711.
26. H. Tellez, J. Druce, T. Ishihara and J. A. Kilner, ECS Trans., 2016, 72, 57–69.
27. F. Tietz, V. A. C. Haanappel, A. Mai, J. Mertens and D. Stöver, J. Power Sources, 2006, 156, 20–22.
28. J. Druce, H. Téllez, M. Burriel, M. D. Sharp and L. J. Fawcett, et al , Energy Environ. Sci., 2014, 7, 3593–3599.
29. Y. Chen, H. Téllez, M. Burriel, F. Yang and N. Tsvetkov, et al , Chem. Mater., 2015, 27, 5436–5450.
30. E. Bucher, W. Sitte, F. Klauser and E. Bertel, Solid State Ionics, 2011, 191, 61–67.
31. E. Bucher, W. Sitte, F. Klauser and E. Bertel, Solid State Ionics, 2012, 208, 43–51.
32. D. Kim, J. W. Park, B. H. Yun, J. H. Park and K. T. Lee, ACS Appl. Mater. Interfaces, 2019, 11, 31786–31792.
33. M. De Ridder, R. G. Van Welzenis, H. H. Brongersma and U. Kreissig, Solid State Ionics, 2003, 158, 67–77.
34. K. V. Hansen, K. Norrman and M. Mogensen, Surf. Interface Anal., 2006, 38, 911–916.
35. J. A. Kilner, B. C. H. Steele and L. Ilkov, Solid State Ionics, 1984, 12, 89–97.
36. Z. Shen, S. J. Skinner and J. A. Kilner, Phys. Chem. Chem. Phys., 2019, 21, 13203–13215.
37. D. M. Smyth, Ferroelectrics, 2009, 380, 1–13.
38. J. A. Van Den Berg, M. A. Reading, P. Bailey, T. Q. C. Noakes and C. Adelmann, et al. , Appl. Surf. Sci., 2013, 281, 8–16.
39. J. C. Vickerman and I. S. Gilmore, Surface analysis – the principal techniques, 2nd edn, 2009, pp. 1–666.
40. H. Téllez, R. J. Chater, S. Fearn, E. Symianakis and H. H. Brongersma, et al. , Appl. Phys. Lett., 2012, 101, 151602.
41. R. A. De Souza, J. Zehnpfenning, M. Martin and J. Maier, Solid State Ionics, 2005, 176, 1465–1471.
42. G. Doucas, Int. J. Mass Spectrom. Ion Phys., 1977, 25, 71–87.
43. R. J. Chater, S. Carter, J. A. Kilner and B. C. H. Steele, Solid State Ionics, 1992, 53–56, 859–867.
44. J. Crank, The mathematics of diffusion, 1979, p. 414.
45. S. H. Kim, K. B. Shim, C. S. Kim, J. T. Chou and T. Oshima, et al. , J. Fuel Cell Sci. Technol., 2010, 7, 0210111–0210116.
46. M. Niania and J. Kilner, Nucl. Instrum. Methods Phys. Res., Sect. B, 2020, 480, 27–32.
47. B. Hagenhoff, Mikrochim. Acta, 2000, 132, 259–271.
48. T. Stephan, J. Zehnpfenning and A. Benninghoven, J. Vac. Sci. Technol., A, 1994, 12, 405–410.
49. A. Staykov, H. Tellez, J. Druce, J. Wu and T. Ishihara, et al. , Sci. Technol. Adv. Mater., 2018, 19, 221–230.
50. M. Riva, M. Kubicek, X. Hao, G. Franceschi and S. Gerhold, et al. , Nat. Commun., 2018, 9, 3710.
51. A. Schmid, G. M. Rupp and J. Fleig, Chem. Mater., 2018, 30, 4242–4252.
52. X.-K. Gu and E. Nikolla, ACS Catal., 2017, 7, 5912–5920.
53. J. E. ten Elshof, M. H. R. Lankhorst and H. J. M. Bouwmeester, J. Electrochem. Soc., 1997, 144, 1060.
54. Y. A. Mastrikov, R. Merkle, E. Heifets, E. A. Kotomin and J. Maier, J. Phys. Chem. C, 2010, 114, 3017–3027.
55. S. Benson, Doctoral thesis, Imperial College London, 1998.
56. A. Mineshige, J. Izutsu, M. Nakamura, K. Nigaki and J. Abe, et al. , Solid State Ionics, 2005, 176, 1145–1149.
57. K. K. Hansen and K. V. Hansen, Solid State Ionics, 2007, 178, 1379–1384.
58. O. Celikbilek, C.-A. Thieu, F. Agnese, E. Calì and C. Lenser, et al. , J. Mater. Chem. A, 2019, 7, 25102–25111.
59. F. Morin, G. Trudel and Y. Denos, Solid State Ionics, 1997, 96, 129–139.
60. K. Szot and W. Speier, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 5909–5926.
61. H. Téllez, A. Aguadero, J. Druce, M. Burriel and S. Fearn, et al. , J. Anal. At. Spectrom., 2014, 29, 1361–1370.
62. S. J. Cooper, M. Niania, F. Hoffmann and J. A. Kilner, Phys. Chem. Chem. Phys., 2017, 19, 12199–12205.
63. J. F. Ziegler, M. D. Ziegler and J. P. Biersack, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1818–1823.
64. M. Kubicek, G. M. Rupp, S. Huber, A. Penn and A. K. Opitz, et al. , Phys. Chem. Chem. Phys., 2014, 16, 2715–2726.
65. O. Schulz, M. Martin, C. Argirusis and G. Borchardt, Phys. Chem. Chem. Phys., 2003, 5, 2308–2313.
66. T. Horita, Solid State Ionics, 1998, 108, 383–390.
67. I. Wærnhus, N. Sakai, H. Yokokawa, T. Grande and M.-A. Einarsrud, et al. , Solid State Ionics, 2007, 178, 907–914.
68. H. Kishimoto, N. Sakai, T. Horita, K. Yamaji and M. Brito, et al. , Solid State Ionics, 2007, 178, 1317–1325.
69. Y. Li, J. A. Kilner, J. R. Liu, W. K. Chu and G. A. Wagner, et al. , Appl. Phys. Lett., 1995, 2738, 2738.
70. I. Sakaguchi, H. Haneda, J. Tanaka and T. Yanagitani, J. Am. Ceram. Soc., 1996, 79, 1627–1632.
71. K. Develos-Bagarinao, H. Kishimoto, J. De Vero, K. Yamaji and T. Horita, Solid State Ionics, 2016, 288, 6–9.
72. W. Araki, T. Yamaguchi, Y. Arai and J. Malzbender, Solid State Ionics, 2014, 268, 1–6.
73. P. E. Vullum, H. L. Lein, M. A. Einarsrud, T. Grande and R. Holmestad, Philos. Mag., 2008, 88, 1187–1208.
74. D. Mori, H. Oka, Y. Suzuki, N. Sonoyama and A. Yamada, et al. , Solid State Ionics, 2006, 177, 535–540.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ta06058e

---