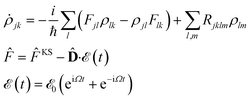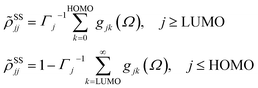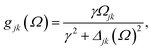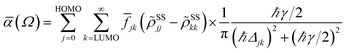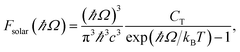Exploring the properties of Ag₅–TiO₂ interfaces: stable surface polaron formation, UV-Vis optical response, and CO₂ photoactivation

Abstract

Using a combination of first-principles modelling, X-ray absorption spectroscopy, and diffuse reflectance spectroscopy measurements, we explore the properties of Ag₅-modified TiO₂ surfaces. A general electron polarization phenomenon associated with surface polarons on TiO₂ has been revealed theoretically and confirmed experimentally. First, the Ag₅ cluster donates an electron to TiO₂, leading to the formation of polaronic Ti³⁺ 3d¹ states on the rutile TiO₂(110) surface. The analysis of polarization effects in the nearby electronic structure accompanying the polaron formation is confirmed with X-ray absorption spectroscopy measurements at the Ti K-edge of TiO₂ nanoparticles. Next, the UV-Vis optical absorption spectrum of the polaronic state is also computationally modelled and an enlargement of the polaron wavefunction is predicted. Moreover, we find an overall improvement of the UV-Vis optical response of the material through diffuse reflectance spectroscopy measurements. Finally, we predict that charge-transfer processes at the Ag₅–TiO₂ interface triggered by solar photons might allow for a photoinduced activation of CO₂ by sunlight.

---

1 Introduction

Highly stable metal clusters of subnanometer size, as required in industrial applications, have recently emerged as a new generation of catalysts and photocatalysts with fascinating properties arising from their molecule-like electronic structures. As opposed to metal nanoparticles in the visible region,¹ these ‘atomic’ or sub-nanometer-sized clusters neither sustain their metallicity, nor show their plasmonic behaviour. Instead, the presence of a molecule-like HOMO–LUMO gap drastically transforms their chemical and physical properties, thus creating innovative materials for applications including luminescence,² sensing,³ therapeutics,⁴ energy conversion,⁵ catalysis,⁶ and electrochemistry.^7,8 Nowadays, these so-called atomic quantum clusters (AQCs) can be synthesized by kinetic control using electrochemical methods,^9–11 showing an exceptional chemical and thermo-dynamical stability in solution over the whole pH range.⁹ As discussed in ref. 9, high monodispersity of synthesized AQCs (e.g., Cu₅) has been achieved since the method of cluster synthesis is extremely size-selective. Moreover, the air stability of AQCs (e.g., Cu₅) with respect to oxidation up to a temperature of 150 °C has been experimentally observed.¹² The resistance of Cu₅ clusters against an irreversible oxidation by a single O₂ molecule has been explained in theoretical studies.^12–14

It is well known that new catalytic and optical properties with technological projections are acquired by certain materials when modified with AQCs.¹⁵ The TiO₂ surface has been previously selected as the AQC support due to its abundance, non-toxicity, biological inertness, and chemical stability, being one of the most popular materials for (photo-)catalytic applications and solar energy conversion. However, its large band-gap (3–3.2 eV) makes ultraviolet irradiation necessary to trigger photo-catalytic reactions. The UV part is less than 8% of the solar radiation so that the reaction rate divided by the photon flux is typically less than 10% for TiO₂-based photocatalysts.^16,17 Several techniques have been developed to extend the photoactivity of TiO₂ to the visible region, most of which involve the direct modification of the electronic structure of the bulk. Very recently, in a joint theoretical–experimental study,¹⁵ we have proposed an alternative technique relying on the deposition of a single monolayer of Cu₅ clusters. It takes advantage of the slightly different electronic structure at the phase boundary and the ability to create electron–hole pairs close to the surface. As a result, much more energy can be harvested from sunlight, and the coated titanium dioxide stores this energy temporarily in the form of charge pairs, electrons and holes, which is a perfect prerequisite to follow-up chemistry.¹⁸ Moreover, a very recent theoretical study¹⁹ has indicated that TiO₂-supported Cu₅ clusters might allow CO₂ activation through sunlight, as well as a spontaneous decomposition, leading to CO desorption.

AQCs made of a few silver atoms seem to display better chemical and physical properties. The stability of Ag_n clusters (n ≤ 5) on the rutile surface has also been theoretically analysed,²⁰ predicting an enhanced light absorbance intensity of the material upon their deposition, as well as the appearance of secondary broad peaks with positions depending on the size and shape of the supported clusters. In particular, intense peaks have been identified in the visible region of the spectrum for the specific case of the Ag₅ AQC.²⁰ In this work, for completeness, the visible spectrum of Ag₅-modified TiO₂ surfaces is experimentally determined using diffuse reflectance spectroscopy. Theoretically, the following relevant aspects are addressed: (1) the existence of surface polarons on TiO₂ through surface activation with Ag₅ AQCs; (2) the stability of the resulting polaronic states as compared to non-polaronic ones as previously reported;^20–22 and (3) the UV-Vis optical absorption spectrum of the polaronic states.

Polaron formation is a fundamental and well-known phenomenon in transition metal oxides, for example, reduced titanium dioxide surfaces (e.g., for a comprehensive overview see ref. 23). Excess electrons from surface defects such as oxygen vacancies and Ti interstitials locally couple to lattice distortions forming small polarons,²⁴ typically hosted at Ti sites close to the defects. The existence of intrinsic small polarons as self-trapped electrons at Ti⁴⁺ ions in rutile TiO₂ (i.e., forming stable Ti³⁺ 3d¹ states) has been both theoretically predicted^23,25–31 and experimentally confirmed.^32–34 Gono et al.³⁵ have theoretically shown that the presence of surface polarons reduces overpotentials in the oxygen evolution reaction (OER). This reaction is the major problem to solve in water splitting. Thus, the quest for experimental systems forming stable surface polarons (clusters on TiO₂ melt at temperatures greater than 700 °C) opens new ways to the experimental work on new catalysts. Very recently, a direct observation of magnetic polarons in a doped Fermi–Hubbard system has been reported by Koepsell and co-workers.³⁶

A theoretical analysis of polaronic states has been provided in studies of Cu_n–TiO₂ (n ≤ 5) interfaces.^15,37 X-ray absorption spectroscopy measurements at the Cu K-edge have confirmed the theoretical prediction that the 3d levels of the Cu₅ clusters become depopulated upon adsorption on TiO₂ for both polaronic and non-polaronic states.¹⁵ However, no conclusive experimental evidence of the modifications of the electronic structure of the Ti atoms upon deposition of Cu₅ AQCs on TiO₂ nanoparticles has been found (see the ESI of ref. 15). In this work, X-ray absorption spectroscopy measurements at the Ti K-edge provide unambiguous evidence that these modifications occur at the Ag₅/TiO₂ interface. Moreover, the experimentally determined modifications are related to electronic polarization effects due to the formation of polarons (Ti³⁺ 3d¹ states). In this way, we extend previous experimental studies proving the existence of Ti³⁺ 3d¹ states in reduced TiO₂ samples,^32–34 including their direct views through scanning tunneling microscopy.³⁴ Furthermore, photo-excitation spectra of the polaronic state with light in the UV-Vis region of the solar radiation are also presented. Clearly, the photoexcitation of polarons is still an unexplored area, for which the first ground-breaking experimental studies have been very recently reported.³⁸

Finally, the possibility of using TiO₂-supported Ag₅ AQCs for photocatalysis applications is also studied. Due to its importance in the context of climate change and global warming (see ref. 39 for a very recent and comprehensive review on heterogeneous CO₂ reduction), the photoactivation of CO₂ over Ag₅ has been addressed. A deterrent in the CO₂ elimination is the high stability of the C=O bond, which necessitates an energy as high as 7.8 eV (ref. 40) in order to be broken in the gas phase. The radical CO₂˙⁻ is a clear precursor state for CO₂ dissociation due to its weakened C=O bond. The question analysed in this work is twofold: (1) whether CO₂ can be trapped in a dispersion-dominated physisorption state and (2) if it is irradiated with visible light, whether this molecule can be transformed into the radical CO₂˙⁻ over TiO₂-supported Ag₅ clusters, as already found for copper clusters.¹⁹

The different topics covered in this work are addressed by applying density functional theory (DFT), time-dependent DFT, and an approach combining DFT with reduced density matrix theory. We chose a DFT-D3 ansatz^41,42 on the basis of its excellent performance in describing the adsorption of the Ag₂ cluster on the rutile TiO₂(110) surface.²⁰ For an appropriate determination of the electronic structure, we employed the HSE06 hybrid functional of Heyd, Scuseria and Ernzerhof^43,44 on top of the structures optimized via the DFT-D3 approach instead. It has been previously shown that the HSE06 functional allows description of localized midgap states below the conduction band which are associated with polarons in reduced TiO₂ (ref. 45) and Cu₅-modified TiO₂ surfaces.¹⁵ In order to calculate the UV-Vis absorption spectra, we employed reduced density matrix (RDM) theory within the Redfield approximation,⁴⁶ combined with DFT calculations using the HSE06 functional. This combination of RDM and DFT, proposed by Micha and collaborators,^47–49 has been successfully applied to silver^20,50–52 and copper^15,19 clusters on semiconductor TiO₂ and silicon surfaces.^{15,19,20,50–53}

The results from our computational calculations and spectroscopy (diffuse reflectance and X-ray absorption) measurements are presented and discussed in Section 2. This section is split in several subsections in order to emphasize at each step the importance of the presence of polarons and, in the last subsection, the prediction of CO₂ photo-activation is briefly described. Section 3 summarizes the main findings. Finally, in Section 4, further details about the materials used as well as the experimental and computational methods developed are provided.

2 Results and discussion

2.1 Surface polaron formation at the Ag₅/TiO₂ interface

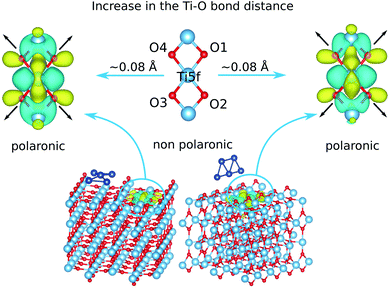
We carried out structural optimizations and interaction energy calculations with the Perdew–Burke–Ernzerhof (PBE) density functional and the Becke–Johnson (BJ) damping⁴¹ for the D3 dispersion correction, including spin-polarization. We refer to this combination as the PBE-D3(BJ) scheme. The Hubbard DFT+U term⁵⁴ was added in PBE-D3(BJ) minimizations to describe localized 3d-electrons on Ti cations.

The optimization of the bare cluster Ag₅ gives rise to a planar trapezoidal structure as in experimental observations.⁵⁵ We then inserted the Ag₅ cluster into our slab model and optimized the whole Ag₅-slab geometries. The pyramidal- and trapezoidal-shaped Ag₅ structures shown in Fig. 1 are thus predicted. Both structures are highly stable, with adsorption energies (−4.53 eV for the pyramidal-shaped geometry at the PBE-D3(BJ)/U level) being of the same order of magnitude as in previous studies.^20,21 Next, we used the wavefunctions calculated at the PBE-D3(BJ)/U level in a follow-up HSE06 calculation at the relaxed geometries. It was thus found that the Ag₅ cluster donates its unpaired electron to the TiO₂ surface and loses its magnetic moment in either pyramidal- and trapezoidal-shaped structures. Using a Bader decomposition scheme,⁵⁶ we estimated charge donations of about −1 and −0.8|e| from the Ag₅ cluster for pyramidal- and trapezoidal-shaped geometries, respectively. As can be observed in Fig. 1, the donated electron becomes localized in one specific 3d orbital lying at the surface plane and centered at the Ti(5f) atom right below the Ag₅ cluster.

Fig. 1 Figure illustrating the formation of small polarons at fivefold coordinated titanium atoms (Ti_5f) next to adsorbed Ag₅ clusters, adopting both pyramidal- (left) and trapezoidal-shaped (right) structures.

The charge trapping via the localization of one electron on the Ti(5f) atom is correlated with the typical lattice distortion accompanying the formation of a small polaron in reduced TiO₂ surfaces (see, e.g., ref. 23). Thus, as we can see in Fig. 1, the oxygen ions depart from the Ti atom hosting the polaron by 0.08 Å in average. For the pyramidal-shaped Ag₅ structure, the polaronic solution is −0.9 eV more stable than the non-polaronic counterpart. For the latter, the “extra” electronic charge donated by the Ag₅ cluster becomes delocalized over several neighboring Ti atoms. As reported in ref. 20 for non-polaronic Ag₅–TiO₂ states, the pyramidal-like structure is preferred over the trapezoidal-shaped arrangement also in polaronic solutions. The adsorption energy differences are ca. 0.3 and 1.5 eV at the HSE06 level and PBE-D3(BJ)/U levels, respectively. This is consistent with previous studies, reporting the hollow site as the most favored position for single Ag atoms adsorbed on both rutile^20,57 and anatase²² TiO₂ surfaces. Accordingly, as shown in Fig. 1, four Ag atoms locate at hollow sites in the pyramidal-shaped structure. The central Ag atom is localized on top of one fivefold (5f) Ti atom instead.

Besides the Ti(5f) ion, alternative locations of the polarons exist with similar energies in hydroxylated and reduced TiO₂(110) surfaces.^26,27 Very recent molecular dynamics simulations under experimental conditions²³ indicate that a subsurface Ti atom is the most stable polaron site on reduced TiO₂(110) surfaces. The stabilization of the surface polaron induced by the Ag₅ cluster is favored by an attractive electrostatic interaction between the localized Ti³⁺ 3d¹ electron and the positively charged Ag₅ cluster. As pointed out in a theoretical–experimental study,⁵⁸ an adsorbate (a CO molecule) is capable of promoting polaron transfer from the subsurface to surface sites also in reduced TiO₂ samples. Similar to the case of the Ag₅/TiO₂ interface, the favored surface location is caused by an attractive (repulsive) interaction of the CO molecule with the surface (subsurface) polaron.

2.2 Polarization effects induced by surface polarons

In order to analyze the polarization effects induced by the polaronic charge, we calculated the net population (number of electrons) of d-type orbitals centered at Ti atoms for Ag₅-modified and unmodified TiO₂ surfaces. We considered the two different (trapezoidal and pyramidal) Ag₅ isomers and both polaronic and non-polaronic states. We found the main modifications in the population of 3d(Ti) orbitals upon Ag₅ adsorption while those of s(Ti) and p(Ti) orbitals (not shown) were kept almost unperturbed. As can be deduced from Table 1, a net depopulation of 3d(Ti) orbitals can be observed upon the polaron formation (see Table 1). This is clearly seen when comparing the 3d(Ti) orbital populations in the unmodified (2nd column) and Ag₅-modified (3rd and 4th columns) TiO₂ surfaces hosting the polaron. Note that this is also clearly apparent in the population difference between polaronic (3rd and 4th columns) and non-polaronic (last column) states.

Table 1 Net population (number of electrons) of d(Ti) orbitals in the unmodified TiO₂ surface (2nd column) and the modified TiO₂ surface bearing supported Ag₅ clusters in both pyramidal- and trapezoidal-shaped structures (3rd and 4th columns). For the most stable pyramidal-shaped isomer, the d(Ti) orbital population is also presented for the non-polaronic state (last column). The population of d and p orbitals of surface titanium and oxygen atoms (referred to as Ti_S0 and O_S0) is presented for the pyramidal-shaped isomer in polaronic and non-polaronic states. The difference between the occupation of orbitals with majority and minority spin components is also indicated as values between parenthesis

	Unmodified TiO2	Ag5/TiO2 (pyramidal polaronic)	Ag5/TiO2 (trapezoidal polaronic)	Ag5/TiO2 (pyramidal non-polaronic)
d(Ti)	173 (0)	172 (1)	172 (1)	175 (1)
d(TiS0)		41 (1)		42 (1)
p(OS0)		93 (0)		92 (0)

---

The depopulation of 3d(Ti) orbitals might be an outcome challenging common intuition. As a localized Ti³⁺ 3d¹ electron state, the polaron is in fact characterized by excess charge (i.e., one “extra” electron) trapped at the Ti site hosting it. Accordingly, the unpaired electron of the Ag₅ cluster becomes trapped at the 3d orbital of one specific Ti(5f) atom. As a result, the difference in the population of 3d(Ti) orbitals with majority and minority spin components is unity (3rd and 4th columns of Table 1). However, we must consider that the polaron becomes effectively screened by the polarization of the surrounding electronic cloud and it is not only manifested in structural lattice distortions. This polarization is also manifested in the formation of a delocalized hole accompanying the trapped Ti³⁺ 3d¹ electron in the 3d-network of occupied orbitals centered at neighboring (mostly surface) Ti atoms. Actually, this polarization effect extends to subsurface layers. As a result, the net population of 3d(Ti) orbitals decreases in the Ag₅-modified polaronic state with respect to that existing in the unmodified TiO₂ surface. In a slightly simplified picture, the localized Ti³⁺ 3d¹ electron attracts positively charged Ti⁴⁺ centers, which become even more positively charged upon polaron formation in order to favour the attractive electrostatic electron–Ti⁴⁺ attraction. The electronic charge is transferred to the p orbitals of neighboring O²⁻ ions which, being repelled by the localized Ti³⁺ 3d¹ electron, move away from it (see Fig. 1). Note that this polarization effect holds for both trapezoidal- and pyramidal-shaped structures of the Ag₅ cluster.

The finding that the polaron formation (as a localized Ti³⁺ 3d¹ electron state) is accompanied by a polarization of the crystal electronic cloud becomes even more clear, when the analysis of orbital populations is restricted to 3d(Ti) and 2p(O) orbitals of titanium and oxygen atoms located at the polaron plane. Thus, as can be observed when comparing these populations in polaronic and non-polaronic states (values indicated in the 2nd and 4th columns and 2nd and 3rd rows, of Table 1), the electron, having left an effective hole delocalized over the 3d-network of surface Ti atoms, is transferred to 2p orbitals of oxygen atoms lying at the polaron plane. It can be noted from Table 1 that one electron located at 3d orbitals of titanium atoms in the non-polaronic state becomes localized at 2p orbitals of oxygen atoms in the polaronic counterpart. The Bader charge of surface oxygen atoms is also larger (by ca. 0.6|e|) in the polaronic state, as opposed to the surface titanium atoms.

2.3 Experimental evidence of polarization effects induced by surface polarons

We found experimental evidence of the described modifications in the electronic structure of Ti atoms through X-ray absorption near edge structure (XANES) spectroscopy. This technique is characterized by a high chemical selectivity. Fig. 2 shows the XANES spectra at the Ti K-edge of bare TiO₂ nanoparticles (NPs) and TiO₂ NPs bearing supported Ag₅ AQCs. We observed a shift of the edge position (ca. 0.1 eV) when adding Ag₅ AQCs to the TiO₂ NPs. An additional peak at 4990 eV was also found. As previously shown,⁵⁹ the multiple structure appearing immediately after the main 1s → 4p transition emerges from a two-electron transition. It consists in the simultaneous excitation of one core electron, associated with 1s → n4p transitions, and one valence electron.⁵⁹ In particular, resonances appearing at ca. 4990 eV are attributed to 2p(O) → 3d(Ti) transitions.⁵⁹ The increase of the XANES area in this region indicates charge transfer from Ti atoms to the ligands (i.e., oxygen ions), resulting in a decrease of the Ti electron density at the 3d levels in average. Thus, the experimental measurements confirm our finding that there is an effective depopulation of 3d(Ti) orbitals favouring 2p(O) orbitals as a result of the polaron formed. As will be next discussed, our interpretation is further supported by the theoretical modelling of the polaron photo-excitation.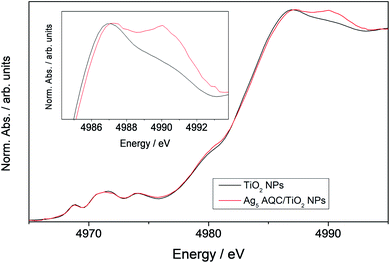

Fig. 2 XANES spectra at the Ti K-edge of TiO₂ NPs (black line) and the Ag₅ atomic quantum cluster (AQC) supported on TiO₂ NPs (red line).

As mentioned in the introduction, no modification of the XANES spectra at the K-edge of Ti atoms was found in the case of the Cu₅ cluster¹⁵ as the adsorbate so that no unambiguous proof of the polaron formation could be provided. On the one hand, one key difference between Ag₅ and Cu₅ as adsorbates is that the 3d orbitals of the latter present a very pronounced hybridization with 2p orbitals of oxygen atoms from the TiO₂ surface. Hence, from our analysis above, the polarization process, which involves the transfer of electronic charge from 3d(Ti) to 2p(O) orbitals, might be somehow constraint at the Cu₅/TiO₂ interface. On the other hand, the employment of smaller TiO₂ nanoparticles has allowed for a larger Ag₅–TiO₂ contact region than in our previous work.¹⁵

We note that the depopulation of 3d(Ti) orbitals is the same for Ag₅ and Cu₅ clusters. Also, we obtained similar values for the surface polaron formed from oxygen vacancies in the reduced TiO₂(110) rutile surface (see Section S1 of the ESI†). Hence, we have provided general microscopic details of polarons: the mechanism leading to their internal structure through the polarization effects in the electronic structure of the environment. This important aspect of the polaron formation is deduced theoretically not from a model Hamiltonian but from our extended ab initio calculations. The strategy followed has been obviously motivated by the presence of Ag₅ clusters which seems to be determinant.

2.4 UV-Vis optical response of surface polarons

Fig. 4 (bottom panel) shows the photo-absorption spectra of the Ag₅-modified TiO₂ surface, with the Ag₅ cluster in the most stable (i.e., pyramidal-shaped) structure. The photo-adsorption spectrum for the trapezoidal-shaped structure is very similar (see Section S2.2 of the ESI†). For the sake of clarity, the density of states is presented in the upper panel of Fig. 4 while the most relevant frontier orbitals are shown in Fig. 3, with the Ti³⁺ 3d¹ electron characterizing the highest-energy single-occupied (referred to as SOMO) orbital of the system (see also Fig. 3 and Section S2 of the ESI†). As can be observed in the projected electronic density of states, the localized Ti³⁺ state (marked with a yellow arrow in the upper panel of Fig. 5) appears about 1.2 eV below the bottom conduction band. The same value was reported by Di Valentin et al. for a Ti(5f) 3d¹ state in hydroxylated and reduced rutile TiO₂(110) surfaces.²⁵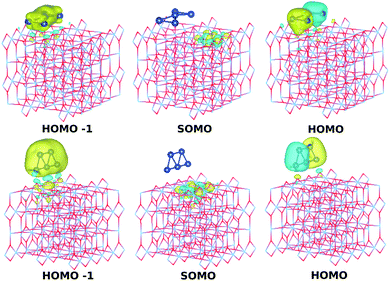

Fig. 3 Picture showing isosurfaces of the frontier “singly occupied” (or occupied only by a single spin component) molecular orbital (referred to as SOMO) as well as the highest-energy and second “doubly occupied” (or occupied by two spin components) molecular orbitals (referred to as HOMO and HOMO−1). The energy positions of the SOMO, HOMO, and HOMO−1 orbitals for the pyramidal-shaped structure of the Ag₅ cluster are indicated in the upper panel of Fig. 4.

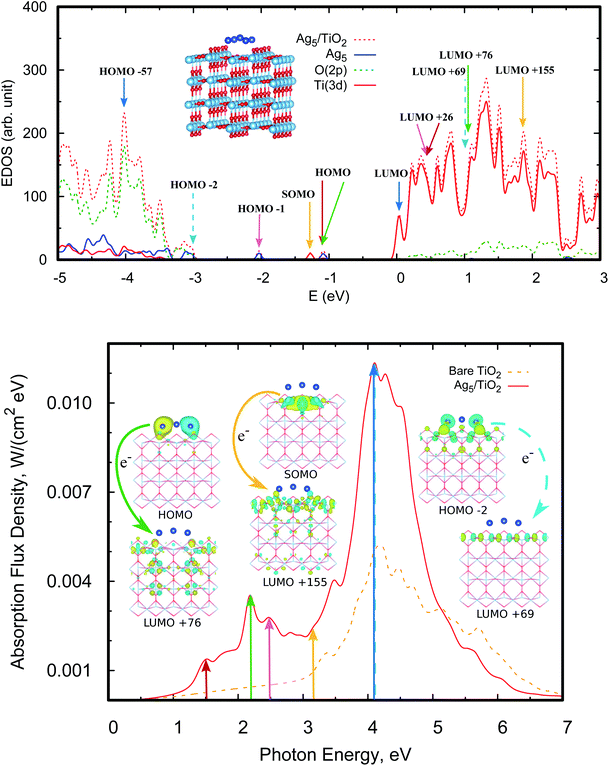Fig. 4 Upper panel: electronic density of states (EDOS) of the Ag₅–TiO₂(110) system. We also indicate the positions of the donor and acceptor orbitals involved in the main photo-induced transitions shown in the bottom panel (see also orbital pictures in Fig. 3). The zero of energy corresponds to the Fermi level, defined here as the highest occupied level. The projected density of states (PDOS) onto O(2p), Ti(3d), and orbitals centered at the Ag₅ cluster is also shown. The arrows indicate the bands responsible for the peaks shown in the photo-absorption spectrum (bottom panel), with the positions of the donor and acceptor orbitals also indicated. Bottom panel: photo-absorption spectra of the TiO₂(110) surface, without adsorbates (red lines) and with the adsorbed Ag₅ cluster (blue lines) in the most stable configuration. The insets present the orbitals involved in the photo-excitation processes (see also Section S2 of the ESI†).

Fig. 5 Comparison of the theoretical and experimental absorbance in the visible region. The experimental absorbance A has been calculated via diffuse reflectance spectroscopy (DRS) measurements from the diffuse reflectance signal R_d as A = log₁₀(1/R_d). The units of absorbance are arbitrary units.

Moving to the photo-excitation processes, the first thing to note from Fig. 4 is that the excitation of the Ti³⁺ 3d¹ electron with a photon energy at the end of the visible region (marked with a yellow arrow at about 3.1 eV) leads to its transfer to 3d orbitals of Ti atoms spread all over the TiO₂ surface. Essentially, the delocalized hole accompanying the formation of the polaronic Ti³⁺ 3d¹ state becomes filled, indicating the existence of the delocalized hole itself. This is further confirmed by an analysis of the acceptor orbital, being mainly composed of 3d states of surface Ti atoms (ca. 64%). Alternatively, our finding could also be viewed as the photo-induced conversion of a small polaron into a large polaron. Previous experimental measurements⁶⁰ have shown that visible light excitation of Ti³⁺ centers on reduced TiO₂ nanoparticles leads to the transfer of the localized 3d¹ electrons into the conduction TiO₂ band.

2.5 Improvement of the UV-Vis optical response of TiO₂: experimental confirmation

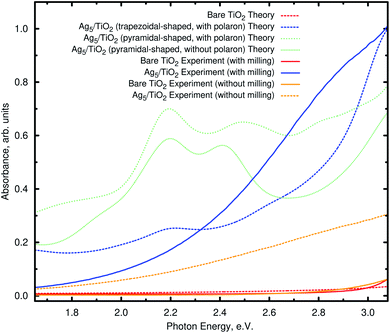
As found for non-polaronic states²⁰ and the Cu₅/TiO₂ interface,¹⁵ it can be noted from Fig. 4 (bottom panel) that the Ag₅ cluster increases the UV and extends into the visible the optical response of TiO₂. Fig. 5 shows the comparison of the theoretical and experimental absorbance in the visible region going from 1.65 to about 3.08 eV. All the DRS spectra show the typical behavior expected in TiO₂-based semiconductors consisting of a nearly flat region, at small photon energies, that is dominated by reflection and scattering due to the high refractive index of the investigated material. The milling process decreases the nanoparticle size increasing the surface area. In this way, the amount on deposited clusters increases and the light absorption is higher (by about a factor of three) than for nanoparticles without milling. The abrupt increase when radiation becomes more intensively absorbed with increasing photon energy corresponds to an onset of transmission near the optical absorption. The experiment corroborates the theoretical prediction that Ag₅ clusters are capable of extending the optical response of TiO₂ into the visible.

As can be seen in the bottom panel of Fig. 4, the main absorption peaks in the visible (pink and forest-green arrows) involve the electron transfer from ‘isolated’ midgap states (the HOMO−1 and HOMO orbitals) to acceptor Ti(3d) states in the TiO₂ conduction band (the LUMO+26 and LUMO+76 orbitals). In contrast with the case of the Cu₅/TiO₂ interface,¹⁵ the frontier HOMO−1 orbital bears a dominant Ag(5s) atomic contribution (see Section S2 of the ESI†) and not chemical mixing of Cu(3d) orbitals with O(2p) and Ti(3d) states. For the Ag₅–TiO₂ system, there is also photo-induced electron transfer from frontier Ag(4d) orbitals having chemical mixing with O(2p) and Ti(3d) states such as the HOMO−2 orbital (see Section S2 of the ESI†). However, the associated absorbance contribution (dotted blue arrow in Fig. 4) is located in the UV and not the visible region.

Our results are consistent with previous studies^15,20 indicating that the main mechanism driving photoabsorption is a single electron ‘jumping’ from 5s (Ag₅) or 3d (Cu₅) orbitals to the conduction band, leaving behind a long-lived ‘hole’ at the subnanometer clusters. Similar to the case of the Cu₅–TiO₂ interface,¹⁵ the Ag₅ cluster induces a spatial separation of photogenerated holes and electrons. It can be noted from the orbital pictures of Fig. 4 that the acceptor state bears a depleted region of charge (empty region) at the Ag₅–TiO₂ layer, hindering electron–hole recombination and then, improving the photocatalyst efficiency of TiO₂.⁶¹

2.6 Prediction of CO₂ photo-activation

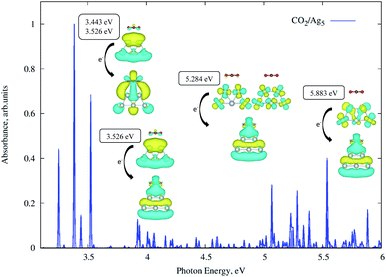
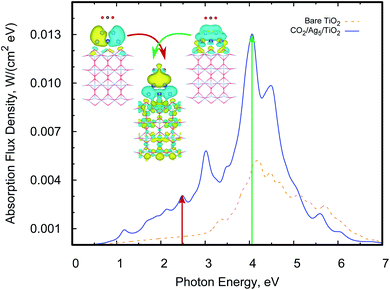
A previous theoretical study¹⁹ has indicated that subnanometer Cu₅ clusters could enable the photo-activation of the CO₂ molecule and we analyse here if similar conclusions hold for unsupported and TiO₂-supported Ag₅ clusters. By relaxing the whole CO₂/Ag₅ geometry (see the inset of Fig. 6), we estimated a physisorption energy of −0.10 (−0.12) eV for the CO₂ molecule over the Ag₅ cluster at the MP2 (DFT-D3) level. We also estimated the Helmholtz free energy of formation,⁶² finding that the CO₂/Ag₅ complex is still stable at room temperature but by −0.03 eV only. Follow-up TDDFT calculations of the UV-Vis spectrum (see Fig. 6) show that the bare Ag₅ clusters induce CO₂ activation with photon energies in the UV region (from about 3.4 eV).

Fig. 6 UV-Vis absorption spectra for CO₂ physisorbed on unsupported Cu₅ clusters, as obtained at the TDDFT level with the PBE-D3(BJ) scheme. The orbitals responsible of the most relevant transitions involving electron transfer from the Cu₅ cluster to the physisorbed CO₂ molecule are also shown. The insets present density isosurfaces of these orbitals. A cluster model has been used (see the Methods section).

When considering TiO₂-supported Ag₅ clusters as the photocatalysts, we find that the physisorption state and energy (0.11 eV) are very similar to the case of the unsupported cluster. However, it can be noted from Fig. 7 that a photon energy in the visible region is already capable of inducing CO₂ activation. The transition responsible for the peak in the visible involves an electron “jump” from the HOMO orbital and the final state is the CO₂˙⁻ radical attached to the Ag₅-supported cluster. It is well-known that the radical CO₂˙⁻ is a clear precursor-state for dissociation of the CO₂ molecule due to its weakened C=O bond.

Fig. 7 UV-Vis absorption spectra for CO₂ physisorbed on TiO₂-supported Ag₅ clusters (blue lines). The spectra on the same surface without adsorbates are also shown (dotted orange lines). The red and green arrows indicate the position of the most intense peaks involving a transition to orbitals with high density on the carbon atom. The inset presents the orbitals involved in the photo-excitation process associated with the indicated peaks. A periodic model has been used (see the Methods section).

Also, we found that both the physisorption and the photo-activation of CO₂ are possible over the pyramidal-shaped Ag₅ isomer shown in Fig. 1, with an almost identical physisorption energy (−0.12 eV). The order of magnitude of our estimated physisorption energies are the same as in previous studies on CO₂ capture through TiO₂ nanoparticles (between −0.16 and −0.28 eV in ref. 63). In view of the similar properties of Ag_n clusters (n < 5) when adsorbed on rutile and anatase phases,^20,22 we expect that the photoinduced activation of CO₂ occurs also on anatase-supported Ag₅ clusters. We also calculated the UV-Vis spectra of CO₂ adsorbed on the bare TiO₂ for one specific configuration (over the Ti(5f) site). However, no transition with a significant oscillator strength has been found for a photo-excited electron from the bare TiO₂ surface to the CO₂ molecule. This outcome also indicates that the Ag₅ cluster is responsible for the predicted CO₂ photoactivation.

3 Conclusions

The very recent development of cutting-edge experimental techniques making the synthesis of subnanometer metal clusters possible is pushing our understanding of molecule-like catalysts and photocatalysts far beyond the theory developed for metal nanoparticles and bulk materials. As an example, it has been previously shown how new photocatalytic and optical properties with technological projections are acquired by TiO₂ surfaces upon deposition of Cu₅ clusters.^15,19 In this work, we computationally and experimentally explored the properties of Ag₅-modified TiO₂ surfaces instead, taking advantage of the high monodispersity of the method for Ag₅ cluster synthesis.

On the one hand, we have clearly shown that these Ag₅ clusters are capable of inducing the formation of stable surface polarons, as localized Ti³⁺ 3d¹ states, as well as photogenerated large polarons at the Ag₅/TiO₂ interface of the material. Moreover, new fundamental insights have been gained on general electronic polarization effects accompanying the formation of surface polarons (along with the well-known structural distortion of the crystal lattice). This phenomenon has been manifested as a depopulation of titanium 3d orbitals favouring oxygen 2p orbitals, as experimentally observed through X-ray absorption spectroscopy at the Ti K-edge and theoretically predicted by applying state-of-the-art computational modelling. The self-trapped Ti³⁺ 3d¹ electron repels nearby oxygen ions and attracts nearby titanium cations which, in turn, affects their electronic structure, causing the transfer of electronic charge from Ti⁴⁺ cations to O²⁻ ions. On the other hand, our results point out that TiO₂-supported Ag₅ clusters are not only visible-light photo-active materials but are also potential photocatalysts for CO₂ reduction.

From a practical perspective, the modification of TiO₂ surfaces with subnanometer Ag₅ clusters has revealed a new way of stabilizing surface polarons and producing at the surface a kind of polaronic 2D material, which could be used for further experimental and theoretical studies of polaron interactions, currently a matter of high relevance.⁶⁴ From a broader perspective, the main novelty of our present work is that we revealed theoretically and confirmed experimentally an electron polarization phenomenon associated with a surface polaron formation for the first time. At present, the experimental observation along with the theoretical interpretation suggests an important step for the fundamental understanding of surface polarons and photoexcitation.

4 Materials and methods

4.1 Materials

Ag₅ clusters were synthesized and characterized according to a previously developed electrochemical method,^10,11 using a Ag electrode.¹¹ The experimental method for Ag₅ cluster synthesis and full characterization has been described in ref. 65. TiO₂ titanium dioxide nanoparticles were purchased from GetNanoMaterials,⁶⁶ in the form of nanopowders, which according to the supplier are composed of particles with a primary particle size (99.9%) of 5 nm.

4.2 Experimental methods

We carried out X-ray absorption spectroscopy measurements (XAS) in the XANES (X-ray absorption near edge structure) regions at the XAFS2 beamline⁶⁷ of the Laboratório Nacional de Luz Síncrotron (LNLS), Campinas, Brazil. These XANES measurements were performed in transmission mode using a Si(111) crystal monochromator around the Ti K-edge (4966 eV) at ambient temperature using three ion chambers as detectors. Harmonics were attenuated by detuning to 50% of the peak intensity. We determined the sample absorption between the first two chambers. For calibration purposes, the third chamber was used to measure a metallic Ti reference. In order to achieve an edge-step close to unity in the XAS measurements, we calculated the optimum amount of material. Powdered samples were dispersed in 10 ml of isopropyl alcohol and then filtered through a 0.45 μm pore size MF-Millipore™ membrane filter. We normalized XANES data by standard methods using ATHENA software which is part of the IFEFFIT package.⁶⁸

We obtained the optical absorption spectra through diffuse reflectance spectroscopy (DRS) using a Shimadzu ISR-2600 Plus spectrophotometer. The setup includes an integrating sphere with two detectors, a photomultiplier and an InGaAs detector. The DRS spectra were collected at room temperature in the range between 200 and 700 nm with a step of 1.0 nm using standard BaSO₄ (Nacalai Tesque) as a reference. DRS was obtained by determining the ratio of intensities of diffusely reflected radiation from the sample and from the standard.

4.3 Computational methods

4.3.1 Periodic calculations. We carried out the periodic electronic structure calculations with the Vienna Ab initio Simulation Package (VASP 5.4.4),^69,70 following the same computational approach reported in previous work on the Cu₅–TiO₂(110) and CO₂/Cu₅–TiO₂(110) interactions.^15,19

Electron–ion interactions are described by the projector augmented-wave method,^70,71 using PAW-PBE pseudopotentials as implemented in the program. The electrons of the O(2s, 2p), C(2s, 2p), Ti(3s, 4s, 3p, 3d) and Ag(4d, 5s) orbitals are treated explicitly as valence electrons. A plane wave basis set with a kinetic energy cutoff of 700 eV is used. A Gaussian smearing of 0.05 eV is employed to account for partial occupancies, and the Brillouin zone sampled at the Γ point.⁷² The convergence criterion was 10⁻⁴ eV for the self-consistent electronic minimization. Geometries were relaxed with a force threshold of 0.02 eV Å⁻¹.

The TiO₂ surface is modelled via periodic slabs, using a 4 × 2 supercell (four TiO₂ trilayers giving ca. 13 Å slab width). Ag₅ adsorption and CO₂ physisorption are assumed on one side of the slab, with 38 Å of vacuum above it.⁷³

Adsorption energies of the Ag₅ cluster on the surface are derived via

E_int = E_{Ag5/TiO2(110)} − E_Ag5 − E_TiO2(110)

where E_{Ag5/TiO2(110)} is the total energy of the system, E_TiO2(110) is the energy of the substrate, and E_Ag5 denotes the energy of the bare silver cluster. When considering the adsorption of CO₂ on TiO₂-supported Ag₅ clusters, the interaction energies are derived via

E_int = E_{CO2/Ag5–TiO2(110)} − E_CO2 − E_{Ag5–TiO2(110)}

with E_{CO2/Ag5–TiO2(110)} as the total energy of the system, E_Ag5 − E_TiO2(110) as the energy of the supported-TiO₂–Ag₅ cluster, and E_CO2 stands for the energy of the free (gas-phase) CO₂ molecule. All these values were calculated in the same supercell slab for the sake of consistency.

The geometries were optimized with the PBE-D3(BJ) scheme with the Hubbard term (DFT+U) added and including spin-polarization. We used the same value of U (4.2 eV) reported in previous studies of TiO₂-modified copper clusters.^15,37 For the dispersion-dominated Ag₂/TiO₂ interaction,²⁰ the PBE-D3(BJ) interaction energies agreed to within 10% with reference values obtained with the domain-based pair natural orbital correlation approach DLPNO-CCSD(T)⁷⁴ as well as the symmetry-adapted perturbation theory [SAPT(DFT)] method.^75,76 The performance of the PBE-D3(BJ) approach against higher levels of ab initio theory has also been tested for the estimation of the CO₂ physisorption energy on TiO₂-supported Cu₅ clusters.¹⁹ An agreement to within 10% was found between PBE-D3(BJ) and second-order Möller–Plesset perturbation theory (MP2) levels.

We used the optimized geometries, obtained at the PBE+U/D3 level in final HSE06 calculations. The HSE06 exchange–correlation functional uses a screened Coulomb potential for increased efficiency on metallic systems.^43,44 It has been the preferred approach in previous studies of optical and other electronic properties of TiO₂.^77–79 We applied the HSE06 approach using a HF/GGA mixing ratio of 25 : 75 with a screening parameter of 0.11 bohr⁻¹, as recommended in ref. 44. At a variance with our previous study of TiO₂-supported Ag_n clusters (n < 5),²⁰ all calculations are spin-polarized and all atoms and ions from the supercell models were relaxed.

4.3.2 Reduced density matrix treatment. We calculated the UV-Vis absorption spectra using the computational approach previously applied to TiO₂-supported Cu₅ clusters.¹⁵ The relaxation processes involved are described by the reduced density matrix (RDM) approach in the Redfield approximation,⁴⁶ based on orbitals taken from calculations employing the HSE06 hybrid functional. This combined RDM-DFT treatment developed by Micha and Kilin^47,48 is already a well-established tool in describing the optical spectra of subnano metal clusters adsorbed on semiconductor surfaces⁸⁰ (see, e.g., ref. 20 and 50–52).

Very briefly, in the presence of a monochromatic electromagnetic field 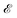of frequency Ω, the evolution equation for the reduced density ρ in the Schrödinger picture takes the form

where F̂^KS denotes the effective Kohn–Sham Hamiltonian (the indices refer to its representation in the Kohn–Sham basis set), D̂ is the electric dipole moment operator, and R_jklm stands for the Redfield coefficients, i.e. the Kohn–Sham components of the relaxation tensor. The latter is defined as in ref. 46 and is implemented as described in ref. 47.

Within the Redfield approximation, the relaxation tensor incorporates not only fast electronic dissipation due to electronic fluctuations in the medium, but also the relatively slow relaxation due to vibrations of the atomic lattice. It is convenient to perform coordinate transformation into a rotating frame accounting for the electromagnetic field oscillation. This is described by the equations

[small rho, Greek, tilde]_ij(t) = ρ_ij(t)exp(iΩt), ε_i > ε_j

[small rho, Greek, tilde]_ij(t) = ρ_ij(t)exp(−iΩt), ε_i < ε_j

[small rho, Greek, tilde]_ii(t) = ρ_ii(t)

where ε_i is the energy of the i-th Kohn–Sham orbital. Time averaging over the fast terms in the equation of motion for the RDM yields
as stationary-state solutions for the diagonal elements.⁴⁷ In this, HOMO and LUMO denote the lowest-energy unoccupied and the highest-energy occupied molecular orbital, respectively. Γ_j is a depopulation rate, and the sum terms g_jk are given by
with γ denoting the decoherence rate, Ω_jk as the Rabi frequencies given by 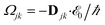, and Δ_jk(Ω) = Ω − (ε_j − ε_k) as detunings. The diagonal elements provide the populations of the KS orbitals. The population relaxation rate ℏΓ and the decoherence rate ℏγ are kept fixed to values of 0.15 meV and 150 meV (27 ps and 27 fs). These values have been chosen according to known rates for phonon decay and electronic density excitations in semiconductors (see, e.g., ref. 81).

In terms of the stationary populations, the absorbance is given by^{20,51,52,82,83}

where f̄_jk is an oscillator strength per active electron.⁸⁴ The solar flux absorption spectrum is then expressed as

F(ℏΩ) = [small alpha, Greek, macron](Ω)F_solar(ℏΩ)ℏΩ,

where the solar flux is approximated by the black body flux distribution, normalized to an incident photon flux of 1 kW m⁻²,
with C_T the flux normalization constant and the temperature T set to 5800 K.

4.3.3 Cluster model calculations. Cluster model calculations were performed for the interaction between CO₂ and the bare Ag₅ cluster by applying the PBE-D3(BJ) scheme and the MP2 method with the ORCA⁸⁵ suite of programs (version 4.0.1.2). For this purpose, we used an atom-centered def2-TZVPP⁸⁶ basis set for carbon, oxygen, and silver atoms. When optimizing the geometries in the CO₂–Ag₅ cluster, the atoms of both CO₂ and Cu₅ sub-systems were allowed to relax. We also calculated Helmholtz free energies of formation^62,87 using the thermochemistry output of ORCA.⁸⁵ Next, we carried out time-dependent DFT (TDDFT) calculations of the UV-Vis spectra using the PBE-D3(BJ) scheme.

Author contributions

Conceptualization and coordination, M. P. d. L. C.; theoretical work, P. L. C., S. M. A., M. P. d. L. C.; experimental work, J. M. R. L., L. J. G., D. B., M. A. L. Q., F. R.; writing manuscript, M. P. d. L. C.; editing, P. L. C., J. M. R. L., L. J. G., D. B., S. M. A., M. A. L. Q., F. R., M. P. d. L. C.; all authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been partly supported by the Spanish Agencia Estatal de Investigación (AEI) and the Fondo Europeo de Desarrollo Regional (FEDER, UE) under Grant No. MAT2016-75354-P, FIS2017-83473-C2-1-P, by La Caixa Foundation (LCF/PR/PR12/11070003), Ramon Areces Foundation (Project CIVP18A3940), and European Commission through FEDER and H2020 program (0681InveNNta1E; Bac-To-Fuel 825999); MINECO, Spain (MAT2015-67458-P – cofinanced with FEDER Funds – and CTQ2013-44762-R), Xunta de Galicia, Spain (GRC ED-431C2017/22; AEMAT ED431E2018/08), and by ANPCyT (2017-1220 and 2017-3944) and UNLP (Project 11/X790), Argentina. The CESGA super-computer center (Spain) is acknowledged for having provided the computational resources used in this work. Partial support by Laboratório Nacional de Luz Síncrotron (LNLS, Campinas, Brazil) under proposals 20170352 and 20180490 is also acknowledged. D. B. expresses gratitude for a postdoctoral grant from Xunta de Galicia, Spain (ED481D 2017/021). P. L. C. expresses her gratitude for a contract for graduate students from the “Garantía Juvenil” program from the Comunidad de Madrid. M. P. de. L. C. is greatly thankful to David A. Micha and Tijo Vazhappilly for having shared the original code to calculate the absorption coefficients and to Alexander O. Mitrushchenkov and Andreas W. Hauser for very useful discussions.

References

1. M. Zhou, C. Zeng, Y. Chen, S. Zhao, M. Y. Sfeir, M. Zhu and R. Jin, Nat. Commun., 2016, 7, 13240.
2. B. S. González and M. A. López-Quintela, Functional Nanometer-Sized Clusters of Transition Metals: Synthesis, Properties and Applications, The Royal Society of Chemistry, 2014, pp. 25–50.
3. S. M. Copp, A. Gorovits, S. M. Swasey, S. Gudibandi, P. Bogdanov and E. G. Gwinn, ACS Nano, 2018, 12, 8240–8247.
4. V. Porto, E. Borrajo, D. Buceta, C. Carneiro, S. Huseyinova, B. Domínguez, K. J. E. Borgman, M. Lakadamyali, M. F. Garcia-Parajo, J. Neissa, T. García-Caballero, G. Barone, M. C. Blanco, N. Busto, B. García, J. M. Leal, J. Blanco, J. Rivas, M. A. López-Quintela and F. Domínguez, Adv. Mater., 2018, 30, 1801317.
5. M. A. Abbas, P. V. Kamat and J. H. Bang, ACS Energy Lett., 2018, 3, 840–854.
6. L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079.
7. R. Passalacqua, S. Parathoner, G. Centi, A. Halder, E. C. Tyo, B. Yang, S. Seifert and S. Vajda, Catal. Sci. Technol., 2016, 6, 6977–6985.
8. A. Halder, L. A. Curtiss, A. Fortunelli and S. Vajda, J. Chem. Phys., 2018, 148, 110901.
9. S. Huseyinova, J. Blanco, F. G. Requejo, J. M. Ramallo-López, M. C. Blanco, D. Buceta and M. A. López-Quintela, J. Phys. Chem. C, 2016, 120, 15902–15908.
10. D. Buceta, N. Busto, G. Barone, J. M. Leal, F. Domínguez, L. J. Giovanetti, F. G. Requejo, B. García and M. A. López-Quintela, Angew. Chem., Int. Ed., 2015, 54, 7612–7616.
11. V. Porto, E. Borrajo, D. Buceta, C. Carneiro, S. Huseyinova, B. Domínguez, K. J. E. Borgman, M. Lakadamyali, M. F. Garcia-Parajo, J. Neissa, T. García-Caballero, G. Barone, M. C. Blanco, N. Busto, B. García, J. M. Leal, J. Blanco, J. Rivas, M. A. López-Quintela and F. Domínguez, Adv. Mater., 2018, 30, 1801317.
12. P. Concepción, M. Boronat, S. García-García, E. Fernández and A. Corma, ACS Catal., 2017, 7, 3560–3568.
13. E. Fernández, M. Boronat and A. Corma, J. Phys. Chem. C, 2015, 119, 19832–19846.
14. A. Zanchet, P. López-Caballero, A. O. Mitrushchenkov, D. Buceta, M. A. López-Quintela, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 27064–27072.
15. M. P. de Lara-Castells, A. W. Hauser, J. M. Ramallo-López, D. Buceta, L. J. Giovanetti, M. A. López-Quintela and F. G. Requejo, J. Mater. Chem. A, 2019, 7, 7489–7500.
16. Q. Guo, C. Zhou, Z. Ma, Z. Ren, H. Fan and X. Yang, Chem. Soc. Rev., 2016, 45, 3701–3730.
17. P. Salvador and C. Gutierrez, J. Phys. Chem., 1984, 88, 3696–3698.
18. A. L. Linsebigler, G. Q. Lu and J. T. Yates Jr, Chem. Rev., 1995, 95, 735–758.
19. P. López-Caballero, A. W. Hauser and M. P. de Lara-Castells, J. Phys. Chem. C, 2019, 123, 23064–23074.
20. M. P. de Lara-Castells, C. Cabrillo, D. A. Micha, A. O. Mitrushchenkov and T. Vazhappilly, Phys. Chem. Chem. Phys., 2018, 20, 19110–19119.
21. S. Tan, A. Argondizzo, J. Ren, L. Liu, J. Zhao and H. Petek, Nat. Photonics, 2017, 11, 806–812.
22. A. R. Puigdollers, P. Schlexer and G. Pacchioni, J. Phys. Chem. C, 2015, 119, 15381–15389.
23. M. Reticcioli, M. Setvin, M. Schmid, U. Diebold and C. Franchini, Phys. Rev. B, 2018, 98, 045306.
24. Polarons are distinguished as small or large polarons depending on the spatial extent of the polaron wavefunction and the associated structural distortion, as compared with the lattice constant a of the crystal. Intrinsic polarons in rutile TiO₂ (i.e., self-trapped electrons at Ti⁴⁺ ions) are characterized as small polarons.
25. C. Di Valentin, G. Pacchioni and A. Selloni, Phys. Rev. Lett., 2006, 97, 166803.
26. N. A. Deskins, R. Rousseau and M. Dupuis, J. Phys. Chem. C, 2009, 113, 14583–14586.
27. S. Chrétien and H. Metiu, J. Phys. Chem. C, 2011, 115, 4696–4705.
28. P. Déak, B. Aradi and T. Brauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 1–8.
29. D. Berger, H. Oberhofer and K. Reuter, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 17, 29949–29957.
30. L. Yan, J. E. Elenewski, W. Jiang and H. Chen, Phys. Chem. Chem. Phys., 2015, 17, 29949–29957.
31. A. Selloni, in Titania and Its Outstanding Properties: Insights from First Principles Calculations, ed. W. Andreoni and S. Yip, Springer International Publishing, Cham, 2018, pp. 1–23.
32. P. Krüger, S. Bourgeois, B. Domenichini, H. Magnan, D. Chandesris, P. Le Fèvre, A. M. Flank, J. Jupille, L. Floreano, A. Cossaro, A. Verdini and A. Morgante, Phys. Rev. Lett., 2008, 100, 055501.
33. S. Yang, A. T. Brant, N. C. Giles and L. E. Halliburton, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 125201.
34. M. Setvin, C. Franchini, X. Hao, M. Schmid, A. Janotti, M. Kaltak, C. G. Van de Walle, G. Kresse and U. Diebold, Phys. Rev. Lett., 2014, 113, 086402.
35. P. Gono, J. Wiktor, F. Ambrosio and A. Pasquarello, ACS Catal., 2018, 8, 5847–5851.
36. J. Koepsell, J. Vijayan, P. Sompet, F. Grusdt, T. A. Hilker, E. Demler, G. Salomon, I. Bloch and C. Gross, Nature, 2019, 572, 358–362.
37. N. Seriani, C. Pinilla and Y. Crespo, J. Phys. Chem. C, 2015, 119, 6696–6702.
38. H. Sezen, H. Shang, F. Bebensee, C. Yang, M. Buchholz, A. Nefedov, S. Heissler, C. Carbogno, M. Scheffler, P. Rinke and C. Wöll, Nat. Commun., 2015, 6, 6901.
39. S. Xu and E. A. Carter, Chem. Rev., 2019, 119, 6631–6669.
40. S. Xie, Q. Zhang, G. Liu and Y. Wang, Chem. Commun., 2016, 52, 35–59.
41. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
42. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
43. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
44. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106.
45. P. Deák, B. Aradi and T. Frauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155207.
46. V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VCH, 2011.
47. D. S. Kilin and D. A. Micha, J. Phys. Chem. C, 2009, 113, 3530–3542.
48. D. A. Micha, Adv. Quantum Chem., 2015, 71, 195–220.
49. D. A. Micha, Molecular Interactions: Concepts and Methods, Wiley, 2019, pp. 1–400.
50. D. S. Kilin and D. A. Micha, J. Phys. Chem. Lett., 2010, 1, 1073–1077.
51. T. Vazhappilly, D. S. Kilin and D. A. Micha, J. Phys. Chem. C, 2012, 116, 25525–25536.
52. R. H. Hembree, T. Vazhappilly and D. A. Micha, J. Chem. Phys., 2017, 147, 224703.
53. T. Vazhappilly, M. P. de Lara-Castells and D. A. Micha, Mol. Phys., 2019, 117, 2267–2274.
54. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
55. T. L. Haslett, K. A. Bosnick and M. Moskovits, J. Chem. Phys., 1998, 108, 3453–3457.
56. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
57. T. Vazhappilly, M. P. de Lara-Castells and D. Micha, Mol. Phys., 2019, 117, 2267–2274.
58. M. Reticcioli, I. Sokolović, M. Schmid, U. Diebold, M. Setvin and C. Franchini, Phys. Rev. Lett., 2019, 122, 016805.
59. M. F. Ruiz-López and A. Muñoz Páez, J. Phys.: Condens. Matter, 1991, 3, 8981.
60. K. Komaguchi, T. Maruoka, H. Nakano, I. Imae, Y. Ooyama and Y. Harima, J. Phys. Chem. C, 2010, 114, 1240–1245.
61. Z. Zhang and J. T. Yates Jr, Chem. Rev., 2012, 112, 5520–5551.
62. X. Yu, A. R. Oganov, Q. Zhu, F. Qi and G. Qian, Phys. Chem. Chem. Phys., 2018, 20, 30437–30444.
63. U. Tumuluri, J. D. Howe, W. P. Mounfield, M. Li, M. Chi, Z. D. Hood, K. S. Walton, D. S. Sholl, S. Dai and Z. Wu, ACS Sustainable Chem. Eng., 2017, 5, 9295–9306.
64. M. Kang, S. W. Jung, W. J. Shin, Y. Sohn, S. H. Ryu, T. K. Kim, M. Hoesch and K. S. Kim, Nat. Mater., 2018, 17, 676–680.
65. J. Blanco, PhD thesis, University of Santiago de Compostela, Spain, 2017.
66. URL: http://www.getnanomaterials.com/nanoparticles/titaniumdioxide-1/tio2-110-5-nm-anatase-1.
67. S. J. A. Figueroa, J. C. Mauricio, J. Murari, D. B. Beniz, J. R. Piton, H. H. Slepicka, M. F. M. F. de Sousa, A. M. Espíndola and A. P. S. Levinsky, J. Phys.: Conf. Ser., 2016, 712, 012022.
68. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
69. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
70. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
71. P. E. Blöch, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
72. Test calculations showed that interaction energies at the potential minimum using a 5 × 5 × 1 Monkhorst–Pack⁸⁸k-point mesh are within ca. 0.01 eV with those calculated at the Γ point.
73. This large vacuum region allows the description of long-range tails of the cluster–surface interaction potentials while avoiding unphysical overlaps of electronic densities.
74. C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106.
75. A. J. Misquitta, B. Jeziorski and K. Szalewicz, Phys. Rev. Lett., 2003, 91, 033201.
76. A. Heßelmann and G. Jansen, Chem. Phys. Lett., 2003, 367, 778–784.
77. J. Anderson and C. G. Van de Walle, Phys. Status Solidi B, 2010, 248, 799–804.
78. A. Janotti, J. B. Varley, P. Rinke, N. Umezawa, G. Kresse and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085212.
79. V. Francesc, L. Oriol, C. K. Kyoung, Y. L. Jin and I. Francesc, J. Comput. Chem., 2017, 38, 781–789.
80. This approximation is valid for long relaxation times in comparison with the duration of the transient energy exchange between the adsorbate and its medium.
81. K. Ozawa, S. Yamamoto, R. Yukawa, R.-Y. Liu, N. Terashima, Y. Natsui, H. Kato, K. Mase and I. Matsuda, J. Phys. Chem. C, 2018, 122, 9562–9569.
82. T. Vazhappilly and D. A. Micha, J. Phys. Chem. C, 2014, 118, 4429–4436.
83. A. Halder, L. A. Curtiss, A. Fortunelli and S. Vajda, J. Chem. Phys., 2018, 148, 110901.
84. This is the purely dissipative contribution to the absorbance. We assume a thin slab, neglecting any dispersive effects, i.e., assuming a refraction index of ca. 1.
85. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
86. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
87. A. W. Hauser, J. Gomes, M. Bajdich, M. Head-Gordon and A. T. Bell, Phys. Chem. Chem. Phys., 2013, 15, 20727–20734.
88. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.

---

Footnote

† Electronic supplementary information (ESI) available: Complementary results from the first-principles modelling: polaronic states in reduced TiO₂(110) surfaces, and characterization of the most relevant orbitals in the photoexcitation of the Ag₅/TiO₂(110) system. See DOI: 10.1039/d0ta00062k

---