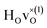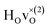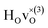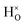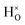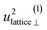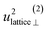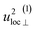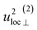Open Access Article
Open Access ArticleThe role of oxygen vacancies on the vibrational motions of hydride ions in the oxyhydride of barium titanate†
Carin
Eklöf-Österberg
a,
Laura
Mazzei
 b,
Erik Jedvik
Granhed
b,
Erik Jedvik
Granhed
 b,
Göran
Wahnström
b,
Göran
Wahnström
 b,
Reji
Nedumkandathil
c,
Ulrich
Häussermann
c,
Aleksander
Jaworski
c,
Andrew J.
Pell
b,
Reji
Nedumkandathil
c,
Ulrich
Häussermann
c,
Aleksander
Jaworski
c,
Andrew J.
Pell
 c,
Stewart F.
Parker
c,
Stewart F.
Parker
 d,
Niina H.
Jalarvo
d,
Niina H.
Jalarvo
 e,
Lars
Börjesson
b and
Maths
Karlsson
e,
Lars
Börjesson
b and
Maths
Karlsson
 *a
*a
aDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, SE-412 96 Göteborg, Sweden. E-mail: maths.karlsson@chalmers.se; Tel: +46 31 772 6770
bDepartment of Physics, Chalmers University of Technology, SE-412 96 Göteborg, Sweden
cDepartment of Materials and Environmental Chemistry, Stockholm University, SE-10691 Stockholm, Sweden
dISIS Neutron and Muon Source, STFC Rutherford Appleton Laboratory, Oxfordshire OX11 0QX, UK
eChemical and Engineering Materials Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831-6475, USA
First published on 23rd March 2020
Abstract
Perovskite-type oxyhydrides, BaTiO3−xHx, represent a novel class of hydride ion conducting materials of interest for several electrochemical applications, but fundamental questions surrounding the defect chemistry and hydride ion transport mechanism remain unclear. Here we report results from powder X-ray diffraction, thermal gravimetric analysis, nuclear magnetic resonance spectroscopy, inelastic neutron scattering (INS), and density functional theory (DFT) simulations on three metal hydride reduced BaTiO3 samples characterized by the simultaneous presence of hydride ions and oxygen vacancies. The INS spectra are characterized by two predominating bands at around 114 (ω⊥) and 128 (ω∥) meV, assigned as fundamental Ti–H vibrational modes perpendicular and parallel to the Ti–H–Ti bond direction, respectively, and four additional, weaker, bands at around 99 (ω1), 110 (ω2), 137 (ω3) and 145 (ω4) meV that originate from a range of different local structures associated with different configurations of the hydride ions and oxygen vacancies in the materials. Crucially, the combined analyses of INS and DFT data confirm the presence of both nearest and next-nearest neighbouring oxygen vacancies to the hydride ions. This supports previous findings from quasielastic neutron scattering experiments, that the hydride ion transport is governed by jump diffusion dynamics between neighbouring and next-nearest neighbouring hydride ion–oxygen vacancy local structures. Furthermore, the investigation of the momentum transfer dependence of the INS spectrum is used to derive the mean square displacement of the hydride ions, which is shown to be in excellent agreement with the calculations. Analysis of the mean square displacement confirms that the hydrogen vibrational motions are localized in nature and only very weakly affected by the dynamics of the surrounding perovskite structure. This insight motivates efforts to identify alternative host lattices that allow for a less localization of the hydride ions as a route to higher hydride ion conductivities.
1 Introduction
Perovskite-type oxyhydrides ATiO3−xHx (A = Ba, Sr, Ca, x < 0.6), in which some of the oxide ions are replaced by hydride ions, have recently emerged as a novel class of mixed electronic-ionic conductors with potential application in energy storage and conversion.1–3 Understanding the defect chemistry and hydride ion conduction mechanism in these materials is of great importance for developing efficient synthesis routes that allow the development of new oxyhydrides with tailored ionic and electronic conductivity for certain applications, but neither the defect chemistry nor hydride ion conduction mechanism are fully understood. Recent results from quasielastic neutron scattering (QENS),4 isotope exchange,5,6 combined isotope exchange with depth profiling analysis7 and first-principles calculations7,8 suggest a vacancy-assisted diffusion mechanism. However, a mechanism based on the transformation into a proton and then interstitial diffusion has been also discussed in the past.1,7–10The oxyhydrides ATiO3−xHx are formed through a topochemical approach by reacting ATiO3 with, e.g., CaH2, which gives rise to the substitution of oxide ions by hydride ions. Among these, BaTiO3−xHx exhibits the highest amount of hydride ions with a concentration up to x ≈ 0.6. The substitutional hydride ion acts as a donor, contributing to n type conductivity in the initially empty Ti4+ 3d band,8–10 and conductivity measurements of BaTiO3−xHx shows that it is electronically conducting.1,11,12 The conductivities as reported on BaTiO3−xHx are, however, somewhat conflicting in that both semiconducting1 and metallic-like12 conductivity has been reported. The semiconducting behaviour was suggested to relate to the presence of localized electronic states within the bandgap,8 which are associated with electron polarons. A polaron in this case refers to when an electron is localized on a titanium ion that resides next to a hydride ion and thereby changes the valence of the titanium ion from +4 to +3.
Recently, we showed, in a combined density functional theory (DFT) calculations and inelastic neutron scattering (INS) study of BaTiO3−xHy□x−y with y = 0.1 and x = 0.18, that the electrons rather tend to form a delocalized state where they are shared among all Ti4+ ions, thus forming a bandstate configuration.13 In particular, the INS technique was used to determine the vibrational spectrum of BaTiO3−xHx, which was shown to be characterized by two intense peaks at approximately 113 and 128 meV, respectively, assigned as vibrational motions of the hydride ions. The DFT calculations showed that these vibrational modes are essentially localized, i.e. show, unlike collective phonons, little dispersion.13 This stems from the large mass difference between the hydrogen and the other atoms in the lattice and means that the vibrational motions of the hydride ions can be treated as decoupled from both the vibrational dynamics of the perovskite lattice structure and the vibrational dynamics of other hydride ions. In other words, one can study such vibrations as if they were virtually isolated from the surrounding system. In addition to the main vibrational bands at 113 and 128 meV, the INS spectrum of BaTiO3−xHx is also characterized by an array of weaker bands at higher frequencies, tentatively assigned as higher-order transitions of the two main vibrational modes.13
Here, we report on a study of the local structure and vibrational dynamics of three metal hydride reduced BaTiO3 samples, which are characterized by varying concentrations of hydride ions and oxygen vacancies. The techniques used are powder X-ray diffraction (PXRD), thermal gravimetric analysis (TGA), nuclear magnetic resonance (NMR) spectroscopy, INS, and DFT calculations. Analyses of the intensity and momentum transfer (Q) of the INS spectral bands provide unique information to characterize the local coordination of hydride ions, such as vibrational frequencies and relative occupation of different hydride ion sites, distinguish between fundamental modes and higher-order transitions, and to derive the mean square displacements (MSD) of the hydride ions. The results provide experimental evidence to the fact that the hydride ion vibrational dynamics are localized in nature and only weakly affected by the dynamics of the surrounding perovskite framework.
2 Experimental details
2.1 Sample preparation
Two reduced BaTiO3 samples, which in the following are termed CA2 and CA3, were prepared by mixing powders of BaTiO3 (500 nm particle size, 99.9% purity, ABCR GmbH) and CaH2 (99.99%, Sigma Aldrich) in an Ar filled glove box in the molar proportion 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.25 (that is BaTiO3
2.25 (that is BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H = 1
H = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.5) and 1
4.5) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8 (that is BaTiO3
0.8 (that is BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H = 1
H = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6) for CA2 and CA3, respectively. Approximately 10 g of this mixture was pressed into pellets with a mass of about 1 g. The pellets were placed inside sealed stainless steel ampules and heated in an evacuated silica jacket to a temperature of 600 °C for two days. A third sample, termed NAB, was prepared by mixing powders of BaTiO3 and NaBH4 (98%, ABCR GmbH) in an Ar filled glove box in the molar proportion
1.6) for CA2 and CA3, respectively. Approximately 10 g of this mixture was pressed into pellets with a mass of about 1 g. The pellets were placed inside sealed stainless steel ampules and heated in an evacuated silica jacket to a temperature of 600 °C for two days. A third sample, termed NAB, was prepared by mixing powders of BaTiO3 and NaBH4 (98%, ABCR GmbH) in an Ar filled glove box in the molar proportion![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.45 (that is BaTiO3
0.45 (that is BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H = 1
H = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.8). Pellets of this mixture were heated to a temperature of 600 °C for two days. The dark-blue coloured products were washed 3–4 times with a mixture of 0.1 M NH4Cl and methanol (CA2), 0.1 M acetic acid (CA3), or 0.1 M hydrochloric acid (NAB) in order to remove excess metal hydride and the byproducts CaO (CA2 and CA3) and NaBO2 (NAB). Finally, CA2, CA3 and NAB were dried under dynamic vacuum at 120 °C for about one day. For the sample preparation of CA1, see ref. 4.
1.8). Pellets of this mixture were heated to a temperature of 600 °C for two days. The dark-blue coloured products were washed 3–4 times with a mixture of 0.1 M NH4Cl and methanol (CA2), 0.1 M acetic acid (CA3), or 0.1 M hydrochloric acid (NAB) in order to remove excess metal hydride and the byproducts CaO (CA2 and CA3) and NaBO2 (NAB). Finally, CA2, CA3 and NAB were dried under dynamic vacuum at 120 °C for about one day. For the sample preparation of CA1, see ref. 4.
2.2 Powder X-ray diffraction
PXRD patterns were collected at ambient temperature on a Panalytical X'Pert Alpha1 diffractometer operated with Cu Kα1 radiation and in θ–2θ diffraction geometry. The powder samples were mounted on a Si wafer zero-background holder and diffraction patterns were measured in a 2θ range of 10–90° with a step size of 0.013°. The Rietveld method as implemented in the FullProf program was used for structure and phase analysis.2.3 Thermal gravimetric analysis
TGA experiments were carried out using a TA instruments Discovery system. The samples, each weighing approximately 15 mg, were heated in a platinum crucible from room temperature to 900 °C with a heating rate of 5 °C min−1. A dry air gas flow of 20 ml min−1 was applied.2.4 Nuclear magnetic resonance spectroscopy
The 1H MAS NMR experiments were performed at a magnetic field of 9.4 T (400.12 MHz 1H Larmor frequency) and a MAS rate of 30.00 kHz on a Bruker Avance-III spectrometer equipped with a 2.5 mm MAS probehead. Acquisitions involved rotor-synchronized, double-adiabatic spin-echo sequence14,15 with a 90° excitation pulse of length 1.2 μs followed by two 50.0 μs tanh/tan short high-power adiabatic pulses (SHAPs)16,17 with 5 MHz frequency sweep. All pulses operated at a nutation frequency of 208 kHz. For each sample 4096 signal transients with 5 s relaxation delays were accumulated. Shifts were referenced with respect to tetramethylsilane (TMS) at 0 ppm.2.5 Inelastic neutron scattering
The INS experiments were performed on three instruments; on MERLIN18,19 and TOSCA20,21 at the ISIS Neutron and Muon Source (ISIS) at the Rutherford Appleton Laboratory, U.K., and on VISION22 at the Spallation Neutron Source (SNS) at the Oak Ridge National Laboratory, U.S. For the present work, the key difference between the spectrometers is that MERLIN enables both momentum (Q, Å−1) and energy (ω, meV) transfer to be measured independently, whereas TOSCA and VISION follow a fixed trajectory in (Q, ω) space.The experiment on MERLIN was performed on CA2 and CA3. Approximately 10 g of each sample was loaded into an aluminium sachet and the sachet into a thin-walled aluminium can. INS spectra were measured using three different incident energies of the neutrons: Ei = 200 meV (5 meV, 400 Hz), 400 meV (12 meV, 550 Hz) and 600 meV (16 meV, 600 Hz), where the numbers within the parentheses refer to the resolution in energy and to the chopper frequency. Measurements were taken at T = 10, 240, and 280 K for CA2, and at T = 10 K for CA3. The time-of-flight data were first converted into INS maps, S(Q, ω), using the software MANTID,23 and the maps were subsequently analyzed using both the software MSLICE24 and DAVE.25 The very same samples (CA2 and CA3), using the same sample cells, were also measured on TOSCA at T < 10 K. Additionally, 10 g of CA1, was also measured on TOSCA, with a flat sample cell, at T < 10 K.
The experiment on VISION was performed on 10 g of NAB, at T < 10 K. The sample was thinly distributed inside an aluminum package that was subsequently rolled into a 54 mm long annuli with a diameter of 29 mm. An aluminum can, which was vacuum sealed using aluminum foil, was used as a sample holder. The software DAVE was used for the analysis of S(Q, ω).25
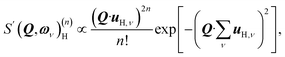 | (1) |
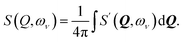 | (2) |
When the displacements uH,ν, associated with the local vibrational modes, are relatively close to each other, they can be approximated by
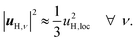 | (3) |
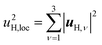 | (4) |
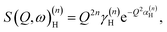 | (5) |
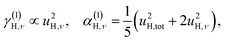 | (6a) |
| u2H,tot = u2H,loc + u2H,lattice, | (6b) |
| γ(2)H,ν ∝ u4H,ν, | (7a) |
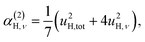 | (7b) |
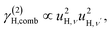 | (7c) |
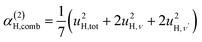 | (7d) |
By differentiation of eqn (5) one can further derive that the maximum of S(Q, ω)(n)H occurs when
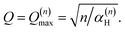 | (8) |
| α(1)H,ν ≈ α(2)H,ν ≈ α(2)H,comb ≃ u2H,loc/3, |
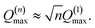 | (9) |
| u2H,loc = 2·|uH,⊥|2 + |uH,∥|2, | (10) |
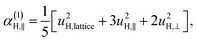 | (11a) |
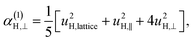 | (11b) |
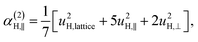 | (11c) |
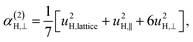 | (11d) |
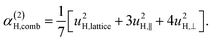 | (11e) |
3 Computational details
3.1 Density functional theory calculations
The DFT calculations were performed using the projector augmented wave (PAW) method31,32 as implemented in the VASP33,34 software together with the PBE35 exchange–correlation functional. A supercell containing 40 atoms constructed from a 2 × 2 × 2 stacking of primitive unit cells was used in most calculations. We denote this the defect cell. The introduction of a hydride ion in the defect cell implies a defect concentration of 12.5%. The same defect cell was used for the calculation of the combined defect of a hydride ion and an oxygen vacancy in various configurations. For the defect cell a Monkhorst–Pack k-point mesh of 6 × 6 × 6 was used together with a plane wave cut-off energy of 500 eV. The calculations were converged to energies within 10−7 eV for the electronic structure and to forces within 10−4 eV Å−1 for the ionic relaxations.3.2 Vibrational density of states
The vibrational frequencies and eigenmodes were obtained using the frozen phonon method in the harmonic approximation as implemented in Phonopy.36 Calculations of the force constants of the dynamical matrix were conducted in the defect cell equivalent to a supercell of 2 × 2 × 2 primitive BaTiO3 unit cells. The convergence was checked with respect to supercell size by augmenting the defect cell dimension with a factor 2 in each direction to a 2 × 2 × 2 defect cell of 320 atoms for the This explicitly includes the zone-boundary points in the calculation. The difference for the phonon spectrum between the primitive and augmented defect cell was negligible and for the combined defect of both a hydride ion and an oxygen vacancy the smaller cell was used.
This explicitly includes the zone-boundary points in the calculation. The difference for the phonon spectrum between the primitive and augmented defect cell was negligible and for the combined defect of both a hydride ion and an oxygen vacancy the smaller cell was used.
The projected vibrational density of states (PDOS) from a phonon calculation can be expressed as36
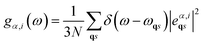 | (12) |
The MSD was calculated through
| 〈|uα,i(T)|2〉 = ∫fi(ω, T)gα,i(ω)dω, | (13) |
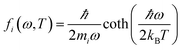 | (14) |
4 Results
4.1 Average-structural and thermogravimetric analysis
The average (long-range) structural and thermal properties of the four samples, CA1, CA2, CA3, and NAB were investigated with PXRD, TGA, and 1H MAS NMR. The results of the average structural and thermal characterisation of CA1, CA2 and NAB were reported and discussed elsewhere.4,13 The characterisation of CA3, together with that of CA2 and NAB, can be found in Fig. S1–S2 and Table S1 (PXRD), Fig. S3 (TGA), and Fig. S4 (1H MAS NMR) in the ESI† and a summary of the results for all the samples can be found in Table 1. On the basis of the average-structural analysis and TGA the composition of the metal hydride reduced BaTiO3 samples are reformulated as BaTiO3−xHy□x−y with x ≈ 0.7 and y ≈ 0.04 for NAB, with x ≈ 0.35 and y ≈ 0.08 for CA2, and with x ≈ 0.18 and y ≈ 0.12 for CA3 (cf.Table 1). The heterogeneous nature of CA2 and CA3 (as suggested from the PXRD pattern) may be due to a phase segregation into a O vacancy rich and H rich phase. However, at this point this remains unclear.| Sample ID | Synthesis conditions | Lattice parameter (Å) | x H from TG | x □ from TG | y H from NMR | Formula BaTiO3−xHy□x−y |
|---|---|---|---|---|---|---|
| a x H refers to a reaction BaTiO3H + 0.75xO2 → BaTiO3 + 0.5xH2O; x□ refers to a reaction BaTiO3H + 0.5xO2 → BaTiO3. | ||||||
| CA1 | BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CaH2 = 1 CaH2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.3 (BaTiO3 0.3 (BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H = 1 H = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.6), 700 °C, 3 days 0.6), 700 °C, 3 days |
4.0055(2) | 0.18 | 0.17 | 0.10 | x = 0.18 |
| y = 0.1 | ||||||
| [H] > [□] | ||||||
| CA3 | BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CaH2 = 1 CaH2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.8 (BaTiO3 0.8 (BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H = 1 H = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6), 600 °C, 2 days 1.6), 600 °C, 2 days |
I: 4.0075(1) 88(2)% | 0.19 | 0.18 | 0.12 | x = 0.18 |
| II: 4.0183(1) 12% | y = 0.12 | |||||
| [H] > [□] | ||||||
| CA2 | BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CaH2 = 1 CaH2 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.25 (BaTiO3 2.25 (BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H = 1 H = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.5), 600 °C, 2 days 4.5), 600 °C, 2 days |
I: 4.0119(1) 79(2)% | 0.37 | 0.35 | 0.08 | x = 0.35 |
| II: 4.0295(2) 21% | y = 0.08 | |||||
| [H] < [□] | ||||||
| NAB | BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NaBH4 = 1 NaBH4 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.45 (BaTiO3 0.45 (BaTiO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H = 1 H = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.8), 600 °C, 2 days 1.8), 600 °C, 2 days |
4.0044(1) | 0.75 | 0.70 | 0.04 | x = 0.7 |
| y = 0.04 | ||||||
| [H] ≪ [□] | ||||||
4.2 Inelastic neutron scattering
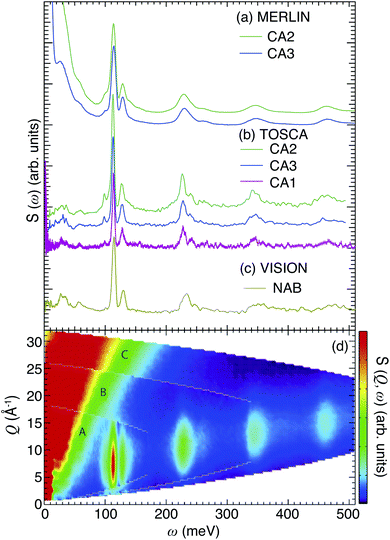
Above 90 meV all spectra are characterized by a series of contributions, where the most intense is located at around 110 meV, and the others are centered at approximately 230, 350 and 460 meV, respectively. In agreement with previous studies, these contributions relate to either fundamental Ti–H vibrational modes or higher-order transitions of these modes,10,13 whereas the bands at <90 meV are assigned to vibrational modes of the perovskite structure.13 This assignment is further supported by the fact that the INS spectrum and the computed vibrational density of states of BaTiO3 (Fig. S5–S7†) are essentially flat at >90 meV. More specifically, the region between 90 and 150 meV is characterized by two strong peaks at 100 and 130 meV, and a small side band at around 90 meV. These features are assigned to the localized vibrations of the hydrogen,10,13 whereas the bands at higher energies, >150 meV, are assigned to higher-order transitions of these modes. This assignment is in agreement with the fact that these higher-energy bands are located at approximately two, three, and four times the frequency of the fundamental bands between 90 and 130 meV as noted above, and is further supported by the relative intensities of the bands.
We also notice the lack of an O–H stretch band, which is generally manifested as a broad continuum from approximately 440 meV (≈3600 cm−1) down to 370 meV (≈3000 cm−1) or even lower energy and which confirms that the hydrogen species in the oxyhydride of BaTiO3 are situated on vacant O sites rather than bound to oxygens of the perovskite structure. This is also confirmed by our 1H NMR results (Fig. S4†), in which the negative shifts are an indication of Ti–H species. No positive shifts, which would indicate the presence of Ti–O–H protic species, are observed.37
Fig. 1(d) shows, as an example, S(Q, ω) of CA2, as obtained from the MERLIN experiment with three different energies of the incident neutrons, 200 meV (A), 400 meV (B) and 600 meV (C). Notice how the maximum intensity of the higher-energy bands generally occurs at larger Q values as the transition energy increases [Fig. 1(d)], exactly as one expects for higher-order transitions.28 This further supports the assignment of the higher-frequency INS modes to higher-order transitions of H vibrational fundamentals. For a more quantitative analysis of the INS spectra, we have performed a peak fit analysis and band assignment, which is described below.
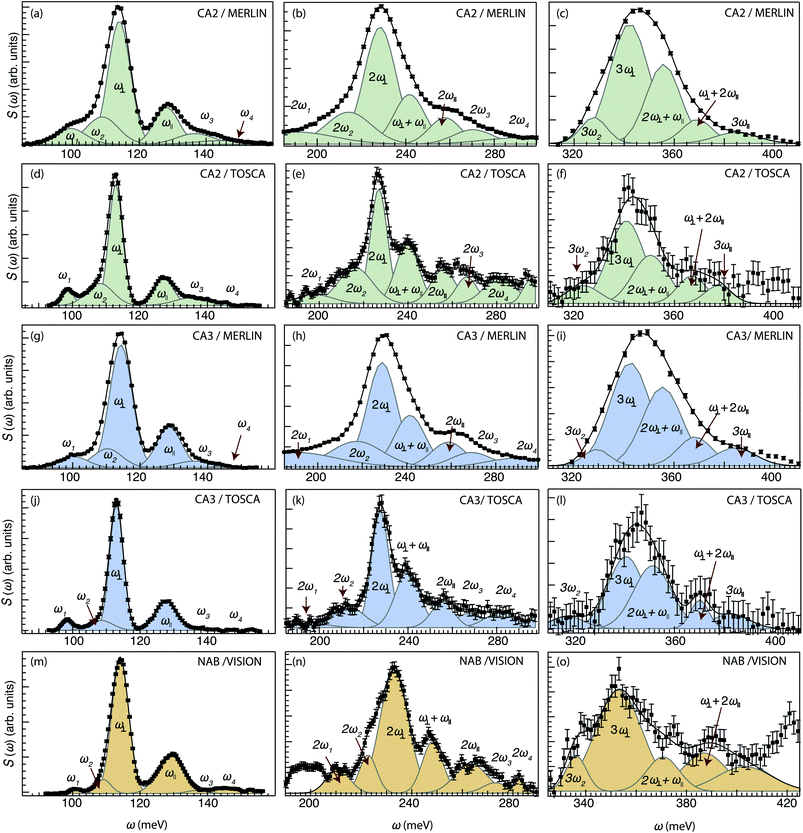
For CA2, we find that the low-frequency region (85–160 meV) can be divided into six Gaussian components [Fig. 2(a and d)]. The two strongest bands, at ω ≈ 114 and 128 meV, are assigned to the fundamental Ti–H vibrational modes ω⊥ and ω∥, respectively. Four weaker bands are located at ≈99 (ω1), 110 (ω2), 137 (ω3) and 145 (ω4) meV, respectively. The presence of several bands related to H motions manifests the coexistence of several different H sites in the material.
The bands in the intermediate frequency range (180–300 meV) can be adequately fit with seven Gaussians [Fig. 2(b and e)]. The three largest bands, at approximately 230, 240, and 255 meV, are assigned, based on their frequencies and relative intensities with respect to each other and the bands at lower frequencies, as 2ω∥, 2ω⊥ and ω∥ + ω⊥, i.e. to overtones and combinations of the (main) fundamental contributions ω∥ and ω⊥. In a similar manner, the remaining four bands are assigned as 2ω1, 2ω2, 2ω3 and 2ω4. Regarding possible combination modes related to ω1–ω4, we assume that they lie in the same frequency range as the overtones and combination of ω∥ and ω⊥. Because they are less intense with respect to these latter ones, it is not possible to observe them.
The bands in the higher-frequency range (300–410 meV) can be adequately fit to five Gaussians, which are assigned as third-order transitions, i.e. 3ω2, 3ω∥, 3ω⊥, 2ω∥ + ω⊥ and ω∥ + 2ω⊥ [Fig. 2(c and f)].
For the other two samples, CA3 and NAB [Fig. 2(g–l) and (m–o)], we find that the peak fit analyses of the INS spectra yield comparable results to that of CA2. This is an important result that points toward no major differences in the local coordination environment of the hydride ions between the three samples. For CA2, we also recorded INS MERLIN spectra at elevated temperatures, T = 240 and T = 280 K (Fig. S8†), which show no large spectral differences between the different temperatures. All the fit parameters are summarized in Table 2.
| TOSCA | MERLIN | VISION | |||||
|---|---|---|---|---|---|---|---|
| Sample | CA3 | CA2 | CA3 | CA2 | CA2 | CA2 | NAB |
| T (K) | 10 | 10 | 9 | 9 | 240 | 280 | 10 |
| ω 1 | 98.4 | 98.5 | 100 | 99 | 100 | 100 | 101 |
| ω 2 | 108.4 | 108.1 | 110 | 109 | 109 | 109 | 109 |
| ω ⊥ | 112.9 | 112.8 | 114 | 114 | 114 | 114 | 114 |
| ω ∥ | 127.7 | 127.1 | 129 | 128 | 127 | 127 | 129 |
| ω 3 | 137.7 | 135.7 | 136 | 137 | 136 | 136 | 137 |
| ω 4 | 147.0 | 145.4 | 144 | 144 | 142 | 143 | 147 |
| 2ω1 | 195.5 | 198.1 | 189 | 190 | 19 | 90 | 211 |
| 2ω2 | 213.2 | 215.4 | 218 | 214 | 214 | 214 | 223 |
| 2ω⊥ | 227.5 | 226.9 | 229 | 228 | 228 | 228 | 233 |
| ω ⊥ + ω⊥ | 239.8 | 239.6 | 241 | 242 | 242 | 242 | 248 |
| 2ω∥ | 255.5 | 255.9 | 259 | 258 | 258 | 257 | 263 |
| 2ω3 | 267.4 | 266.4 | 269 | 270 | 271 | 271 | 273 |
| 2ω4 | 282.3 | 281.4 | 289 | 292 | 294 | 296 | 283 |
| 3ω2 | 317.6 | 323.8 | 329 | 328 | 336 | ||
| 3ω⊥ | 340.8 | 340.9 | 343 | 342 | 353 | ||
| 2ω⊥ + ω⊥ | 351.4 | 350.5 | 355 | 356 | 371 | ||
| ω ⊥ + 2ω⊥ | 370.0 | 366.9 | 368 | 369 | 387 | ||
| 3ω∥ | 382.2 | 377.3 | 384 | 385 | 403 | ||
Note that the peak fit analysis for a specific sample as recorded on MERLIN and TOSCA both give essentially the same fit parameters, suggesting that the peak fit analysis is robust.
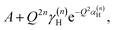 with n = 1 and where the constant A has been added in order to account for the possibility of a background in the spectra. For the bands assigned as second order transitions, in the medium-energy range, the S(Q) curves were fitted using the same equation but with n = 2. Fig. 3 shows S(Q) for (a) ω∥ and 2ω∥, and (b) ω⊥ and 2ω⊥ for CA2. As expected, the maximum of the INS signal occurs at larger Q values as the order of the transition increases.
with n = 1 and where the constant A has been added in order to account for the possibility of a background in the spectra. For the bands assigned as second order transitions, in the medium-energy range, the S(Q) curves were fitted using the same equation but with n = 2. Fig. 3 shows S(Q) for (a) ω∥ and 2ω∥, and (b) ω⊥ and 2ω⊥ for CA2. As expected, the maximum of the INS signal occurs at larger Q values as the order of the transition increases.
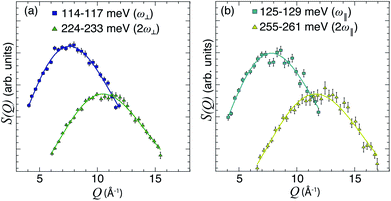 | ||
| Fig. 3 (a and b) S(Q) curves for CA2 at T = 9 K, as obtained after integration of S(Q, ω) over the indicated ω ranges (see legend), together with fits according to eqn (5) with n = 1 and 2, respectively. | ||
The fit parameters (γH and αH) are shown in Table 3. We observe that the γH and αH values are overall larger for CA2 compared to CA3. Since αH is proportional to u2H,int, the hydride ions thus move with somewhat larger vibrational amplitude in CA2. As for the temperature dependence (investigated for CA2 only), γH decreases as a function of increasing temperature, whereas for αH we observe no apparent temperature dependence.
| Sample | CA3 | CA2 | CA2 | CA2 |
|---|---|---|---|---|
| T (K) | 9 | 9 | 240 | 280 |
| (a) γ H (arb units) | ||||
| ω 1 | 1.46(7) | 1.9(1) | 1.7(1) | 1.5(1) |
| ω 2 | 2.27(9) | 3.6(1) | 4.0(2) | 4.1(2) |
| ω ⊥ | 11.0(2) | 11.5(2) | 10.5(3) | 9.94(30) |
| ω ∥ | 3.7(1) | 3.9(2) | 3.3(2) | 3.3(1) |
| ω 3 | 1.36(5) | 1.6(1) | 1.8(1) | 1.7(1) |
| ω 4 | 0.91(6) | 1.00(5) | 1.14(6) | 1.18(5) |
| 2ω1 | 0.0086(3) | 0.0090(5) | 0.0091(4) | 0.0091(3) |
| 2ω2 | 0.0144(4) | 0.0200(6) | 0.0228(5) | 0.0222(5) |
| 2ω⊥ | 0.0477(7) | 0.052(1) | 0.0467(7) | 0.0454(6) |
| ω ⊥ + ω∥ | 0.0212(5) | 0.0243(8) | 0.0249(6) | 0.0243(6) |
| 2ω∥ | 0.0130(3) | 0.0142(5) | 0.0145(3) | 0.0147(3) |
| 2ω3 | 0.00858(2) | 0.0100(4) | 0.0103(3) | 0.0098(3) |
| 2ω4 | 0.0064(2) | 0.068(4) | 0.0077(2) | 0.0078(2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| (b) αH (10−2 Å2) | ||||
| ω 1 | 1.40(2) | 1.58(2) | 1.44(3) | 1.64(2) |
| ω 2 | 1.54(2) | 1.75(2) | 1.73(3) | 1.70(2) |
| ω ⊥ | 1.78(1) | 1.74(1) | 1.82(1) | 1.86(1) |
| ω ∥ | 1.59(1) | 1.64(1) | 1.59(2) | 1.56(2) |
| ω 3 | 1.19(1) | 1.31(2) | 1.30(2) | 1.29(1) |
| ω 4 | 0.99(2) | 1.09(1) | 1.12(2) | 1.10(1) |
| 2ω1 | 1.73(2) | 1.76(2) | 1.71(2) | 1.70(1) |
| 2ω2 | 1.75(1) | 1.83(2) | 1.83(1) | 1.85(1) |
| 2ω⊥ | 1.79(1) | 1.82(1) | 1.82(1) | 1.83(1) |
| ω ⊥ + ω∥ | 1.60(1) | 1.66(1) | 1.67(1) | 1.67(1) |
| 2ω∥ | 1.44(1) | 1.48(1) | 1.49(1) | 1.49(1) |
| 2ω3 | 1.31(1) | 1.38(1) | 1.38(1) | 1.36(1) |
| 2ω4 | 1.23(1) | 1.28(1) | 1.26(1) | 1.28(1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| (c) MSD (10−2 Å2) | ||||
| u 2H,⊥ | 1.72(6) | 1.8(2) | 1.82(2) | 1.87(7) |
| u 2H,∥ | 1.14(6) | 1.3(2) | 1.25(2) | 1.23(7) |
| u 2H,lattice | 1.0(3) | 0.4(9) | 0.61(1) | 0.5(4) |
| u 2H,loc | 4.58(13) | 4.9(4) | 4.89(4) | 5.0(2) |
We also consider the effect of the order of the transition (n) on the peak fitted parameters. As for the γH values, these decrease as a function of increasing n, which reflects the fact that higher-order transitions occur less likely than fundamental transitions. We also observe that γ(n)H,⊥ > γ(n)H,∥, which reflects the fact that there are two perpendicular components and one parallel component of the hydride ion motion (Fig. 4). As for the αH values, these are virtually unaffected by the order of the transition, which is as expected for the overtone progression of an almost isotropic oscillator.
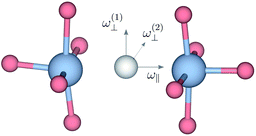 | ||
| Fig. 4 Sketch indicating the direction of the ω⊥ and ω∥ Ti–H vibrational motions in metal hydride reduced BaTiO3. | ||
By using the αH values from Table 3 as input in expressions for the αH coefficients [eqn (11)] we have derived the corresponding MSD of the hydride ions, u2H,⊥, u2H,∥, u2H,loc = 2·u2H,⊥ + u2H,∥ and u2H,lattice (Table 3). In agreement with the αH values, the hydride ions in the CA2 sample are manifested by larger local MSDs than the ones for CA3. Additionally, we remark that u2H,loc > u2H,lattice, as one would expect for localized vibrational modes.
4.3 Density functional theory calculations
DFT calculations were used to compute the hydride ion vibrational frequencies and MSD for three different configurations, containing a hydride ion and an oxygen vacancy as a first, second and third nearest neighbour, respectively. These configurations are denoted as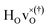 with † = 1, 2, 3. All configurations are neutral with three electrons in the conduction band. Fig. 5 illustrates a
with † = 1, 2, 3. All configurations are neutral with three electrons in the conduction band. Fig. 5 illustrates a 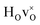 supercell where the numbers in the figure indicate the possible oxygen vacancy positions. With the oxygen vacancy as a second nearest neighbour there are two crystallographically non-equivalent positions (denoted as 2 and 2′). The configuration we consider is where the oxygen vacancy is located in the direction perpendicular to the Ti–H bond, i.e. † = 2. The respective hydride ion frequencies, relative ground state energies ΔE, and the multiplicity g for the three different configurations are presented in Table 4.
supercell where the numbers in the figure indicate the possible oxygen vacancy positions. With the oxygen vacancy as a second nearest neighbour there are two crystallographically non-equivalent positions (denoted as 2 and 2′). The configuration we consider is where the oxygen vacancy is located in the direction perpendicular to the Ti–H bond, i.e. † = 2. The respective hydride ion frequencies, relative ground state energies ΔE, and the multiplicity g for the three different configurations are presented in Table 4.
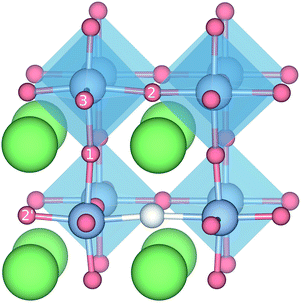 | ||
| Fig. 5 Illustration of the different configurations containing both a HO and a vO defect. The different positions for the oxygen vacancy are indicated by the numbers 1, 2, and 3. | ||
The energetically most favourable position is the one in which the oxygen is the second nearest neighbour, 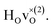 The energy of the first nearest neighbour configuration
The energy of the first nearest neighbour configuration 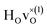 is about 0.1 eV higher. This is not surprising since a repulsion of the two positively charged defects is to be expected. Also with the oxygen vacancy as third nearest neighbour the relative ground state energy is about 0.1 eV higher. The second nearest neighbour position 2′ and the other possible configurations containing the combination of a vacancy and a hydride ion in this supercell size exhibit all relative ground state energies >0.15 eV and are not discussed further.
is about 0.1 eV higher. This is not surprising since a repulsion of the two positively charged defects is to be expected. Also with the oxygen vacancy as third nearest neighbour the relative ground state energy is about 0.1 eV higher. The second nearest neighbour position 2′ and the other possible configurations containing the combination of a vacancy and a hydride ion in this supercell size exhibit all relative ground state energies >0.15 eV and are not discussed further.
With respect to the probability for the occupancy of a particular configuration †, this can be expressed as
| P(†) ∝ g(†)exp[−E(†)/kBT], | (15) |
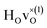 and
and 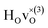 are present.
are present.
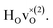 The different colours represent different Cartesian directions and the total DOS for the hydride ion, which is the sum over the three Cartesian directions, is marked with grey color. The two intense peaks at >90 meV are assigned to hydrogen motions in directions parallel (ω∥) and perpendicular (ω⊥) to the Ti–H bond direction, whereas there are only small contributions from hydrogen motions at lower energies of the spectrum. Specifically, these low-energy hydrogen motions are associated with the participation of hydrogen in the collective lattice modes of the perovskite framework. The intensity of these modes is very weak and has been amplified by a factor of 100 in Fig. 6 for improved visibility.
The different colours represent different Cartesian directions and the total DOS for the hydride ion, which is the sum over the three Cartesian directions, is marked with grey color. The two intense peaks at >90 meV are assigned to hydrogen motions in directions parallel (ω∥) and perpendicular (ω⊥) to the Ti–H bond direction, whereas there are only small contributions from hydrogen motions at lower energies of the spectrum. Specifically, these low-energy hydrogen motions are associated with the participation of hydrogen in the collective lattice modes of the perovskite framework. The intensity of these modes is very weak and has been amplified by a factor of 100 in Fig. 6 for improved visibility.
 | ||
Fig. 6 PDOS for the hydride ion in the 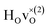 configuration along the 3 Cartesian directions (colour) together with the total DOS (gray). The intensity for frequencies below 90 meV are amplified by a factor 100. The weight factor f(ω, T) [see eqn (14)] is also shown for two different temperatures. configuration along the 3 Cartesian directions (colour) together with the total DOS (gray). The intensity for frequencies below 90 meV are amplified by a factor 100. The weight factor f(ω, T) [see eqn (14)] is also shown for two different temperatures. | ||
Table 4 shows the vibrational frequencies for the localized hydrogen modes in the three different defect configurations, containing a hydride ion and an oxygen vacancy as first, second and third nearest neighbour, respectively. Included in the table are also the hydride vibrational frequencies in a structure without oxygen vacancies, for the case when the extra electron is delocalized over all Ti4+ ions (bandstate) and where the excess electron is localized on a titanium atom nearest neighbour to the hydride ion (polaron state), which have been computed previously.13
We remark that the results presented here are computed using a 2 × 2 × 2 supercell, corresponding to the chemical composition BaTiO2.75H0.125□0.125. To test for possible concentration dependencies of the (calculated) vibrational frequencies, we have also computed the frequencies in a 3 × 3 × 3 supercell, corresponding to BaTiO2.926H0.037□0.037, for both cases of a structure without oxygen vacancies (bandstate) and a structure with second nearest neighbouring vacancies. The corresponding results are summarized in Fig. S6.† The frequencies for 1, 2 and 3 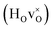 -defects, in a 3 × 3 × 3 supercell have also been computed, corresponding to the compositions BaTiO2.926H0.037□0.037, BaTiO2.926H0.074□0.074, and BaTiO2.926H0.111□0.111, respectively. The oxygen vacancy is in all cases located at a second nearest neighboring oxygen site, the most stable configuration. The corresponding results are summarized in Fig. S7.† In all cases we find very sharp vibrational peaks which clearly shows the localized nature of the hydride ion vibrational motion. The very sharp nature of the peaks is a direct evidence for the localized nature. The local surrounding for a hydride ion in the different numerically investigated cases differ slightly which results in small shifts of the corresponding frequencies. In the INS measurement a weighted average is then obtained and it shows up as a broadening of the measured peak.
-defects, in a 3 × 3 × 3 supercell have also been computed, corresponding to the compositions BaTiO2.926H0.037□0.037, BaTiO2.926H0.074□0.074, and BaTiO2.926H0.111□0.111, respectively. The oxygen vacancy is in all cases located at a second nearest neighboring oxygen site, the most stable configuration. The corresponding results are summarized in Fig. S7.† In all cases we find very sharp vibrational peaks which clearly shows the localized nature of the hydride ion vibrational motion. The very sharp nature of the peaks is a direct evidence for the localized nature. The local surrounding for a hydride ion in the different numerically investigated cases differ slightly which results in small shifts of the corresponding frequencies. In the INS measurement a weighted average is then obtained and it shows up as a broadening of the measured peak.
From the results in Table 4 we can observe that the hydrogen vibrational frequencies for the 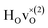 configuration are very similar to both the
configuration are very similar to both the 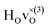 configuration and to the bandstate configuration. All configurations, except the bandstate configuration, break the degeneracy of the perpendicular mode, but only very weakly. The exception is the
configuration and to the bandstate configuration. All configurations, except the bandstate configuration, break the degeneracy of the perpendicular mode, but only very weakly. The exception is the 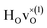 configuration, where there is a significant downshift of about 12 meV of one of the perpendicular modes, the one in the plane containing the vacancy. Based on this we expect the vibrational spectrum to be similar regardless of the vacancy concentration, and if the
configuration, where there is a significant downshift of about 12 meV of one of the perpendicular modes, the one in the plane containing the vacancy. Based on this we expect the vibrational spectrum to be similar regardless of the vacancy concentration, and if the 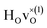 configuration is present, a peak at lower frequencies should be present. Furthermore, we observe that the formation of a polaron shifts the frequency of the parallel mode, by about 15 meV, while the perpendicular modes remain essentially unchanged. This feature may thus be used as a means to determine the respective contribution of the bandstate and polaron state configurations in the material, in the case both states co-exist.
configuration is present, a peak at lower frequencies should be present. Furthermore, we observe that the formation of a polaron shifts the frequency of the parallel mode, by about 15 meV, while the perpendicular modes remain essentially unchanged. This feature may thus be used as a means to determine the respective contribution of the bandstate and polaron state configurations in the material, in the case both states co-exist.
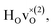 divided into local and lattice contributions, at T = 0 and 300 K
divided into local and lattice contributions, at T = 0 and 300 K
Included in Fig. 6 is also the weight factor f(ω, T) [see eqn (14)] at two different temperatures, T = 0 K and 300 K, together with the vibrational DOS. From the weight factor we observe that low frequency vibrations give a larger contribution to the MSD compared with high frequency vibrations and their contribution also increases more rapidly when the temperature is increased. For example, when the temperature is increased from T = 0 K to 300 K, a mode with frequency ℏω = 22 meV gets an increased weight by a factor of 2.5, while a mode with frequency ℏω = 120 meV only gets a factor of 1.02 increase. This implies that u2ext has a significant temperature dependence compared to u2int (cf.Table 5). At low frequencies, ℏω < 30 meV, the mode ω(1)⊥ has the largest contribution to the vibrational DOS and hence u2ext(1)⊥ has the largest temperature dependence (cf.Table 5).
5 Discussion
In agreement with our previous work on metal hydride reduced BaTiO3 materials,13,37 the spectra show no indications of O–H groups or other interstitial hydrogen species present in any of the materials. This establishes that the hydrogen species are present as hydride ions located on vacant oxygen sites of the perovskite structure, and not as protonic species, virtually independent of the level of hydride ion and oxygen vacancy concentrations as investigated here. In this context, we have followed the approach of Liu et al.7,8 and investigated the possibility, in BaTiO3, of what has been referred to as an indirect interstitial mechanism, in which the hydride ion is transformed to a proton, by donating two extra electrons to Ti ions, and then diffuses by interstitial diffusion. We found that in BaTiO3 the required energy for this process is 2.4 eV, which, in agreement with previous results,7,8 is considerably larger than the typical activation energy for hydride-ion conduction in this system (<0.5 eV).4,8 Thus, we have no reason to expect that the indirect interstitial mechanism takes place in BaTiO3, which is in full accordance with the absence of any signature of O–H species in the vibrational spectra.The comparison of the experimental results with the results from DFT calculations show that the vibrational spectra can be largely divided into three different regions; a low-energy (<90 meV) region related to lattice vibrations, a medium-energy (90–150 meV) region related to local hydride ion vibrations, and a higher energy (>150 meV) region related to higher-order transitions. Specifically, the INS spectra for all three samples are characterized by two intense bands at approximately 114 (ω⊥) and 128 (ω∥) meV, which are assigned to fundamental Ti–H vibrational modes perpendicular and parallel and to the Ti–H–Ti bond direction, respectively. Additionally, the INS spectra contain four weaker bands, at approximately 99 (ω1), 110 (ω2), 137 (ω3) and 145 (ω4) meV, as a result of small differences in the local coordination of the hydride ions in the materials.
When comparing these experimental results with the DFT calculations, one should note that the use of the PBE functional generally underestimates the vibrational frequencies by about 7 meV for ω⊥ and 2 meV for ω∥, compared with the more accurate HSE functional.13 With this discrepancy taken into account, the calculated frequencies of around ω⊥ = 104–106 meV and ω∥ = 124–127 meV for both the 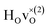 and
and 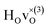 configuration, as well as the bandstate configuration
configuration, as well as the bandstate configuration 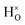 (band), are in excellent agreement with the experimental values of ω⊥ = 114 meV and ω∥ = 128 meV. The exception is the
(band), are in excellent agreement with the experimental values of ω⊥ = 114 meV and ω∥ = 128 meV. The exception is the 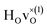 configuration, which is characterized by a hydride ion and an oxygen vacancy as first nearest neighbour and for which the ω(2)⊥ mode is downward-shifted to 93 meV in the calculations. Considering an underestimation of 7 meV of the frequency of this band, it matches almost perfectly with the frequency of the 99 (ω1) meV band in the experimental spectrum. From this we infer that the positioning of the oxygen vacancy with respect to the hydride ion has only a small effect on the vibrational spectra, except when the oxygen vacancy is first nearest neighbour to the hydride ion. Furthermore, we note that the highest-frequency band at approximately 145 (ω4) meV is in very good agreement with the frequency of the ω∥ mode for the polaron state. It follows that, even though the bandstate configuration is the dominating configuration of the hydride ions, our results tentatively indicate the presence of a non-negligible amount of electron polarons, at least in the sample CA2.
configuration, which is characterized by a hydride ion and an oxygen vacancy as first nearest neighbour and for which the ω(2)⊥ mode is downward-shifted to 93 meV in the calculations. Considering an underestimation of 7 meV of the frequency of this band, it matches almost perfectly with the frequency of the 99 (ω1) meV band in the experimental spectrum. From this we infer that the positioning of the oxygen vacancy with respect to the hydride ion has only a small effect on the vibrational spectra, except when the oxygen vacancy is first nearest neighbour to the hydride ion. Furthermore, we note that the highest-frequency band at approximately 145 (ω4) meV is in very good agreement with the frequency of the ω∥ mode for the polaron state. It follows that, even though the bandstate configuration is the dominating configuration of the hydride ions, our results tentatively indicate the presence of a non-negligible amount of electron polarons, at least in the sample CA2.
The new insight into the local structure and vibrational dynamics of the metal hydride reduced BaTiO3 samples, containing the simultaneous presence of hydride ions and oxygen vacancies, can be linked to the nature of diffusional dynamics of the hydride ions. In our previous work, we investigated the nature of diffusional hydride ion dynamics in CA1, CA2, and NAB, by QENS techniques. Analyses of QENS spectra measured at low (T = 225 and 250 K) and high (T = 400–700 K) temperature show that the dynamics can be adequately described by established models of jump diffusion. At low temperature, T ≤ 250 K, all of the models feature a characteristic jump distance of about 2.8 Å, thus of the order of the distance between neighboring oxygen atoms or oxygen vacancies of the perovskite structure and a mean residence time between successive jumps of the order of 0.1 ns. At higher temperatures, >400 K, the jump distance increases to about 4 Å, thus of the order of the distance between next-nearest neighboring oxygen atoms or oxygen vacancies, with a mean residence time of the order of picoseconds. Our present results confirm the existence of these specific local structural configurations and hence support these previous findings on the mechanism of hydride ion transport in perovskite type oxyhydrides based on BaTiO3.
Further insight into the nature of the hydride ion sites comes from the analysis of the MSD of the hydride ions. Crucially, the combined analyses of INS and DFT data show that hydrogen vibrational motions are very localized in nature and only very weakly affected by the dynamics of the surrounding perovskite structure.
6 Conclusions
We investigated the local coordination environment of hydride ions in three metal hydride reduced BaTiO3 samples characterized by the simultaneous presence of hydride ions and oxygen vacancies, using a combination of powder X-ray diffraction, thermal gravimetric analysis, nuclear magnetic resonance, inelastic neutron scattering, and density functional theory calculations. We show that the hydride ions are located on oxygen positions of the perovskite structure and that the hydride ion vibrational dynamics are characterized by two main bands, at 114 meV (ω⊥) and 128 (ω∥) meV, respectively, assigned as Ti–H vibrational modes perpendicular and parallel to the Ti–H–Ti bond direction, and four additional, weaker, bands near the ω⊥ and ω∥ bands, associated with variations of the local coordination environment of the hydride ions in the materials.Crucially, the combined analyses of INS and DFT data confirm the presence of both nearest neighbour and next-nearest neighbouring oxygen vacancies to the hydride ions. This supports previous findings from quasielastic neutron scattering experiments, that the hydride ion transport is governed by jump diffusion dynamics between neighbouring and next-nearest neighbouring hydride ion–oxygen vacancy configurations. Analysis of the MSD of the hydride ions, as determined both experimentally and theoretically, confirms that the hydrogen vibrational motions are very localized in nature and only very weakly affected by the dynamics of the surrounding perovskite structure.
Author contributions
C. E.-Ö., L. M. and M. K. performed and interpreted the INS experiments, assisted by S. F. P. and N. H. J. The DFT simulations were performed and interpreted by E. J. G., under guidance of G. W. The NMR spectroscopy experiments were performed and interpreted by A. J., under guidance of A. J. P. The samples were synthesized by R. N., under guidance of U. H. The study was designed by M. K., together with U. H. and G. W. All authors provided critical comments on the work and to the writing of the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the Swedish Foundation for Strategic Research (grant no. ICA10-0001), the Swedish Research Council (grant no. 2014-3980 and 2016-03441) and the Swedish Energy Agency (grant no. 36645-1 and no. 45410-1). A portion of this research used resources at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. The STFC is thanked for access to neutron beam facilities.References
- Y. Kobayashi, O. J. Hernandez, T. Sakaguchi, T. Yajima, T. Roisnel, Y. Tsujimoto, M. Morita, Y. Noda, Y. Mogami, A. Kitada, M. Ohkura, S. Hosokawa, Z. Li, K. Hayashi, Y. Kusano, J. eun Kim, N. Tsuji, A. Fujiwara, Y. Matsushita, K. Yoshimura, K. Takegoshi, M. Inoue, M. Takano and H. Kageyama, Nat. Mater., 2012, 11, 507–511 CrossRef CAS PubMed
.
- T. Sakaguchi, Y. Kobayashi, T. Yajima, M. Ohkura, C. Tassel, F. Takeiri, S. Mitsuoka, H. Ohkubo, T. Yamamoto, J. Kim, N. Tsuji, A. Fujihara, Y. Matsushita, J. Hester, M. Avdeev, K. Ohoyama and H. Kageyama, Inorg. Chem., 2012, 51, 11371–11376 CrossRef CAS PubMed
.
- T. Yamamoto, R. Yoshii, G. Bouilly, Y. Kobayashi, K. Fujita, Y. Kususe, Y. Matsushita, K. Tanaka and H. Kageyama, Inorg. Chem., 2015, 54, 1501–1507 CrossRef CAS PubMed
.
- C. Eklöf-Österberg, R. Nedumkandathil, U. Häussermann, A. Jaworski, A. J. Pell, M. Tyagi, N. Jalarvo, B. Frick, A. Faraone and M. Karlsson, J. Phys. Chem. C, 2019, 123, 2019–2030 CrossRef
.
- Y. Tang, Y. Kobayashi, K. Shitara, A. Konishi, A. Kuwabara, T. Nakashima, C. Tassel, T. Yamamoto and H. Kageyama, Chem. Mater., 2017, 29, 8187–8194 CrossRef CAS
.
- F. Takeiri, K. Aidzu, T. Yajima, T. Matsui, T. Yamamoto, Y. Kobayashi, J. Hester and H. Kageyama, Inorg. Chem., 2017, 56, 13035–13040 CrossRef CAS PubMed
.
- X. Liu, T. S. Bjørheim, L. Vines, Ø. S. Fjellvåg, C. Granerød, Ø. Prytz, T. Yamamoto, H. Kageyama, T. Norby and R. Haugsrud, J. Am. Chem. Soc., 2019, 141, 4653–4659 CrossRef CAS PubMed
.
- X. Liu, T. Bjørheim and R. Haugsrud, J. Mater. Chem. A, 2017, 5, 1050–1056 RSC
.
- J. Zhang, G. Gou and B. Pan, J. Phys. Chem. C, 2014, 118, 17254–17259 CrossRef CAS
.
- Y. Iwazaki, T. Suzuki and S. Tsuneyuki, J. Appl. Phys., 2010, 108, 083705 CrossRef
.
- T. Yajima, A. Kitada, Y. Kobayashi, T. Sakaguchi, G. Bouilly, S. Kasahara, T. Terashima, M. Takano and H. Kageyama, J. Am. Chem. Soc., 2012, 134, 8782–8785 CrossRef CAS PubMed
.
- G. Bouilly, T. Yajima, T. Terashima, W. Yoshimune, K. Nakano, C. Tassel, Y. Kususe, K. Fujita, K. Tanaka, T. Yamamoto, Y. Kobayashi and H. Kageyama, Chem. Mater., 2015, 27, 6354–6359 CrossRef CAS
.
- E. Jedvik Granhed, A. Lindman, C. Eklöf-Österberg, M. Karlsson, S. F. Parker and G. Wahnström, J. Mater. Chem. A, 2019, 7, 16211–16221 RSC
.
- A. J. Pell and G. Pintacuda, Prog. Nucl. Magn. Reson. Spectrosc., 2015, 84–85, 33–72 CrossRef CAS PubMed
.
- A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271 CrossRef CAS PubMed
.
- T.-L. Hwang, P. Van Zijl and M. Garwood, J. Magn. Reson., 1998, 133, 200–203 CrossRef CAS PubMed
.
- G. Kervern, G. Pintacuda and L. Emsley, Chem. Phys. Lett., 2007, 435, 157–162 CrossRef CAS
.
- ISIS – Merlin, http://www.isis.stfc.ac.uk/instruments/merlin.
- R. Bewley, R. Eccleston, K. McEwen, S. Hayden, M. Dove, S. M. Bennington, J. Treadgold and R. Coleman, Phys. B, 2006, 385–386, 1029–1031 CrossRef CAS
.
- S. F. Parker, F. Fernandez-Alonso, A. J. Ramirez-Cuesta, J. Tomkinson, S. Rudic, R. S. Pinna, G. Gorini and J. Fernández Castañon, J. Phys.: Conf. Ser., 2014, 554, 012003 CrossRef
.
- S. F. Parker, C. J. Carlile, T. Pike, J. Tomkinson, R. J. Newport, C. Andreani, F. P. Ricci, F. Sachetti and M. Zoppi, Phys. B, 1998, 241–243, 154–156 Search PubMed
.
- web-page: https://neutrons.ornl.gov/vision.
- O. Arnold,
et al.
, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS
.
- R. Coldea, ISIS, Rutherford Appleton Laboratory, Mslice, http://mslice.isis.rl.ac.uk/MainPage/, 2004.
- R. Azuah, L. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. Brown, J. Copley and R. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358 CrossRef CAS PubMed
.
- V. F. Sears, Neutron News, 1992, 3, 26–37 CrossRef
.
-
P. C. H. Mitchell, S. F. Parker, A. Ramirez-Cuesta, and J. Tomkinson, Vibrational Spectroscopy with Neutrons, Word Scientific, Singapore, 2005 Search PubMed
.
- L. Mazzei, A. Perrichon, A. Mancini, G. Wahnström, L. Malavasi, S. F. Parker, L. Börjesson and M. Karlsson, J. Mater. Chem. A, 2019, 7, 7360–7372 RSC
.
- J. Tomkinson, S. F. Parker and D. Lennon, J. Chem. Phys., 2010, 133, 034508 CrossRef PubMed
.
- S. F. Parker, S. M. Bennington, A. J. Ramirez-Cuesta, G. Auffermann, W. Bronger, H. Herman, K. P. J. Williams and T. Smith, J. Am. Chem. Soc., 2003, 125, 11656–11661 CrossRef CAS PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS
.
- R. Nedumkandathil, A. Jaworski, J. Grins, D. Bernin, M. Karlsson, C. Eklöf-Österberg, A. Neagu, C.-W. Tai, A. Pell and U. Häussermann, ACS Omega, 2018, 3, 11426–11438 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ta11912d |
| This journal is © The Royal Society of Chemistry 2020 |