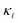Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combined treatment of phonon scattering by electrons and point defects explains the thermal conductivity reduction in highly-doped Si
Bonny
Dongre
 *a,
Jesús
Carrete
*a,
Jesús
Carrete
 a,
Shihao
Wen
a,
Shihao
Wen
 b,
Jinlong
Ma
b,
Jinlong
Ma
 b,
Wu
Li
b,
Natalio
Mingo
b,
Wu
Li
b,
Natalio
Mingo
 c and
Georg K. H.
Madsen
c and
Georg K. H.
Madsen
 a
a
aInstitute of Materials Chemistry, TU Wien, A-1060 Vienna, Austria. E-mail: bonny.dongre@tuwien.ac.at; Tel: +43 1 58801165307
bInstitute for Advanced Study, Shenzhen University, Shenzhen 518060, China
cLITEN, CEA-Grenoble, 17 rue des Martyrs, 38054 Grenoble Cedex 9, France
First published on 6th December 2019
Abstract
The mechanisms causing the reduction in lattice thermal conductivity in highly P- and B-doped Si are looked into in detail. Scattering rates of phonons by point defects, as well as by electrons, are calculated from first principles. Lattice thermal conductivities are calculated considering these scattering mechanisms both individually and together. It is found that at low carrier concentrations and temperatures phonon scattering by electrons is dominant and can reproduce the experimental thermal conductivity reduction. However, at higher doping concentrations the scattering rates of phonons by point defects dominate the ones by electrons except for the lowest phonon frequencies. Consequently, phonon scattering by point defects contributes substantially to the thermal conductivity reduction in Si at defect concentrations above 1019 cm−3 even at room temperature. Only when, phonon scattering by both point defects and electrons are taken into account, excellent agreement is obtained with the experimental values at all temperatures.
1 Introduction
With the characteristic lengths of nanoscale devices approaching the mean free paths of the heat-carrying phonons,1 the need for a detailed and predictive understanding of thermal conductivity is more stark today than ever. In the last few decades, the usage of highly doped (1019–1021 cm−3) semiconductor materials in electronics and energy devices has become prevalent, serving the purpose of achieving enhanced functional properties.2 For these systems, predictive models are especially important because the increased phonon scattering due to point defects and additional charge carriers can result in a substantial drop in thermal conductivity.Owing to its high abundance, non-toxicity, and ease of dopability, Si continues to be the linchpin of the semiconductor industry. Highly P- and B-doped Si are routinely used as source/drain materials in transistors to avoid unwanted Schottky junctions.3 Furthermore, highly-doped Si has also found usage in photovoltaics,4 microelectromechanical systems,5 and microelectronics,6,7 to cite a few applications. In thermoelectric applications the advantage of using highly-doped Si is twofold:8–10 the thermoelectric figure of merit is, on the one hand, proportional to the electronic power factor, which increases with increasing carrier concentration, and, on the other, inversely proportional to the thermal conductivity. A recent advancement in the synthesis of such highly-doped systems was achieved by Rohani et al.,11 who were able to dope Si nanoparticles with boron beyond its equilibrium solubility limit.
The lattice contribution to the thermal conductivity 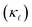 dominates in Si. Phonon scattering by point defects (PDPS) and by electrons (EPS), were identified as the two main contributors to the
dominates in Si. Phonon scattering by point defects (PDPS) and by electrons (EPS), were identified as the two main contributors to the 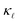 reduction in highly-doped Si.9,10,12,13 Zhu et al.10 reported a ≈ 36% reduction in
reduction in highly-doped Si.9,10,12,13 Zhu et al.10 reported a ≈ 36% reduction in 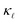 in fine-grained, highly P-doped Si, and asserted that EPS is the major contributor to the
in fine-grained, highly P-doped Si, and asserted that EPS is the major contributor to the 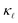 reduction. In contrast, Ohishi et al.9 attributed the
reduction. In contrast, Ohishi et al.9 attributed the 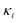 reduction in single-crystal, highly P- and B-doped Si solely to intrinsic anharmonic phonon–phonon scattering and PDPS.
reduction in single-crystal, highly P- and B-doped Si solely to intrinsic anharmonic phonon–phonon scattering and PDPS.
The aforementioned disagreement highlights the problem in studying thermal transport when employing fitted models based on strongly-simplified assumptions about the underlying phonon band structures and scattering mechanisms. Important progress towards a more predictive treatment of 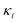 in doped Si was made recently by Liao et al.,13 who performed an ab initio study of n- and p-doped Si and showed that, EPS at a carrier concentration of p ≈ 1021 cm−3 can result in a ≈ 45% reduction in
in doped Si was made recently by Liao et al.,13 who performed an ab initio study of n- and p-doped Si and showed that, EPS at a carrier concentration of p ≈ 1021 cm−3 can result in a ≈ 45% reduction in 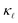 at room temperature. The calculations reproduce how
at room temperature. The calculations reproduce how 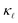 is lower in p-doped samples than in n-doped ones, in agreement with the experiments.14,15 However, they do not capture the magnitude of the reduction observed in B-doped p-type single-crystal Si, which at a doping level of 5 × 1020 cm−3 amounts to more than 70%.14
is lower in p-doped samples than in n-doped ones, in agreement with the experiments.14,15 However, they do not capture the magnitude of the reduction observed in B-doped p-type single-crystal Si, which at a doping level of 5 × 1020 cm−3 amounts to more than 70%.14
In the present work, we investigate the precise mechanisms responsible for the 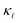 reduction observed in highly-doped Si. We calculate
reduction observed in highly-doped Si. We calculate 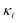 by employing the Boltzmann transport equation (BTE) for phonons, using only inputs in the form of interatomic force constants (IFCs) and electron–phonon coupling (EPC) matrix elements obtained from density functional theory. We extend the earlier work on EPS13 and include also the PDPS from first principles. At high defect concentrations, we find that the PDPS rates dominate the EPS rates at all frequencies except the lowest ones and contribute substantially to the
by employing the Boltzmann transport equation (BTE) for phonons, using only inputs in the form of interatomic force constants (IFCs) and electron–phonon coupling (EPC) matrix elements obtained from density functional theory. We extend the earlier work on EPS13 and include also the PDPS from first principles. At high defect concentrations, we find that the PDPS rates dominate the EPS rates at all frequencies except the lowest ones and contribute substantially to the 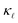 reduction at all temperatures. On the other hand, EPS dominates at low defect concentrations due to a fundamentally different frequency and concentration dependence. As a result, a correct quantitative prediction of the
reduction at all temperatures. On the other hand, EPS dominates at low defect concentrations due to a fundamentally different frequency and concentration dependence. As a result, a correct quantitative prediction of the 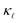 dependence on defect concentration and temperature is obtained only when both EPS and PDPS are taken into account.
dependence on defect concentration and temperature is obtained only when both EPS and PDPS are taken into account.
2 Methodology
Within the relaxation-time approximation, the lattice thermal conductivity tensor can be expressed as16,17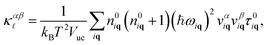 | (1) |
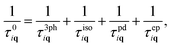 | (2) |
2.1 Point-defect phonon scattering
The phonon scattering rates by point defects, 1/τpdiq, can be calculated as:18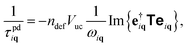 | (3) |
| T = (1 − Vg+)−1V. | (4) |
The matrix element of g+ projected on the atom pairs lη and l′η′ is given as:19
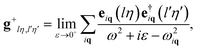 | (5) |
| V = VM + VK, | (6) |
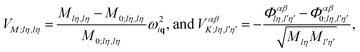 | (7) |
2.2 Electron-phonon scattering
The phonon scattering rates by electrons can be expressed as:13,20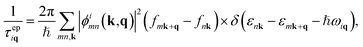 | (8) |
The EPC matrix element can be computed within density functional perturbation theory as:21
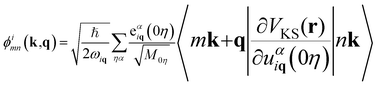 | (9) |
3 Computational details
For calculating the PDPS rates, the total energy as well as the force calculations are carried out using the projector-augmented-wave method22 as implemented in the VASP code,23–25 within the local density approximation (LDA)26,27 to the exchange and correlation energy. For completeness and comparison to LDA we also calculate the PDPS rates with the Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional.28 The volume of the unit cell is relaxed until the energy is converged within 10−8 eV. The 2nd- and 3rd-order IFCs are extracted using 5 × 5 × 5 supercell of the rhombohedral primitive cell containing 250 atoms using just the Γ-point. For the 2nd-order IFC calculations we use the Phonopy29 software package and for the 3rd-order IFCs we use THIRDORDER.PY from the ShengBTE package.16 The same supercell size was used to calculate the IFCs for the defect-laden structures. To compute the PDPS rates, the Green's functions are calculated on a 38 × 38 × 38 q-point mesh using the linear tetrahedron method30 for integration over the Brillouin zone. The scattering rates are then calculated on 35 × 35 × 35 q-point mesh.For the calculation of EPS rates, the EPC matrix elements are first computed on coarse grids and then interpolated to dense grids with the Wannier function interpolation method.31,32 The interpolations are performed using Quantum Espresso33 and the built-in EPW package34 with norm-conserving pseudopotentials. Likewise, both the LDA and PBE exchange and correlation functionals are considered. The initial k and q grids are both 6 × 6 × 6, which are interpolated to 35 × 35 × 35 meshes needed for the thermal conductivity calculations. The energy conservation δ-function is treated by Gaussian function with self-adaptive broadening parameters.21
Finally, the bulk thermal conductivity is also calculated using the 35 × 35 × 35 q-point mesh with the ALMABTE35 package. Due to the dense q-mesh the thermal conductivity is converged down to 40 K.
4 Results and discussion
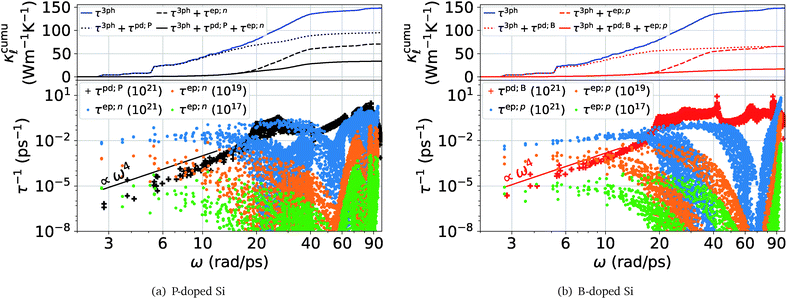
Fig. 1 shows a comparison between the PDPS and EPS rates for both n- and p-doped Si, in the bottom panels. The PDPS depends on the actual defect type present in the system. We have studied the substitutional BSi(−1) and PSi(+1) defects, which are the most common doping elements and also those studied experimentally. The PDPS has a trivial dependence on the defect concentration [eqn (3)] and is shown for only one defect concentration (1021 cm−3). In a rigid band approximation, the EPS is dependent only on the carrier concentration through the distribution function in eqn (8). The EPS is shown for three different carrier concentrations in Fig. 1 and the corresponding chemical potentials are shown in Fig. 2 (inset). Our LDA EPS rates compare well with the PBE rates reported by Liao et al.13 The LDA rates are slightly higher than the PBE ones which results in a correspondingly higher reduction due to EPS in LDA as compared to PBE. However, this does not have any major effect on the interpretation of our results.
reduction due to EPS in LDA as compared to PBE. However, this does not have any major effect on the interpretation of our results.
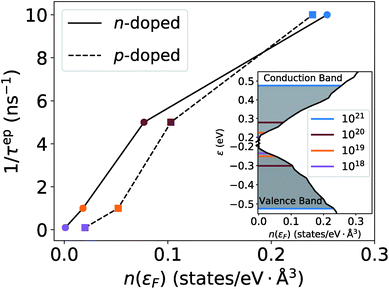 | ||
| Fig. 2 The low-frequency EPS rates for different concentrations as a function of the electronic density of states. The marker colors correspond to the doping levels in the inset. | ||
If we first consider the low frequency (ω < 12 rad ps−1) behavior, the PDPS rates exhibit a simple Rayleigh ω4 behavior and the EPS rates for a given carrier concentration are close to being independent of ω. Plotting the EPS rates as a function of the electronic density of states (DOS), obtained at the electron chemical potential corresponding to a given doping concentration, shows an almost linear dependence (Fig. 2). The EPS rates thus behave in accordance with a simple τ−1 ∝ n(ε) model36 at low frequencies. With a n(ε) ∝ε1/2 behavior of the electronic DOS, the low-frequency EPS rates will scale approximately as ndef1/3 with the carrier/defect concentration as opposed to the linear scaling of the PDPS rates evident from eqn (3). These simple relations are in accordance with the expectation that EPS will dominate over PDPS at low temperatures and defect concentrations while PDPS will become increasingly important at high defect concentrations.
At the same time, it is clear from Fig. 1 that for ω > 12 rad ps−1 the calculated rates deviate substantially from the aforementioned simple relations. The cumulative 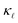 plots in the respective top panels in Fig. 1 (blue curves) illustrate that modes with ω > 12 rad ps−1 carry about two-thirds of the heat at 300 K. Simply extrapolating the low frequency behavior would lead to a strong overestimation of the scattering. This is especially so for the EPS rates where a simple extrapolation would result in a strong overestimation of the predicted
plots in the respective top panels in Fig. 1 (blue curves) illustrate that modes with ω > 12 rad ps−1 carry about two-thirds of the heat at 300 K. Simply extrapolating the low frequency behavior would lead to a strong overestimation of the scattering. This is especially so for the EPS rates where a simple extrapolation would result in a strong overestimation of the predicted 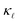 suppression. The cumulative plots in the top panels of Fig. 1 also show for PDPS (dotted lines), at a large defect concentration, that the contribution to
suppression. The cumulative plots in the top panels of Fig. 1 also show for PDPS (dotted lines), at a large defect concentration, that the contribution to 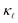 for frequencies higher than 20 rads ps−1 is only ≈15% in case of BSi(−1) defect and ≈40% in case of PSi(+1). In contrast, the EPS causes a majority reduction in
for frequencies higher than 20 rads ps−1 is only ≈15% in case of BSi(−1) defect and ≈40% in case of PSi(+1). In contrast, the EPS causes a majority reduction in 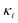 by frequencies below 20 rads ps−1, for both P- and B-doping.
by frequencies below 20 rads ps−1, for both P- and B-doping.
Next, in Fig. 3, we look into the individual contributions from the EPS (dashed lines) and PDPS (dotted lines) to the room temperature thermal conductivity reduction for increasing doping concentrations and compare them to the experimental 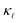 data from Slack.14 In accordance with the analysis of the scattering rates, EPS dominates the reduction of
data from Slack.14 In accordance with the analysis of the scattering rates, EPS dominates the reduction of 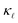 at low carrier concentrations. In the case of n-doped Si, EPS alone is almost enough to explain the experimental point at 2 × 1019 cm−3. However, at higher carrier concentrations, EPS alone clearly underestimates both the absolute reduction of
at low carrier concentrations. In the case of n-doped Si, EPS alone is almost enough to explain the experimental point at 2 × 1019 cm−3. However, at higher carrier concentrations, EPS alone clearly underestimates both the absolute reduction of 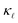 and the trend. Interestingly, PDPS captures the trend correctly for large defect concentrations, but also underestimates the absolute
and the trend. Interestingly, PDPS captures the trend correctly for large defect concentrations, but also underestimates the absolute 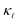 reduction. At a doping concentration of 1021 cm−3, the EPS and PDPS contribute almost equally in
reduction. At a doping concentration of 1021 cm−3, the EPS and PDPS contribute almost equally in 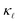 reduction for B doping. Even though both EPS and PDPS contribute substantially to
reduction for B doping. Even though both EPS and PDPS contribute substantially to 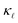 reduction in Si, neither can explain the absolute reduction in
reduction in Si, neither can explain the absolute reduction in 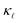 on its own. Only when both are taken into consideration in eqn (2) is the experimentally observed reduction of
on its own. Only when both are taken into consideration in eqn (2) is the experimentally observed reduction of 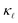 reproduced. This is shown by the black and red solid lines in Fig. 3. Apart from a slight underestimation of
reproduced. This is shown by the black and red solid lines in Fig. 3. Apart from a slight underestimation of 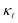 in case of B-doping, the calculated value of
in case of B-doping, the calculated value of 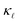 considering both EPS and PDPS agree very well with the experimental values available for concentrations ∼1019–1021 cm−3 both in value and trend, Fig. 3.
considering both EPS and PDPS agree very well with the experimental values available for concentrations ∼1019–1021 cm−3 both in value and trend, Fig. 3.
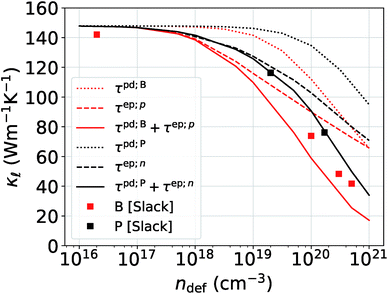 | ||
Fig. 3 Comparison of the reduction in  caused by EPS and PDPS individually and combined together vs. increasing doping concentration. The filled squares are from the experimental data in ref. 14. caused by EPS and PDPS individually and combined together vs. increasing doping concentration. The filled squares are from the experimental data in ref. 14. | ||
Besides the work of Slack et al.14 used for Fig. 3, there is a general lack of systematic experimental data on the thermal conductivity of single-crystal Si with varying doping concentrations. In order to gain further confidence in our results, we compare them to the more recent experimental data from ref. 15, which were measured on single-crystal Si films. Even at low defect concentrations, ndef = 1017–1018 cm−3, these samples exhibit a substantially lower  than the bulk samples.15 However, a good agreement with the experimental curves can be obtained by adding a simple boundary scattering term, 1/τBiq = |viq|/L with L = 10 µm, to eqn (2) to emulate the effect of a film, as seen in Fig. 4 (purple line). Adding now the effect of the PDPS and EPS, we calculate the variation of
than the bulk samples.15 However, a good agreement with the experimental curves can be obtained by adding a simple boundary scattering term, 1/τBiq = |viq|/L with L = 10 µm, to eqn (2) to emulate the effect of a film, as seen in Fig. 4 (purple line). Adding now the effect of the PDPS and EPS, we calculate the variation of 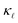 as a function of temperature for both B- and P-doped Si films, shown in Fig. 4. For B-doping, when we include the PDPS and EPS along with the boundary scattering, we see that there is only a slight reduction from the purple line for the 1018 cm−3 doping level (dashed red lines). Nevertheless, this results in an excellent agreement with the experimental data at that concentration (red circles), throughout the temperature range. Keeping the boundary scattering constant, when the doping concentration is increased to 1019 cm−3, a large reduction in
as a function of temperature for both B- and P-doped Si films, shown in Fig. 4. For B-doping, when we include the PDPS and EPS along with the boundary scattering, we see that there is only a slight reduction from the purple line for the 1018 cm−3 doping level (dashed red lines). Nevertheless, this results in an excellent agreement with the experimental data at that concentration (red circles), throughout the temperature range. Keeping the boundary scattering constant, when the doping concentration is increased to 1019 cm−3, a large reduction in 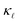 is observed (solid red line) which also agrees well with the experimental data (red circles). Similarly, for the P-doped calculations, we obtain an excellent agreement with the experiments except for a slight underestimation in
is observed (solid red line) which also agrees well with the experimental data (red circles). Similarly, for the P-doped calculations, we obtain an excellent agreement with the experiments except for a slight underestimation in 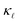 at temperatures below 80 K for 1018 cm−3 doped case. However, this is still under the uncertainties in experimental data.
at temperatures below 80 K for 1018 cm−3 doped case. However, this is still under the uncertainties in experimental data.
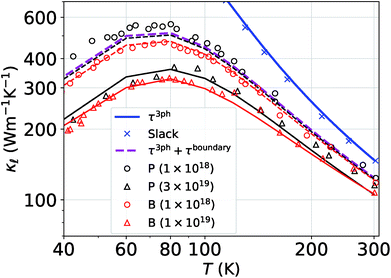 | ||
Fig. 4
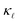 vs. temperature curves for the B(red)- and P(black)-doped Si considering the three-phonon, PDPS, EPS, and boundary scattering (at 10 µm). The open triangles and circles are the experimental data obtained from ref. 15. The solid and dashed (black and red) lines correspond to the calculations done at experimental carrier concentrations.
vs. temperature curves for the B(red)- and P(black)-doped Si considering the three-phonon, PDPS, EPS, and boundary scattering (at 10 µm). The open triangles and circles are the experimental data obtained from ref. 15. The solid and dashed (black and red) lines correspond to the calculations done at experimental carrier concentrations. | ||
We then make predictions for the highly-doped cases (1020 and 1021 cm−3) as there is no experimental thermal conductivity data available for such high doping levels. These are shown in Fig. 5. At room temperature, we find more than 60% reduction as compared to the bulk value at 1020 cm−3 doping level and 90% at 1021 cm−3 for B doping, and 40% and 80% for P doping, respectively. Fig. 5 also shows the individual contributions to the 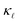 reduction by EPS and PDPS in the case of B doping at a doping concentration of 1021 cm−3, revealing their characteristic effects on the thermal conductivity over the temperature range. The reduction in
reduction by EPS and PDPS in the case of B doping at a doping concentration of 1021 cm−3, revealing their characteristic effects on the thermal conductivity over the temperature range. The reduction in 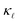 caused by PDPS overtakes the one by EPS at ≈250 K. This behavior highlights the importance of PDPS at high doping concentrations in Si and also emphasizes that, at temperatures higher than 300 K, PDPS is the most dominant scattering mechanism besides the intrinsic anharmonic scattering. We have also performed calculations including an L = 10 µm boundary scattering term, however at such high doping concentrations the EPS and PDPS dominate the boundary scattering throughout the temperature range and only a small effect at very low temperatures was found on the calculated
caused by PDPS overtakes the one by EPS at ≈250 K. This behavior highlights the importance of PDPS at high doping concentrations in Si and also emphasizes that, at temperatures higher than 300 K, PDPS is the most dominant scattering mechanism besides the intrinsic anharmonic scattering. We have also performed calculations including an L = 10 µm boundary scattering term, however at such high doping concentrations the EPS and PDPS dominate the boundary scattering throughout the temperature range and only a small effect at very low temperatures was found on the calculated 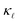 . This observation is also in agreement with Fu et al.37 who observed significant contribution of EPS towards room-temperature
. This observation is also in agreement with Fu et al.37 who observed significant contribution of EPS towards room-temperature  reduction in highly-doped Si nanowires of 1 µm diameter.
reduction in highly-doped Si nanowires of 1 µm diameter.
 | ||
Fig. 5 Prediction of 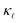 for highly P- and B-doped Si. Also shown is the comparison of EPS and PDPS to for highly P- and B-doped Si. Also shown is the comparison of EPS and PDPS to  reduction considered at a concentration of 1021 cm−3. reduction considered at a concentration of 1021 cm−3. | ||
It is important to note how the present case is very different from our previous work on SiC.38,39 In the present work, we observe a significant contribution of both EPS and PDPS to 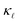 of a highly-doped system; whereas in our previous work we observed that PDPS was sufficient on its own to correctly predict the
of a highly-doped system; whereas in our previous work we observed that PDPS was sufficient on its own to correctly predict the 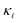 of B-doped cubic SiC owing to the resonant phonon scattering that boron causes.38,39 The resonant scattering was at least one to two orders of magnitude higher than that caused by other defects and resulted in a drastic reduction (approximately two orders of magnitude at room temperature) in the thermal conductivity even at relatively modest defect concentrations (≈1020 cm−3). Boron does not cause resonant scattering in Si and therefore the contribution of both EPS and PDPS are comparable.
of B-doped cubic SiC owing to the resonant phonon scattering that boron causes.38,39 The resonant scattering was at least one to two orders of magnitude higher than that caused by other defects and resulted in a drastic reduction (approximately two orders of magnitude at room temperature) in the thermal conductivity even at relatively modest defect concentrations (≈1020 cm−3). Boron does not cause resonant scattering in Si and therefore the contribution of both EPS and PDPS are comparable.
5 Conclusions
We have calculated the ab initio lattice thermal conductivity of highly P- and B-doped Si considering phonon scattering caused by three phonon processes, isotopes, point defects, and electrons. We illustrate that at low doping concentrations EPS causes a higher reduction in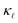 as compared to PDPS owing to a near constant behavior of EPS rates at low frequencies. At low concentrations EPS alone is sufficient to reproduce the absolute reduction in
as compared to PDPS owing to a near constant behavior of EPS rates at low frequencies. At low concentrations EPS alone is sufficient to reproduce the absolute reduction in 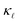 . However, at high doping concentrations it fails to reproduce the absolute values and the trend of
. However, at high doping concentrations it fails to reproduce the absolute values and the trend of 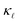 reduction. PDPS has a substantial contribution to
reduction. PDPS has a substantial contribution to 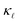 reduction at high doping concentrations and neither EPS nor PDPS is sufficient on its own to reproduce the experimental
reduction at high doping concentrations and neither EPS nor PDPS is sufficient on its own to reproduce the experimental 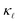 values. Only when the effect of all the scattering mechanisms are considered together, we get a good agreement with the experimental values across the temperature range. At a doping concentration of 1021 cm3, we observe almost 90% reduction in the room temperature thermal conductivity of B-doped Si as compared to the bulk, whereas, 80% reduction in case of P doping is found. This is mainly because of the higher PDPS rates of the B defects than those of P defects. Neither EPS nor PDPS can be captured by conventional parameterized models. Together with our previous works on doping diamond, SiC, GaN and GaAs,38,40–42 we show that, at temperatures above 300 K, PDPS is the most dominant scattering mechanism in highly B- and P-doped Si and cannot be neglected.
values. Only when the effect of all the scattering mechanisms are considered together, we get a good agreement with the experimental values across the temperature range. At a doping concentration of 1021 cm3, we observe almost 90% reduction in the room temperature thermal conductivity of B-doped Si as compared to the bulk, whereas, 80% reduction in case of P doping is found. This is mainly because of the higher PDPS rates of the B defects than those of P defects. Neither EPS nor PDPS can be captured by conventional parameterized models. Together with our previous works on doping diamond, SiC, GaN and GaAs,38,40–42 we show that, at temperatures above 300 K, PDPS is the most dominant scattering mechanism in highly B- and P-doped Si and cannot be neglected.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge support from the European Union's Horizon 2020 Research and Innovation Action under Grant No. 645776 (ALMA), the French (ANR) and Austrian (FWF) Science Funds under project CODIS (ANR-17-CE08-0044-01 and FWF-I-3576-N36), and the Natural Science Foundation of China under Grant No. 11704258. We also thank the Vienna Scientific Cluster for providing the computational facilities (project numbers 645776: ALMA and 1523306: CODIS).References
- D. G. Cahill, P. V. Braun, G. Chen, D. R. Clarke, S. Fan, K. E. Goodson, P. Keblinski, W. P. King, G. D. Mahan, A. Majumdar, H. J. Maris, S. R. Phillpot, E. Pop and L. Shi, Appl. Phys. Rev., 2014, 1, 011305 Search PubMed.
- V. I. Fistul, Heavily doped semiconductors, Springer Science & Business Media, 2012, vol. 1 Search PubMed.
- S. M. Sze and K. K. Ng, Physics of semiconductor devices, John wiley & sons, 2006 Search PubMed.
- H. Ehsani, I. Bhat, J. Borrego, R. Gutmann, E. Brown, R. Dziendziel, M. Freeman and N. Choudhury, J. Appl. Phys., 1997, 81, 432–439 CrossRef CAS.
- E. J. Ng, V. A. Hong, Y. Yang, C. H. Ahn, C. L. M. Everhart and T. W. Kenny, J. Microelectromech. Syst., 2015, 24, 730–741 CAS.
- R. Beyers, D. Coulman and P. Merchant, J. Appl. Phys., 1987, 61, 5110–5117 CrossRef CAS.
- M. van Dort, P. Woerlee and A. Walker, Solid-State Electron., 1994, 37, 411–414 CrossRef CAS.
- N. Neophytou, X. Zianni, H. Kosina, S. Frabboni, B. Lorenzi and D. Narducci, Nanotechnology, 2013, 24, 205402 CrossRef PubMed.
- Y. Ohishi, J. Xie, Y. Miyazaki, Y. Aikebaier, H. Muta, K. Kurosaki, S. Yamanaka, N. Uchida and T. Tada, Jpn. J. Appl. Phys., 2015, 54, 071301 CrossRef.
- T. Zhu, G. Yu, J. Xu, H. Wu, C. Fu, X. Liu, J. He and X. Zhao, Adv. Electron. Mater., 2016, 2, 1600171 CrossRef.
- P. Rohani, S. Banerjee, S. Sharifi-Asl, M. Malekzadeh, R. Shahbazian-Yassar, S. J. L. Billinge and M. T. Swihart, Adv. Funct. Mater., 2019, 29, 1807788 CrossRef.
- B. Abeles, Phys. Rev., 1963, 131, 1906–1911 CrossRef.
- B. Liao, B. Qiu, J. Zhou, S. Huberman, K. Esfarjani and G. Chen, Phys. Rev. Lett., 2015, 114, 115901 CrossRef.
- G. A. Slack, J. Appl. Phys., 1964, 35, 3460–3466 CrossRef CAS.
- M. Asheghi, K. Kurabayashi, R. Kasnavi and K. E. Goodson, J. Appl. Phys., 2002, 91, 5079–5088 CrossRef CAS.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- B. Dongre, J. Carrete, N. Mingo and G. K. H. Madsen, MRS Commun., 2018, 8, 1119–1123 CrossRef CAS.
- N. Mingo, K. Esfarjani, D. A. Broido and D. A. Stewart, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 045408 CrossRef.
- E. N. Economou, Green's functions in quantum physics, Springer, 1983, vol. 3 Search PubMed.
- J. M. Ziman, Electrons and phonons: the theory of transport phenomena in solids, Oxford university press, 2001 Search PubMed.
- W. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 075405 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- P. Lambin and J. P. Vigneron, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 3430–3437 CrossRef.
- F. Giustino, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 165108 CrossRef.
- N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Rev. Mod. Phys., 2012, 84, 1419–1475 CrossRef CAS.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- S. Poncé, E. Margine, C. Verdi and F. Giustino, Comput. Phys. Commun., 2016, 209, 116–133 CrossRef.
- J. Carrete, B. Vermeersch, A. Katre, A. van Roekeghem, T. Wang, G. K. H. Madsen and N. Mingo, Comput. Phys. Commun., 2017, 220, 351–362 CrossRef CAS.
- B. Xu and M. J. Verstraete, Phys. Rev. Lett., 2014, 112, 196603 CrossRef.
- B. Fu, G. Tang and Y. Li, Phys. Chem. Chem. Phys., 2017, 19, 28517–28526 RSC.
- A. Katre, J. Carrete, B. Dongre, G. K. H. Madsen and N. Mingo, Phys. Rev. Lett., 2017, 119, 075902 CrossRef PubMed.
- B. Dongre, J. Carrete, A. Katre, N. Mingo and G. K. H. Madsen, J. Mater. Chem. C, 2018, 6, 4691–4697 RSC.
- N. A. Katcho, J. Carrete, W. Li and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 094117 CrossRef.
- A. Katre, J. Carrete, T. Wang, G. K. H. Madsen and N. Mingo, Phys. Rev. Mater., 2018, 2, 050602 CrossRef CAS.
- A. Kundu, F. Otte, J. Carrete, P. Erhart, W. Li, N. Mingo and G. K. H. Madsen, Phys. Rev. Mater., 2019, 3, 094602 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |