Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Responsive drop method: quantitative in situ determination of surfactant effectiveness using reconfigurable Janus emulsions†
Saveh
Djalali
 ,
Bradley D.
Frank
and
Lukas
Zeininger
,
Bradley D.
Frank
and
Lukas
Zeininger
 *
*
Department of Chemistry, Max Planck Institute of Colloids and Interfaces, Am Muehlenberg 1, 14476 Potsdam, Germany. E-mail: lukas.zeininger@mpikg.mpg.de
First published on 2nd November 2020
Abstract
Characterization of surfactant effectiveness and thus an evaluation of their performance in a wide range of emulsion technologies requires a precise determination of key parameters including their critical micelle concentrations as well as their ability to lower the surface tension at interfaces. In this study, we describe a new approach to quantify marginal variations in interfacial tension of surfactant stabilized fluid interfaces. The method is based on a unique chemical-morphological coupling inside bi-phasic oil-in-water Janus emulsions that undergo dynamic morphological transitions in response to changes in the surfactant type, concentration, ratio, and configuration. Variations in Janus droplet morphologies are readily monitored in situ using a simple side-view imaging setup, resulting in a fast, convenient, cost-effective, time-, and sample-saving technique for the characterization of classical surfactant systems. In addition, the reported method facilitates monitoring of triggered changes in surfactant effectiveness, e.g. invoked by external triggers, and thus proves particularly useful for the in situ analysis of stimuli-responsive surfactants and emulsions.
1 Introduction
Surfactants, including emulsifiers, detergents, dispersants, and foaming, wetting, and coating agents are technologically commonplace on the largest scale as they play an important role in cleaning, manufacturing, oil recovery, and other processes.1–4 Surfactants are designed to lower the surface tension of liquid–liquid, liquid–gas, or solid–liquid interfaces and are therefore central components of many medical, cosmetic, food, consumer, and performance materials.5 Crucial to selecting a suitable surfactant for a specific application is a thorough investigation and characterization of its effectiveness that includes the determination of key parameters such as its critical micelle concentration (CMC) as well as its potential to lower the surface tension at interfaces.Above a particular concentration, i.e. the CMC, surfactants form thermodynamically stable micelles which causes sharp changes in measurable physical properties. Many methods have been developed to identify the CMC value by measuring these changes in physical parameters such as surface or interfacial tension, electric conductivity, absorbance, or fluorescence.6 Most common techniques for determining the interfacial tensions at liquid–liquid interfaces are based on force or optical tensiometers, such as the Du-Noüy ring, Wilhelmy plate, pendant drop, or spinning drop methods.7
Each of these methods allow precise determination of interfacial tensions between two fluids within a certain interfacial tension regime. Whereas force tensiometers provide the most accurate results for fluid interfaces with high interfacial tensions (γ = 40–60 mN m−1), which includes classical oil–water systems, the spinning drop method, for instance, is specifically designed for the quantification of ultralow interfacial tensions (γ < 1 mN m−1) such as found in aqueous multiphase systems. However, for the characterization of surfactant stabilized oil–water interfaces, and thus the extraction of CMC values, a method tailored towards an intermediate interfacial tension regime between γ = 2–20 mN m−1 is desirable. In addition, most conventional techniques are usually associated with one or several of the following drawbacks: incapability to produce a real-time signal that prevents an in situ analysis of surfactant systems, involvement of tedious synthesis e.g. of chemical (fluorescent) probes, the need for expensive and/or complicated equipment, requirement of additional computational add-ons, and/or methods are time- and sample-consuming because a series of surfactant solutions with different concentrations must be prepared and characterized individually.8–11
The development of novel responsive and triggerable materials combined with advances in imaging techniques hold promise to provide alternative cost-effective, rapid, and material gentle pathways for visualizing detectable changes of physical parameters in surfactant solutions and thus to circumvent complications associated with conventional techniques. In this context, liquid–liquid transduction schemes, such as oil-in-water emulsions are appealing because they allow the investigation of surfactants within their designated environment. However, traditionally, variations in the surfactant effectiveness and thus variation of interfacial tensions result only in qualitative results, e.g. changes in droplet size or stability.12–14
In contrast, Janus emulsions, i.e. droplets comprised of two dispersed fluids, have the intrinsic advantage that interfacial tension variations transduce into a change in the internal shape of the droplets whereas the overall emulsion stability remains intact. The internal droplet morphology of Janus emulsions is exclusively controlled by a balance of interfacial tensions, i.e. the droplet geometries can be controllably altered after emulsification by triggering changes in the surfactant effectiveness,15,16 and examples of the latter include stimuli-responsive or cleavable surfactants.17 Owing to this unique morphological response to targeted chemical stimuli, Janus emulsions have been exploited in a number of applications, including as tunable microlenses,18 optical waveguides,19–21 scaffolds for the fabrication of anisotropic solid objects,22,23 motile particle systems,24,25 and as transducers and signal amplifiers in improved chemo- and biosensing platforms.26–29
Herein, we leverage the exquisitely sensitive chemical-morphological coupling inside Janus emulsions for the development of a new simple and broadly applicable method for the quantitative characterization of surfactants. Specifically, we monitored the morphological response of Janus emulsions comprising two immiscible oils dispersed within an aqueous surfactant solution to variations in surfactant type, concentration, ratio, and configuration, using a customized side-view imaging setup (Fig. 1). We demonstrate that marginal variations in interfacial tensions suffice to cause significant variations in droplet shape, which enables a precise determination of surfactant CMC values. In addition, our method allows to quantitatively compare the effectiveness of various cationic, anionic, and nonionic surfactants via determination of the interfacial tensions of surfactant stabilized fluid interfaces. Besides a convenient and precise investigation of conventional surfactant systems, the in situ observation of interfacial tensions proves particularly useful for the characterization of switchable surfactants.
2 Results and discussion
For the preparation of emulsion droplets for our study we selected heptane and perfluorodecalin as our constituent droplet oil phases. The two hydrophobic oils are immiscible at room temperature but mix with gentle heating above their upper critical solution temperature (TC = 38 °C). Using an established thermal phase separation approach,17 Janus emulsions are readily obtained by emulsifying a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio of the two oils above their TC in an aqueous solution containing a mixture of surfactants. Cooling below TC induces phase separation and yields structured Janus emulsion droplets with highly uniform composition and morphology. In response to the type, ratio, and concentration of the surrounding surfactants the morphology of the resulting droplets can be dynamically switched between encapsulated (HC/FC/W and FC/HC/W) and intermediate Janus configurations.
1 volume ratio of the two oils above their TC in an aqueous solution containing a mixture of surfactants. Cooling below TC induces phase separation and yields structured Janus emulsion droplets with highly uniform composition and morphology. In response to the type, ratio, and concentration of the surrounding surfactants the morphology of the resulting droplets can be dynamically switched between encapsulated (HC/FC/W and FC/HC/W) and intermediate Janus configurations.
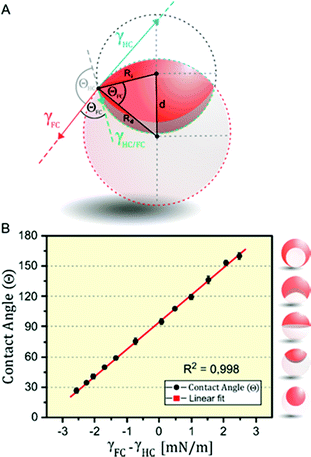
The internal morphologies of as-produced Janus emulsion droplets are highly uniform across a sample, as they solely reflect the force-balance of surface tensions acting at the individual interfaces. The equilibrium angles between different phases can be obtained by the Neumann construction (Fig. 2A).30,31 For the case of working temperatures close to the critical temperature of the internal fluids, the overall droplet shape is nearly spherical because the interfacial tension between the droplet phases γHC/FC are much smaller than the interfacial tensions between the droplet constituents and the aqueous medium γHC and γFC. In addition, for droplets with diameters on the order of 100 μm, the internal interface can be considered to be spherical, because the ratio of gravitational to surface tension forces is negligible. Within these limits, any changes in the values of external interfacial tensions do not affect the overall spherical droplet shape but cause variations in the curvature of the interface between the gravity aligned internal droplet phases. These physical relationships reveal that for the special case of a droplet in the ‘perfect’ Janus state, i.e. a droplet comprised of two perfect hemispheres, the two external interfacial tensions are equal (γHC = γFC).
Marginal variations from this equilibrium induced by variations in the surfactant effectiveness cause immediate variations in the droplet morphology and an either concave or convex shaped internal interface that can be readily observed and monitored by a horizontal imaging setup. To quantitatively describe the droplet morphology as a function of the surfactant type, ratio, and concentration, we used the contact angle θFC at the triple phase contact line, as determined by side-view micrographs of the respective droplet configurations.26 With the internal curvature being set by the balance of interfacial tensions at the external droplet interfaces (i.e. θHC + θFC → π) the contact angle θFC can be used as the sole parameter for describing the morphology of the droplet. Applying the law of cosines, the contact angles were determined from the two circles that define the inner and outer interfaces of the droplets, according to eqn (1) (with Ri: radius of inner droplet; Rd: radius of Janus droplet; and d: distance between the centers of the two circles):
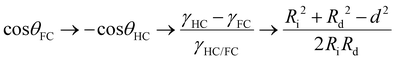 | (1) |
To allow for fast and convenient contact angle analysis we implemented an image processing program to calculate the average contact angles of a sample. The program uses an adaptive thresholding algorithm to distinguish areas with higher transparency from the opaque regions of the higher refractive index and dyed hydrocarbon phases and calculates θFC from the respective circles according to formula (1) (see ESI† for details).
To translate these considerations into a method that allows for an in situ determination of interfacial tensions, we next recorded a calibration curve, in which we plotted the droplet contact angles as a function of the quantity γFC − γHC (Fig. 2B). Therefore, we measured the tensions of heptane–water (γHC) and perfluorodecaline–water (γFC) interfaces for a variety of HC-surfactant (SDS) and FC-surfactant (Zonyl-FS300) concentrations and ratios using the pendant-drop method. The resulting linear correlation validates the interfacial tension difference γFC − γHC to serve as the sole parameter determining the droplet configuration and thus any given contact angle that lies within the dynamic range of droplet reconfiguration can be translated into an interfacial tension value. The calibration curve further reveals that a difference in the balance of interfacial tension of Δγ = ±6.8 mN m−1 suffices to completely invert a droplet's morphology from an encapsulated double emulsion to the inverted encapsulated state. Synonymously, marginal changes in interfacial tension in the order of Δγ = ±0.5 mN m−1 suffice to induce significant and easily detectable changes in contact angle of 13°, which creates a rapid, precise, and sensitive method for the determination of interfacial tensions.
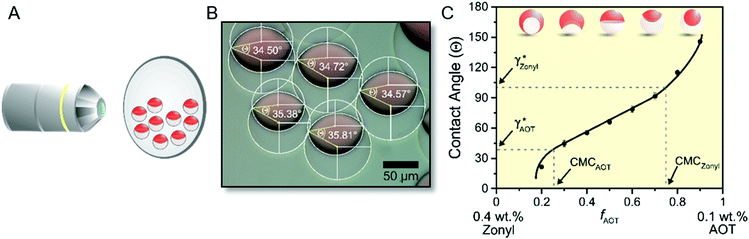
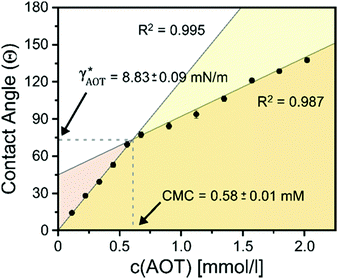
To test this ‘responsive drop’ method for the determination of CMC values, we investigated a series of well-established ionic and nonionic hydrocarbon surfactants. In our experiments, we kept the surfactant stabilizing the FC phase (Zonyl FS-300) at a constant concentration close to its CMC as an internal standard and to maintain the overall droplet stability. To invoke dynamic droplet responses we started with a droplet in its encapsulated form (HC/FC/W) and dynamically increased the concentration of the HC surfactant in the continuous phase. An ‘opening up’ of the droplet morphology associated with changes in the HC/W interfacial tension were monitored using the side-view imaging setup and a typical graph showing the contact angle evolution vs. a HC-surfactant (here: AOT) concentration is displayed in Fig. 3. Similar curves were obtained for all other surfactants tested (Fig. S9–S15, ESI†). The graphs reveal an abrupt change of slope in the evolution of the droplet contact angles illustrating the sharp change in interfacial tension decrease once the surfactant CMC is reached. Analysis of the resulting plots enabled a precise determination of the CMC values of the tested surfactants, and the experimentally measured values agreed well with reported literature values (Table 1).32
| Surfactant | CMC [mM] (responsive drop method) | CMC [mM] (literature values)32 | γ HC* [mN m−1] (responsive drop method) | γ HC* [mN m−1] (pendant drop method) |
|---|---|---|---|---|
| SDS | 8.44 ± 0.17 | 8.10–8.60 | 5.07 ± 0.11 | 5.13 ± 0.24 |
| Brij 58 | 0.076 ± 0.012 | 0.080 | 11.39 ± 1.82 | 10.79 ± 0.54 |
| AOT | 0.584 ± 0.011 | 0.680 | 8.83 ± 0.09 | 9.11 ± 0.27 |
| Triton-X100 | 0.258 ± 0.003 | 0.18–0.25 | 7.60 ± 0.08 | 8.21 ± 0.53 |
| CTAB | 1.00 ± 0.05 | 0.95–1.32 | 7.28 ± 0.38 | 7.05 ± 0.35 |
| Tween 20 | 0.063 ± 0.001 | 0.06–0.08 | 13.46 ± 0.09 | 13.06 ± 0.45 |
Next, with the linear calibration curve (Fig. 2B) at hand, the contact angle at the HC-surfactant CMC could be directly translated into an interfacial tension value γHC*, which serves as a measure of the surfactant's efficiency to stabilize oil–water interfaces. The extracted γHC* values were in good agreement to values obtained using the pendant drop method (Table 1). Notably, in the presence of higher surfactant concentrations the extraction of accurate γHC* values using the pendant drop proved much more difficult and time- and sample-consuming as compared to the in situ extraction via Janus droplet contact angles, because it is difficult to maintain a stable drop volume for longer periods of time, which demonstrates the versatility of the complex hydrocarbon–fluorocarbon droplets’ response for the investigation of a wide range of surfactants and interfaces.
Leveraging the immediate response of the Janus droplets to dynamic variations in surfactant effectiveness, we extended our investigation towards an in situ monitoring of a switchable surfactant system. Stimuli-responsive surfactants that undergo changes in their surfactant effectiveness in response to (bio-)chemical or physical triggers are attractive because they provide a handle to affect colloidal aggregation, emulsion stability, the release of encapsulants, and interfacial activity.33,34 A thorough investigation of such systems is difficult as often triggering events cause irreversible changes in the system composition or structure and a characterization is limited to their thermodynamically stable configurations.
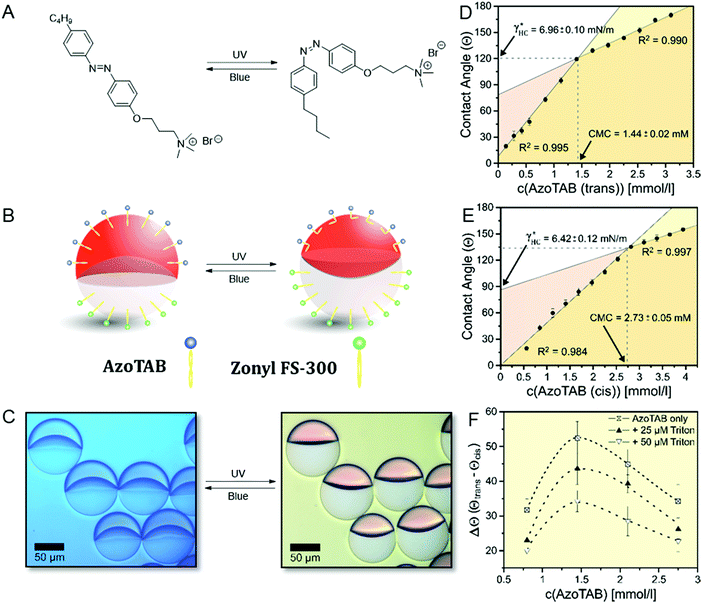
As an example of a switchable stimuli-responsive surfactant, we synthesized a light-responsive surfactant (AzoTAB),35,36 consisting of an azobenzene moiety that can undergo a reversible photo-induced cis–trans isomerization depending on the incident wavelength (Fig. 4A). By photo-switching the thermodynamically stable trans-isomers into the bent cis-form by UV-irradiation (λ = 360 nm) a change in hydrophobicity is induced that causes variations in the surfactant properties. As a consequence, in Janus droplets stabilized with this surfactant in combination with a FC-surfactant a morphology change is readily observed (Fig. 4B and C). This change is reversible and the decrease in interfacial area of the HC/W interface can be reversed by an irradiation with blue (λ = 470 nm) light. Using the ‘responsive drop method’, we followed in situ the morphological transition between the two isomers and readily determined their CMC and their potential to stabilize the HC/W interface by switching between UV and blue light, respectively, as displayed in Fig. 4D and E. As a result, we observed a significant variation of the surfactant CMC from 1.44 mM for the trans to 2.73 mM for the cis-isomer, however only minor changes in the HC/W interfacial tension at their respective CMC (γtrans* = 6.96 mN m−1vs. γcis* = 6.42 mN m−1). Thus, under consideration of these findings, we identified that a maximum change in droplet morphology of θFC = 69.4° is evoked at concentrations close to the CMC of the trans-isomer and that the overall variation in HC/W interfacial tension and therefore droplet response can be fine-tuned and tailored towards a specific requirement by adjusting the concentration of the stimuli-responsive surfactant (Fig. 4F). Similarly, we observed that the overall dynamic range of the droplets’ morphological transition can be reduced when adding an additional non-responsive HC surfactant (Triton-X100) to the system. These results demonstrate that beside innovations in the characterization of classical surfactants the in situ read out capability offers particular practicability for the investigation of systems involving stimuli-responsive surfactants and emulsions.
3 Conclusions
In conclusion, we have developed a new ‘responsive drop method’ for an in situ quantitative determination of both surfactant CMCs and interfacial tension values for surfactant stabilized oil–water interfaces. Responsive Janus emulsions serve as transducers to visualize marginal variations in interfacial tensions at oil–water interfaces in response to variations in the surfactant effectiveness, including their type, ratio, concentration, and configuration. The method presented here is general, and broadly applicable to a wide range of classical and stimuli-responsive surfactants and liquid combinations. Besides offering a powerful economical, simple, and fast alternative for the characterization of widely used surfactants, this method enables an in situ monitoring of dynamic variations in surfactant effectiveness, e.g. in response to physical or (bio-)chemical triggers that provides valuable insights for the investigation of stimuli-responsive surfactants and emulsions and thus will contribute to a better understanding of their application in a wide range of optical, electrical and sensing platforms.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are thankful for funding by the Max Planck Society and gratefully acknowledge financial support through the Emmy-Noether program of the German Research Foundation (DFG) (grant no: ZE1121-3). Open Access funding provided by the Max Planck Society.References
- L. L. Schramm, Surfactants: fundamentals and applications in the petroleum industry, Cambridge University Press, 2000 Search PubMed.
- E. Kissa, Fluorinated surfactants and repellents, CRC Press, 2001, vol. 97 Search PubMed.
- P. Raffa, D. A. Z. Wever, F. Picchioni and A. A. Broekhuis, Chem. Rev., 2015, 115, 8504–8563 CrossRef CAS.
- L. Zeininger, L. M. S. Stiegler, L. Portilla, M. Halik and A. Hirsch, Chem. Open, 2018, 7, 282–287 CAS.
- T. F. Tadros, Applied surfactants: principles and applications. John Wiley & Sons, 2006 Search PubMed.
- R. M. Pashley and M. E. Karaman, Applied colloid and surface chemistry, John Wiley & Sons, 2004 Search PubMed.
- S. Hartland, Surface and interfacial tension: measurement, theory, and applications, CRC Press, 2004 Search PubMed.
- S. Wu, F. Liang, D. Hu, H. Li, W. Yang and Q. Zhu, Anal. Chem., 2020, 92, 4259–4265 CrossRef CAS.
- A. Fluksman and O. Benny, Anal. Methods, 2019, 11, 3810–3818 RSC.
- S. Deodhar, P. Rohilla, M. Manivannan, S. P. Thampi and M. G. Basavaraj, Langmuir, 2020, 36, 8100–8110 CrossRef CAS.
- H. Xi Yuan and M. J. Rosen, J. Colloid Interface Sci., 1988, 124, 652–659 CrossRef.
- Y. Liu, P. G. Jessop, M. Cunningham, C. A. Eckert and C. L. Liotta, Science, 2006, 313, 958–960 CrossRef CAS.
- G. Ren, L. Wang, Q. Chen, Z. Xu, J. Xu and D. Sun, Langmuir, 2017, 33, 3040–3046 CrossRef CAS.
- M. Pavlovic, A. Plucinski, L. Zeininger and B. V. K. J. Schmidt, Chem. Commun., 2020, 56, 6814–6817 RSC.
- H. Hasinovic, S. E. Friberg, I. Kovach and J. Koetz, J. Dispersion Sci. Technol., 2013, 34, 1683–1689 CrossRef CAS.
- I. Kovach, S. E. Friberg and J. Koetz, J. Dispersion Sci. Technol., 2017, 38, 594–597 CrossRef CAS.
- L. D. Zarzar, V. Sresht, E. M. Sletten, J. A. Kalow, D. Blankschtein and T. M. Swager, Nature, 2015, 518, 520–524 CrossRef CAS.
- S. Nagelberg, et al. , Nat. Commun., 2017, 8, 14673 CrossRef.
- S. Savagatrup, D. Ma, H. Zhong, K. S. Harvey, L. C. Kimerling, A. M. Agarwal and T. M. Swager, ACS Sens., 2020, 5, 1996–2002 CrossRef CAS.
- L. Zeininger, E. Weyandt, S. Savagatrup, K. S. Harvey, Q. Zhang, Y. Zhao and T. M. Swager, Lab Chip, 2019, 19, 1327–1331 RSC.
- A. E. Goodling, S. Nagelberg, B. Kaehr, C. H. Meredith, S. I. Cheon, A. P. Saunders, M. Kolle and L. D. Zarzar, Nature, 2019, 566, 523–527 CrossRef CAS.
- L. Ge, J. Cheng, D. Wei, Y. Sun and R. Guo, Langmuir, 2018, 34, 7386–7395 CrossRef CAS.
- R. V. Balaj, S. W. Cho, P. Singh and L. D. Zarzar, Polym. Chem., 2020, 11, 281–286 RSC.
- C. A. Zentner, A. Concellón and T. M. Swager, ACS Cent. Sci., 2020, 6, 1460–1466 CrossRef CAS.
- A. Concellón, C. A. Zentner and T. M. Swager, J. Am. Chem. Soc., 2019, 141, 18246–18255 CrossRef.
- L. Zeininger, S. Nagelberg, K. S. Harvey, S. Savagatrup, M. B. Herbert, K. Yoshinaga, J. A. Capobianco, M. Kolle and T. M. Swager, ACS Cent. Sci., 2019, 5, 789–795 CAS.
- C.-J. Lin, L. Zeininger, S. Savagatrup and T. M. Swager, J. Am. Chem. Soc., 2019, 141, 3802–3806 CrossRef CAS.
- Q. Zhang, L. Zeininger, K.-J. Sung, E. A. Miller, K. Yoshinaga, H. D. Sikes and T. M. Swager, ACS Sens., 2019, 4, 180–184 CrossRef CAS.
- M. Pavlovic, M. Antonietti, B. V. K. J. Schmidt and L. Zeininger, J. Colloid Interface Sci., 2020, 575, 88–95 CrossRef CAS.
- J. Guzowski, P. M. Korczyk, S. Jakiela and P. Garstecki, Soft Matter, 2012, 8, 7269–7278 RSC.
- P.-G. De Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and wetting phenomena: drops, bubbles, pearls, waves, Springer Science & Business Media, 2013 Search PubMed.
- P. Mukerjee and K. J. Mysels, Critical Micelle Concentrations in Aqueous Surfactant Systems, National Bureau of Standards, Washington, 1971 Search PubMed.
- P. Brown, C. P. Butts and J. Eastoe, Soft Matter, 2013, 9, 2365–2374 RSC.
- Y. Suzuki, K. H. Nagai, A. Zinchenko and T. Hamada, Langmuir, 2017, 33, 2671–2676 CrossRef CAS.
- K. Jia, X. Zhang, L. Zhang, L. Yu, Y. Wu, L. Li, Y. Mai and B. Liao, Langmuir, 2018, 34, 11544–11552 CrossRef CAS.
- E. Chevallier, A. Mamane, H. A. Stone, C. Tribet, F. Lequeux and C. Monteux, Soft Matter, 2011, 7, 7866–7874 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Materials and methods, droplet preparation, surfactant characterization. See DOI: 10.1039/d0sm01724h |
| This journal is © The Royal Society of Chemistry 2020 |