Open Access Article
Open Access ArticleAcoustic bubble dynamics in a yield-stress fluid†
Brice
Saint-Michel‡
 and
Valeria
Garbin‡
and
Valeria
Garbin‡
 *
*
Department of Chemical Engineering, Imperial College London, London SW7 2AZ, UK
First published on 13th October 2020
Abstract
Yield-stress fluids naturally trap small bubbles when their buoyancy applies an insufficient stress to induce local yielding of the material. Under acoustic excitation, trapped bubbles can be driven into volumetric oscillations and apply an additional local strain and stress that can trigger yielding and assist their release. In this paper we explore different regimes of microbubble oscillation and translation driven by an ultrasound field in a model yield-stress fluid, a Carbopol microgel. We first analyse the linear bubble oscillation dynamics to measure the local, high-frequency viscosity of the material. We then use acoustic pressure gradients to induce bubble translation and examine the elastic part of the response of the material below yielding. We find that, at moderate pressure amplitude, the additional stresses applied by volumetric oscillations and acoustic radiation forces do not lead to any detectable irreversible bubble motion. At high pressure amplitude, we observe non-spherical shape oscillations that result in erratic bubble motion. The critical pressures we observe differ from the predictions of a recent model of shape oscillations in soft solids. Based on our findings, we discuss possible reasons for the lack of bubble release in Carbopol and suggest other systems in which ultrasound-assisted bubble rise may be observed.
1 Introduction
Yield-stress fluids encompass a wide range of materials including foams, suspensions, emulsions and microgels.1,2 These materials exhibit a threshold in applied stress, called the yield stress, below which the material behaves like a solid, and above which it flows like a liquid. A clear manifestation of the yield stress is the presence of trapped bubbles, when their buoyancy force is too small to yield the material. Trapped bubbles can be beneficial, for instance when they are used to impart texture to a food product, or they can be detrimental as they can negatively affect the thermal conductivity or optical transparency of a material. Strategies to control the amount and size distribution of trapped bubbles are therefore important in processing of formulations and advanced materials. There is some experimental evidence that driving bubbles into volumetric oscillations in yield-stress fluids can assist their removal,3 but the effect of oscillations on yielding is poorly understood. This lack of understanding is particularly detrimental to the development of controlled bubble removal methods.Understanding bubble dynamics in yield-stress fluids is particularly challenging since their rheology is not even fully understood in the case of simple shear. Yield-stress fluids are only well-understood in the limit of very small shear stresses where a linear elastic behaviour is recovered, or for large, steady stresses for which their flow rheology usually obeys the Herschel–Bulkley equation.1 For intermediate stresses, experimental results performed under steady or large amplitude oscillatory shear4 have evidenced that yield-stress fluids exhibit non-linear,5 time-dependent, cooperative6 behaviour. Such features are only captured by the most recent microscopic7 and continuum mechanics models.8
The capacity of a yield-stress fluid to entrap bubbles up to a critical effective radius Rc can be expressed as the dimensionless number Yc−1 = 2ρlgRc/3σY, where ρl is the liquid density, g is the acceleration due to gravity and σY is the yield stress of the material.9 Even with the most conservative estimate, a yield stress of only 10 Pa causes trapping of bubbles up to 2Rc = 6 mm in diameter. Removing bubbles below the critical size can be achieved by centrifuging,10 applying a vacuum, or by using low-frequency (∼100 Hz) vibrations to suppress the yield stress in fragile granular networks.11 These techniques alter the physical parameters at play in the definition of Yc−1 rather than fundamentally altering this criterion.
Bubbles are however not passive under the application of vibrations and acoustic excitations, as the dynamic pressure field drives them into volumetric oscillations.12 Oscillating bubbles apply a local strain field to the surrounding material, which in turn reacts by exerting a stress onto the bubble, altering the oscillation dynamics. Bubble dynamics in Newtonian liquids12 and soft solids13 is now a well-established topic, motivated e.g. by the direct role played by bubble collapse in therapeutic laser or ultrasound tissue ablation.14,15 Bubble radius time profiles are now even used either in the linear regime16 or the strongly non-linear, cavitation regime17 to extract local rheological properties of soft solids.
In yield-stress fluids, oscillating bubbles may apply a strain that is sufficient to locally yield the material, defining a yielded, fluid region. Bubble rise may then proceed in this confined region even if their size is well below Rc. The size and shape of this region has a key influence on the bubble rising velocity, and ultimately in the efficiency of the removal process. While the shape of the yielded region has been investigated in great detail for passive bubble rise,9,18 the case of oscillating bubbles has only been examined very recently.19,20 Building upon the progress in modelling both bubble dynamics in soft materials13 and the rheology of yield-stress fluids,21 these articles confirm that bubble rise is indeed possible for bubbles below Rc;19 they also compute the minimum oscillation amplitude required to initiate yielding.20 To the best of our knowledge, these numerical and theoretical results have not yet been compared to experiments: experimental articles so far have focused on the case of bubble removal in a shear-thinning, viscoelastic surrounding fluid22 and removal in yield-stress fluids for bubbles already close to the static rise radius at rest, Rc.3
In this article, we conduct experiments to test the criterion for medium yielding and bubble removal that we previously derived,20 using a Carbopol microgel as a model yield-stress fluid. We investigate the oscillation dynamics of initially spherical bubbles (100–200 μm) excited by a standing-wave ultrasound field with controlled frequency (19–30 kHz), acoustic pressure amplitude, and spatial distribution of pressure gradients. We measure the resonance curve of the bubbles, their mobility in a pressure gradient and the onset of non-spherical shape oscillations. We extract the viscosity and linear elastic modulus of the material, and compare these measurements to the predictions of the model.20 We finally conclude on the efficiency of bubble removal through bubble oscillation in yield-stress fluids.
2 Bubble dynamics in yield-stress fluids
2.1 Governing equations for bubble oscillations
We briefly recall here the physics of the linear oscillations of a spherical bubble in a yield-stress fluid we derived in a previous article.20 We will show in Section 3.4 that the assumptions of spherical bubble and linear dynamics are reasonable given the size of the bubbles and the rheological properties of the fluid that we use in the experiments.A bubble with equilibrium radius R0 is driven into volumetric oscillations under an acoustic excitation at a frequency f, i.e. a sinusoidal applied pressure p(t) = p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(2πft) far away from the bubble. The time-dependent radius, R(t), is:
sin(2πft) far away from the bubble. The time-dependent radius, R(t), is:
| R(t) = R0[1 +ζ(t)]. | (1) |
Applying the momentum and the mass conservation for the fluid between the spherical bubble surface r = R(t) and r → ∞ yields a generalised Rayleigh–Plesset equation valid for arbitrary fluids.23 Previously our group has derived a model for bubble dynamics in yield-stress fluids by combining the generalised Rayleigh–Plesset equation23 with the elasto-visco-plastic rheological model proposed by Saramito.21 The details of the full model can be found in ref. 20. We recall here that for small-amplitude oscillations and below the yield point, the rheological model reduces to a Kelvin–Voigt viscoelastic solid of linear elastic modulus G and solvent viscosity ηs. A Taylor expansion of the momentum balance valid at order 1 in ζ may then be derived following the classical linear theory of bubble dynamics:24
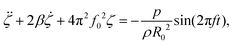 | (2) |
Eqn (2) is a standard second-order linear differential equation that we can reformulate in the frequency domain. We then obtain the second-order transfer function for the bubble oscillation amplitude ζ in the spirit of earlier works on bubble spectroscopy:16,25,26
ζ(t) = ζ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) sin(2πft + ϕ) sin(2πft + ϕ) | (3a) |
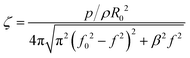 | (3b) |
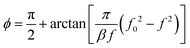 | (3c) |
The amplitude part of the transfer function [eqn (3b)] gives the resonance curve of the bubble. The phase lag between the bubble oscillation and the pressure field ϕ made explicit in eqn (3c) spans from π for f ≪ f0 in the low frequency case to 0 for f ≫ f0 in the high frequency case.
The natural oscillation frequency f0 based on the model of Saramito21 is derived in ref. 20:
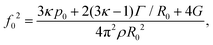 | (4) |
For very soft materials for which G ≪ p0, and for sufficiently large bubbles, i.e. for R0 ≫ Γ/p0 = 1.0 μm, we recover the standard Minnaert frequency27 for a given bubble radius R0:
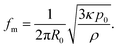 | (5) |
Eqn (5) may be used as well to derive a resonant radius Rm for a given oscillation frequency f. We also recall the predictions for the damping parameter β:20,26
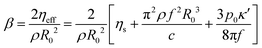 | (6) |
The three terms at the right hand side of eqn (6) respectively account for viscous dissipation proportional to the solvent viscosity ηs in the Kelvin–Voigt model; acoustic scattering of the bubble, and thermal dissipation, in which the dimensionless quantity κ′ is related to the polytropic exponent κ introduced earlier.24 Appendix B shows the relative magnitude of each contribution to β for our experiments. The relative uncertainty on these quantities is discussed in ESI,† Section S1.
2.2 Acoustic radiation forces
Gradients in a pressure field exert a force F = −V∇p on objects of volume V. In a standing wave field p(x,t) = p(x)sin(2πft), the average force 〈F〉 applied on an incompressible object of fixed volume V over one oscillation cycle is zero. Because bubbles expand and contract in response to oscillations in pressure, the same pressure gradient applies a larger net force on the object when its radius is large than when it is small. This leads to a net force over one oscillation period called Bjerknes force:28〈F(x) 〉 = −2πR03∇p(x)ζ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos(ϕ). cos(ϕ). | (7) |
For a driving frequency f and an equilibrium bubble size R0, small bubbles for which cos(ϕ) = −1 will move towards high pressure areas (named anti-nodes) whereas large bubbles for which cos(ϕ) = +1 will move towards low pressure areas (nodes), a classical result in Newtonian fluids.29 Bjerknes forces are non-linear as both ∇p and ζ are proportional to the applied pressure. They are particularly efficient at pushing and pulling bubbles against gravity when the relative pressure gradient |∇p/p| is high.
Following eqn (3b) the pressure p required to obtain a constant oscillation amplitude ζ for all bubble radii R0 is much higher far away from the resonance condition than at resonance. As a consequence, for an imposed oscillation amplitude ζ the pressure gradient ∇p in eqn (7) and the Bjerknes forces will also be stronger away from resonance. We will use this strategy in Section 4.3 to apply strong Bjerknes forces while remaining in the linear range of the bubble oscillation amplitude ζ.
Recent articles have related the force applied to spherical objects and their displacement in purely elastic30 or Kelvin–Voigt viscoelastic solids,31 which can then be applied to yield-stress fluids for relatively small deformations. Assuming the pressure gradient ∇p at location x is directed alongside z we have:
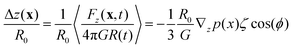 | (8) |
Eqn (8) remains valid as long as the oscillations do not alter the properties of the fluid. Interestingly, it provides a measurement of G that is unaffected by Γ and p0 in contrast with eqn (4). We will use eqn (8) to measure G in Section 4.3.
2.3 Yielding criteria and impact on bubble dynamics
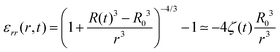 | (9) |
The Kelvin–Voigt model, assumed to be valid below yielding, expresses the applied stress as a sum of an elastic stress Gε and a viscous stress ηs![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/b_i_char_e0a1.gif) . For sufficiently large oscillation amplitudes, the elastic stresses may satisfy the von Mises yield criterion20,33 in a corona of fluid surrounding the bubble. The material then follows a Kelvin–Voigt rheology only outside of the yielded region, including at its edge, located at a distance rY from the centre of the bubble:
. For sufficiently large oscillation amplitudes, the elastic stresses may satisfy the von Mises yield criterion20,33 in a corona of fluid surrounding the bubble. The material then follows a Kelvin–Voigt rheology only outside of the yielded region, including at its edge, located at a distance rY from the centre of the bubble:
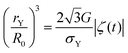 | (10) |
Eqn (10) defines the extent rY of the yielded region as a function of time. Fluid yielding starts when the yielded region exceeds the bubble size at rest R0 at least once during an oscillation cycle. This simplified yielding criterion reads 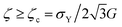 and we hypothesise it is a necessary condition to initiate irreversible bubble rise.
and we hypothesise it is a necessary condition to initiate irreversible bubble rise.
In the yielded region, the purely elastic component of the Kelvin–Voigt model becomes a Maxwell element,21 keeping its elastic modulus G and adding a non-linear plastic degree of deformation of viscosity ηevp, traditionally defined as K![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) n−1 in rotational rheology. The elasto-plastic crossover time of the yielded material is (K/G)1/n: the yielded material remains predominantly elastic below this time scale while plastic deformation dominates above it. Bubble oscillation dynamics is then only affected by yielding when the applied frequency satisfies 2πf(K/G)1/n ≤ 1, in agreement with numerical simulations.20
n−1 in rotational rheology. The elasto-plastic crossover time of the yielded material is (K/G)1/n: the yielded material remains predominantly elastic below this time scale while plastic deformation dominates above it. Bubble oscillation dynamics is then only affected by yielding when the applied frequency satisfies 2πf(K/G)1/n ≤ 1, in agreement with numerical simulations.20
Bubbles also apply a constant stress onto the fluid due to buoyancy or acoustic radiation forces. Hence, these forces will act on the yielded material during the whole time N/f of the acoustic excitation. Irreversible bubble displacement may then be observed provided that f/N(K/G)1/n ≤ 1.
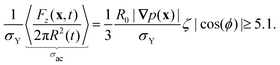 | (11) |
3 Materials and methods
3.1 Carbopol microgel preparation and properties
The yield-stress fluid we use in this article is a Carbopol ETD 2050 microgel (Lubrizol Corporation, Wickliffe, Ohio, USA) of concentration 0.15% w/v that has been extensively studied in the literature.5,35–37 The Carbopol primary particles are made of crosslinked polyacrylic acid, which swells at high pH to form a jammed assembly of soft particles with a diameter of several microns.36Following classical preparation protocols,5,37 we first let the Carbopol flakes dissolve in MilliQ water (18.2 MΩ cm) for 1 hour under gentle agitation before adding 1% v/v 1 M NaOH to adjust the pH to 7. The fluid is then stirred for 20 minutes by an overhead mixer (RW 20 fitted with a R1303 dissolver impeller, IKA, Staufen im Breisgau, Germany) at 2000 rpm. We then place the fluid in a vacuum chamber until all bubbles that have been incorporated during mixing are removed. The fluid is finally left to equilibrate overnight.
We characterise the rheology of the Carbopol microgel using a rotational rheometer (MCR 302, Anton Paar, Graz, Austria). We perform flow curves and oscillatory measurements, from which we deduce σY and G following standard fits;1 both data series are displayed in Appendix A. We measure the sound velocity in the fluid c using a separate acoustic setup. We assume that its density is equal to that of water at room temperature and we choose a surface tension Γ based on dedicated experiments eliminating the impact of elastic stresses.38 We finally use the standard heat diffusivity D of air from classical sources39 to compute the thermal dissipation coefficient κ′ from Section 2.1. The values of these parameters are compiled in Table 1.
| Name | Fluid | Symbol | Value | Unit |
|---|---|---|---|---|
| Polytropic index | κ | 1.30 | ||
| Ambient pressure | Air | p 0 | 1.013 × 105 | Pa |
| Heat diffusivity | Air | D | 1.9 × 10−5 | m2 s−1 |
| Viscosity | Water | η 0 | 1.0 × 10−3 | Pa s |
| Specific gravity | Water | ρ | 9.98 × 102 | kg m−3 |
| Sound velocity | Carbopol | c | 1.495 × 103 | m s−1 |
| Surface tension | Carbopol | Γ | 6.2 × 10−2 | N m−1 |
| Flow index | Carbopol | n | 0.36 | |
| Flow consistency | Carbopol | K | 5.0 | Pa sn |
| Yield stress | Carbopol | σ Y | 5.3 | Pa |
| Shear modulus | Carbopol | G | 36.0 | Pa |
3.2 Ultrasound excitation and high-speed imaging
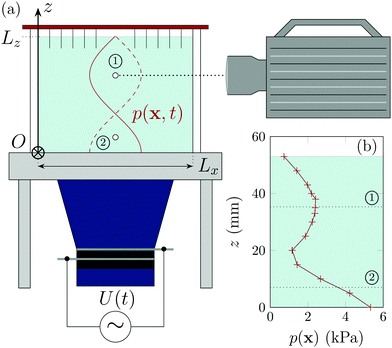
Our experiments take place in a parallelepipedic container filled with the yield-stress fluid, as sketched in Fig. 1. The walls of the containers are either made of glass or duralumin, ensuring total internal reflection of the incident acoustic wave. A lid fitted with needles partially dipped in the fluid is used at the top of the device to prevent sloshing while maintaining the total internal reflection with air.We apply acoustic excitations using a Langevin transducer (Steminc, Doral, Florida, U.S.A.) oscillating between f = 19.45 and 29.2 kHz. We drive the transducer using a waveform generator (33210A, Agilent, Santa Clara, USA) coupled to a linear amplifier (AG 1021, T&C Power Conversion, Rochester, USA). The amplifier gain controls the voltage U applied to the transducer and ultimately the applied pressure amplitude p(x,t) during the experiment. We always work at relatively low input voltage and amplifier gain to prevent non-linear distortion of the amplifier or transducer response.
The container dimensions Lx = 10.2 cm, Ly = 5 cm, and Lz are adapted to produce a resonant standing wave pattern at the applied frequency f, where the pressure amplitude p(x) varies mostly alongside ez. This pattern, shown in Fig. 1(a), corresponds to the (0, 0, 3/2) room mode of the container.40 Pressure measurements using a polyvinylidene fluoride hydrophone (RP 42s, RP Acoustics, Leutenbach, Germany) along the vertical line at the centre of the container [presented in Fig. 1(b)] are compatible with the predicted room mode; they also show that the distortion level is small. We then define two locations named ① and ② (see Fig. 1). The first location corresponds to the pressure anti-node at two-thirds of the cell height for which the pressure gradient ∇p(x1) is zero. It is used in Sections 4.1 and 4.2. The second location is chosen below the pressure node to achieve both a significant pressure and pressure gradient so as to maximise acoustic radiation forces, as explained in Section 2.2. At this location and for an applied frequency f = 19.45 kHz used throughout Section 4.3, we measure a relative pressure gradient |∇p(x2)/p(x2)| in the vertical direction equal to 82 m−1. Given the efficiency of the resonant setup p(x2)/U = 0.13 kPa V−1 at this location, the acoustic pressure gradient |∇p(x2)| exceeds the hydrostatic pressure gradient for voltages U ≥ 1 V.
We align the high-speed camera (Fastcam SA5, Photron, Tokyo, Japan) at location 1 or 2 by imaging the tip of the hydrophone. We then remove the hydrophone and inject a bubble of initial radius ≤300 μm with a small syringe in the frame of the camera before fine-tuning its position through careful manual pushing. Such a procedure inevitably modifies the internal stresses of the fluid around the bubble. Following ref. 26, we consider the slow bubble dissolution (reported in ESI,† Section S2) as a sweep over the initial bubble radii R0 and we then produce a resonance curve [eqn (3b)] for a constant frequency f and varying R0. At the start of the camera acquisition, a burst of N = 200 to 3000 sinusoidal cycles is sent by the waveform generator to the amplifier and the transducer. The camera records images up to 250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 frames per second, corresponding to ∼10 images per oscillation period. We set the total acquisition time to measure both the bubble response to the acoustic excitation and its subsequent relaxation. We report in our acquisitions a small source of vibration at f = 130 Hz. It impacts bubble position measurements but does not affect the measured bubble radius and shape.
000 frames per second, corresponding to ∼10 images per oscillation period. We set the total acquisition time to measure both the bubble response to the acoustic excitation and its subsequent relaxation. We report in our acquisitions a small source of vibration at f = 130 Hz. It impacts bubble position measurements but does not affect the measured bubble radius and shape.
3.3 Bubble contour detection and decomposition into Legendre and Fourier modes
The data processing of video acquisitions is inspired by two recent works.16,41 In short, our Matlab routines normalise raw images and apply a luminosity threshold in order to retrieve the location of the bubble centroid x(t) and its mean radius R(t) = R0[1 + ζ(t)] as a function of time.We then perform a Fourier transform of the radius time series and pay a particular attention to ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/char_e102.gif) (ν) when ν is a multiple or a sub-multiple of the oscillation frequency f. Significant harmonic content indicates that we are no longer working in the linear bubble oscillation framework described in Section 2.
(ν) when ν is a multiple or a sub-multiple of the oscillation frequency f. Significant harmonic content indicates that we are no longer working in the linear bubble oscillation framework described in Section 2.
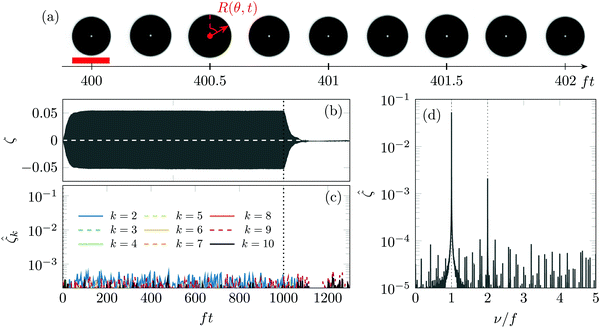
We also study whether bubbles remain spherical during the oscillations by examining the two-dimensional outline of the bubbles. To do so, we plot 360 lines originating at the bubble centroid, with equally spaced polar angles θ, defined from the vertical direction as shown in Fig. 2(a). We define the local bubble radius R0[1 + ζ(θ,t)] as the point where each line crosses the bubble edge. We then define the bubble orientation θ0(t) as the angle for which R(θ0 + θ,t) lies closest to R(θ0 − θ,t). In earlier studies,26,41–43 bubble outlines usually show a clear k-fold symmetry, which is empirically assumed to correspond to the degree, or mode, k of the spherical harmonics Ykm describing the three dimensional shape of the bubble. Following the same approach, we project the bubble shape outline ζ(θ,t) on the Legendre polynomials of degree k, Pk(cos(θ)).41 We may then define the instantaneous amplitude of a shape mode k, ζk(t):
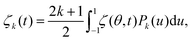 | (12) |
![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) k(ν,t) of the bubble shape modes:
k(ν,t) of the bubble shape modes: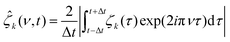 | (13) |
We pay close attention to ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) k(t) =
k(t) = ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) k(f/2,t), as f/2 is the frequency at which shape oscillations arise in Newtonian fluids and Kelvin–Voigt materials.29,44 The time window size used to compute the spectrograms Δt = 2/f allows us to capture this component accurately.
k(f/2,t), as f/2 is the frequency at which shape oscillations arise in Newtonian fluids and Kelvin–Voigt materials.29,44 The time window size used to compute the spectrograms Δt = 2/f allows us to capture this component accurately.
3.4 Characteristic quantities and dimensionless groups
The small bubbles (75 μm ≤ R0 ≤ 300 μm) we consider in this article correspond to very small Bond–Eötvös numbers,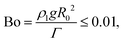 | (14) |
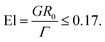 | (15) |
We then expect bubbles to remain spherical at rest, as hypothesised in Section 2. The yielding parameter for such bubbles is also small,
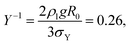 | (16) |
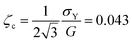 | (17) |
We can finally compute the ratio of the elasto-plastic crossover time scale in the yielded material to that of the bubble oscillations, as defined in Section 2.3. We refer to it as the Deborah number of our experiments:
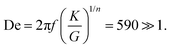 | (18) |
Hence, even if the material has yielded, it will remain predominantly elastic, and we do not expect the bubble oscillations dynamics to be affected by yielding. However, if the material has yielded due to bubble oscillations, irreversible bubble displacement may occur due to buoyancy and acoustic radiation forces, which are applied continuously during N ≥ 1000 cycles, resulting in a time scale ratio f/N(K/G)1/n = De/2πN below unity.
We may lastly define the Péclet number comparing heat diffusion in the air to its advection due to bubble oscillations: Pe = 2πfR02/D = 160. For this range of Péclet numbers, thermal dissipation is the dominant contribution to the damping term β (see Appendix B) and the polytropic exponent is κ = 1.30.24
4 Experimental results
4.1 Linear response: general observations
We first show, for a typical experiment, the criteria we use to define spherical and linear bubble oscillations. Fig. 2(a) shows an image sequence of bubble oscillation after the end of the transient regime at location ①. We also show in Fig. 2(b) the bubble oscillation amplitude ζ(t), which highlights the typical time scale ∼100/f needed for the transient state to vanish. The bubble radius at rest before and long after the oscillations are equal, ruling out any significant gas diffusion into or out of the bubble. Fig. 2(c) confirms that bubbles remain spherical as the shape oscillation modes![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) k remain at a very low level before, during and after the acoustic excitation. We then set the noise threshold for shape oscillations to 10−3 for the rest of this article. Fig. 2(d) confirms the linearity in time of the bubble response. The bubble oscillation spectrum
k remain at a very low level before, during and after the acoustic excitation. We then set the noise threshold for shape oscillations to 10−3 for the rest of this article. Fig. 2(d) confirms the linearity in time of the bubble response. The bubble oscillation spectrum ![[small zeta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e102.gif) (ν) shows a peak at ν = f and harmonic content is almost absent aside from a small peak at ν = 2f. In all our experiments, spherical bubble oscillations are also linear in the time domain.
(ν) shows a peak at ν = f and harmonic content is almost absent aside from a small peak at ν = 2f. In all our experiments, spherical bubble oscillations are also linear in the time domain.
4.2 Resonance curve
We then measure the resonance curve [eqn (3b)] of bubbles in the linear regime, sweeping over their initial radius R0. Fig. 3 highlights the excellent agreement between the measured oscillation amplitude ζ from a series of experiments conducted at a constant pressure amplitude and the prediction of eqn (3b). We first verify that the fitted pressure amplitude p = 1.73 kPa matches independent pressure measurements using the hydrophone (data not shown). All experiments show neither any significant shape oscillation nor any non-linear behaviour in the time domain. By fitting the solvent viscosity to the data, and estimating uncertainties on thermal and acoustic damping from eqn (6), as detailed in ESI,† Section S1, we obtain an estimate for the solvent viscosity, ηs = 1.3 ± 3.0 mPa s, compatible with the viscosity of water η0 = 1.0 mPa s, in agreement with the assumptions of the rheological model.21 Other sets of data (not shown) performed at 19.45 ≤ f ≤ 29.2 kHz are less precise but systematically include the viscosity of water in their confidence intervals.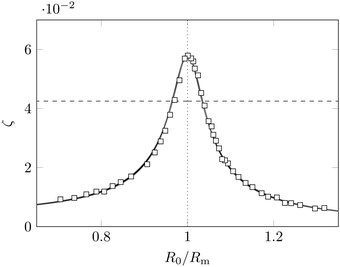 | ||
| Fig. 3 Resonance curve of a bubble in Carbopol obtained for an oscillation frequency of 21.5 kHz and an acoustic pressure amplitude p = 1.73 kPa. The number of cycles has been set to 1000. The Minnaert resonance radius is Rm = 148 μm. The dashed horizontal line represents the onset of Carbopol yielding deduced from eqn (10). Squares represent experimental data. The solid black line is a fit of the linear data following eqn (3b), with two free parameters, the solvent viscosity ηs (included in the damping term β) and the applied pressure p. The 95% confidence interval region is smaller than the size of the markers. | ||
Close to R0 = Rm, the experiments in Fig. 3 satisfy the yielding criterion ζ ≥ ζc, yet follow the exact same trend as the other experiments. Material yielding has therefore no impact on the bubble dynamics. This result confirms the prediction made in Sections 2.3 and 3.4 that elastic stresses do not have time to relax in the yielded material and on the time scale of the oscillations. More surprisingly, we note that none of the experiments for which yielding is expected shows any noticeable displacement of the centre of the bubble.
4.3 Response to acoustic radiation forces
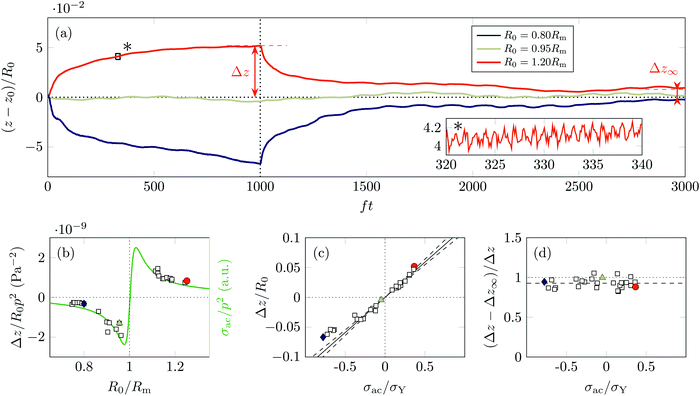
In Section 4.2 we did not observe any significant displacement of bubbles driven into oscillations at location ①, where they are subject only to the buoyancy force. Next we test the effect of acoustic radiation forces [eqn (11)] on bubble displacement, by looking at bubbles positioned at location ② where they are subject also to acoustic pressure gradients.Fig. 4(a) shows the vertical position of the bubble centroid z(t) for three experiments. Bubbles smaller (respectively larger) than the resonant radius Rm show a net downwards (respectively upwards) motion towards the pressure anti-node (respectively pressure node), in line with the change of sign of cos(ϕ) in eqn (3c). The inset of Fig. 4(a) highlights the zero-average oscillatory part of the acoustic radiation forces [averaged out in eqn (7)], clearly noticeable and superposed with the slower displacement related to the Bjerknes force.
Bubble trajectories are non-trivial: they cannot be fitted by a simple exponential law related to the Kelvin–Voigt solid visco-elastic relaxation time ftKV = ηs/G, which amounts to less than one oscillation cycle, nor to the time needed for the transient regime to die out, which corresponds to around 100 cycles, or even the typical elasto-plastic relaxation time of the yielded material, given by De/2πN = 1, also close to N = 100 cycles (see Fig. 2). We can rule out viscous or plastic responses of the fluid as the bubble centroid does not reach a constant, finite velocity dz/dt. They are however not long enough to be completely conclusive regarding more complex, non-linear responses of the fluid, such as creep.5
Fig. 4(b) examines the sensitivity of bubbles to acoustic radiation forces as a function of their size, defined as the normalised displacement Δz/R0p2 as Bjerknes forces are quadratic in pressure amplitude (see Section 2.2). Our experimental data superposes well with the theoretical expression for the average stress applied onto the bubble σac/p2 from eqn (3b), (3c) and (7), which suggests a linear relation between bubble stress and strain.
Fig. 4(c) directly plots the acoustic radiation strain Δz/R0 as a function of the corresponding stress, normalised here by the yield stress σY. We compute here the stress using experimental values of ζ, R0, p and |∇p| and we choose cos(ϕ) based on eqn (3c). The data confirms the linear trend suggested from Fig. 4(b) at low applied stresses and shows a noticeable non-linear deviation for higher stresses. As yielding due to the oscillation amplitude has no impact on the bubble mobility (see ESI,† Section S3), this deviation may only stem from a non-linear behaviour of the emission setup or non-linear elasticity of the Carbopol. We measure the slope of the linear trend at low stress in Fig. 4(c) to extract an estimate of the linear elastic modulus of the surrounding medium G = 44.4 ± 3.5 Pa, following eqn (8). This value is in fair agreement with that obtained from bulk oscillatory rheology, G = 36.0 Pa.
Fig. 4(d) shows the recovered strain 2000 cycles after the end of the acoustic excitation. The recovery is close to 100% for all experiments, which confirms the elastic nature of the deformation shown in Fig. 4(c) expected for experiments conducted for σac/σY ≤ 5.1. Irreversible bubble motion can then only be achieved for higher applied pressure and oscillation amplitude ζ. As we will see in Section 4.4, we could not perform such experiments due to the onset of bubble shape oscillations.
4.4 Shape oscillations
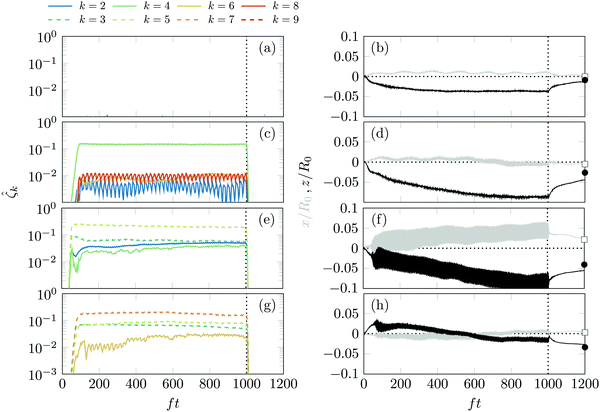
Fig. 5 highlights four shape oscillation modes 4 ≤ k ≤ 7 that have been clearly identified in experiments at location ①. Less than half of the experimental data is sufficiently clear to define unambiguously a shape mode number k. Several experiments (see last row of Fig. 5) instead show a complex outline, which likely results from the projection in the imaging plane of a three-dimensional mode Ymk with m ≠ {0, k, −k} and a random orientation. In all cases, the frequency of the shape oscillations is f/2, confirming that shape oscillations also result from a sub-harmonic instability in yield-stress fluids.
We report in Fig. 6 the shape oscillations observed as a function of both R0 and p for seven slowly dissolving bubbles, identified by a roman numeral from i to vii. Multiple acquisitions have been conducted on each bubble, with the pressure p kept constant throughout their dissolution. The critical pressure of shape oscillations reaches a single local minimum close to R0 = Rm; further away from Rm, it quickly grows and ultimately exceeds the maximum pressure achieved in our setup for R0 ≤ 0.8Rm and R0 ≥ 1.3Rm. Our data indicates that the shape number k in our experiments increases with R0, in qualitative agreement with models44,45 and experiments in Newtonian fluids.42,47
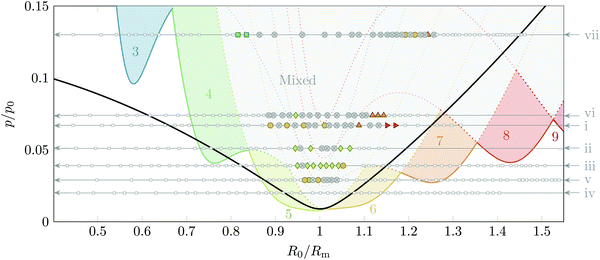 | ||
| Fig. 6 Phase diagram for bubble shape oscillations as a function of the applied pressure p/p0 and the initial radius of bubbles R0/Rm for an excitation frequency f = 22.5 kHz. Experimental data have been acquired throughout the dissolution of seven bubbles, identified with roman numerals i to vii from earliest to latest data series. As the applied pressure p is kept constant for each bubble, the seven data series form horizontal series of points, starting from high values of R0 and ending for low values of R0, following the direction of the grey arrows. Individual acquisitions for each data series are shown as symbols. The modes that we could define without any ambiguity are plotted as red rightwards pointing triangles (k = 8), orange upwards pointing triangles (k = 7), yellow circles (k = 6), light green diamonds (k = 5) and green squares (k = 4). Most acquisitions with shape oscillations have a non-clear mode [e.g. last row of Fig. 5]; they are plotted as crossed circles. The small white squares represent stable spherical oscillations. The critical pressure for each shape mode, computed from ref. 44 and eqn (3b), is shown as a line with the same colour coding as the experiments. Above these lines lie coloured regions where only one oscillation mode k can grow, and a broader grey region where multiple shape modes may grow. The black solid line depicts the threshold for fluid yielding defined combining eqn (3b) and (10). | ||
We overlay in Fig. 6 the predicted critical pressure pc,k derived in Appendix C by combining eqn (3b) and the critical bubble oscillation amplitude ζc,k above which spherical oscillations are linearly unstable. We choose the value of the viscosity we fitted in Section 4.2, ηs = 1.3 mPa s and the elastic modulus measured in Section 4.3, G = 44.4 Pa. A large amount of experiments shows stable spherical oscillations whereas the model predicts they are linearly unstable with respect to shape oscillation modes 4 to 8. The model however correctly predicts that modes 5 and 6 are favoured for R ≃ Rm in agreement with the low values of pc,5 and pc,6 in this region.
Fig. 7 shows the strong impact of shape oscillations on bubble motion. The first three bubbles [Fig. 7(a–f)] show motion towards an antinode in agreement with their initial size R0 ≤ Rm. The presence of a clear shape mode enhances bubble mobility, as shown in Fig. 7(c and d) for k = 4. We also observe spurious motion in the direction transverse to the pressure gradient when a single bubble shape mode k is no longer clearly identified [as seen in Fig. 7(e and f)]. We also have observed reversals of the bubble direction of motion following the onset of shape oscillations [Fig. 7(g and h)]. In general we conclude that while shape oscillations increase bubble displacement, the direction of motion can no longer be controlled.
5 Discussion
5.1 Precision and relevance of the solvent viscosity measurement
The experimental bubble oscillation amplitude ζ in the linear regime may be fitted to the theoretical resonance curve to extract the oscillation damping parameter β. After carefully subtracting from β the dominant acoustic and thermal contributions, we measure a fluid viscosity ηs = 1.3 mPa s. An analysis of the fitting procedure and the uncertainties on β shows that this value is not statistically different from the viscosity of water used as the solvent here, and in agreement with the rheological model.20,21 This low value seems surprising considering the bulk oscillatory rheology of Carbopol (see Appendix A) which rather suggests a viscosity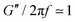 Pa s in the linear regime for low frequencies f = 1 Hz, while the Kelvin–Voigt model we use assumes a constant viscosity below yielding for all frequencies.
Pa s in the linear regime for low frequencies f = 1 Hz, while the Kelvin–Voigt model we use assumes a constant viscosity below yielding for all frequencies.
Indeed, real hydrogels and yield-stress fluids under oscillatory shear do not show a constant viscosity as a function of f: classical rheological measurements show that their loss modulus G′′ behaves as a constant or as slowly increasing power laws of f50 leading to a decreasing viscosity G′′/2πf. These power law scalings may be reproduced by fractional derivative models50 but their microscopic origin remain insufficiently understood.7 The value of the viscosity deduced from G′′ in oscillatory rheology may therefore not be particularly meaningful. In contrast, viscous or close-to-viscous scaling of the stress has been experimentally observed in yield-stress fluids at high frequencies and strain rates.51,52 At such frequencies, dissipation due to the solvent, scaling as ηsf, may become the dominant contribution to G′′, and the material could then recover a Kelvin–Voigt rheology. Our results suggest that bubble oscillations experiments fit into this high-frequency limit and allow a proper measurement of the solvent viscosity.
5.2 Linear response to Bjerknes forces
We have used in Section 4.3 the constant (or zero-frequency) part of the acoustic radiation force to perform an equivalent of step-stress tests, but at a local scale R0. For moderate acoustic stresses σac ≤ σY, we measure a linear strain–stress relation at the end of oscillations, from which we deduce an independent measurement of the local linear elastic modulus of the fluid below yielding, G = 44.4 ± 3.5 Pa, comparable to that obtained using bulk rheology, G = 36 Pa. All quantities used to derive G are either directly measured or estimated from the resonance curve: hence, in contrast with previous works,53 our measurement is truly independent from bulk rheology.The complex time dependence of the displacement shown in Fig. 4(a) is reminiscent of creep behaviour.5 Creep is however usually associated to irreversible strain and a non-linear stress–strain relation in bulk rheology experiments, both of which are not observed here. Interestingly, fully reversible creep motion up to the yield point has also been reported in experiments in which acoustic radiation forces are used to push small spheres.53 The relatively small pressure gradients applied in our experiments according to eqn (11) then cannot alone initiate bubble rise. Performing experiments of longer duration may reveal whether the response to acoustic radiation forces indeed follows a power law or an exponential profile with time, which could be helpful to validate the recent, advanced models of yield-stress fluids.7,8
5.3 Absence of irreversible rising motion
Several experiments satisfy the bubble oscillation yielding criterion ζ ≥ ζc and apply acoustic radiation stresses σac comparable with the yield stress for a sufficiently long time to let elastic stresses relax. Yet, they do not suffice to induce irreversible bubble motion and we do not observe the finite average rising speed predicted in the recent numerical simulations of ref. 19. The yielding criterion ζc = 0.043 we have derived is then a necessary condition, but not sufficient, to induce bubble rise at a useful rate for removal applications.One explanation for this lack of irreversible motion is that the steady-state bubble rise velocity is too small to be observed. Firstly, the yielded region remains under 1.25 times the size of the bubble radius, increasing drag by a factor 40 compared to the unconfined case.54 Secondly, the plastic viscosity in the yielded material stays significantly higher than the solvent viscosity. The corresponding rising velocities may therefore be too small to be resolved in experiments.
Additional factors may prevent irreversible rising motion. For instance, the von Mises yield criterion [eqn (10)] has been shown to fail for bulk yielding in extension, as already reported in other simple yield-stress fluids.55–57 Another possibility lies in finite-size effects given the relatively small size of the bubble compared to the constitutive elements of Carbopol. Local restructuration around slowly-growing bubbles has been recently evidenced in sparse networks of microfibrillated cellulose, which impacts their bubble retention capacity.58 It is difficult to know at the moment whether this scenario applies in our case, since Carbopol is soft-jammed and isotropic and the strain rates at play are high. We may finally question the relevance of the very notions of yielding and unyielding in our experiment since the oscillation timescale 1/f can be below that of the microscopic plastic rearrangements used in yield-stress fluids models.7,8
5.4 Nature and onset of shape oscillations
The critical pressure pck above which we experimentally observe shape oscillations is significantly higher in Carbopol thant what we expect from a linear instability analysis in Kelvin–Voigt materials44 if we use the fluid properties we derived in Sections 4.2 and 4.3. Yield-stress fluids are known to exhibit residual stresses at rest, with unknown spatial distribution. We expect non-homogeneous residual stresses around the bubble to impact bubble shape oscillations by altering the critical pressure pc,k depending on the compatibility between the geometry of the shape modes and that of the residual stresses. Further analysis of the bubble shapes, conducted in ESI,† Section S4, shows that residual stresses induce a very small (0.5%) residual deformation of the bubble at rest. Under acoustic excitation, the bubble shape modes do neither respect the orientation nor the symmetry of these residual deformations. Hence we do not observe any direct impact of residual stresses on bubble shape oscillations even though we cannot rule out their influence. Using a solvent with a higher viscosity in experiments would be particularly helpful to either reconcile experimental data with the linear instability model44 or to prove that it is not applicable to yield-stress fluids.5.5 Consequences on acoustic bubble removal performance
Shape oscillations imply unpredictable bubble motion that inevitably reduces the efficiency of any directed motion induced by acoustic radiation forces or bubble buoyancy. We notice that the window of operation for bubble removal, lying above the black line and below the coloured symbols of Fig. 6, is limited especially since the yielding criterion of eqn (10) does not warrant bubble rise. Bubble removal using acoustic excitation in Carbopol could then be performed using stronger pressure gradients, for instance using focused ultrasound beams. We suspect Carbopol is particularly resistant to the removal process due to its very wide linear elastic regime, as shown in bulk rheology (Appendix A). Bubble removal should be easier in almost any other yield-stress fluid as they break down under much smaller strains.59,60 Increasing ηs could also improve bubble removal by raising the critical pressure at which shape oscillations arise.6 Conclusion
In this article, we have investigated how a small bubble oscillating at a high frequency interacts with Carbopol, a model yield-stress fluid. Bubbles of different sizes allow us to perform bubble spectroscopy25,26 and extract a viscosity ηs = 1.3 mPa s of the fluid at high frequency and for a finite extensional deformation, in agreement with the solvent viscosity of water and as expected from a previous numerical study.20 We have also used pressure gradients to apply acoustic radiation forces on bubbles, from which we measure the local linear shear modulus of the fluid G = 44.4 Pa, in fair agreement with bulk rheology. As long as the oscillations remain spherical, bubble motion is fully reversible given the range of acoustic radiation stresses |σac| ≤ σY achieved in our experiment. In particular, motion reversibility appears unaffected by the oscillatory yielding criterion derived by De Corato et al.20Experiments performed at higher pressure always resulted in non-spherical shape oscillations. As shape oscillations result in an unpredictable bubble motion in all directions, acoustic bubble removal is quite inefficient in Carbopol. Future studies should explore the applicability of acoustic bubble removal in more fragile networks, corresponding to a wide range of attractive colloidal and athermal yield stress fluids in which spherical bubble oscillations largely beyond the yield point are possible, resulting in a strong decrease of both bubble confinement and plastic viscosity during its assisted motion.
Conflicts of interest
There are no conflicts to declare.Appendix
A Carbopol rheology
We characterise the rheology the Carbopol microgel using a standard rotational rheometer (MCR 302) working with a cone-plate geometry fitted with sandpaper discs (grit P1500) to suppress wall slip. Before every test, we apply a pre-shear step at![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1500 s−1 for 30 s and a rest step at σ = 0 Pa for 20 s. We perform two consecutive flow curves for decreasing and increasing shear rates
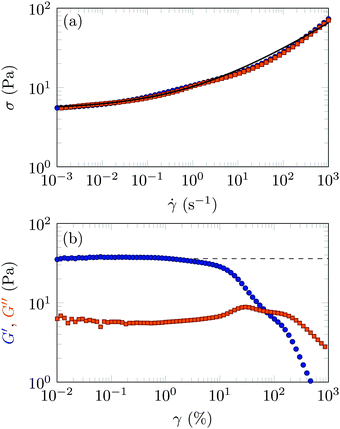
= 1500 s−1 for 30 s and a rest step at σ = 0 Pa for 20 s. We perform two consecutive flow curves for decreasing and increasing shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) between 0.001 s−1 and 1500 s−1, choosing 5 s steps and 10 points per decade. Amplitude sweeps are conducted at a frequency of 1 Hz for increasing shear strains γ between 0.01% to 1000%, and we choose to acquire 15 points per decade and average over 10 oscillation cycles. Our data are presented in Fig. 8.
between 0.001 s−1 and 1500 s−1, choosing 5 s steps and 10 points per decade. Amplitude sweeps are conducted at a frequency of 1 Hz for increasing shear strains γ between 0.01% to 1000%, and we choose to acquire 15 points per decade and average over 10 oscillation cycles. Our data are presented in Fig. 8.
Fig. 8(a) shows the flow curves of the fluid. The data fit to a Herschel–Bulkley law, σ = σY + K![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) n is fair and yields n = 0.36, K = 5.0 Pa sn, and σY = 5.3 Pa. The two consecutive flow curves superpose well, meaning that fluid thixotropy is negligible. In Fig. 8(b), we identify the linear modulus of the Carbopol G with the storage part of the elastic modulus G′ in the linear visco-elastic plateau for which G′ ≫ G′′; this plateau spans from γ ≥ 0.01% to γ = 10%. We obtain G = 36.0 Pa. We also notice that the storage modulus is rather insensitive to the applied frequency f in the range accessible to the rheometer, 0.1 Hz to 10 Hz (data not shown).
n is fair and yields n = 0.36, K = 5.0 Pa sn, and σY = 5.3 Pa. The two consecutive flow curves superpose well, meaning that fluid thixotropy is negligible. In Fig. 8(b), we identify the linear modulus of the Carbopol G with the storage part of the elastic modulus G′ in the linear visco-elastic plateau for which G′ ≫ G′′; this plateau spans from γ ≥ 0.01% to γ = 10%. We obtain G = 36.0 Pa. We also notice that the storage modulus is rather insensitive to the applied frequency f in the range accessible to the rheometer, 0.1 Hz to 10 Hz (data not shown).
B Contributions to damping of bubble oscillations
We compare in Fig. 9 the relative magnitude of the three contributions to dissipation detailed in eqn (6). We respectively note: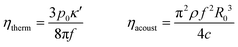 | (19) |
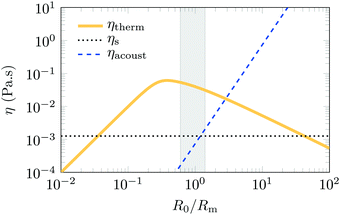 | ||
| Fig. 9 Thermal, viscous and acoustic damping under linear bubble oscillation plotted as effective viscosities for an applied frequency f = 22.5 kHz. The thermal and acoustic contributions are directly plotted from eqn (6), while the value of ηs has been fitted to the resonance curve in Section 4.2. The greyed out region is our usual operating range. | ||
C Threshold for shape oscillations in soft materials
We recall here the predictions of ref. 44, who derived the critical bubble oscillation amplitude above which shape oscillations may be observed in a neo-Hookean, Kelvin–Voigt viscoelastic solid. Defining intermediate quantities: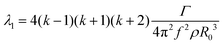 | (20) |
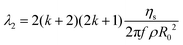 | (21) |
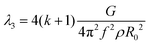 | (22) |
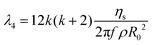 | (23) |
The critical amplitude ζc,k above which a shape mode k develops may be expressed as:
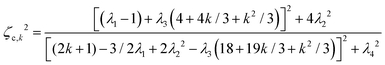 | (24) |
Since our experiments show that bubble oscillations up to the shape oscillation threshold are linear in the time domain, we may combine eqn (3b) and (24) to derive explicitly the critical pressure pc,k for all modes k. One surprising consequence of eqn (24) is that, despite modelling the three-dimensional growth of spherical harmonics Ymk generally defined by two shape modes k and m, the critical pressure of the model is independent of m.
Close to R0 = Rm, the critical pressure pc,k reaches a minimum for all modes k because it corresponds to the resonance condition of spherical oscillations. In addition, shape modes have a natural oscillation frequency, given by:
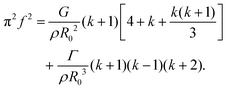 | (25) |
When f is imposed, eqn (25) defines a radius at which a given shape mode k resonates, corresponding to the minima of the coloured tongues in Fig. 6. In some particular cases (here, for k = 5 and 6), both the spherical mode and the shape mode resonate around Rm, resulting in particularly low critical pressures pc,5 and pc,6, as observed in Fig. 6 and in the experiments.
Acknowledgements
The authors wish to thank M. De Corato, J. Tsamopoulos and Y. Dimakopoulos for stimulating discussions and their critical reading of the paper. They also thank D. Baresch for his help with the design of the experimental setup. This work is supported by European Research Council Starting Grant No. 639221 (V. G.).Notes and references
- P. Coussot, J. Non-Newtonian Fluid Mech., 2014, 211, 31–49 CrossRef CAS.
- D. Bonn, M. M. Denn, L. Berthier, T. Divoux and S. Manneville, Rev. Mod. Phys., 2017, 89, 035005 CrossRef.
- S. Stein and H. Buggisch, J. Appl. Math. Mech., 2000, 80, 827–834 Search PubMed.
- K. Hyun, M. Wilhelm, C. O. Klein, K. S. Cho, J. G. Nam, K. H. Ahn, S. J. Lee, R. H. Ewoldt and G. H. McKinley, Prog. Polym. Sci., 2011, 36, 1697–1753 CrossRef CAS.
- P. Lidon, L. Villa and S. Manneville, Rheol. Acta, 2017, 56, 307–323 CrossRef CAS.
- J. Goyon, A. Colin, G. Ovarlez, A. Ajdari and L. Bocquet, Nature, 2008, 454, 84 CrossRef CAS.
- A. Nicolas, E. E. Ferrero, K. Martens and J.-L. Barrat, Rev. Mod. Phys., 2018, 90, 045006 CrossRef CAS.
- C. J. Dimitriou and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2019, 265, 116–132 CrossRef CAS.
- Y. Dimakopoulos, M. Pavlidis and J. Tsamopoulos, J. Non-Newtonian Fluid Mech., 2013, 200, 34–51 CrossRef CAS.
- A. D. Mazzeo, M. E. Lustrino and D. E. Hardt, Polym. Eng. Sci., 2012, 52, 80–90 CrossRef CAS.
- J. A. Koch, D. I. Castaneda, R. H. Ewoldt and D. A. Lange, Cem. Concr. Res., 2019, 115, 31–42 CrossRef CAS.
- M. S. Plesset and A. Prosperetti, Annu. Rev. Fluid Mech., 1977, 9, 145–185 CrossRef CAS.
- B. Dollet, P. Marmottant and V. Garbin, Annu. Rev. Fluid Mech., 2019, 51, 331–355 CrossRef.
- C. C. Coussios and R. A. Roy, Annu. Rev. Fluid Mech., 2008, 40, 395–420 CrossRef.
- C. W. Barney, C. E. Dougan, K. R. McLeod, A. Kazemi-Moridani, Y. Zheng, S. Ye, Z. Tiwari, I. Sacligil, R. A. Riggleman, S. Cai, J.-H. Lee, S. R. Peyton, G. N. Tew and A. J. Crosby, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 9157–9165 CrossRef CAS.
- A. Jamburidze, M. De Corato, A. Huerre, A. Pommella and V. Garbin, Soft Matter, 2017, 13, 3946–3953 RSC.
- J. B. Estrada, C. Barajas, D. L. Henann, E. Johnsen and C. Franck, J. Mech. Phys. Solids, 2018, 112, 291–317 CrossRef.
- Y. Holenberg, O. M. Lavrenteva, A. Liberzon, U. Shavit and A. Nir, J. Non-Newtonian Fluid Mech., 2013, 193, 129–143 CrossRef CAS.
- G. Karapetsas, D. Photeinos, Y. Dimakopoulos and J. Tsamopoulos, J. Fluid Mech., 2019, 865, 381–413 CrossRef CAS.
- M. De Corato, B. Saint-Michel, G. Makrigiorgos, Y. Dimakopoulos, J. Tsamopoulos and V. Garbin, Phys. Rev. Fluids, 2019, 4, 073301 CrossRef.
- P. Saramito, J. Non-Newtonian Fluid Mech., 2009, 158, 154–161 CrossRef CAS.
- S. Iwata, Y. Yamada, T. Takashima and H. Mori, J. Non-Newtonian Fluid Mech., 2008, 151, 30–37 CrossRef CAS.
- A. Prosperetti, Phys. Fluids, 1982, 25, 409–410 CrossRef.
- A. Prosperetti, J. Acoust. Soc. Am., 1977, 61, 17–27 CrossRef.
- S. M. van der Meer, B. Dollet, M. M. Voormolen, C. T. Chin, A. Bouakaz, N. de Jong, M. Versluis and D. Lohse, J. Acoust. Soc. Am., 2007, 121, 648–656 CrossRef CAS.
- F. Hamaguchi and K. Ando, Phys. Fluids, 2015, 27, 113103 CrossRef.
- M. Minnaert, London, Edinburgh Dublin Philos. Mag. J. Sci., 1933, 16, 235–248 CrossRef.
- L. A. Crum, J. Acoust. Soc. Am., 1975, 57, 1363–1370 CrossRef.
- T. G. Leighton, A. J. Walton and M. J. W. Pickworth, Eur. J. Phys., 1990, 11, 47 CrossRef.
- Y. A. Ilinskii, G. D. Meegan, E. A. Zabolotskaya and S. Y. Emelianov, J. Acoust. Soc. Am., 2005, 117, 2338–2346 CrossRef CAS.
- M. W. Urban, I. Z. Nenadic, S. A. Mitchell, S. Chen and J. F. Greenleaf, J. Acoust. Soc. Am., 2011, 130, 1133–1141 CrossRef.
- C. W. Macosko, Rheology: Principles, Measurements and Applications, Wiley-VCH, New York, 1994 Search PubMed.
- R. Hill, The mathematical theory of plasticity, Oxford University Press, 1998, vol. 11 Search PubMed.
- D. Sikorski, H. Tabuteau and J. R. de Bruyn, J. Non-Newtonian Fluid Mech., 2009, 159, 10–16 CrossRef CAS.
- J.-M. Piau, J. Non-Newtonian Fluid Mech., 2007, 144, 1–29 CrossRef CAS.
- P. Lefrançois, E. Ibarboure, B. Payré, E. Gontier, J.-F. L. Meins and C. Schatz, J. Appl. Polym. Sci., 2015, 132, 42761 CrossRef.
- M. Dinkgreve, M. Fazilati, M. Denn and D. Bonn, J. Rheol., 2018, 62, 773–780 CrossRef CAS.
- L. Jørgensen, M. Le Merrer, H. Delanoë-Ayari and C. Barentin, Soft Matter, 2015, 11, 5111–5121 RSC.
- CRC Handbook of Chemistry and Physics, ed. J. Rumble, CRC Press, 2019 Search PubMed.
- P. M. Morse and R. H. Bolt, Rev. Mod. Phys., 1944, 16, 69 CrossRef.
- M. Guédra, S. Cleve, C. Mauger, P. Blanc-Benon and C. Inserra, Phys. Rev. E, 2017, 96, 063104 CrossRef.
- M. Versluis, D. E. Goertz, P. Palanchon, I. L. Heitman, S. M. van der Meer, B. Dollet, N. de Jong and D. Lohse, Phys. Rev. E, 2010, 82, 026321 CrossRef.
- V. Poulichet, A. Huerre and V. Garbin, Soft Matter, 2017, 13, 125–133 RSC.
- K. Murakami, R. Gaudron and E. Johnsen, Ultrason. Sonochem., 2020, 67, 105170 CrossRef CAS.
- A. O. Maksimov and T. G. Leighton, Acta Acust. Acust., 2001, 87, 322–332 Search PubMed.
- F. Mekki-Berrada, P. Thibault and P. Marmottant, Phys. Fluids, 2016, 28, 032004 CrossRef.
- S. Cleve, M. Guédra, C. Mauger, C. Inserra and P. Blanc-Benon, J. Fluid Mech., 2019, 875, 597–621 CrossRef CAS.
- K. Foteinopoulou and M. Laso, Ultrasonics, 2010, 50, 758–776 CrossRef CAS.
- A. A. Doinikov, J. Fluid Mech., 2004, 501, 1–24 CrossRef.
- A. Jaishankar and G. H. McKinley, Proc. – R. Soc. Edinburgh, Sect. A: Math., 2013, 469, 20120284 CrossRef.
- T. G. Mason, Rheol. Acta, 2000, 39, 371–378 CrossRef CAS.
- M. Caggioni, V. Trappe and P. T. Spicer, J. Rheol., 2020, 64, 413–422 CrossRef CAS.
- P. Lidon, L. Villa and S. Manneville, Soft Matter, 2019, 15, 2688–2702 RSC.
- J. Happel and H. Brenner, Low Reynolds number hydrodynamics, Springer, 1983, DOI:10.1007/978-94-009-8352-6.
- K. Niedzwiedz, H. Buggisch and N. Willenbacher, Rheol. Acta, 2010, 49, 1103–1116 CrossRef CAS.
- X. Zhang, O. Fadoul, E. Lorenceau and P. Coussot, Phys. Rev. Lett., 2018, 120, 048001 CrossRef CAS.
- S. Varchanis, S. J. Haward, C. C. Hopkins, A. Syrakos, A. Q. Shen, Y. Dimakopoulos and J. Tsamopoulos, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12611–12617 CrossRef CAS.
- J. Song, M. Caggioni, T. M. Squires, J. F. Gilchrist, S. W. Prescott and P. T. Spicer, Rheol. Acta, 2019, 58, 217–229 CrossRef CAS; J. Song, M. Caggioni, T. M. Squires, J. F. Gilchrist, S. W. Prescott and P. T. Spicer, Rheol. Acta, 2019, 58, 231–239 CrossRef.
- D. E. V. Andrade and P. Coussot, Soft Matter, 2019, 15, 8766–8777 RSC.
- S. Saha, B. Saint-Michel, V. Leynes, B. P. Binks and V. Garbin, Rheol. Acta, 2020, 59, 255–266 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01044h |
| ‡ Present address: Department of Chemical Engineering, Delft University of Technology, Delft 2629 HZ, The Netherlands. E-mail: v.garbin@tudelft.nl |
| This journal is © The Royal Society of Chemistry 2020 |