Electrohydrodynamics of droplets and jets in multiphase microsystems
Cheng
Qi
a,
Yao
Li
a,
Zhou
Liu
*b and
Tiantian
Kong
 *c
*c
aCollege of Mechatronics and Control Engineering, Shenzhen University, Shenzhen 518000, Guangdong, China
bCollege of Chemistry and Environmental Engineering, Shenzhen University, Shenzhen 518000, Guangdong, China. E-mail: zhouliu@szu.edu.cn
cDepartment of Biomedical Engineering, School of Medicine, Shenzhen University, Shenzhen 518000, Guangdong, China. E-mail: ttkong@szu.edu.cn
First published on 17th August 2020
Abstract
Electrohydrodynamics is among the most promising techniques for manipulating liquids in microsystems. The electric stress actuates, generates, and coalesces droplets of small sizes; it also accelerates, focuses, and controls the motion of fine jets. In this review, the current understanding of dynamic regimes of electrically driven drops and jets in multiphase microsystems is summarized. The experimental description and underlying mechanism of force interplay and instabilities are discussed. Conditions for controlled transitions among different regimes are also provided. Emerging new phenomena either due to special interfacial properties or geometric confinement are emphasized, and simple scaling arguments proposed in the literature are introduced. The review provides useful perspectives for investigations involving electrically driven droplets and jets.
1 Introduction
Electrohydrodynamics (EHD) can be considered as fluid mechanics involving electric force effects.1 EHD is one of the most effective techniques to manipulate liquids with small volumes in microsystems, and it has been extensively employed in a wide range of applications from liquid handling to material fabrication.2–8 Most problems in EHD are the evolution of electrically charged fluids by surface or volumetric forces, originating from a net charge density or a permittivity gradient.9 Enormously rich EHD phenomena have been reported in multiphase microsystems, including steady, non-steady and periodic flows resulting from the interplay of electric and hydrodynamic forces associated with fluids in motion. These phenomena are further complicated by the geometric confinement and multiphase interfaces in these systems.The earliest record of an EHD experiment goes back to the far past when W. Gilbert found the formation of a conical shape of a spherical water droplet on a dry surface beneath a charged rod in the seventeenth century.10 Rapid development of research on electrically driven jets and disintegration of electrified jets began in the 1960s,11–22 which led to an active field of electrospray in the 1980s–1990s.9–15,25–28 The thriving of electrospray is motivated by its applications in ionizing biomolecules and fabricating nanoparticles.6,32 In the 2000s, the discovery of whipping instability for electrically forced jets gave rise to broad interest in electrospinning, since it produces large quantities of nanofibers from a wide range of polymers.33–42 Meanwhile, featuring the ability to manipulate liquids of small volume, microfluidics shows great promise as micro-total-analysis-systems for miniaturized biochemical/biological reactions.43–48 Liquid droplets of small volumes have been manipulated passively and actively in microfluidics, in which an electric field has been utilized for droplet generation,49 droplet colascence,50 droplet splitting50 and directional movement of droplets.50 In recent years, the development of electrohydrodynamic printing for patterns and structures in high resolution has been successful. It is driven by emerging applications such as flexible electronics and energy storage materials.3,51–57
Over the years, the understanding of the dynamic behaviors of droplets and jets exposed to an electric field has laid the cornerstone for their manipulation in various scenarios, which are the workhorse for electrospray, electrospinning, electrowetting and all associated applications. While most existing reviews focused on applications of electrohydrodynamics of droplets and jets, few of them focus on compiling their fundamental physics. The operation modes and underlying physics of electrospray and electrospinning have been reviewed,9,28,40,58–61 for instance, a comprehensive and in-depth review on the physics of cone-jets in electrospray is recommended;2 however, new developments of electrified liquid jets/filaments of multiphase systems in confined geometry have not been put into perspective with the existing consensus.
Therefore, this review discusses dynamic responses of droplets and jets charged by electric fields in multiphase microsystems, emphasizing recent developments. Multiphase microflows are laminar with dominant capillary effects, composed of two or more contacting fluidic phases, for example, water–oil or liquid–gas phases. To avoid making the scope of this review overbroad, another branch of EHD, electrokinetics, always occurring in conducting electrolytes, is not discussed here, which may merit a separate review. We start in Section 2 by describing the principle balancing laws and dimensionless numbers with definitive parameters for electrohydrodynamic drops and jets. In Section 3, we introduce general models for droplets in response to applied electric fields including electrowetting and electrodeformation, explaining how electric stress interacts with surface tension effects for a single droplet. Subsequently, we elucidate rich operation modes of electrocoalescence for a pair of droplets and for a droplet and an interface under the influence of an electric field, along with the principle electrohydrodynamics involved in the process. We then devote Section 4 to describing the dynamics of electrically driven microjets that transit from an electrified meniscus, along with the associated instabilities. We mainly focus on Rayleigh–Plateau (RP) instability, coiling instability, and whipping instability. Apart from summarizing the important consensus of electrically driven microjets, we explore in detail the emergence of electrocoiling instability as well as the crossover of RP, coiling and whipping instabilities for charged liquid filaments or confined microjets in Section 4. Finally, we close this review with a perspective and outlook in Section 5.
2 Physical mechanisms: balancing laws and dimensionless numbers
The dynamic behaviors we discuss in this review include electrowetting, electrocoalescence, electrospray, electrocoiling and electrospinning. Typically, a liquid meniscus or droplet is characterized by its radius a. It can be supplied by a flow rate Q, emerging from an electrified conducting nozzle with a charging voltage of U, or it can be placed in an applied electric field with a field intensity E. The electric field is set up by two electrodes separated by a distance of L. These two electrodes can be in point-to-point, nozzle-to-plate, or plate-to-plate configurations. The working liquid is mostly a newtonian fluid characterized by a density of ρ, viscosity of μ, interfacial tension of γ, electrical conductivity of K and relative dielectric constant of ε.To compare the relative importance of gravitational, surface tension, viscous, inertial, and electrical effects, dimensionless numbers such as Weber, Bond, Reynolds, Ohnesorge, capillary and electrocapillary are used. The Weber number We ∼ ρQ2/Lc3γ and the capillary number Ca = μv/γ denote the ratio of the inertial and the viscous to the surface tension effect, respectively. The Bond number Bo = ρLc2g/γ, and the electrocapillary number Cae = ε0εE2Lc/γ compare the gravitational and electric stress relative to the surface tension effect, respectively. The Ohnesorge number Oh = μ/(γρLc)0.5 measures the relative importance of the viscous effect to the combined capillary and inertial effects, and the Reynolds number Re = ρvLc/μ estimates the ratio of the inertial to the viscous effect. In these dimensionless numbers, Lc refers to the characteristic length-scale of the problem that needs to be described.
3 Electrohydrodynamic droplets in multiphase microsystems
Droplets respond to an applied electric field in a variety of ways, spanning a wide spectrum of multiphase problems. This attribute enables controlled droplet manipulation by an electric field,62 giving rise to several fundamental applications, such as digital microfluidics63,64 and de-emulsification in oil recovery.65,66 We start with the electrowetting of droplets, where the contact angle of droplets deposited on a solid substrate changes by using an electric field. We then introduce the deformation of a single droplet placed in an electric field, followed by the deformation and coalescence of a pair of two neighboring droplets in an electric field. The electric-driven coalescence of two droplets, or of a droplet and an interface, exhibits rich operating regimes, which we classified into “coalescence”, “non-coalescence”, and “partial coalescence”, respectively (Fig. 1). These three dynamic regimes are reviewed sequentially in the separate sections.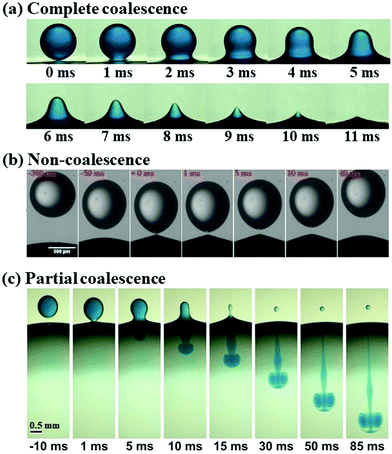 | ||
| Fig. 1 Illustration of three classical dynamic regimes of droplet–interface interaction: (a) complete coalescence (reproduced with permission from ref. 67, Copyright 2020, Elsevier Ltd);67 (b) non-coalescence, where the droplet bounces off the interface (reproduced with permission from ref. 68, Copyright 2020, American Chemical Society);68 and (c) partial coalescence, with a smaller secondary droplet left above the interface (reproduced with permission from ref. 69, Copyright 2012, American Physical Society).69 | ||
3.1 Electrowetting
Electrowetting is a phenomenon in which the wetting angle between a liquid droplet and a substrate can be modified by a tunable electric field.70–72 With the electric field applied, the interfacial energy between the liquid and the substrate is changed, which affects the macroscopic contact angle of the droplet on a substrate,72 as shown in Fig. 2. The relationship between the modified contact angle θ and the applied voltage U can be estimated as:71,73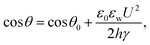 | (1) |
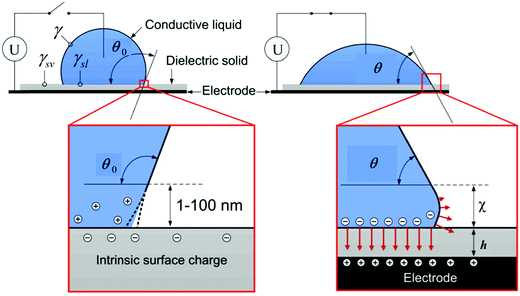 | ||
| Fig. 2 Schematic of the electrowetting of a conductive liquid droplet on a substrate. Reproduced with permission from ref. 72. Copyright 2012, Taylor & Francis.72 | ||
In microsystems, by configuring the electrodes and programming the applied voltage, a substrate with controllable local surface hydrophilicity can be fabricated. Such a substrate enables the actuation of liquid droplets through the electrowetting force,74–76 which inspires the field of digital microfluidics, widely used for applications including chemical reactions,77 display technology78 and micro-lenses.79
3.2 Electrodeformation
The electric responses of a droplet suspended in another immiscible liquid is of fundamental importance. Under an external electric field, the interplay of the electric stress and the surface tension deforms the droplet to adopt different shapes, which can be characterized as: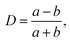 | (2) |
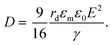 | (3) |
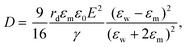 | (4) |
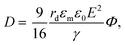 | (5) |
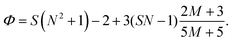 | (6) |
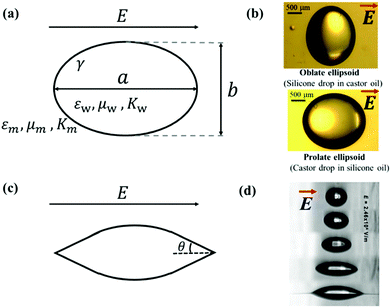 | ||
| Fig. 3 (a) Deformation of a droplet suspended in another immiscible liquid under an external electric field. (b) Drops with oblate and prolate shapes under an applied electric field.82 (c) Conical meniscus formed at the ends of a droplet in a strong electric field. The semi-angle of the cone is denoted as θ. (d) Tip streaming mode. Sequences of 225 μm droplets exposed to an electric field with an electric field strength E = 2.46 × 10−6 V m−1. Reproduced with permission from ref. 84. Copyright 2005, American Chemical Society.84 | ||
In eqn (6), S ≡ εm/εw, N ≡ Km/Kw, and M ≡ μm/μw, where Km and μm denote the electrical conductivity and viscosity of the surrounding medium, and μw indicates the viscosity of the drop. With an applied electric field, a prolate shape is formed for Φ > 1, while an oblate shape is obtained for Φ < 1. This model is in qualitative agreement with the result by Allan and Mason.80
The above-mentioned theories and equations depict small deformations of droplets subjected to an applied electric field. The deformation increases with an increase in the electric field intensity. If the applied electric field is sufficiently strong, a conical meniscus may form at the two ends of the droplet, as shown schematically in Fig. 3(c). The theoretical value of the cone angle θ is intensively studied for a dielectric droplet suspended in another dielectric fluid,18,85,86 a conducting droplet in a dielectric fluid,87–90 and a leaky dielectric droplet in a dielectric fluid.62,85,91–94 When the electric field strength is exceedingly strong, the surface of the droplet can no longer hold excess surface charges, leading to the disintegration of the droplet via different modes. For instance, in a leaky dielectric droplet, thin jets from the conical tips of the original droplet could develop and break up into tiny droplets, exhibiting the “tip streaming” mode as shown in Fig. 3(d).84 G. I. Taylor found that if the conical tip has a semi-angle of θ = 49.3°, the electric stress balances the surface tension, forming a stable conical tip, also known as the Taylor cone-jet.21
3.3 Electrocoalescence
Two bare droplets upon contact always coalesce into one to minimize the surface energy.95,96 Under an applied electric field, deformed droplets can interact with each other, which enriches the dynamics of droplet coalescence (Fig. 1).8,97–101 The coalescence of neighboring droplets driven by electric stress is termed electrocoalescence (Fig. 1a).62,87,88,102,103 In the presence of an electric field, neutral water droplets are polarized. The induced electric stress overcomes the surface tension, and two stretched neighboring droplets approach each other. In the meantime, the induced charges of opposite sign on the closest surfaces of the two droplets generate a dipole–dipole interaction force, F, bringing the further aggregation of droplets.104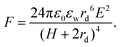 | (7) |
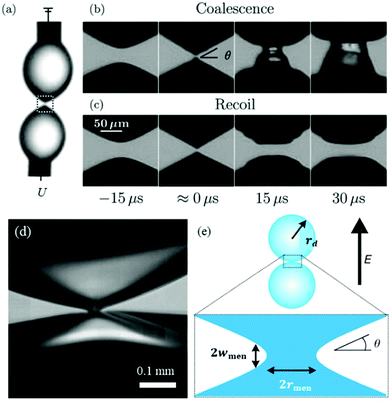 | ||
| Fig. 4 (a) A voltage U is applied across a pair of droplets pinned on needles.107 (b) Prior to contact, each droplet deforms into a cone with angle θ. At lower voltages, the droplets immediately coalesce.107 (c) At higher voltages, the droplets contact and then recoil.107 Reproduced with permission from ref. 107. Copyright 2009, American Physical Society. (d) High-magnification, high speed image of the temporary meniscus bridge between two bouncing water drops in silicone oil. The dark regions are water, and the brighter areas within the water are reflections.106 (e) Definition sketch of the meniscus bridge.106 Reproduced with permission from ref. 106. Copyright 2009, Springer Nature. | ||
3.4 Non-coalescence
In an electric field, two deformed droplets do not always coalesce, even though they are oppositely charged.105 Under a sufficiently large electric field, the droplets could briefly contact each other by forming a cone–cone geometry, and they tend to recoil, bounce or pinch-off rather than coalesce (Fig. 4c).106 To account for the pinch-off phenomenon, a crude capillary pressure model was developed. Considering a meniscus bridge with a conical geometry, its capillary pressure can be approximated by the Young–Laplace equation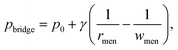 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tan
tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Similarly, the capillary pressure in the bulk of the droplets with a radius of rd is expressed by pdrop = p0 + γ(1/R1 + 1/R2), where R1 and R2 are the principal radii of curvature. For a spherical droplet, it yields R1 = R2 = rd and hence pdrop = p0 + 2γ/rd. The pressure difference between the bulk of the drop and the bridge is
θ. Similarly, the capillary pressure in the bulk of the droplets with a radius of rd is expressed by pdrop = p0 + γ(1/R1 + 1/R2), where R1 and R2 are the principal radii of curvature. For a spherical droplet, it yields R1 = R2 = rd and hence pdrop = p0 + 2γ/rd. The pressure difference between the bulk of the drop and the bridge is 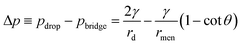 . The radius of the bridge is much smaller than that of the droplet, rmen ≪ rd, resulting in an approximation of the pressure difference
. The radius of the bridge is much smaller than that of the droplet, rmen ≪ rd, resulting in an approximation of the pressure difference 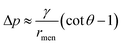 . Therefore, the sign of the pressure difference and corresponding flow direction solely depend upon the angle θ: for θ > 45°, the pressure is higher in the bridge (Δp < 0) and hence it drives the fluid wherein into the droplet and results in pinch-off (Fig. 4c and d).
. Therefore, the sign of the pressure difference and corresponding flow direction solely depend upon the angle θ: for θ > 45°, the pressure is higher in the bridge (Δp < 0) and hence it drives the fluid wherein into the droplet and results in pinch-off (Fig. 4c and d).
It is the critical cone angle of the meniscus bridge connecting two droplets upon contact that determines whether they coalesce or pinch-off, as the applied electric field intensity increases.106 To date, various models have been put forward to predict this transitional cone angle. Certain assumptions have been made about key physical elements, giving rise to different predictions of the critical cone angle and bridge morphology. The crude capillary pressure model106 predicts a critical cone angle of about 45°, and this angle was later refined to 30.8° in follow-up work of the same group by re-modeling the curvatures in the meniscus bridge explicitly. In the remodeling, deformations of the meniscus bridge are assumed self-similar as droplets coalesce, and this self-similar shape is assumed to be the profile resulting from minimizing the surface area under the constraint of volume conservation.107 The profile of the bridge region was, therefore, determined independently of any dynamic effects in surrounding cones.107 A theory of mean curvature flow from cones was developed, which governs how a cone can evolve to reduce its surface area as quickly as possible, leading to a critical cone angle of 24°.108 However, the model still neglects dynamic influences as it does not involve conservation of mass and momentum. Taking fluid inertia into consideration, a volume-of-fluid technique predicted that the critical cone angle was about 25°, where inviscid droplets were assumed.109 The model was then modified to include the viscous stress in numerical simulations, predicting that the critical cone angle is reduced (around 19°) as the droplets’ viscosity is increased.110
In the above studies, the values of the critical cone angle were obtained in droplet-in-gas systems where the dynamics of the surrounding gas is ignored. If the droplets are immersed in a liquid medium, it may impose a significant effect on the coalescence-to-pinch off transition. Considering silicon oils with different viscosities as the surrounding medium, the critical cone angle measured in the droplet-in-oil system is much larger than that measured in the droplet-in-gas system. The angle becomes larger as the viscosity of the surrounding medium increases, and it reduces for droplets with higher conductivity.111 For a highly conductive droplet, it may burst after recoil at a sufficiently strong electric field caused by Rayleigh instability (Fig. 5).112,113
 | ||
| Fig. 5 Breakup of a water droplet with a conductivity of 820 μS cm−1 at a DC voltage of 1.5 kV applied vertically.113 Reproduced with permission from ref. 113. Copyright 2015, Springer Nature. | ||
Besides a remarkably larger critical cone angle in droplet-in-oil than droplet-in-air systems, the dynamic interactions between droplets are also dissimilar. In a gas, the liquid bridge connecting two water droplets breaks up immediately during non-coalescence, while for droplets suspended in castor oil, the liquid bridge thickens at first, and then dramatically thins, followed by pinching off.114 The oscillation and breakup of the liquid bridge were supposed to be affected by its profile. The competing meridional and azimuthal curvatures of the bridge could make the interior pressure either positive or negative, resulting in growth or vanishing of the liquid bridge.114
If droplets are immersed in conductive liquids rather than dielectric liquids under an applied electric field, unexpected tip shapes may appear. For instance, when immersed in silicone and castor oils, water droplets exhibit cone–cone and cone–dimple structures in the pre-contact phase, respectively (Fig. 6).115 The distinct structures may relate to the fact that the conductivity of silicone oil is around 100 times smaller than that of castor oil.115 By adding additives to silicone oil to improve its conductivity, cone–dimple structures could occur as well.115
 | ||
| Fig. 6 Non-coalescence of DI water droplets adopting the cone–cone structure in (a) silicone oil and the cone–dimple structure in (b) castor oil under a voltage applied horizontally.115 Reproduced with permission from ref. 115. Copyright 2018, Cambridge University Press. | ||
The relative separation distance between neighboring droplets can impact their dynamics under an applied electric field. In the configuration of two droplets pinned to the cathode and anode, respectively, supplying a DC electric field, three dynamic regimes, classical coalescence, fuse-and-split, and periodic non-coalescence, were observed.116 Above a sufficiently large electric field, the electric stress overcomes surface tension, and brings two droplets into contact. Subsequently, the coalescence dynamics of these two droplets depend on their relative separation distance, defined by the ratio of the distance to the droplet radius. As the relative separation increases, the two droplets go through the coalescence, fuse-and-split, and periodic non-coalescence regimes (Fig. 7).116 A similar influence of the relative separation was found when an AC electric field is applied. Under an AC electric field, three dynamic regions, droplet coalescence, non-coalesced droplets with evolving deformation, and non-coalesced droplets with steady deformation, are observed with increasing relative separation distance.101
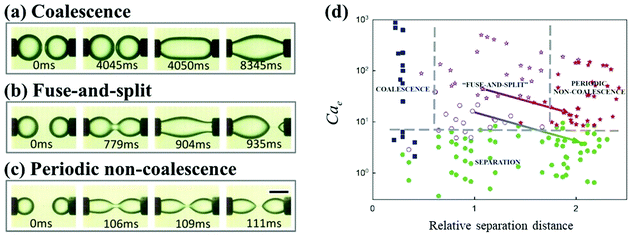 | ||
| Fig. 7 As the separation distance between two droplets increases, the dynamic regimes of (a) classical coalescence, (b) fuse-and-split, and (c) periodic non-coalescence occur in sequence.116 (d) State diagram for the dynamic behaviors of droplet pairs, based on the electrocapillary number Cae and the relative separation distance.116 Reproduced with permission from ref. 116. Copyright 2015, AIP Publishing. | ||
Geometric confinement can affect the coalescence dynamics of droplets. For instance, the non-coalescence underwent multiple cycles when two droplets are pinned and charged by a metallic nozzle. Free droplets bounce away after brief contact and pinch off under an applied electric field. Pinned and charged droplets go through multiple cycles of contact and pinch-off, where the liquid bridge oscillates repeatedly. A similar phenomenon is observed for particle-laden droplets immersed in dielectric oils. Owing to the presence of particles at droplet surfaces, a liquid bridge formed from the uncovered surface and then broke up; it also oscillates repeatedly for multiple cycles due to geometric fixation of particle shells (Fig. 8).117 Similar oscillatory dynamics of two bare droplets was also reported when situated in an alternating electric field.118
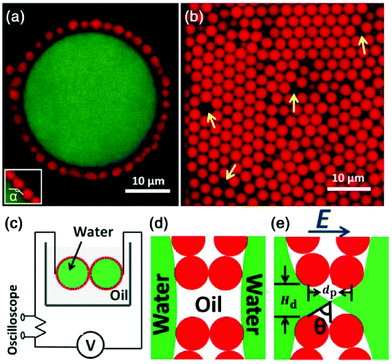 | ||
| Fig. 8 (a) The 2D confocal slice of a typical Pickering emulsion droplet, where a large saltwater droplet is coated with particles. (b) The arrangement of particles in the shell, where yellow arrows point to some typical defects. (c) Diagram of the experimental setup. (d) A cartoon illustrating the separation of water droplets in the absence of an electric field. (e) With a high enough DC electric field, a liquid bridge is formed through defects. dp is the particle diameter, Hd is the defect size, and θ is the cone angle. Reproduced with permission from ref. 117. Copyright 2013, American Physical Society.117 | ||
3.5 Partial coalescence
Upon encountering an interface, the droplet may coalesce completely with the interface, or it could bounce away from the interface under a strong enough electric field. Sometimes, however, only a part of the droplet can coalesce with the interface, leaving behind a daughter droplet. This distinct phenomenon is also called partial coalescence, and it could occur either in the absence or presence of an electric field. In the absence of an electric field, partial-coalescence has been extensively studied119–124 since Charles and Mason125 observed fine secondary droplets left above the interface after a primary droplet coalesces with a liquid–liquid interface in the 1960s. Before coalescence, the primary water droplet rests at the interface, which is separated from the bulk water pool by a thin intervening film of oil. As the film drains and eventually ruptures, the droplet starts coalescing driven by a liquid bridge connected to the interface. There are two phenomena reported: complete coalescence and partial coalescence, where smaller secondary droplets are produced (Fig. 9). | ||
| Fig. 9 The partial coalescence of an aqueous drop and an air/water interface. Each frame is taken 3 ms apart. As the process begins (first frame), the drop shape evolves from a spherical shape to a column (fourth frame) that pinches off and a secondary drop is formed. The time of coalescence begins at the first frame and ends at the seventh frame, where the secondary drop attains a spherical shape. Reproduced with permission from ref. 119. Copyright 2006, AIP Publishing.119 | ||
In partial or complete coalescence, there are three forces of main importance: capillary, inertial and viscous forces, where the capillary force drives the process while viscosity and/or inertia oppose the motion.119 Two timescales in terms of viscosity and inertia are defined by
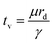 | (9) |
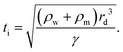 | (10) |
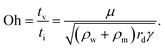 | (11) |
In the presence of an electric field, partial coalescence was first reported by Torza and Mason.126 Under the effect of an electric field, the electrostatic stress can locally change the droplet–interface shape, accelerate the rupture of the thin oil film, and hence promote the process of coalescence substantially.127 If the strength of the applied electric field is too high, only a part of the droplet can coalesce with the interface, resulting in partial coalescence. The critical strength of the electric field was found to depend on the surface tension, radius, conductivity, permittivity, density of the droplet, and the frequency of the AC or pulsed electric field.67,128 In the absence of an electric field, the Ohnesorge number indicates the transition from complete to partial coalescence,122,123,127 while under an electric field, partial coalescence can occur at a critical electrocapillary number, reportedly around 0.055 and regardless of the Ohnesorge number.68
The partial coalescence under a strong electric field may result from charge transfer during the process.69,129 Beyond a critical strength of the electric field, a droplet approaches the interface, encounters it and partially coalesces with it, during which secondary smaller droplets are formed. Subsequently, the residual droplets move away from the interface and toward one side of the electrode. After partial coalescence, the coalesced droplet and residual droplet may acquire opposite charges. One would expect that the ionic conductivity of the primary droplet plays an important role in determining the volume of the secondary droplet and the amount of charges it acquired. However, it was experimentally reported that the charge and volume of the secondary droplet are independent of the ionic conductivity of the primary droplet.69 The charge convection by a capillary jet with high velocity dominates conduction in the charge transfer, rendering the conductivity irrelevant.69 In contrast to this experimental observation,69 a numerical simulation reported that the ionic concentration of primary droplets affects the size and charge of residual secondary droplets, by applying a multiphase electrokinetic model to microdroplets. The discrepancy between the numerical simulation and experimental observation resulted from different charge separation and transfer dynamics between micro-sized and macro-sized droplets.130 The volume of secondary droplets after partial coalescence has attracted much attention, and reportedly it can be influenced by various parameters, including the initial size of primary droplets,131 the droplet–interface distance,130–132 the conductivity,69,130,132,133 permittivity,127,132 viscosity,127,132 and interfacial tension127,132,134,135 of the droplet, the strength of the electric field,131–133 the waveform and frequency of the pulsatile electric field,136 and the electrode configurations.135
4 Electrohydrodynamic free jets in multiphase microsystems
Electrified liquid free jets have enormously rich physics and wide-spread applications, including ink-jet printing,3 drug encapsulation4,6,137,138 and tissue engineering.139 In this section, we discuss electrified microjets, in which a stream of liquid is charged by an electric field along the flow direction. Several instabilities can occur including Rayleigh–Plateau instability, coiling instability, and charge-induced whipping instability, enriching the flow regimes/modes (Fig. 10).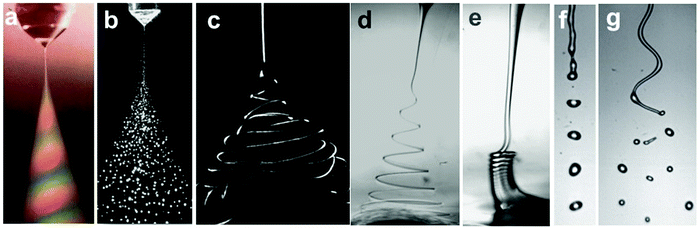 | ||
| Fig. 10 Representative optical images of (a and b) electrospray in air (reproduced with permission from ref. 27, Copyright 1994, Elsevier Ltd, and ref. 59, Copyright 2001, John Wiley and Sons);27,59 (c) chaotic electrospinning in air (reproduced with permission from ref. 141, Copyright 2007, Elsevier Ltd);140 (d) helical electrospinning in liquids;141 (e) electrocoiling in liquids;141 (f) electrodripping (reproduced with permission from ref. 142, Copyright 2017, American Physical Society);142 and (g) whipping jet breaking up into droplets (reproduced with permission from ref. 142, Copyright 2014, American Physical Society).142 | ||
In classical studies of electrified jets, the charging nozzle and the ground substrate are separated by a large enough distance to ensure that the electric field near the nozzle is mainly dependent on local conditions.58 Upon charging the meniscus, charges supplied by conduction from the bulk liquid accumulate at the surface. Normal and tangential electrostatic stresses arise from the accumulated surface charges. The meniscus narrows to increase the capillary pressure to balance the normal electrostatic stress. Meanwhile, the tangential electrostatic stress sets the jet in motion, and a high-speed thin jet emits from the tip of the meniscus. The thin jet can break up into droplets downstream due to axis-symmetric instabilities, exploited in electrospray for nanoparticles,4,6,137,138 or it elongates and thins away from the nozzle, until it bends off-axis due to a lateral whipping instability, extensively used in electrospinning for nanofibers.35,41,143–145 In both cases, the viscous effect of the jet is neglected owing to a sufficiently small capillary number in electrospray or a small Reynolds number in electrospinning.
Enforced by the trend of miniaturized manufacturing, the distance between the nozzle and the plate is significantly reduced to facilitate electrohydrodynamic writing.3,54–56,146 As such, the electrified jet can no longer be considered as a free jet but an electrified liquid bridge/filament. The existence of a nearby plate not only interferes with the generated electric field, but also decelerates the jet approaching the plate.141,147,148 For spinnable liquids, the interplay between the inertial and the viscous effect can be overturned as the nozzle-to-plate distance reduces, and other unstable modes, for instance, coiling instability, can occur.141,147,148 A viscous thin liquid filament can exhibit a coiling instability, also known as “liquid rope coiling”, which arises from an axial compressive stress that bends the jet.149–151 The compressive stress can result from the deceleration of the jet along the axial direction, for example, when a liquid jet encounters a substrate. The coiling instability can also be observed for electrified thin jets impinging on substrates.141,148,152,153
Although these instabilities have been well studied separately, the cross-over and co-existence of these instabilities for electrified liquid jets of multiphase systems under diverse geometric and fluidic parameters are inadequately discussed. For instance, a whipping jet can break up into droplets by Rayleigh–Plateau instability, and an electrified viscous jet in immiscible liquids can transit between coiling and whipping by varying the charging levels. Therefore, a systematic overview and physical analysis of these instabilities induced by electrical thinning for electrified jets are crucial to understand their dynamics and facilitate relevant applications.
4.1 Electrospray and the cone-jet mode
For a noncharged meniscus, it drips at a nozzle when the capillary effect dominates, at We < 1 and Ca < 1. When its flow rate or viscous shear increases, the dripping to jetting transition can occur at either We > 1 or Ca > 1, where the inertial or viscous effect dominates over the capillary effect, respectively.154,155 At a low electrical charging level, characterized by Cae ≪ 1, the slightly charged meniscus also drips since the capillary effect prevails; it also shifts from dripping to jetting when the inertial or viscous effect becomes important. Under constant Q, slightly charged liquid jets have a higher dripping frequency and thus break up into smaller detached droplets, compared with noncharging cases.28,156 As the charging level increases, both the intermittent cone-jet and spindle mode of the electrohydrodynamic jet can occur depending on the flow rate. Under this circumstance, the combination of the electrostatic and the inertial effect balances the surface tension effect, We < 1 and Cae ∼ 1.28,157–159 At a high charging level, the electric stress is sufficiently strong to reach Cae ∼ 1, the electrostatic and the surface tension effects balance, and the liquid meniscus deforms into a conical shape with a thin jet emitting from the tip of the cone. Within a narrow combination of flow rates and applied voltages, the cone shape is steady and a fine jet emits continuously, which is also known as the steady cone-jet mode (Fig. 11).60 The formation of tiny droplets in air or in other gases results in aerosols or sprays, and thus this process is named electrospray.27,28,156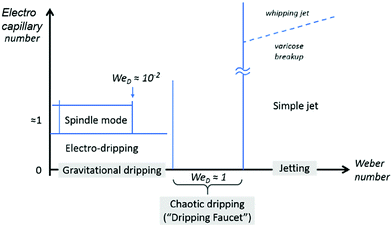 | ||
| Fig. 11 The illustrative phase map of operation modes for electrospray characterized by the Weber number and electrocapillary number. The modes in grey boxes are modes for a noncharged meniscus. Reproduced with permission from ref. 58. Copyright 2018, Elsevier Ltd.58 | ||
The stable cone-jet mode in electrospray relies on the perfect balance between electrostatic and capillary stresses satisfied by the deformed meniscus. In the absence of flow, G. I. Taylor analyzed the local hydrostatic equilibrium between normal electrostatic and capillary stresses, deducing the Taylor cone angle theoretically.21,160 The cone is intrinsically unstable since the capillary stress diverges at its tip. Any perturbation decreasing the angle can cause an imbalance of electric over capillary stresses, leading to a net pulling force that makes the cone even sharper. Eventually the tip of the cone is accelerated by the increased electrostatic stress, and a tiny jet emits from the cone tip, reducing the liquid volume and restoring the original cone angle. By feeding an appropriate liquid flow that equals the volume released from the jet, the cone can maintain global stability.28,30,60,156
The steady cone-jet mode exists for limited liquids with a limited combination of flow rates and applied voltages.28–30,60,156 The sprayed liquids should have suitable physical properties that enable a potential drop from the cone base to the cone tip, providing a stabilizing electric tangential stress. The cone-jet mode breaks down if the imposed flow rate Q is smaller than a minimum flow rate Qmin, where the hydrodynamic tf ∼ Lcrc2/Q becomes comparable to the charge relaxation time te = ε0ε/K, where Lc and rc are the characteristic length and radius of the cone-jet.30,31,161,162 By taking rc ∼ (Qε0(ε − 1)0.5/K)1/3 and Lc ∼ rcε0γ/ρKQ, Qmin ∼ εε0γ/ρK(ε − 1)0.5 is needed for a stable cone-jet mode.30,31,162 This scaling holds for Oh < 1 and predicts that Qmin decreases as the electrical conductivity of the working liquid increases. For small nozzles with sizes comparable to the length-scale of the cone-jet transitional region Lc, the viscous timescale becomes comparable with te, and the scaling of Qmin shows independence from the electrical conductivity of the working liquid.163 Instead, Qmin depends strongly on the nozzle size,163 which suggests that the capillary force stabilizes the electrified liquid meniscus and is involved in the minimum flow rate stability limit.161,163
The key process in electrospray is the cone-to-jet transition and the jet breakup for fine droplets. The emitted fine jet exhibits delayed breakup. Numerous efforts have been devoted to analyzing the stability of liquid jets charged by axial electric fields.1,21,23,36,160,164,165 Particularly, the thin jet of leaky dielectric liquids is surprisingly stable against capillary breakup.1,12,16,23,24 In the presence of both surface charge and a tangential electric field, the tangential electric shear stress stabilizes the fine jet of finite conductivity and delays the capillary breakup.1,36,166
At the base of the cone, charges are mainly transported by conduction, while at the jet region, charges are mainly convected. It is generally accepted that between the cone and jet downstream, the cone-to-jet transitional neck region controls the conduction-to-convection charge transfer and the jet diameter.9,31,162,167,168 In many cases of classic electrospray, the electric current I and the droplet radius rd scale with the imposed flow rate Q;26 the scaling exponent depends on the liquid properties but shows no dependence on the applied field intensity E.30,31,162 The normal stress balance demands ε0E2 ∼ γ/Lc. Thus, 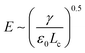 is determined by the Taylor cone, and the current at the neck region is
is determined by the Taylor cone, and the current at the neck region is 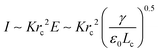 .9,31 In the transitional region, the reduced electrical power IU ∼ Krc2γ/ε0 should be on the same order of kinetic energy ρv2(a2v), and thus rd ∼ rc ∼ (ε0ρQ3/Kγ)1/6,9,31 indicating that the size of the emitted drop scales with Q0.5. If the transitional neck region is sufficiently small, the current I ∼ (γKQ)1/2 (Fig. 12).26,30,31,138,168–170 Several important studies analyze experimentally and theoretically the dependence of the scaling exponent of I–Q on the dimensionless experimental and geometric parameters, and physical properties of the working liquid.26,30,31,138,168–170 The verified range of each power law is limited, and a power law validated for any range of governing parameters may not exist.
.9,31 In the transitional region, the reduced electrical power IU ∼ Krc2γ/ε0 should be on the same order of kinetic energy ρv2(a2v), and thus rd ∼ rc ∼ (ε0ρQ3/Kγ)1/6,9,31 indicating that the size of the emitted drop scales with Q0.5. If the transitional neck region is sufficiently small, the current I ∼ (γKQ)1/2 (Fig. 12).26,30,31,138,168–170 Several important studies analyze experimentally and theoretically the dependence of the scaling exponent of I–Q on the dimensionless experimental and geometric parameters, and physical properties of the working liquid.26,30,31,138,168–170 The verified range of each power law is limited, and a power law validated for any range of governing parameters may not exist.
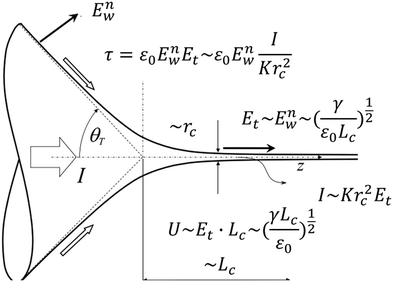 | ||
| Fig. 12 Schematic showing the variables used for the scaling of the characteristic jet size and electric intensity for a steady Taylor cone-jet. Reproduced with permission from ref. 9. Copyright 2018, Elsevier Ltd.9 | ||
Intriguingly, the current–flow rate characteristics are related to the geometric configurations.171,172 The dependence of the current on the flow rates, no matter what the exponent, holds for classic electrospray where the nozzle size is larger than the jet size by several orders of magnitude. In such cases, the imposed electric field decreases significantly towards the emitted jet downstream, and it does not contribute to the surface charge transport, or the conduction-to-convection transfer region (Fig. 13).171,172 The current is solely convected by the imposed flow rates. However, the current–flow rate characteristics do not hold in miniaturized devices, for instance, microfluidic devices.171 In such devices, the nozzle size is tens of micrometers, and the jet size is only one order-of-magnitude smaller; consequently, the tangential electric field is strong in the jet region and it affects the transportation of surface charges. As a result, the dominating convection current near the tip of the cone is driven by tangential electric stress, and thus it exhibits no dependence on the flow rates, but scales linearly with the applied electric field intensity.171
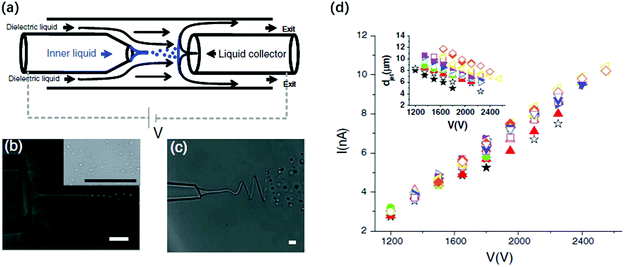 | ||
| Fig. 13 (a) Schematic illustration of the miniaturized device where the electrified liquid jet generates small droplets in co-flow dielectric liquids, and these droplets are collected by a conducive liquid collector;171 microscopic images of (b) a charged straight jet breaking up into droplets171 and (c) a charged whipping jet breaking up into droplets downstream;171 and (d) a linear plot of the applied voltage against the measured current of the electrified liquid jet.171 Reproduced with permission from ref. 171. Copyright 2010, American Physical Society. | ||
Multiphase electrospray, where the electrified liquid sprays in static liquid baths or in flowing liquid streams, generates emulsions rather than sprays/aerosols (Fig. 14).173,174 The typical liquid media are dielectric liquids with small dielectric constants to ensure that an electric potential is exerted on the spraying liquids. The liquid-in-liquid interfacial tension is usually lower than the surface tension of the liquid, avoiding the dielectric breakdown of air and consequent influences of space charges.175 More importantly, the viscosity, interfacial tension and flow shear of the medium liquids can be conveniently tuned, providing additional control over the formation of the emitted jet and sizes of the formed droplets. Multiphase electrospray can also refer to co-axial electrospray, where a compound cone-jet is formed and complex emulsion droplets are generated.6,137,176–178
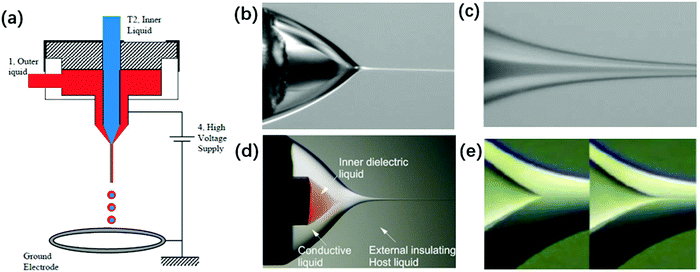 | ||
| Fig. 14 (a) Schematic of a typical experimental setup for coaxial electrospray. Reproduced with permission from ref. 6. Copyright 2002, The American Association for the Advancement of Science.6 The structure of a coaxial compound Taylor-cone and its cone-jet (b and c) in air. Reproduced with permission from ref. 6. Copyright 2002, The American Association for the Advancement of Science.6 (d and e) In insulating liquids, the meniscus of the inner liquid emits a jet as its flow rate increases. Reproduced with permission from ref. 176. Copyright 2007, American Physical Society.176 | ||
Combining the cone-jet mode in electrospray and hydrodynamic flow focusing in microfluidics may enable the generation of monodisperse sub-micron droplets with complex structures, including multi-layered and multi-compartmental droplets.167,179–184 Both electrospray and hydrodynamic flow focusing share similar governing equations for jet stability and breakup.138 It is thus intuitive that by combining electric and hydrodynamic flow focusing in microfluidics, uniform droplets with sub-micron sizes and complex structures may be obtained. As such, an electrical field, either direct-current (DC) or alternating-current (AC), has been incorporated in microfluidics to facilitate the generation of droplets from orifices.181,182,185–189 In most cases, monodisperse droplets are generated in an electrodripping regime with low applied field intensity, and these droplets of low charging levels are centered by the focusing flow of the continuous phase.181,186 When the field intensity increases, a conical meniscus can be observed, and the size of the generated droplets decreases significantly, but these droplets of high charging levels discharge at the nearest walls of the microchannels. The wall effect of the microchannels makes the collection of tiny droplets challenging, which can be addressed by introducing a third liquid collector that also functions as the opposite electrode.4,171 The third liquid collector should be conductive oils, and immiscible with both the aqueous core phase and the insulating shell phase.4,171
4.2 Electrocoiling and coiling instability
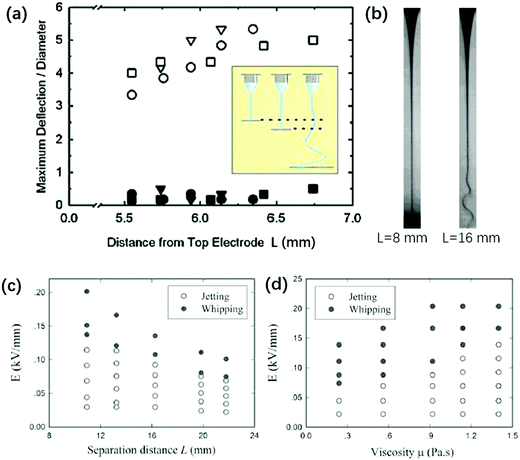
The bending, folding and coiling of liquid streams are ubiquitous fluid mechanical phenomena that occur on the geographical, macro and microscale, for instance, the folding of magma, and the coiling of honey and shampoo.149–151,190–195 When liquid streams with sufficiently large viscosity are compressed, such as when they are hindered by substrates or they enter a diverging channel,196 they become wider or bend to satisfy mass conservation. Similar to Euler elastic bucking, a sufficiently thin liquid stream that is compressed bends and coils.197 The coiling of viscous jets and folding of viscous sheets in air have been investigated experimentally, numerically and theoretically.149–151,198 The key experimental parameters are the falling height L, and the volumetric flow rate of the jet, Q. Depending on the falling height, jet coiling can be categized into viscous, gravitational and inertial regimes.149–151 Under a fixed flow rate, the falling height dictates the jet velocity and radius, thus governing the force balances for coiling frequency Ω and amplitude R. However, in geometrically constrained microsystems, varying the morphology of a viscous microjet hydrodynamically to a large extent becomes difficult. The falling height L is restricted and cannot be varied over a wide range, and the jet cannot attain a large end-velocity nor a small radius by changing L. Surface tension, important in microsystems, inhibits the formation of a thin jet, since it drives the breakup of any sufficiently slender jet into a string of droplets. Therefore, electric stress, which can change both the shape and dynamics of liquid jets, is utilized for controlling viscous microjets.Charging a viscous microjet along its axial direction extruded from a metallic nozzle of radius r0, at a height L, can trigger its coiling.148 With no applied voltage, the extruded viscous flow forms a straight jet, which slightly widens near the substrate owing to the forced deceleration. With an applied voltage, the viscous microjet accelerates and becomes thinner. The more it accelerates after exiting the nozzle, the more it was forced to decelerate depositing on the substrate, creating a larger axial compressive stress. Analogously, the electric stress acts like mechanical compressive stress, and the two ends of the viscous jet are pushed inwards to the midplane (Fig. 15).141 The viscous compression can be characterized by μvmax/L, where vmax = Q/πrmin2 is the local velocity at the minimum radius of the jet, rmin.141 The surface tension effect, γ/r0, plays an important stabilizing role in microsystems, since it favors an axis-symmetric jet of smaller surface area than a coiled one. At a critical applied voltage, the sufficiently large electric stress generates sufficient compression that dominates the surface tension, bending the jet. This predicts that the coiling of the charged jet should occur at the critical capillary number Ca ∼ μvmax/γ exceeding the characteristic jet dimension L/r0 (Fig. 15a–c).141
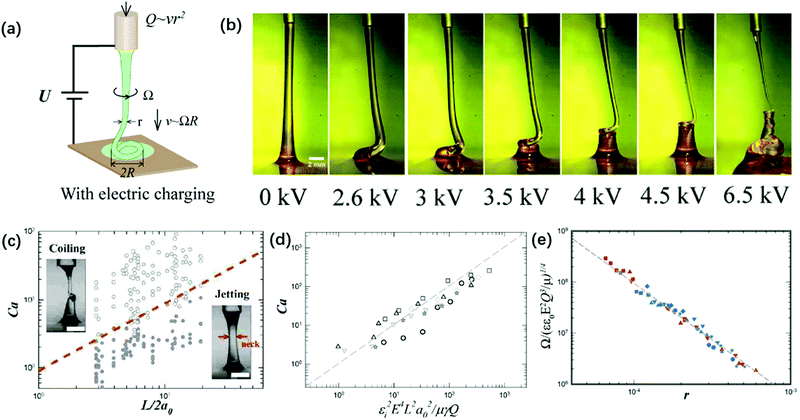 | ||
| Fig. 15 (a) Schematic of the experimental setup for the charged viscous coiling jet;148 (b) serial optical images showing that a viscous jet can be induced to coil at a critical applied voltage, and the applied voltage enhances the coiling instability;148 (c) a state diagram for jetting and coiling of an electrified viscous filament characterized by the dimensionless capillary number and geometric parameter;141 (d) a log–log plot showing the dependence of the critical capillary number for the transition of coiling on geometric, experimental and fluidic parameters;141 and (e) a log–log plot showing the dependence of the coiling frequency by torque balance based on experimental and fluidic parameters.148 | ||
The determining factor for the jetting-to-coiling transition is controlled by the minimum radius of the jet rmin decreased by the applied electric stress. For a highly viscous jet, the scaling law of rmin ∼ μU0a0/εε0E2L along the axial direction can be deduced by solving its simplified governing equation of a balance between the viscous and electric stress terms. Thus, the critical applied field intensity can be estimated as Ecoiling ∼ (μv0γ)1/4L−1/4r0−3/2ε0−1/2 (Fig. 15).141 As the straight jet is triggered to coil, the coiling frequency also increases as the field intensity E further increases. Since the jet radius r decreases with increasing E, decreasing r leads to increasing coiling frequency Ω ∼ r−2, and thus the jet coils faster at a higher E. Since the coiling motion is steady with constant Ω and R, the viscous torque that resists the bending and twisting μr4v/R2191 must balance the electric torque ε0εE2rR2, and thus Ω ∼ (ε0εE2Q3/μr9)1/4 (Fig. 15e).148
With a large applied electric force, the fast coiling of a thin jet is a “liquid sewing machine”. It piles up into a nano-pillar with constant radius,152 or it deposits curved nanofibers with a variety of rich periodic morphologies on a translating substrate.146 This electric-field assisted deposition of thin fibers enabled by a small nozzle-to-plate distance is also explored in near-field electrospinning.199–202 In near-field electrospinning, the emitted thin jet does not develop whipping instability; instead, as the electrified jet hits the nearby substrate, it bends and coils.199–202 As such, the periodic morphologies including meanders, translating coils and alternating loops can be varied by changing the applied voltage while keeping the same translation speed of both the nozzle and substrate (Fig. 16).146 Electrocoiling-guided printing is similar to printing by inertial coiling203–205 in that in both the patterns switching is governed by varying the speed difference between the end velocity of the jet impinging the substrate and the translational speed.206 In electrocoiling, the jet impinging velocity can be conveniently tuned by programming the applied voltage, and thus the switching between patterns is fast and precise. In comparison, the speed difference between the jet impinging velocity and the translational speed is changed either by varying the nozzle-to-plate distance or programming the translational speed in inertial coiling. Frequent changes in both mechanical movements can cause undesired vibrations and residual motions, leading to uncontrolled patterns.146 Therefore, electrocoiling-guided programmed printing can achieve complex patterns assembled from periodic curved lines with high precision, nanoscale resolution and fast speed.
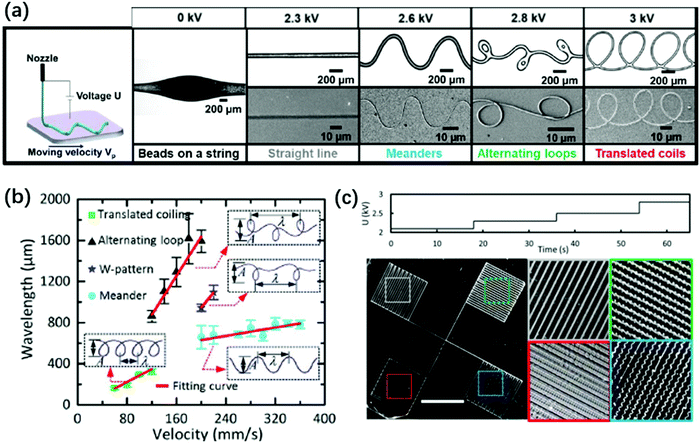 | ||
| Fig. 16 (a) Schematic and microscopic images of electrocoiling-guided printing. The coiling jet charged by increasing voltages rotates at increasing frequencies, and it is coupled with a linear translation stage with a constant velocity of Vp for printing curved nanofibers of various morphologies, including meanders, alternating loops and translating coils. Reproduced with permission from ref. 146. Copyright 2019, Royal Society of Chemistry.146 (b) A state diagram indicating that the fiber pattern is controlled by the impinging velocity of the electrified jet on the substrate. Reproduced with permission from ref. 207. Copyright 2017, Elsevier Ltd.207 (c) Microscopic images of four different structures printed by programming the applied voltage in stair-up wave forms. Reproduced with permission from ref. 146. Copyright 2019, Royal Society of Chemistry.146 | ||
The horizontal coiling of a viscous jet in another co-flow liquid is also observed in microfluidic channels, upon entering a divergent channel or exiting a nozzle. The liquid two-phase system can be miscible liquids with negligible interfacial tension,196,208 or immiscible liquids with low interfacial tension, 10−5 mN m−1.209 The viscosity ratio of the inner to the outer phase is usually large, exceeding 102.196,208,209 The coiling jet in the horizontal channel appears like the rotation of the coiling jet in vertical fall, except that the shear force from the co-flow sheath phase in the channel acts like the gravitational or inertial force in the vertical case. Intriguingly, when an axial electric field is applied to the coiling/folding jet, the jet becomes wider and the coiling frequency decreases.166,209 At a critical applied voltage, the coiling jet is completely uncoiled into a straight one (Fig. 17).166,209 The electric field suppresses the coiling instability in horizontal microchannels. The applied electric field not only compresses the coiling jet, but also exerts an outward normal electrostatic stress that widens the jet, owing to the softness of the jet interface. The increase in the jet radius decreases the coiling frequency, Ω ∼ r−2, and eventually unfolds the jet.72 The geometry factors have a prominent influence on the interplay of electric, hydrodynamic and surface tension effects on the liquid jet, which contribute to the rich physical phenomena of electrohydrodynamic multiphase flows.
 | ||
| Fig. 17 (a) Schematic showing the charging of a folding jet in an immiscible insulating liquid;166 (b) schematic illustration of the applied electric stress on the jet interface;166 and (c) serial microscope images of the folding jet unfolding at a critical electric field intensity, and its folding frequency decreasing as the applied field intensity increases, indicating that the folding instability is suppressed by the applied electric field. Reproduced with permission from ref. 166. Copyright 2015, American Physical Society. | ||
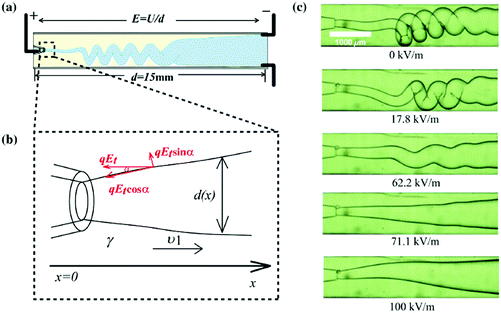
4.3 Electrospinning and whipping instability
As a thin jet continuously thins and accelerates under an axial electric field, charges accumulate at the jet surfaces and the repulsion between them becomes significant. When a small portion of the highly charged jet moves off-axis, the charges lined up along the rest of the jet will push this portion outwards away from the axis, leading to a lateral instability also known as whipping instability.36,40,172,210–212 The movement of the jet under lateral instability generates additional tensile stress, further thinning the jet. For typical polymer solutions, their high viscosity and shear thinning property delay the capillary breakup, facilitating fiber formation.35,143,145,213,214The charging level is dictated by the jet velocity under a fixed flow rate. To trigger the whipping instability, a sufficient charge density demands a sufficiently large velocity of the jet.36,40 Thus, the nozzle-to-plate distance L is typically large in electrospinning to allow full development of the end velocity of the jet. The faraway substrate is assumed to have no effect on the jet morphology and development in theoretical and numerical analysis of electrospinning. By computing the local electric field and the jet shape and stability analysis, growth rates of varicose and lateral perturbations of charged free jets are compared, and when electrospinning occurs is predicted.36,40 At increasing electric field intensity and surface charge density, the capillary instability is suppressed, and the jet will continue thinning until whipping occurs.35,36,40
The onset of whipping instability strongly depends on whether there exists a sufficiently large charge density σ ∼ Ir/2Q at the jet interface, as the jet thins and the conduction current vanishes.36,40 Unlike in electrospray, the current in electrospinning scales approximately linearly with the applied field intensity E and the volumetric flow rate Q.36,40 The surface charge density is influenced by the conductivity of the jet, and jets with higher conductivity tend to have a larger density of surface charges. This can also be used to explain why the minimum flow rate for jets with higher conductivity is lower in electrospray.74 The viscosity does not affect the onset of whipping, provided a sufficiently large nozzle-to-plate distance L in which the jet thinning is dominated by the inertial effect, r ∼ z−0.25,16,30 where z denotes the axial distance. However, high viscosity delays the capillary breakup since the viscous Rayleigh–Plateau instability has a smaller growth rate than the inviscid one.
When the charge repulsion dominates the stabilizing surface tension, the charged thin jet loses stability and bends away from the centerline, γ/r < σ2/ε. As the jet whips, its radius further reduces owing to the tensile stretch, which increases the capillary pressure γ/r and diminishes the charge repulsion σ2/ε ∼ I2ar2/4εQ2.215 Ultimately, the terminal diameter of the whipping jet can be estimated when these two terms balance, rmin ∼ (Q/I)2/3(εγ)1/3.215
By shortening the nozzle-to-plate distance L, a whipping jet can be stabilized. This was explained by the gas ionization due to close electrode separation, which neutralizes some surface charges and stabilizes the whipping jet.216 It is experimentally shown that a higher current is measured at shorter electrode separation, and increasing humidity can increase the “straight segment” of the jet (Fig. 18a and b). The stability of the electrified jet can be enhanced by partial neutralization of surface charges by electrons produced via gas ionization. However, by replacing air with silicone oils and eliminating the gas ionization effect, reducing L still stabilizes the jet and makes whipping disappear (Fig. 18c). This phenomenon can be explained simply by the fact that a smaller L leads to a slower-thinning jet, since the electrified jet is forced to decelerate near the substrate, leading to reduced surface charges and thus improved stability.141
 | ||
| Fig. 18 (a) The nozzle-to-plate distance L affects the stability against whipping. At L ∼ 5.5–7 mm, the electrified liquid jet shows no centerline deflection and no whipping (solid symbols); at L = 25.1 mm, the electrified liquid jet whips and the centerline deflection increases by an order of magnitude (open symbols).216 (b) Microscopic images of an electrified glycerin jet connecting the nozzle and substrate with L = 8 mm and 16 mm, respectively.216 State diagram for jetting and whipping of an electrified liquid filament characterized by (c) E − μ (Q = 20 mL h−1, L = 16.4 mm) and (d) E − L (Q = 5 mL h−1, μ = 0.56 Pa s) planes, respectively. Reproduced with permission from ref. 216. Copyright 2008, American Physical Society. | ||
The small nozzle-to-plate distance L changes the interplay between inertial and viscous stresses. For L > Lc = μA/ρQ, where A is the cross-sectional area of the nozzle, and Re > 1, changing the viscosity does not affect the jet profile,35,36,40,217 while for L < Lc and Re < 1, the viscosity does affect the jet profile and hence the onset of the whipping instability. The prolonged stability against whipping is more pronounced with smaller L and larger μ, for an electrified jet in silicone oil (Fig. 18c and d).141 This is rationalized by the fact that both factors contribute to a larger rmin along the axial direction.141 A larger rmin decreases the surface convection, leading to smaller surface charge density, and thus suppresses charge repulsion. To trigger whipping of a viscous and short electrified liquid jet, a higher E should be applied.141
Multiphase electrospinning refers to electrified jet whipping in liquids, also known as wet-electrospinning. A liquid-in-liquid two-phase system has advantages over a liquid-in-air system for electrospinning.39,173,213 The former has a lower interfacial tension and thus requires a lower intensity of the applied electric field for electrospinning. Moreover, dielectric oils typically have much higher dielectric breakdown field strength than ambient air, avoiding effects of space charges. More importantly, the violent movement of the whipping jet is slower in liquids than in air,83 enabling quantitative analysis of the whipping structure, including the frequency and amplitude.212,218
Intriguingly, the fluidic parameters of the outer liquid significantly affect the whipping structure. Steady and helicoidal whipping structures of ethylene glycol (17 mPa s), glycerin (927 mPa s), and lecithin from soybean (7.5 Pa s) jets are observed in silicone oils with viscosities under 10 mPa s,141,218 for wide combinations of flow rates and voltages (Fig. 19). Their structures resemble a helix with a linearly increasing amplitude. In contrast, most whipping occurring in air or hexane (0.2 mPa s) is chaotic (Fig. 19).212,218,219 By comparing the characteristic capillary, viscous and inertial times of the inner and outer liquid, respectively, it was found that a helicoidal steady-state whipping structure is observed when the longest time scale is that of the outer liquid; otherwise chaotic whipping occurs when the longest characteristic time scale is that of the inner liquid.218
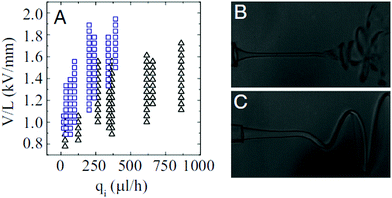 | ||
| Fig. 19 (A) State diagram for chaotic and helical whipping of an electrified liquid jet in an immiscible dielectric liquid, characterized by the applied field intensity and the flow rate of the inner liquid (the parameters of the outer phase are kept constant). Representative images of (B) chaotic and (C) helical whipping, in which the outer liquids are silicone oils with a viscosity of 0.5 cP and 9.4 cP, respectively.218 | ||
In liquid–liquid two-phase systems with low interfacial tension, the crossover of coiling and whipping for electrified liquid jets with small L < Lc was first discovered. Applying a charging electric field to a viscous liquid filament that connects the nozzle and substrate, it exhibits three dynamic regimes: “jetting”, “coiling” and “whipping”, as the charging voltage increases (Fig. 20). The onsets of both coiling and whipping instabilities are controlled by the minimum radius along the jet, the scaling of which is related to both the viscosity and nozzle-to-plate separation. As the critical local capillary number and electrocapillary number at the minimum radius are reached, the jet starts to coil or whip, respectively.63 These results enrich the overall physical picture of electrically forced jets, and establish guidelines to integrate a novel electrocoiling phenomenon into printing of functional materials.
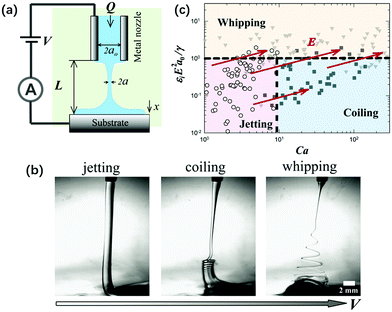 | ||
| Fig. 20 (a) Schematic of the experimental setup for an electrified liquid filament in a dielectric liquid with low interfacial tension; (b) representative optical images of “jetting”, “coiling” and “whipping” for the electrified liquid filament under small L, as the applied field intensity increases, respectively; and (c) a state diagram summarizing the dynamic behaviors of an electrified liquid filament characterized by the capillary and the electrocapillary number.141 | ||
5 Outlook
The diverse applications of fine drops and jets and the need for precise control over their sizes and motions have given rise to continued development of electrically driven flows. Electrohydrodynamics is a versatile platform to shape liquid interfaces to produce fine droplets and jets with large quantities. In this review, the principles of electrowetting, electrodeformation, electrocoalescence of charged microdroplets, electrospray of a liquid meniscus, and electrocoiling and electrospinning of liquid microjets have been discussed concisely. Apart from outlining key physical fundamentals that are generally accepted by the classical literature, we also have included rich dynamics of liquid drops and jets in microscale geometric confinement, since the advances in microfabrication bring new ideas and phenomena to electrohydrodynamic flows. For steady operational regimes, the underlying balances and scaling laws are analyzed for predicting transitions between dynamic regimes and features of produced drops and jets.The past decades have witnessed significant progress in fundamental aspects of electrohydrodynamics of droplet jets. For instance, electrospray and electrospinning are considered as mature technologies that are widely used for applications. There still exist challenges worthy of being addressed in the future. Studies of the “critical angle” which characterizes the transition between “coalescence” and “non-coalescence” represent an example. Previous experimental studies reveal that the critical angle could change depending on the properties of the droplets as well as the surroundings.110,111,115 Although several theoretical explanations are proposed to predict such a critical angle and agree well with the experimental results qualitatively, most of them made certain assumptions about key physical elements and hence could only be applied in limited experimental situations. A comprehensive one that can generalize our understanding and findings of the “critical angle” is still needed. In these studies, an assumption of a uniform electric field has been always made for simplicity even though the electric field is essentially nonuniform such as in electrode configurations of pin–plate or pin–pin. It may, at least in part, give rise to a discrepancy between experimental and theoretical results. Actually, the use of nonuniform electric fields is of practical significance in the oil and petroleum industries since it may remarkably improve the performance of electrocoalescence.220–222 By taking the nonuniformity of electric fields into consideration, the fundamental mechanism for complete, partial or non-coalescence of droplets deserves further investigation.
In addition, the rheological properties of the fluid studied in most problems are normally Newtonian. However, a lot of applications based on EHD involve sample fluids with complex physical properties. For instance, the crude oil in oil recovery, biological samples and colloidal suspensions are non-Newtonian fluids.223,224 At the microscale, non-Newtonian effects could be significant and further enrich the EHD phenomena of droplets. Of particular interest are interactions between colloidal suspensions and electric fields, since fluid properties such as viscosity can be changed by electric fields.225 The application of electric fields may either enhance226 or weaken227,228 the fluid viscosity. This electrorheology effect needs to be studied in-depth.
Moreover, droplets and jets with complex interfaces may display new electrohydrodynamic phenomena. Stabilizers, such as molecular and particulate surfactants, are often added to prevent interface collapse. Although the electric manipulation of droplets stabilized by a molecular surfactant has been intensively studied, an understanding of EHD of interfaces stabilized by lipids, block/graft copolymers, polypeptides and particles would also be of great significance. It is worth exploring these systems further for the sake of controlling droplet-based bioreactors. Especially, interfaces assembled from amphiphilic biomolecules represent artificially formed membranes. Investigation of their electric responses and manipulation could provide us with insights to understand the biological systems of cells.
In return, the emergence and understanding of new EHD phenomena also advance burgeoning applications. For instance, electro-coiling and near-field electrospinning provide versatile ways of depositing fine fibers with periodic conductive structures. These conductive helical patterns with structural stretchability have potential for flexible electronics. For these applications, the deposited ink contains conductive materials, including conductive polymers and inorganic nanomaterials. The ink composition alters its response to an electric field and leads to new phenomena, which requires future studies for controlling their dynamics and deposited structures precisely.
To conclude, new experiments and physics associated with electrohydrodynamics of droplets and jets thrive as new elements, such as composited interfaces, ultra-soft interfaces, stimuli-responsive interfaces, and confined boundaries, are involved. These new elements alter the force balance, change the relative importance of timescales, and require new models for description. Electrohydrodynamic multiphase microflows remain a complex, fascinating, and multidisciplinary field in soft matter physics that continually fosters scientific curiosity, which will keep moving forward by new problems, experiments, and models.
Nomenclature
| A | The cross-sectional area of the nozzle |
| a | The axis of the ellipsoidal droplet parallel to the electric field |
| b | The axis of the ellipsoidal droplet perpendicular to the electric field |
| D | Deformation |
| d p | Particle diameter |
| E | Electric field intensity |
| E t | The tangential electric field intensity |
| E n w | The normal electric field intensity of the working liquid |
| F | Force |
| g | Gravitational acceleration |
| H | Distance between the near surfaces of the droplets |
| H d | The size of defects in a particle-laden surface |
| h | Thickness of a substrate |
| I | Electric current |
| K | Electrical conductivity |
| K d | Electrical conductivity of a drop |
| K m | Electrical conductivity of the medium |
| K w | Electrical conductivity of the working liquid |
| L | Distance between the electrodes, nozzle-to-plate distance |
| L c | Characteristic length-scale |
| p | Pressure |
| p 0 | Ambient pressure |
| p bridge | Pressure in the bridge |
| p drop | Pressure in the bulk droplet |
| p | Pressure difference |
| q | Electric charge density |
| Q | Flow rate |
| Q min | The minimum flow rate |
| R | Amplitude |
| r | Jet radius |
| r min | The minimum jet radius along the z direction |
| r d | Droplet radius |
| r men | Radius of the meniscus bridge |
| r 0 | Nozzle radius |
| r c | Characteristic length-scale along the radial direction of a jet |
| t | Timescale |
| t e | Charge relaxation time |
| t f | Hydrodynamic time |
| t i | Timescale in terms of inertia |
| t v | Timescale in terms of viscosity |
| U | Electric voltage |
| v | Velocity |
| V p | Moving velocity of the substrate |
| v max | The local velocity at the minimum jet radius |
| v 0 | Velocity at the nozzle |
| w men | The width of the meniscus bridge |
| z | Axial direction |
Greek symbols
| γ | Interfacial tension |
| ε | Relative dielectric constant |
| ε 0 | Vacuum permittivity |
| ε w | Dielectric constant of the working liquid |
| ε m | Dielectric constant of the medium |
| θ | Angle |
| θ 0 | Initial contact angle |
| θ T | Angle of the Taylor cone |
| μ | Viscosity |
| μ m | Viscosity of the medium |
| μ w | Viscosity of the working liquid |
| ρ | Density |
| ρ w | Density of the working liquid |
| ρ m | Density of the medium |
| σ | Charge density |
| τ | The electric stress |
| Φ | The discriminating function |
| Ω | Coiling frequency |
Non-dimensional parameters
| M ≡ μm/μw | |
| N ≡ Km/Kw | |
| S ≡ εm/εw | |
| We | Weber number |
| Ca | Capillary number |
| Re | Reynolds number |
| Oh | Ohnesorge number |
| Cae | Electrocapillary number |
| Bo | Bond number |
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This research was supported by National Natural Science Foundation of China (NSFC 21706161). The authors are also thankful for the support of the Guangdong Province Universities and Colleges Pearl River Scholar Funded Scheme (2018) and Shenzhen Overseas High-level Talents Key Foundation for Innovation and Entrepreneurship.References
- J. R. Melcher and G. I. Taylor, Annu. Rev. Fluid Mech., 1969, 1, 111–146 CrossRef.
- A. I. Zhakin, Phys.-Usp., 2012, 55, 465–488 CrossRef CAS.
- J.-U. Park, M. Hardy, S. J. Kang, K. Barton, K. Adair, D. K. Mukhopadhyay, C. Y. Lee, M. S. Strano, A. G. Alleyne, J. G. Georgiadis, P. M. Ferreira and J. A. Rogers, Nat. Mater., 2007, 6, 782–789 CrossRef CAS.
- S. Chakraborty, I. C. Liao, A. Adler and K. W. Leong, Adv. Drug Delivery Rev., 2009, 61, 1043–1054 CrossRef CAS.
- K. Roh, D. C. Martin and J. Lahann, Nat. Mater., 2005, 4, 759–763 CrossRef CAS.
- I. G. Loscertales, A. Barrero, I. Guerrero, R. Cortijo, M. Marquez and A. M. Gañán-Calvo, Science, 2002, 295, 1695–1698 CrossRef CAS.
- E. Brouzes, M. Medkova, N. Savenelli, D. Marran, M. Twardowski, J. B. Hutchison, J. M. Rothberg, D. R. Link, N. Perrimon and M. L. Samuels, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 14195–14200 CrossRef CAS.
- A. R. Abate, T. Hung, P. Mary, J. J. Agresti and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 19163–19166 CrossRef CAS.
- A. M. Gañán-Calvo, J. M. López-Herrera, M. A. Herrada, A. Ramos and J. M. Montanero, J. Aerosol Sci., 2018, 125, 32–56 CrossRef.
- G. I. Taylor and M. D. Van Dyke, Proc. R. Soc. London, Ser. A, 1969, 313, 453–475 Search PubMed.
- J. Zeleny, Phys. Rev., 1907, 25, 305–333 Search PubMed.
- J. R. Melcher and E. P. Warren, J. Fluid Mech., 1971, 47, 127–143 CrossRef.
- M. Cloupeau and B. Prunet-Foch, J. Electrost., 1990, 25, 165–184 CrossRef CAS.
- F. J. De La Mora, J. Fluid Mech., 1992, 243, 561–574 CrossRef.
- J. Zeleny, Proc. Cambridge Philos. Soc., 1915, 18, 71 Search PubMed.
- A. M. Gañán-Calvo, J. Fluid Mech., 1997, 335, 165–188 CrossRef.
- A. Barrero, A. M. Gañán-Calvo, J. Dávila, A. Palacios and E. Gómez-González, J. Electrost., 1999, 47, 13–26 CrossRef CAS.
- H. A. Stone, J. R. Lister and M. P. Brenner, Proc. R. Soc. London, Ser. A, 1999, 455, 329–347 CrossRef.
- J. R. Melcher, Phys. Fluids, 1968, 11, 2604 CrossRef.
- G. I. Taylor, Proc. 12th Int. Cong. Applied Mechanics, Springer, 1968.
- G. I. Taylor, Proc. R. Soc. London, Ser. A, 1964, 280, 383–397 Search PubMed.
- M. Mutoh, S. Kaieda and K. Kamimura, J. Appl. Phys., 1979, 50, 3174 CrossRef CAS.
- D. A. Saville, Phys. Fluids, 1970, 13, 2987–2994 CrossRef.
- D. A. Saville, Annu. Rev. Fluid Mech., 1997, 29, 27–64 CrossRef.
- K. Tang and A. Gomez, Phys. Fluids, 1994, 6, 2317–2332 CrossRef.
- J. Fernández de la Mora and I. G. Loscertales, J. Fluid Mech., 1994, 260, 155–184 CrossRef.
- C. Pantano, A. M. Gañán-Calvo and A. Barrero, J. Aerosol Sci., 1994, 25, 1065–1077 CrossRef CAS.
- M. Cloupeau and B. Prunet-Foch, J. Aerosol Sci., 1994, 25, 1021–1036 CrossRef CAS.
- P. Atten, IEEE Trans. Dielectr. Electr. Insul., 1996, 3, 1–17 CrossRef CAS.
- A. M. Gañán-Calvo, Phys. Rev. Lett., 1997, 79, 217–220 CrossRef.
- A. M. Gañán-Calvo, J. Davila and A. Barrero, J. Aerosol Sci., 1997, 28, 249–275 CrossRef.
- J. B. Fenn, M. Mann, C. K. Meng, S. F. Wong and C. M. Whitehouse, Science, 1989, 246, 64–71 CrossRef CAS.
- H. Fong, I. Chun and D. H. Reneker, Polymer, 1999, 40, 4585–4592 CrossRef CAS.
- Z. M. Huang, Y. Z. Zhang, M. Kotaki and S. Ramakrishna, Compos. Sci. Technol., 2003, 63, 2223–2253 CrossRef CAS.
- Y. M. Shin, M. M. Hohman, M. P. Brenner and G. C. Rutledge, Appl. Phys. Lett., 2001, 78, 1149 CrossRef CAS.
- M. M. Hohman, M. Shin, G. Rutledge and M. P. Brenner, Phys. Fluids, 2001, 13, 2201 CrossRef CAS.
- H. Yoshimoto, Y. M. Shin, H. Terai and J. P. Vacanti, Biomaterials, 2003, 24, 2077–2082 CrossRef CAS.
- J. Doshi and D. H. Reneker, Conf. Rec. 1993 IEEE Ind. Appl. Conf. Twenty-Eighth IAS Annu. Meet., 1993, 35, 151–160.
- A. L. Yarin, S. Koombhongse and D. H. Reneker, J. Appl. Phys., 2001, 89, 3018–3026 CrossRef CAS.
- M. M. Hohman, M. Shin, G. Rutledge and M. P. Brenner, Phys. Fluids, 2001, 13, 2221–2236 CrossRef CAS.
- D. Li and Y. Xia, Adv. Mater., 2004, 16, 1151–1170 CrossRef CAS.
- F. Yang, R. Murugan, S. Wang and S. Ramakrishna, Biomaterials, 2005, 26, 2603–2610 CrossRef CAS.
- H. A. Stone, A. D. Stroock and A. Ajdari, Annu. Rev. Fluid Mech., 2004, 36, 381–411 CrossRef.
- M. Joanicot and A. Ajdari, Science, 2005, 309, 887–888 CrossRef CAS.
- X. Casadevall i Solvas and A. deMello, Chem. Commun., 2011, 47, 1936–1942 RSC.
- S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220 RSC.
- G. M. Whitesides, Nature, 2006, 442, 368–373 CrossRef CAS.
- R. K. Shah, H. C. Shum, A. C. Rowat, D. Lee, J. J. Agresti, A. S. Utada, L.-Y. Chu, J.-W. Kim, A. Fernandez-Nieves, C. J. Martinez and D. A. Weitz, Mater. Today, 2008, 11, 18–27 CrossRef CAS.
- P. Zhu and L. Wang, Lab Chip, 2017, 17, 34–75 RSC.
- D. R. Link, E. Grasland-Mongrain, A. Duri, F. Sarrazin, Z. Cheng, G. Cristobal, M. Marquez and D. A. Weitz, Angew. Chem., Int. Ed., 2006, 45, 2556–2560 CrossRef CAS.
- H. Lee, B. Seong, J. Kim, Y. Jang and D. Byun, Small, 2014, 10, 3918–3922 CrossRef CAS.
- A. Reiser, M. Lindén, P. Rohner, A. Marchand, H. Galinski, A. S. Sologubenko, J. M. Wheeler, R. Zenobi, D. Poulikakos and R. Spolenak, Nat. Commun., 2019, 10, 1–8 CrossRef CAS.
- B. W. An, K. Kim, H. Lee, S.-Y. Kim, Y. Shim, D.-Y. Lee, J. Y. Song and J.-U. Park, Adv. Mater., 2015, 27, 4322–4328 CrossRef CAS.
- D. Wang, X. Zhao, Y. Lin, J. Liang, T. Ren, Z. Liu and J. Li, Nanoscale, 2018, 10, 9867–9879 RSC.
- M. S. Onses, E. Sutanto, P. M. Ferreira, A. G. Alleyne and J. A. Rogers, Small, 2015, 11, 4237–4266 CrossRef CAS.
- Y. Huang, N. Bu, Y. Duan, Y. Pan, H. Liu, Z. Yin and Y. Xiong, Nanoscale, 2013, 5, 12007–12017 RSC.
- K. S. Park, J. Baek, Y. Park, L. Lee, Y.-E. K. Lee, Y. Kang and M. M. Sung, Adv. Mater., 2016, 28, 2874–2880 CrossRef CAS.
- J. Rosell-Llompart, J. Grifoll and I. G. Loscertales, J. Aerosol Sci., 2018, 125, 2–31 CrossRef CAS.
- A. Gomez and W. Deng, Aerosol Meas., 2011, 435–448 CAS.
- J. Fernández de La Mora, Annu. Rev. Fluid Mech., 2007, 39, 217–243 CrossRef.
- M. M. Hohman, M. Shin, G. Rutledge and M. P. Brenner, Phys. Fluids, 2001, 13, 2201–2220 CrossRef CAS.
- J. C. Baygents, N. J. Rivette and H. A. Stone, J. Fluid Mech., 1998, 368, 359–375 CrossRef CAS.
- K. Choi, A. H. C. Ng, R. Fobel and A. R. Wheeler, Annu. Rev. Anal. Chem., 2012, 5, 413–440 CrossRef CAS.
- A. R. Wheeler, Science, 2008, 322, 539–540 CrossRef CAS.
- J. S. Eow, M. Ghadiri, A. O. Sharif and T. J. Williams, Chem. Eng. J., 2001, 84, 173–192 CrossRef CAS.
- V. Alvarado and E. Manrique, Energies, 2010, 3, 1529–1575 CrossRef.
- Y. Sun, D. Yang, L. He, X. Luo and Y. Lü, Chem. Eng. Sci., 2019, 208, 115136 CrossRef CAS.
- V. Anand, V. A. Juvekar and R. M. Thaokar, Langmuir, 2020, 36, 6051–6060 CrossRef CAS.
- B. S. Hamlin, J. C. Creasey and W. D. Ristenpart, Phys. Rev. Lett., 2012, 109, 1–5 CrossRef.
- G. Beni and S. Hackwood, Appl. Phys. Lett., 1981, 38, 207–209 CrossRef CAS.
- F. Mugele and J.-C. Baret, J. Phys.: Condens. Matter, 2005, 17, R705 CrossRef CAS.
- W. C. Nelson and C.-J. Kim, J. Adhes. Sci. Technol., 2012, 26, 1747–1771 CrossRef CAS.
- H. Chang and L. Yeo, Electrokinetically driven microfluidics and nanofluidics, Cambridge University Press, 2010 Search PubMed.
- M. G. Pollack, R. B. Fair and A. D. Shenderov, Appl. Phys. Lett., 2000, 77, 1725–1726 CrossRef CAS.
- R. B. Fair, Microfluid. Nanofluid., 2007, 3, 245–281 CrossRef CAS.
- I. Barbulovic-Nad, H. Yang, P. S. Park and A. R. Wheeler, Lab Chip, 2008, 8, 519–526 RSC.
- P. Paik, V. K. Pamula and R. B. Fair, Lab Chip, 2003, 3, 253–259 RSC.
- R. A. Hayes and B. J. Feenstra, Nature, 2003, 425, 383–385 CrossRef CAS.
- B. Berge and J. Peseux, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 3, 159–163 CrossRef CAS.
- R. S. Allan and S. G. Mason, Proc. R. Soc. London, Ser. A, 1962, 267, 45–61 Search PubMed.
- C. T. O’Konski and H. C. Thacher Jr, J. Phys. Chem., 1953, 57, 955–958 CrossRef.
- M. S. Abbasi, H. Farooq, H. Ali, A. H. Kazim, R. Nazir, A. Shabbir, S. Cho, R. Song and J. Lee, Materials, 2020, 13, 2984 CrossRef CAS.
- G. I. Taylor, A. D. McEwan and L. N. J. de Jong, Proc. R. Soc. London, Ser. A, 1966, 291, 159–166 Search PubMed.
- R. L. Grimm and J. L. Beauchamp, J. Phys. Chem. B, 2005, 109, 8244–8250 CrossRef CAS.
- G. Supeene, C. R. Koch and S. Bhattacharjee, J. Colloid Interface Sci., 2008, 318, 463–476 CrossRef CAS.
- R. J. Haywood, M. Renksizbulut and G. D. Raithby, AIChE J., 1991, 37, 1305–1317 CrossRef CAS.
- P. R. Brazier-Smith, S. G. Jennings and J. Latham, Proc. R. Soc. London, Ser. A, 1971, 325, 363–376 Search PubMed.
- P. R. Brazier-Smith, Phys. Fluids, 1971, 14, 1–6 CrossRef.
- O. A. Basaran, T. W. Patzek, R. E. Benner Jr and L. E. Scriven, Ind. Eng. Chem. Res., 1995, 34, 3454–3465 CrossRef CAS.
- O. A. Basaran and L. E. Scriven, Phys. Fluids A, 1989, 1, 799–809 CrossRef CAS.
- J. Q. Feng, Proc. R. Soc. London, Ser. A, 1999, 455, 2245–2269 CrossRef CAS.
- J. Q. Feng and T. C. Scott, J. Fluid Mech., 1996, 311, 289–326 CrossRef CAS.
- T. Tsukada, T. Katayama, Y. Ito and M. Hozawa, J. Chem. Eng. Jpn., 1993, 26, 698–703 CrossRef CAS.
- M. J. Miksis, Phys. Fluids, 1981, 24, 1967–1972 CrossRef CAS.
- D. G. A. L. Aarts, H. N. W. Lekkerkerker, H. Guo, G. H. Wegdam and D. Bonn, Phys. Rev. Lett., 2005, 95, 164503 CrossRef.
- A. Menchaca-Rocha, A. Martínez-Dávalos, R. Nunez, S. Popinet and S. Zaleski, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 63, 46309 CrossRef CAS.
- C. Priest, S. Herminghaus and R. Seemann, Appl. Phys. Lett., 2006, 89, 134101 CrossRef.
- K. Ahn, J. Agresti, H. Chong, M. Marquez and D. A. Weitz, Appl. Phys. Lett., 2006, 88, 264105 CrossRef.
- X. Niu, F. Gielen, A. J. demello and J. B. Edel, Anal. Chem., 2009, 81, 7321–7325 CrossRef CAS.
- M. Zagnoni and J. M. Cooper, Lab Chip, 2009, 9, 2652–2658 RSC.
- A. R. Thiam, N. Bremond and J. Bibette, Phys. Rev. Lett., 2009, 102, 1–4 CrossRef.
- J. Latham and I. W. Roxburgh, Proc. R. Soc. London, Ser. A, 1966, 295, 84–97 CAS.
- G. I. Taylor, Proc. R. Soc. London, Ser. A, 1968, 306, 423–434 Search PubMed.
- X. Zhang, O. A. Basaran and R. M. Wham, AIChE J., 1995, 41, 1629–1639 CrossRef CAS.
- P.-G. de Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and Wetting Phenomena, Springer, New York, New York, NY, 2004, pp. 33–67 Search PubMed.
- W. D. Ristenpart, J. C. Bird, A. Belmonte, F. Dollar and H. A. Stone, Nature, 2009, 461, 377–380 CrossRef CAS.
- J. C. Bird, W. D. Ristenpart, A. Belmonte and H. A. Stone, Phys. Rev. Lett., 2009, 103, 1–4 CrossRef.
- S. Helmensdorfer and P. Topping, Europhys. Lett., 2013, 104(3), 34001 CrossRef.
- C. T. Bartlett, G. A. Généro and J. C. Bird, J. Fluid Mech., 2015, 763, 369–385 CrossRef.
- J. Lu, S. Fang and C. M. Corvalan, Phys. Rev. E, 2016, 93, 1–5 Search PubMed.
- X. Chen, P. Liu, C. Qi, T. Wang, Z. Liu and T. Kong, Appl. Phys. Lett., 2019, 115(2), 023701 CrossRef.
- J. Wang, B. Wang and H. Qiu, Sci. Rep., 2014, 4, 7123 CrossRef CAS.
- Y. Huo, J. Wang, H. Qiu, Z. Zuo and Y. Fan, Exp. Fluids, 2015, 56, 1–9 CrossRef.
- S. Roy, V. Anand and R. M. Thaokar, J. Fluid Mech., 2019, 878, 820–833 CrossRef CAS.
- V. Anand, S. Roy, V. M. Naik, V. A. Juvekar and R. M. Thaokar, J. Fluid Mech., 2019, 859, 839–850 CrossRef CAS.
- Z. Liu, H. M. Wyss, A. Fernandez-Nieves and H. C. Shum, Phys. Fluids, 2015, 27, 082003 CrossRef.
- G. Chen, P. Tan, S. Chen, J. Huang, W. Wen and L. Xu, Phys. Rev. Lett., 2013, 110, 1–5 Search PubMed.
- S. Choi and A. V. Saveliev, Phys. Rev. Fluids, 2017, 2, 1–10 Search PubMed.
- H. Aryafar and H. P. Kavehpour, Phys. Fluids, 2006, 18(7), 072105 CrossRef.
- X. Chen, S. Mandre and J. J. Feng, Phys. Fluids, 2006, 18, 51705 CrossRef.
- Z. Mohamed-Kassim and E. K. Longmire, Phys. Fluids, 2004, 16, 2170–2181 CrossRef CAS.
- F. Blanchette and T. P. Bigioni, Nat. Phys., 2006, 2, 254–257 Search PubMed.
- B. Ray, G. Biswas and A. Sharma, J. Fluid Mech., 2010, 655, 72–104 Search PubMed.
- J. D. Paulsen, R. Carmigniani, A. Kannan, J. C. Burton and S. R. Nagel, Nat. Commun., 2014, 5, 3182 Search PubMed.
- G. E. Charles and S. G. Mason, J. Colloid Sci., 1960, 15, 236–267 CrossRef CAS.
- S. Torza and S. G. Mason, Science, 1969, 163, 813–814 CrossRef CAS.
- H. Aryafar and H. P. Kavehpour, Langmuir, 2009, 25, 12460–12465 CrossRef CAS.
- D. Yang, M. Ghadiri, Y. Sun, L. He, X. Luo and Y. Lü, Chem. Eng. Res. Des., 2018, 136, 83–93 CrossRef CAS.
- B. B. Wang, X. D. Wang, W. M. Yan and T. H. Wang, Langmuir, 2015, 31, 7457–7462 CrossRef CAS.
- R. Pillai, J. D. Berry, D. J. E. Harvie and M. R. Davidson, Chem. Eng. Sci., 2017, 169, 273–283 CrossRef CAS.
- M. Mousavichoubeh, M. Ghadiri and M. Shariaty-Niassar, Chem. Eng. Process., 2011, 50, 338–344 CrossRef CAS.
- B. Li, Z. Wang, V. Vivacqua, M. Ghadiri, J. Wang, W. Zhang, D. Wang, H. Liu, Z. Sun and Z. Wang, Chem. Eng. Sci., 2020, 213, 115360 CrossRef CAS.
- S. Sunder and G. Tomar, Eur. J. Mech., 2020, 81, 114–123 CrossRef.
- M. Mousavichoubeh, M. Shariaty-Niassar and M. Ghadiri, Chem. Eng. Sci., 2011, 66, 5330–5337 CrossRef CAS.
- B. Li, K. Yu, J. Xu, Z. Wang, J. Wang, W. Zhang, D. Wang, H. Xu, Z. Sun and Z. Wang, Int. J. Multiphase Flow, 2020, 125, 103211 CrossRef CAS.
- S. H. Mousavi, M. Ghadiri and M. Buckley, Chem. Eng. Sci., 2014, 120, 130–142 CrossRef CAS.
- P. Davoodi, F. Feng, Q. Xu, W. C. Yan, Y. W. Tong, M. P. Srinivasan, V. K. Sharma and C. H. Wang, J. Controlled Release, 2015, 205, 70–82 CrossRef CAS.
- A. Barrero and I. G. Loscertales, Annu. Rev. Fluid Mech., 2007, 39, 89–106 CrossRef.
- T. J. Sill and H. A. von Recum, Biomaterials, 2008, 29, 1989–2006 CrossRef CAS.
- T. Han, D. H. Reneker and A. L. Yarin, Polymer, 2007, 48, 6064–6076 CrossRef CAS.
- T. Kong, H. A. Stone, L. Wang and H. C. Shum, Proc. Natl. Acad. Sci. U. S. A., 2018, 01053 Search PubMed.
- W. Yang, H. Duan, C. Li and W. Deng, Phys. Rev. Lett., 2014, 112, 054501 CrossRef CAS.
- G. C. Rutledge and S. V. Fridrikh, Adv. Drug Delivery Rev., 2007, 59, 1384–1391 CrossRef CAS.
- A. Greiner and J. H. Wendorff, Angew. Chem., Int. Ed., 2007, 46, 5670–5703 CrossRef CAS.
- D. H. Reneker and A. L. Yarin, Polymer, 2008, 49, 2387–2425 CrossRef CAS.
- J. Li, T. Kong, J. Yu, K. H. Lee, Y. H. Tang, K. W. Kwok, J. T. Kim and H. C. Shum, Lab Chip, 2019, 19, 1953–1960 RSC.
- J. Tian, J. Li, A. Sauret, T. Kong, X. Wu, Y. Lu and H. C. Shum, Phys. Rev. Appl., 2019, 12, 1 Search PubMed.
- T. Kong, J. Li, Z. Liu, Z. Zhou, P. H. Y. Ng, L. Wang and H. C. Shum, Sci. Rep., 2016, 6, 19606 CrossRef CAS.
- N. M. Ribe, M. Habibi and D. Bonn, Annu. Rev. Fluid Mech., 2012, 44, 249–266 CrossRef.
- M. Maleki, M. Habibi, R. Golestanian, N. Ribe and D. Bonn, Phys. Rev. Lett., 2004, 93, 214502 CrossRef CAS.
- N. M. Ribe, Proc. R. Soc. London, Ser. A, 2004, 460, 3223–3239 CrossRef.
- H. Y. Kim, M. Lee, K. J. Park, S. Kim and L. Mahadevan, Nano Lett., 2010, 10, 2138–2140 CrossRef CAS.
- S. I. Nagahiro and Y. Hayakawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 8–11 CrossRef.
- B. Ambravaneswaran, H. Subramani, S. Phillips and O. Basaran, Phys. Rev. Lett., 2004, 93, 034501 CrossRef.
- A. S. Utada, A. Fernandez-Nieves, H. A. Stone and D. A. Weitz, Phys. Rev. Lett., 2007, 99, 1–4 CrossRef.
- M. Cloupeau and B. Prunet-Foch, J. Electrost., 1989, 22, 135–159 CrossRef CAS.
- C. H. Chen, D. A. Seville and I. A. Aksay, Appl. Phys. Lett., 2006, 89, 87–90 Search PubMed.
- X. Li, S. Wei, L. Chen, G. Qu, H. Zhang, Z. Liu, L. Wang, T. Kong and T. Wang, Sci. Rep., 2017, 7, 1–7 CrossRef.
- Z. Z. Chong, S. H. Tan, A. M. Gañán-Calvo, S. B. Tor, N. H. Loh and N. T. Nguyen, Lab Chip, 2016, 16, 35–58 RSC.
- G. I. Taylor, Proc. R. Soc. London, Ser. A, 1969, 313, 453–475 Search PubMed.
- A. Ponce-Torres, N. Rebollo-Munõz, M. A. Herrada, A. M. Ganãn-Calvo and J. M. Montanero, J. Fluid Mech., 2018, 857, 142–172 CrossRef CAS.
- A. M. Gañán-Calvo, N. Rebollo-Muñoz and J. M. Montanero, New J. Phys., 2013, 15(3), 033035 CrossRef.
- W. J. Scheideler and C. Chen, Appl. Phys. Lett., 2014, 104, 024103 CrossRef.
- S. Sankaran and D. A. Saville, Phys. Fluids A, 1992, 5, 1081–1083 CrossRef.
- Á. G. Marín and D. Lohse, Phys. Fluids, 2010, 22(12), 122104 CrossRef.
- T. Kong, Z. Liu, L. Wang and H. C. Shum, Phys. Rev. Appl., 2015, 3, 034010 CrossRef.
- A. Gañán-Calvo, Phys. Rev. Lett., 2007, 98, 98–101 Search PubMed.
- A. M. Gañán-Calvo, J. Aerosol Sci., 1999, 30, 863–872 CrossRef.
- F. J. Higuera, J. Fluid Mech., 2004, 513, 239–246 CrossRef.
- A. M. Gañán-Calvo, J. C. Lasheras, J. Dávila and A. Barrero, J. Aerosol Sci., 1994, 25, 1121–1142 CrossRef.
- V. R. Gundabala, N. Vilanova and A. Fernández-Nieves, Phys. Rev. Lett., 2010, 105, 154503 CrossRef CAS.
- F. J. Higuera, J. Fluid Mech., 2006, 558, 143 CrossRef.
- A. Barrero, J. M. López-Herrera, A. Boucard, I. G. Loscertales and M. Márquez, J. Colloid Interface Sci., 2004, 272, 104–108 CrossRef CAS.
- X. Chen, L. Jia, X. Yin, J. Cheng and J. Lu, Phys. Fluids, 2005, 17, 1–8 Search PubMed.
- Á. G. Marín, I. G. Loscertales and A. Barrero, Biomicrofluidics, 2012, 6(4), 044104 CrossRef.
- Á. Marín, I. Loscertales, M. Márquez and A. Barrero, Phys. Rev. Lett., 2007, 98, 1–4 CrossRef.
- J. M. López-Herrera, A. Barrero, A. López, I. G. Loscertales and M. Márquez, J. Aerosol Sci., 2003, 34, 535–552 CrossRef.
- I. G. Loscertales, A. Barrero, M. Márquez, R. Spretz, R. Velarde-Ortiz and G. Larsen, J. Am. Chem. Soc., 2004, 126, 5376–5377 CrossRef CAS.
- S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364 CrossRef CAS.
- A. M. Gañán-Calvo, J. M. López-Herrera and P. Riesco-Chueca, J. Fluid Mech., 2006, 566, 421 CrossRef.
- H. Kim, D. Luo, D. Link, D. A. Weitz, M. Marquez and Z. Cheng, Appl. Phys. Lett., 2007, 91, 133106 CrossRef.
- J. Guerrero, Y. W. Chang, A. A. Fragkopoulos and A. Fernandez-Nieves, Small, 2019, 1904344, 1–15 Search PubMed.
- A. F. Mejia, P. He, D. Luo, M. Marquez and Z. Cheng, J. Colloid Interface Sci., 2009, 334, 22–28 CrossRef CAS.
- A. F. Mejia, P. He, M. Netemeyer, D. Luo, M. Marquez and Z. Cheng, Soft Matter, 2010, 6, 4885–4894 RSC.
- T. Si, C. Yin, P. Gao, G. Li, H. Ding, X. He, B. Xie and R. X. Xu, Appl. Phys. Lett., 2016, 108, 1–5 Search PubMed.
- P. He, H. Kim, D. Luo, M. Marquez and Z. Cheng, Appl. Phys. Lett., 2010, 96, 16–19 Search PubMed.
- E. Castro-Hernández, P. García-Sánchez, J. Alzaga-Gimeno, S. H. Tan, J.-C. Baret and A. Ramos, Biomicrofluidics, 2016, 10(4), 043504 CrossRef.
- S. H. Tan, B. Semin and J. C. Baret, Lab Chip, 2014, 14, 1099–1106 RSC.
- Z. Nie, M. Seo, S. Xu, P. C. Lewis, M. Mok, E. Kumacheva, G. M. Whitesides, P. Garstecki and H. A. Stone, Microfluid. Nanofluid., 2008, 5, 585–594 CrossRef CAS.
- R. W. Griffiths and J. S. Turner, Geophys. J. Int., 1988, 95, 397–419 CrossRef.
- L. Mahadevan, W. Ryu and A. Samuel, Nature, 1998, 392, 140 CrossRef CAS.
- M. Matovich and J. Pearson, Ind. Eng. Chem. Fundam., 1969, 8, 512 CrossRef CAS.
- S. M. Suleiman, Phys. Fluids, 1981, 24, 1 CrossRef.
- R. W. Freeman and L. L. Tavlarides, Phys. Fluids, 1979, 22, 782 CrossRef.
- J. Cruickshank and B. Munson, J. Fluids Eng., 1982, 104, 360 CrossRef.
- T. Cubaud and T. Mason, Phys. Rev. Lett., 2006, 96, 114501 CrossRef.
- M. Le Merrer, D. Quéré and C. Clanet, Phys. Rev. Lett., 2012, 109, 8–11 CrossRef.
- N. Ribe, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 036305 CrossRef.
- D. Sun, C. Chang, S. Li and L. Lin, Nano Lett., 2006, 6, 839–842 CrossRef CAS.
- C. Chang, K. Limkrailassiri and L. Lin, Appl. Phys. Lett., 2008, 93, 1–3 Search PubMed.
- Y. S. Park, J. Kim, J. M. Oh, S. Park, S. Cho, H. Ko and Y. K. Cho, Nano Lett., 2020, 20, 441–448 CrossRef CAS.
- X. X. He, J. Zheng, G. F. Yu, M. H. You, M. Yu, X. Ning and Y. Z. Long, J. Phys. Chem. C, 2017, 121, 8663–8678 CrossRef CAS.
- N. M. Ribe, J. R. Lister and S. Chiu-Webster, Phys. Fluids, 2006, 18, 124105 CrossRef.
- S. Chiu-Webster and J. R. Lister, J. Fluid Mech., 2006, 569, 89 CrossRef.
- S. W. Morris, J. H. P. Dawes, N. M. Ribe and J. R. Lister, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 1–12 CrossRef.
- P.-T. Brun, B. Audoly, N. M. Ribe, T. S. Eaves and J. R. Lister, Phys. Rev. Lett., 2015, 114, 174501 CrossRef.
- Y. Huang, Y. Ding, J. Bian, Y. Su, J. Zhou and Y. Duan, Nano Energy, 2017, 40, 432–439 CrossRef CAS.
- C. Chung, D. Choi, J. M. Kim, K. H. Ahn and S. J. Lee, Microfluid. Nanofluid., 2009, 8, 767–776 CrossRef.
- Y. Song, Z. Liu, T. Kong and H. C. Shum, Chem. Commun., 2013, 49, 1726–1728 RSC.
- A. L. Yarin, S. Koombhongse and D. H. Reneker, J. Appl. Phys., 2001, 89, 3018–3026 CrossRef CAS.
- D. H. Reneker and A. L. Yarin, J. Appl. Phys., 2000, 87, 4531–4547 CrossRef CAS.
- G. Riboux, Á. G. Marín, I. G. Loscertales and A. Barrero, J. Fluid Mech., 2011, 671, 226–253 CrossRef.
- Y. M. Shin, M. M. Hohman, M. P. Brenner and G. C. Rutledge, Polymer, 2001, 42, 09955–09967 CrossRef CAS.
- J. H. Park and G. C. Rutledge, Macromolecules, 2017, 50, 5627–5642 CrossRef CAS.
- S. V. Fridrikh, J. H. Yu, M. P. Brenner and G. C. Rutledge, Phys. Rev. Lett., 2003, 90, 144502 CrossRef.
- S. Korkut, D. A. Saville and I. A. Aksay, Phys. Rev. Lett., 2008, 100, 1–4 CrossRef.
- A. F. Spivak and Y. A. Dzenis, Appl. Phys. Lett., 1998, 73, 3067–3069 CrossRef CAS.
- J. Guerrero, J. Rivero, V. R. Gundabala, M. Perez-Saborid and A. Fernandez-Nieves, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13763–13767 CrossRef CAS.
- W. Arne, N. Marheineke, M. Perez-Saborid, J. Rivero-Rodriguez, R. Wegener and M. Wieland, SIAM J. Appl. Math., 2017, 1–24 CAS.
- H. Hadidi, R. Kamali and M. K. D. Manshadi, Eur. J. Mech., 2020, 80, 206–215 CrossRef.
- S. Luo, J. Schiffbauer and T. Luo, Phys. Chem. Chem. Phys., 2016, 18, 29786–29796 RSC.
- S. Mhatre and R. Thaokar, Chem. Eng. Process., 2015, 96, 28–38 CrossRef CAS.
- D. Dan and G. Jing, J. Pet. Sci. Eng., 2006, 53, 113–122 CrossRef CAS.
- B. Sebastian and P. S. Dittrich, Annu. Rev. Fluid Mech., 2018, 50, 483–504 CrossRef.
- P. M. Vlahovska, Annu. Rev. Fluid Mech., 2019, 51, 305–330 CrossRef.
- R. G. Larson, The structure and rheology of complex fluids, Oxford Univ. Press, Oxford, 1999 Search PubMed.
- H.-F. Huang, M. Zahn and E. Lemaire, J. Electrost., 2011, 69, 442–455 CrossRef CAS.
- E. Lemaire, L. Lobry, N. Pannacci and F. Peters, J. Rheol., 2008, 52, 769–783 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |
