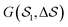Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Free-energy landscape of polymer-crystal polymorphism†
Chan
Liu
a,
Jan Gerit
Brandenburg
 bc,
Omar
Valsson
bc,
Omar
Valsson
 a,
Kurt
Kremer
a,
Kurt
Kremer
 a and
Tristan
Bereau
a and
Tristan
Bereau
 *ad
*ad
aMax Planck Institute for Polymer Research, 55128 Mainz, Germany
bInterdisciplinary Center for Scientific Computing, University of Heidelberg, 69120 Heidelberg, Germany
cDigital Organization, Merck KGaA, 64293 Darmstadt, Germany
dVan 't Hoff Institute for Molecular Sciences and Informatics Institute, University of Amsterdam, Amsterdam 1098 XH, The Netherlands. E-mail: t.bereau@uva.nl
First published on 3rd September 2020
Abstract
Polymorphism rationalizes how processing can control the final structure of a material. The rugged free-energy landscape and exceedingly slow kinetics in the solid state have so far hampered computational investigations. We report for the first time the free-energy landscape of a polymorphic crystalline polymer, syndiotactic polystyrene. Coarse-grained metadynamics simulations allow us to efficiently sample the landscape at large. The free-energy difference between the two main polymorphs, α and β, is further investigated by quantum-chemical calculations. The results of the two methods are in line with experimental observations: they predict β as the more stable polymorph under standard conditions. Critically, the free-energy landscape suggests how the α polymorph may lead to experimentally observed kinetic traps. The combination of multiscale modeling, enhanced sampling, and quantum-chemical calculations offers an appealing strategy to uncover complex free-energy landscapes with polymorphic behavior.
I. Introduction
The complex interplay of molecular interactions can lead to a material exhibiting multiple distinct forms in its solid state.1 This polymorphism often results in wildly different material properties, making the study of polymorphism both essential for quality control in manufacture, and also a fascinating structure–property problem. Beyond structure and property, the intermediate processing of a material has a key impact on the resulting polymorph. Fundamentally, this stems from two ingredients: (i) the underlying free-energy landscape being sufficiently rugged to display several low-lying metastable states; and (ii) the exceedingly slow kinetics exhibited in the solid phase, preventing a full/ergodic kinetic relaxation.The screening of polymorphs has traditionally exclusively been performed experimentally, in spite of the significant costs involved. Computational methods hold the promise of predicting polymorphic stability before going to the laboratory. In the context of molecular crystals, especially pharmaceuticals and porous (organic) cages, a considerable body of work has recently emerged.2–13 The modeling of polymorphism holds two challenges: sampling and modeling accuracy. The free-energy landscape exhibits an overwhelming number of configurations, of which only an infinitesimal fraction competes in terms of low-lying states. Furthermore, correctly ranking the relative free energies of each conformer requires computational methods that are accurate enough (of the order of thermal energy, kBT) to reproduce the underlying interactions. Many methods exist to tackle these two challenges, out of which we mention the use of an appropriately-tuned force-field for sampling and electronic-structure methods (e.g., density functional theory) for energetic characterization.14–16
Here, we focus on polymers, which not only embody countless industrial applications, but also for which we critically lack a detailed picture of their free-energy landscape. Evidently, the increased number of atoms per molecule involved will lead to higher structural correlations, significantly larger barriers, and much longer timescales compared to molecular crystals of small molecules. While many semicrystalline polymers possess only a single type of unit cell, there are exceptions: syndiotactic polystyrene (sPS), for instance, is well-known for its complex crystal polymorphism.
In this work, we aim at unraveling the underlying free-energy landscape of sPS, to better understand the body of experimental evidence gathered around its polymorphs. We focus on the thermally-induced processing aspect – the α and β polymorphs, shown in Fig. 1.18–23 They share the same intrachain conformations, but with different interchain-packing structures. The α and β forms of sPS are further classified into limiting disordered forms, α′ and β′, and limiting ordered forms, α′′ and β′′.18,20,22,24 The processing conditions impact the forms experimentally observed.22,24Fig. 1 displays the limiting ordered forms.
 | ||
| Fig. 1 (a) Molecular structure of polystyrene and the CG-mapping scheme of the Fritz model.17 (b) Left: Longitudinal view of an all-trans chain conformation; Right: transverse section of the experimentally-resolved α and β forms. In the transverse sections, each polymer chain is represented by three CG beads (highlighted in red dashed circles). The red solid lines represent cross-sectional vectors pointing from the backbone to the bisector of its two closest side chains. | ||
Experimental evidence has pointed out the strong impact of the processing conditions: starting material, initial temperature, and cooling rate.18,22,24–28 They hint at a highly complex free-energy landscape. The relative stability between the α and β polymorphs is noteworthy: (i) starting from a high initial temperature, fast (slow) cooling will lead to the α (β) forms; (ii) under an identical slow cooling rate, melt crystallization starting under 230 °C and above 260 °C will yield the α and β polymorphs, respectively, while intermediate temperatures generate mixtures thereof. These results suggest that given sufficient mobility thanks to a high initial temperature and a slow enough cooling rate, the preferred packing structure corresponds to the β form. In the case of stiffened chains and/or reduced molecular mobility, the α polymorph is preferred. These observations of the structural properties of sPS indicate that crystallization to the α form results from a kinetically-controlled process, while β would be the thermodynamically stable form. Our understanding, therefore, falls short in several ways: how the free-energy landscape translates into the apparent differences between the two forms, and also a more mechanistic insight regarding the origin of these effects.
While computational studies of polymer crystal polymorphs remain to date extremely limited, we note the work of Tamai and co-workers on nanoporous cavity structures in the α and β forms,29 the diffusion of gases,30,31 the orientational motion of guest solvents,32,33 and the adsorption of small molecules.34–36 These studies helped understand the structural features of some of these forms. Unfortunately, the atomistic resolution involved strongly limits the timescale that can be reached with the simulations – on the order of nanoseconds. This prevents both the observation of self assembly and also polymorph interconversion, thereby hindering access to the free-energy landscape.
To address the time-scale issue, we turn to coarse-grained (CG) modeling. By lumping several atoms into one larger superparticle or bead, CG models can sample significantly faster, while offering a systematic connection to the reference chemistry.37 Some of us recently applied a structure-based CG model aimed at reproducing certain thermodynamic aspects of sPS.17 Despite a parametrization and validation performed exclusively in the melt, we found remarkable transferability to the crystalline phase: not only does the CG model stabilize the α and β polymorphs, the melting temperatures of the two phases were found to be in excellent agreement.38 Our study aimed at an exploration of the self-assembly mechanisms of sPS, using a temperature-based enhanced-sampling molecular dynamics (MD) technique – parallel tempering. In the present work, we instead turn to methods based on collective variables (CVs), specifically metadynamics.39,40 We will show that an appropriate choice of CVs can lead to convergence of the simulations, and offer us access to a great diversity of structural forms. We present for the first time the free-energy landscape of polymorphism of a polymer crystal.
We further challenge the calculations of the free-energy difference between α and β polymorph stability by means of quantum-chemical calculation at the density functional theory (DFT) level. The results show excellent agreement with the CG simulations given the change in resolution. Critically, we find in both cases the preferential stabilization of the β phase – in line with experiments.
II. Results and discussion
A. Metadynamics
In the Methods section, we present collective variables (CVs) that are capable of distinguishing five different phases of sPS (Section IV B). A significant distinction between these phases is essential to also enable the discovery of other intermediate phases. A further requirement is the absence of hidden barriers that would hinder dynamics along the CVs.39 To alleviate possible artifacts due to an inappropriate choice of CVs, we tested several of them and later re-weighted all simulations to the same CV space. This further allows us to empirically check the convergence of our simulations.We focus on a two-dimensional CV exploration, as a balance between exploration and convergence: a three-dimensional CV-space exploration can require excessive memory and presents challenges to converge due to the curse of dimensionality. We note that extensions of the method, such as bias-exchange and parallel-bias metadynamics, can help along these lines.41–44 We herein present four combinations of CVs (referenced in Table S1, ESI†) based on orientational features between the v2 transverse vectors (Fig. 1b). Variants of 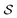 focus on specific angles, while the second Legendre polynomial P2 probes the overall ordering: (i)
focus on specific angles, while the second Legendre polynomial P2 probes the overall ordering: (i) 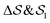 ; (ii)
; (ii) 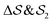 ; (iii)
; (iii) 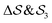 ; (iv)
; (iv) 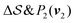 .
.
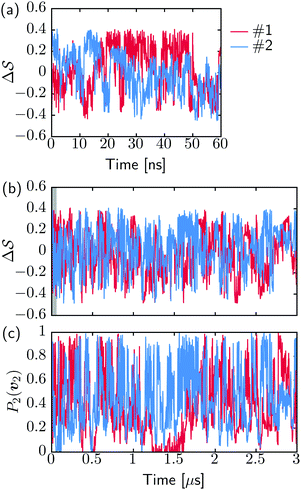
Fig. 2 shows a metadynamics simulation at T = 400 K driven by the combination of CVs 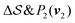 using two walkers. The walkers were initiated from the two crystalline phases α and β. The simulations are able to transition many times between the main polymorphs, starting at around 20 ns (Fig. 2a). The results highlight that the ability of the CVs to distinguish α from β helps ensure large conformational transitions (Fig. S2, ESI†). We note however the absence of conformations in the amorphous phase, due to both our sampling below the transition temperature (roughly 450 K) and our protocol's restraining box range and chain direction (see Section IV C).
using two walkers. The walkers were initiated from the two crystalline phases α and β. The simulations are able to transition many times between the main polymorphs, starting at around 20 ns (Fig. 2a). The results highlight that the ability of the CVs to distinguish α from β helps ensure large conformational transitions (Fig. S2, ESI†). We note however the absence of conformations in the amorphous phase, due to both our sampling below the transition temperature (roughly 450 K) and our protocol's restraining box range and chain direction (see Section IV C).
B. Polymorphic stability
Having established that our combination of CVs enables a satisfactory transition between major polymorphs, we turn to the question of convergence. To assess convergence, we run metadynamics in the CV space of our four combinations, and marginalize the free-energy landscape to only display their common CV: the SMAC difference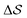 . Fig. 3 compares the free-energy surface as a function of the CV
. Fig. 3 compares the free-energy surface as a function of the CV 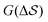 . We have marked the α and β polymorphs according to values of the CV from unbiased MD simulations (see the ESI†). All four curves agree within roughly 5 kJ mol−1 across the range of
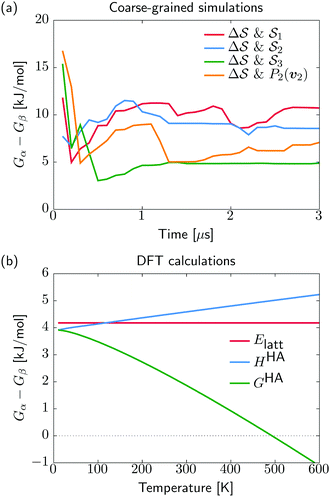
. We have marked the α and β polymorphs according to values of the CV from unbiased MD simulations (see the ESI†). All four curves agree within roughly 5 kJ mol−1 across the range of 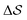 values, despite their sampling along different complementary CVs. Convergence as a function of simulation time is further displayed in Fig. 4a, which focuses on the free-energy difference between the α and β polymorphs, Gα − Gβ. We find that all curves converge after roughly 1 to 2 μs. We do see variations between simulations reminiscent of the spread in panel (a). Given the remarkable complexity of probing the free-energy landscape of polymer crystals, we consider this level of agreement as an encouraging indicator of the level of convergence of our simulations.
values, despite their sampling along different complementary CVs. Convergence as a function of simulation time is further displayed in Fig. 4a, which focuses on the free-energy difference between the α and β polymorphs, Gα − Gβ. We find that all curves converge after roughly 1 to 2 μs. We do see variations between simulations reminiscent of the spread in panel (a). Given the remarkable complexity of probing the free-energy landscape of polymer crystals, we consider this level of agreement as an encouraging indicator of the level of convergence of our simulations.
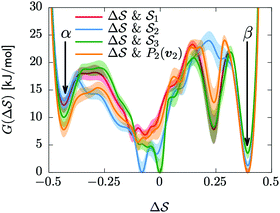 | ||
Fig. 3 Convergence of the free-energy calculations. Comparison of four metadynamics simulations at T = 400 K with different CVs (see labels) projected on 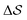 . . | ||
Metadynamics simulations on different system sizes lead to similar free-energy profiles (see Fig. S5, ESI†), whether changing the number of chains in the box or the number of monomers per chain. We rationalize the lack of system-size dependence in two ways: (i) the lack of dependence on the number of chains can be explained by the collective nature of the transitions, where the box is so small that all chains transition to a new phase at once; and (ii) the free-energy barriers do not scale with the number of monomers, because the transitions are orthogonal to the chain direction, as indicated by the order parameters P2(v1) and P2(v2) (see Fig. S2, ESI†). As such, the size regime we work with appears to have a lack of system-size dependency, despite the extensivity of the free energy. Identifying this scaling would require the simulation of much larger simulation boxes, for instance because multiple structures could occur (concurrent with grain boundaries).
Having identified the two polymorphs as local minima with a rationalization of kinetic routes in between them, we try to further establish their relative thermodynamic stability. For this, we start from the experimentally determined structures and employ quantum mechanical methods for local structure relaxations and prediction of their temperature dependent free energy (see Section IV D). In contrast to the molecular dynamics simulations, our DFT results do not describe anharmonicities of the energy surface, potentially neglecting some thermal effects. On the other hand, the described interactions are at a quantum-mechanical level, physically more sound, and thus expected to be more accurate compared to the classical potentials used in our molecular dynamics. We note that while the α and β polymorphs for the quantum-mechanical calculations are taken from experimental structures, the coarse-grained references stem from the simulations. Our recent analysis of the CG model indicated a faithful stabilization of the α structure but discrepancies in the β structure, likely due to side-chain packing issues.38 Using experimental and simulation β structures for the quantum-mechanical calculations and CG simulations, respectively, allows us to account for the limited resolution of the CG model.
We show in Fig. 4b the quantum-mechanical energy difference between the two polymorphic forms. In a static picture at 0 K, sPS β is predicted to be more stable by 4 kJ mol−1. Upon heating to 400 K, the enthalpy difference increases by 1 kJ mol−1, while the free energy difference decreases by 3 kJ mol−1. At elevated temperatures of about 500 K, form α is predicted to be more stable, which is, however, not experimentally observable due to the amorphous phase. The stability difference at room temperature is in excellent agreement with the estimations from our dynamics simulations, indicating a stabilization of β by 5–10 kJ mol−1. The smaller stability difference predicted by DFT is in line with our experience from molecular crystals, where higher quality interaction energy models typically lead to smaller energy gaps between polymorphs.14 The overall analysis matches the experimental expectation that form α crystallizes on rapid cooling from elevated temperatures, while β forms in slow cooling experiments.45
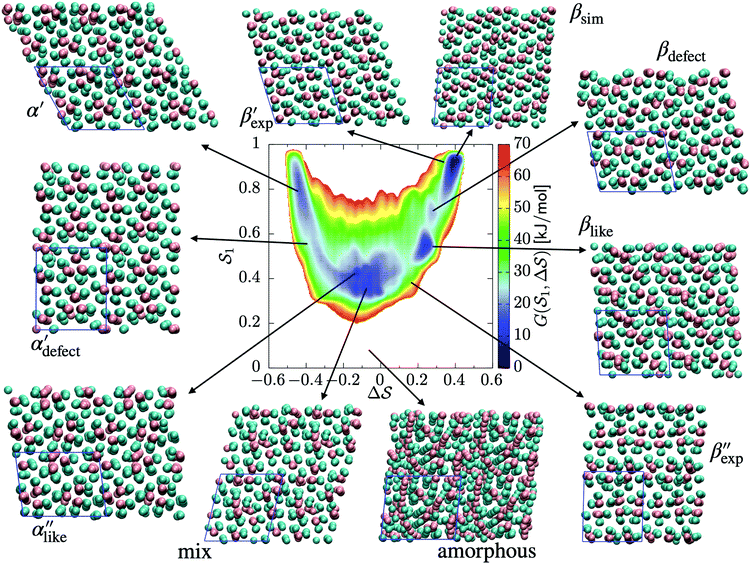
The analysis reported in Fig. 4 shows that the β form is systematically better stabilized than the competing α form. The 1D landscape clearly separates α from β at the left and right sides of the range, respectively. These are separated by both α/β mixtures and the amorphous phases at around 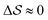 . Interestingly, we observe a significantly lower free-energy barrier upon going from the amorphous phase to the pure α polymorph, compared to that for the β polymorph: while the former is between 10 and 15 kJ mol−1 high, the other is up to 20 kJ mol−1. The β form is more stable across the CV space, but the α form is easier to obtain from the mixture and amorphous phases – a kinetic effect. This can help rationalize the kinetic-trap behavior of the α form found experimentally.45 Some of us previously identified an overpopulation of the α form when probed in simulation box geometries concomitant to the α unit cell, suggesting a templating mechanism.38
. Interestingly, we observe a significantly lower free-energy barrier upon going from the amorphous phase to the pure α polymorph, compared to that for the β polymorph: while the former is between 10 and 15 kJ mol−1 high, the other is up to 20 kJ mol−1. The β form is more stable across the CV space, but the α form is easier to obtain from the mixture and amorphous phases – a kinetic effect. This can help rationalize the kinetic-trap behavior of the α form found experimentally.45 Some of us previously identified an overpopulation of the α form when probed in simulation box geometries concomitant to the α unit cell, suggesting a templating mechanism.38
C. Free-energy landscape of sPS
As an extension to Fig. 3, Fig. 5 shows a representation of the free-energy landscape for the CV combination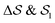 . Stability is color coded from blue to red. We observe a large diversity of phases with distinct structural features. Notably, we find many more structures than our previous study based on parallel tempering.38
. Stability is color coded from blue to red. We observe a large diversity of phases with distinct structural features. Notably, we find many more structures than our previous study based on parallel tempering.38
We first analyze structures similar to the α polymorph. Of particular interest are symmetries around triplets of chains that form the fundamental symmetric unit of α structures (see Fig. 1b). As compared to our previous work that used parallel tempering, we observe a broader variety of relative orientations between chain triplets. Small but noticeable variations can be found among the α-type structures on the landscape. The differentiation between α′ and α′′ is made more difficult by imposing 12 chains in our simulation box, while the unit cell of α contains only 9 chains.20 We emphasize the difference between apparently distinct forms stabilized in our simulations: α′, 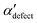 and
and 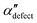 , shown in Fig. 5. All triplets of chains, represented by groups of tan-colored beads, exhibit virtually identical orientations in α′ and little variation in
, shown in Fig. 5. All triplets of chains, represented by groups of tan-colored beads, exhibit virtually identical orientations in α′ and little variation in 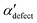 : the angles between side-chain vectors are almost all strictly at 120°, leading to
: the angles between side-chain vectors are almost all strictly at 120°, leading to 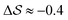 .
. 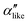 , on the other hand, displays two different triplet orientations, analogous to the experimentally resolved α′′. The angles between side-chain vectors do not always correspond to 120°, leading to
, on the other hand, displays two different triplet orientations, analogous to the experimentally resolved α′′. The angles between side-chain vectors do not always correspond to 120°, leading to 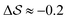 , located near the mixture phases. Our simulations do not stabilize the α′′ polymorph, which may be due to the number of chains being incongruent with the unit cell, or possibly limitations in the CG force field in reproducing fine steric features.17,38
, located near the mixture phases. Our simulations do not stabilize the α′′ polymorph, which may be due to the number of chains being incongruent with the unit cell, or possibly limitations in the CG force field in reproducing fine steric features.17,38
In line with our previous study, we find an alternate form to the experimentally-resolved22,24 limiting disordered β′ and limiting ordered β′′ polymorphs as the most global minimum of sPS: βsim, where we highlighted the difference in layering.38 While the parallel tempering simulations led to neither experimental form, the metadynamics simulations successfully sampled them, albeit at too high free energy: the 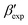 and
and 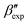 forms sit at about 30 and 50 kJ mol−1 higher than the global minimum, respectively. We argued before that the simple description of the side-chain sterics likely had a detrimental effect on the stability of the β polymorphs. This effect was motivated by a discrepancy in the melting temperature from CG simulations, as compared to reference atomistic simulations: in excellent agreement for the α form, but with too-low stability for β. In the context of the present work, these structural artifacts likely give rise to shifts in the free-energy landscape shown in Fig. 5.
forms sit at about 30 and 50 kJ mol−1 higher than the global minimum, respectively. We argued before that the simple description of the side-chain sterics likely had a detrimental effect on the stability of the β polymorphs. This effect was motivated by a discrepancy in the melting temperature from CG simulations, as compared to reference atomistic simulations: in excellent agreement for the α form, but with too-low stability for β. In the context of the present work, these structural artifacts likely give rise to shifts in the free-energy landscape shown in Fig. 5.
III. Conclusion
In this paper, we study the free-energy landscape of syndiotactic polystyrene (sPS) using computational methods to get microscopic insight into polymorphic interconversion. The development of adequate collective variables (CVs) applied to metadynamics, together with the use of a remarkably transferable coarse-grained (CG) model, allows us for the first time to cross the significant barriers between polymorphs in polymer crystals. Minute structural differences between polymorphs require finely-tuned CVs to account for the small variations. Rather than relying on a single CV combination, running metadynamics simulations on several such combinations and re-weighting them help us test for convergence of the simulations. We find excellent agreement between four such combinations, despite the significant barriers exerted by the system.We rely on a combination of two different SMAC variables46 to build a free-energy landscape. The β form clearly stands as the global minimum, even though we observe fine differences between the simulated and experimental layerings, arguably an artifact of the side-chain representation in the CG model. Encouragingly, we do observe the two experimental 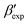 and
and 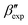 structures in the metadynamics runs. The α form is between 5 and 10 kJ mol−1 less stable than the global minimum. As a complementary approach, we used quantum mechanical models to compute the temperature dependent relative stability of the α and β polymorphs. We predict the stability to be slightly smaller (1 kJ mol−1), but can overall confirm the CG simulations.
structures in the metadynamics runs. The α form is between 5 and 10 kJ mol−1 less stable than the global minimum. As a complementary approach, we used quantum mechanical models to compute the temperature dependent relative stability of the α and β polymorphs. We predict the stability to be slightly smaller (1 kJ mol−1), but can overall confirm the CG simulations.
Remarkably, we find a significantly lower free-energy barrier upon going from the amorphous phase to α rather than β. This lowered activation could partially explain the α polymorph's tendency to be identified as a kinetic trap. It also complements our previous observation: α is overstabilized in box geometries congruent with its unit cell, a templating mechanism of sorts. Differences in nucleation rates may further help drive the system in the direction of α, although this is beyond the scope of this work.
Varying the system size will naturally affect the results: smaller simulation boxes are more likely to suffer from incompatibilities with different crystal units, resulting in artificially low stabilization. On the other hand, the significant free-energy barriers will become more challenging to cross as simulation boxes grow. The present study demonstrates that a multiscale approach can provide insight and complementary information to experiments on polymer-crystal polymorphism.
IV. Simulation methods
A. Coarse-grained simulations
We rely on a previously-developed coarse-grained (CG) model for syndiotactic polystyrene (sPS), referred to hereafter as the Fritz model.17 It maps each monomer onto two types of CG beads: “A” for the chain backbone and “B” for the phenyl ring (Fig. 1a). The model represents PS as a linear chain of alternating A and B CG beads, supplemented by sophisticated bonded potentials to ensure accurate structures, including the correct tacticity – enabling the crystallization of sPS. The bonded interactions were obtained by direct Boltzmann inversion of distributions obtained from atomistic simulations of single chains in a vacuum. The nonbonded potentials are derived using the conditional reversible work (CRW) method:47,48 constrained-dynamics runs with the all-atom model of two short chains in a vacuum.B. Collective variables
Metadynamics acts on the selected CVs to drive the system and cross free-energy barriers. This puts an essential emphasis on the choice of CVs, known to be extremely system and process dependent.39 A large variety of CVs have been used, for instance, distances, angles, or dihedrals formed by atoms or groups of atoms,49 coordination numbers,41,50,51 and Steinhardt parameters.52–54Crystallization is typically characterized by long-range order. For example, cluster symmetries are often probed via the Steinhardt parameter, Ql,55,56 which represents the rotationally-invariant spherical harmonics of order l. Q4 and Q6, in particular, have been studied in the context of Lennard-Jones particles,52 ice,53 and calcium carbonate nanoparticles.54 To study polymorphism in sPS, however, we have found the Steinhardt parameter to inefficiently distinguish crystalline forms (see Fig. S3, ESI†). We rationalize this by the lack of differentiation for transverse vectors (see Fig. 1b). This has led us to the development of CVs that are tailored to sPS.
Fig. 1b shows a longitudinal view of a chain conformation, as well as transverse sections of the two main polymorphs of interest: the experimentally-determined α and β structures.24 We herein propose two sets of vectors: one longitudinal vector, v1, and one transverse vector, v2. v1 is oriented along the backbone, and it is defined as the interparticle vector between two consecutive monomers (i.e., backbone beads). As for the transverse vector v2, for each monomer, it originates from the second backbone and points to the bisector of the two closest side chains. Fig. 1b indicates that typical angles for the α and β polymorphs are roughly 120° and 180°, respectively. Note that here, to improve the efficiency of computation, the side-chain vector is an average over each whole molecule. Effectively this assumes a homogeneous configuration across the chain, in line with the system sizes considered here.
Because these two polymorphs consist of identical chain conformations, no differences can be extracted from intrachain statistics. Instead, differences between polymorphs are concentrated in the interchain configurations. As such, any CV that is able to distinguish between polymorphs ought to focus on interchain geometries. By symmetry, the most noticeable differences occur along the transverse sections. These differences can be displayed more intuitively by the distribution of angles between neighboring transverse vectors v2 (see Fig. S1, ESI†), which is derived from unbiased MD simulations at 300 K. In the following discussion, we will introduce two kinds of CVs that are functions of these transverse angles.
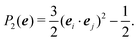 | (1) |
| Kn(θij − θn) = e−((θij−θn)2/2σn2). | (2) |
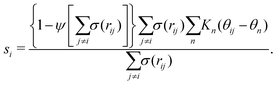 | (3) |
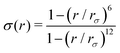 and ψ(r) = exp(−r/rψ), where rσ and rψ (see Table S1, ESI†) provide a balance to keep the CV local, while incorporating enough numbers. The quantity is then averaged over all si:
and ψ(r) = exp(−r/rψ), where rσ and rψ (see Table S1, ESI†) provide a balance to keep the CV local, while incorporating enough numbers. The quantity is then averaged over all si: 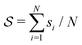 .
.
Based on the angle distributions of Fig. S1 (ESI†), we construct a number of SMAC CVs using various sets of reference angles to optimally distinguish between sPS phases. Table S1 (ESI†) lists the set of CVs we used in this work. For instance, the main peaks for the α and β phases led to the definition of SMAC CVs 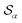 and
and 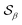 , centered at 120° and 170°, respectively. To emphasize both features at once, we constructed a CV based on their difference:
, centered at 120° and 170°, respectively. To emphasize both features at once, we constructed a CV based on their difference: 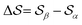 . This can be observed by monitoring the CV during unbiased MD simulations (Fig. S2c, ESI†). Three additional SMAC CVs are presented in Table S1 (ESI†).
. This can be observed by monitoring the CV during unbiased MD simulations (Fig. S2c, ESI†). Three additional SMAC CVs are presented in Table S1 (ESI†).
C. Metadynamics
Well-tempered metadynamics simulations were performed at 400 K.40,60–65 The bias deposition stride was set to be 0.5 ps, and the bias factor was 20. The Gaussian-bias width was set to 0.01 for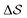 , and 0.05 otherwise. The initial Gaussian heights were all set to 3 kJ mol−1. Each simulation consisted of multiple walkers:66 In metadynamics, we refer to a biased run that explores the CV-space as a walker, while multiple walkers simultaneously explore and carve the same free-energy landscape. This method can significantly speed up the convergence of the simulations, as all walkers contribute to a single, combined free-energy landscape. In this work, 2 walkers were run in parallel and initialized from the α and β forms, respectively. All simulations were performed using GROMACS 5.1.467 and PLUMED 2.4.68,69 Simulations were carried out in the isothermal–isobaric ensemble at P = 1 bar using the velocity-rescale thermostat70 and the anisotropic Parrinello–Rahman barostat.71 We ensured stable variations in the simulation box by restraining the range of allowed geometries (5 < a2 < 9; 5 < b2 < 9; 6 < c2 < 8 nm2). We also restrained the direction of each chain to lie within 30° of the box's z component. This avoided significant collective rotations of the chains with respect to the simulation box, leading to alignments along the other coordinates. Such a scheme merely aims at forcing all chains to loosely lie within an arbitrarily-chosen z axis. This helped avoid artifacts when calculating longitudinal and transverse vectors, especially at higher temperatures. More details can be found in the ESI.†
, and 0.05 otherwise. The initial Gaussian heights were all set to 3 kJ mol−1. Each simulation consisted of multiple walkers:66 In metadynamics, we refer to a biased run that explores the CV-space as a walker, while multiple walkers simultaneously explore and carve the same free-energy landscape. This method can significantly speed up the convergence of the simulations, as all walkers contribute to a single, combined free-energy landscape. In this work, 2 walkers were run in parallel and initialized from the α and β forms, respectively. All simulations were performed using GROMACS 5.1.467 and PLUMED 2.4.68,69 Simulations were carried out in the isothermal–isobaric ensemble at P = 1 bar using the velocity-rescale thermostat70 and the anisotropic Parrinello–Rahman barostat.71 We ensured stable variations in the simulation box by restraining the range of allowed geometries (5 < a2 < 9; 5 < b2 < 9; 6 < c2 < 8 nm2). We also restrained the direction of each chain to lie within 30° of the box's z component. This avoided significant collective rotations of the chains with respect to the simulation box, leading to alignments along the other coordinates. Such a scheme merely aims at forcing all chains to loosely lie within an arbitrarily-chosen z axis. This helped avoid artifacts when calculating longitudinal and transverse vectors, especially at higher temperatures. More details can be found in the ESI.†
D. Quantum-chemical methods
Quantum-chemical methods are used to simulate the relative thermodynamical stability of the two sPS polymorphs. The two polymorphic forms identified by the metadynamics simulations and experimentally characterized in the literature have been taken as starting points for local geometry optimization. Phonon modes are computed to confirm the stationary points as local minima and to give access to the temperature-dependent harmonic Gibbs free energy| GHA(T,P) = Elatt + GHAvib(T) + PV. | (4) |
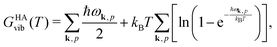 | (5) |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Christine Peter for insightful discussions, as well as Bingqing Cheng, Robinson Cortes-Huerto, and Hsiao-Ping Hsu for critical reading of the manuscript. CL was supported by the Max Planck Graduate Center. TB was partially supported by the Emmy Noether program of the Deutsche Forchungsgemeinschaft (DFG). Open Access funding provided by the Max Planck Society.References
- H. G. Brittain, et al., Polymorphism in pharmaceutical solids, Drugs Pharm. Sci., 1999, 95, 183–226 Search PubMed.
- R. J. Gdanitz, Ab initio prediction of molecular crystal structures, Curr. Opin. Solid State Mater. Sci., 1998, 3(4), 414–418 CrossRef CAS.
- J. Bernstein and J. M. Bernstein, Polymorphism in Molecular Crystals, Oxford University Press, vol. 14, 2002 Search PubMed.
- M. Jansen, K. Doll and J. Christian Schön, Addressing chemical diversity by employing the energy landscape concept, Acta Crystallogr., Sect. A: Found. Crystallogr., 2010, 66(5), 518–534 CrossRef CAS.
- J. T. A. Jones, T. Hasell, X. Wu, J. Bacsa, K. E. Jelfs, M. Schmidtmann, S. Y. Chong, D. J. Adams, A. Trewin, F. Schiffman, F. Cora, B. Slater, A. Steiner, G. M. Day and A. I. Cooper, Modular and predictable assembly of porous organic molecular crystals, Nature, 2011, 474(7351), 367–371 CrossRef CAS.
- Y. A. Abramov, Current computational approaches to support pharmaceutical solid form selection, Org. Process Res. Dev., 2012, 17(3), 472–485 CrossRef.
- E. O. Pyzer-Knapp, H. P. G. Thompson, F. Schiffmann, K. E. Jelfs, S. Y. Chong, M. A. Little, A. I. Cooper and G. M. Day, Predicted crystal energy landscapes of porous organic cages, Chem. Sci., 2014, 5(6), 2235–2245 RSC.
- A. J. Cruz-Cabeza, S. M. Reutzel-Edens and J. Bernstein, Facts and fictions about polymorphism, Chem. Soc. Rev., 2015, 44(23), 8619–8635 RSC.
- M. A. Neumann, J. van de Streek, F. P. A. Fabbiani, P. Hidber and O. Grassmann, Combined crystal structure prediction and high-pressure crystallization in rational pharmaceutical polymorph screening, Nat. Commun., 2015, 6, 7793 CrossRef CAS.
- S. L. Price and S. M. Reutzel-Edens, The potential of computed crystal energy landscapes to aid solid-form development, Drug Discovery Today, 2016, 21(6), 912–923 CrossRef.
- S. L. Price and J. G. Brandenburg, Molecular crystal structure prediction, in Non-Covalent Interactions in Quantum Chemistry and Physics, Elsevier, 2017, pp. 333–363 Search PubMed.
- A. Pulido, L. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Functional materials discovery using energy–structure–function maps, Nature, 2017, 543(7647), 657–664 CrossRef CAS.
- G. M. Day and A. I. Cooper, Energy-structure-function maps: Cartography for materials discovery, Adv. Mater., 2017, 30(37), 1704944 CrossRef.
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, A. D. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell and R. Car, et al., Report on the sixth blind test of organic crystal structure prediction methods, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72(4), 439–459 CrossRef CAS.
- N. Marom, R. A. DiStasio, V. Atalla, S. Levchenko, A. M. Reilly, J. R. Chelikowsky, L. Leiserowitz and A. Tkatchenko, Many-body dispersion interactions in molecular crystal polymorphism, Angew. Chem., Int. Ed., 2013, 52(26), 6629–6632 CrossRef CAS.
- J. Hoja, H.-Y. Ko, M. A. Neumann, R. Car, R. A. DiStasio and A. Tkatchenko, Reliable and practical computational description of molecular crystal polymorphs, Sci. Adv., 2019, 5(1), eaau3338 CrossRef.
- D. Fritz, V. A. Harmandaris, K. Kremer and N. F. A. van der Vegt, Coarse-grained polymer melts based on isolated atomistic chains: simulation of polystyrene of different tacticities, Macromolecules, 2009, 42(19), 7579–7588 CrossRef CAS.
- C. De Rosa, G. Guerra, V. Petraccone and P. Corradini, Crystal structure of the α-form of syndiotactic polystyrene, Polym. J., 1991, 23(12), 1435 CrossRef CAS.
- P. Corradini, C. De Rosa, G. Guerra, R. Napolitano, V. Petraccone and B. Pirozzi, Conformational and packing energy of the crystalline α modification of syndiotactic polystyrene, Eur. Polym. J., 1994, 30(10), 1173–1177 CrossRef CAS.
- C. De Rosa, Crystal structure of the trigonal modification (α form) of syndiotactic polystyrene, Macromolecules, 1996, 29(26), 8460–8465 CrossRef CAS.
- L. Cartier, T. Okihara and B. Lotz, The α superstructure of syndiotactic polystyrene: A frustrated structure, Macromolecules, 1998, 31(10), 3303–3310 CrossRef CAS.
- C. De Rosa, M. Rapacciuolo, G. Guerra, V. Petraccone and P. Corradini, On the crystal structure of the orthorhombic form of syndiotactic polystyrene, Polymer, 1992, 33(7), 1423–1428 CrossRef CAS.
- Y. Chatani, Y. Shimane, T. Ijitsu and T. Yukinari, Structural study on syndiotactic polystyrene: 3. crystal structure of planar form i, Polymer, 1993, 34(8), 1625–1629 CrossRef CAS.
- G. Guerra, V. M. Vitagliano, C. De Rosa, V. Petraccone and P. Corradini, Polymorphism in melt crystallized syndiotactic polystyrene samples, Macromolecules, 1990, 23(5), 1539–1544 CrossRef CAS.
- Y. S. Sun and E. M. Woo, Relationships between polymorphic crystals and multiple melting peaks in crystalline syndiotactic polystyrene, Macromolecules, 1999, 32(23), 7836–7844 CrossRef CAS.
- E. M. Woo, Y. S. Sun and M. Lu Lee, Crystal forms in cold-crystallized syndiotactic polystyrene, Polymer, 1999, 40(15), 4425–4429 CrossRef CAS.
- R. H. Lin and E. M. Woo, Melting behavior and identification of polymorphic crystals in syndiotactic polystyrene, Polymer, 2000, 41(1), 121–131 CrossRef CAS.
- Y.-S. Sun and E. M. Woo, Morphology and crystal structure of cold-crystallized syndiotactic polystyrene, Polymer, 2001, 42(5), 2241–2245 CrossRef CAS.
- Y. Tamai and M. Fukuda, Nanoscale molecular cavity in crystalline polymer membranes studied by molecular dynamics simulation, Polymer, 2003, 44(11), 3279–3289 CrossRef CAS.
- G. Milano, G. Guerra and F. Müller-Plathe, Anisotropic diffusion of small penetrants in the δ crystalline phase of syndiotactic polystyrene: a molecular dynamics simulation study, Chem. Mater., 2002, 14(7), 2977–2982 CrossRef CAS.
- Y. Tamai and M. Fukuda, Fast one-dimensional gas transport in molecular capillary embedded in polymer crystal, Chem. Phys. Lett., 2003, 371(1–2), 217–222 CrossRef CAS.
- Y. Tamai and M. Fukuda, Reorientational dynamics of aromatic molecules clathrated in δ form of crystalline syndiotactic polystyrene, Chem. Phys. Lett., 2003, 371(5–6), 620–625 CrossRef CAS.
- Y. Tamai, Y. Tsujita and M. Fukuda, Reorientational relaxation of aromatic molecules in the molecular cavity of crystalline syndiotactic polystyrene studied by molecular dynamics simulation, J. Mol. Struct., 2005, 739(1–3), 33–40 CrossRef CAS.
- S. Figueroa-Gerstenmaier, C. Daniel, G. Milano, G. Guerra, O. Zavorotynska, J. G. Vitillo, A. Zecchina and G. Spoto, Storage of hydrogen as a guest of a nanoporous polymeric crystalline phase, Phys. Chem. Chem. Phys., 2010, 12(20), 5369–5374 RSC.
- S. Figueroa-Gerstenmaier, C. Daniel, G. Milano, J. G. Vitillo, O. Zavorotynska, G. Spoto and G. Guerra, Hydrogen adsorption by δ and ε crystalline phases of syndiotactic polystyrene aerogels, Macromolecules, 2010, 43(20), 8594–8601 CrossRef CAS.
- L. Sanguigno, F. Cosentino, D. Larobina and G. Mensitieri, Molecular simulation of carbon dioxide sorption in nanoporous crystalline phase of sydiotactic polystyrene, Soft Mater., 2011, 9(2–3), 169–182 CrossRef CAS.
- W. G. Noid, Perspective: Coarse-grained models for biomolecular systems, J. Chem. Phys., 2013, 139(9), 09B201_1 CrossRef.
- C. Liu, K. Kremer and T. Bereau, Polymorphism of syndiotactic polystyrene crystals from multiscale simulations, Adv. Theor. Simul., 2018, 1(7), 1800024 CrossRef.
- A. Laio and F. L. Gervasio, Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science, Rep. Prog. Phys., 2008, 71(12), 126601 CrossRef.
- O. Valsson, P. Tiwary and M. Parrinello, Enhancing important fluctuations: Rare events and metadynamics from a conceptual viewpoint, Annu. Rev. Phys. Chem., 2016, 67(1), 159–184 CrossRef CAS.
- S. Piana and A. Laio, A bias-exchange approach to protein folding, J. Phys. Chem. B, 2007, 111(17), 4553–4559 CrossRef CAS.
- F. Marinelli, F. Pietrucci, A. Laio and S. Piana, A kinetic model of trp-cage folding from multiple biased molecular dynamics simulations, PLoS Comput. Biol., 2009, 5(8), e1000452 CrossRef.
- F. Baftizadeh, P. Cossio, F. Pietrucci and A. Laio, Protein folding and ligand-enzyme binding from bias-exchange metadynamics simulations, Curr. Phys. Chem., 2012, 2(1), 79–91 CrossRef CAS.
- J. Pfaendtner and M. Bonomi, Efficient sampling of high-dimensional free-energy landscapes with parallel bias metadynamics, J. Chem. Theory Comput., 2015, 11(11), 5062–5067 CrossRef CAS.
- E. M. Woo, Y.-S. Sun and C.-P. Yang, Polymorphism, thermal behavior, and crystal stability in syndiotactic polystyrene vs. its miscible blends, Prog. Polym. Sci., 2001, 26(6), 945–983 CrossRef CAS.
- F. Giberti, M. Salvalaglio, M. Mazzotti and M. Parrinello, Insight into the nucleation of urea crystals from the melt, Chem. Eng. Sci., 2015, 121, 51–59 CrossRef CAS.
- E. Brini, V. Marcon and N. F. A. van der Vegt, Conditional reversible work method for molecular coarse graining applications, Phys. Chem. Chem. Phys., 2011, 13(22), 10468–10474 RSC.
- G. Deichmann and N. F. A. van der Vegt, Conditional reversible work coarse-grained models of molecular liquids with coulomb electrostatics-a proof of concept study on weakly polar organic molecules, J. Chem. Theory Comput., 2017, 13(12), 6158–6166 CrossRef CAS.
- F. L. Gervasio, A. Laio and M. Parrinello, Flexible docking in solution using metadynamics, J. Am. Chem. Soc., 2005, 127(8), 2600–2607 CrossRef CAS.
- G. Bussi, F. Luigi Gervasio, A. Laio and M. Parrinello, Free-energy landscape for β hairpin folding from combined parallel tempering and metadynamics, J. Am. Chem. Soc., 2006, 128(41), 13435–13441 CrossRef CAS.
- G. Fiorin, A. Pastore, P. Carloni and M. Parrinello, Using metadynamics to understand the mechanism of calmodulin/target recognition at atomic detail, Biophys. J., 2006, 91(8), 2768–2777 CrossRef CAS.
- F. Trudu, D. Donadio and M. Parrinello, Freezing of a Lennard-Jones fluid: From nucleation to spinodal regime, Phys. Rev. Lett., 2006, 97(10), 105701 CrossRef.
- D. Quigley and P. M. Rodger, Metadynamics simulations of ice nucleation and growth, J. Chem. Phys., 2008, 128(15), 154518 CrossRef CAS.
- D. Quigley and P. Mark Rodger, Free energy and structure of calcium carbonate nanoparticles during early stages of crystallization, J. Chem. Phys., 2008, 128, 221101 CrossRef CAS.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Icosahedral bond orientational order in supercooled liquids, Phys. Rev. Lett., 1981, 47(18), 1297 CrossRef CAS.
- P. J. Steinhardt, D. R. Nelson and M. Ronchetti, Bond-orientational order in liquids and glasses, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28(2), 784 CrossRef CAS.
- M. Jae Ko, N. Waheed, M. S. Lavine and G. C. Rutledge, Characterization of polyethylene crystallization from an oriented melt by molecular dynamics simulation, J. Chem. Phys., 2004, 121(6), 2823–2832 CrossRef.
- N. Waheed, M. J. Ko and G. C. Rutledge, Molecular simulation of crystal growth in long alkanes, Polymer, 2005, 46(20), 8689–8702 CrossRef CAS.
- E. E. Santiso and B. L. Trout, A general set of order parameters for molecular crystals, J. Chem. Phys., 2011, 134(6), 064109 CrossRef.
- A. Barducci, G. Bussi and M. Parrinello, Well-tempered metadynamics: a smoothly converging and tunable free-energy method, Phys. Rev. Lett., 2008, 100(2), 020603 CrossRef.
- A. Laio and M. Parrinello, Escaping free-energy minima, Proc. Natl. Acad. Sci. U. S. A., 2002, 99(20), 12562–12566 CrossRef CAS.
- A. Barducci, M. Bonomi and M. Parrinello, Metadynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1(5), 826–843 CAS.
- C. Abrams and G. Bussi, Enhanced sampling in molecular dynamics using metadynamics, replica-exchange, and temperature-acceleration, Entropy, 2014, 16(1), 163–199 CrossRef.
- J. F. Dama, M. Parrinello and G. A. Voth, Well-tempered metadynamics converges asymptotically, Phys. Rev. Lett., 2014, 112(24), 240602 CrossRef.
- P. Tiwary and M. Parrinello, A time-independent free energy estimator for metadynamics, J. Phys. Chem. B, 2014, 119(3), 736–742 CrossRef.
- P. Raiteri, A. Laio, F. Luigi Gervasio, C. Micheletti and M. Parrinello, Efficient reconstruction of complex free energy landscapes by multiple walkers metadynamics, J. Phys. Chem. B, 2006, 110(8), 3533–3539 CrossRef CAS.
- M. James Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, Gromacs: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1, 19–25 CrossRef.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Plumed 2: New feathers for an old bird, Comput. Phys. Commun., 2014, 185(2), 604–613 CrossRef CAS.
- The PLUMED Consortium. Promoting transparency and reproducibility in enhanced molecular simulations. Nat. Methods, 16:670-673, 2019. For the full list of researches from the PLUMED Consortium, see https://www.plumed-nest.org/consortium.html.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity rescaling, J. Chem. Phys., 2007, 126(1), 014101 CrossRef.
- M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52(12), 7182–7190 CrossRef CAS.
- K. Burke, Perspective on density functional theory, J. Chem. Phys., 2012, 136, 150901 CrossRef.
- A. D. Becke, Perspective: Fifty years of density-functional theory in chemical physics, J. Chem. Phys., 2014, 140, 18A301 CrossRef.
- H. S. Yu, S. L. Li and D. G. Truhlar, Perspective: Kohn-sham density functional theory descending a staircase, J. Chem. Phys., 2016, 145, 130901 CrossRef.
- R. J. Maurer, C. Freysoldt, A. M. Reilly, J. G. Brandenburg, O. T. Hofmann, T. Bjöorkman, S. Lebègue and A. Tkatchenko, Advances in density-functional calculations for materials modeling, Annu. Rev. Mater. Res., 2019, 49(3), 1–3 CrossRef CAS.
- J. G. Brandenburg, E. Caldeweyher and S. Grimme, Screened exchange hybrid density functional for accurate and efficient structures and interaction energies, Phys. Chem. Chem. Phys., 2016, 18, 15519–15523 RSC.
- E. Caldeweyher and J. G. Brandenburg, Simplified dft methods for consistent structures and energies of large systems, J. Phys.: Condens. Matter, 2018, 30, 213001 CrossRef.
- R. Sure and S. Grimme, Chem. – Eur. J., 2017, 23, 5687–5691 CrossRef.
- S. Roesel, H. Quanz, C. Logemann, J. Becker, E. Mossou, L. C. Delgado, E. Caldeweyher, S. Grimme and P. R. Schreiner, London dispersion enables the shortest intermolecular hydrocarbon h⋯h contact, J. Am. Chem. Soc., 2017, 139, 428–7431 Search PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Dispersion-corrected mean-field electronic structure methods, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS.
- G. J. O. Beran, Modeling polymorphic molecular crystals with electronic structure theory, Chem. Rev., 2016, 116(9), 5567–5613 CrossRef CAS.
- J. Klimeš and A. Michaelides, Perspective: Advances and challenges in treating van der Waals dispersion forces in density functional theory, J. Chem. Phys., 2012, 137, 120901 CrossRef.
- A. Erba, J. Baima, I. Bush, R. Orlando and R. Dovesi, Large-scale condensed matter dft simulations: Performance and capabilities of the crystal code, J. Chem. Theory Comput., 2017, 13, 5019–5027 CrossRef CAS.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- R. Sure and S. Grimme, Corrected small basis set Hartree–Fock method for large systems, J. Comput. Chem., 2013, 34, 1672–1685 CrossRef CAS.
- M. Cutini, B. Civalleri, M. Corno, R. Orlando, J. G. Brandenburg, L. Maschio and P. Ugliengoa, Assessment of different quantum mechanical methods for the prediction of structure and cohesive energy of molecular crystals, J. Chem. Theory Comput., 2016, 12, 3340–3352 CrossRef CAS.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(11), 7260–7268 CrossRef CAS.
- B. Aradi, B. Hourahine and T. Frauenheim, Dftb+, a sparse matrix-based implementation of the dftb method, J. Phys. Chem. A, 2007, 111(26), 5678–5684 CrossRef CAS.
- J. G. Brandenburg and S. Grimme, Accurate Modeling of Organic Molecular Crystals by Dispersion-Corrected Density Functional Tight Binding (DFTB), J. Phys. Chem. Lett., 2014, 5, 1785–1789 CrossRef CAS.
- J. G. Brandenburg, J. Potticary, H. A. Sparkes, S. L. Price and S. R. Hall, Thermal expansion of carbamazepine: Systematic crystallographic measurements challenge quantum chemical calculations, J. Phys. Chem. Lett., 2017, 8, 4319–4324 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01342k |
| This journal is © The Royal Society of Chemistry 2020 |