Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cluster prevalence in concentrated ring-chain mixtures under shear
Maximilian
Liebetreu
 * and
Christos N.
Likos
* and
Christos N.
Likos

Faculty of Physics, University of Vienna, Boltzmanngasse 5, 1090 Vienna, Austria. E-mail: maximilian.liebetreu@univie.ac.at
First published on 28th August 2020
Abstract
Semiflexible ring polymers are known to exhibit clustering behavior and form stacks in concentrated solutions. Recently, weak shear was suggested to re-orient these stacks with flow, a phenomenon more easily visible in more concentrated solutions [Liebetreu et al., ACS Appl. Polym. Mater., 2020, 2(8), 3505–3517, DOI: 10.1021/acsapm.0c00522]. In this work, we investigate the impact of mixing linear chains and rings in a similar system under shear, studying clustering in the presence of semiflexible, rod-like chains. We present a correlation between chain monomer fraction and clustering behavior as linear chains take up less space, thus decreasing the system's effective density and, subsequently, clustering. However, we suggest mixtures with a low chain concentration to maintain or potentially enhance clustering at equilibrium while this effect is destroyed under shear. The mixing of chains and rings may therefore be used to create more strongly organized structures susceptible to reorientation via weak shear.
1 Introduction
In recent years, the importance of polymer topology for dynamical and rheological properties has gained significant importance. Polymers come in a host of different topologies such as linear chains, stars, dendrimers and rings, and the impact of topological differences on polymer dynamics in dilute solution has been studied extensively both in equilibrium1–5 and a variety of out-of-equilibrium situations6–8 such as shear flow. Special attention has been given to dynamics under spatial constraints,9–11 and it has recently been shown that linear chains and rings move through narrow segmented channels at different radial distances.12 Spatial constraints imposed via an increase of monomer density have also been studied extensively for melts13,14 as well as semi-dilute suspensions.15,16Polymers of diverse topology often occur naturally. Examples for ring-shaped polymers include plasmids and the kinetoplast from the mitochondria of trypanosome parasites.17 Synthetically, polymer topology can be controlled through the use of optical tweezers,18 and double-stranded DNA rings have been manufactured to produce catenanes,19–23 a group of interlinked rings.
Semiflexible rings in concentrated solutions are known to exhibit a self-organized, amorphous cluster phase in equilibrium.15,16,24 In this phase, rings form long stacks without net translational and orientational order. On such stacks, rings are strongly correlated to each other as well as to rings on neighboring stacks. These rings are typically of oblate shape, but some of them may also exhibit a prolate shape and thread through other rings in order to reside within a given stack. Dynamically, the cluster phase results in a cluster glass,25 an arrested form of matter in which the cluster structures are locked into place but individual rings can hop between clusters, similar to individual particles in cluster crystals.26 In addition to pure ring solutions or melts, mixtures of rings and linear chains have also attracted considerable attention recently, both theoretically and experimentally, due to the rich dynamics they display, and in particular with a focus on the mechanism of threading of the rings by the chain and the ensuing constraint release mechanism.27–33 Furthermore, mixtures of long linear chains and polymer rings have been shown to exhibit an increased viscosity as compared to pure chain solutions.34–36
Recently, semiflexible rings have been shown to exhibit pronounced clustering behavior even under weak shear, whereas strong shear destroys clusters.37 Such sheared clusters have been shown to re-orient due to the imposed shear and form bands aligned with flow independent of consideration or disregard of fully-developed hydrodynamic interactions. Stacks aligned in this manner maintain their orientation even after cessation of shear. This effect is more pronounced in concentrated solutions and more difficult to isolate for semi-dilute systems. In this work, we investigate the effect of mixing semiflexible linear chains and rings on the overall clustering behavior in the system. We employ Molecular Dynamics simulations of semiflexible polymers coupled to a solvent modeled by Multi-Particle Collision Dynamics38,39 without fully-developed hydrodynamic interactions40,41 and study the impact of steady shear on the system. Varying the chain monomer fraction while keeping the number of monomers constant at three distinct concentrations in the semi-dilute regime, we find that high chain monomer fractions typically make the system behave similarly as it would for pure ring solutions at lower monomer densities. We link this effect to the effective density and topological state of the system, the former decreasing with increasing chain monomer fraction. However, mixing in only a few chains conversely improves clustering behavior as chains get trapped inside of stacks of rings and help stabilizing these structures. Under shear, the investigated properties progressively lose their dependence on chain stoichiometry, converging towards values dictated by monomer density as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) grows. Not only could this effect be used to improve clustering behavior in ring solutions, it might simultaneously simplify reorientation of clusters in a particular direction using weak shear.
grows. Not only could this effect be used to improve clustering behavior in ring solutions, it might simultaneously simplify reorientation of clusters in a particular direction using weak shear.
2 Methods
2.1 Numerical model
We perform Molecular Dynamics (MD) simulations to study semiflexible polymers in the bulk under shear. To this end, we employ the Kremer–Grest bead-spring model42,43 and an additional bending potential to introduce rigidity.16 The equations of motion are integrated by Velocity-Verlet.44,45 We use polymer rings of contour length NR = 50 and chains of contour length NC = 25, ensuring that rings and chains, when fully stretched, are of about the same length and still fit inside the simulation box of volume V = (50 × 50 × 50)σ3 where σ is the length scale of the Lennard-Jones interaction of the Kremer–Grest model. We couple the molecular-dynamics part of the simulation to a solvent modeled by Multi-Particle Collision Dynamics38,39 (MPCD) with a modification to disable fully-resolved hydrodynamic interactions40,41 in the interest of computational efficiency. Viscous heating is prevented by employing a Maxwellian cell-level thermostat.39 Lastly, we employ Lees-Edwards boundary conditions46 to establish a linear velocity profile corresponding to planar Couette flow such that the expected solvent velocity vs(r) =![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) y
y![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , in which
, in which ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the imposed shear rate, r = (x,y,z) denotes an arbitrary location, and
is the imposed shear rate, r = (x,y,z) denotes an arbitrary location, and ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , ŷ, and ẑ indicate flow-, gradient- and vorticity directions.
, ŷ, and ẑ indicate flow-, gradient- and vorticity directions.
We use the standard set of MPCD parameters38,39 corresponding to solvent particle mass m = 1, collision angle α = 130°, and collision cell side length a = σ. We set the number of solvent particles per collision cell to 〈Nc〉 = 10 and correspondingly the mass of a polymer bead to M = m〈Nc〉 = 10. The MPCD timestep was set to h = 0.1[(kBT)−0.5m0.5σ]. This combination of parameters creates a solvent with viscosity ηs = 8.70[(kBT)0.5m0.5σ−2].
Similarly, we use a well-established set of MD parameters used by Poier et al.16 to study cluster-glass phases of semiflexible rings, as well as in subsequent works on similar systems.11,24,37 This choice of parameters corresponds to Weaks-Chandler-Andersen potential parameters ε = kBT and σ as a unit of length, FENE potential VFENE(r) = −εkR02/σ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[1 − (r/R0)2] with spring constant k = 15kBT/ε and critical bond extension R0 = 1.5σ, and lastly a bending potential acting on consecutive bonds at an angle ϕ to each other: Vbend(ϕ) = εκB(1 − cos(ϕ))2 with rigidity constant κB = 30kBT/ε. For rings in equilibrium at contour length NR = 50, this model yields a radius of gyration of 〈Rg,0〉 ≈ 6.5σ and an expected bond length of 〈lb〉 = 0.96σ. For chains at contour length NC = 25, one obtains 〈Rg,0〉 ≈5.5σ. We employ an MD timestep of δt = 0.002[(kBT)−0.5m0.5σ], which is sufficient to prevent concatenation.
ln[1 − (r/R0)2] with spring constant k = 15kBT/ε and critical bond extension R0 = 1.5σ, and lastly a bending potential acting on consecutive bonds at an angle ϕ to each other: Vbend(ϕ) = εκB(1 − cos(ϕ))2 with rigidity constant κB = 30kBT/ε. For rings in equilibrium at contour length NR = 50, this model yields a radius of gyration of 〈Rg,0〉 ≈ 6.5σ and an expected bond length of 〈lb〉 = 0.96σ. For chains at contour length NC = 25, one obtains 〈Rg,0〉 ≈5.5σ. We employ an MD timestep of δt = 0.002[(kBT)−0.5m0.5σ], which is sufficient to prevent concatenation.
2.2 Simulation details
Because of the vast number of monomers in our system and the use of Lees–Edwards boundary conditions,46 we employ our own custom code written in C++/CUDA47 to run efficiently on GPUs. This code has been tested extensively and successfully utilized in previous works.37,48,49 It combines several optimization methods like parallelized MPCD,50 particle sorting,51 Verlet- and cell lists,52 and an adaptation of the cell-list algorithm for Lees–Edwards.53We set the size of our simulation box to V = (50 × 50 × 50)σ3 and investigate a set of different monomer densities ρ = N/V = {0.364, 0.456, 0.600}σ−3 for monomer counts N. For Fig. 2 and 3 and Fig. 6, we have chosen to use a gray color gradient for ρ = 0.364σ−3, blue color gradient for ρ = 0.456σ−3 and a red color gradient for ρ = 0.6σ−3. Building upon the effective density employed by Bernabei et al.15 and Slimani et al.,25 we define an effective density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) = [CR·〈VR〉 + CC·〈VC〉]/V where CX corresponds to ring- (R) or chain (C) count and 〈VX〉 to the estimated expected volume of the corresponding objects. Note that
= [CR·〈VR〉 + CC·〈VC〉]/V where CX corresponds to ring- (R) or chain (C) count and 〈VX〉 to the estimated expected volume of the corresponding objects. Note that ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) always refers to the effective density as measured at equilibrium. Bernabei et al.15 took the cubed equilibrium diameter of gyration Dg,03 as a volume estimate. However, in the case of chains, this would severly overestimate the average proximity and overlap of objects in the system. Therefore, as an estimate for these volumes, we instead use the eigenvalues λα of the gyration tensor
always refers to the effective density as measured at equilibrium. Bernabei et al.15 took the cubed equilibrium diameter of gyration Dg,03 as a volume estimate. However, in the case of chains, this would severly overestimate the average proximity and overlap of objects in the system. Therefore, as an estimate for these volumes, we instead use the eigenvalues λα of the gyration tensor 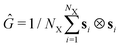 1 (where ⊗ is the dyadic product and si is the vector from the object's center-of-mass to the position of particle i) such that 〈VX〉 = 〈λ1〉·〈λ2〉·〈λ3〉. We further define the chain monomer fraction as QCR = CCNC/N, i.e., the fraction of number of monomers belonging to chains, CCNC, to the total number N of monomers in the system. Accordingly, low values of QCR indicate a system dominated by rings. The effective equilibrium densities
1 (where ⊗ is the dyadic product and si is the vector from the object's center-of-mass to the position of particle i) such that 〈VX〉 = 〈λ1〉·〈λ2〉·〈λ3〉. We further define the chain monomer fraction as QCR = CCNC/N, i.e., the fraction of number of monomers belonging to chains, CCNC, to the total number N of monomers in the system. Accordingly, low values of QCR indicate a system dominated by rings. The effective equilibrium densities ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) for different values of ρ and QCR can be found in Table 1 below.
for different values of ρ and QCR can be found in Table 1 below.
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) for a variety of different chain monomer fractions QCR and monomer densities ρ
for a variety of different chain monomer fractions QCR and monomer densities ρ
| Q CR |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (ρ = 0.364σ−3) (ρ = 0.364σ−3) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (ρ = 0.456σ−3) (ρ = 0.456σ−3) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) (ρ = 0.600σ−3) (ρ = 0.600σ−3) |
|---|---|---|---|
| 0.00 | 3.00 | 3.66 | 4.72 |
| 0.10 | 2.60 | 3.14 | 3.96 |
| 0.25 | 2.49 | 2.77 | 3.16 |
| 0.50 | 1.77 | 2.24 | 2.44 |
| 0.75 | 1.19 | 1.50 | 1.79 |
| 0.90 | 0.78 | 0.92 | 1.24 |
| 1.00 | 0.44 | 0.56 | 0.71 |
We follow the method set forth by Bernabei et al.15 and employed as well in subsequent works16,25 to identify stacks of rings. To this end, we define the director di of a ring i to be equivalent to the eigenvector corresponding to the smallest eigenvalue of the gyration tensor Ĝ. As such, di is always perpendicular to the plane in which the open semiflexible ring resides. We can then employ the following criteria for deciding whether any ring i is on the same stack as a ring j:
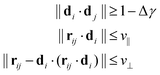 | (1) |
We prepare our mixtures by taking a fully equilibrated system of rings in the cluster-glass phase, cutting random rings open, and allowing the system to equilibrate again. The same initial equilibrated pure-ring system was used for preparing all simulations, and the same initial equilibrated ring-chain mixtures were used for varying shear rates ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) at constant chain monomer fraction QCR to enable highlighting of shear and chain fraction, and maintaining system comparability. We define the Weissenberg number54Wi0 =
at constant chain monomer fraction QCR to enable highlighting of shear and chain fraction, and maintaining system comparability. We define the Weissenberg number54Wi0 = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ·τR,0, a quantity computed from shear rate
·τR,0, a quantity computed from shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and relaxation time τR,0 of a semiflexible ring in dilute solution in equilibrium. We then simulate each system for about t = 3 × 106[(kBT)−0.5m0.5σ], with the exact number varying slightly due to runtime restrictions on the employed GPU cluster. By fitting the autocorrelation function Φ(t) of the end-to-end vector for chains and the maximum-distance vector between beads i and i + NR/2 for rings with f(t) = a0e−t/τ1 + (1 − a0)e−t/τ2, we obtain
and relaxation time τR,0 of a semiflexible ring in dilute solution in equilibrium. We then simulate each system for about t = 3 × 106[(kBT)−0.5m0.5σ], with the exact number varying slightly due to runtime restrictions on the employed GPU cluster. By fitting the autocorrelation function Φ(t) of the end-to-end vector for chains and the maximum-distance vector between beads i and i + NR/2 for rings with f(t) = a0e−t/τ1 + (1 − a0)e−t/τ2, we obtain 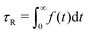 .55 We determine the dilute-equilibrium relaxation times τR,0 ≅ 62
.55 We determine the dilute-equilibrium relaxation times τR,0 ≅ 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000[(kBT)−0.5m0.5σ] for the chains and τR,0 ≅ 46
000[(kBT)−0.5m0.5σ] for the chains and τR,0 ≅ 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000[(kBT)−0.5m0.5σ] for our rings.
000[(kBT)−0.5m0.5σ] for our rings.
3 Results and discussion
3.1 Ring clustering behavior in ring-chain mixtures
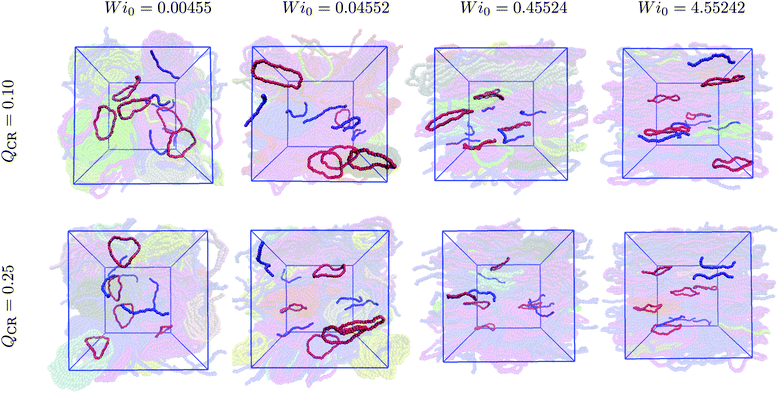
Semiflexible rings in concentrated solutions in equilibrium exhibit clustering behavior and self-organize into stacks.15,16,24,25 Under sufficiently weak shear, these stacks reorient and align with the flow direction.37 In this work, we demonstrate the changes introduced by mixing chains and rings into the same system. Specifically, we cut open some of the rings, thus keeping the monomer density ρ constant.First, we look at the centers-of-mass of the polymers in our system to obtain an overall view of the ensuing phenomenon after imposing shear. In Fig. 1, we show centers-of-mass of rings (red) and chains (blue) for Wi0 spanning four orders of magnitude and QCR between 0.0 and 0.5 with ρ = 0.6σ−3. At equilibrium, the rings in the system look equally as organized into clusters at QCR = {0.0, 0.1, 0.25}, whereas shorter clusters can be discerned at QCR = 0.5. As Wi0 increases, stacks begin to align with the flow.37 At Wi0 = 0.04552, we observe regular alignment for QCR = {0.0, 0.1}, similarly pronounced alignment for QCR = 0.25 and clusters already breaking for QCR ≥ 0.5. At Wi0 = 0.45524, stacks are fully aligned for QCR = {0.0, 0.1}, start dissembling for QCR = 0.25 and are mostly broken for QCR ≥ 0.5. As Wi0 is increased another order of magnitude, very few and only short clusters can be seen independent of QCR.
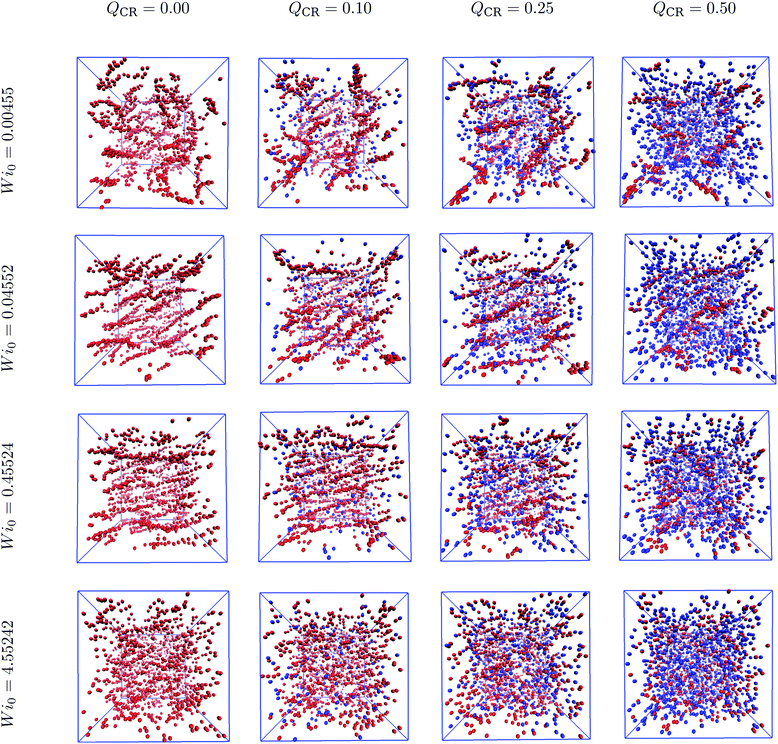 | ||
| Fig. 1 Cluster phase in chain-ring mixtures. Centers-of-mass of rings (red) and chains (blue) for a variety of different Weissenberg numbers Wi0 and chain monomer fractions QCR. The simulation box is shown in blue, and the system is projected onto the flow-gradient plane. The snapshots were created using VMD,56 and the corresponding monomer density is ρ = 0.6σ−3. Left to right: Increasing chain monomer fraction QCR at constant Weissenberg number Wi0. Top to bottom: Increasing Weissenberg number Wi0 at constant chain monomer fraction QCR. | ||
Intuitively, we expect that low values of QCR would yield similar results to a pure-ring solution or even slightly improve clustering. Additionally, it seems that higher values of QCR might cause clusters to align and eventually also dissemble at comparatively lower Wi0. Increasing QCR past QCR ≅ 0.25 severely reduces clustering in the system when compared to lower QCR values.
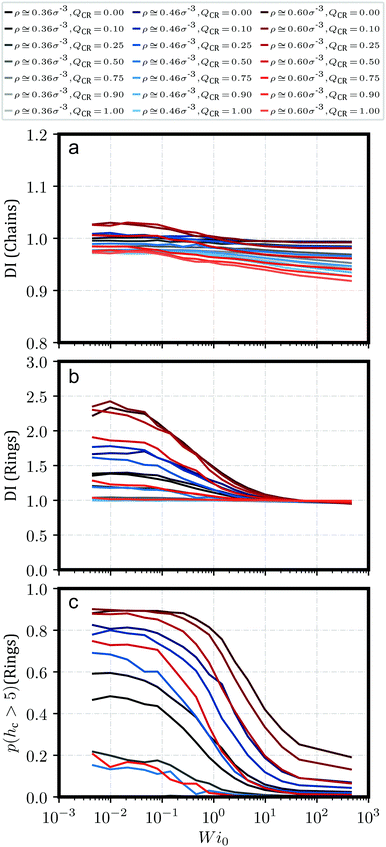
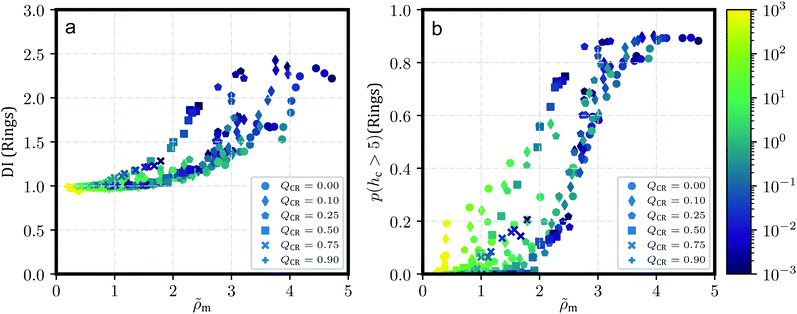
We can verify and quantify this behavior using the dispersion index DI of the centers-of-mass of our rings and chains as described by Kam et al.57 and also Liebetreu and Likos;37 this quantity is shown in Fig. 2a and b. To this end, we introduce a cubic grid of cell length l = 2.5σ and measure sample mean μ of the number of centers-of-mass per cell. We label the sample standard deviation of this quantity s. The dispersion index DI is then calculated as DI = s2/μ. Characteristically, a value of DI = 1 indicates a random arrangement of centers-of-mass in accordance with a Poisson distribution. Values of DI < 1 point at more-than-random uniformity, for example grid-like symmetry for all individual centers-of-mass, whereas DI > 1 signifies clustering. It should be noted that the justification for employing this parameter is mostly a comparative one. In Fig. 2c, we provide the probability p(hc > 5) for a ring to belong to a stack with more than 5 members, which produces a similar graph. The advantage of DI, however, is that the choice of 5 members for p(hc > 5) is arbitrary and not necessarily indicative of clustering. Moreover, removing rings from a given system can drastically alter p(hc > 5), while DI should be more robust under such changes and provide a more robust measure for clustering when altering QCR. In addition, the dispersion index DI always has a reference value of 1 to indicate clustering or uniformity in the system.
 | ||
| Fig. 3 Polymeric viscosity η against Weissenberg number Wi0 for a variety of different monomer densities ρ and chain monomer fractions QCR. | ||
Fig. 2 shows the dispersion index DI both for chains (Fig. 2a) and for rings (Fig. 2b). DI for chains is, across shear rates and effective densities ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) , at around DI ≲ 1. A notable exception occurs for the most concentrated solution ρ = 0.6σ−3 at QCR = {0.1, 0.25}, where chains appear to exhibit some weak clustering behavior following the strong clustering of the rings in that system. Curiously, this exception is also visible in Fig. 2b for the rings, where equilibrium values of DI at QCR = {0.1, 0.25} exceed DI at QCR = 0. A similar effect can be discerned at QCR = 0.1 for semi-concentrated solutions at ρ = 0.456σ−3, whereas it vanishes for the most dilute concentration investigated, ρ = 0.364σ−3. Looking at the effective densities
, at around DI ≲ 1. A notable exception occurs for the most concentrated solution ρ = 0.6σ−3 at QCR = {0.1, 0.25}, where chains appear to exhibit some weak clustering behavior following the strong clustering of the rings in that system. Curiously, this exception is also visible in Fig. 2b for the rings, where equilibrium values of DI at QCR = {0.1, 0.25} exceed DI at QCR = 0. A similar effect can be discerned at QCR = 0.1 for semi-concentrated solutions at ρ = 0.456σ−3, whereas it vanishes for the most dilute concentration investigated, ρ = 0.364σ−3. Looking at the effective densities ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) , the effect is visible where
, the effect is visible where ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) ≳ 3.0 (compare Table 1), which we will therefore treat as an estimate for a stabilization threshold in this context. This threshold is also discussed later in the context of Fig. 7 for momentary effective densities
≳ 3.0 (compare Table 1), which we will therefore treat as an estimate for a stabilization threshold in this context. This threshold is also discussed later in the context of Fig. 7 for momentary effective densities ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m, where these transitions are shown to be linked to
m, where these transitions are shown to be linked to ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m, but also influenced by QCR and, subsequently, topology.
m, but also influenced by QCR and, subsequently, topology.
The weak clustering of the chains could point at chains becoming trapped inside or between clusters of rings – an observation difficult to quantify, but one which agrees well with our visual impression of the system from Fig. 1. It seems plausible that this trapping could potentially stabilize the clusters under shear, protecting them from breaking into smaller clusters even at high shear rates, but we do not observe such an effect. In fact, for increasing shear, the same behavior can be seen for all the investigated systems: DI decreases with shear, and ultimately, DI for rings starts to converge against DI ≅ 1 independent of ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) or QCR. It appears the chains in this work, at least, are either too short or too rigid to effectively tangle the rings and hold them in place. However, small non-zero values of QCR seem to at least improve clustering behavior in equilibrium, and they do not appear to influence the slope of DI as shear increases, given
or QCR. It appears the chains in this work, at least, are either too short or too rigid to effectively tangle the rings and hold them in place. However, small non-zero values of QCR seem to at least improve clustering behavior in equilibrium, and they do not appear to influence the slope of DI as shear increases, given ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) ≳ 3.0 (compare Table 1).
≳ 3.0 (compare Table 1).
Finally, we plot the probability p(hc > 5) for a randomly-selected ring to be part of a stack with a ring count hc > 5 in Fig. 2c. Unsurprisingly, this probability decreases consistently with increasing shear as clusters start to break apart. Curiously, at ρ = {0.456, 0.6}σ−3, low values of QCR cause well-separated graphs at high shear and overlapping graphs near equilibrium, even though there are less rings in the system as QCR increases.
This provides further evidence that a small amount of chains can enhance cluster formation, or at the very least does not disrupt it. The observed improvement is, however, small, and we cannot confirm without reasonable doubt that the effect is not just the result of some noise. On the other hand, the consistent behavior across different densities ρ for values of QCR = {0.0, 0.1} and the unchanging values obtained for p(hc > 5) at low values of Wi as shown in Fig. 2c indicate that future investigations of the system at these parameters might provide further evidence for the effect discussed here, and potentially show that clustering is not just equal but stronger under the addition of a few chains at QCR ≅ 0.1, at least for sufficient overall densities ρ.
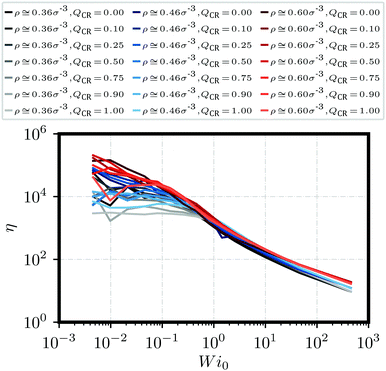
Next, we look at the rheological properties of the system through the polymeric viscosity58η = −σxy/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) where σxy is the flow-gradient element of the stress tensor as computed from the modified Kramers expression59
where σxy is the flow-gradient element of the stress tensor as computed from the modified Kramers expression59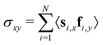 where fi is the total force acting on bead i. We have already established from Fig. 2 that the chains in this work do not effectively tangle the rings to keep them on formed clusters as shear increases. Fig. 3 confirms this effect through clear shear-thinning qualitatively independent of
where fi is the total force acting on bead i. We have already established from Fig. 2 that the chains in this work do not effectively tangle the rings to keep them on formed clusters as shear increases. Fig. 3 confirms this effect through clear shear-thinning qualitatively independent of ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) and QCR. We suggest that both the rigidity of the chains and their shortness might be detrimental to shear thickening, with some chains getting trapped within the stacks, but then aligning with them or simply capable of escaping a given stack without causing too much friction.
and QCR. We suggest that both the rigidity of the chains and their shortness might be detrimental to shear thickening, with some chains getting trapped within the stacks, but then aligning with them or simply capable of escaping a given stack without causing too much friction.
We establish a direct correlation between polymeric viscosity η and monomer density ρ, highlighted by three distinct bands at high shear in Fig. 3. This also indicates that any topological influence becomes drastically reduced at high shear, and that the main factor for polymeric viscosity in this regime is the monomer density ρ rather than the effective density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) or the chain monomer fraction QCR. Across all investigated mixtures, there seems to be a shear regime in which low values of QCR lead to lower relative viscosities η when compared to graphs of higher QCR at equal ρ. Unfortunately, the effect is difficult to see and more difficult to isolate. We suggest this occurs because, as clusters are broken apart by shear, chains might cause additional friction and align at a different rate than rings. We will revisit this question in Section 3.3.
or the chain monomer fraction QCR. Across all investigated mixtures, there seems to be a shear regime in which low values of QCR lead to lower relative viscosities η when compared to graphs of higher QCR at equal ρ. Unfortunately, the effect is difficult to see and more difficult to isolate. We suggest this occurs because, as clusters are broken apart by shear, chains might cause additional friction and align at a different rate than rings. We will revisit this question in Section 3.3.
3.2 Stack orientation under shear
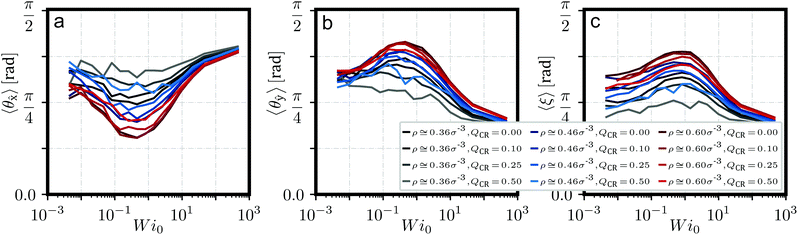
We have defined the director d of a ring as its plane normal, computed from the eigenvector of its gyration tensor Ĝ corresponding to its smallest eigenvalue. The clusters formed under equilibrium are typically oriented randomly. Under shear, those stacks start to align themselves with flow until they eventually break apart.37 We show quantitative evidence of this phenomenon in Fig. 4, which describes angles 〈θ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) 〉 of stack axis to flow, 〈θŷ〉 of stack axis to gradient and 〈ξ〉 of stack axis to individual ring directors d. The stack axis is computed as the main principle component via Ĝ of the set of centers-of-mass of rings on that stack.
〉 of stack axis to flow, 〈θŷ〉 of stack axis to gradient and 〈ξ〉 of stack axis to individual ring directors d. The stack axis is computed as the main principle component via Ĝ of the set of centers-of-mass of rings on that stack.
An important feature of these angles is that they show the alignment of stacks as shear increases, up to about Wi0 ≅ 0.5, where we find a minimum for 〈θ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) 〉 in Fig. 4a. For Wi0 ≳ 0.5, clusters break apart and long aggregates become increasingly unlikely. Another indicator for this behavior is p(hc > 5) in Fig. 2c, which shows a rapid decline for Wi0 ≳ 0.5 across all values of
〉 in Fig. 4a. For Wi0 ≳ 0.5, clusters break apart and long aggregates become increasingly unlikely. Another indicator for this behavior is p(hc > 5) in Fig. 2c, which shows a rapid decline for Wi0 ≳ 0.5 across all values of ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) and QCR. If one compares 〈θŷ〉 to 〈ξ〉 in Fig. 4b and c, one can see 〈ξ〉 mimicking the behavior of 〈θŷ〉 shifted to slightly higher values of Wi0. We suggest that stacks, which are expected to have a much higher relaxation time than individual rings, respond to shear before individual rings do, thus causing stacks to align even as rings still maintain their equilibrium orientations. Only at higher shear rates, when rings start to align as well, do the clusters break apart.
and QCR. If one compares 〈θŷ〉 to 〈ξ〉 in Fig. 4b and c, one can see 〈ξ〉 mimicking the behavior of 〈θŷ〉 shifted to slightly higher values of Wi0. We suggest that stacks, which are expected to have a much higher relaxation time than individual rings, respond to shear before individual rings do, thus causing stacks to align even as rings still maintain their equilibrium orientations. Only at higher shear rates, when rings start to align as well, do the clusters break apart.
The observed alignment effect with shear becomes less pronounced for higher values of QCR across all investigated monomer densities ρ. We suggest that this is simply due to less and shorter clusters forming under such conditions as chains become increasingly system-dominating, an observation taken from Fig. 2. Such short clusters can also be detected as a side effect of the employed algorithm for detecting these stacks when rings in the system become increasingly aligned in the same way and happen to pass each other. This effect becomes increasingly pronounced at high shear and directly influences the angles as seen here. For high values of QCR, the system is dominated by chains, and the few clusters which might form will be increasingly short and short-lived, showing this side-effect even close to equilibrium.
In the context of chains potentially helping the alignment of clusters under shear, no such effect can be discerned here. At QCR = {0.1, 0.25}, the graphs for ρ = 0.6σ−3 are almost indistinguishable, so we can conclude that the addition of only a few chains does not significantly alter the alignment of stacks under shear. Overall, the alignment here seems to follow similar rules for when chain monomer fractions start affecting the system as we described before from Fig. 2.
3.3 Individual chains and rings in the mixture
We visualize some typical configurations of rings (red) and chains (blue) in the aforementioned simulations at QCR = {0.1, 0.25} in Fig. 5. One can identify the alignment of both rings and chains as shear increases, as well as spot the onset of twisting for rings, which is more pronounced for still higher values of the shear rate.37 Chains instead exhibit stretching. Tumbling, which occurs for both chains and rings in these simulations, is difficult to visualize from snapshots. It should be noted that here, we can even see a more complete alignment of rings into the flow-vorticity plane for Wi0 = 0.45524 and QCR = 0.25 when compared to QCR = 0.10 at equal Wi0, as well as the onset of stack destruction as shown in Fig. 1 and 2. This observation provides further evidence that as rings align with the flow, clusters start breaking. At constant monomer density ρ, increasing the chain monomer fraction QCR means creating a more chain-dominated system in which the remaining rings have more space to orient themselves (![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) will be lower if ρ is kept constant).
will be lower if ρ is kept constant).
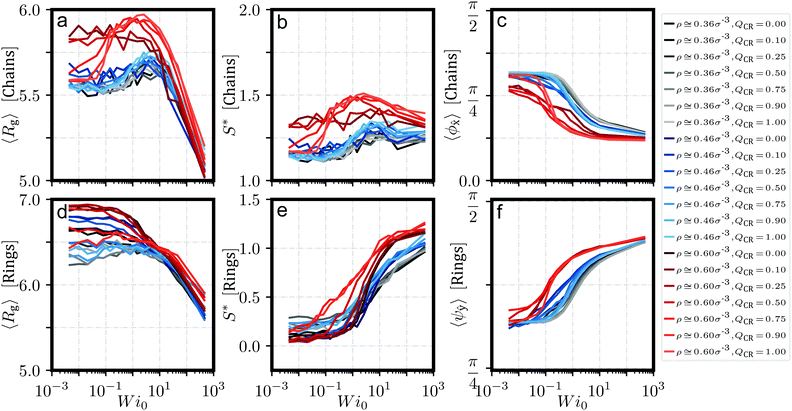
In Fig. 6, we present instructive properties of individual chains and rings. First, we define the radius of gyration 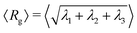 for eigenvalues λ1 ≥ λ2 ≥ λ3 of the gyration tensor Ĝ1,60 and visualize it in Fig. 6a and d. Its value typically scales proportional to effective density
for eigenvalues λ1 ≥ λ2 ≥ λ3 of the gyration tensor Ĝ1,60 and visualize it in Fig. 6a and d. Its value typically scales proportional to effective density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) . Semiflexible chains exhibit swelling under shear as they stretch and elongate up to a maximum value, then deflate as shear increases further due to tumbling (Fig. 6a). Rings do not exhibit swelling; their rigidity causes them to not stretch enough to balance out a twisting which is entropically favorable to stretching. Instead, rings deflate under shear (Fig. 6d). However, this twisting nevertheless makes them resemble a prolate object, and their form mimicks that of the chains in strong shear.
. Semiflexible chains exhibit swelling under shear as they stretch and elongate up to a maximum value, then deflate as shear increases further due to tumbling (Fig. 6a). Rings do not exhibit swelling; their rigidity causes them to not stretch enough to balance out a twisting which is entropically favorable to stretching. Instead, rings deflate under shear (Fig. 6d). However, this twisting nevertheless makes them resemble a prolate object, and their form mimicks that of the chains in strong shear.
To quantify this behavior, we define the prolateness S* which inhibits values from −0.25 (a circle) to 2 (a straight line) and describes how ellipsoidal a shape is. Via the eigenvalues λi of Ĝ, S* can be computed in the following fashion:1,60
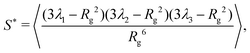 | (2) |
We confirm from Fig. 6c and f that chains align themselves with the flow axis while rings align themselves into the flow-vorticity plane, which confirms our observations from Fig. 5. Note that we are measuring angles to an axis, so we are biasing our values away from perfect alignment.
We finally turn our attention to the question of the impact of the effective density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) on clustering behavior, which is summarized in Fig. 7. The main question here is whether the clustering behavior discussed around the findings presented in Fig. 2 is mainly dictated by effective density
on clustering behavior, which is summarized in Fig. 7. The main question here is whether the clustering behavior discussed around the findings presented in Fig. 2 is mainly dictated by effective density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) rather than by the topological effects introduced by mixing chains and rings. To this end, we define the momentary effective density
rather than by the topological effects introduced by mixing chains and rings. To this end, we define the momentary effective density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m, similarly to the effective density
m, similarly to the effective density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) , with the volume computed from averaged gyration tensor eigenvalues 〈λi〉 not at equilibrium, but instead in any given mixture at Wi0 > 0.
, with the volume computed from averaged gyration tensor eigenvalues 〈λi〉 not at equilibrium, but instead in any given mixture at Wi0 > 0.
As the shear rate and the chain monomer fraction QCR increase, the quantity ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m decreases accordingly because rings and chains stretch and deform, reducing thereby the volumes of the ellipsoids of inertia 〈VC〉 and 〈VR〉. The values scanned by the quantity
m decreases accordingly because rings and chains stretch and deform, reducing thereby the volumes of the ellipsoids of inertia 〈VC〉 and 〈VR〉. The values scanned by the quantity ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m in mixtures across varying Wi0, ρ and QCR lie in the same range, independently of the details of the mixture stoichiometry. If the topological differences between chains and rings were negligible and instead their different sizes caused the phenomena discussed in this work, then we should see all values of DI and p(hc) in Fig. 7 collapse onto a single graph, respectively. This is clearly not the case here, therefore topology is important.
m in mixtures across varying Wi0, ρ and QCR lie in the same range, independently of the details of the mixture stoichiometry. If the topological differences between chains and rings were negligible and instead their different sizes caused the phenomena discussed in this work, then we should see all values of DI and p(hc) in Fig. 7 collapse onto a single graph, respectively. This is clearly not the case here, therefore topology is important.
There are other possibilities: if the different clustering strengths are tied only to monomer densities ρ and topological differences had no effect, we should see three distinct graphs each showing slightly different dependence on ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m. This could apply here at least in parts of the figure, but it is not an exhaustive explanation. Besides, we have already established that clustering is stronger for high values of ρ, so this influence is not surprising. Alternatively, if QCR was the sole driving force behind clustering strength, we should see the same markers at the same values for DI and p(hc) for varying
m. This could apply here at least in parts of the figure, but it is not an exhaustive explanation. Besides, we have already established that clustering is stronger for high values of ρ, so this influence is not surprising. Alternatively, if QCR was the sole driving force behind clustering strength, we should see the same markers at the same values for DI and p(hc) for varying ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m, respectively. This is not the case here, either.
m, respectively. This is not the case here, either.
Similarly, we can get another indication for the decreasing significance of topology for high values of Wi0: this is easiest to see in Fig. 7a where we find overlapping same-colored data points at the lowest exhibited values of ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m, meaning that at these shear rates,
m, meaning that at these shear rates, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m is almost the same independent of QCR. Here, we see overlapping datapoints only in the high-shear regime, and the same markers are not always found at the same values of DI or p(hc). It is no surprise that ρ would be the main driving force behind clustering strength - this has already been established in Fig. 2. However, on top of this, we show here that QCR has a significant impact of its own on clustering behavior in the system, one that is not only caused by the difference in
m is almost the same independent of QCR. Here, we see overlapping datapoints only in the high-shear regime, and the same markers are not always found at the same values of DI or p(hc). It is no surprise that ρ would be the main driving force behind clustering strength - this has already been established in Fig. 2. However, on top of this, we show here that QCR has a significant impact of its own on clustering behavior in the system, one that is not only caused by the difference in ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m, especially for moderate shear Wi0 ∈ [10−1, 101]. Again, if that were the case and the topological difference had less impact than the difference in size, we should see the scatterplots collapse onto single graphs such that the quantities shown in Fig. 7 would depend only on
m, especially for moderate shear Wi0 ∈ [10−1, 101]. Again, if that were the case and the topological difference had less impact than the difference in size, we should see the scatterplots collapse onto single graphs such that the quantities shown in Fig. 7 would depend only on ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m, which is not the case.
m, which is not the case.
Close to equilibrium, momentary effective densities ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) m are heavily influenced by QCR as shapes are distinctly different, but at least for QCR ∈ [0.0, 0.25], the impact on clustering is negligible, confirming our previous observations about mixing in chains and the parameter regimes in which it impacts the system the strongest. Most importantly, we can discern distinct graphs, meaning that even at same initial effective densities, different clustering behavior can be achieved by varying QCR.
m are heavily influenced by QCR as shapes are distinctly different, but at least for QCR ∈ [0.0, 0.25], the impact on clustering is negligible, confirming our previous observations about mixing in chains and the parameter regimes in which it impacts the system the strongest. Most importantly, we can discern distinct graphs, meaning that even at same initial effective densities, different clustering behavior can be achieved by varying QCR.
4 Conclusions
In this work, we have investigated the effect of cutting open semiflexible rings in a concentrated solution to create a chain-ring mixture. We have denoted the chain monomer fraction as QCR. We find that small values of QCR do not significantly alter the clustering- and general behavior of the solvent, and values QCR ≳ 0.5 make clustering progressively unlikely. Under weak shear, the addition of chains alters neither clustering behavior nor cluster alignment. However, the addition of chains does significantly alter the effective densities![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) observed in the system. For high Weissenberg numbers Wi0, topological influences become negligible as both chains and rings become highly elongated and tumble. In this regime, monomer density ρ takes precedence over QCR or
observed in the system. For high Weissenberg numbers Wi0, topological influences become negligible as both chains and rings become highly elongated and tumble. In this regime, monomer density ρ takes precedence over QCR or ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) .
.
Initially, chains might get trapped within clusters, but their length is not sufficient to entangle the stacks, and under shear, the stacks break apart using the same mechanism as described before.37 We find that the addition of a small number of chains into a system of semiflexible rings (low values of QCR) does not appear to affect the clustering behavior of the system, neither with nor without shear. Therefore, experimental investigation of such systems should not require polymer blends that only, exclusively, feature rings.
Future work in this direction should investigate especially the regime of QCR ∈ [0.0, 0.25] and Wi0 ∈ [10−3, 100] in which chains might aid the system in clustering. Of particular interest will be the variation of rigidity, either in general or only for the chains to increase the overall entanglement in the system. For this subset of shear rates and chain monomer fractions, additional investigations could also alter chain contour length. It is possible that, for chains of the same contour length as the rings, their effect on clustering behavior might be much stronger, and we encourage the tools developed and presented in this work be applied to further, similar investigations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The computational results presented have been achieved in part using the Vienna Scientific Cluster (VSC). M. L. has been supported by the uni:docs Doctoral Fellowship Programme of the University of Vienna.Notes and references
- J. Aronovitz and D. Nelson, J. Phys., 1986, 47, 1445–1456 CrossRef CAS
.
- A. Y. Grosberg, A. Feigel and Y. Rabin, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 6618–6622 CrossRef CAS
.
- S. S. Jang, T. Çaǵin and W. A. Goddard, J. Chem. Phys., 2003, 119, 1843–1854 CrossRef CAS
.
- N. T. Moore, R. C. Lua and A. Y. Grosberg, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 13431–13435 CrossRef CAS
.
- A. Narros, A. J. Moreno and C. N. Likos, Macromolecules, 2013, 46, 3654–3668 CrossRef CAS
.
- A. Prhashanna, S. Khan and S. Chen, Colloids Surf., A, 2016, 506, 457–466, DOI:10.1016/j.colsurfa.2016.07.003
.
- T. Yamamoto and N. Masaoka, Rheol. Acta, 2015, 54, 139–147 CrossRef CAS
.
- L. Weiss, A. Nikoubashman and C. N. Likos, ACS Macro Lett., 2017, 6, 1426–1431 CrossRef CAS
.
- S. F. Edwards, Proc. Phys. Soc., 1967, 91, 513–519 CrossRef CAS
.
- S. F. Edwards, J. Phys. A, 1968, 1, 15–28 CrossRef
.
- P. Poier, S. A. Egorov, C. N. Likos and R. Blaak, Soft Matter, 2016, 12, 7983–7994 RSC
.
- L. B. Weiss, C. N. Likos and A. Nikoubashman, Macromolecules, 2019, 52, 7858–7869 CrossRef CAS
.
- D. Vlassopoulos, T. Pakula, G. Fytas, J. Roovers, K. Karatasos and N. Hadjichristidis, Europhys. Lett., 1997, 39, 617–622 CrossRef CAS
.
- A. Y. Grosberg, Soft Matter, 2014, 10, 560–565 RSC
.
- M. Bernabei, P. Bacova, A. J. Moreno, A. Narros and C. N. Likos, Soft Matter, 2013, 9, 1287–1300 RSC
.
- P. Poier, C. N. Likos, A. J. Moreno and R. Blaak, Macromolecules, 2015, 48, 4983–4997 CrossRef CAS
.
- A. R. Klotz, B. W. Soh and P. S. Doyle, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 121–127 CrossRef CAS
.
- Y. Arai, R. Yashuda, K. Akashi, Y. Harada, H. Miyata, K. Kinoshita Jr. and H. Itoh, Nature, 1999, 399, 446–448 CrossRef CAS
.
- L. Hu, C.-H. Lu and I. Willner, Nano Lett., 2015, 15, 2099–2103 CrossRef CAS
.
- C.-H. Lu, A. Cecconello, X.-J. Qi, N. Wu, S.-S. Jester, M. Famulok, M. Matthies, T.-L. Schmidt and I. Willner, Nano Lett., 2015, 15, 7133–7173 CrossRef
.
- C.-H. Lu, A. Cecconello and I. Willner, J. Am. Chem. Soc., 2016, 138, 5172–5185 CrossRef CAS
.
- Z. Ahmadian, I. Chubak, C. N. Likos and M. R. Ejtehadi, Soft Matter, 2020, 16, 3029–3038, 10.1039/c9sm02374g
.
- P. M. Rauscher, K. S. Schweizer, S. J. Rowan and J. J. de Pablo, Macromolecules, 2020, 53, 3390–3408 CrossRef CAS
.
- P. Poier, P. Bacová, A. J. Moreno, C. N. Likos and R. Blaak, Soft Matter, 2016, 12, 4805–4820 RSC
.
- M. Z. Slimani, P. Bacova, M. Bernabei, A. Narros, C. N. Likos and A. J. Moreno, ACS Macro Lett., 2014, 3, 611–616 CrossRef CAS
.
- A. Moreno and C. N. Likos, Phys. Rev. Lett., 2007, 99, 107801 CrossRef
.
- D. G. Tsalikis and V. G. Mavrantzas, ACS Macro Lett., 2014, 3, 763–766 CrossRef CAS
.
- D. G. Tsalikis, V. G. Mavrantzas and D. Vlassopoulos, ACS Macro Lett., 2016, 5, 755–760 CrossRef CAS
.
- S. Goossen, M. Krutyeva, M. Sharp, A. Feoktystov, J. Allgaier, W. Pyckhout-Hintzen, A. Wischnewski and D. Richter, Phys. Rev. Lett., 2015, 115, 148302 CrossRef
.
- D. Vlassopoulos, Rheol. Acta, 2016, 55, 613–632 CrossRef CAS
.
- G. D. Papadopoulos, D. G. Tsalikis and V. G. Mavrantzas, Polymers, 2016, 8, 283 CrossRef
.
- D. G. Tsalikis, P. V. Alatas, L. D. Peristeras and V. G. Mavrantzas, ACS Macro Lett., 2018, 7, 916–920 CrossRef CAS
.
- M. Kruteva, J. Allgaier and D. Richter, Macromolecules, 2017, 50, 9482–9493 CrossRef CAS
.
- J. D. Halverson, W. B. Lee, G. S. Grest, A. Y. Grosberg and K. Kremer, J. Chem. Phys., 2011, 134, 204904 CrossRef
.
- J. D. Halverson, W. B. Lee, G. S. Grest, A. Y. Grosberg and K. Kremer, J. Chem. Phys., 2011, 134, 204905 CrossRef
.
- J. D. Halverson, G. S. Grest, A. Y. Grosberg and K. Kremer, Phys. Rev. Lett., 2012, 108, 038301 CrossRef
.
- M. Liebetreu and C. N. Likos, ACS Appl. Polym. Mater., 2020, 2(8), 3505–3517, DOI:10.1021/acsapm.0c00522
.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605–8613 CrossRef CAS
.
- G. Gompper, T. Ihle, D. Kroll and R. Winkler, Adv. Polym. Sci., 2008, 221, 1–91 Search PubMed
.
- N. Kikuchi, A. Gent and J. M. Yeomans, Eur. Phys. J. E, 2002, 9, 63–66 CrossRef CAS
.
- M. Ripoll, R. G. Winkler and G. Gompper, Eur. Phys. J. E, 2007, 23, 349–354 CrossRef CAS
.
- G. S. Grest and K. Kremer, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3628–3631 CrossRef CAS
.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS
.
- L. Verlet, Phys. Rev., 1967, 159, 98–103 CrossRef CAS
.
- W. C. Swope, H. C. Andersen, P. H. Berens and K. R. Wilson, J. Chem. Phys., 1982, 76, 637–649 CrossRef CAS
.
- A. W. Lees and S. F. Edwards, J. Phys. C, 1972, 5, 1921–1929 CrossRef
.
- J. Nickolls, I. Buck, M. Garland and K. Skadron, Queue, 2008, 6, 40–53 CrossRef
.
- M. Liebetreu, M. Ripoll and C. N. Likos, ACS Macro Lett., 2018, 7, 447–452 CrossRef CAS
.
- M. Liebetreu and C. N. Likos, Commun. Mater., 2020, 1, 4 CrossRef
.
- E. Westphal, S. Singh, C.-C. Huang, G. Gompper and R. Winkler, Comput. Phys. Commun., 2014, 185, 495–503 CrossRef CAS
.
- M. P. Howard, A. Z. Panagiotopoulos and A. Nikoubashman, Comput. Phys. Commun., 2018, 230, 10–20 CrossRef CAS
.
- W. Mattson and B. M. Rice, Comput. Phys. Commun., 1999, 119, 135–148 CrossRef CAS
.
- J. S. Sims and N. Martys, J. Res. Natl. Inst. Stand. Technol., 2004, 109, 267–277 CrossRef CAS
.
- J. L. White, J. Appl. Polym. Sci., 1964, 8, 2339–2357 CrossRef CAS
.
- L. Tubiana, A. Rosa, F. Fragiacomo and C. Micheletti, Macromolecules, 2013, 46, 3669–3678 CrossRef CAS
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS
.
- K. M. Kam, L. Zeng, Q. Zhou, R. Tran and J. Yang, J. Manuf. Syst., 2013, 32, 154–166 CrossRef
.
-
M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press Inc., New York, 1987 (2009) Search PubMed
.
-
R. B. Bird, O. Hassager, R. C. Armstrong and C. F. Curtiss, Dynamics of Polymeric Liquids, John Wiley & Sons, New York, 2nd edn, 1987 Search PubMed
.
- J. Rudnik and G. Gaspari, J. Phys. A: Math. Gen., 1986, 19, L191–L193 CrossRef
.
| This journal is © The Royal Society of Chemistry 2020 |