DOI:
10.1039/D0SM01164A
(Paper)
Soft Matter, 2020,
16, 9838-9843
Controlled propagation and jamming of a delamination front†
Received
25th June 2020
, Accepted 28th August 2020
First published on 3rd September 2020
Abstract
We study the birth and propagation of a delamination front in the peeling of a soft, weakly adhesive layer. In a controlled-displacement setting, the layer partially detaches via a subcritical instability and the motion continues until arrested, by jamming of the two lobes. Using numerical solutions and scaling analysis, we quantitatively describe the equilibrium shapes and obtain constitutive sensitivities of jamming process to material and interface properties. We conclude with a way to delay or avoid jamming altogether by tunable interface properties.
1 Introduction
The crawling motion of a caterpillar serves as a common pedagogical analogue to dislocation theory;1,2 although the soft bodied larva may not be able to push forward the entire length of its body simultaneously, without much effort it can form an arch at its hind, and work that arch forward to conquer a short distance. In a metal crystal, the caterpillar is representative of one sheet of atoms, and the arch, of one atomic spacing, which promotes deformation by moving. Clearly, these representations are oversimplified. On the one hand, the motion of an arch cannot accurately predict the behaviour in the bulk of a crystalline material. On the other hand, the locomotion of caterpillars is now known to be conspicuously more complex.3 Regardless, studying and understanding physical phenomena that appear in the simplified model can ultimately feedback into our understanding of the analogous system. In this paper, we report on a jamming phenomenon that appears following the nucleation and propagation of a peeling arch in compliant, weakly adhesive layers. The arch is formed by subjecting the layer to a controlled in-plane compressive displacement at one end. Its motion is then resisted by the adhesive forces, until it is completely arrested by jamming, thus producing stick-slip behaviour in a fully controlled manner.
The motion of a ruck in a puckered carpet, serves as a similar and common analogue to dislocation theory and has been extensively studied in recent years.4–7 There, the motion is resisted by gravitational forces. In contrast, here we consider the resistance due to adhesive forces between the layer and a substrate.8 This not only mimics the atomic interactions between sheets, but also applies to a myriad of additional physical systems: the stick-slip behavior of the delamination front is akin to a Shallamach wave,9–11 and is considered to be a fundamental mechanism in earthquakes;12–14 evolution of geological formations also involves inter-layer binding forces;15,16 adhesion and peeling are key mechanisms in emerging methods for fabrication and patterning of nanowires and flexible electronics;17–19 several additional examples appear in biology, where the control and propagation of adhesive interfaces is used to promote motility both at the level of a single cell20,21 and at the level of an entire organism.22–24 For further reading, a comprehensive review of the literature and applications related to delamination of thin films is provided in a recent work by Davidovitch and Démery25 where they analyze the role of different length scales in the process.
2 Observation
The delamination and jamming behavior described above is demonstrated by a proof-of-concept observation in Fig. 1. A soft layer of Polydimethylsiloxane (PDMS) is placed on a glass plate and compressed by controlling the horizontal displacement of its end, u0. The resulting horizontal and vertical displacements of the layer are denoted by u(x) and v(x), respectively, where x, the material coordinate, is measured from the loaded end, such that u0 = u(0). Initially, the layer deforms in the plane while the adhesive bond appears to remain intact, until, at a critical displacement uc, an arch forms thus delaminating a length l = lc of the undeformed layer. As this quasistatic process continues, the arch length, la = l − u0, of the delaminated region varies until the two sides of the arch come into contact, and are joined by the adhesive forces, thus arresting the peeling process. In the present formulation, all length scales are nondimensionalized with respect to the thickness of the layer, h.
 |
| | Fig. 1 Controlled delamination in a PDMS layer of thickness h = 5 mm and elastic modulus E = 30 kPa,26 adhered to a rigid glass plate. Displacement control was used and a zero-slope boundary condition on the left end was devised. Three trials were carried out (see ESI† for details on sample preparation, experimental setup, additional trials and video of the experiment). | |
In this work, we facilitate this model system, which permits control over the entire delamination process, and employ an analytical model and scaling arguments to ask: how do the properties of the layer and the adhesive interface influence the conditions for formation and jamming of the delamination front? Can these material properties be tuned to allow the delamination front to propagate indefinitely?
A key property that must be accounted for, to answer these questions, is the nature of the adhesive interaction between the layer and the substrate. Considering small strains and weak bonding, such as the van der Waals forces that attach the elastomer layer to the glass in our model system (Fig. 1), we account for the effect of the deformation of the adhesive bonds, prior to their detachment, as previously suggested in Cohen et al.23 Accordingly, we divide the interface interactions into elastic and inelastic components. The bond stiffness, k, governs the elastic resistance to tangential (in-plane) sliding prior to detachment, and the surface energy, Γ, represents the energy required to debond a unit area of the surface.
3 Model
For the mathematical derivation, we consider a semi-infinite elastic layer that is bonded to the surface and occupies the region 0 < x < ∞, in its undeformed state. Upon displacement of the end (x = 0) by an amount u0, a section of length l delaminates to form an arch, while the rest of the layer (x > l) experiences compression u′(x) < 0, but remains adhered to the surface. The horizontal span of the arch can be calculated from the integral| |  | (1) |
where θ(x) is the local angle between the arch tangent and the substrate, and changes in length of the detached region are neglected.‡ The displacement of the end that is accommodated by formation of the arch is thus| | 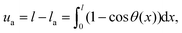 | (2) |
whereas, the displacement accommodated by the in-plane motion of the adhered part is| |  | (3) |
Accordingly, we write the kinematic constraint on the total deformation of the end
The shape of the layer is determined by minimizing the total energy of the system for any prescribed u0. In our formulation, the shape of the layer is fully described by the two functions θ(x) and u(x) for a given detached length l. The total energy Π invested in deforming the layer comprises of contributions from two parts: the delaminated region of the layer, and the adhered region of the layer.
Delaminated region
The energy of the delaminated region comprises of the bending energy and the surface energy invested in breaking the bonds between the layer and the substrate,| |  | (5) |
where E is the Young's modulus, and I is the area moment of inertia of a layer of unit width. Here, assuming l ≫ 1 we neglect contributions due to in-plane compression of the detached region.§
Adhered region
The energy of the adhered region includes elastic energy stored by the in-plane compression of the layer, and the energy stored in extending the adhesive bonds| |  | (6) |
The adhesive bonds (before their detachment) can be thought of as a bed of springs with stiffness k, per unit area, and therefore the second term in eqn (6) is the energy invested in stretching the springs.
With the above contributions, we can write the total energy for an arbitrary set [θ(x),u(x);l], as the sum Π = Πd + Πa. An equilibrium solution is an extremum of this energy functional. However, to be admissible, it must also obey the kinematic constraint (4). To enforce this constraint we augment the energy functional by an additional term
| |  | (7) |
where
F is a Lagrange multiplier that can be interpreted as a generalized force applied at
x = 0, to ensure the displacement
u0.
Finally, the augmented energy functional is given by adding the separate contributions Π = Πd + Πa + C, which by inserting eqn (5)–(7) reads,
| |  | (8) |
A stable equilibrium shape for an imposed displacement u0 is found through a two step minimization procedure: first, we find the shape that minimizes the energy for a prescribed detached length l; then we find the minimum energy solution among all values of l, including the fully adhered solution for which l = 0. Mathematically we can write
| |  | (9) |
The optimal solutions obtained in the first minimization follow from the Euler–Lagrange formulation, which results in two differential equations, readily written in nondimensional form as
| | θ″ − 12f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 0 for x ∈ [0,l] θ = 0 for x ∈ [0,l] | (10) |
| | | λ2u″ − u = 0 for x ∈ [l,∞], | (11) |
where the dimensionless number,
λ2 =
E/
kh, emerges naturally from the formulation, and the dimensionless force
is derived using
I =
h3/12, and ensures balance of horizontal forces at
x =
l.
Integration of (10) is performed numerically to determine θ(x), which is then used to obtain the displacements
| |  | (13) |
Here we consider situations in which a zero angle is maintained on both ends of the arch, namely
θ(
x = 0) =
θ(
x =
l) = 0. Hence, the numerical solution is obtained
via a shooting method.
In the adhered region, eqn (11) is integrated analytically. Here, the displacement is expected to decay in the remote field, namely u(x → ∞) → 0, while its slope, at x = l, balances the force f. Accordingly, we have
| | | (u(x),v(x)) = (λfe(l−x)/λ,0) for x ∈ [l,∞). | (14) |
From this result, it is apparent that
λ serves as a characteristic decay length in the adhered region. The dimensionless force,
f, is obtained by the requirement of displacement continuity at
x =
l.
The solutions obtained through this procedure are equilibrium configurations for a prescribed detached length l. Hence, they are independent of the surface energy, Γ, which enters the formulation in the second minimization procedure (9), where an optimal l is obtained by comparison among the energetic states. This is done separately for each prescribed displacement u0.
4 Numerical results
Representative results are shown in Fig. 2, where we examine the sensitivity of the process to the dimensionless characteristic decay length, and the dimensionless counterpart of the surface energy| |  | (15) |
respectively. The length of the delaminated region, l, is shown as a function of u0 in Fig. 2a. In all cases, delamination of a finite region appears as a first order transition, where the critical displacement, uc, depends on both λ and γ. Quite interestingly, λ influences the barrier for delamination, but has a negligible effect on the shape of the curve that follows and, thus, on the shape of the arched region. Prior to the delamination, the response is linear and is dictated solely by the elastic properties through λ, as shown by the force–displacement curves in Fig. 2b. Then, at uc a sudden drop in the applied force is observed and followed by a monotonic decrease as displacement progresses. The corresponding sensitivity of the shape of the layer is shown in Fig. 2c for three representative values of u0. The curves clearly indicate negligible effect of λ on the shape, once the delamination has taken place. Higher γ leads to a smaller detached section as it increases the energetic cost of delamination.
 |
| | Fig. 2 Theoretical results for three combinations of (λ,γ) provided as multiplications of the base pair λ0 = 10, γ0 = 10−3: (a) evolution of detached length l with applied displacement u0 shows a jump at a critical displacement at u0 = uc. Increasing γ delays detachment and leads to a smaller detached length; increasing λ only delays detachment. Scaling predictions, indicated by dotted gray lines, are in agreement with numerical results. (b) Applied force f undergoes a drop at u0 = uc as the peeling initiates. Only λ controls the slope of the initial linear part of the f–u0 curve, prior to detachment. Higher γ leads to a lower peak-force and earlier detachment. (c) The corresponding shapes at different values of u0 are shown for the three cases. In determining the delaminated shape λ is shown to have negligible impact (red and green curves), while increasing γ delays detachment and decreases the delaminated length for a given u0. | |
To study the jamming limit, we examine the evolution of the archlength as shown by the black curves in Fig. 3, for different values of γ. In all cases, following the initial detachment, the arch increases its length up to a maximal value, beyond which the tendency is reversed and the arch begins to contract with increasing u0, until it jams. This limit is estimated here by the intersection between the two sides of the layers’ mid-line. Upon jamming, the shapes of the arched region in different layers are self-similar, namely jamming occurs once the ratio la/u0 ∼ 0.2 is obtained, as shown by the dashed gray line in Fig. 3.
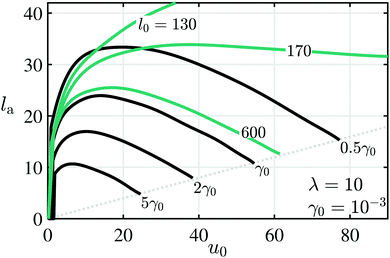 |
| | Fig. 3 Jamming transition shown for λ = 10 with four values of γ = (5, 2, 1, 0.5)γ0 with γ0 = 10−3: archlength, la, is plotted as function of the applied displacement. The black curves represent cases with spatially constant surface energy (γ). The dashed gray line marks the points where the lobes of the layer come into self contact and jamming is initiated. If the surface energy decays spatially with γ = γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−x/l0), the jamming can be delayed or avoided altogether by tuning the decay length, as shown by the green-colored curves for three values (l0 = 130, 170, 600). exp(−x/l0), the jamming can be delayed or avoided altogether by tuning the decay length, as shown by the green-colored curves for three values (l0 = 130, 170, 600). | |
5 Scaling analysis
The sensitivities observed in Fig. 2 can be further clarified by a scaling analysis. We consider arch formation under the assumption u0 ≪ l and, thus, θ ≪ 1. At this limit, eqn (10) can be integrated analytically, which upon implementation of boundary conditions, reads θ(x) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πx/l), where the compatibility requirement (4) translates to A2 = 4(u0 − ul)/l, and force balance implies ul = λf = λπ2/3l2. Now, we substitute these relationships into (8) and omit small terms under the assumption λ/l4 ≪ 1, to obtain the total energy
sin(2πx/l), where the compatibility requirement (4) translates to A2 = 4(u0 − ul)/l, and force balance implies ul = λf = λπ2/3l2. Now, we substitute these relationships into (8) and omit small terms under the assumption λ/l4 ≪ 1, to obtain the total energy| | | Π ∼ Eh(π2u0/3l2 + 2γl) | (16) |
which admits a minimal value at| |  | (17) |
Corresponding curves are shown by the dotted gray lines in Fig. 2a, and agree well with the numerical results for moderate displacements, u0.
Next, to estimate the critical values at which the arch forms, i.e. (uc,lc), we compare the total energy invested in deforming the layer into the arched configuration (by inserting (17) into (16)), with that of the layer in a fully adhered state, i.e. Π = Eh(u02/2λ). Initially, the flat configuration is energetically favorable. Then, the arch emerges when these energies intersect, which after some algebra and by substitution of (18) reads
We find a striking agreement between this relation and the results obtained
via the numerical scheme, which are shown in the form of a phase portrait in
Fig. 4. According to
(18), at the limit of infinite bond stiffness (
λ → 0), which is commonly assumed in theories for interfacial fracture, an arch would form immediately upon loading with
uc = 0, and would result in
lc = 0, thus showing the importance of accounting for the bond stiffness to determine the nucleation limit.
 |
| | Fig. 4 Phase portrait showing constant critical displacement curves on the γ–λ plane as obtained from numerical results, and matches well with scaling predictions. The result from experimental observations is indicated on the figure with γ = (2.63 ± 0.296) × 10−2 and λ = 0.6 ± 0.058. | |
6 Discussion and concluding remarks
To confirm the results of the above formulation, we now return to our observation in Fig. 1. Recall from Fig. 2 that γ controls both the critical displacement uc and the subsequent evolution of l with u0, while λ only affects uc. In order to fit the model to the experimental data, we first obtain the γ that best captures the l > 0 part of the l − u0 curve. Then, keeping γ fixed, we tune λ to match the experimentally observed uc. The outcome of this fitting process is shown in Fig. 5 (see ESI† for two additional cases). We show the mid-line curves of the PDMS sample at different displacements in comparison with theoretical shapes. The discrepancy in the arch shape for small u0, where the arch is shallow, is due to the extensibility of the layer. This effect becomes less significant as u0 increases. At larger displacements, when jamming is approached, symmetry breakage may occur due to gravity, which is neglected in the present model.¶ From the fitting process outlined above, we have for the PDMS layer γ ∼ 3.2 × 10−2 and λ ∼ 0.7 for a trial showed in Fig. 5. The combined results from the three trials give γ = (2.63 ± 0.296) × 10−2 and λ = 0.6 ± 0.058 (these values are also indicated in Fig. 4), which from eqn (15) translate to dimensional values Γ ∼ (3.95 ± 0.44) × 10−3 N mm−1 and k ∼ (1.76 ± 0.34) × 10−2 N mm−3. These values agree with representative values in the literature.23,27 The present peeling method thus provides a novel technique to measure these properties, which are otherwise difficult to obtain. Since the adhesive properties of PDMS are coupled with stiffness, their individual control is an experimental challenge that is left for future work.
 |
| | Fig. 5 Comparison between observation and theory. The dashed black curves represent experimental mid-line curves from Fig. 1; they are superimposed on gray curves which represent the best-fitting model predictions. Two fitting parameters – γ and λ – were used to fit the model to the experiment. In total, three trial were carried out (see ESI† for additional trials). | |
Finally, a key result of this work is the identification of the terminal jammed state and its dependence on the layer properties. While intermediate configurations are unstable to perturbations of the applied force, the jammed state is expected to be most ubiquitous in the natural world. Moreover, recent works have demonstrated that by employing surface wrinkling and kirigami techniques to control interface morphology, it is possible to tune the surface adhesive properties.28,29 Therefore, given our understanding of this phenomenon, it is now possible to tune the system not only to prescribe the jamming distance, but to avoid jamming completely. As an example, the latter can be achieved by spatially varying the surface energy, as shown in Fig. 3. This potential of active control raises the question as to whether caterpillars or even cells exploit similar in-plane mechanisms to form an arch and control their motion, and can artificial smart systems do the same?
Conflicts of interest
There are no conflicts to declare.
Notes and references
- F. Nabarro, S. Afr. J. Sci., 1989, 85, 589 Search PubMed.
- J. Hirth, Metall. Trans. A, 1985, 16, 2085–2090 CrossRef.
- L. Van Griethuijsen and B. Trimmer, Biol. Rev., 2014, 89, 656–670 CrossRef.
- J. M. Kolinski, P. Aussillous and L. Mahadevan, Phys. Rev. Lett., 2009, 103, 174302 CrossRef.
- N. Balmforth, R. Craster and I. Hewitt, Proc. R. Soc. A, 2015, 471, 20140740 CrossRef.
- A. A. Lee, C. Le Gouellec and D. Vella, Extreme Mech. Lett., 2015, 5, 81–87 CrossRef.
- D. Vella, A. Boudaoud and M. Adda-Bedia, Phys. Rev. Lett., 2009, 103, 174301 CrossRef.
- T. J. Wagner and D. Vella, Soft Matter, 2013, 9, 1025–1030 RSC.
- A. Schallamach, Wear, 1971, 17, 301–312 CrossRef.
- C. J. Rand and A. J. Crosby, Appl. Phys. Lett., 2006, 89, 261907 CrossRef.
- G. Briggs and B. Briscoe, Philos. Mag. A, 1978, 38, 387–399 CrossRef.
- W. Brace and J. Byerlee, Science, 1966, 153, 990–992 CrossRef CAS.
- S. Maegawa and K. Nakano, Wear, 2010, 268, 924–930 CrossRef CAS.
- O. Ronsin, T. Baumberger and C. Hui, J. Adhes., 2011, 87, 504–529 CrossRef CAS.
- H. Ramberg and O. Stephansson, Tectonophysics, 1964, 1, 101–120 CrossRef.
- S. Schmalholz, Y. Podladchikov and J.-P. Burg, J. Geophys. Res.: Solid Earth, 2002, 107, ETG-1 Search PubMed.
- M. M. Shulaker, H. Wei, N. Patil, J. Provine, H.-Y. Chen, H.-S. Wong and S. Mitra, Nano Lett., 2011, 11, 1881–1886 CrossRef CAS.
- P. M. Reis, F. Corson, A. Boudaoud and B. Roman, Phys. Rev. Lett., 2009, 103, 045501 CrossRef CAS.
- D. Vella, J. Bico, A. Boudaoud, B. Roman and P. M. Reis, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10901–10906 CrossRef CAS.
- U. S. Schwarz and S. A. Safran, Rev. Mod. Phys., 2013, 85, 1327 CrossRef CAS.
- F. Ziebert and I. S. Aranson, npj Comput. Mater., 2016, 2, 16019 CrossRef.
-
E. R. Trueman, Locomotion of soft-bodied animals, Edward Arnold, 1975 Search PubMed.
- T. Cohen, C. U. Chan and L. Mahadevan, Soft Matter, 2018, 14, 1771–1779 RSC.
- D. Labonte, C. J. Clemente, A. Dittrich, C.-Y. Kuo, A. J. Crosby, D. J. Irschick and W. Federle, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 1297–1302 CrossRef CAS.
-
B. Davidovitch and V. Démery, Rucks and folds: delamination from a flat rigid substrate under uniaxial compression, 2020 Search PubMed.
-
S. Chockalingam, C. Roth, T. Henzel and T. Cohen, 2020, arXiv preprint arXiv:2007.11090.
- A. Sofla, E. Seker, J. P. Landers and M. R. Begley, J. Appl. Mech., 2010, 77(3), 031007 CrossRef.
- P.-C. Lin, S. Vajpayee, A. Jagota, C.-Y. Hui and S. Yang, Soft Matter, 2008, 4, 1830–1835 RSC.
- D.-G. Hwang, K. Trent and M. D. Bartlett, ACS Appl. Mater. Interfaces, 2018, 10, 6747–6754 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01164a |
| ‡ It has been verified that displacements due to compression of the delaminated region are negligible. |
| § Recall that all lengths in the formulation are nondimensionalized with respect to the thickness of the layer. |
| ¶ The effect of gravity has been treated by others4,5 and is not the focus of the current work. |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Zoë
Lemon
a,
Christine
Roth
ab and
Tal
Cohen
a,
Zoë
Lemon
a,
Christine
Roth
ab and
Tal
Cohen
 *ac
*ac


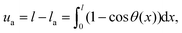






![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = 0 for x ∈ [0,l]
θ = 0 for x ∈ [0,l]

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2πx/l), where the compatibility requirement (4) translates to A2 = 4(u0 − ul)/l, and force balance implies ul = λf = λπ2/3l2. Now, we substitute these relationships into (8) and omit small terms under the assumption λ/l4 ≪ 1, to obtain the total energy
sin(2πx/l), where the compatibility requirement (4) translates to A2 = 4(u0 − ul)/l, and force balance implies ul = λf = λπ2/3l2. Now, we substitute these relationships into (8) and omit small terms under the assumption λ/l4 ≪ 1, to obtain the total energy




