Contact network changes in ordered and disordered disk packings
Abstract
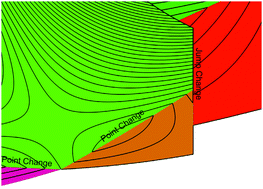
We investigate the mechanical response of packings of purely repulsive, frictionless disks to quasistatic deformations. The deformations include simple shear strain at constant packing fraction and at constant pressure, “polydispersity” strain (in which we change the particle size distribution) at constant packing fraction and at constant pressure, and isotropic compression. For each deformation, we show that there are two classes of changes in the interparticle contact networks: jump changes and point changes. Jump changes occur when a contact network becomes mechanically unstable, particles “rearrange”, and the potential energy (when the strain is applied at constant packing fraction) or enthalpy (when the strain is applied at constant pressure) and all derivatives are discontinuous. During point changes, a single contact is either added to or removed from the contact network. For repulsive linear spring interactions, second- and higher-order derivatives of the potential energy/enthalpy are discontinuous at a point change, while for Hertzian interactions, third- and higher-order derivatives of the potential energy/enthalpy are discontinuous. We illustrate the importance of point changes by studying the transition from a hexagonal crystal to a disordered crystal induced by applying polydispersity strain. During this transition, the system only undergoes point changes, with no jump changes. We emphasize that one must understand point changes, as well as jump changes, to predict the mechanical properties of jammed packings.


 Please wait while we load your content...
Please wait while we load your content...