Peak force visible microscopy†
Haomin
Wang
 a,
Le
Wang
a,
Yuequn
Shang
a,
Le
Wang
a,
Yuequn
Shang
 b,
Sajedehalsadat
Yazdanparast Tafti
c,
Wenpeng
Cao
c,
Zhijun
Ning
b,
Sajedehalsadat
Yazdanparast Tafti
c,
Wenpeng
Cao
c,
Zhijun
Ning
 b,
X. Frank
Zhang
c and
Xiaoji G.
Xu
b,
X. Frank
Zhang
c and
Xiaoji G.
Xu
 *a
*a
aDepartment of Chemistry, Lehigh University, 6 East Packer Ave., Bethlehem, PA 18015, USA. E-mail: xgx214@lehigh.edu
bSchool of Physical Science and Technology, ShanghaiTech University, 100 Haike Road, Shanghai 201210, China
cDepartment of Bioengineering, Lehigh University, 111 Research Drive, Bethlehem, PA 18015, USA
First published on 3rd August 2020
Abstract
The optical responses of molecules and materials provide a basis for chemical measurement and imaging. The optical diffraction limit in conventional light microscopy is exceeded by mechanically probing optical absorption through the photothermal effect with atomic force microscopy (AFM). However, the spatial resolution of AFM-based photothermal optical microscopy is still limited, and the sample surface is prone to damage from scratching due to tip contact, particularly for measurements on soft matter. In this article, we develop peak force visible (PF-vis) microscopy for the measurement of visible optical absorption of soft matter. The spatial resolution of PF-vis microscopy is demonstrated to be 3 nm on green fluorescent protein-labeled virus-like particles, and the imaging sensitivity may approach a single protein molecule. On organic photovoltaic polymers, the spatial distribution of the optical absorption probed by PF-vis microscopy is found to be dependent on the diffusion ranges of excitons in the donor domain. Through finite element modeling and data analysis, the exciton diffusion range of organic photovoltaics can be directly extracted from PF-vis images, saving the need for complex and delicate sample preparations. PF-vis microscopy will enable high-resolution nano-imaging based on light absorption of fluorophores and chromophores, as well as deciphering the correlation between the spatial distribution of photothermal signals and underlying photophysical parameters at the tens of nanometer scale.
Introduction
Ultraviolet and visible light excites electronic resonances. After light absorption, the excited states relax and the energy is converted into heat through a phenomenon that is known as the photothermal effect.1 The photothermal effect has been utilized across several disciplines, such as photothermal therapy,2 manipulation of nanoparticle properties,3 and photothermal spectro-microscopy.4 In photothermal imaging, a pump beam is used to heat the sample, then a probe beam is applied to detect the photothermal expansion caused by the first beam. Detection of the photothermal response yields high sensitivity. Gold nanoparticles down to the size of 1.4 nm can be measured.5 However, the spatial resolution of far-field photothermal microscopy is still bound by Abbe's diffraction limit,6 to about half of the light wavelength.The diffraction limit can be bypassed by mechanically probing the photothermal effect with a sharp tip with dimensions much less than the wavelength of incident photons, through atomic force microscopy (AFM).7 Moreover, the metallic AFM tip generates a spatially confined field enhancement under light illumination, with a size far below the diffraction limit. As a result, the small sample volume right beneath the tip is excited by the field enhancement to generate photothermal expansion, which causes the AFM cantilever to oscillate through mechanical excitation. Several photothermal AFM infrared (AFM-IR) imaging techniques have been developed, including photothermally induced resonance (PTIR)8 and peak force infrared (PFIR) microscopy.9 Signal contribution from photothermal expansion also exists in photoinduced force microscopy (PiFM).10,11 These infrared imaging methods deliver spatial resolution much better than the optical diffraction limit. As an infrared imaging technique, PFIR microscopy has distinct advantages among these methods: it has the highest spatial resolution of ∼6 nm,12,13 can simultaneously measure multimodal properties of the sample, and is suitable for liquid-phase operation without sample damage.14,15 These advantages stem from the non-invasive peak force tapping (PFT) mode utilized in PFIR microscopy. The PFT mode allows intermittent and brief tip–sample contact for accurate force measurement, while maintaining minimal tip indentation to avoid sample scratching. The detection mechanism of both PTIR microscopy and PiFM has been extended to visible excitation.16,17 However, the detection mechanism of PFIR microscopy has yet to be utilized for non-infrared excitations.
In this article, we expand the operation mechanism of PFIR microscopy into the visible light regime. We named this method peak force visible (PF-vis) microscopy, as a sub-branch of peak force photothermal microscopy. PF-vis microscopy can probe the optical absorption of materials and yields a spatial resolution of 3 nm, superseding that of PFIR microscopy in the infrared region. The high sensitivity and spatial resolution of PF-vis microscopy in imaging fluorophore-labeled samples and fluorescence molecules are demonstrated. PF-vis microscopy can also be used to study organic photovoltaic (OPV) blends to reveal the distribution of the donor domains. With the help of an exciton diffusion model, the spatial distribution of the photothermal response in the donor domains is used to recover the exciton diffusion range, which is a much-needed property for OPV research.
Experimental
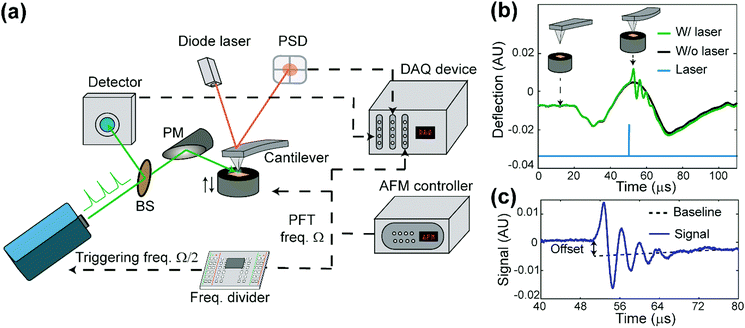
The apparatus of PF-vis microscopy is illustrated in Fig. 1a. A Q-switch pulsed 532 nm laser with 7 ns pulse duration (CST-L-532Q, Ultralasers) is used as the light source. An AFM instrument (Multimode 8, Bruker) is operated in the peak force tapping (PFT) mode. To acquire the precise timing of the laser pulses, a beam splitter (4% reflection) is installed at 45° before the laser source to direct a small portion of light into an optical detector (Si amplified detector, Thorlabs). The rest of the visible light is focused onto the tip–sample region by a silver-coated parabolic mirror of 0.25 numerical aperture. In the PFT mode, the AFM sample stage is vertically oscillated by a piezo actuator at a frequency of Ω (2 kHz in our experiment), while the cantilever is held stationary. The same driving frequency of Ω is routed out from the controller to a custom-made frequency divider to generate a waveform with frequency Ω/2, which is phase synchronized with the PFT to trigger the laser pulses. As a result, PFT cycles are consecutively associated with and without a laser pulse. Vertical cantilever deflections are obtained by an AFM built-in position-sensitive detector (PSD). Signals from the optical detector and the PSD, as well as the trigger waveform with the frequency Ω from the AFM controller, are all routed into a high-speed data acquisition (DAQ) card (PXI-5122, National Instruments) to process signals in LabVIEW (LabVIEW 2013, National Instruments) in real-time. Cantilever deflection curves obtained in such PFT cycles are shown in Fig. 1b. For PFT cycles with laser illumination, the sample undergoes rapid photothermal expansion, and the cantilever is pushed up, causing the cantilever to oscillate at a higher contact resonant frequency (hundreds of kHz). The alternating laser pulse delivery scheme allows background subtraction and extraction of the laser-induced photothermal expansion from cantilever deflections in real time, as shown in Fig. 1c.PF-vis microscopy reads out signals from the laser-induced cantilever deflections. Fig. 1b shows the detected cantilever deflections and timing of the laser pulse in the time domain. Corresponding tip-sample configurations during PFT cycles are illustrated as the inset. For samples that absorb photons at 532 nm, a regular force curve without a laser pulse (black curve), and a photothermal-excited force curve due to laser pulse illumination (green curve) are displayed. The timing of the laser pulse is adjusted to be right at the maximal cantilever indentation, which is known as the peak force set point when the tip is in momentary but firm contact with the sample. Fig. 1c shows the baseline offset and ringdowns of the cantilever's contact resonance, which provides two aspects of the rapid photothermal expansion. In this article, the amplitude of the Fourier transform of ringdown oscillations is used as the PF-vis signal. As the AFM tip scans across the sample surface, PF-vis signals are registered for each pixel, and a photothermal expansion image can be composed. In addition, mechanical information, such as modulus and adhesion extracted from the PFT force curves, is registered simultaneously by the AFM controller. The detailed apparatus setup and sample preparations can be found in Note S1 (ESI†).
Results
Imaging green fluorescent protein-labelled virus-like particles
The fluorescence process is accompanied by internal conversions, which generate heat that causes photothermal effects. After photon absorption, fluorescent molecules are instantaneously excited to a higher vibrational state before the emission of fluorescence. In general, the fluorescence quantum yield is less than unity, and the excess energy is converted into heat through vibrational relaxation, such as nonradiative quenching.18 Accompanying photothermal effects lead to indirect fluorescence detection, such as thermal lens spectroscopy.19 Here, we use a sharp AFM probe in PF-vis microscopy to locally detect photothermal expansions of green fluorescent protein (GFP)-labeled virus-like-particles (VLPs).
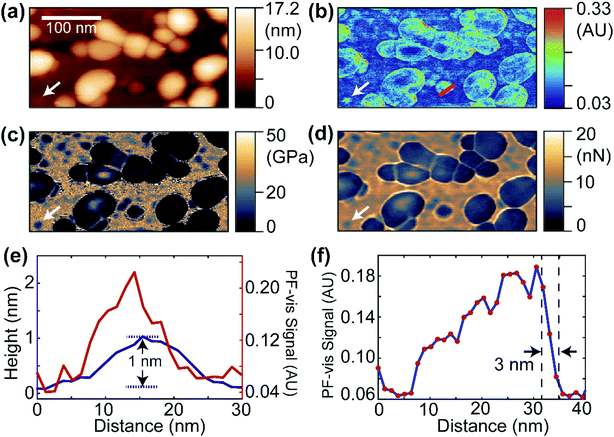
Fig. 2 displays the PF-vis microscopy results of GFP-labeled VLPs under ambient conditions. The VLPs (a kind gift from Dr Wendy Maury, University of Iowa) were nonpathogenic Ebola virus glycoprotein-pseudotyped VLPs, and were generated by co-transfecting HEK 293 T cells with a plasmid expressing Ebola virus VP40 fused to a green fluorescent protein (GFP), and a plasmid expressing Ebola virus glycoprotein, at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio.20,21 The AFM topography image is shown in Fig. 2a, where the majority of VLPs have sizes of 30–80 nm and heights of 10–17 nm. Fig. 2b shows a PF-vis image of the same region with the excitation of the 532 nm laser. Each GFP-labeled VLP, regardless of size, is revealed by stronger 532 nm absorption than the mica substrate. The PF-vis image also suggests that the distribution of GFPs on VLPs is not homogenous: GFPs are more attached to the periphery of the VLPs. This is consistent with the fact that VP40 is a matrix protein that is positioned under the glycoprotein and makes up the shell of the particle. There should be multiple VP40-GFPs in the periphery lining up in the vertical direction and, hence, the photothermal effects should be more prominent in the periphery. Some small hotspots are also present on the substrate, which are small particles formed by unattached GFPs, likely due to VLP degradation.
1 ratio.20,21 The AFM topography image is shown in Fig. 2a, where the majority of VLPs have sizes of 30–80 nm and heights of 10–17 nm. Fig. 2b shows a PF-vis image of the same region with the excitation of the 532 nm laser. Each GFP-labeled VLP, regardless of size, is revealed by stronger 532 nm absorption than the mica substrate. The PF-vis image also suggests that the distribution of GFPs on VLPs is not homogenous: GFPs are more attached to the periphery of the VLPs. This is consistent with the fact that VP40 is a matrix protein that is positioned under the glycoprotein and makes up the shell of the particle. There should be multiple VP40-GFPs in the periphery lining up in the vertical direction and, hence, the photothermal effects should be more prominent in the periphery. Some small hotspots are also present on the substrate, which are small particles formed by unattached GFPs, likely due to VLP degradation.
Interestingly, a small particle absorbing strongly at 532 nm can be observed in Fig. 2b, which is marked by the white arrow, and the same position is also marked in Fig. 2a–d. The same particle is present in the reduced Young's modulus and adhesion images shown in Fig. 2c and d. It has a smaller modulus and adhesion than the mica substrate, indicating that the particle is composed of soft VP40-GFPs. In Fig. 2e, the PF-vis signal profile across this particle is plotted along with the AFM height. The PF-vis profile has a width of approximately 15 nm, which is ∼17 times better than the optical diffraction limit. A height of only 1 nm from the mica substrate is obtained for this particle, indicating that this particle could be a single or a small aggregate of VP40-GFP molecules, given that the structure of GFP protein has a cylindrical shape of about 2.5 nm in diameter and 4 nm height in free space.22 The AFM width was measured to be roughly 20 nm for the particle, since the lateral resolution of AFM is a convolution of sample geometry and tip radius (∼30 nm in this case). Fig. 2e demonstrates the high imaging sensitivity of PF-vis microscopy, possibly reaching single-molecule level. Another PF-vis image of a possible single dye-labeled streptavidin molecule is provided in Fig. S1 (ESI†).
To estimate the spatial resolution, a PF-vis signal profile across a VLP from Fig. 2b is plotted in Fig. 2f, where a spatial resolution of 3 nm is obtained from the width between 90% and 10% of the difference between the signal maximum and minimum across the edge. The 3 nm spatial resolution exceeds the 6 nm spatial resolution of PFIR microscopy with an infrared laser source, and is much finer than the ∼20 nm resolution obtained by PTIR microscopy. Similar spatial resolutions of 3–5 nm were also estimated from other locations from Fig. 2b and Fig. S1 (ESI†), and are displayed in Fig. S2 (ESI†). Such a high-resolution results from the intermittent PFT operation and the large photothermal effect in the visible range. Compared with super-resolution fluorescence microscopy,23 PF-vis microscopy is not susceptible to and actually benefits from fluorescence quenching, as it measures the local photothermal expansion resulting from light absorption. Also, the photothermal effect does not require fluorophores that emit light, it only requires chromophores that absorb light.
Imaging of and extracting intrinsic properties from organic photovoltaic blends
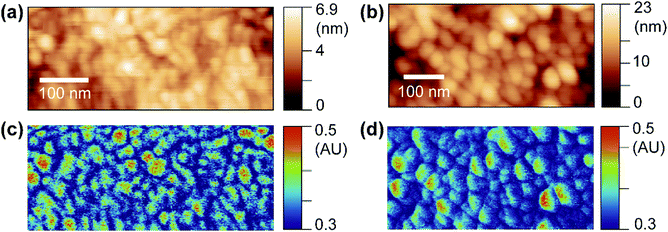
OPVs have shown great potential in visible optoelectronic conversion due to their low-cost, flexible, long-lasting, and non-toxic features.24 The key functional layer in OPVs consists of spatially phase-separated donor and acceptor domains in a blend mixture. Excitons generated by photons diffuse towards donor–acceptor interfaces in the mixture, which is called the bulk heterojunction (BHJ) and undergo charge separation to generate electric current.25,26 Phase-separated donor and acceptor domains in BHJs are usually on the nanometer scale, and the geometry of the phase separation plays an important role in effective light–current conversion.27 Here, we use PF-vis microscopy to image and extract intrinsic exciton properties from OPV blends. In the two investigated OPV blends, poly(3-hexylthiophene-2,5-diyl) (P3HT) and poly[(9,9-dioctylfluorenyl-2,7-diyl)-alt-(4,4′-(N-(4-sec-butylphenyl)diphenylamine))] (TFB) are used as donors, and [6,6]-phenyl C61 butyric acid methyl ester (PCBM) is used as the acceptor in both.PF-vis microscopy measurements on the two kinds of OPV blend samples are shown in Fig. 3. Nanoscale phase separations are observed in the AFM topography images shown in Fig. 3a and b, but no further information can be extracted. In the PF-vis images shown in Fig. 3c and d, two types of domains are present: one type of domain absorbs strongly at 532 nm, while only a faint signature is observed for the other type. In OPV blends, light energy is mostly absorbed by donors to generate excitons. Since P3HT and TFB are used as donor molecules, and the same PCBM molecule is used as the acceptor molecule in the two blends, one can conclude that P3HT-rich and TFB-rich domains form larger islands in the two blend films and PCBM-rich domains fill in the lower interstices. This phase separation was further confirmed by modulus and adhesion measurements, as P3HT and TFB polymer films have lower modulus and adhesion values than those of PCBM (see Fig. S3, ESI†). One notable difference between the two PF-vis images is present when evaluating PF-vis signal distributions on donor domains in detail. For most P3HT domains, the PF-vis signal distribution is roughly symmetric, the center of the domains has a higher intensity and a lower intensity is observed at the periphery. In contrast, for most TFB domains, the signal distribution is asymmetric, with a higher signal intensity located on the left side of the domains. PF-vis images with different scan angles are shown in Fig. S4 (ESI†), confirming that the asymmetric signal distribution is not caused by scan artifacts.
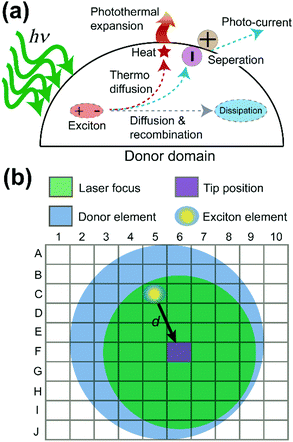
Why do the donor domains of the P3HT:PCBM and the TFB:PCBM blend films show different signal distributions of the photothermal expansion? To answer this question, exciton behavior in OPV donor domains was examined in detail. Fig. 4a illustrates multiple routes that can be taken by excitons in the donor domain. Two major paths are adopted by excitons to diffuse the absorbed energy. In the first path, excitons travel towards the interface between donor and acceptor. From there, the exciton dissociates into a separate electron and hole, generating electric currents. This is the preferred process for OPV applications. In the second path, the exciton undergoes the process of thermo diffusion and recombination to reach the dissipation state. In general, the heat generated during the second process can cause the donor domain to expand due to the released thermal energy. The efficiency of both processes depends on the lifetime or the decay length of the exciton. The longer the decay length, the higher the possibility that the exciton can reach the interface, and the greater the heat and current generation.26 Moreover, the lifetime of excitons is in the order of nanoseconds,26 which is much shorter than the μs-level cantilever vibrations detected in PF-vis microscopy (Fig. 1c). What is then measured by PF-vis microscopy is the net result of exciton distributions after the decay. Therefore, a finite element analysis can be applied to simulate exciton distributions on the donor domain by treating every element as an exciton generation source and considering the decay length. The scheme of finite element analysis is shown in Fig. 4b.
In the finite element analysis, the element size is set as 1 × 1 nm2. The heat generated at each element is proportional to the local density of excitons generated from and diffused to the element and can be written as:
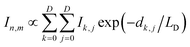 | (1) |
In PF-vis operation, excitons are generated by the tip-enhanced light field. Thus, other factors related to element-wise exciton generation should also be considered and added to eqn (1). These effects include the non-symmetric illumination field due to the incident light direction (see Fig. 5), the limited size of the focus spot (Fig. 4b), and the actual geometry of donor domains. A modified eqn (1) is then written as:
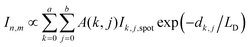 | (2) |
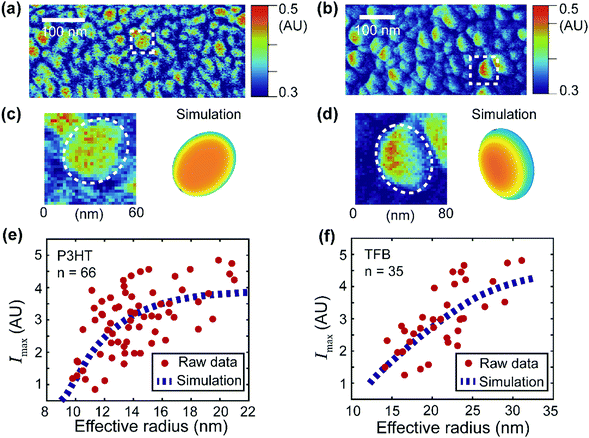 | ||
| Fig. 6 Simulation of the signal distribution of the donor domains and extraction of the apparent exciton diffusion length for two OPV blends. (a and b) PF-vis images of P3HT:PCBM and TFB:PCBM, respectively. They are identical to Fig. 3c and d. (c and d) Zoomed-in images of an observed P3HT-rich domain (enclosed by the white box in (a)) and a TFB-rich domain (enclosed by the white box in (b)). Simulations based on eqn (2) are illustrated for comparison. (e) Maximal signal intensity Imaxversus the effective radius of the P3HT donor domains. Data were obtained from 66 P3HT-rich donor domains in (a). The raw data were then fitted with the numerical simulation (based on eqn (2)). The best fit was obtained with LD = 2.4 nm with an R-squared value of 0.35. (f) Maximal signal intensity Imaxversus the effective radius of the TFB donor domains. Data were obtained from 35 TFB-rich donor domains in (b). The best fit was obtained with LD = 11 nm with an R-squared value of 0.51. | ||
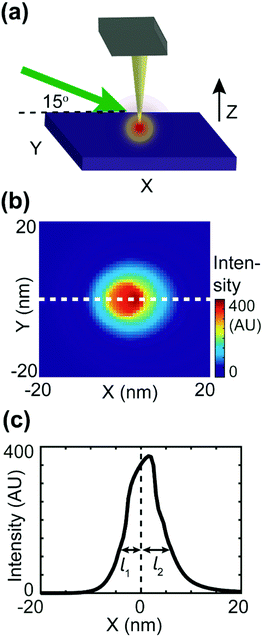
To estimate the asymmetric term A(k,j), an FDTD simulation was conducted, as shown in Fig. 5. As shown in Fig. 5b, the intensity decay length of the asymmetric focus spot is direction-dependent, as the maximum decay length (l2) aligns with the X-axis and the minimum decay length (l1) aligns with the direction of negative X. In the actual simulation, we also set the value of A(k,j) to be direction-dependent with a general expression A(k,j) = exp(−dk,j/l), with the decay length l ranging between l1 = 2 nm and l2 = 18 nm. The signal distribution difference between donor domains of P3HT and TFB turns out to result from the interplay between the asymmetric focus spot in PF-vis operation and the exciton diffusion length LD.
Planar elliptical domain shapes are used in the simulation to approximate the actual geometry. In the simulation of the P3HT-rich domain shown in Fig. 6c, an ellipse with a long axis of 60 nm and a short axis of 40 nm is used. In the simulation of the TFB-rich domain shown in Fig. 6d, an ellipse with a long axis of 80 nm and a short axis of 40 nm is used. The focus spot diameter is set as 30 nm, and diffusion lengths of 2.4 nm and 11 nm are used for P3HT- and TFB-rich domains, respectively. These diffusion lengths were obtained by applying simulation-based fits to experimental data and will be introduced later. As a result, a symmetric P3HT-rich domain and an asymmetric TFB-rich domain are reproduced, which accommodate the experimentally observed signal distributions. In the case of P3HT domains, the exciton diffusion length is small. The overall photothermal expansion signal is less affected by the asymmetric focus spot and appears symmetric. However, in the case of TFB domains, the diffusion length is large, and the distribution of excitons is more affected by the asymmetric focus spot. Consequently, the signal of TFB domains appears non-symmetric. Note that the simulations do not fully reproduce the experimental features because of the simplicity of the model. For example, eqn (2) assumes a pure donor domain. Nevertheless, in practice, a mixture of donor–acceptor pairs could exist at the molecular level.28,29
Despite its simplicity, eqn (2) can still be used to extract the apparent exciton diffusion length LD. According to eqn (2), if we assume that the focus condition is the same (A(k,j) and the spot size kept the same) in all PF-vis measurements, the PF-vis signal only depends on the apparent diffusion length LD and donor domain geometry. Therefore, we can plot the maximal PF-vis signal extracted from multiple donor domains versus the domain size, and extract the apparent diffusion length LD by comparing the experimental data with the simulation. Such a procedure is shown in Fig. 6(e and f). In these two simulation-based fittings, the A(k,j) term is set to 1, the focus spot diameter is set to 30 nm, and ratios between the long axis and the short axis are set as 1.5 for both P3HT and TFB domains. By applying proper values of LD, we observe that the best fit (within 99% of the maximum R-squared value) occurs with LD = 2.0–2.8 nm for P3HT domains and LD = 8–22 nm for TFB domains. These results are in agreement with diffusion lengths of 3 nm for P3HT and 9 nm for TFB measured by the conventional fluorescence quenching and transient absorption methods.30,31 The consistency of the apparent LD obtained by PF-vis microscopy with the diffusion length measured by conventional methods suggests that PF-vis microscopy can be utilized to extract useful parameters in situ for OPV devices from PF-vis images.
Discussion
The high sensitivity of PF-vis microscopy is contributed by four factors: first, the tip-enhancement of the metallic tip increases the field usually by two orders of magnitude, compared with the regular far-field illumination. Secondly, the energy per photon in the visible region is about ten times larger than that of infrared, so the photothermal effect is stronger. Thirdly, the metallic tip in close contact with the sample can assist fluorescence quenching, leading to more energy being dissipated through non-radiative heat channels, rather than through radiative fluorescence. Lastly, nanosecond laser pulses are used in our experiment. Even for a single chromophore under the tip, there could be multiple excitation–relaxation events that generate heat within the pulse duration. The high spatial resolution comes from the gentle tip–sample contact during the peak force tapping with the peak force setpoint of only several nano Newtons. Although the tip radius is about 30 nm in this study, sub-10 nm spatial resolution is achievable because the contact area of the tip and sample is smaller than the tip radius.With the high sensitivity and 3 nm spatial resolution, PF-vis microscopy is suitable for imaging fluorescent molecules, and provides complementary details to the super-resolution fluorescence microscopies in situations that do not permit extrinsic fluorophore labels. Because PF-vis microscopy measures the local photothermal expansion, it also serves as a complementary tool to reveal the distribution of fluorescent molecules in a complex biological system where fluorescence quenching becomes a problem. Compared with other common methods that are used in measuring the exciton diffusion length in OPV samples, such as photoluminescence quenching31,32 and transient absorption spectroscopy,30 PF-vis microscopy can directly measure the apparent diffusion length, requiring fewer specialties in sample preparation and less expensive laser sources. It does not require homogeneous thin films or crystals, but rather it focuses on the in situ and in operando properties of photo-active donor–acceptor blends, thus providing useful information for practical applications. Upon completion of a single PF-vis microscopy scan, donor and acceptor domains can be distinguished, and the apparent exciton diffusion length can be estimated at the same time.
Further improvement in the accuracy of the measured apparent diffusion length can be achieved by considering local morphology variations of the donor domains and applying a 3D finite element analysis. In the finite element analysis, the ellipse approximation used in our current model could be further modified domain by domain to account for the actual geometry. An exciton reflection term can be further added into our model to better characterize signal intensity at domain peripherals. The feasibility of finite element analysis also allows for taking the exciton behavior at domain interfaces into consideration and performing iterative calculations to reach a steady state at the expense of computational complexity. Instrument-wise, the single-frequency laser source used in this study can be upgraded to a broadband UV-vis-NIR source, so that detailed spectroscopic analysis can be performed on OPV samples to unravel the interplay between different charge-transfer states.
Conclusions
In conclusion, mechanical detection of visible absorption through photothermal expansion has been demonstrated on soft matter by using PF-vis microscopy. The noninvasiveness of PF-vis microscopy helps deliver the spatial resolution of 3 nm on GFP-labeled VLPs, and high chemical sensitivity towards the single-molecular level. The PF-vis signal also correlates with the exciton diffusion range of donor domains in OPV blends. Through a finite element analysis, characteristic exciton diffusion lengths for P3HT:PCBM and TFB:PCBM blends were calculated from in situ PF-vis images. Super-resolution nano-imaging of fluorophores and chromophores in complex biological systems is expected to be achieved with PF-vis microscopy. It is also expected to be a useful platform for deciphering the correlation between the photothermal signal and underlying photophysical parameters at the nanoscale.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Faculty Innovation Grant of Lehigh University. The authors also acknowledge Dr. Lisa Fredin and Dr. Ivan Biaggio for helpful discussions relating to this work, and Devon S. Jakob and Joseph González-Fialkowski for proofreading the manuscript.Notes and references
- M. Terazima, N. Hirota, S. E. Braslavsky, A. Mandelis, S. E. Bialkowski, G. J. Diebold, R. J. D. Miller, D. Fournier, R. A. Palmer and A. Tam, Pure Appl. Chem., 2004, 76, 1083–1118 CAS.
- X. Huang and M. A. El-Sayed, Alexandria J. Med, 2011, 47(1), 1–9 CrossRef.
- J. Tan, S. Namuangruk, W. Kong, N. Kungwan, J. Guo and C. Wang, Angew. Chem., Int. Ed., 2016, 55, 13979–13984 CrossRef CAS PubMed.
- A. Gaiduk, P. V. Ruijgrok, M. Yorulmaz and M. Orrit, Chem. Sci., 2010, 1, 343–350 RSC.
- L. Cognet, S. Berciaud, D. Lasne and B. Lounis, Anal. Chem., 2008, 80(7), 2288–2294, DOI:10.1021/ac086020h.
- E. Abbe, Archiv für mikroskopische Anatomie, 1873, 9, 413–418 CrossRef.
- A. Dazzi and C. B. Prater, Chem. Rev., 2017, 117, 5146–5173 CrossRef CAS PubMed.
- A. Dazzi, R. Prazeres, E. Glotin and J. M. Ortega, Opt. Lett., 2005, 30, 2388–2390 CrossRef CAS PubMed.
- L. Wang, H. Wang, M. Wagner, Y. Yan, D. S. Jakob and X. G. Xu, Sci. Adv., 2017, 3, e1700255 CrossRef PubMed.
- L. Wang, H. M. Wang, D. Vezenov and X. J. G. Xu, J. Phys. Chem. C, 2018, 122, 23808–23813 CrossRef CAS.
- J. Jahng, E. O. Potma and E. S. Lee, Anal. Chem., 2018, 90, 11054–11061 CrossRef CAS PubMed.
- D. S. Jakob, L. Wang, H. Wang and X. G. Xu, Anal. Chem., 2019, 91, 8883–8890 CrossRef CAS PubMed.
- W. Li, H. Wang, X. G. Xu and Y. Yu, Langmuir, 2020, 36(22), 6169–6177, DOI:10.1021/acs.langmuir.0c00627.
- H. Wang, E. Janzen, L. Wang, J. H. Edgar and X. G. Xu, Nano Lett., 2020, 20, 3986–3991 CrossRef CAS PubMed.
- H. Wang, J. M. González-Fialkowski, W. Li, Y. Yu and X. G. Xu, ChemRxiv, 2020, Preprint.
- A. M. Katzenmeyer, G. Holland, K. Kjoller and A. Centrone, Anal. Chem., 2015, 87, 3154–3159 CrossRef CAS PubMed.
- J. Jahng, D. A. Fishman, S. Park, D. B. Nowak, W. A. Morrison, H. K. Wickramasinghe and E. O. Potma, Acc. Chem. Res., 2015, 48, 2671–2679 CrossRef CAS PubMed.
- B. R. Masters, J. Biomed. Opt., 2013, 18, 039901 CrossRef.
- M. Liu and M. Franko, Int. J. Thermophys., 2016, 37, 67 CrossRef.
- S. P. Timoshenko and S. Woinowsky-Krieger, Theory of plates and shells, McGraw-hill, 1959 Search PubMed.
- S. Moller-Tank, A. S. Kondratowicz, R. A. Davey, P. D. Rennert and W. Maury, J. Virol., 2013, 87, 8327 CrossRef CAS PubMed.
- S. J. Remington, Protein Sci., 2011, 20, 1509–1519 CrossRef CAS PubMed.
- B. Huang, M. Bates and X. Zhuang, Annu. Rev. Biochem., 2009, 78, 993–1016 CrossRef CAS PubMed.
- C. Brabec, U. Scherf and V. Dyakonov, Organic photovoltaics: materials, device physics, and manufacturing technologies, John Wiley & Sons, 2011 Search PubMed.
- S. M. Menke and R. J. Holmes, Energy Environ. Sci., 2014, 7, 499–512 RSC.
- O. V. Mikhnenko, P. W. M. Blom and T.-Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867–1888 RSC.
- B. P. Lyons, N. Clarke and C. Groves, Energy Environ. Sci., 2012, 5, 7657–7663 RSC.
- N. D. Treat, M. A. Brady, G. Smith, M. F. Toney, E. J. Kramer, C. J. Hawker and M. L. Chabinyc, Adv. Energy Mater., 2011, 1, 82–89 CrossRef CAS.
- B. A. Collins, J. R. Tumbleston and H. Ade, J. Phys. Chem. Lett., 2011, 2, 3135–3145 CrossRef CAS.
- A. Bruno, L. X. Reynolds, C. Dyer-Snaith, J. Nelson and S. A. Haque, J. Phys. Chem. C, 2013, 117, 19832–19838 CrossRef CAS.
- M. Sim, J. Shin, C. Shim, M. Kim, S. B. Jo, J.-H. Kim and K. Cho, J. Phys. Chem. C, 2014, 118, 760–766 CrossRef CAS.
- P. Irkhin and I. Biaggio, Phys. Rev. Lett., 2011, 107, 017402 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting materials for peak force visible microscopy. See DOI: 10.1039/d0sm01104e |
| This journal is © The Royal Society of Chemistry 2020 |