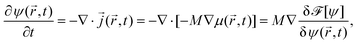Open Access Article
Open Access ArticleTransient coarsening and the motility of optically heated Janus colloids in a binary liquid mixture†
Juan Ruben
Gomez-Solano
 a,
Sutapa
Roy
a,
Sutapa
Roy
 bc,
Takeaki
Araki
d,
S.
Dietrich
bc and
Anna
Maciołek
bc,
Takeaki
Araki
d,
S.
Dietrich
bc and
Anna
Maciołek
 *bce
*bce
aInstituto de Fisica, Universidad Nacional Autonoma de México, Apdo. Postal 20-364, 01000, Ciudad de México, Mexico
bMax-Planck-Institut für Intelligente Systeme, Heisenbergstr. 3, 70569 Stuttgart, Germany
cIV. Institut für Theoretische Physik, Universität Stuttgart, Pfaffenwaldring 57, 70569 Stuttgart, Germany
dDepartment of Physics, Kyoto University, Kyoto 606-8502, Japan
eInstitute of Physical Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, PL-01-224 Warsaw, Poland. E-mail: amaciolek@ichf.edu.pl
First published on 4th August 2020
Abstract
A gold-capped Janus particle suspended in a near-critical binary liquid mixture can self-propel under illumination. We have immobilized such a particle in a narrow channel and carried out a combined experimental and theoretical study of the non-equilibrium dynamics of a binary solvent around it – lasting from the very moment of switching illumination on until the steady state is reached. In the theoretical study we use both a purely diffusive and a hydrodynamic model, which we solve numerically. Our results demonstrate a remarkable complexity of the time evolution of the concentration field around the colloid. This evolution is governed by the combined effects of the temperature gradient and the wettability, and crucially depends on whether the colloid is free to move or is trapped. For the trapped colloid, all approaches indicate that the early time dynamics is purely diffusive and characterized by composition layers travelling with constant speed from the surface of the colloid into the bulk of the solvent. Subsequently, hydrodynamic effects set in. Anomalously large nonequilibrium fluctuations, which result from the temperature gradient and the vicinity of the critical point of the binary liquid mixture, give rise to strong concentration fluctuations in the solvent and to permanently changing coarsening patterns not observed for a mobile particle. The early time dynamics around initially still Janus colloids produces a force which is able to set the Janus colloid into motion. The propulsion due to this transient dynamics is in the direction opposite to that observed after the steady state is attained.
1 Introduction
Inspired by biological molecular motors, in recent years there has been an upsurge of research efforts to construct artificial devices, which deliver mechanical work or propel themselves in a liquid environment. It has been demonstrated experimentally that a micron-sized Janus particle, half-coated with metal and suspended in a near critical binary solvent, self-propels after illumination with light of low intensity.1,2 Ever since, this type of light activated self-propellers has been intensively used for studying active matter. The phenomena, which have been explored this way, range from clustering and phase separation in dense suspensions,3 over the circular motion4 and gravitaxis5 of asymmetric self-propelled objects, to phototactic behavior6,7 and self-propulsion in viscoelastic fluids7–10 and dense colloidal suspensions.11Another important direction of research aims at understanding the self-propulsion mechanism in these systems, which is rather complex. The source of the active motion is provided by the local demixing of a binary solvent, which is observed around the Janus colloid after its illumination by light of sufficient intensity, such that the metal cap is heated above the lower critical temperature Tc of the solvent. Evidence has been gathered that the onset of the motion as well as its direction and its speed depend sensitively on system parameters, such as the wetting properties of both hemispheres of the Janus particle, the intensity of the illumination, the particle size, or the average composition of the solvent.
Hydrodynamic models shed light on the processes occurring at steady state, i.e., after a local demixing has been completed and a droplet, rich in the species preferred by the hot hemisphere of the Janus particle, has been formed.7,12–14 However, the relevance of the diffusive dynamics, which dominates the coarsening process at early and transient times, is still unclear. So far, the early stage diffusive dynamics of a local demixing near a Janus particle has been studied only for temperature quenches, which do not cross the binodal of demixing.15 Deeper quenches have been studied only for homogeneously heated particles.16
This has motivated us to combine experiment and theory in order to investigate the non-equilibrium coarsening dynamics around a hot spherical Janus particle suspended in a binary solvent. This is a challenging task because of technical limitations of both approaches. Concerning the experiments, one has to use large particles in order to be able to resolve the coarsening patterns. On the other hand, simulations for large particles are restricted by the availability of computing power. Accordingly, a quantitatively reliable comparison of the corresponding results is not always possible. We used an optical microscope to measure the time evolution of the surface layers and the subsequent growth of a droplet near the heated golden hemisphere. After implementing a suitable confinement, a single colloidal particle can be immobilized, which allows one to perform accurate measurements of the composition profiles around the particle as a function of time. In order to be able to judge the relevance of hydrodynamic effects in the transient dynamics, we compare the experimental data with the results obtained from two models, i.e., purely diffusive model B and model H which includes hydrodynamics.
We find that the coarsening dynamics around immobilized Janus particles is more involved than the one observed for a self-propelling particle: the coarsening patterns which form around a fixed particle at later times are not observed around a mobile particle. Such patterns might, however, be relevant for Janus particles in optical potentials, which have been recently studied in the context of, e.g., clustering17 or of microscopic engines powered by the local demixing of a critical binary liquid mixture.18 The transient dynamics has consequences for the self-propulsion. We observe that the Janus particle starts to move long before the stationary-state droplet is formed near its hot hemisphere. Interestingly, in these transient states the direction of self-propulsion is opposite to the one in the stationary state.
2 Experiment
2.1 Experimental setup
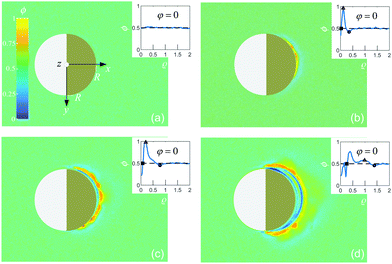
We use spherical colloids (radius R = 11.6 ± 0.4 μm) made of silica and half-coated by thermal evaporation with a layer of gold (thickness 20 nm). The gold caps are chemically functionalized with either 11-mercaptoundecanoic acid dissolved in ethanol or 1-octadecanethiol dissolved in ethanol to make them strongly hydrophilic or hydrophobic, respectively, while the uncapped silica hemispheres remain hydrophilic in all our experiments. The particles are suspended in a binary liquid mixture of propylene glycol n-propyl ether (PnP) and water, the lower critical point of which is Tc = 31.9 °C and 0.4 PnP mass fraction.19 The binary solvent is at its critical composition. At such a concentration, by quickly increasing the temperature from below to above Tc, the bulk of this binary fluid demixes by spinodal decomposition.20 A very small volume (∼μl) of the dilute colloidal suspension is kept within a thin sample cell composed of two parallel glass plates, the separation of which (h ≈ 2R) is fixed by the diameter of the particle, as shown in Fig. 1(a). Under such a strong confinement, the largest particles (R = 12 μm) are totally immobile while the smallest ones (R = 11.2 μm) experience a large hydrodynamic friction. The lateral lengths of the cell along x and y are both 1 cm, i.e., approximately 400 times the particle diameter. The cell is kept at T0 = 28.0 °C, in order to maintain the bulk fluid in the mixed phase. The colloid of interest is chosen in such a way that both capped and uncapped hemispheres are equally visible from below the sample cell, i.e. in the x–y plane, as shown in Fig. 2(a–d). Then, an inverse temperature quench is induced around the colloid at time t = 0 by perpendicularly applying green laser illumination (λ = 532 nm) onto the sample in the z direction, as sketched in Fig. 1(a). Due to the absorption peak of gold around λ = 532 nm and the poor absorption of silica and of the surrounding fluid at that wavelength, the temperature non-isotropically increases around the particle surface. For the applied laser intensity (≈2 μW μm−2), the final temperature of the cap is T0 + ΔT = 35.8 °C, which is 3.9 °C above Tc, thus resulting in a local demixing of the binary fluid around the colloid.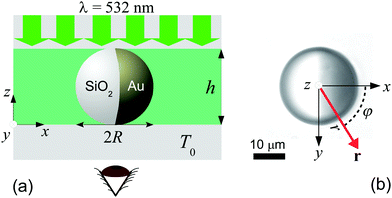 | ||
Fig. 1 (a) Schematic representation of the side-view (x–z plane) of the experimental setup. The coarsening of the binary liquid mixture (green) around the colloid is recorded from below (see the eye) the sample cell at a temperature T0. The sample cell is composed of two glass plates (grey). The thick green arrows indicate the illumination by green laser light with wavelength λ = 532 nm. (b) The camera image of a Janus colloid with the coordinates ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) = (x = r = (x = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, y = r φ, y = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ) is used to describe the coarsening dynamics of the surrounding binary liquid mixture in the x–y plane. The dark area on the right side of the colloid corresponds to the golden cap. The origin of the coordinate system is at the point where the spherical colloid touches the surface of the bottom glass plate. For presentation purposes in (a) the coordinate system is shifted to the left. Fig. 1(b) corresponds to the projection onto the colloid to the plane z = 0 (see (a)). The polar coordinates φ and r of φ) is used to describe the coarsening dynamics of the surrounding binary liquid mixture in the x–y plane. The dark area on the right side of the colloid corresponds to the golden cap. The origin of the coordinate system is at the point where the spherical colloid touches the surface of the bottom glass plate. For presentation purposes in (a) the coordinate system is shifted to the left. Fig. 1(b) corresponds to the projection onto the colloid to the plane z = 0 (see (a)). The polar coordinates φ and r of ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) within the plane z = 0 are indicated in (b). The red vector within the plane z = 0 are indicated in (b). The red vector ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) with | with |![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) | = r is the projection of the three-dimensional vector onto the plane z = 0. | = r is the projection of the three-dimensional vector onto the plane z = 0. | ||
We investigate the coarsening dynamics of the fluid at t ≥ 0 until its final steady-state temperature and concentration profiles are attained. For this purpose, using a collimated beam from a second light source which illuminates the sample cell from above (z ≫ h), in combination with a CCD camera located below (z < 0), we record images (in the x–y plane) of the light which traverses the fluid around a single colloid and arrives at the CCD sensor with a sampling frequency of 150 frames per second and a spatial resolution of 0.080 μm per pixel. The relevant coordinates r = (x = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, y = r
φ, y = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ) to describe the coarsening dynamics of the binary fluid are illustrated in Fig. 1(b), where r is the radial distance from the south pole of the colloid and φ is the azimuthal angle with respect to the x axis pointing from the uncapped to the capped hemisphere. The third coordinate z of the three-dimensional space does not appear here because the imaging lens, which is positioned beneath the bottom of the sample, provides an image integrated over the vertical coordinate z.
φ) to describe the coarsening dynamics of the binary fluid are illustrated in Fig. 1(b), where r is the radial distance from the south pole of the colloid and φ is the azimuthal angle with respect to the x axis pointing from the uncapped to the capped hemisphere. The third coordinate z of the three-dimensional space does not appear here because the imaging lens, which is positioned beneath the bottom of the sample, provides an image integrated over the vertical coordinate z.
Due to the difference between the refractive index of water and PnP within the temperature range of the experiments (30 ± 5 °C), n = 1.331 ± 0.001 and n = 1.410 ± 0.002, respectively, we can perform shadowgraph visualization21–23 of the phases rich in each component during the coarsening process. In the mixed phase at T0 < Tc, the refractive index of the quiescent binary liquid is homogeneous, i.e., n(r,φ,z) = const. for r > R and 0 < z < h, thus leading to a constant light intensity I0 arriving at the camera, i.e., I(r,φ) = I0 for r > R. After the temperature quench, spatial variations of the refractive index due to local disturbances in the concentration field of the fluid give rise to deviations ΔI(r,φ) = I(r,φ) − I0 of the light intensity I(r,φ) from the unperturbed intensity I0:23
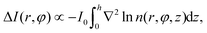 | (1) |
2.2 Experimental results
Depending on the wetting properties of the gold hemisphere, two distinct coarsening patterns can develop. This is demonstrated in Fig. 2 and 3 for a hydrophilic and a hydrophobic cap, respectively, where, after the quench, we show various stages of the image intensity ϕ := const × ΔI (arbitrary units). We assign ϕ = 0.5 to the fully mixed fluid while ϕ > 0.5 and ϕ < 0.5 represent locally PnP-rich and water-rich regions, respectively. We have estimated the resolution δϕ of the image intensity ϕ from its standard deviation for an image of the fully mixed binary liquid mixture. Therefore, any variation of ϕ less than δϕ is pure noise caused by the fluctuations of the intensity on the colormap. The value we found is δϕ = 0.03.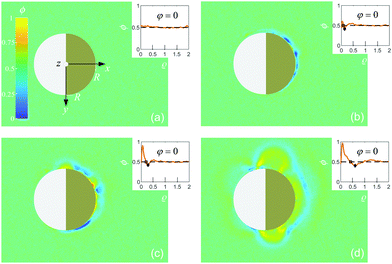 | ||
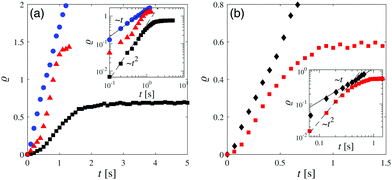
| Fig. 3 Experimental image intensity profile (as in Fig. 2) during the coarsening of the binary liquid mixture around a Janus colloid with a hydrophobic cap at four times after the quench: (a) t = 0, (b) t = 0.13 s, (c) t = 0.27 s, and (d) t = 0.53 s; insets: corresponding radial profiles ϕ(ρ = (R − r)/R) for φ = 0. The symbols represent the location of the transient water-rich layer (black diamond) and the PnP droplet thickness (red square). | ||
We have checked that before and just at the inverse temperature quench, i.e., for t ≤ 0, one has ϕ = 0.5 constant in space and time, as shown in Fig. 2(a) and 3(a). In order to characterize the coarsening dynamics, we determine the radial profile of ϕ along the main particle axis, i.e., for φ = 0, as a function of the distance from the capped particle surface, normalized by the particle radius:  . Certain examples of such radial profiles are plotted in the insets of Fig. 2 and 3.
. Certain examples of such radial profiles are plotted in the insets of Fig. 2 and 3.
3 Simulation models
In order to understand the observed non-equilibrium dynamics of a binary liquid mixture surrounding an immobilized Janus particle after an inverse temperature quench, we adopt two distinct frameworks. The first one assumes purely diffusive dynamics and is the extension of the Cahn–Hilliard–Cook (CHC)-type model, based on the Ginzburg–Landau free energy functional, to non-isothermal systems.15,16 This approach was used to study coarsening of the solvent structure surrounding a homogeneous colloidal particle, which emerges after a temperature quench at the entire colloid surface. However, these earlier studies did not take into account heat diffusion through the particle, and they considered homogeneous particles. The second approach includes hydrodynamics and is based on the “fluid particle dynamics” (FPD) method, which describes dynamical couplings between the particle, the concentration, and the flow field.25–31 This method, extended to a non-isothermal situation, was used to demonstrate that the illumination-induced motion of a Janus particle in binary solvents is not due to diffusiophoresis but rather due to Marangoni-like effects.143.1 Diffusive dynamics
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) =
,t) = ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (T(
(T(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) − Tc)/Tc and of the concentration field ψ(
,t) − Tc)/Tc and of the concentration field ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) around the Janus particle, after the temperature quench of the cap, is described by the modified CHC equation, concertedly with the heat diffusion equation:
,t) around the Janus particle, after the temperature quench of the cap, is described by the modified CHC equation, concertedly with the heat diffusion equation: | (2) |
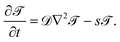 | (3) |
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) < 0 for the mixed phase.
,t) < 0 for the mixed phase. ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 is the reduced inverse quench temperature of the cap. The magnitude of the sink term s in eqn (3) controls the location of the critical isotherm around the colloid. The Gaussian white noise ζ obeys the relation 〈ζ(
1 is the reduced inverse quench temperature of the cap. The magnitude of the sink term s in eqn (3) controls the location of the critical isotherm around the colloid. The Gaussian white noise ζ obeys the relation 〈ζ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t)ζ(
,t)ζ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′,t′)〉 = −2ζ0(
′,t′)〉 = −2ζ0(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )∇2δ(
)∇2δ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) −
− ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′)δ(t − t′); ζ0(
′)δ(t − t′); ζ0(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the strength of the noise. Here,
) is the strength of the noise. Here, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) |
|![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1| = Dth/Dm is the Lewis number,32 which is the ratio of the thermal diffusivity Dth and the mutual diffusivity Dm of the solvent.
1| = Dth/Dm is the Lewis number,32 which is the ratio of the thermal diffusivity Dth and the mutual diffusivity Dm of the solvent.
We employ a no-concentration-flux boundary condition (b.c.) on the surface of the colloid. The selective surface adsorption on the colloid surface gives rise to the static so-called Robin b.c.33,34
(ê![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ·∇ψ( ·∇ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) + αsψ( ) + αsψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ))| ))|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) = hs = hs | (4) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) refers to the surface of the colloid, and ê
refers to the surface of the colloid, and ê![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) is the unit vector perpendicular to
is the unit vector perpendicular to ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) pointing into it. We assume that the surface enrichment parameters are αs,c (αs,l) and that the symmetry breaking surface fields are hs,c (hs,l) on the cap (on the left hemisphere) of the colloid. All surface parameters are made dimensionless (see Appendix A). The Janus colloid is kept confined between two identical parallel walls. We apply the surface b.c. (eqn (4)) to these walls with the surface parameters αs,w and hs,w. The cap of the colloid is always maintained at the inverse quench temperature
pointing into it. We assume that the surface enrichment parameters are αs,c (αs,l) and that the symmetry breaking surface fields are hs,c (hs,l) on the cap (on the left hemisphere) of the colloid. All surface parameters are made dimensionless (see Appendix A). The Janus colloid is kept confined between two identical parallel walls. We apply the surface b.c. (eqn (4)) to these walls with the surface parameters αs,w and hs,w. The cap of the colloid is always maintained at the inverse quench temperature ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1:
1:![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )| )|![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) c = c = ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1, 1, | (5) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) c stands for the surface of the cap. In order to consider the heat flow across the colloid (from the cap towards the left surface), eqn (3) without the sink term is solved inside the colloid for
c stands for the surface of the cap. In order to consider the heat flow across the colloid (from the cap towards the left surface), eqn (3) without the sink term is solved inside the colloid for ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) =
= ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) c, which differs from that in the solvent. A smooth variation of the temperature across the surface of the left hemisphere is ensured by adopting the following b.c.:
c, which differs from that in the solvent. A smooth variation of the temperature across the surface of the left hemisphere is ensured by adopting the following b.c.:∇![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) | |![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) l,out = ∇ l,out = ∇![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) | |![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) l,in. l,in. | (6) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) l,out and
l,out and ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) l,in refer to the outside and the inside of the surface of the left hemisphere, respectively.
l,in refer to the outside and the inside of the surface of the left hemisphere, respectively.
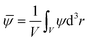 | (7) |
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) = 0 is conserved as function of time. V is the volume available for a binary solvent. The initial temperature throughout the system is set below Tc in a system with a lower critical point:
= 0 is conserved as function of time. V is the volume available for a binary solvent. The initial temperature throughout the system is set below Tc in a system with a lower critical point: ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) i(
i(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = −1, which together with the value of the amplitude
) = −1, which together with the value of the amplitude ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ≃ 46.3 (see Appendix A) implies Ti ≃ 0.98Tc. At t = 0, the cap is quenched to a temperature
≃ 46.3 (see Appendix A) implies Ti ≃ 0.98Tc. At t = 0, the cap is quenched to a temperature ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 and the subsequent dynamics is studied by simultaneously solving the heat diffusion equation for the solvent and for the colloid (as mentioned above). The experimental inverse quench temperature 35.8 °C translates into the reduced temperature
1 and the subsequent dynamics is studied by simultaneously solving the heat diffusion equation for the solvent and for the colloid (as mentioned above). The experimental inverse quench temperature 35.8 °C translates into the reduced temperature ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 ≃ 6 (which implies T1 ≃ 1.13Tc) for our simulation model. For numerical purposes, we consider αs = 0.5 and hs = −0.2 both on the top and the bottom confining surfaces and αs,l = αs,c = 0.5 on both sides of the Janus colloid. We set hs,l = −0.2 on the left side and hs,c = −2 on the capped side of the hydrophilic–hydrophilic colloid. For the hydrophilic–hydrophobic particle we take hs,l = −0.2 and hs,c = 2. We set C = 4, s = 0.001,
1 ≃ 6 (which implies T1 ≃ 1.13Tc) for our simulation model. For numerical purposes, we consider αs = 0.5 and hs = −0.2 both on the top and the bottom confining surfaces and αs,l = αs,c = 0.5 on both sides of the Janus colloid. We set hs,l = −0.2 on the left side and hs,c = −2 on the capped side of the hydrophilic–hydrophilic colloid. For the hydrophilic–hydrophobic particle we take hs,l = −0.2 and hs,c = 2. We set C = 4, s = 0.001, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) = 100, and
= 100, and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) c = 3
c = 3![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) . We assume that the typical molecular size v0 (see eqn (17)) is equal to the amplitude ξ0− = 0.1 nm of the bulk correlation length (above Tc for the lower critical point). The CHC theory units are then r0 = 0.35 nm for a length and t0 = 10−7 s for time (see Appendix A). The noise amplitude ζ0 is taken to be uniform in space and equal to 10−4. Unless mentioned otherwise, Lx = Ly = 120, Lz = 26, and R = 10 in units of r0. Finite-element representation of the spatial derivatives combined with the Euler time integrator is used to solve the corresponding equations with the time step δt = 0.001 of integration (in units of t0). In order to implement the b.c. on a spherical colloid a trilinear interpolation method36 is used.
. We assume that the typical molecular size v0 (see eqn (17)) is equal to the amplitude ξ0− = 0.1 nm of the bulk correlation length (above Tc for the lower critical point). The CHC theory units are then r0 = 0.35 nm for a length and t0 = 10−7 s for time (see Appendix A). The noise amplitude ζ0 is taken to be uniform in space and equal to 10−4. Unless mentioned otherwise, Lx = Ly = 120, Lz = 26, and R = 10 in units of r0. Finite-element representation of the spatial derivatives combined with the Euler time integrator is used to solve the corresponding equations with the time step δt = 0.001 of integration (in units of t0). In order to implement the b.c. on a spherical colloid a trilinear interpolation method36 is used.
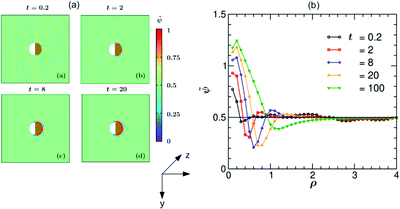
In Fig. 5 we present simulation results for the dynamics of the local structure formation around a hydrophilic–hydrophilic colloid (hs,l = −0.2, hs,c = −2). As in the experiment, the cap is more hydrophilic (hs,c < hs,l). The rescaled concentration field ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = (ψ(
,t) = (ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) + 1)/2 shown in Fig. 5(a) is constructed such that ψ > 0.5 corresponds to the PnP-rich phase and ψ < 0.5 to the water-rich phase (corresponding to hs < 0), as the experimental data do. At very early times (t = 0.2) surface layers form near the cap. With increasing time they propagate into the bulk and become thicker. It is interesting to note that at later times (t = 8) the surface layers enter also the region near the uncapped, weakly hydrophilic side of the Janus colloid. This is due to the heat flow across the colloid. At late times, the Janus particle becomes covered by a water-rich droplet, which is much thicker on the capped side of the colloid. The condensation of asymmetric droplets around the Janus colloid was found also for temperature quenches which do not cross the binodal.15 We note that for such quenches this phenomenon is due to the combination of the Soret and surface effects.15,16 Thus it involves a different mechanism than the one occurring due to the deep quenches considered here. In Fig. 5(b) the corresponding rescaled OP profile
,t) + 1)/2 shown in Fig. 5(a) is constructed such that ψ > 0.5 corresponds to the PnP-rich phase and ψ < 0.5 to the water-rich phase (corresponding to hs < 0), as the experimental data do. At very early times (t = 0.2) surface layers form near the cap. With increasing time they propagate into the bulk and become thicker. It is interesting to note that at later times (t = 8) the surface layers enter also the region near the uncapped, weakly hydrophilic side of the Janus colloid. This is due to the heat flow across the colloid. At late times, the Janus particle becomes covered by a water-rich droplet, which is much thicker on the capped side of the colloid. The condensation of asymmetric droplets around the Janus colloid was found also for temperature quenches which do not cross the binodal.15 We note that for such quenches this phenomenon is due to the combination of the Soret and surface effects.15,16 Thus it involves a different mechanism than the one occurring due to the deep quenches considered here. In Fig. 5(b) the corresponding rescaled OP profile ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) along the x-axis is plotted as a function of the radial distance ρ = (r − R)/R from the colloid surface. On top of the depth averaging, these data are averaged over 10 independent initial configurations and are presented at five times. Additional information about the formation of the layers can be gained by inspecting the vector snapshots of the OP flux which is defined as the spatial gradient of ψ(
,t) along the x-axis is plotted as a function of the radial distance ρ = (r − R)/R from the colloid surface. On top of the depth averaging, these data are averaged over 10 independent initial configurations and are presented at five times. Additional information about the formation of the layers can be gained by inspecting the vector snapshots of the OP flux which is defined as the spatial gradient of ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) normalized to one (see Fig. S1 in the ESI†).
,t) normalized to one (see Fig. S1 in the ESI†).
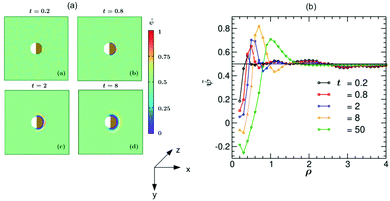 | ||
Fig. 5 (a) Theoretical evolution snapshots of the rescaled concentration field ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = (ψ( ,t) = (ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) + 1)/2 during the coarsening of a binary solvent under a time-dependent temperature gradient around a hydrophilic–hydrophilic Janus colloid confined between two parallel slabs kept at z = 0 and Lz. In the color code, ,t) + 1)/2 during the coarsening of a binary solvent under a time-dependent temperature gradient around a hydrophilic–hydrophilic Janus colloid confined between two parallel slabs kept at z = 0 and Lz. In the color code, ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) > 0.5 and <0.5 refer to the PnP-rich and the water-rich phase, respectively. Far away from the colloid one can see bicontinuous coarsening patterns characteristic of spinodal decomposition. Surface layers form due to the surface-directed spinodal-decomposition mechanism. With increasing time, these layers broaden and increase in number. The snapshots correspond to the bottom view (Fig. 1(b)) and are depth-averaged (see the main text). Time is given in units of t0 = 10−6 s. The side bar provides the color code for the values of > 0.5 and <0.5 refer to the PnP-rich and the water-rich phase, respectively. Far away from the colloid one can see bicontinuous coarsening patterns characteristic of spinodal decomposition. Surface layers form due to the surface-directed spinodal-decomposition mechanism. With increasing time, these layers broaden and increase in number. The snapshots correspond to the bottom view (Fig. 1(b)) and are depth-averaged (see the main text). Time is given in units of t0 = 10−6 s. The side bar provides the color code for the values of ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) . The brownish color indicates that the right hemisphere is capped. We do not specify wettability of the cap via a color code. (b) Rescaled theoretical OP profiles . The brownish color indicates that the right hemisphere is capped. We do not specify wettability of the cap via a color code. (b) Rescaled theoretical OP profiles ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) ( (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) after depth-averaging and averaged over 10 initial conditions along the x-axis around a hydrophilic–hydrophilic Janus colloid as a function of the radial distance ρ = (r − R)/R from the surface of the colloid. Time is given in units of t0 = 10−6 s. ,t) after depth-averaging and averaged over 10 initial conditions along the x-axis around a hydrophilic–hydrophilic Janus colloid as a function of the radial distance ρ = (r − R)/R from the surface of the colloid. Time is given in units of t0 = 10−6 s. | ||
Next, we present results for a hydrophilic–hydrophobic colloid (hs,l = −0.2, hs,c = 2). All other system parameters are the same as in the case of a hydrophilic–hydrophilic colloid. Using the same color code as in Fig. 5(a), in Fig. 6(a) we present depth-averaged, evolving snapshots. The capped (right) and uncapped (left) hemispheres of the Janus colloid favor the PnP-rich and water-rich phases, respectively. The formation of bicontinuous patterns, as they are characteristic of spinodal decomposition,37 and of surface layers proceeds in a way similar to what is shown in Fig. 5(a). This is readily visible in Fig. 6(b) where the corresponding rescaled OP profile ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) (depth-averaged and averaged over 10 independent initial configurations) as a function of ρ is shown. In contrast to the case of the hydrophilic–hydrophilic colloid shown in Fig. 5(a), for the hydrophilic–hydrophobic colloid an asymmetric droplet, condensed at the Janus particle, consists of two parts with phases of opposite character: a water-rich part of a droplet, which is thin and covers only partly the hydrophilic hemisphere, and a PnP-rich part of a droplet, which is thick and extends beyond the capped hemisphere of the Janus particle (see Fig. 6(a)). The relative size of these parts depends on the surface fields, the initial temperature of the system, and the quench temperature. The temporal evolution of the OP flux around a hydrophilic–hydrophobic colloid is shown in Fig. S2 in ESI.†
,t) (depth-averaged and averaged over 10 independent initial configurations) as a function of ρ is shown. In contrast to the case of the hydrophilic–hydrophilic colloid shown in Fig. 5(a), for the hydrophilic–hydrophobic colloid an asymmetric droplet, condensed at the Janus particle, consists of two parts with phases of opposite character: a water-rich part of a droplet, which is thin and covers only partly the hydrophilic hemisphere, and a PnP-rich part of a droplet, which is thick and extends beyond the capped hemisphere of the Janus particle (see Fig. 6(a)). The relative size of these parts depends on the surface fields, the initial temperature of the system, and the quench temperature. The temporal evolution of the OP flux around a hydrophilic–hydrophobic colloid is shown in Fig. S2 in ESI.†
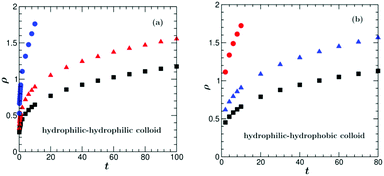
From the OP profiles for a hydrophilic–hydrophilic colloid ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) (depth-averaged and averaged over 10 initial configurations) we determined the time dependence of the position of the transient water-rich layer by inferring it from the second minimum of ψ(ρ), of the position of the transient PnP-rich layer by inferring it from the first maximum of ψ(ρ), and of the thickness of the water-rich droplet around the Janus colloid by inferring it from the zero crossing of ψ(ρ). Similarly, for the hydrophilic–hydrophobic colloid, the time dependence of the position of the transient PnP-rich layer is determined by inferring it from the second maximum of ψ(ρ), of the position of the transient water-rich layer is determined by inferring it from the first minimum of ψ(ρ), and of the thickness of the PnP-rich droplet around the Janus colloid is determined by inferring it from the zero crossing of ψ(ρ). The corresponding results are plotted in Fig. 7.
,t) (depth-averaged and averaged over 10 initial configurations) we determined the time dependence of the position of the transient water-rich layer by inferring it from the second minimum of ψ(ρ), of the position of the transient PnP-rich layer by inferring it from the first maximum of ψ(ρ), and of the thickness of the water-rich droplet around the Janus colloid by inferring it from the zero crossing of ψ(ρ). Similarly, for the hydrophilic–hydrophobic colloid, the time dependence of the position of the transient PnP-rich layer is determined by inferring it from the second maximum of ψ(ρ), of the position of the transient water-rich layer is determined by inferring it from the first minimum of ψ(ρ), and of the thickness of the PnP-rich droplet around the Janus colloid is determined by inferring it from the zero crossing of ψ(ρ). The corresponding results are plotted in Fig. 7.
In the case of coarsening around a hydrophobic cap, there are more discrepancies between the experimental and the simulation results. In the experiment, the time evolution of the transient PnP-rich transient layer could not be measured because, although present, this layer was hardly visible and its position was difficult to infer from the second maximum of the radial profile of ψ. In the simulations this layer moves with a constant speed of ca. 11.5 μm s−1 for t ≳ 10. The measurements show that the transient water-rich layer moves with a constant speed of ca. 15 μm s−1 for t ≳ 10 (black squares in Fig. 4(b)), whereas in the simulations the motion of the transient water-rich layer is nonlinear (blue triangles in Fig. 7(b)). The thickness of the PnP-rich droplet (red squares in Fig. 7(b)) does not follow the power law ∼t2 found in the experiment at early times (inset of Fig. 4(b)). In the experiment, at t = 0.53 the layer structure is destroyed and one observes a flower-like structure around the hot cap of the colloid due to hydrodynamic effects, which will be studied in the next section.
3.2 Hydrodynamic model
Within this approach, the Janus particle of radius R is represented by a smooth shape function as
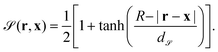 | (8) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) represents the width of the smooth interface such that, in the limit of d
represents the width of the smooth interface such that, in the limit of d![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) → 0,
→ 0, ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) is unity and zero in the interior and exterior of the particle, respectively. We also define the particle orientation function
is unity and zero in the interior and exterior of the particle, respectively. We also define the particle orientation function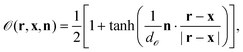 | (9) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) is a sharpness parameter of the particle orientation. Roughly, one has
is a sharpness parameter of the particle orientation. Roughly, one has ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) = 1 if n·(r − x)/|r − x| > d
= 1 if n·(r − x)/|r − x| > d![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) , while
, while ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) = 0 if n·(r − x)/|r − x| < −d
= 0 if n·(r − x)/|r − x| < −d![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) . In this study, we set d
. In this study, we set d![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) = 0.033 in order to assure that the surface properties change smoothly within a few lattice constants. In the limit of d
= 0.033 in order to assure that the surface properties change smoothly within a few lattice constants. In the limit of d![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) → 0, one has
→ 0, one has ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) = 1 around the cap (n·(r − x) > 0), while
= 1 around the cap (n·(r − x) > 0), while ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) = 0 otherwise.
= 0 otherwise.
In order to describe a binary liquid mixture in an inhomogeneous temperature field, we employ the dynamic van der Waals theory39–44 extended to incompressible binary liquid mixtures. The concentration field of the binary liquid mixture ψ(r) is coupled to the surface of the Janus particle with the energy E given by
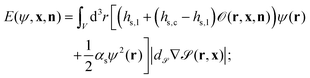 | (10) |
We assume that the time development of the concentration field ψ(r,t) is governed by
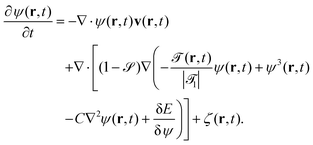 | (11) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) + αsψ(r)]|d
+ αsψ(r)]|d![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ∇r
∇r![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) | represents the wetting interaction on the particle surface. The diffusion flux inside the particle vanishes due to the term (1 −
| represents the wetting interaction on the particle surface. The diffusion flux inside the particle vanishes due to the term (1 − ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ); ζ(r,t) is the Gaussian white noise introduced earlier (see Section 3.1.1).
); ζ(r,t) is the Gaussian white noise introduced earlier (see Section 3.1.1).
The time development of the temperature field is given by
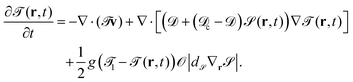 | (12) |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) c and
c and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) are the thermal diffusion constants inside the particle and of the binary solvent, respectively. The last term on the right hand side of eqn (11) is introduced in order to fix the temperature on the cap of the particle. The cap is represented by
are the thermal diffusion constants inside the particle and of the binary solvent, respectively. The last term on the right hand side of eqn (11) is introduced in order to fix the temperature on the cap of the particle. The cap is represented by ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) |d
|d![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) ∇
∇![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) |, and g is a parameter related to the heating power.||
|, and g is a parameter related to the heating power.||
We consider the hydrodynamic flow v(r) in the limit of low Reynolds numbers, in which the effect of inertia is negligible. The flow field v(r) is obtained by solving the following differential equations:
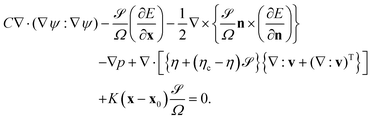 | (13) |
The particle position and its orientation are transported by the hydrodynamic flow v and its vorticity according to
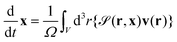 | (14) |
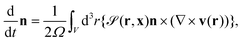 | (15) |
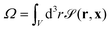 is the particle volume.
is the particle volume.
![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) 3 are the simple cubic lattice coordinates in lattice space, whereas the position x of the center of the particle is in the off-lattice space, i.e., the components of x are floating point numbers. The time increment is δt = 0.005. The system size is 240 × 240 × 52. Periodic boundary conditions are employed in the x and y directions. On the other hand, we employ non-slip boundary conditions for the flow field on the bottom (z = 1) and top (z = 52) planes. The concentration fluxes vanish on these walls, too. The temperature at these walls is fixed to
3 are the simple cubic lattice coordinates in lattice space, whereas the position x of the center of the particle is in the off-lattice space, i.e., the components of x are floating point numbers. The time increment is δt = 0.005. The system size is 240 × 240 × 52. Periodic boundary conditions are employed in the x and y directions. On the other hand, we employ non-slip boundary conditions for the flow field on the bottom (z = 1) and top (z = 52) planes. The concentration fluxes vanish on these walls, too. The temperature at these walls is fixed to ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) i = −1 and after the quench that on the cap is controlled to be
i = −1 and after the quench that on the cap is controlled to be ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 = 6 with g = 10. The thermal diffusion constants are
1 = 6 with g = 10. The thermal diffusion constants are ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) = 100 and
= 100 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) c = 3
c = 3![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) . These walls act as a heat reservoir. The particle radius is R = 20. Initially, the particle is placed at the center of the cell and is oriented in the (1,0,0)-direction. In the present study, the particle position and orientation are almost fixed at their initial values owing to the harmonic potential K(x − x0)2/2. The parameters in the hydrodynamic eqn (13) are taken to be C = 4, K = 100, η = 0.5, and ηs = 25. For the length unit d
. These walls act as a heat reservoir. The particle radius is R = 20. Initially, the particle is placed at the center of the cell and is oriented in the (1,0,0)-direction. In the present study, the particle position and orientation are almost fixed at their initial values owing to the harmonic potential K(x − x0)2/2. The parameters in the hydrodynamic eqn (13) are taken to be C = 4, K = 100, η = 0.5, and ηs = 25. For the length unit d![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) (eqn (9)) we take the typical value 2 nm. The time unit is given by t0 = d
(eqn (9)) we take the typical value 2 nm. The time unit is given by t0 = d![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) 2/Dm. Assuming Dm ≃ 1.1 × 10−10 m2 s−1 gives t0 ≃ 3.6 × 10−8 s. The amplitude ζ0 of the noise is the same as in the purely diffusive model, i.e., 10−4.
2/Dm. Assuming Dm ≃ 1.1 × 10−10 m2 s−1 gives t0 ≃ 3.6 × 10−8 s. The amplitude ζ0 of the noise is the same as in the purely diffusive model, i.e., 10−4.
In order to mimic an experimental system, we consider two kinds of Janus particles with different surface fields. One particle has a strongly hydrophilic cap and a weakly hydrophilic tail, for which we set hs,c = −2.0 and hs,l = −0.2. The other particle has a strongly hydrophobic cap and a weakly hydrophilic tail with hs,c = 2.0 and hs,l = −0.2. The top and bottom walls of the cell are weakly hydrophilic, for which we set hwall = −0.2. The surface enrichment parameter is αs = 0.5. We note that the choice of the surface interaction parameter is the same as in the diffusive model.
For the initial configuration we assume that the concentration field is ψ = 0 throughout and that the temperature is T = −1 everywhere. The flow is absent. The particle is placed at the center of the cell and it is oriented along the x-axis. The particle position and orientation are almost fixed during the simulations.
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 0) for distances up to about x/R = 2. For larger distances it attains the background temperature
= 0) for distances up to about x/R = 2. For larger distances it attains the background temperature ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) i = −1. On the uncapped side, the temperature is higher than the critical temperature up to about x/R = −1. We find that the temperature field is almost independent of the wettability parameters hs,c and hs,l.
i = −1. On the uncapped side, the temperature is higher than the critical temperature up to about x/R = −1. We find that the temperature field is almost independent of the wettability parameters hs,c and hs,l.
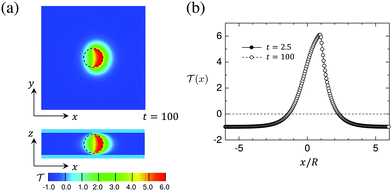 | ||
Fig. 8 (a) Snapshot of the temperature field around a hydrophilic–hydrophilic Janus particle in the x–y and x–z planes passing through the particle center of the system. The temperature at the bottom and the top walls of the cell is fixed at ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) i = −1 and the temperature of the surface of the capped hemisphere of the particle is quenched to i = −1 and the temperature of the surface of the capped hemisphere of the particle is quenched to ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 = 6. The average concentration (see eqn (7)) is 1 = 6. The average concentration (see eqn (7)) is ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) = 0 and conserved as function of time. The black circle represents the particle, which is oriented to the right, i.e., the heated particle cap is oriented towards n = (1, 0, 0). (b) The profiles of the temperature field = 0 and conserved as function of time. The black circle represents the particle, which is oriented to the right, i.e., the heated particle cap is oriented towards n = (1, 0, 0). (b) The profiles of the temperature field ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (x) at t = 2.5 and t = 100 de facto coincide. (x) at t = 2.5 and t = 100 de facto coincide. ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (x) = 0 corresponds to the (lower) critical temperature Tc. Time is given in units of t0 = 3.6 × 10−8 s. (x) = 0 corresponds to the (lower) critical temperature Tc. Time is given in units of t0 = 3.6 × 10−8 s. | ||
The time evolution of the concentration field coupled to the solvent flow is depicted in Fig. 9(a and b) for the hydrophilic–hydrophilic and hydrophilic–hydrophobic particle, respectively. The snapshots are taken at the same cross-sectional x–y plane as the temperature field shown in Fig. 9(a). Only at very early times after the thermal quench one can see the formation of layers which propagate from the surface of the Janus particle into the bulk. Later, the evolution of the coarsening patterns near the capped side of the colloid becomes more complex (see the Movies S1 and S2 in the ESI†). In the course of time, fluctuations of the concentration field appear mostly at the outermost part of the phase-separating region but also close to the surface of the colloid along the border line between capped and uncapped hemispheres. The pattern emerging at t = 100 is already quite complex such as the nucleation of a small droplet further away from the surface. Remarkably, at this late stage of the time evolution, the concentration pattern near the left side of the colloid is determined entirely by the capped side. Fig. 10 presents this pattern in the x–z plane passing through the center of a colloid. One can clearly see the phase separation of the binary solvent in the vicinity of the colloid. In the case of the hydrophilic–hydrophilic colloid, a region rich in the phase with ψ < 0 (water-rich, red) has a shape of a droplet which surrounds the uncapped part of the colloid. Near the surface of the capped hemisphere, both phases are present. Further away from it, only the phase with ψ > 0 (PnP-rich, blue) prevails. The coarsening pattern around the hydrophilic–hydrophobic colloid is similar, only with the phase with ψ > 0 being replaced by the phase with ψ < 0. This demonstrates that within the hydrodynamic approach used here the wettability of the uncapped hemisphere is not important, provided the corresponding surface fields are weak. In the present examples the wettabilities of the capped hemispheres of both types of Janus particles are opposite to each other, but their strengths are the same. In this case, the figures showing the coarsening patterns look the same but with a different coloring.
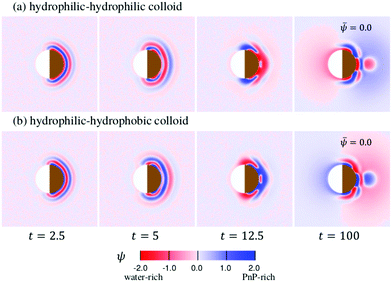 | ||
Fig. 9 The pattern evolution of the concentration field ψ of a mixture with ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) = 0 (see eqn (7)) outside a Janus particle and conserved as function of time, which has (a) a strongly hydrophilic cap (hs,c = −2.0) and a weakly hydrophilic tail (hs,l = −0.2); (b) a strongly hydrophobic cap (hs,c = 2.0) and a weakly hydrophilic tail (hs,l = −0.2). The brownish color indicates that the right hemisphere is capped. We do not specify wettability of the cap via a color code. = 0 (see eqn (7)) outside a Janus particle and conserved as function of time, which has (a) a strongly hydrophilic cap (hs,c = −2.0) and a weakly hydrophilic tail (hs,l = −0.2); (b) a strongly hydrophobic cap (hs,c = 2.0) and a weakly hydrophilic tail (hs,l = −0.2). The brownish color indicates that the right hemisphere is capped. We do not specify wettability of the cap via a color code. | ||
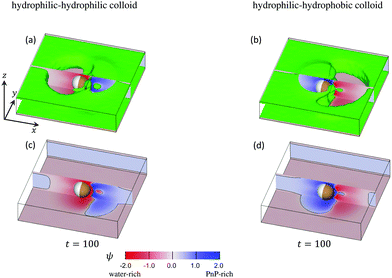 | ||
Fig. 10 Three-dimensional snapshots of ψ reveal the complexity of the coarsening patterns around a Janus particle at t = 100 after illumination. The mixture is at its critical concentration, i.e., ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) = 0. The panels (a) and (b) correspond to a strongly hydrophilic cap (hs,c = −2.0) and a weakly hydrophilic tail (hs,l = −0.2) whereas the panels (b) and (d) correspond to a strongly hydrophobic cap (hs,c = 2.0) and a weakly hydrophilic tail (hs,l = −0.2). The cross sections of the concentration field at the x–z plane passing through the particle center are shown in red-blue color, in line with Fig. 11 for t = 100. In front of and behind this x–z plane, in (a) and (b) we show (in green) the isosurfaces ψ = 0. They consist of a pair of horizontal, flat sheets (one at the top and one at the bottom) connected by curved vertical surfaces. The sheets are slightly separated from the weakly hydrophilic confining walls at the bottom and at the top (with the top wall not shown) by a thin film rich in water (marked reddishly). The connecting surfaces comprise the external borders of two nonspherical blobs: one rich in water (reddish areas to the left (right)) of the Janus colloid in (a) (in (b)) and the second (smaller) rich in PnP (blueish areas to the right (left)) of the colloid in (a) (in (b)). The wavy interface ψ = 0 between these two blobs lies slightly to the right of the capped hemisphere. Close to the hot capped hemisphere (marked in brown) one can see strong fluctuation of the concentration field, in particular, a droplet (in green) of the water-rich phase in (a) and the PnP-rich phase in (b). In the panels (c) and (d) the isosurfaces ψ = 0 are removed and one can see the concentration field at the bottom wall. The interface positions ψ = 0 on the bottom and on the x–z plane are indicated by black curves. Periodic boundary conditions are applied along the x-axis. = 0. The panels (a) and (b) correspond to a strongly hydrophilic cap (hs,c = −2.0) and a weakly hydrophilic tail (hs,l = −0.2) whereas the panels (b) and (d) correspond to a strongly hydrophobic cap (hs,c = 2.0) and a weakly hydrophilic tail (hs,l = −0.2). The cross sections of the concentration field at the x–z plane passing through the particle center are shown in red-blue color, in line with Fig. 11 for t = 100. In front of and behind this x–z plane, in (a) and (b) we show (in green) the isosurfaces ψ = 0. They consist of a pair of horizontal, flat sheets (one at the top and one at the bottom) connected by curved vertical surfaces. The sheets are slightly separated from the weakly hydrophilic confining walls at the bottom and at the top (with the top wall not shown) by a thin film rich in water (marked reddishly). The connecting surfaces comprise the external borders of two nonspherical blobs: one rich in water (reddish areas to the left (right)) of the Janus colloid in (a) (in (b)) and the second (smaller) rich in PnP (blueish areas to the right (left)) of the colloid in (a) (in (b)). The wavy interface ψ = 0 between these two blobs lies slightly to the right of the capped hemisphere. Close to the hot capped hemisphere (marked in brown) one can see strong fluctuation of the concentration field, in particular, a droplet (in green) of the water-rich phase in (a) and the PnP-rich phase in (b). In the panels (c) and (d) the isosurfaces ψ = 0 are removed and one can see the concentration field at the bottom wall. The interface positions ψ = 0 on the bottom and on the x–z plane are indicated by black curves. Periodic boundary conditions are applied along the x-axis. | ||
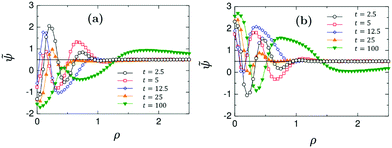
Profiles of the rescaled concentration field ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = (ψ(
,t) = (ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) + 1)/2 along the x-axis as a function of the radial distance ρ = (r − R)/R from the surface of Janus particles, are shown in Fig. 11(a and b). They correspond to the snapshots shown in Fig. 9(a and b), respectively. Only at early times (t = 2.5) the profiles look similar to those obtained from the diffusive model as shown in Fig. 7. For later times, strong concentration fluctuations deform the radial structure of the profiles. The time evolution of the concentration profiles near the left side of the Janus colloids reveals the role of the capped hot side (see Fig. S3 and S4 in ESI†). The left side is always hydrophilic and at early times one can see a very small water-rich layer near it. If the cap is hydrophilic, this layer becomes much thicker at late times. If the cap is hydrophobic, at later times this layer is smeared out by a PnP-rich concentration wave traveling from the right side of the Janus colloid.
,t) + 1)/2 along the x-axis as a function of the radial distance ρ = (r − R)/R from the surface of Janus particles, are shown in Fig. 11(a and b). They correspond to the snapshots shown in Fig. 9(a and b), respectively. Only at early times (t = 2.5) the profiles look similar to those obtained from the diffusive model as shown in Fig. 7. For later times, strong concentration fluctuations deform the radial structure of the profiles. The time evolution of the concentration profiles near the left side of the Janus colloids reveals the role of the capped hot side (see Fig. S3 and S4 in ESI†). The left side is always hydrophilic and at early times one can see a very small water-rich layer near it. If the cap is hydrophilic, this layer becomes much thicker at late times. If the cap is hydrophobic, at later times this layer is smeared out by a PnP-rich concentration wave traveling from the right side of the Janus colloid.
The above results raise the issue concerning the origin of the strong concentration fluctuations observed within the hydrodynamic approach. It is well established that thermal fluctuations in liquids in the presence of stationary temperature gradients are anomalously large and very long-ranged.45 They occur as a result of a coupling between temperature and velocity fluctuations. It is to be expected that in liquid mixtures a temperature gradient induces long-ranged concentration fluctuations via the Soret effect. Moreover, these nonequilibrium fluctuations have to be coupled to the critical concentration fluctuations. Indeed, we observe that the concentration fluctuations appear mostly in that region where the temperature is critical or close to its critical value.
4 Conclusions
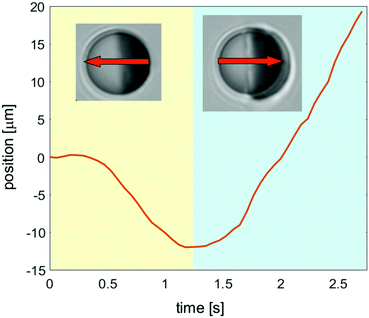
The important conclusion from our study is that at early times after applying laser illumination to the sample, the coarsening dynamics around Janus colloids is dominated by diffusion. It is characterized by the formation of transient layers propagating with constant speed from the surface of the Janus particle into the bulk. In the case of an immobilized particle, after a transient time the coarsening process is dominated by hydrodynamic effects with the patterns continually varying in time.These spatio-temporal patterns are different if the particle size is small enough so that it can move between the two parallel confining walls (h > 2R, Fig. 1(a)). The transient layering precedes the formation of a droplet, which characterizes the stationary state of the fluid surrounding a moving colloid. In Fig. 12, we show our data for the position of the center of a mobile colloid during the transient demixing (yellow area) and in the steady state (blue area). The arrows indicate the corresponding directions of motion. For these measurements we have used 2,6-lutidine–water as a binary solvent, and the particle has a hydrophobic golden cap on the right hemisphere. The particle can move through the fluid because it is slightly smaller in diameter 2R than the thickness h of the sample cell. The laser illumination is turned on at the beginning of the video (see Movie S3 in ESI†). During the first 0.4 seconds, the colloid remains at rest, but thereafter it starts to move with rather constant speed in the direction opposite to the golden cap (right hemisphere), while the transient layers develop. Finally, after 1.2 seconds it reverses its direction of motion, once the droplet has almost reached its final size. The speed during the initial transient is about 8 microns per second, so that the effect of the reversal of the direction is rather large.
Because the colloid remains at rest during the first 0.4 seconds, we can employ our simulation models developed for fixed particle in order to calculate the body force due to the concentration flux acting on a fixed colloid immediately after an inverse temperature quench. We have used a purely diffusive approach, which we found to be an appropriate description of the early time dynamics. The force is calculated as
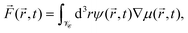 | (16) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = ∇(δ
,t) = ∇(δ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) [ψ]/δψ(
[ψ]/δψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t)) follows from the free energy functional of the CHC theory (see Appendix A).
,t)) follows from the free energy functional of the CHC theory (see Appendix A). ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif)
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) refers to the volume of the colloid. In Fig. 13, we present numerical results for the three Cartesian components of
refers to the volume of the colloid. In Fig. 13, we present numerical results for the three Cartesian components of ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) acting on a hydrophilic–hydrophobic Janus colloid after an inverse temperature quench was applied at t = 0. The results correspond to Lx = Ly = Lz = 100, R = 5,
,t) acting on a hydrophilic–hydrophobic Janus colloid after an inverse temperature quench was applied at t = 0. The results correspond to Lx = Ly = Lz = 100, R = 5, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) i = −1,
i = −1, ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 = 8, s = 0.001,
1 = 8, s = 0.001, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) = 100,
= 100, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) c = 300, αs,l = αs,c = 0.5, hs,l = 2, and hs,c = −2. One can see that after some transient the magnitude of the x-component of the force increases, and that beyond a certain time it starts to decrease. The force vanishes at about t ≃ 100 when the steady state is achieved, i.e., after the local demixing has been completed, and a droplet, rich in the species preferred by the hot hemisphere of the Janus particle, has been formed. The strength of the x-component is much bigger than the strengths of the y- and z-components. This is the reason for the onset of the particle motion in x-direction. Once the colloid is set into motion, our simulation model does no longer apply. The constant speed, observed between 0.5 and 1.0 seconds (Fig. 12), indicates that the total force acting on the particle is zero, although the coarsening process has not yet attained its steady state. It is plausible that at these early times the body force
c = 300, αs,l = αs,c = 0.5, hs,l = 2, and hs,c = −2. One can see that after some transient the magnitude of the x-component of the force increases, and that beyond a certain time it starts to decrease. The force vanishes at about t ≃ 100 when the steady state is achieved, i.e., after the local demixing has been completed, and a droplet, rich in the species preferred by the hot hemisphere of the Janus particle, has been formed. The strength of the x-component is much bigger than the strengths of the y- and z-components. This is the reason for the onset of the particle motion in x-direction. Once the colloid is set into motion, our simulation model does no longer apply. The constant speed, observed between 0.5 and 1.0 seconds (Fig. 12), indicates that the total force acting on the particle is zero, although the coarsening process has not yet attained its steady state. It is plausible that at these early times the body force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) is vanishingly small and concurrently, hydrodynamic forces are still absent. The initial motion of a colloid is stopped by fluid resistance. But in the meantime hydrodynamic effects become relevant for the coarsening process, giving rise to a propulsion force which changes the direction of motion of the colloid.
,t) is vanishingly small and concurrently, hydrodynamic forces are still absent. The initial motion of a colloid is stopped by fluid resistance. But in the meantime hydrodynamic effects become relevant for the coarsening process, giving rise to a propulsion force which changes the direction of motion of the colloid.
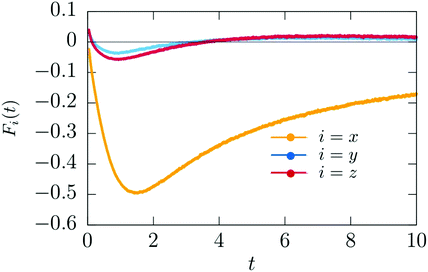 | ||
Fig. 13 Time dependence of the x, y, and z components of the theoretical body force ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (t) (eqn (16)) acting on the Janus particle after the temperature quench. Time is given in units of t0 = 10−6 s. (t) (eqn (16)) acting on the Janus particle after the temperature quench. Time is given in units of t0 = 10−6 s. | ||
It would be interesting to explore the dependence of the transient dynamics on the intensity of the laser illumination. For deeper inverse temperature quenches, the coarsening dynamics is faster and it takes place in a larger area around the colloid. This may influence the initial speed of the mobile Janus particle as well as the onset time at which the reversal of the propulsion direction occurs.
Control over the propulsion direction is an issue of interest concerning the behavior of active particles.46,47 For the present system the observed reversal of the propulsion direction is a sort of “switch-on effect”, because it results from transient dynamics. As such, it can be switched back and forth only via turning the illumination on and off. We expect that deeper quenches may speed up the switchability, because the dynamics should be faster in that case. Moreover, nonlinear effects in the propagation of the composition waves are also expected to occur at early times if the temperature quench is sufficiently deep so that the full particle surface is heated above Tc. Although intriguing, these effects are beyond the scope of our current investigation and will be the subject of further studies.
Another subject for future studies is the effect of strong confinement on the motion of the Janus particles in our system. We expect that in addition to the fact established for squirmers that the hydrodynamic flow around the particle near the walls is rather different from that in the bulk, an inhomogeneous concentration field would lead to an effective interaction between the wall and the particle. This, together with the convection caused by the Marangoni flow, would affect the particle motion to a certain extend.
Finally, interesting conclusion can be drawn from those results, which are obtained by employing a hydrodynamic model. These results clearly demonstrate the high relevance of nonequilibrium concentration fluctuations, induced by temperature gradients, for the coarsening dynamics. It would be rewarding to study in more detail how these nonequilibrium concentration fluctuations couple to the critical fluctuations in the vicinity of the demixing critical point of the binary liquid mixture.
Conflicts of interest
There are no conflicts of interest to declare.Appendix
A Diffusive model
Within the CHC theory the free energy functional of the solvent is given by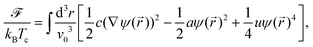 | (17) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (T − Tc)/Tc ≡
(T − Tc)/Tc ≡ ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) τ and Tc as the demixing critical temperature for a binary liquid mixture. Accordingly, a is related to the correlation length of the fluid which diverges upon approaching Tc. Here we consider a lower critical point so that a < 0 for the mixed phase. The length scale v0 is taken to be a microscopic length scale (e.g., the diameter of the molecules of the solvent). For a conserved OP field its time evolution is related to the free energy as
τ and Tc as the demixing critical temperature for a binary liquid mixture. Accordingly, a is related to the correlation length of the fluid which diverges upon approaching Tc. Here we consider a lower critical point so that a < 0 for the mixed phase. The length scale v0 is taken to be a microscopic length scale (e.g., the diameter of the molecules of the solvent). For a conserved OP field its time evolution is related to the free energy as![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) and M being the concentration current and the mobility, respectively. The concentration current is proportional to the gradient of the local chemical potential μ(
and M being the concentration current and the mobility, respectively. The concentration current is proportional to the gradient of the local chemical potential μ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t). This leads to the CHC equation at constant temperature T:
,t). This leads to the CHC equation at constant temperature T: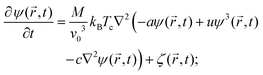 | (18) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) is a Gaussian random white noise which describes the thermal fluctuations:
,t) is a Gaussian random white noise which describes the thermal fluctuations:〈ζ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t)ζ( ,t)ζ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′,t′)〉 = −2(Mv03)kBTc∇2δ( ′,t′)〉 = −2(Mv03)kBTc∇2δ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) − − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) )δ(t − t′) )δ(t − t′) | (19) |
In order to extend the CHC model to the present colloidal system, in which the temperature field depends both on space and time, the coefficient a in eqn (18) is replaced by ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = (
) = (![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (T(
(T(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) − Tc)/Tc) where
) − Tc)/Tc) where ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) is a dimensionless constant. By using suitable substitutions, eqn (18) takes on a modified dimensionless form:
is a dimensionless constant. By using suitable substitutions, eqn (18) takes on a modified dimensionless form:
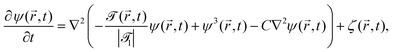 | (20) |
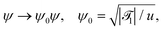 | (21a) |
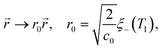 | (21b) |
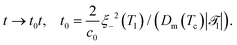 | (21c) |
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 is the reduced quench temperature of the cap, ψ0 is the absolute value of the mean-field bulk OP at T = T1, and C = c/c0 is a dimensionless parameter. In ref. 14–16, which are concerned with shallow quenches, this parameter was set to 1, i.e., the rescaling factor c0 was equal to c. In the present study we assume C = 4, which is appropriate for deep quenches, as considered here, for which the bulk correlation length ξ−(T1) at T1 is comparable to the size of the mesh in the numerical calculations. We assume that the strength ζ0(
1 is the reduced quench temperature of the cap, ψ0 is the absolute value of the mean-field bulk OP at T = T1, and C = c/c0 is a dimensionless parameter. In ref. 14–16, which are concerned with shallow quenches, this parameter was set to 1, i.e., the rescaling factor c0 was equal to c. In the present study we assume C = 4, which is appropriate for deep quenches, as considered here, for which the bulk correlation length ξ−(T1) at T1 is comparable to the size of the mesh in the numerical calculations. We assume that the strength ζ0(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) of the dimensionless noise ζ(
,t) of the dimensionless noise ζ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) is uniform in space and is expressed in units of η0 = ψ0/t0. Dm(Tc) = (M/v03)kBTc is the interdiffusion constant of a binary solvent at the critical temperature.
,t) is uniform in space and is expressed in units of η0 = ψ0/t0. Dm(Tc) = (M/v03)kBTc is the interdiffusion constant of a binary solvent at the critical temperature.
We recall that for the system with a homogeneous temperature T, the mean field bulk correlation length (above Tc in the system with a lower critical point) is given by ξ−(T) = ξ0−|τ|−1/2, where the amplitude 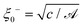 follows from the free energy given by eqn (17). Using the relations
follows from the free energy given by eqn (17). Using the relations ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (
(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) = (
) = (![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) (T(
(T(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) − Tc)/Tc) and ξ− ≃ ξ0−|((T(
) − Tc)/Tc) and ξ− ≃ ξ0−|((T(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) − Tc)/Tc)|−ν with the critical exponent ν ≃ 0.6350 of the three-dimensional Ising model and assuming typical values for the bulk correlation length amplitude for binary liquid mixtures, ξ0− ≃ 0.1 nm,48,49c ≃ 1.85 nm2,15 and for the amplitude
) − Tc)/Tc)|−ν with the critical exponent ν ≃ 0.6350 of the three-dimensional Ising model and assuming typical values for the bulk correlation length amplitude for binary liquid mixtures, ξ0− ≃ 0.1 nm,48,49c ≃ 1.85 nm2,15 and for the amplitude ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = c/(ξ0−)2 ≃ −46.3, we obtain
= c/(ξ0−)2 ≃ −46.3, we obtain ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 = 6 for the quench temperature and r0 ≃ 0.35 nm for the length unit. Approximating Dm(Tc) by a value of Dm at a rather small reduced temperature |(T − Tc)|/Tc = 10−6, which typically is of the order 10−14 m2 s−1,48 renders t0 ≃ 10−7 s for the time unit.
1 = 6 for the quench temperature and r0 ≃ 0.35 nm for the length unit. Approximating Dm(Tc) by a value of Dm at a rather small reduced temperature |(T − Tc)|/Tc = 10−6, which typically is of the order 10−14 m2 s−1,48 renders t0 ≃ 10−7 s for the time unit.
The generic preference of the colloidal surface for one of the two components of the binary mixture is taking account by considering a surface energy contribution 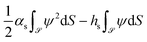 which has to be added to the free energy functional in eqn (17).34 Here,
which has to be added to the free energy functional in eqn (17).34 Here, ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) refers to the surface of the colloid, αs is a surface enhancement parameter, and hs is a symmetry breaking surface field. Upon the substitutions αs → (c/|
refers to the surface of the colloid, αs is a surface enhancement parameter, and hs is a symmetry breaking surface field. Upon the substitutions αs → (c/|![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1|)−1/2αs and hs → ((|
1|)−1/2αs and hs → ((|![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1|/u)1/2/(c/|
1|/u)1/2/(c/|![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1|)−1/2)hs, this contribution leads to the dimensionless static Robin b.c. as given by eqn (4).
1|)−1/2)hs, this contribution leads to the dimensionless static Robin b.c. as given by eqn (4).
Acknowledgements
The work by AM has been supported by the Polish National Science Center (Harmonia Grant No. 2015/18/M/ST3/00403). TA acknowledges the support from JSPS KAKENHI Grant Number JP17K05612, and JST CREST Grant No. JPMJCR1424, Japan. J. R. G.-S. acknowledges support from DGAPA-UNAM PAPIIT Grant No. IA103320.References
- G. Volpe, I. Buttinoni, D. Vogt, H.-J. Kümmerer and C. Bechinger, Soft Matter, 2011, 7, 8810–8815 RSC.
- I. Buttinoni, G. Volpe, F. Kümmel, G. Volpe and C. Bechinger, J. Phys.: Condens. Matter, 2012, 24, 284129 CrossRef PubMed.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef PubMed.
- F. Kümmel, B. ten Hagen, R. Wittkowski, I. Buttinoni, R. Eichhorn, G. Volpe, H. Löwen and C. Bechinger, Phys. Rev. Lett., 2013, 110, 198302 CrossRef PubMed.
- B. Ten Hagen, F. Kümmel, R. Wittkowski, D. Takagi, H. Löwen and C. Bechinger, Nat. Commun., 2014, 5, 4829 CrossRef CAS PubMed.
- J. R. Gomez-Solano, A. Blokhuis and C. Bechinger, Sci. Rep., 2016, 116, 138301 CrossRef PubMed.
- J. R. Gomez-Solano, S. Samin, C. Lozano, P. Ruedas-Batuecas, R. Roij and C. Bechinger, Sci. Rep., 2017, 7, 14891 CrossRef PubMed.
- C. Lozano, J. R. Gomez-Solano and C. Bechinger, New J. Phys., 2018, 20, 015008 CrossRef.
- N. Narinder, C. Bechinger and J. R. Gomez-Solano, Phys. Rev. Lett., 2018, 121, 078003 CrossRef CAS PubMed.
- N. Narinder, J. R. Gomez-Solano and C. Bechinger, New J. Phys., 2019, 21, 093058 CrossRef.
- C. Lozano, J. R. Gomez-Solano and C. Bechinger, Nat. Mater., 2019, 18, 1118 CrossRef CAS PubMed.
- A. Würger, Phys. Rev. Lett., 2015, 115, 188304 CrossRef PubMed.
- S. Samin and R. van Roij, Phys. Rev. Lett., 2015, 115, 188305 CrossRef PubMed.
- T. Araki and A. Maciołek, Soft Matter, 2019, 15, 5243–5254 RSC.
- S. Roy, S. Dietrich and A. Maciołek, Phys. Rev. E, 2018, 97, 042603 CrossRef CAS PubMed.
- S. Roy and A. Maciołek, Soft Matter, 2018, 14, 9326–9335 RSC.
- S. M. Mousavi, I. Kasianiuk, D. Kasyanyuk, S. K. P. Velu, A. Callegari, L. Biancofiore and G. Volpe, Soft Matter, 2019, 15, 5748–5759 RSC.
- F. Schmidt, A. Magazzù, A. Callegari, L. Biancofiore, F. Cichos and G. Volpe, Phys. Rev. Lett., 2018, 120, 068004 CrossRef CAS PubMed.
- P. Bauduin, L. Wattebled, S. Schrödle, D. Touraud and W. Kunz, J. Mol. Liq., 2004, 115, 23–28 CrossRef CAS.
- S. Roy and S. K. Das, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 050602 CrossRef PubMed.
- J. Fineberg, E. Moses and V. Steinberg, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 4939–4942 CrossRef PubMed.
- M. Assenheimer, B. Khaykovich and V. Steinberg, Phys. A, 1994, 208, 373–393 CrossRef CAS.
- C. Mauger, L. Méès, L. Michard, A. Azouzi and S. Valette, Exp. Fluids, 2012, 53, 1895 CrossRef.
- Y. Jayalakshmi, J. Van Duijneveldt and D. Beysens, J. Chem. Phys., 1994, 100, 604 CrossRef CAS.
- H. Tanaka and T. Araki, Phys. Rev. Lett., 2000, 85, 1338–1341 CrossRef CAS PubMed.
- T. Araki and H. Tanaka, J. Phys.: Condens. Matter, 2008, 20, 072101 CrossRef.
- T. Araki and H. Tanaka, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 061506 CrossRef.
- T. Araki and S. Fukai, Soft Matter, 2015, 11, 3470–3479 RSC.
- A. Barbot and T. Araki, Soft Matter, 2017, 13, 5911–5921 RSC.
- H. Tanaka and T. Araki, Europhys. Lett., 2000, 51, 154–1600 CrossRef CAS.
- T. Araki and H. Tanaka, Europhys. Lett., 2004, 65, 214–220 CrossRef CAS.
- W. K. Lewis, Trans. Am. Soc. Mech. Eng., 1922, 1849, 325 Search PubMed.
- H. Diehl and H. Janssen, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 45, 7145 CrossRef PubMed.
- H. Diehl, Int. J. Mod. Phys. B, 1997, 11, 3503 CrossRef.
- M. Allen and D. Tildesley, Computer Simulations of Liquids, Clarendon, Oxford, 1987 Search PubMed.
- L. Surhone, M. Timpledon and S. Marseken, Trilinear Interpolation, Betascript Publishing, United States, 2010 Search PubMed.
- S. Roy and S. K. Das, J. Chem. Phys., 2013, 139, 044911 CrossRef PubMed.
- A. Furukawa, M. Tateno and H. Tanaka, Soft Matter, 2018, 14, 3738–3747 RSC.
- A. Onuki, Phase Transition Dynamics, Cambridge University Press, 2002 Search PubMed.
- A. Onuki, Phys. Rev. Lett., 2005, 94, 054501 CrossRef PubMed.
- A. Onuki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 036304 CrossRef PubMed.
- R. Teshigawara and A. Onuki, Europhys. Lett., 2008, 84, 36003 CrossRef.
- R. Teshigawara and A. Onuki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 021603 CrossRef PubMed.
- R. Teshigawara and A. Onuki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041602 CrossRef PubMed.
- J. Ortiz de Zárate and J. Sengers, Hydrodynamic Fluctuations in Fluids and Fluid Mixtures, Elsevier, Amsterdam, 2006 Search PubMed.
- L. Wang, M. N. Popescu, F. Stavale, A. Ali, T. Gemming and J. Simmchen, Soft Matter, 2018, 14, 6969–6973 RSC.
- H. H. R. Vutukuri, M. Lisiecki, E. Lauga and J. Vermant, Nat. Commun., 2020, 11, 2628 CrossRef CAS PubMed.
- S. Z. Mirzaev, R. Behrends, T. Heimburg, J. Haller and U. Kaatze, J. Chem. Phys., 2006, 124, 144517 CrossRef CAS PubMed.
- E. Gülari, A. F. Collings, R. L. Schmidt and C. J. Pings, J. Chem. Phys., 1972, 56, 6169–6179 CrossRef.
- A. Pelissetto and E. Vicari, Phys. Rep., 2002, 368, 549 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00964d |
| ‡ However, for a water–2,6-lutidine mixture it was demonstrated experimentally24 that close to the lower critical point of demixing the relation between the refractive index and the concentration of the 2,6-lutidine mixture can be well approximated by a linear function. We are not aware of similar studies for the mixture of water and PnP used in the present experiment. |
§ The quantity 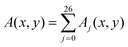 , where Aj(x,y) is its value at the point (x,y) in the jth x–y plane, is called depth-averaged. , where Aj(x,y) is its value at the point (x,y) in the jth x–y plane, is called depth-averaged. |
| ¶ In this section we use the subscript “exp” in order to distinguish the actual time from the reduced simulation time. |
|| The expression g(![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 − 1 − ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (r,t))/2 can be rewritten as H/Cp − s (r,t))/2 can be rewritten as H/Cp − s![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (r,t), where H and Cp are the heating power and the specific heat (see ref. 14). The quantity −s (r,t), where H and Cp are the heating power and the specific heat (see ref. 14). The quantity −s![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) represents the dissipation to the bath (see eqn (3) for the purely diffusive model). In the hydrodynamic model, this dissipation is introduced only at the surface. With fixed temperature at the boundary of the simulation box this controls the location of the critical isotherm around the colloid. The factors g and represents the dissipation to the bath (see eqn (3) for the purely diffusive model). In the hydrodynamic model, this dissipation is introduced only at the surface. With fixed temperature at the boundary of the simulation box this controls the location of the critical isotherm around the colloid. The factors g and ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 are related to H, Cp, and s according to 1 are related to H, Cp, and s according to ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 1 = H/(Cps) and g = 2s. 1 = H/(Cps) and g = 2s. |
| This journal is © The Royal Society of Chemistry 2020 |