Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Tuning the selective permeability of polydisperse polymer networks†
Won Kyu
Kim
 *a,
Richard
Chudoba
*a,
Richard
Chudoba
 bc,
Sebastian
Milster
bc,
Sebastian
Milster
 bd,
Rafael
Roa
bd,
Rafael
Roa
 e,
Matej
Kanduč
e,
Matej
Kanduč
 f and
Joachim
Dzubiella
f and
Joachim
Dzubiella
 *bdg
*bdg
aKorea Institute for Advanced Study, Seoul 02455, Republic of Korea. E-mail: wonkyukim@kias.re.kr
bResearch Group for Simulations of Energy Materials, Helmholtz-Zentrum Berlin für Materialien und Energie, D-14109 Berlin, Germany
cDivision of Theoretical Chemistry, Department of Chemistry, Lund University, P.O. Box 124, SE-22100 Lund, Sweden
dApplied Theoretical Physics-Computational Physics, Physikalisches Institut, Albert-Ludwigs-Universität Freiburg, D-79104 Freiburg, Germany. E-mail: joachim.dzubiella@physik.uni-freiburg.de
eDepartamento de Física Aplicada I, Facultad de Ciencias, Universidad de Málaga, E-29071 Málaga, Spain
fJožef Stefan Institute, SI-1000 Ljubljana, Slovenia
gCluster of Excellence livMatS @ FIT – Freiburg Center for Interactive Materials and Bioinspired Technologies, Albert-Ludwigs-Universität Freiburg, D-79110 Freiburg, Germany
First published on 7th August 2020
Abstract
We study the permeability and selectivity (‘permselectivity’) of model membranes made of polydisperse polymer networks for molecular penetrant transport, using coarse-grained, implicit-solvent computer simulations. In our work, permeability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) is determined on the linear-response level using the solution–diffusion model,
is determined on the linear-response level using the solution–diffusion model, ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) =
= ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Din, i.e., by calculating the equilibrium penetrant partition ratio
Din, i.e., by calculating the equilibrium penetrant partition ratio ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) and penetrant diffusivity Din inside the membrane. We vary two key parameters, namely the network–network interaction, which controls the degree of swelling and collapse of the network, and the network–penetrant interaction, which tunes the selective penetrant uptake and microscopic energy landscape for diffusive transport. We find that the partitioning
and penetrant diffusivity Din inside the membrane. We vary two key parameters, namely the network–network interaction, which controls the degree of swelling and collapse of the network, and the network–penetrant interaction, which tunes the selective penetrant uptake and microscopic energy landscape for diffusive transport. We find that the partitioning ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) covers four orders of magnitude and is a non-monotonic function of the parameters, well interpreted by a second-order virial expansion of the free energy of transferring one penetrant from a reservoir into the membrane. Moreover, we find that the penetrant diffusivity Din in the polydisperse networks, in contrast to highly ordered membrane structures, exhibits relatively simple exponential decays. We propose a semi-empirical scaling law for the penetrant diffusion that describes the simulation data for a wide range of densities and interaction parameters. The resulting permeability
covers four orders of magnitude and is a non-monotonic function of the parameters, well interpreted by a second-order virial expansion of the free energy of transferring one penetrant from a reservoir into the membrane. Moreover, we find that the penetrant diffusivity Din in the polydisperse networks, in contrast to highly ordered membrane structures, exhibits relatively simple exponential decays. We propose a semi-empirical scaling law for the penetrant diffusion that describes the simulation data for a wide range of densities and interaction parameters. The resulting permeability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) turns out to follow the qualitative behavior (including maximization and minimization) of partitioning. However, partitioning and diffusion are typically anti-correlated, yielding large quantitative cancellations, controlled and fine-tuned by the network density and interactions, as rationalized by our scaling laws. We finally demonstrate that even small changes of network–penetrant interactions, e.g., by half a kBT, modify the permselectivity by almost one order of magnitude.
turns out to follow the qualitative behavior (including maximization and minimization) of partitioning. However, partitioning and diffusion are typically anti-correlated, yielding large quantitative cancellations, controlled and fine-tuned by the network density and interactions, as rationalized by our scaling laws. We finally demonstrate that even small changes of network–penetrant interactions, e.g., by half a kBT, modify the permselectivity by almost one order of magnitude.
1 Introduction
Being a key transport property in materials science, the permeability of membranes has been excessively studied for more than a century.1–5 The permeability determines the fundamental ability of functional solutes, such as ions, ligands, proteins, and reactants to penetrate and be transported through dense but permeable membranes of various kinds. Membranes, constituting typically quite crowded environments, are mostly polymer-based, and are ubiquitous in soft matter applications, materials science, and naturally in biological systems. In the latter, bio-hydrogels such as cytoskeletons, mucus gels, and the extracellular matrix (ECM) are complex molecular assemblies composed of hydrated polymer networks.4,6–11 In general, they function as selectively permeable barriers for solutes to penetrate.9 For instance, the ECM constructs a selective barrier around the cells, thereby regulating the transport of signaling molecules.9,12–18 Hence, the permeability of bio-hydrogels plays a decisive role in maintaining life.Other important examples of polymer-network-based membranes can be found in functional soft matter composed of synthetic hydrogels, such as cross-linked poly(N-isopropylacrylamide) (PNIPAM).19 Due to their thermoresponsiveness and relatively sharp volume transition, they are widely used as representative and promising components in emerging material technologies for stimuli-responsive carrier particles, actuators, sensors, or responsive nanoreactors.20–33 In the latter, for instance, the hydrogel embeds nano-sized enzymes or metal nanoparticles catalyzing chemical reactions, which are ultimately controlled by responsive membrane permeability.34–36 In general, responsive polymeric matrices can be expected to control the permeation of solutes (penetrants) in a selective manner, modulated by external stimuli such as temperature, pH, and salinity. The tunable selectivity of permeability (‘permselectivity’)4 thus bears enormous potential for the development of ‘intelligent’, programmable and adaptive membranes for diverse applications ranging from gas separation,37–43 water purification, and filtration44–50 to dialysis and drug delivery.51,52
Typically, the permeability of dense membranes is quantified by the so-called solution–diffusion model on the linear-response level, via3,5,37,38,43,53–60
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) = = ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Din, Din, | (1) |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) = cin/c0, simply given by the ratio between the penetrant concentrations inside the membrane cin and in the bulk reservoir c0, and the diffusivity (diffusion coefficient) Din of the penetrants inside the membrane. In this definition, the permeability of the bulk reservoir reference is thus equal to the free penetrant diffusivity in the bulk reservoir, i.e.,
= cin/c0, simply given by the ratio between the penetrant concentrations inside the membrane cin and in the bulk reservoir c0, and the diffusivity (diffusion coefficient) Din of the penetrants inside the membrane. In this definition, the permeability of the bulk reservoir reference is thus equal to the free penetrant diffusivity in the bulk reservoir, i.e., ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 0 = D0. Definition (1) is based on linear Fick's type of laws,5,56,61 where penetrant flux j is generated by a concentration difference Δc, i.e., j = −
0 = D0. Definition (1) is based on linear Fick's type of laws,5,56,61 where penetrant flux j is generated by a concentration difference Δc, i.e., j = −![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) Δc/L across the membrane of thickness L, and the proportionality constant is given by eqn (1). Note that in the gas separation field, the permeability is often very similarly defined as the product of a solubility coefficient and a diffusion coefficient,37 which may lead to different physical units of
Δc/L across the membrane of thickness L, and the proportionality constant is given by eqn (1). Note that in the gas separation field, the permeability is often very similarly defined as the product of a solubility coefficient and a diffusion coefficient,37 which may lead to different physical units of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) , depending on the exact definition of solubility.62 Other definitions of permeability exist depending on length scales and transport mechanisms, e.g., Knudsen diffusion or convection, which are not applicable to our simulations.63 The elegance of the model represented by eqn (1) is that it is simply based on two intuitive and fundamental properties of a medium in equilibrium, which should be easily accessible in experiments and theoretically tractable.
, depending on the exact definition of solubility.62 Other definitions of permeability exist depending on length scales and transport mechanisms, e.g., Knudsen diffusion or convection, which are not applicable to our simulations.63 The elegance of the model represented by eqn (1) is that it is simply based on two intuitive and fundamental properties of a medium in equilibrium, which should be easily accessible in experiments and theoretically tractable.
However, there is still a growing number of theoretical studies pursuing a better understanding of partitioning39–41,64–71 and diffusivity37,53,55,56,72–94,131 in polymer-based membranes and hydrogels. It is the complexity arising from diverse molecular interactions (e.g., excluded volume and attraction) and conformational structures (cross-linked, ordered, polydisperse) inside the membrane that renders the problem very challenging. Since the pioneering attempts95–99 to tackle this problem, computer simulations have become powerful, requisite tools used to understand the permeability in polymers.100–110 In this context, for instance, we recently presented a simple coarse-grained (CG) simulation model of penetrant transport across a rigid immobile lattice-based membrane, pursuing a better comprehension of permeability, particularly in dense and attractive systems.87 Despite the simplicity of that model, we demonstrated a very intricate behavior of permeability: it varied over many orders of magnitude, and could even be minimized or maximized by tailoring the potential energy landscape for the diffusing penetrants through small variations of membrane attraction, structure, and density. Supported by limited scaling theories, we showed that the possible occurrence of extreme values is far from trivial, being evoked by a strong anti-correlation and substantial (orders of magnitude) cancellation between penetrant partitioning and diffusivity, especially in the case of dense and highly attractive membranes.
In this work, we extend the previous study of a fixed, ordered membrane topology to a more complex and more realistic case of a membrane composed of fluctuating and cross-linked polydisperse polymers to study the transport of diffusive penetrants. For this, we consider a polydisperse tetra-functional network, i.e., each cross-linker connects four polymer strands, which have a polydisperse length distribution. As considered previously,69,87 the system includes the network region and the bulk reservoir region, enabling a direct calculation of partitioning, diffusivity, and thus permeability. We focus on two important control parameters: the polymer network density ϕn (volume fraction), tuned by internal interactions, and the interaction between the network monomers and the penetrants. We calculate the linear-response permeability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) according to eqn (1) and systematically analyze and rationalize our findings by presenting semi-empirical scaling laws. Finally, we demonstrate how minute changes of the interactions can modify the permselectivity of the membrane substantially.
according to eqn (1) and systematically analyze and rationalize our findings by presenting semi-empirical scaling laws. Finally, we demonstrate how minute changes of the interactions can modify the permselectivity of the membrane substantially.
2 Methods
2.1 Simulation model
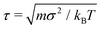 , where m is the unit mass, and kBT = 1/β is the thermal energy. The friction coefficient γ was chosen such that the momentum relaxation time τγ = m/γ = τ, thus the free penetrants’ motion becomes diffusive after 200 time steps.
, where m is the unit mass, and kBT = 1/β is the thermal energy. The friction coefficient γ was chosen such that the momentum relaxation time τγ = m/γ = τ, thus the free penetrants’ motion becomes diffusive after 200 time steps.
For the initial configuration of the network, we considered 4 × 4 × 4 unit cells of a diamond cubic lattice, where Nxlink = 64 × 8 = 512 cross-linkers were located on the lattice points. The unit cell length is 25σ (with σ defining the penetrant size and our length scale) with the initial normalized cross-linker positions per cell, {(0,0,0),(0,0.5,0.5),(0.5,0,0.5),(0.5,0.5,0),(0.25,0.25,0.25), (0.25,0.75,0.75),(0.75,0.25,0.75),(0.75,0.75,0.25)}. In the tetra-functional network, each cross-linker connects four polymer chains. The number of polymer monomers between the (closest neighboring) cross-linkers was randomly drawn from a uniform distribution between 2 and 18, thereby resulting in the polydisperse structure with an average chain length of 10 monomers, and a standard deviation of about 5. With the above construction we ended up with Nm = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 364 monomers in the network, yielding a cross-linker fraction of fxlink = 4.7%. This cross-linker fraction is in the range of typical experimental values for tetra-functional polymer networks, such as cross-linked PNIPAM hydrogels.88–92
364 monomers in the network, yielding a cross-linker fraction of fxlink = 4.7%. This cross-linker fraction is in the range of typical experimental values for tetra-functional polymer networks, such as cross-linked PNIPAM hydrogels.88–92
For initial equilibration, the membrane was placed in the middle of a simulation box of lateral lengths Lx = Ly = 100σ and longitudinal length Lz = 300σ, with periodic boundary conditions in all three Cartesian directions. For a small molecule of typical size σ = 0.4 nm, the longitudinal box length then corresponds to Lz = 120 nm. Note that the periodic boundary conditions lead to an infinitely large membrane in the x and y directions, while the membrane-reservoir regions periodically repeat in the z direction with a spatial period Lz, reminiscent of a stack of lamellar hydrogel layers.116 The membrane was first equilibrated in the NVT ensemble using the force-field described below. We then added Np = 1000 penetrant particles to the bulk reservoir region, and equilibrated the whole system.
In the next step, the longitudinal box length Lz was kept fixed, while Lx and Ly could adjust equivalently according to the NpT ensemble with a given particle number N = Nm + Nxlink + Np = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 876, pressure px = py = p, and temperature T. To maintain the target pressure p on an average, we used the Berendsen barostat with semi-isotropic pressure coupling.117 Since we consider the implicit-solvent model, the anisotropic pressure couples only to the virial coefficients in the x and y directions of the polymer monomers and the penetrants. The value of the lateral pressure defines the network reference states without penetrants and was chosen to be p = 1 bar ≈10−2kBT nm−3. The latter is in fact negligibly small (essentially p ≈ 0) compared to the interactions in our system,67,118 which are of the order of kBT nm−3 ≈ 41 bar ≫ p. The pressure relaxation time τp and bulk modulus Kb for the barostat were chosen in the range of 1 ≤ τp/τ ≤ 2 and 1 ≤ Kb/p ≤ 10, respectively, to maintain reasonable dynamic pressure relaxation comparable to the Langevin momentum relaxation, which depends on the interaction parameters.
876, pressure px = py = p, and temperature T. To maintain the target pressure p on an average, we used the Berendsen barostat with semi-isotropic pressure coupling.117 Since we consider the implicit-solvent model, the anisotropic pressure couples only to the virial coefficients in the x and y directions of the polymer monomers and the penetrants. The value of the lateral pressure defines the network reference states without penetrants and was chosen to be p = 1 bar ≈10−2kBT nm−3. The latter is in fact negligibly small (essentially p ≈ 0) compared to the interactions in our system,67,118 which are of the order of kBT nm−3 ≈ 41 bar ≫ p. The pressure relaxation time τp and bulk modulus Kb for the barostat were chosen in the range of 1 ≤ τp/τ ≤ 2 and 1 ≤ Kb/p ≤ 10, respectively, to maintain reasonable dynamic pressure relaxation comparable to the Langevin momentum relaxation, which depends on the interaction parameters.
After an equilibration time of 1.5 × 105τ, we performed the production simulations typically up to 107δτ = 5 × 104τ. As the finite network membrane is connected to the large bulk reservoir region of solute penetrants, the penetrants can always equilibrate their partitioning between the large bulk reservoir and the (responsive) membrane. The resulting equilibrium density profiles of the monomers as well as the penetrants within the membrane and in the bulk reservoir are considerably homogeneous along the z direction, cf. Fig. S1 in the ESI† demonstrates that the systems are well equilibrated. For the chosen typical molecule size σ = 0.4 nm, the corresponding membrane widths, determined from the monomer concentration profiles, equilibrate then typically from ≃4 to 16 nm. The lateral equilibrated lengths of the simulation box Lx (= Ly) are shown in Table S2 in the ESI.†
Selected two-dimensional radial density distribution functions between the cross-linkers, g2Dxlink(r), shown in Fig. 2, also demonstrate that the equilibration procedure leads to reasonable and homogeneous network structures in the lateral directions (note that g2Dxlink(r) is averaged over thin two-dimensional membrane slabs in the x and y directions, see Fig. S2 in the ESI† for details). Especially in the dense state, apart from some short-ranged packing effects, for r ≳ 3σ, g2Dxlink(r) becomes homogeneous in the lateral directions. For the swollen network, g2Dxlink(r) reveals some more structures with a local peak at 3σ ≲ r ≲ 4σ, reflecting short-range correlations between the crowded cross-linker regions, and a second peak close to the average chain length (i.e., average mesh size in the swollen case) of r ≃ 10σ. Changing the network–penetrant interaction affects these distributions only slightly in the dense systems, while in the swollen case few structures are observed for large attractions between the network and the penetrants (see Fig. S2 in the ESI†), indicating some amount of penetrant-induced homogenization.
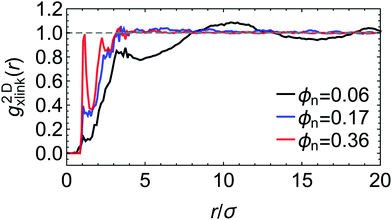 | ||
| Fig. 2 Two-dimensional radial distribution function between the cross-linkers g2Dxlink(r) for three different polymer volume fractions, from swollen (ϕn = 0.06) to collapsed (ϕn = 0.36) states. The network–penetrant interaction parameter is βεnp = 0.1. The distribution function g2Dxlink(r) is averaged over thin 2D membrane slabs in the x and y directions, see the ESI† for details and more data. | ||
The intra-network interaction εnn is interpreted as a measure of solvent quality,69,87,119 thereby controlling the network volume fraction ϕn = (Nm + Nxlink)v0/Vn, where v0 = πσ3/6 is the monomer volume with diameter σ = σnn = σnp, and Vn is the network volume. As discussed in previous works,69,87,119 small/high εnn corresponds to a good/poor solvent leading to a small/high volume fraction, respectively. The network–penetrant interaction εnp governs the strength of attraction between the polymers and the penetrants.
For the bonded interactions of the (semi-flexible) polymers, we employed harmonic stretching (bond) and bending (angle) potentials.69 The bonded polymer parameters were determined via coarse-graining from explicit-water, all-atom simulation results of cross-linked PNIPAM chains, utilizing a force-field from our group's work.120 Since the cross-linker connects monomers of four polymer chains, the network is tetra-functional, and in addition to the m-m-m bending, there are six bending potentials for the m-xlink-m arrangement. Therefore, we have nine different bonded (7 bending (angles), 2 stretching (bonds)) potentials in total and we determined eighteen bonded parameters Kijr, rij0, Kijkθ, and θijk0 by fitting harmonic potentials to the free energies obtained from the all-atom simulations. The details of all the bonded interactions, that is, their calculation from the all-atom (explicit-water) simulations of PNIPAM and their final definition, can be found in the last section in the ESI.†
2.2 Analysis
In order to determine the solution–diffusion permeability given in eqn (1), we need to individually evaluate the partition ratio and the penetrant diffusion inside the network. Note again that we analyze the simulation results in equilibrium, not by measuring any fluxes of the penetrants.The partition ratio, ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) = cin/c0, was computed by counting and averaging the equilibrium number density of penetrants inside the network and bulk reservoir, as similarly done in our previous works.36,69,87 We carefully divided the simulation box into three regions (inner membrane, membrane surface, and bulk reservoir) to sample the concentrations without any effects of the surface and the finite membrane width. See Fig. S1 in the ESI† for details.
= cin/c0, was computed by counting and averaging the equilibrium number density of penetrants inside the network and bulk reservoir, as similarly done in our previous works.36,69,87 We carefully divided the simulation box into three regions (inner membrane, membrane surface, and bulk reservoir) to sample the concentrations without any effects of the surface and the finite membrane width. See Fig. S1 in the ESI† for details.
For the calculation of the penetrant diffusivity in the network, Din, to avoid the surface effect, we generated 20 auxiliary simulation boxes of diamond unit cells of the polydisperse tetra-functional networks periodically repeated in all three dimensions. We included the penetrants for each parameter set of εnn and εnp and we performed additional simulations of these periodic cells (see Fig. S4 in the ESI†). To determine the cell size and the number of the penetrants in the cell, we used the equilibrium values of the penetrant density and the polymer density obtained from the main simulation data. We computed the mean-squared-displacement (MSD) of the penetrants in the networks, averaged over time and particles,121 as shown in the ESI,† Fig. S5 (upper panels), within the dimensionless simulation time range from t = 100 to t = 1000 to obtain diffusivity via MSD = 6Dint, ensuring the normal diffusion,121 which fulfills 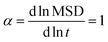 (see Fig. S5 (lower panels) in the ESI†). This auxiliary setup is fully isotropic and can possibly differ from the network structure in the main simulations, where the membrane deformations can be globally anisotropic. We therefore checked the isotropy of the membrane simulations using several shape descriptors.122,123 Our examinations with results shown in Fig. S6 in the ESI,† confirm that the polymeric structure is highly isotropic in the central membrane region throughout the whole range of interaction parameters.
(see Fig. S5 (lower panels) in the ESI†). This auxiliary setup is fully isotropic and can possibly differ from the network structure in the main simulations, where the membrane deformations can be globally anisotropic. We therefore checked the isotropy of the membrane simulations using several shape descriptors.122,123 Our examinations with results shown in Fig. S6 in the ESI,† confirm that the polymeric structure is highly isotropic in the central membrane region throughout the whole range of interaction parameters.
Note that in our implicit-solvent simulations in the NpT ensemble, the penetrant's concentration in the bulk reservoir is not a conserved quantity among the systems (as it would be in a grand canonical ensemble), as the penetrants partition differently in the membrane. Therefore, we intentionally employed small penetrant concentrations in the reservoir and only weak interactions (εpp = 0.1kBT) to reduce non-ideality corrections. To check the effects of a varying reservoir concentration, we compare the partitioning results for two different numbers of penetrants (Np) for all polymer densities at the lowest and highest network–penetrant interaction in Fig. S7 in the ESI.† This comparison indeed reveals a small quantitative difference in the partitioning, but only for large polymer packing fractions and without changing the qualitative picture. Hence, the conclusions based on our generic simulation model should not depend on the ensemble. Actually, our periodic isothermal–isobaric representation (with fixed N) could be adequate to describe permeability experiments using lamellar hydrogel layers.116
We note here that there are other simulation approaches to study the solvent permeability in polymeric networks: Masoud et al. developed DPD (dissipative particle dynamics) CG simulations to investigate the solvent permeability in random networks under external flow.103 Wang et al. developed explicit-solvent simulations to study pressure-driven water transport in a polyamide membrane in the isotropic NpT ensemble.107 A similar all-atom approach was presented by the same authors to study pressure-driven water transport through a CNT (carbon nanotube) membrane pore in the presence of moving walls in the longitudinal direction.104 This method as an alternative to the grand canonical ensemble124 was originally proposed by Ghoufi et al.125 and used to study the water transport through a polyamide membrane.108 These approaches successfully elucidated the permeability of solvents, especially under non-equilibrium situations. However, our approach is different since we focus on the permeability of solutes in an implicit-solvent model in equilibrium, in the absence of pressure gradients. In particular, the chosen solution–diffusion approach has the advantage that effects of partitioning and diffusion on permeability can be studied separately.
3 Results and discussion
3.1 Network density response to solvent quality and penetrants
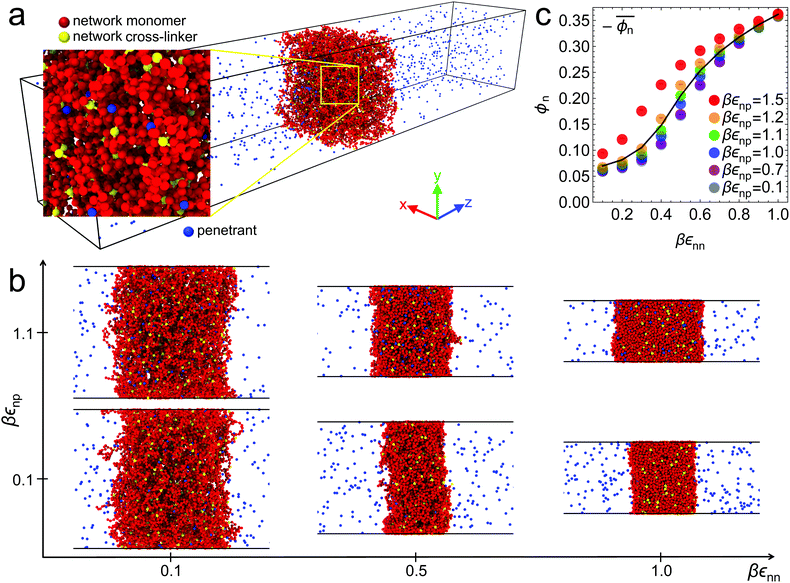
Six representative simulation snapshots of the system are shown in Fig. 1b for different values of the solvent quality parameter εnn and the network–penetrant interaction parameter εnp. The most swollen state is shown by the lower left snapshot, whereas the most compact state is depicted by the upper right snapshot. The polymer network collapses due to strong network–network attractions εnn (poor solvent), otherwise it swells (good solvent). In addition, upon changing the network–penetrant interaction, particularly while using intermediate solvent quality (εnn = 0.5kBT), we note that the larger the attraction εnp, the more packed is the network (lower volume). This is due to the bridging effects of highly attractive penetrants, contracting the network to maximize favorable interaction contacts.69 See Fig. S8 in the ESI† for details of the network volume change depending on the interactions.In this respect, note that for the same solvent quality βεnn = 1, the membrane width is increasing with growing network–penetrant interaction βεnp, i.e., there is a penetrant-induced deformation. Recall that we apply isotropic pressure with independent scaling of the box in the x and y directions with essentially vanishing target pressure, hence the membrane can simply freely deform based on its internal virial. For large network–penetrant attractions, the polymer tends to maximize contacts with penetrants (a volume effect) and therefore the membrane deforms to increase the volume-to-interface ratio.
The global effects of the two interaction parameters are summarized in Fig. 1c, which depicts the network volume fraction ϕn, i.e., the ratio of the volume occupied by the polymers to the entire network volume, as a function of the solvent quality parameter εnn for different values of the network–penetrant interaction εnp. The network undergoes a typical collapse transition as εnn increases at small and intermediate values of εnp, while the transition becomes more gradual when the penetrants are very attractive (εnp = 1.5kBT). This is probably due to local monomer clustering and less structured networks, cf. Fig. S1 (ESI†), indicating a smooth transition. The solid line interpolates between the mean values over the volume fraction 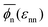 averaged over all simulated εnp values. Also note that the grey data for ϕn(βεnp = 0.1) almost coincide with the purple data for ϕn(βεnp = 0.7) as shown in Fig. 1c.
averaged over all simulated εnp values. Also note that the grey data for ϕn(βεnp = 0.1) almost coincide with the purple data for ϕn(βεnp = 0.7) as shown in Fig. 1c.
3.2 Penetrant partitioning, diffusivity, and permeability
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) , the penetrant diffusion inside the network Din, and the permeability
, the penetrant diffusion inside the network Din, and the permeability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) , as a function of the network volume fraction (a–c) and the network–penetrant interaction parameter (d–f).
, as a function of the network volume fraction (a–c) and the network–penetrant interaction parameter (d–f).
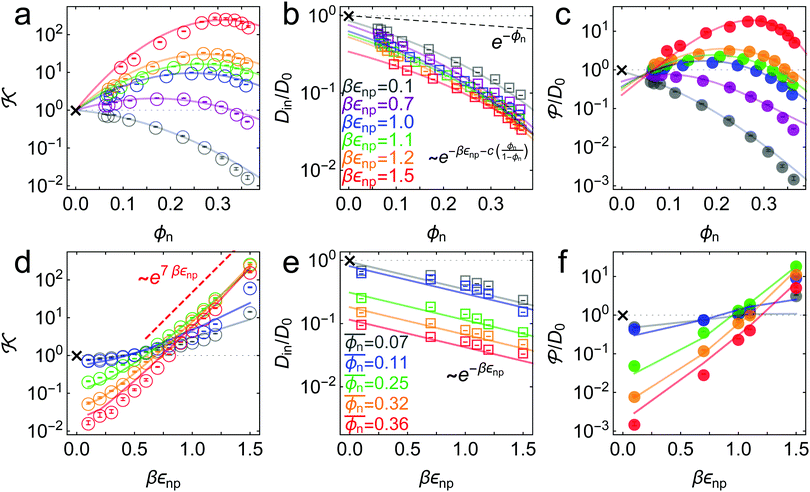 | ||
Fig. 3 Simulation results (symbols) and theoretical fits (solid lines). (a) Partitioning ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) as a function of the network volume fraction for different values of network–penetrant interaction εnp. The solid lines are the fits from virial expansion eqn (2) (see the text and Table S1 in the ESI† and Fig. 4 for details). (b) Penetrant diffusion in the polymer network Din as a function of ϕn. The solid lines are the fits (also depicted in (e)) from the free-volume approach eqn (4) (see Table S3 in the ESI† for the details). The dashed line is e−ϕn as a reference. (c) Permeability as a function of the network volume fraction for different values of network–penetrant interaction εnp. The solid lines are the fits from virial expansion eqn (2) (see the text and Table S1 in the ESI† and Fig. 4 for details). (b) Penetrant diffusion in the polymer network Din as a function of ϕn. The solid lines are the fits (also depicted in (e)) from the free-volume approach eqn (4) (see Table S3 in the ESI† for the details). The dashed line is e−ϕn as a reference. (c) Permeability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) as a function of ϕn. The solid lines are the predictions from eqn (5) using the fitting values from (a) and (b). (d) Partitioning as a function of ϕn. The solid lines are the predictions from eqn (5) using the fitting values from (a) and (b). (d) Partitioning ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) as a function of εnp. The solid lines are the prediction according to the virial expression eqn (2) using the Bnp2 and Bnnp3 values from the fit in (a) and the mean density as a function of εnp. The solid lines are the prediction according to the virial expression eqn (2) using the Bnp2 and Bnnp3 values from the fit in (a) and the mean density 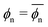 . The data scale roughly as . The data scale roughly as ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) ∼ e7βεnp for dense and attractive polymers (the red dashed line). (e) Penetrant diffusion Din as a function of εnp. The solid lines are the fits according to the exponential (Kramers’) scaling Din/D0 ∼ e−βεnp from eqn (4). (f) Permeability ∼ e7βεnp for dense and attractive polymers (the red dashed line). (e) Penetrant diffusion Din as a function of εnp. The solid lines are the fits according to the exponential (Kramers’) scaling Din/D0 ∼ e−βεnp from eqn (4). (f) Permeability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) as a function of εnp. The solid lines are the predictions from eqn (5) using the fitting values from (a) (see also panels (d) and (e)). The cross symbols in each panel are corresponding reference values in the bulk reservoir. as a function of εnp. The solid lines are the predictions from eqn (5) using the fitting values from (a) (see also panels (d) and (e)). The cross symbols in each panel are corresponding reference values in the bulk reservoir. | ||
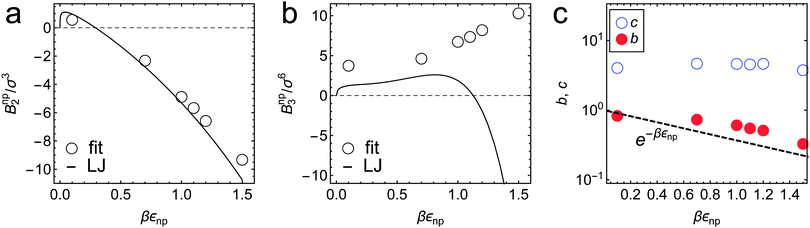 | ||
| Fig. 4 Virial coefficients (a) Bnp2 and (b) Bnnp3 in eqn (2) obtained as fitting parameters in Fig. 3a, shown by symbols for different values of εnp. The exact values of BLJ2 and BLJ3 for LJ potential are shown by the solid lines for comparison. (c) Fitting parameter values b and c in the free-volume scaling theory eqn (3) (see also Fig. 3b). See the ESI† for details. | ||
The partitioning as a function of the network volume fraction, ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (ϕn), exhibits diverse behavior, ranging over four orders of magnitude depending on the interactions, as shown in Fig. 3a. For low network–penetrant interaction parameters εnp,
(ϕn), exhibits diverse behavior, ranging over four orders of magnitude depending on the interactions, as shown in Fig. 3a. For low network–penetrant interaction parameters εnp, ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) decreases monotonically with increasing network density, since the essentially repelled penetrants are excluded by highly packed polymers (see the second virial coefficient of the LJ system as shown in Fig. 4). For higher values of the LJ potential depth εnp, the penetrants are increasingly more attracted to the network. The partitioning
decreases monotonically with increasing network density, since the essentially repelled penetrants are excluded by highly packed polymers (see the second virial coefficient of the LJ system as shown in Fig. 4). For higher values of the LJ potential depth εnp, the penetrants are increasingly more attracted to the network. The partitioning ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) , however, becomes non-monotonic and reaches a maximum around ϕn ≃ 0.3. This partitioning maximization is due to the volume exclusion of the penetrants, which wins over the attraction at high densities.70,87
, however, becomes non-monotonic and reaches a maximum around ϕn ≃ 0.3. This partitioning maximization is due to the volume exclusion of the penetrants, which wins over the attraction at high densities.70,87
The cross-over from penetrant exclusion to enrichment for increasing εnp at fixed polymer density ϕn becomes obvious in Fig. 3d, where we plot ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (εnp). At around βεnp ≃ 0.5–0.7 (depending on details of polymer density) the attraction outvalues the steric obstruction and penetrants are on average preferentially adsorbed rather than being in the bulk reservoir, i.e.,
(εnp). At around βεnp ≃ 0.5–0.7 (depending on details of polymer density) the attraction outvalues the steric obstruction and penetrants are on average preferentially adsorbed rather than being in the bulk reservoir, i.e., ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) > 1. We also observe that partitioning
> 1. We also observe that partitioning ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) (εnp) roughly exhibits an exponential increase with a larger slope as ϕn increases. The exponential increase of partitioning is also found in ordered membranes,87 reflecting that the overall scaling behavior of partitioning (upon changing the interactions) is rather insensitive to the regularity of the network. For dense and attractive polymer networks, we empirically find that
(εnp) roughly exhibits an exponential increase with a larger slope as ϕn increases. The exponential increase of partitioning is also found in ordered membranes,87 reflecting that the overall scaling behavior of partitioning (upon changing the interactions) is rather insensitive to the regularity of the network. For dense and attractive polymer networks, we empirically find that ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) ∼ e7βεnp, as depicted in Fig. 3d. The prefactor 7 reflects the total mean attraction in the dense systems, where the potential wells of many attractive monomers densely overlap.
∼ e7βεnp, as depicted in Fig. 3d. The prefactor 7 reflects the total mean attraction in the dense systems, where the potential wells of many attractive monomers densely overlap.
In order to gain more theoretical insight and develop an analytical framework for describing the data, we perform a virial expansion of the transfer free energy 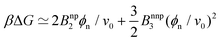 , and apply it to the partition coefficient
, and apply it to the partition coefficient ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) = exp(−βΔG),87 as
= exp(−βΔG),87 as
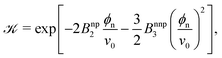 | (2) |
The fitted Bnp2 and Bnnp3 parameters can be found in Fig. 4a and b. We find that the second virial coefficients Bnp2 agree well with the values from the explicit relation 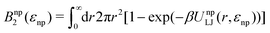 for LJ particles, cf. the solid line in Fig. 4a. However, as shown in Fig. 4b, the third virial coefficient Bnnp3 from the fitting deviates from the explicitly computed values of the LJ fluid. This implies that as the polymer density increases, many-body interactions, in particular at the crowded cross-linker regions,120 play a major role, which is beyond the correlations of a simple LJ liquid. In fact, the fitted Bnnp3 values are always positive, i.e., the many-body effect can be identified as, on average, a repulsive contribution.
for LJ particles, cf. the solid line in Fig. 4a. However, as shown in Fig. 4b, the third virial coefficient Bnnp3 from the fitting deviates from the explicitly computed values of the LJ fluid. This implies that as the polymer density increases, many-body interactions, in particular at the crowded cross-linker regions,120 play a major role, which is beyond the correlations of a simple LJ liquid. In fact, the fitted Bnnp3 values are always positive, i.e., the many-body effect can be identified as, on average, a repulsive contribution.
The data in Fig. 3d are also well described by the virial form, eqn (2), where the solid lines agree with the simulation data. For this, we use eqn (2) with the same virial coefficients obtained from the result shown in Fig. 3a, and assume 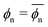 , which is in fact a good approximation particularly for low and high polymer densities. The dependence of the partitioning on the network volume fraction can thus again be explained by a balance between the network–penetrant attraction and exclusion, which is particularly important for high volume fractions.
, which is in fact a good approximation particularly for low and high polymer densities. The dependence of the partitioning on the network volume fraction can thus again be explained by a balance between the network–penetrant attraction and exclusion, which is particularly important for high volume fractions.
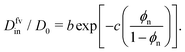 | (3) |
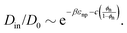 | (4) |
In Fig. 3e we confirm that Din(εnp) indeed tends to exponentially decrease. Hence, the Kramers’ type scaling Din ∝ e−βεnp for the diffusion limited escape from a single attractive well75 fits well, such that our prediction from eqn (4) holds. It is interesting that the energy barrier in the dense systems (i.e., the micro-roughness of the energy landscape) is simply described by εnp and not by multiples of it, as we observed in the more ordered systems.87 Apparently, the random structure (e.g., polydispersity of the network) in thermal fluctuations smoothens out the roughness significantly. Note again that the overall mean attraction (i.e., the mean of the landscape in contrast to its roughness) is much higher than εnp, since we needed 7εnp to fit the partition ratio above. We remark here that our semi-empirical scaling law eqn (4) has limitations since it does not behave well when ϕn → 0, where Din/D0 should go up to unity. However, this highly dilute membrane limit with little influence on transport is not interesting anyway for applications and selectivity-control.
We recall that in the literature there are in fact various proposals for scaling theories of diffusivity, depending on microscopic diffusion mechanisms and length scales.75,76 In Fig. S9 in the ESI,† we present several appropriate scaling theories for the diffusivity, which are compared to our simulation results. We concluded that for our systems, eqn (4) performs the best throughout the range of ϕn, including the dense regimes.
It is interesting that the diffusivity is a simple monotonic function of ϕn. In fact, this result is very different from our previous finding for regular topologies, that is, membranes made of a fixed (static) fcc (face-centered-cubic) or simple-cubic lattice of LJ spheres.87 There, we found that the diffusivity is rather a complex function of the density of the membranes. We rationalized the effect by the roughness of a potential landscape, which for ordered potential wells on a regular lattice can be a very rapidly changing function of membrane density in certain density regions.87 But in the case here, the fluctuations and the polydispersity of the polymer network smoothen out the sharp density effects on the energy landscape and all diffusivities scale similarly exponentially, qualitatively almost independent of parameter εnp.
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) =
= ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Dinversus the packing fraction. The permeability varies by about 4 orders of magnitude in our parameter range. Due to the generic monotonic behavior of the diffusion, the nature of the permeability depending on the volume fraction reflects essentially the one of the partition ratio
Dinversus the packing fraction. The permeability varies by about 4 orders of magnitude in our parameter range. Due to the generic monotonic behavior of the diffusion, the nature of the permeability depending on the volume fraction reflects essentially the one of the partition ratio ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) , while the diffusivity only quantitatively scales the results. Hence, we find that for small interactions εnp, the permeability monotonically decreases with density, whereas for stronger interactions, it becomes a non-monotonic function of density. Therefore, as an important finding, the permeability can be maximized in our network model system. For the largest network–penetrant attraction, the permeability is maximized at around ϕn ≃ 0.28 by a factor of around 20 when compared to the bulk reservoir reference permeability
, while the diffusivity only quantitatively scales the results. Hence, we find that for small interactions εnp, the permeability monotonically decreases with density, whereas for stronger interactions, it becomes a non-monotonic function of density. Therefore, as an important finding, the permeability can be maximized in our network model system. For the largest network–penetrant attraction, the permeability is maximized at around ϕn ≃ 0.28 by a factor of around 20 when compared to the bulk reservoir reference permeability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) = D0 (the cross symbol).
= D0 (the cross symbol).
Having well-performing scaling laws for ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) and Din from eqn (2) and (4), now we attempt to empirically construct a scaling law for the permeability, via their product, eqn (1),
and Din from eqn (2) and (4), now we attempt to empirically construct a scaling law for the permeability, via their product, eqn (1),
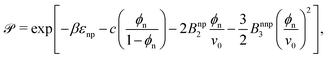 | (5) |
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) can therefore be understood viaeqn (2) and (4). The solid lines in Fig. 3c are the predictions from eqn (5) using the fitting parameters determined already in panels a and b, showing very good agreement with the simulation results.
can therefore be understood viaeqn (2) and (4). The solid lines in Fig. 3c are the predictions from eqn (5) using the fitting parameters determined already in panels a and b, showing very good agreement with the simulation results.
The permeability as a function of the network–penetrant interaction, ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (εnp), as shown in Fig. 3f, is an increasing function from the global minimum at around βεnp = 0.1, which substantially depends on membrane density. Here, the selective tuning of
(εnp), as shown in Fig. 3f, is an increasing function from the global minimum at around βεnp = 0.1, which substantially depends on membrane density. Here, the selective tuning of ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) is mainly controlled by the penetrant's excluded volume. The prediction from the empirical scaling eqn (5) indeed agrees well with the simulation data, in particular, capturing the competition and cancellation between the exponentially growing partitioning and the exponentially decreasing diffusion.
is mainly controlled by the penetrant's excluded volume. The prediction from the empirical scaling eqn (5) indeed agrees well with the simulation data, in particular, capturing the competition and cancellation between the exponentially growing partitioning and the exponentially decreasing diffusion.
3.3 Correlations between ![[scr K, script letter K]](https://www.rsc.org/images/entities/h3_char_e148.gif) and Din and tuning of permselectivity
and Din and tuning of permselectivity
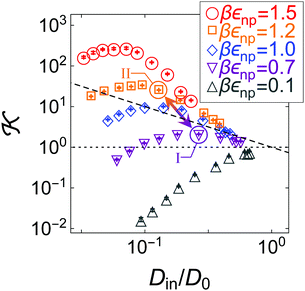
The diagram in Fig. 5 plots the partitioning ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) versus the diffusivity Din and thus presents a landscape visualizing how they are correlated, i.e., a partitioning–diffusivity correlation diagram. The plot shows a wide landscape of the permeability spanning over several orders of magnitude. The black dashed line depicts the iso-permeability line of the bulk reservoir permeability
versus the diffusivity Din and thus presents a landscape visualizing how they are correlated, i.e., a partitioning–diffusivity correlation diagram. The plot shows a wide landscape of the permeability spanning over several orders of magnitude. The black dashed line depicts the iso-permeability line of the bulk reservoir permeability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) /D0 = 1, where the two contributions exactly cancel out. The data in Fig. 5 at low and intermediate polymer densities lead to final permeabilities close to the iso-permeability line, hence exhibiting clear anti-correlations and cancellations. Such cancellations were also observed, even more massively, in membranes constructed of static regular obstacles.87
/D0 = 1, where the two contributions exactly cancel out. The data in Fig. 5 at low and intermediate polymer densities lead to final permeabilities close to the iso-permeability line, hence exhibiting clear anti-correlations and cancellations. Such cancellations were also observed, even more massively, in membranes constructed of static regular obstacles.87
The anti-correlations can be understood by glancing back at our empirical scaling law for permeability, eqn (5). The attraction between monomers and penetrants increases the uptake of penetrants in the membrane roughly exponentially. However, at the same time the attraction enhances the microscopic roughness and deepens local traps, thereby impeding the thermally activated (Kramers) escape, which in turn also leads to an exponential decrease of diffusion. In many regimes, these two effects cancel out, but the exact behavior depends on the details of the variation of the energy landscape.87
In fact, the data do not simply follow one universal trend with some statistical scatter. On the contrary, we observe a set of distinct non-monotonic trends, each of which has its own physical explanation. For example, for the most repulsive penetrants (gray upside triangles) the data diverge substantially downwards, as both partitioning and diffusion decrease with polymer density due to excluded-volume (steric) constraints. In contrast, for the most attractive penetrants (red circles) the permeability stays closer to the bulk permeability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) /D0 = 1 but shows a distinct maximum. The reason for this is that partitioning first increases stronger (beyond unity) than diffusion decreases for increasing polymer density, but then steric exclusion limits the uptake. Diffusion apparently does not decrease as much as partitioning increases because in our fluctuating, polydisperse network the energy landscape for diffusion stays relatively smooth and independent of density, in contrast to highly ordered membranes.87 This knowledge can be harvested to tune and optimize the selectivity of a polymer membrane. In contrast to the ordered membranes,87 however, this work indicates that the diffusivity in fluctuating, disordered networks only rescales the permeability, while the shape of the dependence is dictated by the partitioning behavior. Hence, membrane design for polydisperse networks should focus more on the behavior of solubility in the network than on the mobility.
/D0 = 1 but shows a distinct maximum. The reason for this is that partitioning first increases stronger (beyond unity) than diffusion decreases for increasing polymer density, but then steric exclusion limits the uptake. Diffusion apparently does not decrease as much as partitioning increases because in our fluctuating, polydisperse network the energy landscape for diffusion stays relatively smooth and independent of density, in contrast to highly ordered membranes.87 This knowledge can be harvested to tune and optimize the selectivity of a polymer membrane. In contrast to the ordered membranes,87 however, this work indicates that the diffusivity in fluctuating, disordered networks only rescales the permeability, while the shape of the dependence is dictated by the partitioning behavior. Hence, membrane design for polydisperse networks should focus more on the behavior of solubility in the network than on the mobility.
Hence, the diagram in Fig. 5 presents non-trivial pathways of the permeability ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) along the two variable parameters, density and network–penetrant attraction. This clearly shows how the permeability can be tuned substantially over several orders of magnitude already by a relatively small material parameter space. With this, a significant selective permeability (permselectivity) can be demonstrated depending on the interaction parameter, εnp (which in reality is different for various chemically specific penetrants). For instance, defined as αII,I ≡
along the two variable parameters, density and network–penetrant attraction. This clearly shows how the permeability can be tuned substantially over several orders of magnitude already by a relatively small material parameter space. With this, a significant selective permeability (permselectivity) can be demonstrated depending on the interaction parameter, εnp (which in reality is different for various chemically specific penetrants). For instance, defined as αII,I ≡ ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) II/
II/![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) I,42 the selectivity for the states II (βεnp = 1.2) and I (βεnp = 0.7) depicted by the arrow in Fig. 5 at a packing fraction ϕn ≃ 0.17 amounts to αII,I ≈ 6, which is large. Hence, a small difference in interactions of half a kBT results already in a permeability ratio of almost one order of magnitude.
I,42 the selectivity for the states II (βεnp = 1.2) and I (βεnp = 0.7) depicted by the arrow in Fig. 5 at a packing fraction ϕn ≃ 0.17 amounts to αII,I ≈ 6, which is large. Hence, a small difference in interactions of half a kBT results already in a permeability ratio of almost one order of magnitude.
We note here that there are various mechanisms that govern the selectivity. We limit our study to varying the interaction strengths (εnn and εnp) at fixed penetrant size (σ). Varying the size, in fact, leads to even more complex behavior, such as molecular sieving, once the penetrant size becomes larger than the mesh size of the network.109,110 In this work, we focus on the interaction-dependent permselectivity, where the sieving can be effectively tuned by changing the interactions.
4 Conclusion
We presented extensive (implicit-solvent) coarse-grained simulations and scaling theories for penetrant transport through semi-flexible, cross-linked, and polydisperse polymer networks with a focus on the linear-response permeability, calculated by the equilibrium partitioning and diffusion of the penetrants inside the network. The permeability has been found to be largely tunable by varying the polymer network density and the microscopic interactions between the network and the diffusive penetrants. In particular, significant maximization and minimization of the permeability were found, fine-tuned by the solvent quality and the network–penetrant interactions. The results were rationalized by phenomenological scaling theories that we developed in this work, which include a virial expansion with two-body attractions and many-body exclusion effects for the partitioning, and a combination of the free-volume and Kramers’ escape scaling laws for the diffusivity. Our presented laws, despite their simplicity, capture salient features of the system, showing good agreement with the simulation results.The penetrant diffusivity turned out to be a rather smooth function of the network density, implying substantial effects of the fluctuation and randomness of the polymer network. The highly fluctuating and polydisperse nature of the network averages out the roughness of the energy landscape, which was more pronounced and sensitive to parameter changes in highly ordered, lattice-based and static membrane systems.87 However, it is not clear whether smoothing-out is more a consequence of polydispersity, or just a consequence of the irregular distribution of polymer segments in space, which might also occur in monodisperse fluctuating networks that may be studied in the future.
Nevertheless, permeability revealed a rather intricate, non-monotonic behavior over several orders of magnitude, originating from the complex nature of partitioning, while quantitatively and substantially modified by the anti-correlated and canceling contributions of the diffusion. As a consequence, only small changes of interactions, e.g., by half a kBT can already modify the selectivity of the membrane by a factor of 6. Our study provides a further step in the fundamental understanding and development of a minimal theory to characterize better the permeability in flexible and fluctuating polymer-based membrane systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Matthias Ballauff, Benjamin Rotenberg, Arturo Moncho-Jordá and Changbong Hyeon for fruitful discussions. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No. 646659). W. K. K. acknowledges the support by a KIAS Individual Grant (CG076001) at Korea Institute for Advanced Study. M. K. acknowledges the financial support from the Slovenian Research Agency (research core funding No. P1-0055). The simulations were performed with resources provided by the North-German Supercomputing Alliance (HLRN). We acknowledge the Center for Advanced Computation at Korea Institute for Advanced Study for providing computing resources for this work.References
- T. Graham, Philos. Mag., 1866, 32, 401–420 Search PubMed
.
-
A. Finkelstein, Current Topics in Membranes and Transport, Elsevier, 1984, vol. 21, pp. 295–308 Search PubMed
.
- Q. Al-Awqati, Nat. Cell Biol., 1999, 1, E201 CrossRef CAS
.
- K. P. Lee, T. C. Arnot and D. Mattia, J. Membr. Sci., 2011, 370, 1–22 CrossRef CAS
.
- R. M. Venable, A. Krämer and R. W. Pastor, Chem. Rev., 2019, 119, 5954–5997 CrossRef CAS
.
- D. Shasby, S. Shasby, J. Sullivan and M. Peach, Circ. Res., 1982, 51, 657–661 CrossRef CAS
.
-
J. Wingender, T. R. Neu and H.-C. Flemming, Microbial extracellular polymeric substances, Springer, 1999, pp. 1–19 Search PubMed
.
-
E. D. Hay, Cell biology of extracellular matrix, Springer Science & Business Media, 2013 Search PubMed
.
- J. Witten, K. Ribbeck, V. V. Khutoryanskiy, L. Wu, M. Liu, W. Shan, X. Zhu, L. Li, Z. Zhang and Y. Huang, Nanoscale, 2017, 9, 8080 RSC
.
- C. P. Goodrich, M. P. Brenner and K. Ribbeck, Nat. Commun., 2018, 9, 4348 CrossRef
.
- G. Fuhrmann, Nat. Nanotechnol., 2020, 15, 168–169 CrossRef CAS
.
- J. Taipale and J. Keski-Oja, FASEB J., 1997, 11, 51–59 CrossRef CAS
.
- C. J. Dowd, C. L. Cooney and M. A. Nugent, J. Biol. Chem., 1999, 274, 5236–5244 CrossRef CAS
.
- E. W. Raines, Int. J. Clin. Exp. Pathol., 2000, 81, 173–182 CrossRef CAS
.
- A. M. Garcia, N. Szasz, S. B. Trippel, T. I. Morales, A. J. Grodzinsky and E. H. Frank, Arch. Biochem. Biophys., 2003, 415, 69–79 CrossRef CAS
.
- R. G. Thorne, A. Lakkaraju, E. Rodriguez-Boulan and C. Nicholson, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 8416–8421 CrossRef CAS
.
- L. Zhang, B. S. Gardiner, D. W. Smith, P. Pivonka and A. J. Grodzinsky, J. Theor. Biol., 2010, 263, 20–29 CrossRef CAS
.
- A. D. Theocharis, S. S. Skandalis, C. Gialeli and N. K. Karamanos, Adv. Drug Delivery Rev., 2016, 97, 4–27 CrossRef CAS
.
- A. Halperin, M. Kröger and F. M. Winnik, Angew. Chem., Int. Ed., 2015, 54, 15342–15367 CrossRef CAS
.
- D. M. Vriezema, M. Comellas Aragonès, J. A. A. W. Elemans, J. J. L. M. Cornelissen, A. E. Rowan and R. J. M. Nolte, Chem. Rev., 2005, 105, 1445–1490 CrossRef CAS
.
- S. Carregal-Romero, N. J. Buurma, J. Pérez-Juste, L. M. Liz-Marzán and P. Hervés, Chem. Mater., 2010, 22, 3051–3059 CrossRef CAS
.
- M. A. C. Stuart, W. T. S. Huck, J. Genzer, M. Müller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk, M. Urban, F. Winnik, S. Zauscher, I. Luzinov and S. Minko, Nat. Mater., 2010, 9, 101–113 CrossRef
.
- Y. Lu and M. Ballauff, Prog. Polym. Sci., 2011, 36, 767–792 CrossRef CAS
.
- K. Renggli, P. Baumann, K. Langowska, O. Onaca, N. Bruns and W. Meier, Adv. Funct. Mater., 2011, 21, 1241–1259 CrossRef CAS
.
- P. Tanner, P. Baumann, R. Enea, O. Onaca, C. Palivan and W. Meier, Acc. Chem. Res., 2011, 44, 1039–1049 CrossRef CAS
.
- Y. Guan and Y. Zhang, Soft Matter, 2011, 7, 6375–6384 RSC
.
- P. Hervés, M. Pérez-Lorenzo, L. M. Liz-Marzán, J. Dzubiella, Y. Lu and M. Ballauff, Chem. Soc. Rev., 2012, 41, 5577–5587 RSC
.
- S. Wu, J. Dzubiella, J. Kaiser, M. Drechsler, X. Guo, M. Ballauff and Y. Lu, Angew. Chem., Int. Ed., 2012, 51, 2229–2233 CrossRef CAS
.
- J. Gaitzsch, X. Huang and B. Voit, Chem. Rev., 2015, 116, 1053–1093 CrossRef
.
- S. Campisi, M. Schiavoni, C. Chan-Thaw and A. Villa, Catalysts, 2016, 6, 185 CrossRef
.
- G. Prieto, H. Tüysüz, N. Duyckaerts, J. Knossalla, G.-H. Wang and F. Schüth, Chem. Rev., 2016, 116, 14056–14119 CrossRef CAS
.
- S. H. Petrosko, R. Johnson, H. White and C. A. Mirkin, J. Am. Chem. Soc., 2016, 138, 7443–7445 CrossRef CAS
.
- H. Jia, R. Roa, S. Angioletti-Uberti, K. Henzler, A. Ott, X. Lin, J. Möser, Z. Kochovski, A. Schnegg, J. Dzubiella, M. Ballauff and Y. Lu, J. Mater. Chem. A, 2016, 4, 9677–9684 RSC
.
- S. Angioletti-Uberti, Y. Lu, M. Ballauff and J. Dzubiella, J. Phys. Chem. C, 2015, 119, 15723–15730 CrossRef CAS
.
- R. Roa, W. K. Kim, M. Kanduč, J. Dzubiella and S. Angioletti-Uberti, ACS Catal., 2017, 7, 5604–5611 CrossRef CAS
.
- M. Kanduč, W. K. Kim, R. Roa and J. Dzubiella, Mol. Syst. Des. Eng., 2020, 5, 602–619 RSC
.
- L. M. Robeson, J. Membr. Sci., 1991, 62, 165–185 CrossRef CAS
.
- P. Pandey and R. Chauhan, Prog. Polym. Sci., 2001, 26, 853–893 CrossRef CAS
.
- E. Atci, I. Erucar and S. Keskin, J. Phys. Chem. C, 2011, 115, 6833–6840 CrossRef CAS
.
- K. Falk, B. Coasne, R. Pellenq, F.-J. Ulm and L. Bocquet, Nat. Commun., 2015, 6, 6949 CrossRef CAS
.
- A. Obliger, R. Pellenq, F.-J. Ulm and B. Coasne, J. Phys. Chem. Lett., 2016, 7, 3712–3717 CrossRef CAS
.
- B. D. Freeman, Macromolecules, 1999, 32, 375–380 CrossRef CAS
.
- H. B. Park, J. Kamcev, L. M. Robeson, M. Elimelech and B. D. Freeman, Science, 2017, 356, 1137 CrossRef CAS
.
- M. A. Shannon, P. W. Bohn, M. Elimelech, J. G. Georgiadis, B. J. Mariñas and A. M. Mayes, Nature, 2008, 452, 301–310 CrossRef CAS
.
- G. M. Geise, H.-S. Lee, D. J. Miller, B. D. Freeman, J. E. McGrath and D. R. Paul, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 1685–1718 CrossRef CAS
.
- G. M. Geise, H. B. Park, A. C. Sagle, B. D. Freeman and J. E. McGrath, J. Membr. Sci., 2011, 369, 130–138 CrossRef CAS
.
- D. Menne, F. Pitsch, J. E. Wong, A. Pich and M. Wessling, Angew. Chem., Int. Ed., 2014, 53, 5706–5710 CrossRef CAS
.
- B. Tansel, J. Sager, T. Rector, J. Garland, R. F. Strayer, L. Levine, M. Robert, M. Hummerick and J. Bauer, Sep. Purif. Technol., 2006, 51, 40–47 CrossRef CAS
.
- Z. Tan, S. Chen, X. Peng, L. Zhang and C. Gao, Science, 2018, 360, 518–521 CrossRef CAS
.
- W. Hyk and K. Kitka, J. Environ. Chem. Eng., 2018, 6, 6108–6117 CrossRef CAS
.
- C. S. Brazel and N. A. Peppas, Polymer, 1999, 40, 3383–3398 CrossRef CAS
.
- D. F. Stamatialis, B. J. Papenburg, M. Girones, S. Saiful, S. N. Bettahalli, S. Schmitmeier and M. Wessling, J. Membr. Sci., 2008, 308, 1–34 CrossRef CAS
.
- H. Yasuda, A. Peterlin, C. Colton, K. Smith and E. Merrill, Die Makromol. Chem., 1969, 126, 177–186 CrossRef CAS
.
- D. R. Paul, Sep. Purif. Methods, 1976, 5, 33–50 CrossRef CAS
.
- J. Williams and R. W. Baker, J. Membr. Sci., 1995, 107, 1–21 CrossRef
.
- S. Gehrke, J. Fisher, M. Palasis and M. E. Lund, Ann. N. Y. Acad. Sci., 1997, 831, 179–207 CrossRef CAS
.
- S. C. George and S. Thomas, Prog. Polym. Sci., 2001, 26, 985–1017 CrossRef CAS
.
- M. Ulbricht, Polymer, 2006, 47, 2217–2262 CrossRef CAS
.
- A. Missner and P. Pohl, Chem. Phys. Chem., 2009, 10, 1405–1414 CrossRef CAS
.
- R. W. Baker and B. T. Low, Macromolecules, 2014, 47, 6999–7013 CrossRef CAS
.
-
P. Nelson, Biological physics, WH Freeman, New York, 2004 Search PubMed
.
- R. Sander, Atmos. Chem. Phys., 2015, 15, 4399–4981 CrossRef CAS
.
-
R. W. Baker, Membrane Technology and Applications, John Wiley & Sons, Ltd, 2004 Search PubMed
.
- A. Obliger, M. Jardat, D. Coelho, S. Bekri and B. Rotenberg, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 043013 CrossRef
.
- A. Moncho-Jordá and I. Adroher-Bentez, Soft Matter, 2014, 10, 5810–5823 RSC
.
- I. Adroher-Bentez, S. Ahualli, A. Martn-Molina, M. Quesada-Pérez and A. Moncho-Jordá, Macromolecules, 2015, 48, 4645–4656 CrossRef
.
- A. Erbas and M. Olvera de la Cruz, Macromolecules, 2016, 49, 9026–9034 CrossRef CAS
.
- B. Rotenberg, J.-F. Dufreche, B. Bagchi, E. Giffaut, J.-P. Hansen and P. Turq, J. Chem. Phys., 2006, 124, 154701 CrossRef CAS
.
- W. K. Kim, A. Moncho-Jordá, R. Roa, M. Kanduč and J. Dzubiella, Macromolecules, 2017, 50, 6227–6237 CrossRef CAS
.
- L. Pérez-Mas, A. Martín-Molina, M. Quesada-Pérez and A. Moncho-Jordá, Phys. Chem. Chem. Phys., 2018, 20, 2814–2825 RSC
.
- M. Kanduč, W. K. Kim, R. Roa and J. Dzubiella, ACS Nano, 2019, 13, 11224–11234 CrossRef
.
- H. Yasuda, C. Lamaze and L. D. Ikenberry, Die Makromol. Chem., 1968, 118, 19–35 CrossRef CAS
.
- H. Yasuda, L. Ikenberry and C. Lamaze, Die Makromol. Chem., 1969, 125, 108–118 CrossRef CAS
.
- I. C. Kim and S. Torquato, J. Chem. Phys., 1992, 96, 1498–1503 CrossRef CAS
.
- L. Masaro and X. Zhu, Prog. Polym. Sci., 1999, 24, 731–775 CrossRef CAS
.
- B. Amsden, Macromolecules, 1998, 31, 8382–8395 CrossRef CAS
.
- A. P. Chatterjee, J. Phys.: Condens. Matter, 2011, 23, 375103 CrossRef
.
- Y. Jiao and S. Torquato, Phys. Biol., 2012, 9, 036009 CrossRef
.
- M. Spanner, S. K. Schnyder, F. Höfling, T. Voigtmann and T. Franosch, Soft Matter, 2013, 9, 1604–1611 RSC
.
- A. Godec, M. Bauer and R. Metzler, New J. Phys., 2014, 16, 092002 CrossRef
.
- H. Liasneuski, D. Hlushkou, S. Khirevich, A. Höltzel, U. Tallarek and S. Torquato, J. Appl. Phys., 2014, 116, 034904 CrossRef
.
- X. Zhang, J. Hansing, R. R. Netz and J. E. DeRouchey, Biophys. J., 2015, 108, 530–539 CrossRef CAS
.
- J. Hansing, C. Ciemer, W. K. Kim, X. Zhang, J. E. DeRouchey and R. R. Netz, Eur. Phys. J. E: Soft Matter Biol. Phys., 2016, 39, 53 CrossRef
.
- J. Hansing, J. R. Duke III, E. B. Fryman, J. E. DeRouchey and R. R. Netz, Nano Lett., 2018, 18, 5248–5256 CrossRef CAS
.
- J. Hansing and R. R. Netz, Macromolecules, 2018, 51, 7608–7620 CrossRef CAS
.
- J. Hansing and R. R. Netz, Biophys. J., 2018, 114, 2653–2664 CrossRef CAS
.
- W. K. Kim, M. Kanduč, R. Roa and J. Dzubiella, Phys. Rev. Lett., 2019, 122, 108001 CrossRef CAS
.
- P. Jha, J. Zwanikken, F. Detcheverry, J. de Pablo and M. Olvera de la Cruz, Soft Matter, 2011, 7, 5965–5975 RSC
.
- M. Quesada-Pérez, J. Ramos, J. Forcada and A. Martín-Molina, J. Chem. Phys., 2012, 136, 244903 CrossRef
.
- P. Košovan, T. Richter and C. Holm, Macromolecules, 2015, 48, 7698–7708 CrossRef
.
- H. Kobayashi and R. G. Winkler, Sci. Rep., 2016, 6, 19836 CrossRef CAS
.
- A. Schmid, J. Dubbert, A. A. Rudov, J. Pedersen, P. Lindner, M. Karg, I. Potemkin and W. Richtering, Sci. Rep., 2016, 22736 CrossRef CAS
.
- I. Zadok and S. Srebnik, J. Phys. Chem. B, 2018, 122, 7091–7101 CrossRef CAS
.
- M. Kanduč, W. K. Kim, R. Roa and J. Dzubiella, Macromolecules, 2018, 51, 4853–4864 CrossRef
.
- H. Takeuchi and K. Okazaki, J. Chem. Phys., 1990, 92, 5643–5652 CrossRef CAS
.
- J. Sonnenburg, J. Gao and J. Weiner, Macromolecules, 1990, 23, 4653–4657 CrossRef CAS
.
- F. Müller-Plathe, J. Chem. Phys., 1991, 94, 3192–3199 CrossRef
.
- R. Sok, H. Berendsen and W. Van Gunsteren, J. Chem. Phys., 1992, 96, 4699–4704 CrossRef CAS
.
- F. Müller-Plathe, Acta Polym., 1994, 45, 259–293 CrossRef
.
- P. A. Netz and T. Dorfmüller, J. Chem. Phys., 1997, 107, 9221–9233 CrossRef CAS
.
- D. Hofmann, L. Fritz, J. Ulbrich, C. Schepers and M. Böhning, Macromol. Theory Simul., 2000, 9, 293–327 CrossRef CAS
.
- H. Zhou and S. B. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 021801 CrossRef
.
- H. Masoud and A. Alexeev, Macromolecules, 2010, 43, 10117–10122 CrossRef CAS
.
- L. Wang, R. S. Dumont and J. M. Dickson, J. Chem. Phys., 2013, 138, 124701 CrossRef
.
- H. Li, A. Erbas, J. Zwanikken and M. Olvera de la Cruz, Macromolecules, 2016, 49, 9239–9246 CrossRef CAS
.
- D. Sandrin, D. Wagner, C. Sitta, R. Thoma, S. Felekyan, H. Hermes, C. Janiak, N. de Sousa Amadeu, R. Kühnemuth and H. Löwen,
et al.
, Phys. Chem. Chem. Phys., 2016, 18, 12860–12876 RSC
.
- L. Wang, R. S. Dumont and J. M. Dickson, RSC Adv., 2016, 6, 63586–63596 RSC
.
- M. Ding, A. Szymczyk and A. Ghoufi, J. Membr. Sci., 2016, 501, 248–253 CrossRef CAS
.
- K. Zhang and S. K. Kumar, ACS Macro Lett., 2017, 6, 864–868 CrossRef CAS
.
- K. Zhang, D. Meng, F. Müller-Plathe and S. K. Kumar, Soft Matter, 2018, 14, 440–447 RSC
.
- P. Higgs and R. Ball, J. Phys. France, 1988, 49, 1785–1811 CrossRef CAS
.
- E. Geissler, F. Horkay and A.-M. Hecht, Phys. Rev. Lett., 1993, 71, 645 CrossRef CAS
.
- G. Glatting, R. Winkler and P. Reineker, Macromolecules, 1995, 28, 5906–5909 CrossRef CAS
.
- J. S. Soares and P. Zunino, Biomaterials, 2010, 31, 3032–3042 CrossRef CAS
.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- Y. F. Yue, M. A. Haque, T. Kurokawa, T. Nakajima and J. P. Gong, Adv. Mater., 2013, 25, 3106–3110 CrossRef CAS
.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS
.
- A. Erbas and M. Olvera de la Cruz, ACS Macro Lett., 2015, 4, 857–861 CrossRef CAS
.
- J. Heyda, A. Muzdalo and J. Dzubiella, Macromolecules, 2013, 46, 1231–1238 CrossRef CAS
.
- S. Milster, R. Chudoba, M. Kanduč and J. Dzubiella, Phys. Chem. Chem. Phys., 2019, 21, 6588–6599 RSC
.
- J. Shin, A. G. Cherstvy, W. K. Kim and V. Zaburdaev, Phys. Chem. Chem. Phys., 2017, 19, 18338–18347 RSC
.
- D. N. Theodorou and U. W. Suter, Macromolecules, 1985, 18, 1206–1214 CrossRef CAS
.
- P. Fu and Y. F. Dafalias, Int. J. Solids Struct., 2015, 63, 68–81 CrossRef
.
- H. Eslami, F. Mozaffari, J. Moghadasi and F. Müller-Plathe, J. Chem. Phys., 2008, 129, 194702 CrossRef
.
- A. Ghoufi, D. Morineau, R. Lefort, I. Hureau, L. Hennous, H. Zhu, A. Szymczyk, P. Malfreyt and G. Maurin, J. Chem. Phys., 2011, 134, 074104 CrossRef
.
- J. Haus and K. Kehr, Phys. Rep., 1987, 150, 263–406 CrossRef CAS
.
- S. K. Ghosh, A. G. Cherstvy and R. Metzler, Phys. Chem. Chem. Phys., 2014, 17, 1847–1858 RSC
.
- N. A. Peppas and C. T. Reinhart, J. Membr. Sci., 1983, 15, 275–287 CrossRef CAS
.
- C. T. Reinhart and N. A. Peppas, J. Membr. Sci., 1984, 18, 227–239 CrossRef CAS
.
- S. R. Lustig and N. A. Peppas, J. Appl. Polym. Sci., 1988, 36, 735–747 CrossRef CAS
.
- P. Kumar, L. Theeyancheri, S. Chaki and R. Chakrabarti, Soft Matter, 2019, 15, 8992–9002 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01083a |
| This journal is © The Royal Society of Chemistry 2020 |