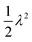Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of temperature in the rigidity-controlled fracture of elastic networks†
Justin
Tauber
 ,
Aimée R.
Kok
,
Aimée R.
Kok
 ,
Jasper
van der Gucht
,
Jasper
van der Gucht
 * and
Simone
Dussi
* and
Simone
Dussi

Physical Chemistry and Soft Matter, Wageningen University, Stippeneng 4, 6708 WE, Wageningen, The Netherlands. E-mail: jasper.vandergucht@wur.nl
First published on 2nd October 2020
Abstract
We study the influence of thermal fluctuations on the fracture of elastic networks, via simulations of the uniaxial extension of central-force spring networks with varying rigidity. Studying their failure response, both at the macroscopic and microscopic level, we find that an increase in temperature corresponds to a more homogeneous stress (re)distribution and induces thermally activated failure of springs. As a consequence, the material strength decreases upon increasing temperature, the microscopic damage spreads over a larger area and a more ductile fracture process is observed. These effects are modulated by network rigidity and can therefore be tuned via the network connectivity and the rupture threshold of the springs. Knowledge of the interplay between temperature and rigidity improves our understanding of the fracture of elastic network materials, such as (biological) polymer networks, and can help to refine design principles for tough soft materials.
1 Introduction
Many soft materials have a microstructure that consists of a disordered network. The building blocks that constitute this network range from stiff fibers1 in paper or textiles, to semiflexible filaments in biological cells and tissues,2–4 to flexible polymer chains in elastomers.5 The network architecture is known to be important for the mechanical response and failure of these materials;1,2,6,7 yet, most theoretical studies describe the failure response via continuum mechanics8 or using a mean-field approach,9 which ignore details of the network topology and neglect the role of structural disorder. Such models thus cannot provide a microscopic understanding of the failure process. Therefore, coarse-grained network models have been developed, which treat the material as a disordered network of elastic springs, and which explicitly take connectivity and disorder into account.10–13 Recent computational studies, complemented with experiments on architectured elastic networks, have shown that under athermal and quasistatic conditions the elastic response and failure behaviour of an elastic network is controlled by both the connectivity of the network and the strength of the individual elements.12–15 The network architecture, in particular its connectivity, determines the network rigidity. Commonly, the average connectivity of a random network is described using the average number of bonds per crosslink. Central-force spring networks, where the elements only resist stretching, are rigid above a connectivity 2d, with d the dimensionality of the network; this is called the isostatic point.16 Below the isostatic point, central-force spring networks are mechanically floppy. However, simulations have shown that even floppy or sub-isostatic networks can be rigidified by an external deformation13,17,18 or by the presence of additional interactions such as a bending rigidity.6,10,11,19–23 These recent studies suggest that if the static network structure and the element strength of a soft athermal material are known, the material response can be predicted based on the physical concept of rigidity.However, these athermal network models completely ignore thermal fluctuations. While this may be justified for networks composed of very stiff fibers, it is highly questionable for softer networks. For example, the mechanics of flexible polymer networks, such as elastomers and hydrogels, are known to be governed by thermal fluctuations and entropy, while network connectivity is usually not taken into consideration.24,25 This raises the question how connectivity and thermal fluctuations interplay for networks consisting of fibers of intermediate stiffness, as found, for example, in many biological materials. Recent Monte Carlo simulations for such networks suggest that in the presence of thermal fluctuations the linear modulus is dependent on both rigidity and temperature. In particular, it is shown that thermal fluctuations can stabilize (sub-isostatic) central-force spring networks at the network level in a similar way to bending interactions.26,27 Also, when looking at failure, it is predicted that the average external force required to break a single element or bond is typically reduced in presence of thermal fluctuations.28,29 However, experiments on polymer networks30 that demonstrate the presence of this thermally activated failure process in network materials also imply that in networks the thermally activated failure is enhanced. These results suggest that, when thermal fluctuations are present, the elastic and failure response can be controlled by temperature, but also by the structure of the network. However, it remains unclear how these two parameters together govern the failure process.
In this paper we explore to what extent network rigidity controls the influence of thermal fluctuations on the failure behaviour of an elastic material. To this end, we study the response of diluted central-force spring networks (see Fig. 1), similar to previous studies.12–14,26,27 To introduce thermal fluctuations into these systems we perform Langevin dynamics simulations, which means that the networks are effectively embedded in an implicit solvent. We find that the strength of the networks is dependent on temperature and that the effect of the thermal fluctuations is coupled to the rigidity of the network. The simple structure of the model allows us to highlight the interplay between rigidity and temperature, and to provide insight in the underlying microscopic mechanisms of stress homogenization and diffuse failure.
2 Model and methods
We consider diluted spring networks with a 2D triangular topology consisting of L × L nodes separated by a distance![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. Nearest neighbors are connected by bonds, which gives a maximum network connectivity zmax = 6. The network is subsequently randomly diluted by removing a fraction 1 − p of the bonds, such that the average connectivity becomes 〈z〉 = pzmax. Periodic boundary conditions are employed in all directions. The bonds are harmonic (linear) springs with spring constant μ and rest length
0. Nearest neighbors are connected by bonds, which gives a maximum network connectivity zmax = 6. The network is subsequently randomly diluted by removing a fraction 1 − p of the bonds, such that the average connectivity becomes 〈z〉 = pzmax. Periodic boundary conditions are employed in all directions. The bonds are harmonic (linear) springs with spring constant μ and rest length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. Excluded volume interactions are not present in the system. During fracture simulations, bonds break irreversibly when their relative extension Δ
0. Excluded volume interactions are not present in the system. During fracture simulations, bonds break irreversibly when their relative extension Δ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /
/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 exceeds a rupture threshold λ, which is the same for all the springs. We will focus on networks with λ = 0.03.
0 exceeds a rupture threshold λ, which is the same for all the springs. We will focus on networks with λ = 0.03.
Simulations are performed using LAMMPS31 and nodes follow Langevin dynamics:
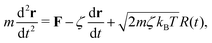 | (1) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , m is the mass, ζ is a friction coefficient, kB the Boltzmann's constant, T the temperature and R(t) white noise with zero-mean. The terms on the right hand side of eqn (1) describe all the contributions to the movement of the nodes: the elastic interaction with the network via the springs (first term), a velocity dependent friction term with the implicit solvent (second term), and a stochastic term which represents random kicks from the molecules in the implicit solvent (third term). The simulation is performed in reduced units with
, m is the mass, ζ is a friction coefficient, kB the Boltzmann's constant, T the temperature and R(t) white noise with zero-mean. The terms on the right hand side of eqn (1) describe all the contributions to the movement of the nodes: the elastic interaction with the network via the springs (first term), a velocity dependent friction term with the implicit solvent (second term), and a stochastic term which represents random kicks from the molecules in the implicit solvent (third term). The simulation is performed in reduced units with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 = 1 as the unit for distance, m = 1 the unit for mass,
0 = 1 as the unit for distance, m = 1 the unit for mass, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) = 1 the unit for energy and kB = 1 the Boltzmann constant. By replacing these reduced units with values corresponding to an experimental system, the results of this model can be expressed in terms relevant for that system. The integration time step is set to δt = 0.001τ, where
= 1 the unit for energy and kB = 1 the Boltzmann constant. By replacing these reduced units with values corresponding to an experimental system, the results of this model can be expressed in terms relevant for that system. The integration time step is set to δt = 0.001τ, where 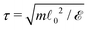 is the unit time of our simulations. The spring stiffness is set to μ = 2000
is the unit time of our simulations. The spring stiffness is set to μ = 2000![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) /
/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 02. In our analysis, we will use the reduced temperature T* = kBT/(μ
02. In our analysis, we will use the reduced temperature T* = kBT/(μ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 02), indicating the ratio between thermal and elastic energies. We set the friction with the implicit solvent to ζ = 10
02), indicating the ratio between thermal and elastic energies. We set the friction with the implicit solvent to ζ = 10![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) τ/
τ/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 02. The friction coefficient controls how quickly fluctuations in the system are damped by the implicit solvent. A high friction coefficient, e.g. a high solvent viscosity, results in fast damping of fluctuations, while a low friction coefficient results in slow damping of fluctuations so that inertia plays a dominant role in the system dynamics. The friction coefficient chosen here corresponds to the intermediate (underdamped) regime. In addition, we can define a time scale τ0 = ζ/μ, the time that a node requires to travel a distance
02. The friction coefficient controls how quickly fluctuations in the system are damped by the implicit solvent. A high friction coefficient, e.g. a high solvent viscosity, results in fast damping of fluctuations, while a low friction coefficient results in slow damping of fluctuations so that inertia plays a dominant role in the system dynamics. The friction coefficient chosen here corresponds to the intermediate (underdamped) regime. In addition, we can define a time scale τ0 = ζ/μ, the time that a node requires to travel a distance ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 if it is subjected to a force μ
0 if it is subjected to a force μ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. For our set of simulations τ0 = 5 × 10−3τ.
0. For our set of simulations τ0 = 5 × 10−3τ.
2.1 Measuring linear modulus and non-affinity
We calculate the linear Young modulus E from the difference in average stress at 0% strain and 1.5% strain. At both strain values the system is equilibrated for 100τ and averaged over 1900τ. The stress σ is defined as the yy-component (along the deformation axis) of the virial stress tensor normalized by μ. In the manuscript we only show the virial stress based on mechanical interactions. Inclusion of the kinetic component of the virial stress does not change the conclusions of this paper (see ESI,† Fig. S3). Due to the thermal fluctuations a hydrostatic component is present, even at 0% strain (see ESI,† Fig. S4). Analysis using the deviatoric stress shows that substracting the hydrostatic component does not alter our conclusion (see ESI,† Fig. S5). We also calculate the non-affinity parameter defined as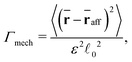 | (2) |
![[r with combining macron]](https://www.rsc.org/images/entities/b_char_0072_0304.gif) is the time averaged position of the individual nodes after an applied deformation and
is the time averaged position of the individual nodes after an applied deformation and ![[r with combining macron]](https://www.rsc.org/images/entities/b_char_0072_0304.gif) aff the position assuming an affine displacement with respect to the time averaged position of individual nodes at rest. ε is the strain and 〈·〉 indicates the average over all nodes. For these simulations, both non-percolating clusters and primary dangling ends (i.e. nodes that are only connected to one bond after dilution) are iteratively removed from the network.
aff the position assuming an affine displacement with respect to the time averaged position of individual nodes at rest. ε is the strain and 〈·〉 indicates the average over all nodes. For these simulations, both non-percolating clusters and primary dangling ends (i.e. nodes that are only connected to one bond after dilution) are iteratively removed from the network.
2.2 Non-linear elasticity and fracture
The network is uniaxially deformed in the y-direction up to 100% strain with a fixed strain rate of![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 0.001τ−1 (i.e. 0.0001% deformation per unit time) while the lateral size is kept constant. We remap the node positions between time steps, temporarily enforcing affine deformation. The deformation is relatively slow compared to the τ0,
= 0.001τ−1 (i.e. 0.0001% deformation per unit time) while the lateral size is kept constant. We remap the node positions between time steps, temporarily enforcing affine deformation. The deformation is relatively slow compared to the τ0, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 5 × 10−6τ0−1, which indicates the system has time to respond to the affine deformation via structural rearrangements. Results for varying
= 5 × 10−6τ0−1, which indicates the system has time to respond to the affine deformation via structural rearrangements. Results for varying ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) are reported in the ESI† (see Fig. S7). A quick equilibration run of 50τ precedes the deformation. The network response is quantified by looking at the stress σ as a function of strain ε. In addition, we follow the instantaneous non-affine response
are reported in the ESI† (see Fig. S7). A quick equilibration run of 50τ precedes the deformation. The network response is quantified by looking at the stress σ as a function of strain ε. In addition, we follow the instantaneous non-affine response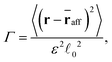 | (3) |
In fracture simulations bonds are broken every 100 steps (i.e. 0.1τ) when the connected nodes are separated by a distance more than ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 + λ
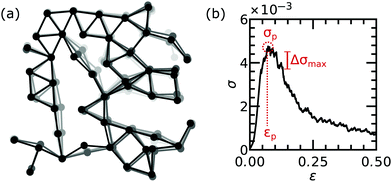
0 + λ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0. While the interval chosen for the evaluation of rupture events influences the stress–strain curves somewhat, it does not affect the conclusions of our paper (see ESI,† Fig. S8 and S9). From the measured stress–strain curves we extract several quantities (see Fig. 1). All quantities are averaged over several configurations and expressed in reduced units. The peak stress σp is defined as the highest measured stress, and the peak strain εp is its corresponding strain value. The maximum stress drop Δσmax is calculated according to a procedure13,32 where we (i) calculate the derivative of the stress–strain curve, (ii) make a list of consecutive data points which have a negative derivative and note the initial and final strain of each interval, (iii) calculate the stress drops by subtracting the stress at the final strain from the stress at the initial strain, (iv) identify the largest stress interval, which corresponds to maximum stress drop Δσmax. For the stress distribution analysis, we make instantaneous histograms of the bond lengths
0. While the interval chosen for the evaluation of rupture events influences the stress–strain curves somewhat, it does not affect the conclusions of our paper (see ESI,† Fig. S8 and S9). From the measured stress–strain curves we extract several quantities (see Fig. 1). All quantities are averaged over several configurations and expressed in reduced units. The peak stress σp is defined as the highest measured stress, and the peak strain εp is its corresponding strain value. The maximum stress drop Δσmax is calculated according to a procedure13,32 where we (i) calculate the derivative of the stress–strain curve, (ii) make a list of consecutive data points which have a negative derivative and note the initial and final strain of each interval, (iii) calculate the stress drops by subtracting the stress at the final strain from the stress at the initial strain, (iv) identify the largest stress interval, which corresponds to maximum stress drop Δσmax. For the stress distribution analysis, we make instantaneous histograms of the bond lengths ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) i during the simulation at every percent strain. Based on these histograms, we calculate the excess kurtosis
i during the simulation at every percent strain. Based on these histograms, we calculate the excess kurtosis
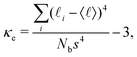 | (4) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 〉 the average bond length. For all these parameters the standard error is calculated as the standard deviation divided by the number of sampled configurations (standard error of the mean). The errors are shown when they are larger than the symbols displayed in the graphs.
〉 the average bond length. For all these parameters the standard error is calculated as the standard deviation divided by the number of sampled configurations (standard error of the mean). The errors are shown when they are larger than the symbols displayed in the graphs.
3 Results and discussion
Using Langevin dynamics simulations, we uniaxially deform diluted triangular central-force spring networks to study both linear and non-linear network mechanics. By analyzing the network response on both a macroscopic and microscopic level, we gain insight into the effects of thermal fluctuations on the fracture process of spring networks as well as how the rigidity controlled failure of networks is affected by thermal fluctuations. Throughout the manuscript we use the reduced temperature T* = kBT/(μ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 02) which is a measure for the energy of the thermal fluctuations relative to the energy required to extend the springs in the network.
02) which is a measure for the energy of the thermal fluctuations relative to the energy required to extend the springs in the network.
3.1 The effect of thermal fluctuations on linear elasticity
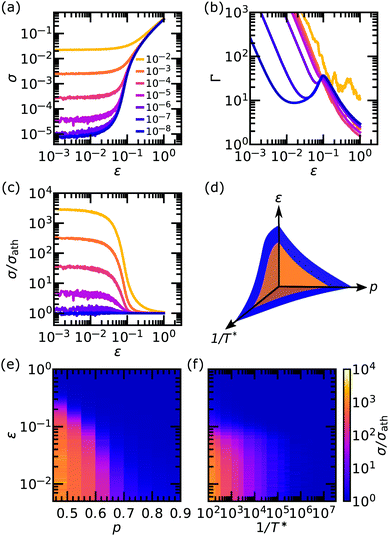
First, we study the effects of thermal fluctuations on the linear elasticity of central-force spring networks to check if the rigidity-dependent elasticity observed via Monte Carlo simulations,26,27 an equilibrium method, can also be observed in our dynamical model based on the Langevin equation (eqn (1)).In Fig. 2(a) we plot the linear modulus E of the network as a function of the network connectivity factor p for several reduced temperatures T*. The linear modulus E describes the resistance of a network to deformation and we observe that networks below the isostatic point of mechanical stability16 (i.e. networks below piso ≈ 0.66) display a finite linear modulus E, which would be absent for athermal systems (in the limit of T = 0). This finite E is an effect of entropic stiffness, a temperature-dependent phenomenon. Please note that this entropic stiffness is a network effect and is not the same as the entropic elasticity arising from individual polymer chains. As reported in literature,26,27 the scaling of the linear modulus with temperature E ∝ Tα depends on both connectivity and temperature itself. By plotting E as a function of T* we extract the scaling exponent α from a power-law fit for three different values of p, as shown in Fig. 2(b). For a sub-isostatic network with a connectivity parameter p = 0.55 the linear modulus scales with α = 0.84, which roughly corresponds to the dependence found in the anomalous regime as defined in ref. 26, where a shear deformation was instead considered. It was argued that the disordered network structure causes this sub-linear dependence. Whilst there is a clear dependence of the linear modulus on the temperature below the isostatic point, the curves for the different temperatures start to converge when approaching a structurally rigid network (Fig. 2(a)). Accordingly, stiff networks display temperature insensitivity (α ≈ 0), as can be seen for a network with p = 0.70 in Fig. 2(b). As T* increases, however, the network connectivity becomes less important as the energetic contribution arising from the structural rigidity becomes negligible compared to the entropic elasticity. This is noticeable in Fig. 2(a) where the curve for T* = 10−2 is roughly flat for the entire p-range, and also in Fig. 2(b) where for p = 0.70, E increases for T* > 10−3. As predicted in ref. 26, we also find a different scaling for networks close to the isostatic point, see, e.g., the curve for p = 0.62 in Fig. 2(b). Although the exponent α is slightly different from the findings of ref. 26 (where shear deformation and different simulation methods were employed), we were also able to obtain critical rescaling as shown in Fig. 2(c). We can conclude that there are different regimes of dependence for the linear modulus on the temperature based on both rigidity and temperature.
 | ||
| Fig. 2 Characterization of the linear elastic response for diluted triangular networks of fixed system size L = 128. (a) Young's modulus E as a function of the connectivity parameter p for different temperatures T*. (b) Temperature dependence of E for networks below, around, and above the isostatic point (value of p indicated in the legend). The dashed lines indicate the power-law fit Tα. (c) Rescaling of Young's modulus according to ref. 26 with a = 1.4, b = 2.8, and zc = 3.78. (d) The non-affinity parameter Γmech at 1.5% strain as a function of p for different temperatures, same legend as (a). Every data point is based on simulations of at least 10 independent configurations. | ||
Furthermore, we find similar rigidity-dependent behaviour of the thermal fluctuations in the non-affinity parameter Γmech (eqn (2)), reported in Fig. 2(d) as a function of p for different T*. The non-affinity of the network describes how much the time-averaged local deformation differs from the global (externally imposed) deformation. At low T* we find a peak in non-affine deformation around the isostatic point (p ≈ 0.66). This peak arises from the tendency of the spring network to minimize internal stress upon deformation. If the spring network is far below the isostatic point, the stress can be reduced significantly by a small amount of non-affine rearrangements while at the isostatic point many non-affine rearrangements are required. At the isostatic point, an increase in T* decreases Γmech, which suggests that thermal fluctuations act as a stabilizing field, similar to the bending rigidity in fiber networks.10 However, we note that the effect of thermal fluctuations is always present, even without external deformations, leading to structural rearrangements in the rest state (see ESI,† Fig. S1). Above the isostatic point, we observe that the non-affinity converges for most values of T* (see ESI,† Fig. S1 for details), which indicates that above the isostatic point the network rigidity dominates the non-affine response. Only if T* > 10−4, we see that thermal fluctuations affect the non-affine response, increasing Γmech. This is in contrast to fiber networks, where the non-affinity decreases with an increase in bending rigidity. We hypothesize that this difference occurs because in the case of fiber networks the fibers have a preference to remain straight to minimize stress caused by fiber bending, while in the case of thermal fluctuations an affine displacement of the nodes will not minimize the stress caused by the randomly oriented thermal fluctuations. Below the isostatic point, the effect of thermal fluctuations on the non-affine response is significant. We observe that at T* = 10−8 the non-affine response is the smallest and that a moderate increase in T* up to T* = 10−6 leads to an increase in the non-affine response, corresponding to what is observed for fiber networks. However, we also observe a decrease in Γmech if the temperature is increased beyond T* = 10−6, which is not observed in fiber networks. It is unclear if this deviation is caused by a fundamental difference between thermal fluctuations and bending rigidity as a stabilizing field or that longer equilibration times are required to gain quantitative information on the non-affine response in this regime (see ESI,† Fig. S1 and S2 for details).
In general, we find that at a global level thermal fluctuations act as a stabilizing field in central-force spring networks, dampening rigidity-dependent behaviour around the isostatic point. However, our results suggest that the random nature of the thermal fluctuations causes significant differences in the local response with respect to stabilizing fields in athermal systems such as bending.
3.2 The effect of thermal fluctuations on non-linear elasticity
In the previous section, we have shown that thermal fluctuations rigidify sub-isostatic networks. Here, we analyze the non-linear elasticity of unbreakable networks to quantify the effect of temperature when networks become more and more strained. The strain-stiffening observed for sub-isostatic networks in the athermal limit has been extensively studied.6,11,18,19,33–36 In Fig. 3(a), we report the stress–strain curves for a network with p = 0.56 at different temperatures. It is evident that the network strain-stiffens for all the T* investigated. We observe that the onset of strain-stiffening is barely dependent on temperature. Furthermore, the stress response becomes independent of T* at high strains, similarly to what has been observed for other stabilizing fields, e.g. bending.11,19Signatures of strain-stiffening can also be observed in the non-affine response of the network. In Fig. 3(b), we report the instantaneous non-affinity parameter Γ, that intrinsically includes both the non-affine contributions from instantaneous thermal fluctuations and structural rearrangements. As a result, high non-affinity values can be observed at low strains, where the size of the non-affine thermal fluctuations is large compared to the applied strain. At low temperatures, a peak can be observed in the non-affine response around the onset strain. At high temperatures, this peak is overshadowed by the non-affine thermal fluctuations. At high strain, the network elasticity is controlled by stretching of the bonds and the network response becomes increasingly affine for most temperatures. Only at T* = 10−2, the non-affine fluctuations are still visible.
To disentangle the effects of temperature and network connectivity, we normalize the stress–strain curve with the ones obtained in the athermal energy-dominated limit. In particular, we plot the stress ratio σ/σath in Fig. 3(c), where we used the data obtained at T* = 10−8 for σath. At this temperature the network behaves according to a network in the athermal limit, but still a small amount of stress is observed i.e. the stress is not zero at small strains even below the isostatic point. A ratio of σ/σath ≈ 1 implies that the mechanical behaviour is basically insensitive to variations in temperature. As can be seen in Fig. 3(c) for a network with p = 0.56, there is a regime of strain in which the stress ratio depends on T* and decreases upon stretching the network more and more. At increasing temperature, this stress ratio is both higher at the start and approaches temperature insensitivity at a higher strain. The start of the decrease in stress ratio for all temperatures occurs at approximately the same strain value, corresponding to the onset of strain-stiffening. This transition could therefore be interpreted as a transition between a regime dominated by thermal fluctuations to a regime dominated by bond stretching. This is analogous to the bending-to-stretching transition observed in fiber networks.11,33,37 We summarize these observations in a mechanical phase diagram sketched in Fig. 3(d), where we can distinguish two regimes: a mechanically-dominated regime (blue) where structural rigidity overpowers the effect of thermal fluctuations and a temperature-controlled regime (orange) where thermal fluctuations play a more important role in the elastic behaviour. The transition between these regimes depends on the reduced temperature T* (and therefore both on the actual temperature T and the bond stiffness μ), the connectivity parameter p and the strain ε. This transition is in general very gradual as can be seen in the two cross-sections of the mechanical phase diagram reported in Fig. 3(e and f) where we show the stress ratio obtained by some of our simulations. When T* is fixed (Fig. 3(e)) and we increase p, we observe a steep decrease in the strain associated to the thermal-stretching transition. Above the isostatic point, the mechanics of the rigid networks is barely affected by thermal fluctuations at this temperature. In Fig. 3(f), we observe that with increasing temperature the stress ratio increases but the strain characterizing the transition seems to reach a limiting value. This limiting value is a result of the onset of strain-stiffening, which is independent of temperature and corresponds to the transition to the elastic regime.
In summary, we identified a rigidity-dependent transition between two regimes where thermal fluctuations are or are not important. In the following sections, we will investigate whether this underlying transition also influences the fracture of these elastic networks.
3.3 The effect of thermal fluctuations on macroscopic fracture
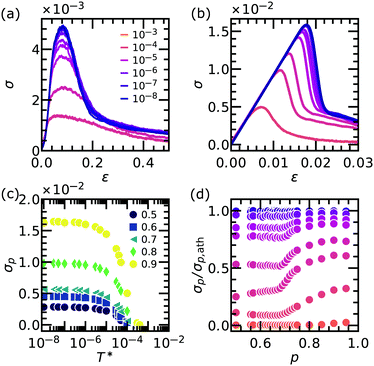
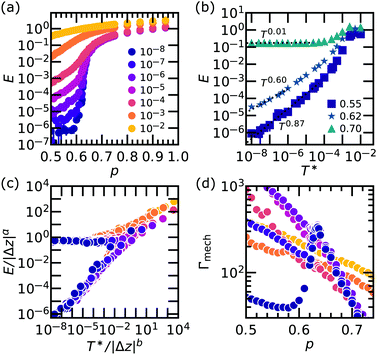
Under athermal conditions, bonds break only after the onset strain, as only at this stage the bonds are under tension. Furthermore, Fig. 3 indicates that the contribution of the thermal fluctuations to the stress in the system is significantly reduced beyond the onset strain. Does this mean that there is only a minor influence of temperature on the failure response?We first focus on macroscopic descriptors and characterize the stress–strain curves obtained from fracture simulations. In Fig. 4(a and b), we show the response of two representative networks with a small rupture threshold λ = 0.03 and different connectivities at several temperatures T*. For the network with p = 0.65 ≃ piso (panel a), a clear decrease in peak stress σp for increasing T* is observed, while a variation in the peak strain εp is less evident as the fracture becomes more ductile and the decrease in stress after the peak is less pronounced. For the very rigid network (p = 0.90, panel b), the decrease in both σp and εp is clearly observed. Similarly, the fracture becomes more ductile for higher T*, even though a clear stress drop is still recognizable at the highest temperature simulated. In both cases, the networks become weaker with increasing T*. Furthermore, when approaching the athermal limit (T* → 0) the peak stress becomes less sensitive to variation in temperature. In Fig. 4(c), we show the temperature dependence of σp for several connectivities with λ = 0.03. The common trend is little variation at low temperatures, almost a plateau that is indicative of approaching the athermal limit, followed by a decrease when temperature is increased, with σp eventually dropping to zero when a temperature of T* ≃ 10−4 is reached. On the one hand, for low T* the peak stress is evidently controlled by the network rigidity, as previously investigated in the athermal limit.12,13 On the other hand, when the thermal energy is of the order of 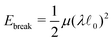 the network structure is irrelevant, as springs spontaneously break and the system shows melting behaviour. We will later describe the melting point using the reduced quantity
the network structure is irrelevant, as springs spontaneously break and the system shows melting behaviour. We will later describe the melting point using the reduced quantity 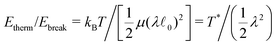 . In between these limits, there is a broad cross-over regime. To better assess the role of rigidity in this intermediate regime, we normalize σp by its value in the athermal limit σp,ath and plot this ratio in Fig. 4(d). The transition between the athermal limit, where σp/σp,ath = 1, and the melting limit, where such a ratio goes to zero, depends on a subtle coupling between connectivity and temperature itself. Far below (p < 0.60) and far above the isostatic point (p > 0.80) the connectivity plays a small role since at every temperature the curve exhibits two plateaus (at small and large p). However, around the isostatic point rigidity and thermal fluctuations are coupled, since at all the intermediate temperatures we can observe a sharp increase in σp/σp,ath upon increasing p, connecting the two limiting plateaus. On passing, we note that the plateau for small p is lower, suggesting that temperature starts to affect failure of very diluted networks earlier than for networks with large p. Furthermore, we speculate that the complex temperature-dependence around the isostatic point arises from locally floppy regions that are rigidified by thermal fluctuations (whose magnitude depends on temperature itself) and are therefore able to sustain and concentrate stress, and break. Since the isostatic point marks the onset of mechanical stability, such an effect is largest for networks close to it.
. In between these limits, there is a broad cross-over regime. To better assess the role of rigidity in this intermediate regime, we normalize σp by its value in the athermal limit σp,ath and plot this ratio in Fig. 4(d). The transition between the athermal limit, where σp/σp,ath = 1, and the melting limit, where such a ratio goes to zero, depends on a subtle coupling between connectivity and temperature itself. Far below (p < 0.60) and far above the isostatic point (p > 0.80) the connectivity plays a small role since at every temperature the curve exhibits two plateaus (at small and large p). However, around the isostatic point rigidity and thermal fluctuations are coupled, since at all the intermediate temperatures we can observe a sharp increase in σp/σp,ath upon increasing p, connecting the two limiting plateaus. On passing, we note that the plateau for small p is lower, suggesting that temperature starts to affect failure of very diluted networks earlier than for networks with large p. Furthermore, we speculate that the complex temperature-dependence around the isostatic point arises from locally floppy regions that are rigidified by thermal fluctuations (whose magnitude depends on temperature itself) and are therefore able to sustain and concentrate stress, and break. Since the isostatic point marks the onset of mechanical stability, such an effect is largest for networks close to it.
3.4 The effect of thermal fluctuations on microscopic fracture
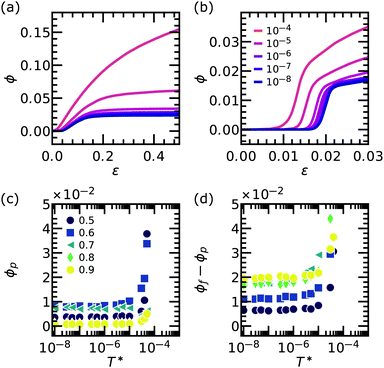
Clearly, the failure response is temperature dependent across the entire connectivity range, but the influence of temperature indeed seems to depend on the distance with respect to the isostatic point i.e. on the network rigidity. Are these differences also apparent at the microscopic level? To investigate this, we monitor the number of broken bonds during the simulations. As shown in Fig. 5(a and b), the fraction of broken bonds ϕ as a function of deformation indicates that higher temperature leads to earlier and overall increased damage. However, the effect of temperature is more significant close to the melting temperature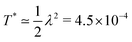 , whereas for lower temperatures the system response is still highly influenced by rigidity. By focusing on the fraction of bonds broken at the peak strain ϕp, counting also the bonds broken during the peak event, as shown in Fig. 5(c), the diverging behaviour when approaching melting is evident. This increase in broken bonds could explain the decrease in material strength σp. The fraction of broken bonds observed here is of the same order of magnitude as the fraction of broken bonds observed in literature for athermal systems where all elements have equal strength.12,13,21 Also the fraction of bonds that break above εp (Fig. 5(d)), the post-peak response, increases close to the melting point, which points towards a prolonged post-peak response, i.e. higher ductility.
, whereas for lower temperatures the system response is still highly influenced by rigidity. By focusing on the fraction of bonds broken at the peak strain ϕp, counting also the bonds broken during the peak event, as shown in Fig. 5(c), the diverging behaviour when approaching melting is evident. This increase in broken bonds could explain the decrease in material strength σp. The fraction of broken bonds observed here is of the same order of magnitude as the fraction of broken bonds observed in literature for athermal systems where all elements have equal strength.12,13,21 Also the fraction of bonds that break above εp (Fig. 5(d)), the post-peak response, increases close to the melting point, which points towards a prolonged post-peak response, i.e. higher ductility.
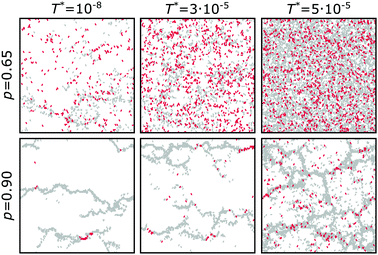
A direct inspection of the simulation snapshots (Fig. 6) suggests that bonds that break up to the peak strain εp (red bonds) are dispersed more homogeneously throughout the sample at a higher temperature. The snapshots also reveal a big difference in the response to temperature between networks around (p = 0.65) and far above the isostatic point (p = 0.90). Around the isostatic point, the damage up to εp is already diffusive in the athermal limit, and its delocalization is enhanced when the temperature is increased. In contrast, the failure response far above the isostatic point shows a clear transition from crack nucleation in the athermal regime to a more diffuse failure response close to the melting point. However, the post peak response at p = 0.90 is clearly still dominated by the propagation of cracks. Nevertheless, at high temperatures we observe the development of multiple cracks, sometimes even not perpendicular to the deformation direction, and evidence of crack merging.
In summary, we show that an increase in temperature leads to an increase in diffuse failure, implying suppression of stress concentration before the peak stress. These observations suggest that thermal fluctuations are responsible for two apparently contrasting effects: on the one hand, they create “instantaneous defects” resulting in more regions with broken bonds, that reduce material strength; on the other hand, the fluctuations allow to delocalize stress away from such defects, delaying the propagation of large cracks. As a result, the damage pattern is diffuse throughout the system.
3.5 Thermal fluctuations increase the length scale of stress redistribution
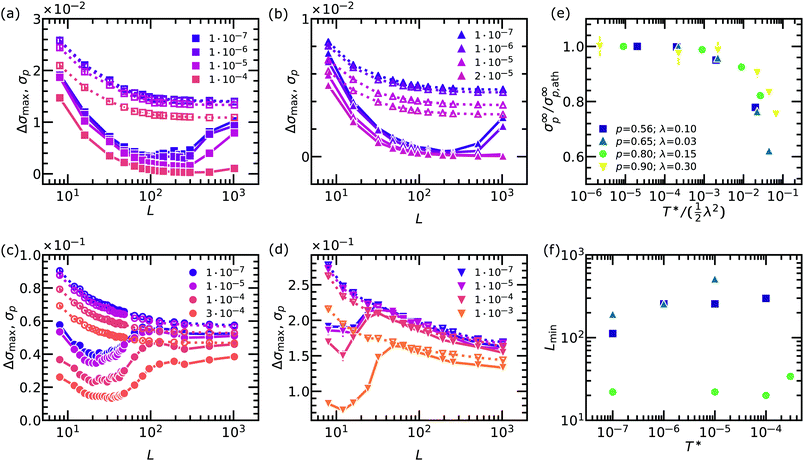
In the last section we have interpreted the effect of thermal fluctuations on the microscopic failure mechanisms in terms of defects and stress concentration. However, it should be realized that the use of these terms in (spring) networks comes with more challenges than the use of these terms in a continuum description of a material. In a disordered network, it proves challenging to identify defects, because the edges of a large void do not necessarily coincide with locations of stress concentration. Moreover, we observe that in networks stress can be redistributed over a large part of the network via non-affine rearrangements of the network. As a result, both the concentration of stress and the failure response in spring networks are dependent on the size of the network. It might therefore be possible to identify a characteristic lengthscale associated to stress concentration (or to stress delocalization) in these spring networks. For example, we have recently13 shown that in athermal systems, brittle (abrupt) fracture always occurs for networks above a certain system size L*. This critical size can be tuned by the network rigidity, i.e. by varying p and λ. The onset of the size-induced brittleness can be determined by looking at the non-monotonic size-dependence of Δσmax. Here we investigate whether temperature affects this critical system size, which can be interpreted as a characteristic lengthscale at which the concentration of stress can be observed. This analysis is therefore another way to further assess the role of temperature on stress concentration.Therefore, we examine how thermal fluctuations affect the macroscopic fracture descriptors for different system sizes, focusing on the maximum stress drop Δσmax that quantifies fracture abruptness. In Fig. 7(a–d), we plot the size-scaling of the maximum stress drop Δσmax (closed symbols) together with the peak stress σp (open symbols) for four combinations of p and λ at different temperatures. In all cases, we observe a monotonic decrease of σp as a function of the system size. These trends can be fitted by a power law σp = (L/α)−β + σ∞p, where σ∞p is the failure stress in the thermodynamic limit (infinite system size), β the size scaling exponent and α a fitting constant. Values for β are comparable to values found in literature.13,22 It is interesting to note that we find a finite value for σ∞p, which is different from many other studies on network failure.38 This is because in our work all elements have the same strength and therefore a finite amount of stress is required at all network sizes to start the failure process. In contrast, some studies reported a vanishing σ∞p since they employed a distribution in element strength extending to zero.38 In Fig. 7(e), we plot σ∞p normalized by its athermal value σ∞p,ath as a function of T* normalized by 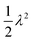 (see ESI,† Fig. S6 for the other fitting parameters). The observed trend underlying a transition from low T* to melting is consistent with the data at fixed system size and fixed rupture threshold λ presented earlier in Fig. 4. Here, we can also appreciate the effect of varying λ in the intermediate temperature regime. For example, the largest λ = 0.30 (downward triangles, networks with p = 0.90) shows a steeper decrease in the normalized fracture stress, suggesting that thermal effects kick in at higher temperatures for these very rigid networks.
(see ESI,† Fig. S6 for the other fitting parameters). The observed trend underlying a transition from low T* to melting is consistent with the data at fixed system size and fixed rupture threshold λ presented earlier in Fig. 4. Here, we can also appreciate the effect of varying λ in the intermediate temperature regime. For example, the largest λ = 0.30 (downward triangles, networks with p = 0.90) shows a steeper decrease in the normalized fracture stress, suggesting that thermal effects kick in at higher temperatures for these very rigid networks.
Finally, we focus on the maximum stress drop Δσmax. From Fig. 7(a–d), we observe that a non-monotonic trend is present in basically all cases, consistent with our previous results in the athermal limit.13 We speculated that the initial decrease, implying a more ductile fracture upon increasing system size, is associated to the rupture and reformation of locally stressed regions (often consisting of aligned springs, and sometimes called force chains12,39–41). However, upon increasing the system size Δσmax starts to increase, suggesting that stress concentration around defects is present in the system, since it fractures in a more abrupt way. At even larger L, Δσmax decreases again, now following the same trend for the peak stress σp that sets the upper bound to the possible stress drop. In Fig. 7(c) the entire trend is visible for the system sizes explored in this work, whereas in the other panels only parts of it are captured. Importantly, for all systems, the trend depends on temperature. In particular, in Fig. 7(f) we quantify the effect of temperature by plotting the system size Lmin corresponding to the minimum Δσmax as a function of T*. We observe that thermal fluctuations increase the value of Lmin, which can be interpreted as a lengthscale for stress concentration. The role of temperature seems particularly relevant at low connectivity, where the stress is already very delocalized in the athermal limit.
In summary, we find that also in the thermodynamic limit there is a crossover from an athermal regime to a melting regime where the failure behaviour is determined by both rigidity and thermal fluctuations. Moreover, thanks to the analysis of Δσmax, we find evidence that temperature increases the region over which stress is delocalized.
3.6 Thermal fluctuations homogenize stress
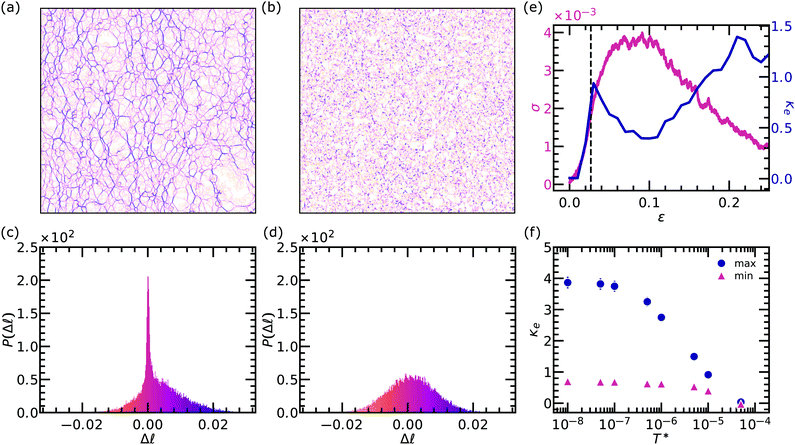
The delocalization of stress is mediated by structural rearrangements in the network. Therefore, if temperature helps to delocalize stress as suggested by Fig. 6 and 7(f), this must be evident in the distribution of stress within the network. In Fig. 8(a and b) we show two snapshots of the same deformed network (p = 0.65) at two different temperatures, together with the associated histograms of the bond deformation Fig. 8(c and d), which is equivalent to the probability distribution of the microscopic stresses since the springs are linear. Both networks are deformed up to 10% strain, which is close to εp and well above the onset strain discussed in Section 3.2. At the lower temperature, the stress is distributed very heterogeneously, as indicated by an asymmetric distribution with an exponential tail containing few bonds carrying a high load. The regions of high stress, typically composed of aligned highly-stressed bonds, that we call force chains, can be readily identified in the simulation snapshot. On the contrary, for the higher temperature, the distribution is symmetric, resembling a Gaussian distribution, and the force chains can not be identified. This indicates that even above the onset strain thermal fluctuations act as a stabilizing field as discussed in Section 3.1 and do affect the distribution of stress in the network. To quantify this heterogeneity, we calculate the excess kurtosis κe of the stress distribution, an indicator of the tail heaviness of a distribution (being zero for a Gaussian). This measure has been recently used to quantify stress heterogeneities in porous materials.42 To illustrate how the heterogeneity of the stress distributions is linked to the macroscopic stress evolution, in Fig. 8(c) we plot both κe and σ as a function of strain for an example simulation run. As observed in most cases, the strain-stiffening of the network is accompanied by a similar increase in kurtosis. The stress distribution becomes more heterogeneous until (approximately) the first bond breaks (the dashed black line in Fig. 8(c)), after which strain softening occurs and the stress distribution becomes more homogeneous. This decrease in heterogeneity is presumably caused by redistribution of the stress after bonds are broken. Strikingly, in correspondence with the peak stress, a local minimum for the kurtosis is observed. The subsequent stress drops are instead accompanied by an increase in κe, and therefore in the microscopic stress heterogeneity. This increase indicates stress concentration somewhere in the network leading to significant bond breakage that does not allow for a larger stress response. To show how the stress heterogeneity changes with temperature, we plot the maximum and the minimum of κe as a function of T* in Fig. 8(d). To determine the minimum kurtosis, we take the smallest value of κe in a strain interval close to the peak strain εp, to avoid lower values that might be found before strain-stiffening. Analogously, for the maximum kurtosis, we only look at the maximum up to and including the peak strain, to avoid post-peak values. Both quantities clearly decrease when the temperature is raised, but follow different curves. In particular, the maximum of κe, that is associated to the network strain-stiffening, is immediately sensitive to temperature changes, in line with our previous observations on the non-linear elasticity (Section 3.2), while the minimum of κe, associated to the fracture peak, exhibits an initial temperature insensitive interval, similarly to the other fracture descriptors investigated above. Furthermore, as the temperature increases, the difference between the maximum and minimum becomes smaller, and eventually both quantities reach zero (homogeneous stress distribution) at the melting temperature. Note that, while we have shown here results only for a given connectivity, the fact that a higher temperature allows for better redistribution of the stress during fracture was a consistent observation in our simulation study.4 Concluding remarks
In this work we explored the relation between rigidity and the failure of central-force spring networks under the influence of thermal fluctuations. Our results demonstrate that thermal fluctuations couple with network rigidity and affect the non-linear mechanics of elastic networks. In general, thermal fluctuations lead to a lower failure strength (Fig. 4), an increased ductility, and an increased fraction of broken bonds (Fig. 5). We have shown that at the microscopic level the failure response is altered with respect to the athermal case in two ways: (i) bond failure can be activated by instantaneous thermal fluctuations, creating additional weak spots, and (ii) stress is delocalized, suppressing the expansion of existing defects (Fig. 6). We reveal that temperature acts as a stabilizing field that resists large structural non-affine deformation within the network (Fig. 2 and 3). Specifically, the thermal fluctuations increase the lengthscale over which stress is redistributed, which can be quantified via the maximum stress drop (Fig. 7) and the excess kurtosis (Fig. 8). Although these trends can be observed for all connectivities, there are distinct damage mechanisms above and below the isostatic point. Above the isostatic point, the failure up to the peak stress shifts from crack nucleation at a single site to a more diffuse failure pattern, while around the isostatic point the failure response is already delocalized in the athermal limit and the fraction of broken bonds is enhanced approaching the melting point (Fig. 6). These distinct failure processes might explain the difference in how the peak strain depends on temperature with respect to rigidity (Fig. 4).We note that at a first glance central-force spring networks subjected to thermal fluctuations behave like athermal networks in a stabilizing field. However, the instantaneous nature of the thermal fluctuations introduces important differences. It is striking that, without any applied deformation, the thermal fluctuations induce structural rearrangements of the average network structure (see ESI,† Fig. S1). Furthermore, providing enough time, the thermal fluctuations allow the failure of bonds even if they are not intrinsically under tension (activated failure), leading to diffuse damage. A final consequence of introducing thermal fluctuations is that time becomes an important parameter. In our simulations the system was deformed at a constant strain rate, i.e. it was driven at a given speed. If the driving speed is too low, the system will melt due to the process of activated failure. If the driving speed is too high, the system has no time for stress relaxation as it is held back by the viscous surroundings. Therefore, the failure response of an elastic network is generally determined by the coupling between the driving speed, viscosity, rigidity and thermal fluctuations. Our study was focused on a regime in which driving and viscosity effects were small (see ESI† for discussion).
This work provides new insight into the relation between the static network structure, thermal fluctuations and the failure response of central-force spring networks. Above all, it shows that rigidity remains a controlling parameter in the failure response of spring networks in the presence of thermal fluctuations, even close to the melting temperature. This suggests that the failure response of thermal networks in experiment, such as semiflexible polymer networks, could be rigidity-dependent as well. The ratio between the energy of the thermal fluctuations, Etherm = kBT, and the energy required to break an elastic element, Ebreak, emerges as a relevant parameter to classify the failure regime of a particular network (either the athermal regime, the cross-over regime, or the melting regime) and could thus be a relevant parameter to classify the failure response of experimental systems. For example, a rough estimate of this ratio for experimental systems  shows us that for a collagen network Etherm/Ebreak ≈ 1 × 10−6, which corresponds to the athermal limit, while the values for a semiflexible network like actin (Etherm/Ebreak ≈ 8 × 10−3) and a flexible polymer network (Etherm/Ebreak ≈ 7 × 10−3) are significantly higher (see ESI† for details). These examples show that it is not just the temperature, but also the type of building block that determines the relevant failure regime. Furthermore, the ratio also makes clear that the temperature sensitivity is not only dependent on the element stiffness μ, but also on extensibility λ. Therefore, it is a possibility that a network with a temperature dependent elastic response at the network level (determined by T*), might not be sensitive to thermal fluctuations in the failure regime (determined by
shows us that for a collagen network Etherm/Ebreak ≈ 1 × 10−6, which corresponds to the athermal limit, while the values for a semiflexible network like actin (Etherm/Ebreak ≈ 8 × 10−3) and a flexible polymer network (Etherm/Ebreak ≈ 7 × 10−3) are significantly higher (see ESI† for details). These examples show that it is not just the temperature, but also the type of building block that determines the relevant failure regime. Furthermore, the ratio also makes clear that the temperature sensitivity is not only dependent on the element stiffness μ, but also on extensibility λ. Therefore, it is a possibility that a network with a temperature dependent elastic response at the network level (determined by T*), might not be sensitive to thermal fluctuations in the failure regime (determined by 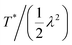 ). Our model predicts that networks with weak crosslinkers, i.e. small λ, are most likely to have a failure response as observed in the cross-over regime.
). Our model predicts that networks with weak crosslinkers, i.e. small λ, are most likely to have a failure response as observed in the cross-over regime.
We hope that our simulation results will stimulate further experimental work aimed at mapping out the roles that rigidity and thermal fluctuations play in governing mechanical failure of elastic networks.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is part of the SOFTBREAK project funded by the European Research Council (ERC Consolidator Grant 682782).References
- R. C. Picu, Soft Matter, 2011, 7, 6768–6785 RSC.
- C. P. Broedersz and F. C. Mackintosh, Rev. Mod. Phys., 2014, 86, 995–1036 CrossRef CAS.
- K. A. Jansen, A. J. Licup, A. Sharma, R. Rens, F. C. MacKintosh and G. H. Koenderink, Biophys. J., 2018, 114, 2665–2678 CrossRef CAS.
- P. H. Kouwer, M. Koepf, V. A. Le Sage, M. Jaspers, A. M. Van Buul, Z. H. Eksteen-Akeroyd, T. Woltinge, E. Schwartz, H. J. Kitto, R. Hoogenboom, S. J. Picken, R. J. Nolte, E. Mendes and A. E. Rowan, Nature, 2013, 493, 651–655 CrossRef CAS.
- C. Creton, Macromolecules, 2017, 50, 8297–8316 CrossRef CAS.
- M. Bouzid and E. Del Gado, Langmuir, 2018, 34, 773–781 CrossRef CAS.
- F. Burla, S. Dussi, C. Martinez-Torres, J. Tauber, J. van der Gucht and G. H. Koenderink, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 8326–8334 CrossRef CAS.
- C. Creton and M. Ciccotti, Rep. Prog. Phys., 2016, 79, 46601 CrossRef.
- F. J. Vernerey, R. Brighenti, R. Long and T. Shen, Macromolecules, 2018, 51, 6609–6622 CrossRef CAS.
- C. P. Broedersz, X. Mao, T. C. Lubensky and F. C. Mackintosh, Nat. Phys., 2011, 7, 983–988 Search PubMed.
- A. Sharma, A. J. Licup, K. A. Jansen, R. Rens, M. Sheinman, G. H. Koenderink and F. C. Mackintosh, Nat. Phys., 2016, 12, 584–587 Search PubMed.
- L. Zhang, D. Z. Rocklin, L. M. Sander and X. Mao, Phys. Rev. Mater., 2017, 1, 052602 Search PubMed.
- S. Dussi, J. Tauber and J. Van Der Gucht, Phys. Rev. Lett., 2020, 124, 18002 CrossRef CAS.
- M. M. Driscoll, B. G. G. Chen, T. H. Beuman, S. Ulrich, S. R. Nagel and V. Vitelli, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10813–10817 CrossRef CAS.
- E. Berthier, J. E. Kollmer, S. E. Henkes, K. Liu, J. M. Schwarz and K. E. Daniels, Phys. Rev. Mater., 2019, 3, 075602 CrossRef CAS.
- J. C. Maxwell, Philos. Mag., 1864, 27, 250–261 Search PubMed.
- M. Wyart, H. Liang, A. Kabla and L. Mahadevan, Phys. Rev. Lett., 2008, 101, 215501 CrossRef CAS.
- J. L. Shivers, S. Arzash, A. Sharma and F. C. MacKintosh, Phys. Rev. Lett., 2019, 122, 188003 CrossRef CAS.
- J. Feng, H. Levine, X. Mao and L. M. Sander, Soft Matter, 2016, 12, 1419–1424 RSC.
- A. Kulachenko and T. Uesaka, Mech. Mater., 2012, 51, 1–14 CrossRef.
- S. Borodulina, H. R. Motamedian and A. Kulachenko, Int. J. Solids Struct., 2018, 154, 19–32 CrossRef CAS.
- S. Deogekar and R. C. Picu, J. Mech. Phys. Solids, 2018, 116, 1–16 CrossRef.
- S. Deogekar, M. R. Islam and R. C. Picu, Int. J. Solids Struct., 2019, 168, 194–202 CrossRef CAS.
- H. M. James and E. Guth, J. Chem. Phys., 1943, 11, 455–481 CrossRef CAS.
- E. M. Arruda and M. C. Boyce, J. Mech. Phys. Solids, 1993, 41, 389–412 CrossRef CAS.
- M. Dennison, M. Sheinman, C. Storm and F. C. Mackintosh, Phys. Rev. Lett., 2013, 111, 095503 CrossRef CAS.
- L. Zhang and X. Mao, Phys. Rev. E, 2016, 93, 022110 CrossRef.
- G. I. Bell, Science, 1978, 200, 618–627 CrossRef CAS.
- J. T. Bullerjahn, S. Sturm and K. Kroy, Nat. Commun., 2014, 5, 4463 CrossRef CAS.
- P. J. Skrzeszewska, J. Sprakel, F. A. de Wolf, R. Fokkink, M. A. Cohen Stuart and J. van der Gucht, Macromolecules, 2010, 43, 3542–3548 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- S. Bonfanti, E. E. Ferrero, A. L. Sellerio, R. Guerra and S. Zapperi, Nano Lett., 2018, 18, 4100–4106 CrossRef CAS.
- P. R. Onck, T. Koeman, T. Van Dillen and E. Van Der Giessen, Phys. Rev. Lett., 2005, 95, 178102 CrossRef CAS.
- A. Sharma, A. J. Licup, R. Rens, M. Vahabi, K. A. Jansen, G. H. Koenderink and F. C. MacKintosh, Phys. Rev. E, 2016, 94, 042407 CrossRef CAS.
- G. Žagar, P. R. Onck and E. Van Der Giessen, Biophys. J., 2015, 108, 1470–1479 CrossRef.
- A. S. G. Van Oosten, M. Vahabi, A. J. Licup, A. Sharma, P. A. Galie, F. C. MacKintosh and P. A. Janmey, Sci. Rep., 2016, 6, 19270 CrossRef CAS.
- G. A. Buxton and N. Clarke, Phys. Rev. Lett., 2007, 98, 238103 CrossRef.
- M. J. Alava, P. K. V. V. Nukala and S. Zapperi, Adv. Phys., 2006, 55, 349–476 CrossRef.
- C. Heussinger and E. Frey, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 24, 47–53 CrossRef CAS.
- R. C. Arevalo, P. Kumar, J. S. Urbach and D. L. Blair, PLoS One, 2015, 10, 0118021 CrossRef.
- L. Liang, C. Jones, S. Chen, B. Sun and Y. Jiao, Phys. Biol., 2016, 13, 066001 CrossRef.
- H. Laubie, F. Radjai, R. Pellenq and F. J. Ulm, Phys. Rev. Lett., 2017, 119, 075501 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01063d |
| This journal is © The Royal Society of Chemistry 2020 |