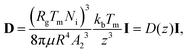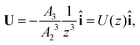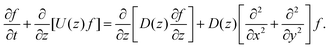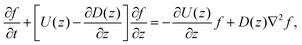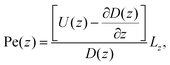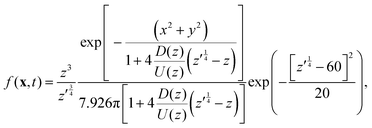DOI:
10.1039/D0SM00558D
(Paper)
Soft Matter, 2020,
16, 5886-5891
Impurity effects in thermal regelation
Received
30th March 2020
, Accepted 17th May 2020
First published on 21st May 2020
Abstract
When a particle is placed in a material with a lower bulk melting temperature, intermolecular forces can lead to the existence of a “premelted” liquid film of the lower melting temperature material. Despite the system being below the melting temperatures of both solids, the liquid film is a consequence of thermodynamic equilibrium, controlled by intermolecular, ionic and other interactions. An imposed temperature gradient drives the translation of the particle by a process of melting and refreezing known as “thermal regelation”. We calculate the rate of regelation of spherical particles surrounded by premelted films that contain ionic impurities. The impurities enhance the rate of motion thereby influencing the dynamics of single particles and distributions of particles, which we describe in addition to the consequences in natural and technological settings.
1 Introduction
Premelted liquid films can separate the surface of a solid from a foreign substrate at temperatures below the solid's bulk melting temperature. The solid melts against the substrate in order to minimize the free energy of the solid–liquid–substrate system.1 Thorough reviews1–3 discuss the theory of premelting and its consequences in a swath of natural and technological settings. One of the consequences of premelting is the translation of a foreign particle through a solid when subjected to a temperature gradient. In this process of thermal regelation the solid melts at the warmer side of the particle and the fluid flows to the colder side and refreezes thereby facilitating the translation. Evidently Gilpin4 first modeled thermal regelation, which was later discussed in the context of interfacial melting5 and frost heave.6 In most settings impurities are present in the films surrounding particles, but the rate of regelation has only been calculated for particles surrounded by pure films. The effect of impurities on the premelting of ice has been calculated for a wide range of planar substrates.7 By combining the key ingredients of pure and impure systems,5–11 we analyze the effects of impurities on the rate of thermal regelation of spherical particles and discuss their implications for environmental and engineering problems, by treating specific materials, in particular ice.
In Section 2, we give the theory for thermal regelation of spherical particles embedded in a solid. First, we describe how impurities in the premelted films that surround the particles control the film thickness. Then, we calculate the translational velocity and displacement of the particle, when it is subjected to a temperature gradient. Lastly, we develop the theory to understand the combined effects of thermal regelation and diffusion on the particle motion. In Section 3, we describe the displacement of particles of different sizes and impurity concentrations for various temperature gradients. The examples we provide are motivated by the dating of ice cores used in paleoclimate research and the manipulation of composite materials, as described in Section 4. We conclude in Section 5.
2 Theory
We analyse the translation of a spherical particle of radius R that is surrounded by a solid, which premelts against the particle forming a thin film of liquid of thickness d, as shown in Fig. 1(b). At temperatures below the solid's bulk melting temperature, Tm, the film's thickness depends on the nature of the intermolecular and coulombic forces operative in the system and is a function of the impurity concentration and the degree of undercooling.7,8 For sufficiently large concentrations,1,7,8 the thickness of the premelted film on a flat substrate (R → ∞) is dominated by colligative effects and is given by| | 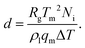 | (1) |
Here Rg is the universal gas constant, ρl is the molar density of the liquid, ΔT = Tm − T is the undercooling, with T is the temperature of the solid/liquid/substrate system, qm is the latent heat of melting per mole of the solid and Ni is the number of moles of impurity per unit surface area of the substrate. The concentrations and the temperatures in which this linear colligative-type relationship between d, Ni and ΔT holds, depends on the nature of the materials in the system.7
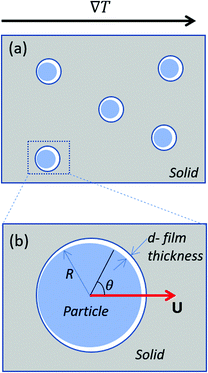 |
| | Fig. 1 (a) Shows particles embedded in a solid subjected to a temperature gradient of ∇T and (b) shows a zoomed view of the particle that is enclosed by the box in (a). The radius and the translational velocity of the particle are denoted by R and U, respectively. The premelted film that separates the solid from the particle is of thickness d. | |
Firstly, for spheres of radius R, so long as d ≪ R, the curvature of the solid–liquid interface is approximately the same as that of the particle–liquid interface. Secondly, for sufficiently large impurity concentrations and particles, then the Gibbs–Thomson effect does not control the film thickness.8 This requires that ΔT > 2Tmγsl/Rρsqm, so that for micron sized particles in ice, where γsl = 0.033 J m−2 is the solid–liquid interfacial free energy, Tm = 273.15 K, and ρsqm ≈ 334 × 106 J m−3, and thus ΔT > 0.05 K. Therefore, unless the system is within 50 mK of the bulk melting point, eqn (1) determines the film thickness for high concentrations and particles larger than about a micron, which is the situation we treat here.
2.1 Rate of thermal regelation
The pressure in the solid (ps) will be different from that in the liquid (pl) and the difference is calculated using the Gibbs–Duhem equation12 and is given by ps − pl ≈ ρsqmΔT/Tm. This pressure difference creates a force acting on the particle given by| | 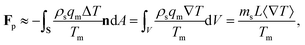 | (2) |
where n is the unit vector normal to the surface (S) of the particle–film system, V is the volume, ms is the mass of the displaced host solid, L is the latent heat of melting per unit mass of the solid and 〈∇T〉 is the temperature gradient averaged over V. We assume that the materials have the same thermal conductivities and the temperature gradient is a constant vector, which implies 〈∇T〉 = ∇T. The force in eqn (2) is a “thermodynamic buoyancy” force13 and it pushes the particle in the direction of the gradient-towards the warmer side of the particle. As the particle moves, the thickness of the film must obey eqn (1), with larger thicknesses at larger temperatures. Therefore, the solid melts on the warm side, and the melt flows through the film to the colder side where it refreezes. The flow is driven by a thermomolecular pressure gradient,13 or temperature gradient induced liquid pressure gradient, and it will exert a hydrodynamic force on the particle governed by lubrication theory.14 At a polar angle θ (Fig. 1(b)) the volume flux from lubrication theory is equated to the particle motion as| | 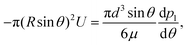 | (3) |
where U is the magnitude of the translational velocity of the particle and μ is the viscosity of the liquid.
Substituting the thickness from eqn (1) into eqn (3) and integrating the latter with respect to θ we obtain the liquid pressure.6 Hence, the hydrodynamic force is given by 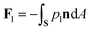 , and integration yields
, and integration yields
| | 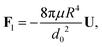 | (4) |
where
d0 is the thickness of the film at the equator of the particle, when its axis is parallel to the temperature gradient. The expression for the hydrodynamic force is the same as that derived for the case of a premelted film without impurities;
5,6 however, here the relationship between
d0 and the undercooling Δ
T is given by
eqn (1). Equating the hydrodynamic and thermodynamic buoyancy forces we obtain the translational velocity of the particle as
| | 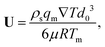 | (5) |
showing that the particle translates parallel to the temperature gradient.
2.2 Particle displacement by thermal regelation
Substituting the thickness from eqn (1) into eqn (5) we can rewrite the latter as| | 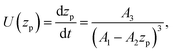 | (6) |
where zp is the position of the particle measured parallel to the temperature gradient, with zp = 0 at t = 0, A1 = ρlqm(Tm − Tint)/Tm, A2 = ρlqm|∇T|/Tm, A3 = ρsqm|∇T|(RgTmNi)3/6μRTm, and Tint is the temperature at the initial position of the particle. Integration of eqn (6) leads to a quartic equation in zp whose solution is| | 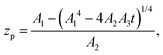 | (7) |
which gives the net displacement of the particle at time t. When zp ≪ A1/A2, then the displacement grows linearly with time, viz., 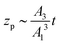 , followed by power law growth.
, followed by power law growth.
2.3 Particle diffusion
Owing to the thermal fluctuations in the premelted film a spherical particle can execute diffusive motion through the host solid. The premelting-controlled diffusivity of the particle is given by D = (3d03/4R3)Ds, where Ds = kBTI/6πμR is the Stokes–Einstein diffusivity of the particle, I is the second-order identity tensor and kB is Boltzmann's constant.15 In a Cartesian coordinate system, whose z-axis is parallel to the temperature gradient with T(z = 0) = Tm, the premelting-controlled diffusivity of the particle located at x = (x,y,z) is given by| | 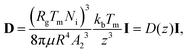 | (8) |
where we have used thickness from eqn (1), with ΔT = z|∇T|, and A2 is the thermomolecular pressure coefficient times |∇T|, as defined following eqn (6).
2.4 Combining thermal regelation and diffusion
The particle translates due to thermal regelation, and using eqn (5), its velocity can be written in the Cartesian coordinate system as| | 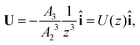 | (9) |
where A3 is defined below eqn (6). Hence, we combine the effects of regelation (eqn (9)) and diffusion (eqn (8)) in a statistical mechanical treatment of particles in the dilute limit as follows. The probability of finding a particle at x = (x,y,z) at time t is given by the probability density f(x,t), which is governed by the following Fokker–Planck-like equation| | 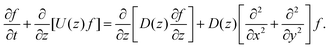 | (10) |
Since the translational velocity and the diffusivity have a non-trivial dependence on z, a complete understanding of this theory requires a numerical treatment. However, rewriting eqn (10) as| | 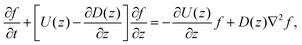 | (11) |
facilitates an analytical interpretation using a “Péclet function” defined as| | 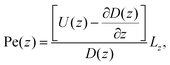 | (12) |
where Lz is the characteristic length scale in the z-direction. Now, we can solve eqn (11) analytically in the large Pe(z) limit, that is when diffusion in the z-direction can be neglected.
3 Results
Our model system consists of silicon particles embedded in ice. We use ice as the solid for two main reasons. Firstly, ice is a material that exhibits all of the phase behavior of general interest in the physical sciences, but with distinct advantages associated with its ready accessibility, transparency and experimental control.1 Therefore, it acts as a test bed for a broad class of materials processes, and of particular relevance here are composite materials. Secondly, ice is an essential astro-geophysical material and thus basic processes, such as particle migration in ice cores, are of great contemporary interest, as described in Section 4. Previously we studied the effects of a wide range of impurity concentrations on interfacial premelting.7 When the concentration is very low and both van der Waals and screened Coulomb interactions control the film thickness, then the substrate material properties are important, and the general theory described in ref. 7 was tested using as one example a silicon substrate. Our analysis here is valid in the high concentration limit of this more general approach, when the film thickness is governed by eqn (1). Because at sufficiently high concentrations, colligative effects dominate independent of the particle material, this limit is useful to demonstrate regelation.
3.1 Thermal regelation alone
Using eqn (7), we plot the displacement of particles of three different sizes versus time in Fig. 2, with Tint = 263.5 K, which corresponds to an undercooling of 10 K. We have set the temperature gradient to 0.1 K m−1, and the concentration of impurities to 100 μM m−2. The biggest particle considered has the smallest displacement, and in 104 years, the particle of radius 10−6 m experiences both linear and nonlinear growth in its displacement. To understand the effects of impurities on thermal regelation, in Fig. 3, we have plotted the displacement of a particle of radius 10−6 m at three different concentrations, with Tint = 263.5 K and |∇T| = 0.1 K m−1. Eqn (5) shows that the translational velocity of the particle is proportional to the thickness of the film at its equator, and that thickness increases with concentration as governed by eqn (1), so that the displacement increases with concentration Ni. In Fig. 4 we show the dependence of the displacement on Tint for a particle of radius 10−6 m starting at three different initial temperatures at a concentration of Ni = 100 μM m−2 and |∇T| = 0.1 K m−1. The particle starting at the smallest undercooling experiences the largest displacement because the thickness of the film increases with Tint.
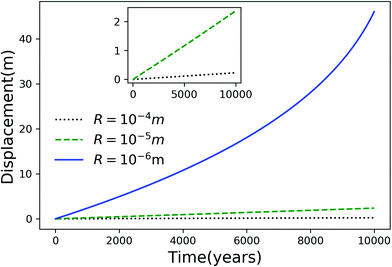 |
| | Fig. 2 Displacement versus time for different particles with Tm − Tint = 10 K, |∇T| = 0.1 K m−1 and Ni = 100 μM m−2. The inset is an expanded view of the plot for the particles with R = 10−4 and 10−5 m. | |
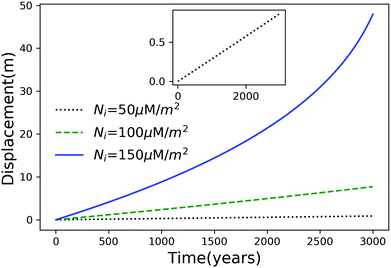 |
| | Fig. 3 Displacement versus time for a particle of radius 10−6 m at three different concentrations with Tm − Tint = 10 K and |∇T| = 0.1 K m−1. The inset is an expanded view of the plot for the particle with Ni = 50 μM m−2. | |
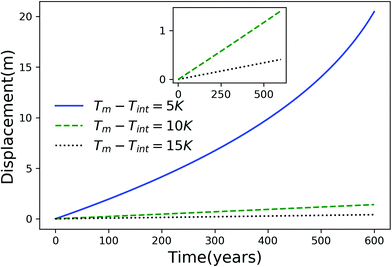 |
| | Fig. 4 Displacement versus time for a particle of radius 10−6 m starting from three different undercoolings with Ni = 100 μM m−2 and |∇T| = 0.1 K m−1. The inset is an expanded view for the particles starting at Tm − Tint = 10 K and 15 K. | |
Fig. 2–4 have time scales of the order of years and length scales of the order of meters. In a lab or composite manufacturing setting, the time and length scales are of the order of minutes to hours and centimeters. Such small scales can be achieved by using a larger temperature gradient and in Fig. 5 we have plotted the displacement of a particle of radius 10−6 m, in a temperature gradient of 1 K cm−1 with Ni = 400 μM m−2. Clearly, by adjusting the magnitude of the temperature gradient and the concentration of impurities, the motion of a particle inside a solid can be controlled on laboratory scales.
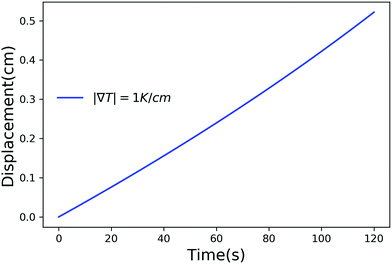 |
| | Fig. 5 Displacement versus time for a particle of radius 10−6 m with Ni = 400 μM m−2, Tm − Tint = 5 K and |∇T| = 1 K m−1. | |
3.2 Thermal regelation and diffusion
As noted above, thermal fluctuations in the premelted films that surround the particles inside a solid facilitates their diffusion through the solid. As shown in eqn (11), the combined effects of thermal regelation and diffusion will determine the evolution of the probability density of particles, f(x,t). We analyze the evolution of f(x,t) by numerically solving eqn (11) for micron-sized silicon particles in ice. In Fig. 6(a and b) we have plotted the evolution along the z and x axes, respectively. The initial distribution is assumed to be a three-dimensional Gaussian, f(x,0) = e−x2−y2−(z−60)2/20/7.926π, peaked at x = {0,0,60}. If the characteristic length scale in eqn (12) is set as 1 m, then Pe is of the order of 108 for the solution presented in the figures. The numerical solution (solid lines) compares well with the large Pe analytical solution of eqn (11) (dotted and dashed lines) given by| | 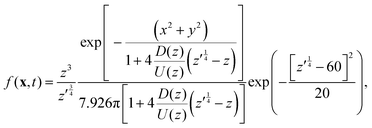 | (13) |
for this particular initial condition, where z′ = z4 + 4A3t/A23. In Fig. 6(a), the advection of the probability density towards higher temperatures (T = Tm at z = 0) is evident and the decay in the probability density is due to the reaction term (∝f) in eqn (11). The growth of density in Fig. 6(b) is a consequence of the advection. Thus, for micron sized silicon particles in ice subjected to a gradient of 0.1 K m−1 with Ni = 100 μM m−2, the advection and the reaction terms in eqn (11) determine the evolution of the probability density. Although we have illustrated the solution of eqn (11) only for a large Pèclet function, clearly the solution behavior can alter between the advection-dominated one seen in Fig. 6 and a diffusion-dominated one depending on the temperature gradient, particle size and/or impurity concentrations.
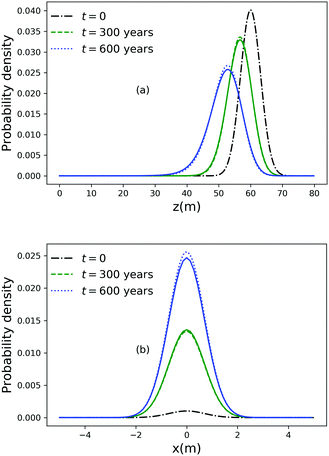 |
| | Fig. 6 (a) Evolution of the probability density along the z axis at x = 0 and y = 0 for particles of radius 10−6 m with Ni = 100 μM m−2, |∇T| = 0.1 K m−1 and T = Tm at z = 0. (b) Evolution of the probability density along the x axis at y = 0 and z = 51. | |
4 Applications: ice and other materials
Thermal regelation of particles can occur in terrestrial ice masses. For example, ice sheets contain deposits of tephra particles from past volcanic eruptions,16 dust particles originating from arid regions17 and DNA remnants from ancient ecosystems.18 Accurate dating of ice core data, such as the isotopic composition, chemical species (in ice and on particles), provides the highest resolution reconstructions of past climates. Layers of volcanic particles are used as absolute time markers for dating the cores.19,20 The time markers are utilised to improve the ice flow models that are used for dating the cores. The particles are typically surrounded by impurities21 and experience a temperature gradient in the lower-oldest and most compressed-part of the ice sheet due to the basal geothermal heat flux.22,23 Therefore, quantifying the translation of particles by thermal regelation and diffusion is important for the dating procedure. The displacements of the order of meters that we find in Section 3 can lead to significant corrections in the dating of deep ice cores.
Because premelting occurs in many materials thermal regelation may be used, for example, as a novel method to tailor the properties of particle-reinforced composites.24,25 During their manufacture, by adjusting the impurity concentration and the temperature gradient, the rate of thermal regelation of particles may be manipulated to achieve the desired distribution of particles. Indeed, premelting enhanced particle diffusion has been proposed as such a manipulation strategy.15
5 Conclusions
Extending the ideas developed in the literature1–8,13,15 we have included the effects of impurities in the theory of thermomolecular pressure driven thermal regelation of spherical particles. In Section 2 we provide the formulae for the speed and displacement of particles. By combining these with their premelting facilitated diffusivity we derive a Fokker–Planck-like equation (eqn (11)) for the evolution of the probability density of particles, f(x,t), in the dilute limit. We illustrate the theory in Section 3 by considering as a model system silicon particles in ice, which can either be considered as a transparent composite material for laboratory studies, or as a setting to examine the redistribution of particles in ice cores studies of paleoclimate. We systematically examined the role of particle size, impurity concentration and temperature gradient. Because of the known sensitivity of premelted film thickness on impurity concentration, for a given particle size we find that particle displacement is very sensitive to impurities and the temperature gradient, which underlies the thermomolecular pressure gradient. As discussed in the analysis surrounding Fig. 6, these effects control the evolution of f(x,t) which can be diffusively or advectively dominated, of particular relevance for the control and manipulation of materials properties and quantifying the particle based time horizons in ice cores. Consequences of these findings are important for interpretation of ice core dating, which often relies on time calibration from volcanic particles, and provide a framework for the manipulation of particles in composite media. In the case of ice core dating, we found that micron sized particles are displaced tens of meters in thousands of years, compromising dating accuracy, and in the case of composite media we found that silicon particles can be moved centimeters through ice on time scales of minutes.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors acknowledge the support of the Swedish Research Council Grant No. 638-2013-9243.
Notes and references
- J. G. Dash, A. W. Rempel and J. S. Wettlaufer, Rev. Mod. Phys., 2006, 78, 695–741 CrossRef CAS.
- J. G. Dash, H. Fu and J. S. Wettlaufer, Rep. Prog. Phys., 1995, 58, 115–167 CrossRef CAS.
- J. S. Wettlaufer and M. G. Worster, Annu. Rev. Fluid Mech., 2006, 38, 427–452 CrossRef.
- R. R. Gilpin, J. Colloid Interface Sci., 1979, 68, 235–251 CrossRef CAS.
-
M. G. Worster and J. S. Wettlaufer, in Fluid Dynamics at Interfaces, ed. W. Shyy and R. Naranyanan, 1999, pp. 339–351 Search PubMed.
- A. W. Rempel, J. S. Wettlaufer and M. G. Worster, J. Fluid Mech., 2004, 498, 227–244 CrossRef CAS.
- J. S. Wettlaufer, Phys. Rev. Lett., 1999, 82, 2516–2519 CrossRef CAS.
- H. Hansen-Goos and J. S. Wettlaufer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031604 CrossRef.
- D. Dedovets, C. Monteux and S. Deville, Science, 2018, 360, 303–306 CrossRef CAS.
-
T. Zhou, M. Mirzadeh, D. Fraggedakis, R. J.-M. Pellenq and M. Z. Bazant, 2019, arXiv preprint arXiv:1909.09332.
- S. S. L. Peppin, J. Fluid Mech., 2020, 886, A16 CrossRef.
-
H. B. Callen, Thermodynamics and an Introduction to Thermostatistics, American Association of Physics Teachers, 1998 Search PubMed.
- A. W. Rempel, J. S. Wettlaufer and M. G. Worster, Phys. Rev. Lett., 2001, 87, 088501 CrossRef CAS PubMed.
-
G. K. Batchelor, An Introduction to Fluid Dynamics, Cambridge University Press, 2000 Search PubMed.
- S. S. L. Peppin, M. J. Spannuth and J. S. Wettlaufer, J. Stat. Phys., 2009, 134, 701–708 CrossRef CAS.
- B. Narcisi, J. R. Petit, B. Delmonte, I. Basile-Doelsch and V. Maggi, Earth Planet. Sci. Lett., 2005, 239, 253–265 CrossRef CAS.
- F. E. Grousset, P. E. Biscaye, M. Revel, J. R. Petit, K. Pye, S. Joussaume and J. Jouzel, Earth Planet. Sci. Lett., 1992, 111, 175–182 CrossRef CAS.
- E. Willerslev, E. Cappellini, W. Boomsma, R. Nielsen, M. B. Hebsgaard, T. B. Brand, M. Hofreiter, M. Bunce, H. N. Poinar, D. Dahl-Jensen, S. Johnsen, J. P. Steffensen, O. Bennike, J.-L. Schwenninger, R. Nathan, S. Armitage, C.-J. de Hoog, V. Alfimov, M. Christl, J. Beer, R. Muscheler, J. Barker, M. Sharp, K. E. H. Penkman, J. Haile, P. Taberlet, M. T. P. Gilbert, A. Casoli, E. Campani and M. J. Collins, Science, 2007, 317, 111–114 CrossRef CAS PubMed.
- N. W. Dunbar, G. A. Zielinski and D. T. Voisins, J. Geophys. Res., 2003, 108, 1–11 CrossRef.
- B. Narcisi, J. R. Petit and M. Tiepolo, Quat. Sci. Rev., 2006, 25, 2682–2687 CrossRef.
- N. W. Dunbar and A. V. Kurbatov, Quat. Sci. Rev., 2011, 30, 1602–1614 CrossRef.
- N. Gundestrup, D. Dahl-Jensen, S. J. Johnsen and A. Rossi, Cold Reg. Sci. Technol., 1993, 21, 399–402 CrossRef.
- A. T. Fisher, K. D. Mankoff, S. M. Tulaczyk, S. W. Tyler, N. Foley and the WISSARD Science Team, Sci. Adv., 2015, 1, 1–9 Search PubMed.
- H. Zhang, I. Hussain, M. Brust, M. F. Butler, S. P. Rannard and A. I. Cooper, Nat. Mater., 2005, 4, 787–793 CrossRef CAS PubMed.
- T. Hanemann and D. V. Szabó, Materials, 2010, 3, 3468–3517 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab
*ab
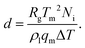
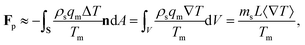
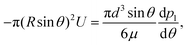
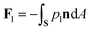 , and integration yields
, and integration yields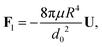
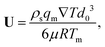
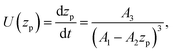
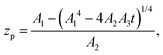
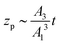 , followed by power law growth.
, followed by power law growth.