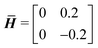Open Access Article
Open Access ArticleA data-driven computational scheme for the nonlinear mechanical properties of cellular mechanical metamaterials under large deformation†
Tianju
Xue
 *a,
Alex
Beatson
b,
Maurizio
Chiaramonte
*c,
Geoffrey
Roeder
b,
Jordan T.
Ash
b,
Yigit
Menguc
c,
Sigrid
Adriaenssens
a,
Ryan P.
Adams
b and
Sheng
Mao
*a,
Alex
Beatson
b,
Maurizio
Chiaramonte
*c,
Geoffrey
Roeder
b,
Jordan T.
Ash
b,
Yigit
Menguc
c,
Sigrid
Adriaenssens
a,
Ryan P.
Adams
b and
Sheng
Mao
 *de
*de
aDepartment of Civil and Environmental Engineering, Princeton University, Princeton, NJ 08544, USA. E-mail: txue@princeton.edu
bDepartment of Computer Science, Princeton University, Princeton, NJ 08544, USA
cFacebook Reality Labs, Redmond, WA 98052, USA. E-mail: mchiaram@fb.com
dDepartment of Mechanics and Engineering Science, BIC-ESAT, College of Engineering, Peking University, Beijing 100871, People's Republic of China. E-mail: maosheng@pku.edu.cn
eDepartment of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
First published on 14th July 2020
Abstract
Cellular mechanical metamaterials are a special class of materials whose mechanical properties are primarily determined by their geometry. However, capturing the nonlinear mechanical behavior of these materials, especially those with complex geometries and under large deformation, can be challenging due to inherent computational complexity. In this work, we propose a data-driven multiscale computational scheme as a possible route to resolve this challenge. We use a neural network to approximate the effective strain energy density as a function of cellular geometry and overall deformation. The network is constructed by “learning” from the data generated by finite element calculation of a set of representative volume elements at cellular scales. This effective strain energy density is then used to predict the mechanical responses of cellular materials at larger scales. Compared with direct finite element simulation, the proposed scheme can reduce the computational time up to two orders of magnitude. Potentially, this scheme can facilitate new optimization algorithms for designing cellular materials of highly specific mechanical properties.
1 Introduction
Cellular mechanical metamaterials (CMMs) with repeating cells are commonly observed in both nature and industry, from biological materials such as honeycombs to synthetic structures such as metallic microlattices. These materials can exhibit unique mechanical properties, such as high stiffness- and/or strength-to-density ratio,1 that are primarily determined by geometries. Traditionally, the study of this field is limited to several simple structures and under relatively small deformation.2 Yet in the past decade, the advent of fabrication technologies such as additive manufacturing3,4 has enabled precise but fast realization of sophisticated cellular architectures made of soft materials, such as elastomers. These materials not only can bear large deformation, but also exhibit novel mechanical properties under that condition, including negative Poisson's ratio (auxeticity),5–7 shape morphing,8 tunable bandstructures9 and energy absorption.10 These novel properties have created an avenue for many exciting engineering applications, e.g., soft actuators, materials with in situ tunable functionalities, reusable energy-absorbing materials, etc.11–16The rapid development on the fabrication side demands a fast and predictive computational method to predict the mechanical behaviors of CMMs. For materials with a relatively small number of cells, one can conduct a direct numerical simulation (DNS) on the whole specimen using the finite element method (FEM).17 However, the mechanical behaviors of soft CMMs are often highly nonlinear and may involve mechanical instability, thus requiring a fine spatiotemporal resolution for DNS calculations. DNS can easily become computationally intractable as CMMs usually consist of a large number of cells. Alternatively, one can conduct a fine-mesh FEM calculation on a representative volume element (RVE), often composed of one or several repeating cells,6 by prescribing appropriate boundary conditions. Such a method can efficiently predict the mechanical response of CMMs under homogeneous deformation. When CMMs are subject to complex loads, such predictions will fail.
When the size of the CMM is much larger than that of the repeating cells, multiscale analysis such as homogenization can be a useful tool. Homogenization, often called “coarse-graining” in the physics community, is often used to predict the macroscopic behavior of composites from their microstructures.18,19 The early development of homogenization primarily focuses on the analytical approach. Following the pioneering work of Eshelby,20 various analytical homogenization methods have been developed for linear materials21–26 and later extended to nonlinear materials.27–30 While these analytical approaches provide useful bounds, they are less accurate when microstructures become sophisticated.31 Computational homogenization is more suitable in this scenario. Reviews of the recent progress in this field can be found in ref. 32–34. Among various methods of computational homogenization, two main categories can be distinguished: concurrent and off-line methods. Concurrent methods integrate the macro- and micro-scale problems through proper mathematical formulations and solve both problems concurrently. For example, the FE2 method is a widely adopted concurrent scheme, and uses FEM to solve problems at both scales.35–40 Another example is given by the spectral method based on Fast Fourier Transform (FFT).41–44 Concurrent methods are powerful and accurate, yet can still be computationally expensive, mainly due to the nested numerical solvers needed to balance calculations at both scales. On the other hand, for off-line methods, the macro- and micro-scale problems are solved separately. Effective constitutive laws are first constructed based on a set of numerical calculations at microscales, and then used to solve problems at macroscales.45,46 Thus, offline methods can avoid the huge cost of nested numerical solvers and in some cases be orders of magnitude faster than the concurrent methods.46,47 Essentially, the constitutive relation can be seen as a multi-dimensional mapping from the microstructural features to the macroscopic response of the material, and the core of offline methods is to efficiently and accurately construct such a mapping. To this end, several techniques46–52 have been developed, including recent efforts using neural networks.53,54
Neural networks (NNs) are massively parametric function approximators inspired by biological neural networks.55 Given a large number of input/output examples, neural networks can often successfully learn functions on high-dimensional spaces. This process of “learning” the function corresponds to identifying an optimal set of parameters, i.e., neural network “weights”, to capture the relationship between inputs and outputs reflected in the training data. Neural networks have been demonstrated to be powerful function approximators for solving challenging engineering tasks, such as language modeling,56 image classification,57 and machine translation.58 More recently, there has been a growing interest in applying neural networks to complex problems in natural sciences, e.g., physics,59–61 chemistry,62 astronomy,63 biomedicine,64 and materials science.65–69
In the present work, we extend previous works on NN-based computational homogenization methods53,54 to model the nonlinear mechanical behavior of cellular mechanical metamaterials under large deformation. For that purpose, we first generate training data by conducting a large number of RVE calculations at the cellular scale. We then train a neural network on those data to approximate the effective strain energy density at the macro-scale, which is a function of the macroscopic strain and microscopic structural parameters. Through this NN-based surrogate model for effective strain energy density, the coarse-grained constitutive relations can be easily obtained, which greatly reduces the computational cost of determining the mechanical behavior of cellular materials at the macro-scale.
This paper is organized as follows. In Section 2, the finite deformation theory of hyperelastic cellular mechanical metamaterials and the specific geometries of this study are described. In Section 3, we propose a neural network-based multiscale computational scheme to determine the mechanical responses of CMMs and describe the procedures to carry out the scheme in Section 4. Numerical examples are presented in Section 5, where our NN-based method is compared with DNS in terms of accuracy and efficiency. In Section 6, we discuss the applicability and the limitations of our NN-based method. Finally we conclude in Section 7.
2 Problem formulation
2.1 Finite deformation elasticity
Consider a homogeneous elastic body in a 3D Euclidean space![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3, where we introduce a fixed Cartesian coordinate system with orthonormal basis {e1,e2,e3}. In an unstressed state, the body occupies a region
3, where we introduce a fixed Cartesian coordinate system with orthonormal basis {e1,e2,e3}. In an unstressed state, the body occupies a region ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) ⊂
⊂ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 (reference configuration) with a boundary ∂
3 (reference configuration) with a boundary ∂![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) whose outward normal is N. Upon mechanical loading, the body deforms and occupies a different region
whose outward normal is N. Upon mechanical loading, the body deforms and occupies a different region ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) t ⊂
t ⊂ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3 (deformed configuration). Deformation can therefore be described as a mapping: φ:
3 (deformed configuration). Deformation can therefore be described as a mapping: φ: ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) →
→ ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) t, which maps any material point X ∈
t, which maps any material point X ∈ ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) to its counterpart x ∈
to its counterpart x ∈ ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) t, i.e.x = φ(X). The corresponding displacement field is defined as u = x − X and the deformation gradient
t, i.e.x = φ(X). The corresponding displacement field is defined as u = x − X and the deformation gradient 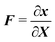 . We denote vectors and tensors with a bold font in contrast to scalars with a normal font.
. We denote vectors and tensors with a bold font in contrast to scalars with a normal font.
The constitutive model of a hyperelastic material can be defined by a strain energy density function (per volume) W, which depends on F, through the right Cauchy–Green tensor C = FTF. The displacement field u can be determined by solving for the stationary point δΨ = 0 of the following functional (in the absence of body force):
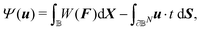 | (1) |
![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) D, where ub is the prescribed displacement field, t is the prescribed traction (force per unit reference area), ∂
D, where ub is the prescribed displacement field, t is the prescribed traction (force per unit reference area), ∂![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) N ∪ ∂
N ∪ ∂![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) D = ∂
D = ∂![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) and ∂
and ∂![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) N ∩ ∂
N ∩ ∂![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) D = ∅. The measures dX and dS are the infinitesimal volume and surface elements in the reference configuration respectively. Alternatively, the above variational problem can be formulated as a boundary value problem:
D = ∅. The measures dX and dS are the infinitesimal volume and surface elements in the reference configuration respectively. Alternatively, the above variational problem can be formulated as a boundary value problem:Div P = 0 in ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) , , |
u = ub on ∂![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) D, D, |
P·N = t on ∂![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) N, N, | (2) |
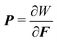 is the first Piola–Kirchoff stress. These problems can be numerically solved by FEM.
is the first Piola–Kirchoff stress. These problems can be numerically solved by FEM.
The formulation described above is applicable to any hyperelastic material, but in this work we focus on CMMs made of soft elastomers and therefore adopt the following form of W:
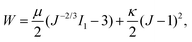 | (3) |
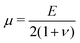 and
and 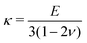 denote the initial shear and bulk moduli, respectively, with E and ν being the material's Young's modulus and Poisson's ratio. The above W is commonly used to model isotropic elastomers that are almost incompressible and we assume ν = 0.3 throughout this work.
denote the initial shear and bulk moduli, respectively, with E and ν being the material's Young's modulus and Poisson's ratio. The above W is commonly used to model isotropic elastomers that are almost incompressible and we assume ν = 0.3 throughout this work.
2.2 Problem geometry
In this work, we focus on a special but widely used class of CMMs: 2D porous cellular solids with a repeating unit cell. We adopt a plane strain setting here, i.e., ui = ui(X1, X2), i = 1,2 and u3 = 0. Previous works6,7 have shown that the mechanical properties of these CMMs highly depend on the shape of the pore. Following previous treatments, our study focuses on pores with four-fold symmetry whose contour can be described by the following parametrization:r(θ) = r0(1 + ξ1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(4θ) +ξ2 cos(4θ) +ξ2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(8θ)), cos(8θ)), | (4) |
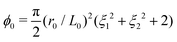 . In this work, we fix L0 = 0.5 and porosity ϕ0 = 0.5.
. In this work, we fix L0 = 0.5 and porosity ϕ0 = 0.5.
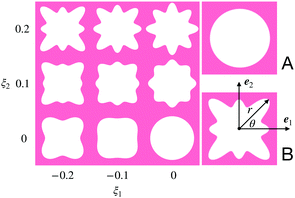 | ||
| Fig. 1 Left: A map from the parameters to the pore shapes indicated by eqn (4). For each (ξ1,ξ2), we get a corresponding pore shape. Right: The two representative pore shapes studied in this work. | ||
Among all the possible pore shapes, we focus on two types (A and B in Fig. 1): pore A is circular, with ξA = (0, 0), and pore B breaks the angular symmetry, with ξB = (−0.2, 0.2). We choose these two shapes as our representative examples for two reasons. First, mechanical instability can be triggered in CMMs made of both unit cells under compression, which leads to an asymmetric mechanical response of the CMMs under tension and compression. Second, even though mechanical instability can be triggered in these two CMMs, they still exhibit very distinct mechanical responses under the same mechanical loading.6,7
3 NN-based multiscale approach
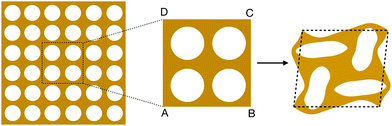
Direct numerical simulation of cellular mechanical metamaterials made of large numbers of unit cells is challenging, especially for CMMs with complicated cellular geometries or that undergo large deformation, mainly due to the large computational cost. The computational expense arises from two factors. First, to resolve detailed cellular geometries, the finite element mesh size must be no larger than microstructural features. Second, since the mechanical responses can be highly nonlinear under large deformation, small time steps are required for DNS to converge. To address these issues, we adopt a multiscale approach called (offline) computational homogenization,53,54 which performs fine-mesh FEM calculations at the RVE level to obtain the coarse-grained constitutive relations, and then uses these relations to predict the mechanical behavior of the material at larger scale.Our computational homogenization approach starts with a study of the representative volume element of the CMM. The choice of RVE is not unique, but it has to be simultaneously large enough to capture the influence of cellular geometries on the overall mechanical behavior and small enough to be considered as a material point for the CMM. For example, as shown in Fig. 2, for a CMM composed of many unit cells with pore A, we have chosen ABCD, a 2 × 2 array of unit cells, as our RVE. This choice of RVE ensures that we capture the mechanical instability that leads to reorganization of the neighboring unit cells.6,7 We emphasize that the above statement relies on the critical assumption of separation of length scales, i.e. the size of the CMM is much larger than that of the unit cell and RVE, without which the homogenization approach is invalid.
To construct the effective strain energy density of this RVE, we conduct a fine-mesh FEM calculation on the RVE under macroscopic deformations ![[F with combining macron]](https://www.rsc.org/images/entities/b_i_char_0046_0304.gif) by prescribing the following periodic boundary conditions:
by prescribing the following periodic boundary conditions:
u(X) = (![[F with combining macron]](https://www.rsc.org/images/entities/b_i_char_0046_0304.gif) − I)·X + u*(X) = − I)·X + u*(X) = ![[H with combining macron]](https://www.rsc.org/images/entities/b_i_char_0048_0304.gif) ·X + u*(X), ·X + u*(X), | (5) |
![[H with combining macron]](https://www.rsc.org/images/entities/b_i_char_0048_0304.gif) denotes the macroscopic displacement gradient.
denotes the macroscopic displacement gradient. ![[F with combining macron]](https://www.rsc.org/images/entities/b_i_char_0046_0304.gif) and
and ![[H with combining macron]](https://www.rsc.org/images/entities/b_i_char_0048_0304.gif) are uniform on the RVE and periodic boundary conditions are applied to ensure
are uniform on the RVE and periodic boundary conditions are applied to ensure 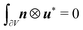 . For example, for the RVE ABCD in Fig. 2, we have u*AD = u*BC and u*AB = u*DC. Essentially, eqn (5) decomposes the total displacement of the RVE into a macroscopic (overall) part ū =
. For example, for the RVE ABCD in Fig. 2, we have u*AD = u*BC and u*AB = u*DC. Essentially, eqn (5) decomposes the total displacement of the RVE into a macroscopic (overall) part ū = ![[H with combining macron]](https://www.rsc.org/images/entities/b_i_char_0048_0304.gif) ·X and a microscopic (fluctuating) part u*.
·X and a microscopic (fluctuating) part u*.
The effective strain energy density ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) can be obtained via the average W over the RVE:
can be obtained via the average W over the RVE: 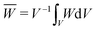 with V being the total volume of the RVE (for plane strain, dV = dX1dX2). Other macroscopic quantities can be obtained in the same fashion. This effective strain energy density
with V being the total volume of the RVE (for plane strain, dV = dX1dX2). Other macroscopic quantities can be obtained in the same fashion. This effective strain energy density ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) is the bridge that connects the microscopic features to macroscopic mechanical responses. In essence,
is the bridge that connects the microscopic features to macroscopic mechanical responses. In essence, ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) should be a function of
should be a function of ![[F with combining macron]](https://www.rsc.org/images/entities/b_i_char_0046_0304.gif) as well as the microstructural features ξ:
as well as the microstructural features ξ: ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) =
= ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) (
(![[F with combining macron]](https://www.rsc.org/images/entities/b_i_char_0046_0304.gif) ,ξ). Once that relation is established, we then treat the RVE as a material point in the CMM and use FEM to find the approximate solution to the stationary point of the following functional:
,ξ). Once that relation is established, we then treat the RVE as a material point in the CMM and use FEM to find the approximate solution to the stationary point of the following functional:
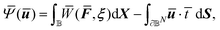 | (6) |
![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) D. Making use of the celebrated Hill–Mandel condition70
D. Making use of the celebrated Hill–Mandel condition70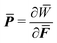 , the above minimization formulation can be shown to be equivalent to the following macroscopic BVP:
, the above minimization formulation can be shown to be equivalent to the following macroscopic BVP:Div ![[P with combining macron]](https://www.rsc.org/images/entities/b_i_char_0050_0304.gif) = 0 in = 0 in ![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) , , |
ū = ūb on ∂![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) D, D, |
![[P with combining macron]](https://www.rsc.org/images/entities/b_i_char_0050_0304.gif) ·N = ·N = ![[t with combining macron]](https://www.rsc.org/images/entities/b_i_char_0074_0304.gif) on ∂ on ∂![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) N. N. | (7) |
![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) as a function of
as a function of ![[F with combining macron]](https://www.rsc.org/images/entities/b_i_char_0046_0304.gif) (more strictly speaking
(more strictly speaking ![[C with combining macron]](https://www.rsc.org/images/entities/b_i_char_0043_0304.gif) ) and ξ. In this work, we adopt a data-driven approach based on neural networks.
) and ξ. In this work, we adopt a data-driven approach based on neural networks.
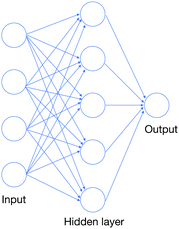
Neural networks (NNs) are powerful computational structures for constructing massively parametric mappings.55 The classic general form of a neural network is the multi-layer perceptron (MLP), made up of fully connected layers.71 The input vector x is processed through several hidden layers and finally to an output vector y. Suppose that the ith layer has m nodes and the i + 1 layer has n of them, the computation between these two layers is given by yi = fi(xi): = σ(wi·xi + bi), where wi ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) n×m and bi ∈
n×m and bi ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) m are the weight matrix and bias vector of the ith layer, and σ is an element-wise nonlinear function, such as a logistic function σ(y) = 1/(1 +e−y) or tanh. We can “stack” these transformations as y = fk(xk) = fk○fk−1(xk−1) = … = fk○…○f1(x) for a MLP with k − 1 hidden layers. We hereby denote this mapping as y = fθ(x) to emphasize that this mapping is under the parameter θ = (w1,w2,…,wk;b1,b2,…,bk). A typical MLP with only one hidden layer is shown in Fig. 3.
m are the weight matrix and bias vector of the ith layer, and σ is an element-wise nonlinear function, such as a logistic function σ(y) = 1/(1 +e−y) or tanh. We can “stack” these transformations as y = fk(xk) = fk○fk−1(xk−1) = … = fk○…○f1(x) for a MLP with k − 1 hidden layers. We hereby denote this mapping as y = fθ(x) to emphasize that this mapping is under the parameter θ = (w1,w2,…,wk;b1,b2,…,bk). A typical MLP with only one hidden layer is shown in Fig. 3.
The weight matrices and bias vectors θ are called the parameters of the neural network and they are optimized through a training procedure that minimizes a loss function reflecting the quality of the fit to data. This training is typically performed via a stochastic optimization procedure such as stochastic gradient descent.72 At each step, one randomly selects a subset of the training examples x each with the corresponding target value y* and computes a loss function ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (y*,y) (for example, the squared Euclidean distance between targets and predictions ‖y* − y‖22). Gradients of this loss function with respect to the parameters are then computed using reverse-mode automatic differentiation and the parameters are updated accordingly.73 This proceeds until a convergence criterion is achieved. After training and other validation and calibration processes, we can then deploy the neural network to make predictions for new inputs.
(y*,y) (for example, the squared Euclidean distance between targets and predictions ‖y* − y‖22). Gradients of this loss function with respect to the parameters are then computed using reverse-mode automatic differentiation and the parameters are updated accordingly.73 This proceeds until a convergence criterion is achieved. After training and other validation and calibration processes, we can then deploy the neural network to make predictions for new inputs.
In this work, we use an MLP to approximate the effective strain energy density, namely ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) NN(
NN(![[C with combining macron]](https://www.rsc.org/images/entities/b_i_char_0043_0304.gif) ,ξ) ≈
,ξ) ≈ ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) (
(![[C with combining macron]](https://www.rsc.org/images/entities/b_i_char_0043_0304.gif) ,ξ). The input vector is a 5-dimensional vector: x = (
,ξ). The input vector is a 5-dimensional vector: x = (![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 11,
11,![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 12,
12,![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 22,ξ1,ξ2) and the output is a scalar y =
22,ξ1,ξ2) and the output is a scalar y = ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) NN. For any given input, the target output is generated by RVE calculations. The goal is to train an MLP which can reproduce the results of these calculations for out-of-sample vectors. After training the MLP, we replace the
NN. For any given input, the target output is generated by RVE calculations. The goal is to train an MLP which can reproduce the results of these calculations for out-of-sample vectors. After training the MLP, we replace the ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) in eqn (6) with
in eqn (6) with ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) NN and solve the macroscopic problem.
NN and solve the macroscopic problem.
We use scikit-learn,74 an open source machine learning framework, to build, train and later test our neural network. All finite element calculations are carried out using an open-source FEM package FEniCS.75
4 Construction of the NN-based computational homogenization scheme
In the previous section, we have outlined an NN-based multiscale computational homogenization scheme, with the goal of obtaining a mapping from macroscopic deformation![[C with combining macron]](https://www.rsc.org/images/entities/b_i_char_0043_0304.gif) and microstructural parameters ξ to the effective strain energy density
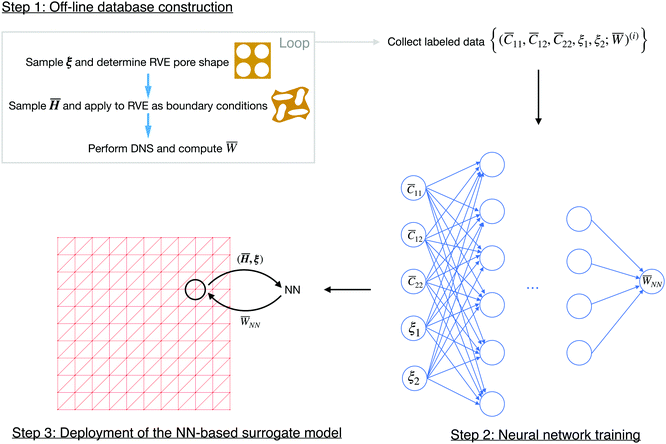
and microstructural parameters ξ to the effective strain energy density ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) . This scheme, as illustrated in Fig. 4, mainly consists of three steps: (1) offline construction of training data, (2) optimization of neural network parameters, and (3) deployment of the NN-based surrogate model for FEM at the macro-scale. In this section, we will describe these steps in detail.
. This scheme, as illustrated in Fig. 4, mainly consists of three steps: (1) offline construction of training data, (2) optimization of neural network parameters, and (3) deployment of the NN-based surrogate model for FEM at the macro-scale. In this section, we will describe these steps in detail.
4.1 Offline generation of training data
As mentioned above, the first step of constructing the NN-based multiscale computational scheme is to construct a proper training database composed of labeled data, each in the form of an input vector and its target output: {(![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 11,
11,![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 12,
12,![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 22,ξ1,ξ2;
22,ξ1,ξ2;![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) )(i)}. The target output
)(i)}. The target output ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) (i) is obtained via finite element calculation of the RVE with the corresponding geometric parameters ξ(i) and subject to the corresponding macroscopic field of
(i) is obtained via finite element calculation of the RVE with the corresponding geometric parameters ξ(i) and subject to the corresponding macroscopic field of ![[C with combining macron]](https://www.rsc.org/images/entities/b_i_char_0043_0304.gif) (i).
(i).
In this work, we focus on CMMs composed of two types of unit cells: those with pore A and pore B, so the choice of ξ(i) is limited: ξ(i) ∈ {ξA,ξB}. However, the choice of the macroscopic field ![[C with combining macron]](https://www.rsc.org/images/entities/b_i_char_0043_0304.gif) (i) is in principle infinite since it varies continuously. Therefore some care is necessary in constructing an effective sampling method for
(i) is in principle infinite since it varies continuously. Therefore some care is necessary in constructing an effective sampling method for ![[C with combining macron]](https://www.rsc.org/images/entities/b_i_char_0043_0304.gif) (i).
(i).
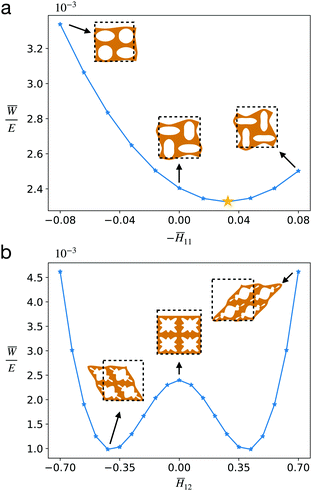
First we must identify a domain over which ![[C with combining macron]](https://www.rsc.org/images/entities/b_i_char_0043_0304.gif) (i) is to be sampled. Such a region should cover the nonlinear mechanical behaviors of primary interest. For example, for CMMs composed of unit cells with pore A, beyond certain compression the CMM undergoes mechanical instability which leads to auxetic behavior. This behavior can be observed for
(i) is to be sampled. Such a region should cover the nonlinear mechanical behaviors of primary interest. For example, for CMMs composed of unit cells with pore A, beyond certain compression the CMM undergoes mechanical instability which leads to auxetic behavior. This behavior can be observed for ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 22 = −0.125,
22 = −0.125, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 12 =
12 = ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 21 = 0 and
21 = 0 and ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 11 ∈ [−0.08, 0.08], as shown in Fig. 5a. The effective Poisson's ratio is calculated to be
11 ∈ [−0.08, 0.08], as shown in Fig. 5a. The effective Poisson's ratio is calculated to be ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) = −0.26 (defined as
= −0.26 (defined as 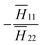 at the star point, where
at the star point, where 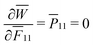 ). As for CMMs made of unit cells with pore B, when subject to both shear and compression, mechanical instability can lead to the bifurcation of microstructures.7 This is observed when
). As for CMMs made of unit cells with pore B, when subject to both shear and compression, mechanical instability can lead to the bifurcation of microstructures.7 This is observed when ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 22 = −0.125,
22 = −0.125, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 11 =
11 = ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 21 = 0 and
21 = 0 and ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 12 ∈ [−0.7, 0.7]. As shown in Fig. 5b, a double well shape of
12 ∈ [−0.7, 0.7]. As shown in Fig. 5b, a double well shape of ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) is observed as a function of
is observed as a function of ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 12 with two energy minima. Therefore, when the CMM is subject to an overall compression
12 with two energy minima. Therefore, when the CMM is subject to an overall compression ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 22 = −0.125, the CMM will bifurcate into two different microstructures that correspond to these two minima.
22 = −0.125, the CMM will bifurcate into two different microstructures that correspond to these two minima.
The inspections above offer insight into a reasonable range of ![[H with combining macron]](https://www.rsc.org/images/entities/b_i_char_0048_0304.gif) for sampling data. The range should be sufficiently wide so that important mechanics are reflected in the database, while it should also be limited so that undesired behaviors like self-contact are avoided with the current FEM simulation. The sampling region chosen for pore A is
for sampling data. The range should be sufficiently wide so that important mechanics are reflected in the database, while it should also be limited so that undesired behaviors like self-contact are avoided with the current FEM simulation. The sampling region chosen for pore A is
{−0.2 ≤ ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 11 ≤ 0.2, −0.2 ≤ 11 ≤ 0.2, −0.2 ≤ ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 12 ≤ 0.2, 12 ≤ 0.2, |
−0.2 ≤ ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 21 ≤ 0.2, −0.2 ≤ 21 ≤ 0.2, −0.2 ≤ ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 22 ≤ 0.2}, 22 ≤ 0.2}, | (8) |
{−0.2 ≤ ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 11 ≤ 0.2, −0.8 ≤ 11 ≤ 0.2, −0.8 ≤ ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 12 ≤ 0.8, 12 ≤ 0.8, |
−0.8 ≤ ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 21 ≤ 0.8, −0.2 ≤ 21 ≤ 0.8, −0.2 ≤ ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 22 ≤ 0.2}. 22 ≤ 0.2}. | (9) |
4.2 Neural network training
Once the database is constructed, the next step is to train a neural network to establish a mapping from input vector x = (![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 11,
11,![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 12,
12,![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 22,ξ1,ξ2) to its target scalar output y =
22,ξ1,ξ2) to its target scalar output y = ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) . We randomly split our database into a training set (90% of the data) and a test set (the rest 10%). Our neural networks will be trained on the training set and the test set is used to ensure good generalizability and avoid overfitting.
. We randomly split our database into a training set (90% of the data) and a test set (the rest 10%). Our neural networks will be trained on the training set and the test set is used to ensure good generalizability and avoid overfitting.
The neural network used here is an MLP with one hidden layer, which as we will show later is able to provide sufficient accuracy for our problem. The logistic function σ(y) = 1/(1 + e−y) is chosen as our activation function, and mean squared error (MSE) is chosen as our loss function: 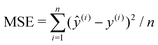 , where n is the number of data points evaluated and ŷ(i) denotes the output of the MLP given input x(i). The neural network is trained using mini-batch stochastic gradient descent with Adam optimizer.77 Hyperparameters such as number of neurons in the hidden layer are first optimized via k-fold cross-validation78 (see ESI†). We obtained the following optimal hyperparameters: learning rate 10−2, batch size 64, and 128 neurons in the hidden layer. We then train our neural networks using these hyperparameters. The training time for the NN is typically within 1 minute on a personal computer. After training of 1000 epochs, our NN model reports a training MSE of 6.11 × 10−5 and a test MSE of 7.67 × 10−5.
, where n is the number of data points evaluated and ŷ(i) denotes the output of the MLP given input x(i). The neural network is trained using mini-batch stochastic gradient descent with Adam optimizer.77 Hyperparameters such as number of neurons in the hidden layer are first optimized via k-fold cross-validation78 (see ESI†). We obtained the following optimal hyperparameters: learning rate 10−2, batch size 64, and 128 neurons in the hidden layer. We then train our neural networks using these hyperparameters. The training time for the NN is typically within 1 minute on a personal computer. After training of 1000 epochs, our NN model reports a training MSE of 6.11 × 10−5 and a test MSE of 7.67 × 10−5.
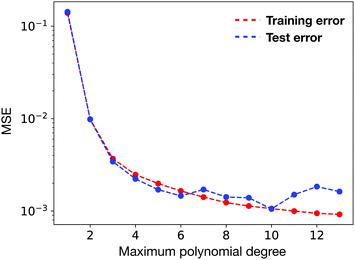
We performed polynomial regression on the same data set as a baseline comparison. As shown in Fig. 7, when the maximum degree of polynomial is increased, the MSE tends to decrease. But when the maximum degree exceeds 10, the regression problem starts to become ill-conditioned and thus results in large MSE.79 The best of polynomial regression reports a test error of 1.05 × 10−3, which is more than an order of magnitude larger than the neural network model.
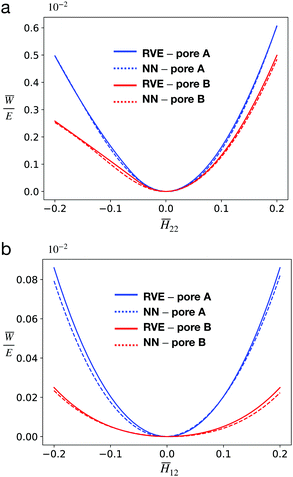
We further validate our NN model in two test cases to serve as our benchmarks by prescribing the following ![[H with combining macron]](https://www.rsc.org/images/entities/b_i_char_0048_0304.gif) :
:
(1) Uniaxial strain: ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 11,
11, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 12,
12, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 21 = 0,
21 = 0, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 22 ≠ 0
22 ≠ 0
(2) Simple shear strain: ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 11,
11, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 21,
21, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 22 = 0,
22 = 0, ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) 12 ≠ 0
12 ≠ 0
We conducted the above two test cases on both unit cells with pore A and pore B and ensured that the ![[H with combining macron]](https://www.rsc.org/images/entities/b_i_char_0048_0304.gif) 's tested here are different from those in the database. The results are shown in Fig. 6, where the effective strain energy obtained via RVE calculation and that from the NN model are compared. It is observed that the NN model agrees with the RVE calculation reasonably well. The errors between NN model and RVE calculation are also small among both benchmarks: the respective MSEs are 2.42 × 10−5 and 4.28 × 10−5.
's tested here are different from those in the database. The results are shown in Fig. 6, where the effective strain energy obtained via RVE calculation and that from the NN model are compared. It is observed that the NN model agrees with the RVE calculation reasonably well. The errors between NN model and RVE calculation are also small among both benchmarks: the respective MSEs are 2.42 × 10−5 and 4.28 × 10−5.
4.3 Deployment of the NN-based surrogate model
Now that we have obtained an optimized NN model of the effective strain energy density![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) NN, we replace the
NN, we replace the ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) in eqn (6) with the obtained
in eqn (6) with the obtained ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) NN. Then, for any given ξ, the solution to the macroscopic problem boils down to finding the stationary point
NN. Then, for any given ξ, the solution to the macroscopic problem boils down to finding the stationary point 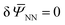 of the following functional:
of the following functional: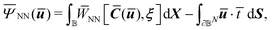 | (10) |
![[Doublestruck B]](https://www.rsc.org/images/entities/char_e165.gif) D.
D.
By extracting out the optimal parameters of the NN model, the explicit functional form of ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) NN(
NN(![[C with combining macron]](https://www.rsc.org/images/entities/b_i_char_0043_0304.gif) ,ξ) is readily available, which can be computed iteratively as described in Section 3. However, to find the stationary point of the above functional
,ξ) is readily available, which can be computed iteratively as described in Section 3. However, to find the stationary point of the above functional 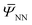 , one needs to efficiently evaluate the derivatives of
, one needs to efficiently evaluate the derivatives of 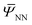 to compute quantities like the first Piola–Kirchhoff stress
to compute quantities like the first Piola–Kirchhoff stress 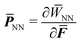 as well as the tangent stiffness tensor
as well as the tangent stiffness tensor 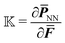 . In this work, we made use of the automatic symbolic differentiation feature provided by the open-source package FEniCS (specifically the UFL component80 of the package) to compute those derivatives. The standard Newton–Raphson method is used to find the root of the nonlinear equations. We use automatic differentiation and other features of FEniCS, so that the code can be written in a concise and near-math fashion, which provides an easier access to broader audiences. Equivalently, the exact same derivatives could be computed analytically53 or via finite differences.54
. In this work, we made use of the automatic symbolic differentiation feature provided by the open-source package FEniCS (specifically the UFL component80 of the package) to compute those derivatives. The standard Newton–Raphson method is used to find the root of the nonlinear equations. We use automatic differentiation and other features of FEniCS, so that the code can be written in a concise and near-math fashion, which provides an easier access to broader audiences. Equivalently, the exact same derivatives could be computed analytically53 or via finite differences.54
5 Numerical examples
In this section, we employed the aforementioned NN-based multiscale approach to study the mechanical behavior of CMMs composed of 2D arrays of cells with different pore shapes and compare that with direct numerical simulation. As shown in Fig. 8, a square-shaped CMM with a length L = 16L0 is studied. The CMM is subject to a uniaxial testing with displacement control. Specifically, a displacement ΔL along the e2 direction is applied at the top with the bottom kept fixed, while the left and right sides of the CMM remain traction free. This uniaxial testing is a standard practice to obtain the stress–strain curve of materials. Here, the engineering strain ε and engineering stress σ of the CMM are defined as follows: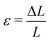 and
and 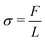 , where
, where 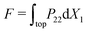 is the total resultant force (per thickness) on the top surface.
is the total resultant force (per thickness) on the top surface.
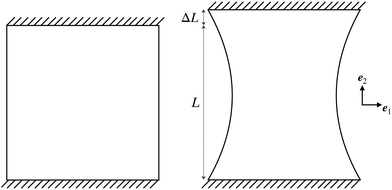 | ||
| Fig. 8 Boundary conditions for uniaxial tests. The upper and lower sides of the plate have fixed displacement conditions while the left and right sides are traction free. | ||
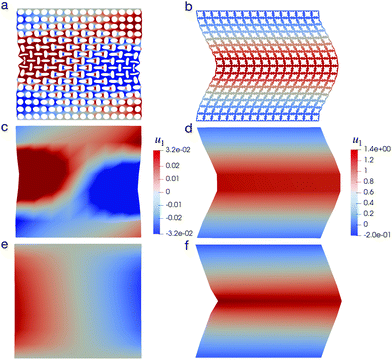
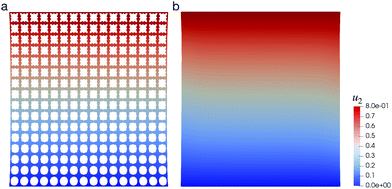
We perform this uniaxial test on a CMM with spatially uniform pore shapes of either pore A or pore B. Previous studies76 suggested that compression can lead to distinct mechanical behaviors of these two CMMs. This phenomenon is indeed observed in Fig. 9, where the deformed shapes of the CMMs under an engineering strain of −10% are shown. Both DNS (Fig. 9a and b) and the NN-based model (Fig. 9e and f) have shown that even under the same compressive loads, the two CMMs develop very different shapes. We also computed the average displacement field over each RVE element of the CMMs using data from DNS. The results are shown in Fig. 9c and d.
Specifically for CMMs with pore A, as mentioned in Section 4.2, a negative Poisson's ratio is expected, i.e., the compression in the e2 direction will lead to a contraction also in the e1 direction. This can be easily observed for the DNS results shown in Fig. 9a, where the CMM starts to contract in the middle region. The NN-based model also produces that result, as shown in Fig. 9e where displacement component u1 is plotted. We can observe that it is positive on the left and negative on the right, which is a clear sign of contraction. As for CMMs with pore B, compression can lead to a bifurcation of the local microstructure, as mentioned in Section 4.2, which again can be observed from the DNS result in Fig. 9b. For the NN-based model, since the microstructural information has been averaged out, such bifurcation can only be inferred indirectly. Recall that in Fig. 5b, the two minima of ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) correspond to nonzero shear deformation with equal and opposite shear components. In Fig. 9f, we observe that under pure compression, the CMM develops a large local shear in the upper and lower part of the material, with opposite shear directions. The results in Fig. 9, whether obtained via DNS or the NN-based approach, are all in qualitative agreement with previous experimental work.6
correspond to nonzero shear deformation with equal and opposite shear components. In Fig. 9f, we observe that under pure compression, the CMM develops a large local shear in the upper and lower part of the material, with opposite shear directions. The results in Fig. 9, whether obtained via DNS or the NN-based approach, are all in qualitative agreement with previous experimental work.6
Beyond visual qualitative comparisons, we obtained a stress–strain (σ–ε) curve for both CMMs to quantitatively assess the accuracy of our NN-based approach. The curves are obtained by varying the applied engineering strain ε from −10% to 10% and the results are shown in Fig. 10. The curves obtained from DNS and the NN-based model are almost identical for both pore A and pore B when under tension, even at large strain up to 10%. The NN-based model can reproduce the results of DNS for pore B for compression, but it starts to deviate from DNS results for pore A when the compression becomes large. This deviation is observed even with a much finer mesh for our NN-based approach.
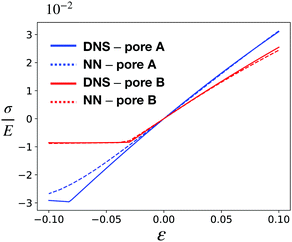 | ||
| Fig. 10 Stress–strain curve for CMMs under uniaxial test with pore A (red) and pore B (blue) obtained via DNS (solid line) and the NN-based model (dashed line). | ||
One possible reason for such behavior is the boundary effect. For CMMs with pore B we can observe some variation of microstructures near the boundary, but the variation is quite smooth and the main effect – the bifurcation into two shear states – is captured by the NN-based model. However for CMMs with pore A, on the left and right boundaries there are strong pore–boundary interactions, resulting in a drastic change in the pore shapes (see ESI†). This boundary effect persists even with the increasing number of composing unit cells. Another possible reason is that there is strong microstructure localization in the case of pore A. We can see that the rotation of the holes is drastic, and the distances between holes are small, thus leading to strong local interactions between the RVEs (Fig. 9a and ESI†). This is in contrast to the case of pore B, where pore rotations vary more smoothly yielding no strong localization (Fig. 9b and ESI†). Moreover, the strongly localized deformations in the case of pore A can lead to contacts between the interior boundaries of the pore, at which point our finite element model becomes invalid (without extension to handle contacts). In conclusion, the strong local variations in the microstructural features may impede the predictive power of our computational scheme. Possible ways of resolving this issue include using a separate model to account for the boundary effects,81 or utilizing more advanced homogenization techniques to deal with the aforementioned localization effects.32,33
Aside from accuracy, we also compared the efficiency of the NN-based approach with DNS. Recall that one of our main motivations to construct such a surrogate-based approach is to reduce the computational complexity of DNS. This computational expense is mainly due to the fact that a small mesh size is needed to resolve the detailed cellular geometries, which results in a large number of degrees of freedom (DoF). Our NN-based model can use a much coarser mesh since the detailed microstructural features have already been averaged out and factored into the effective strain energy density. This significantly reduces the degrees of freedom when solving for the macroscopic behavior of the CMM – of course at the cost of losing the detailed local information of relevant fields. Table 1 summarizes the computational performance of DNS and the NN-based approach when they are used to generate the stress–strain curve in Fig. 10. The NN-based approach needs much fewer DoF to accurately capture the overall mechanics of the CMMs and hence can reduce the computational time by up to two orders of magnitude for both CMM with pore A and that with pore B. Note that for our problem, we used the same increment in ε to obtain the stress–strain curve. For a time-dependent problem, it is also important to examine the numerical stability of both approaches when different time steps are used.
| DoF | Computation time [s] | |
|---|---|---|
| DNS – pore A – compression | 158![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 310 |
5.15 × 102 |
| DNS – pore A – tension | 7.42 × 102 | |
| NN – pore A – compression | 290 | 6.18 |
| NN – pore A – tension | 6.41 | |
| DNS – pore B – compression | 139![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 520 520 |
5.33 × 102 |
| DNS – pore B – tension | 5.19 × 102 | |
| NN – pore B – compression | 290 | 8.20 |
| NN – pore B – tension | 6.94 |
6 Discussion
In the previous section, our NN-based approach is shown to efficiently predict the mechanical behavior of CMMs with homogeneous ξ but an inhomogeneous deformation field. Here we further consider a CMM whose ξ is macroscopically inhomogeneous: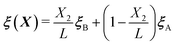 , a linearly varying ξ along the e2 direction. The shape of the CMM is still a square, with size L = 16L0 and under the same uniaxial loading as described in Fig. 8. A maximum strain of 20% is applied to this CMM. Its deformed shape is shown in Fig. 11 when under a tensile strain of 20%. The macroscopic responses for both DNS and the NN-homogenized model agree with each other qualitatively by visual observation. When the applied ε > 0, i.e., tensile loading, we have found that the NN-based approach can reproduce the DNS results very well – as in the case of a CMM with homogeneous ξ. On the other hand, when under compression, the NN-based approach starts to diverge and fails to find a solution even at small compression.
, a linearly varying ξ along the e2 direction. The shape of the CMM is still a square, with size L = 16L0 and under the same uniaxial loading as described in Fig. 8. A maximum strain of 20% is applied to this CMM. Its deformed shape is shown in Fig. 11 when under a tensile strain of 20%. The macroscopic responses for both DNS and the NN-homogenized model agree with each other qualitatively by visual observation. When the applied ε > 0, i.e., tensile loading, we have found that the NN-based approach can reproduce the DNS results very well – as in the case of a CMM with homogeneous ξ. On the other hand, when under compression, the NN-based approach starts to diverge and fails to find a solution even at small compression.
 | ||
| Fig. 11 Deformed configuration of a CMM with non-uniform pore shapes under a uniaxial tension of 20% obtained via (a) DNS and (b) the NN-based approach. Color contours indicate the value of u2. | ||
We suggest two explanations for this phenomenon. First, since ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) is a strongly nonlinear function of ξ, especially when under compression, the ability of our neural network to capture that functional dependence remains uncertain, given that only two different ξ's (ξA and ξB) are included in the training data. Second, since the local mechanical properties of the CMM depend on ξ in a strongly nonlinear fashion, the ξ used in this study can still create a strong local variation. When the characteristic length of that variation is comparable to the RVE size, the assumption of separation of scales can break and in that case our multiscale framework will fail. Particularly in the above example, when the CMM is under uniaxial tension, as shown in Fig. 10, the mechanical properties of CMMs vary smoothly between different ξ's. Therefore, the NN-based approach gives us good agreement with the DNS results in tension. However, when under compression, as the properties vary drastically between different ξ's, our NN-based approach starts to fail.
is a strongly nonlinear function of ξ, especially when under compression, the ability of our neural network to capture that functional dependence remains uncertain, given that only two different ξ's (ξA and ξB) are included in the training data. Second, since the local mechanical properties of the CMM depend on ξ in a strongly nonlinear fashion, the ξ used in this study can still create a strong local variation. When the characteristic length of that variation is comparable to the RVE size, the assumption of separation of scales can break and in that case our multiscale framework will fail. Particularly in the above example, when the CMM is under uniaxial tension, as shown in Fig. 10, the mechanical properties of CMMs vary smoothly between different ξ's. Therefore, the NN-based approach gives us good agreement with the DNS results in tension. However, when under compression, as the properties vary drastically between different ξ's, our NN-based approach starts to fail.
To enhance the fidelity of our NN-based approach for CMMs with complex pore shapes, it is useful to include a larger number of sampled ξ's in the database. This way, our neural networks can better capture the nonlinear dependence of ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) on the geometric parameters ξ. We can validate our results by conducting similar uniaxial tests on CMMs with a homogeneous ξ that are different from those in the training data and compare with DNS results. Once that dependence is established with good accuracy, we can use the NN-based approach to predict the mechanical behavior of CMMs with an arbitrary uniform ξ or those with a non-uniform ξ, which varies “smoothly enough”.
on the geometric parameters ξ. We can validate our results by conducting similar uniaxial tests on CMMs with a homogeneous ξ that are different from those in the training data and compare with DNS results. Once that dependence is established with good accuracy, we can use the NN-based approach to predict the mechanical behavior of CMMs with an arbitrary uniform ξ or those with a non-uniform ξ, which varies “smoothly enough”.
However, for those ξ's that lead to large local variations and with characteristic lengths comparable to the size of RVE, our NN-based approach will fail since it breaks the basic assumption of our multiscale framework. For those CMMs, we have to rely on other approaches like DNS. We must be cautious about the spatial inhomogeneity of the problem that we are solving: be it either in the geometric features or in the deformation field. For the multiscale approach to work, we must ensure that those variations have a negligible influence on the macroscopic problems of interest. In principle, our NN-based multiscale approach only works when the size of the CMM is much larger than that of the RVE and when there is no strong localization effect.
In Section 5 we have demonstrated that our NN-based scheme can capture the mechanics of moderately sized CMMs with reasonable accuracy, but with significant computational savings over DNS. We anticipate further reduction for even larger CMM size. Nevertheless, it is worth noting that the most time-consuming step of our NN-based scheme is not solving the macroscopic problem using the NN-based model, but the generation of the training data. As reported in Section 4.1, it takes about 20 hours to construct the database, although it is trivially parallelizable. Even though it is time-consuming, this generation step is only required once, and the resulting NN-based model can be used to solve multiple problems. Therefore, significant time can still be saved compared to other multiscale methods like FE2 where micro- and macroscopic problems have to be solved at the same time, as pointed out in ref. 53 and 54.
Owing to its great computational efficiency, the NN-based approach proposed in this work can be particularly useful for solving design problems – the reverse engineering of CMMs to achieve specific mechanical properties. Compared with typical multiscale approaches, our approach provides a straightforward way of evaluating the necessary derivatives needed for the sensitivity analysis,82,83 once the functional dependence of ![[W with combining macron]](https://www.rsc.org/images/entities/i_char_0057_0304.gif) on ξ is well established. Therefore we envision that those powerful tools used for structural topological optimization of composite materials can now be used for the design of CMMs under the NN-based framework. However, since our NN-based multiscale approach only works for CMMs with smoothly varying ξ, proper regularization has to be imposed to ensure that the optimal solution that we obtained does not violate that condition. Other structural parameters can also be included for the design of CMM, for example, the porosity of the CMM, the arrangement of the pores (other than the square arrays used in this work), etc.
on ξ is well established. Therefore we envision that those powerful tools used for structural topological optimization of composite materials can now be used for the design of CMMs under the NN-based framework. However, since our NN-based multiscale approach only works for CMMs with smoothly varying ξ, proper regularization has to be imposed to ensure that the optimal solution that we obtained does not violate that condition. Other structural parameters can also be included for the design of CMM, for example, the porosity of the CMM, the arrangement of the pores (other than the square arrays used in this work), etc.
Differentiability and fast deployment are two important motivators for choosing neural networks for this work. Other than neural networks and polynomial regression in Section 4.2, there are many machine learning techniques available, each suitable for different types of problems. For example, decision trees84 are a popular machine learning technique which offers great interpretability; however they are not typically differentiable. Gaussian process regression can be an alternative to neural networks for small datasets, and can sometimes outperform neural networks in terms of accuracy. Yet, there can be great computational cost for deployment once the dataset becomes large.85 The choice of machine learning techniques largely depends on the types of problems and applications considered. Sometimes multiple machine learning techniques can be combined together for optimal performance. In this work, our aim is to demonstrate that neural networks are a promising tool for the design of CMMs. There are limitations – the need to generate a large dataset, the need for smoothly varying ξ – but we expect that future work may be able to compose the model we present with other machine learning techniques to relax these restrictions.
7 Conclusion
In this work, we proposed a neural network based multiscale computational scheme which can be used to predict the overall mechanical behavior of cellular mechanical metamaterials under large deformation. Our scheme adopts a data-driven approach to estimate the functional dependence of the effective strain energy density on complex cellular geometries and finite overall deformation. We first identify a proper RVE of the cellular solid and build an offline training database by varying overall deformation as well as cellular geometries. The database is then used to train and validate a neural network model that can best represent the effective strain energy density as a function of cellular geometries and overall deformation. This neural network model is then treated as a coarse-grained constitutive model of the metamaterial and used to predict its overall mechanical behavior. Under certain conditions, our proposed scheme can significantly reduce the computational time compared with direct numerical simulation while achieving reasonable accuracy, especially when the metamaterial consists of a large number of unit cells. We discussed the limitations of the current scheme and emphasized the types of problems for which it is appropriate. Finally, we discussed the potential of using this to enable efficient rational design of metamaterials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is partially supported by the Princeton Catalysis Initiative at Princeton University. We sincerely thank Dr Dawei Song for helpful and in-depth discussions.Notes and references
-
L. J. Gibson and M. F. Ashby, Cellular solids: structure and properties, Cambridge University Press, 1999 Search PubMed
.
- T. A. Schaedler and W. B. Carter, Annu. Rev. Mater. Res., 2016, 46, 187–210 CrossRef CAS
.
- D. Chen and X. Zheng, Sci. Rep., 2018, 8, 9139 CrossRef PubMed
.
- S. Yuan, C. K. Chua and K. Zhou, Adv. Mater. Technol., 2019, 4, 1800419 CrossRef
.
- K. Bertoldi, P. M. Reis, S. Willshaw and T. Mullin, Adv. Mater., 2010, 22, 361–366 CrossRef CAS PubMed
.
- J. T. Overvelde, S. Shan and K. Bertoldi, Adv. Mater., 2012, 24, 2337–2342 CrossRef CAS PubMed
.
- J. T. Overvelde and K. Bertoldi, J. Mech. Phys. Solids, 2014, 64, 351–366 CrossRef
.
- M. Mirzaali, S. Janbaz, M. Strano, L. Vergani and A. A. Zadpoor, Sci. Rep., 2018, 8, 965 CrossRef CAS PubMed
.
- D. Krishnan and H. T. Johnson, J. Mech. Phys. Solids, 2009, 57, 1500–1513 CrossRef CAS
.
- L. R. Meza, S. Das and J. R. Greer, Science, 2014, 345, 1322–1326 CrossRef CAS PubMed
.
- X. Li and H. Gao, Nat. Mater., 2016, 15, 373 CrossRef CAS
.
- B. Florijn, C. Coulais and M. van Hecke, Soft Matter, 2016, 12, 8736–8743 RSC
.
- K. Bertoldi, V. Vitelli, J. Christensen and M. van Hecke, Nat. Rev. Mater., 2017, 2, 17066 CrossRef CAS
.
- K. Bertoldi, Annu. Rev. Mater. Res., 2017, 47, 51–61 CrossRef CAS
.
- E. Barchiesi, M. Spagnuolo and L. Placidi, Math. Mech. Solids, 2019, 24, 212–234 CrossRef
.
- J. U. Surjadi, L. Gao, H. Du, X. Li, X. Xiong, N. X. Fang and Y. Lu, Adv. Eng. Mater., 2019, 21, 1800864 CrossRef CAS
.
- M. M. Ameen, O. Rokoš, R. Peerlings and M. Geers, Mech. Mater., 2018, 124, 55–70 CrossRef
.
- E. Weinan, B. Engquist, X. Li, W. Ren and E. Vanden-Eijnden, Commun. Comput. Phys., 2007, 2, 367–450 Search PubMed
.
- S. Ahuja, V. Yakhot and I. G. Kevrekidis, Phys. Fluids, 2008, 20, 035111 CrossRef
.
- J. D. Eshelby, Proc. R. Soc. A, 1957, 241, 376–396 Search PubMed
.
- E. Kröner, Z. Phys., 1958, 151, 504–518 CrossRef
.
- Z. Hashin and S. Shtrikman, J. Mech. Phys. Solids, 1963, 11, 127–140 CrossRef
.
- B. Budiansky, J. Mech. Phys. Solids, 1965, 13, 223–227 CrossRef
.
- R. Hill, J. Mech. Phys. Solids, 1965, 13, 213–222 CrossRef
.
- T. Mori and K. Tanaka, Acta Metall., 1973, 21, 571–574 CrossRef
.
- J. Willis, J. Mech. Phys. Solids, 1977, 25, 185–202 CrossRef
.
- R. Hill, J. Mech. Phys. Solids, 1965, 13, 89–101 CrossRef CAS
.
- M. Berveiller and A. Zaoui, J. Mech. Phys. Solids, 1978, 26, 325–344 CrossRef CAS
.
- P. P. Castañeda, J. Mech. Phys. Solids, 1991, 39, 45–71 CrossRef
.
- P. P. Castañeda, J. Mech. Phys. Solids, 1996, 44, 827–862 CrossRef
.
-
J. Segurado, R. A. Lebensohn and J. LLorca, Advances in Applied Mechanics, Elsevier, 2018, vol. 51, pp. 1–114 Search PubMed
.
- M. G. Geers, V. G. Kouznetsova and W. Brekelmans, J. Comput. Appl. Math., 2010, 234, 2175–2182 CrossRef
.
- V. P. Nguyen, M. Stroeven and L. J. Sluys, J. Multiscale Modell., 2011, 3, 229–270 CrossRef
.
- S. Saeb, P. Steinmann and A. Javili, Appl. Mech. Rev., 2016, 68, 050801 CrossRef
.
- F. Feyel, Comput. Mater. Sci., 1999, 16, 344–354 CrossRef CAS
.
- F. Feyel and J.-L. Chaboche, Comput. Methods Appl. Mech. Eng., 2000, 183, 309–330 CrossRef
.
- S. Ghosh, K. Lee and P. Raghavan, Int. J. Solids Struct., 2001, 38, 2335–2385 CrossRef
.
- K. Terada and N. Kikuchi, Comput. Methods Appl. Mech. Eng., 2001, 190, 5427–5464 CrossRef
.
- V. Kouznetsova, M. G. Geers and W. Brekelmans, Comput. Methods Appl. Mech. Eng., 2004, 193, 5525–5550 CrossRef
.
- J. Yvonnet and Q.-C. He, J. Comput. Phys., 2007, 223, 341–368 CrossRef
.
- H. Moulinec and P. Suquet, C. R. Acad. Sci., Ser. IIb: Mec., Phys., Chim., Astron., 1994, 318, 1417–1423 Search PubMed
.
- H. Moulinec and P. Suquet, Comput. Methods Appl. Mech. Eng., 1998, 157, 69–94 CrossRef
.
- D. J. Eyre and G. W. Milton, Eur. Phys. J.: Appl. Phys., 1999, 6, 41–47 CrossRef
.
- J. Michel, H. Moulinec and P. Suquet, CMES (Comput. Modell. Eng. Sci.), 2000, 1, 79–88 Search PubMed
.
- A. Gendy and A. Saleeb, Comput. Mech., 2000, 25, 66–77 CrossRef
.
- J. Yvonnet, E. Monteiro and Q.-C. He, Int. J. Multiscale Comput. Eng., 2013, 11, 201–225 CrossRef
.
- J. Yvonnet, D. Gonzalez and Q.-C. He, Comput. Methods Appl. Mech. Eng., 2009, 198, 2723–2737 CrossRef
.
- N. Takano, M. Zako and Y. Ohnishi, J. Soc. Mater. Sci., Jpn., 1996, 45, 81–86 CrossRef
.
- D. Ryckelynck, J. Comput. Phys., 2005, 202, 346–366 CrossRef
.
- I. Temizer and T. Zohdi, Comput. Mech., 2007, 40, 281–298 CrossRef
.
- R. Chowdhury, B. Rao and A. M. Prasad, Commun. Numer. Methods Eng., 2009, 25, 301–337 CrossRef
.
- F. Fritzen and O. Kunc, Eur. J. Mech., A: Solids, 2018, 69, 201–220 CrossRef
.
- B. Le, J. Yvonnet and Q.-C. He, Int. J. Numer. Meth. Eng., 2015, 104, 1061–1084 CrossRef
.
- X. Lu, D. G. Giovanis, J. Yvonnet, V. Papadopoulos, F. Detrez and J. Bai, Comput. Mech., 2019, 64, 307–321 CrossRef
.
-
S. Haykin, Neural networks: a comprehensive foundation, Prentice-Hall, Inc., 2007 Search PubMed
.
- X. Glorot, A. Bordes and Y. Bengio, International Conference on Machine Learning, 2011, pp. 513–520.
- A. Krizhevsky, I. Sutskever and G. E. Hinton, Neural Information Processing Systems, 2012, pp. 1097–1105.
- D. Bahdanau, K. Cho and Y. Bengio, 2014, arXiv: 1409.0473.
- J. Carrasquilla and R. G. Melko, Nat. Phys., 2017, 13, 431–434 Search PubMed
.
- G. Carleo and M. Troyer, Science, 2017, 355, 602–606 CrossRef CAS
.
- D.-L. Deng, Phys. Rev. Lett., 2018, 120, 240402 CrossRef CAS PubMed
.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed
.
- M. C. Chan and J. P. Stott, Mon. Not. R. Astron. Soc., 2019, 490, 5770–5787 CrossRef
.
- M. Wainberg, D. Merico, A. Delong and B. J. Frey, Nat. Biotechnol., 2018, 36, 829–838 CrossRef CAS PubMed
.
-
T. Xue, A. Beatson, S. Adriaenssens and R. P. Adams, International Conference on Machine Learning, 2020, pp. 8675–8684 Search PubMed
.
- A. Beatson, J. T. Ash, G. Roeder, T. Xue and R. P. Adams, 2020, arXiv:2005.06549.
- Z. Nie, H. Jiang and L. B. Kara, 2018, arxiv: 1808.08914.
- K. Sagiyama and K. Garikipati, 2019, arxiv: 1901.00524.
- H. Zhao, B. D. Storey, R. D. Braatz and M. Z. Bazant, Phys. Rev. Lett., 2020, 124, 060201 CrossRef CAS PubMed
.
- R. Hill, Proc. R. Soc. A, 1972, 326, 131–147 Search PubMed
.
-
T. Hastie, R. Tibshirani and J. Friedman, The elements of statistical learning: data mining, inference, and prediction, Springer Science & Business Media, 2009 Search PubMed
.
- H. Robbins and S. Monro, Ann. Math. Stat., 1951, 400–407 CrossRef
.
- D. E. Rumelhart, G. E. Hinton and R. J. Williams, Learning internal representations by error propagation, California univ san diego la jolla inst for cognitive science technical report, 1985.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed
.
-
A. Logg, K.-A. Mardal and G. Wells, Automated solution of differential equations by the finite element method: The FEniCS book, Springer Science & Business Media, 2012, vol. 84 Search PubMed
.
- I. M. Sobol’, Zh. Vychisl. Mat. Mat. Fiz., 1967, 7, 784–802 Search PubMed
.
- D. P. Kingma and J. Ba, 2014, arxiv: 1412.6980.
- M. Stone, J. R. Stat. Soc.: Ser. B (Methodological), 1974, 36, 111–133 Search PubMed
.
-
C. M. Bishop, Pattern recognition and machine learning, Springer, 2006 Search PubMed
.
-
M. S. Alnæs, Automated Solution of Differential Equations by the Finite Element Method, Springer, 2012, pp. 303–338 Search PubMed
.
- S. Sarkar, M. Cebron, M. Brojan and A. Kosmrlj, 2020, arXiv: 2004.01044.
- G. Allaire, F. De Gournay, F. Jouve and A.-M. Toader, Control Cybernetics, 2005, 34, 59 Search PubMed
.
- H. A. Eschenauer and N. Olhoff, Appl. Mech. Rev., 2001, 54, 331–390 CrossRef
.
-
L. Breiman, J. Friedman, C. J. Stone and R. A. Olshen, Classification and regression trees, CRC Press, 1984 Search PubMed
.
-
C. E. Rasmussen, Summer School on Machine Learning, 2003, pp. 63–71 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00488j |
| This journal is © The Royal Society of Chemistry 2020 |