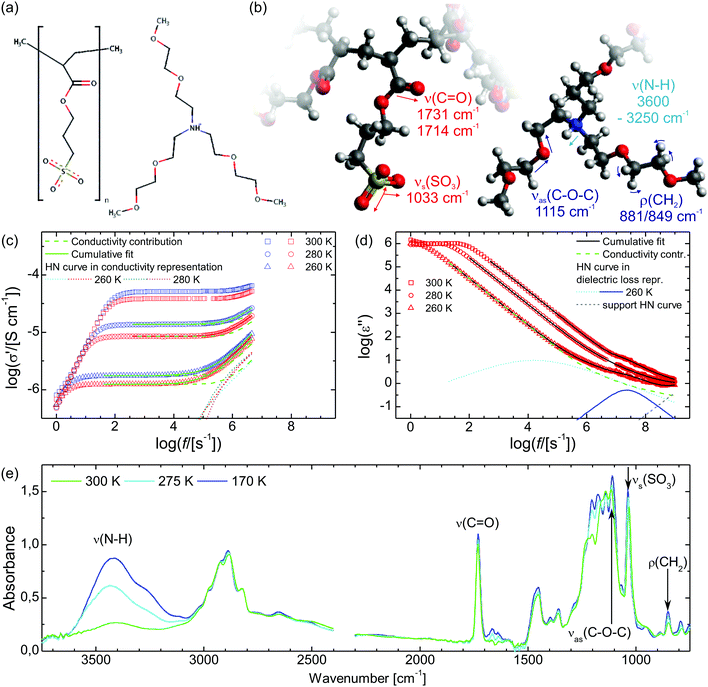
Open Access Article
Open Access ArticleHydrogen bonding and charge transport in a protic polymerized ionic liquid†
Arthur Markus
Anton
 *ab,
Falk
Frenzel
*ab,
Falk
Frenzel
 a,
Jiayin
Yuan
a,
Jiayin
Yuan
 c,
Martin
Tress
c,
Martin
Tress
 ad and
Friedrich
Kremer
ad and
Friedrich
Kremer
 a
a
aLeipzig University, Peter Debye Institute for Soft Matter Physics, Linnéstraße 5, 04103 Leipzig, Germany. E-mail: a.m.anton@outlook.de
bThe University of Sheffield, Department of Physics and Astronomy, Hicks Building, Hounsfield Road, Sheffield S3 7RH, UK
cStockholm University, Department of Materials and Environmental Chemistry, Svante Arrhenius väg 16C, 106 91 Stockholm, Sweden
dUniversity of Tennessee, Department of Chemistry, 1420 Circle Drive,, Knoxville, Tennessee 37996, USA
First published on 9th June 2020
Abstract
Hydrogen bonding and charge transport in the protic polymerized ionic liquid poly[tris(2-(2-methoxyethoxy)ethyl)ammoniumacryloxypropyl sulfonate] (PAAPS) are studied by combining Fourier transform infrared (FTIR) and broadband dielectric spectroscopy (BDS) in a wide temperature range from 170 to 300 K. While the former enables to determine precisely the formation of hydrogen bonds and other moiety-specific quantized vibrational states, the latter allows for recording the complex conductivity in a spectral range from 10−2 to 10+9 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Hz. A pronounced thermal hysteresis is observed for the H-bond network formation in distinct contrast to the reversibility of the effective conductivity measured by BDS. On the basis of this finding and the fact that the conductivity changes with temperature by orders of magnitude, whereas the integrated absorbance of the N–H stretching vibration (being proportional to the number density of protons in the hydrogen bond network) changes only by a factor of 4, it is concluded that charge transport takes place predominantly due to hopping conduction assisted by glassy dynamics (dynamic glass transition assisted hopping) and is not significantly affected by the establishment of H-bonds.
Hz. A pronounced thermal hysteresis is observed for the H-bond network formation in distinct contrast to the reversibility of the effective conductivity measured by BDS. On the basis of this finding and the fact that the conductivity changes with temperature by orders of magnitude, whereas the integrated absorbance of the N–H stretching vibration (being proportional to the number density of protons in the hydrogen bond network) changes only by a factor of 4, it is concluded that charge transport takes place predominantly due to hopping conduction assisted by glassy dynamics (dynamic glass transition assisted hopping) and is not significantly affected by the establishment of H-bonds.
1 Introduction
Polymerized ionic liquids (polyILs) form a unique class of electrolyte materials, which combines the favorable properties of neat ionic liquids (ILs), such as ion conductivity,1 wide electrochemical and thermal stability,2,3 or non-flammability,4 with the macromolecular benefits of polymers like mechanical stability.5,6 Based on the polyILs’ properties they can be used in multifold applications, such as solvents,7,8 in electro- and biochemistry,9,10 engineering,11 or aeronautics.12 Among the wide field of ILs, protic ionic liquids (proILs) represent a subset produced through combining a Brønsted acid with a Brønsted base.13 Because of the proton transfer from the acid to the base, proton donor and acceptor sites are present, which are well suited to form hydrogen bonds (H-bonds). One consequence of this is that the amount of hydrogen bonds within the sample can significantly affect the polyIL's macroscopic properties.14–17 It can be demonstrated that water added to a protic polyIL acts as plasticizer and reduces the (calorimetric) glass transition temperature (Tg) as well as it increases the DC-conductivity at absolute temperatures.18,19Another strategy to modify the polyILs’ conductivity behavior is to place a spacer unit at the IL-like side group attached to the polymer backbone or between the backbone and the IL-like group.20–24 This architecture reduces Tg with increasing spacer length with the result of an increased DC-conductivity at absolute temperatures for the most cases, but a lowered DC-conductivity at Tg-normalized temperatures (T/Tg) for all cases. The same holds true for increasing the size of the counterion.22
For the most (but not all) cases the mechanism of charge transport in non-crystalline polyILs (as well as low molecular weight ILs) can be comprehended as class transition assisted hopping.25–27 In this model hopping of charges is governed by molecular fluctuations, and consequently the conductivity of the materials is predominantly determined by the dynamics of the glassy system.28 This is in particular evidenced by the proportionality between the hopping rate of the charge carriers and relaxation rate of thermally activated fluctuations obeying glassy dynamics. Moreover, this relation can typically be observed over 6 to 8 orders of magnitude and holds true for both low molecular weight ILs29,30 as well as polymeric systems.27,31,32
Recently, Gainaru et al. and Stacy et al. published a model for a direct estimate of ion diffusion on the basis of the conductivity relaxation process and further a qualitative model describing ionic transport as a competition between electrostatic and elastic forces, respectively. In addition to the correlation with the ion size, which determines the particular regime (electrostatic or elastic), the authors suggested an increase of the dielectric permittivity in order to reduce Tg and the energy barrier for small ion conductivity.33,34
In the current manuscript we study the sample material poly[tris(2-(2-methoxyethoxy)ethyl)ammonium acryloxypropyl sulfonate] (PAAPS), which exhibits one of the highest values of DC-conductivity at room temperature for anhydrous (water-free) polymer systems as recently reported in our previous work.31 Even though this material makes use of a reduced Tg by an increased side chain length and counterion size, PAAPS appears highly viscous at room temperature.35 In order to investigate the mechanism of charge transport in this promising material in detail on the molecular scale, we examine a combination of temperature-dependent Fourier transform infrared (FTIR) and broadband dielectric spectroscopy (BDS). Even though FTIR and BDS measurements are routinely employed as separate methods in order to study (poly)ILs, combining them is very uncommon. However, this combination enables us, on the one hand, to follow the temperature-dependent evolution of the macroscopic complex conductivity, and on the other hand, to assess alterations of moiety-specific molecular vibrations.
We follow the formation and deterioration of an extended H-bond network during a cooling-heating cycle. A detailed analysis reveals that the network remains intact during heating giving rise to a pronounced hysteresis, which allows for comparing the DC-conductivity of the identical sample at the same temperature with a tremendous difference in H-bond density. Surprisingly and contrary to the concept of fast proton hopping,17,36 in the case of PAAPS, H-bond formation hinders charge transport. We discuss the charge transport mechanism which is governed by thermally activated molecular fluctuations, whereas hydrogen bonding hinders fluctuations and thus reduces the DC-conductivity. These novel results about which moieties are involved in inter-molecular binding on the microscopic scale and how H-bonds affect the macroscopic conductivity for the particular case of PAAPS suggest a reassessment of the role of H-bonds for conductivity.
2 Materials and methods
2.1 Sample material
The synthesis of the sample material poly[tris(2-(2-methoxyethoxy)ethyl)ammonium acryloxypropyl sulfonate] (PAAPS) has been published by Prescher et al.35 and Frenzel et al.,31 in the former for the repeat unit and in the latter for the polymerized ionic liquid (polyIL, Fig. 1), respectively. The molecular weight of the examined sample was Mn = 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 g mol−1.
500 g mol−1.
2.2 Temperature- and frequency-dependent broadband dielectric spectroscopy
For broadband dielectric spectroscopy (BDS) two devices have been used; in the frequency range of f = 10−2–10+7 s−1 a high-resolution α-analyzer (Novocontrol Technologies GmbH & Co. KG, Germany) and in a range of f = 10+7–10+9 s−1 a 4291A impedance/material analyzer and a high impedance test head (Hewlett Packard, USA). Both spectrometers are equipped with a Quatro temperature controller (temperature accuracy ≤1 K, (Novocontrol Technologies GmbH & Co. KG, Germany)). In the case no error bars are provided, the measurement uncertainty is smaller than the symbol size.Sample cells dedicated to be measured in the first device consisted of a polished brass electrode (40 mm diameter), glass fibers (50 μm diameter) acting as spacers, and a second polished brass electrode (10 mm diameter). In order to remove as much water as possible, a droplet of PAAPS has been placed on the bigger, lower electrode with glass fibers on top and stored at 423 K in high vacuum (10−6 mbar) for at least 12 hours. The smaller, upper electrode has not been placed on top of the sample yet, but experienced the same temperature and atmospheric treatment as the rest of the sample. After the temperature and vacuum treatment, the vacuum chamber was flushed with Argon and the hot upper electrode was put on top of the hot sample, forming the capacitor for the BDS measurements. Dielectric spectra have been recorded from 300 K down to 170 K and back in steps of 5 K with an effective cooling/heating rate of 5 × 10−5 K s−1.
Samples for the high frequency spectrometer were composed of two gold coated brass electrodes (5 mm diameter), two thin Teflon stripes (520 μm thickness) acting as spacers, and a Teflon ring slightly wider than the electrodes in order to hold this arrangement in place. Spectra have been recorded under dry nitrogen atmosphere in the temperature range from 310 K to 170 K and back in steps of 5 K with a cooling/heating rate of 5 K s−1.
2.3 Temperature-dependent infrared spectroscopy
Infrared (IR) spectra have been recorded by means of a Bio-Rad FTS 6000 FTIR spectrometer equipped with a UMA 500 IR microscope and a liquid nitrogen-cooled mercury–cadmium–telluride (MCT) detector (Kolmar Technologies, Inc., USA). The sample temperature has been controlled using a THMS 350V stage (Linkam Scientific Instruments, UK) flushed with dry nitrogen. IR spectra have been recorded from 300 K down to 170 K and back in steps of 5 K with an effective cooling/heating rate of 0.012 K s−1.Samples for IR spectroscopy have been prepared by dissolving the sample material in deionized water (18.2 MΩ cm−1, Milli-Q, Merck, Germany) and drop-casting the solution on an IR-transparent substrate (BaF2, Korth Kristalle GmbH, Germany). This method facilitates the adjustment of the sample thickness by subsequent dropping and drying until the desired absorption is reached. Afterward the sample films have been stored at 423 K in vacuum (10−6 mbar) for at least 12 hours, in order to remove the water used for preparation and absorbed from ambient air. The sample has been transported in dry argon atmosphere and measured in dry nitrogen atmosphere.
3 Results
3.1 Broadband dielectric spectroscopy
A basic study on the sample's dielectric and conductive properties has been published previously.31 Therein, dielectric relaxation processes and conductivity has been studied in the frequency range from 10−2 to 10+7 s−1. The primary α relaxation has been ascribed to fluctuations of transient dipole moments, whereas the secondary β relaxation to fluctuations of the carboxyl group. Furthermore, PAAPS emerged as a polyIL exhibiting one of the highest values of DC-conductivity at 300 K so far published for anhydrous (water-free) polyILs.31,37 In order to investigate the mechanism of charge transport in detail, we expand the frequency range for BDS measurements up to 10+9 s−1 (Fig. 1). The detriment of the high DC-conductivity interfering with the primary relaxation process in dielectric loss spectra ε′′(ω) is circumvented by fitting a superposition of a conductivity contribution and a relaxation process in the real part of the complex conductivity σ′(ω) (Fig. 1c).38 In detail we make use of| σ*(ω) = iωε0ε*, | (1) |
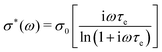 | (2) |
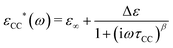 | (3) |
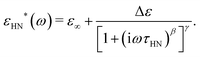 | (4) |
When fitting in the σ′-representation, on the one hand, the value of σ0 can be directly obtained from the measured plateau level and, on the other hand, the increase of the AC-conductivity at higher frequencies is properly described through the random free-energy barrier model.38,39 Consequently, the relaxation process in the measured curves (as sum of conductivity and relaxation) is accounted for by a CC function instead of the more general HN function,40 because a CC function is symmetric and only one side of the relaxation process can be seen in the spectra.
The thus obtained mean relaxation times of this process confirm the extrapolation of values determined previously for the α-relaxation at lower temperatures (Fig. 2a).31 Making use of the relaxation time for the α-relaxation τα-CC as well as the values of the DC-conductivity σ0 and critical frequency of the charge transport ωc, the relaxation times for the secondary process (as HN function) are determined on the basis of a combination of dielectric loss spectra in the ε′′-representation in the frequency ranges of 10−2 to 10+7 s−1 and 10+7 to 10+9 s−1 (Fig. 1d). The relaxation times for the secondary β-relaxation also agree with the values determined at lower temperatures (Fig. 2a).31 When we approximate the thermal activation of the α- and β-relaxation times with a Vogel–Fulcher–Tammann (VFT) and an Arrhenius functions,40 the rates of both processes are separated by less than 1 decade for Tg/T ≤ 0.74 and do intersect at Tg/T = 0.72.
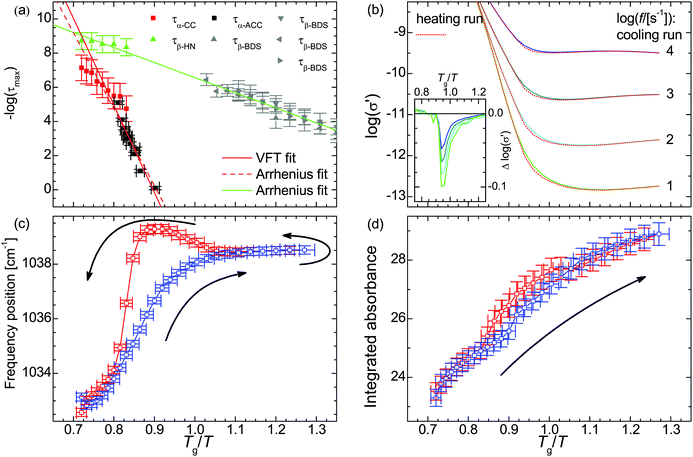 | ||
Fig. 2 (a) Relaxation time of the primary τα and secondary relaxation processes τβ in PAAPS (red and green symbols: spectra measured using the described combination of normal and high frequency dielectric spectroscopy; τα-CC primary relaxation derived in the σ′-representation using a Cole–Cole (CC) function; τβ-HN secondary relaxation derived in the ε′′-representation using a Havriliak–Negami (HN) function; black and grey symbols: spectra measured by means of BDS and alternating current chip calorimetry (ACC), data taken from Frenzel et al., ref. 31; τα-ACC primary relaxation derived by means of ACC; τβ-BDS secondary relaxation derived by using a HN function in the normal frequency BDS range (10−2 to 10+7 s−1); solid red line: VFT fit; solid green line and dashed red line: Arrhenius fits). (b) Real part σ′ of the complex conductivity function depending on the inverse temperature scaled with the glass transition temperature Tg = 216 K. The inset depicts the difference between the cooling and heating run; at the same temperature σ0 is up to 20% smaller during the heating run than during previous cooling. (c) Frequency position ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) and (d) integrated absorbance Aint of the symmetric SO3 stretching vibration νs(SO3). The blue and red symbols denote data recorded during the cooling run from 300 K to 170 K and the reversed heating, respectively. The logarithm in panels a and b is to base 10. and (d) integrated absorbance Aint of the symmetric SO3 stretching vibration νs(SO3). The blue and red symbols denote data recorded during the cooling run from 300 K to 170 K and the reversed heating, respectively. The logarithm in panels a and b is to base 10. | ||
In the conductivity spectra (Fig. 1c), it is evident that the plateau of the DC-conductivity at a particular temperature is higher in the case of the cooling run as compared to the subsequent heating. Similarly, in the temperature-dependent representations of the conductivity spectra for particular frequencies (Fig. 2b), the decrease of the conductivity (because of cooling) takes place at lower temperatures (higher values of Tg/T) than the respective increase of conductivity during the subsequent heating run; we observe a hysteresis for the DC-conductivity. The maximum difference between the conductivity during the heating and previous cooling run is
Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10(σ′) = log10(σ′)|heating − log10(σ′)|cooling log10(σ′) = log10(σ′)|heating − log10(σ′)|cooling | (5) |
| = −0.10 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) s−1]) = 1 to 5; for lower frequencies a more pronounces hysteresis can be observed (Fig. S2 in the ESI†).
s−1]) = 1 to 5; for lower frequencies a more pronounces hysteresis can be observed (Fig. S2 in the ESI†).
3.2 Infrared spectroscopy
Within the IR spectra of PAAPS we identify absorption peaks and bands specific for charged and uncharged moieties within the polymer side chain as well as the cation (Table 1). Among them, the quaternary ammonium group is the only hydrogen bond donor; in contrast, the ether group in the cation as well as the carboxyl and sulfonate groups in the polymer side chains are hydrogen bond acceptors (determined by means of the Hydrogen Bond Donor/Acceptor Plugin in Mavin by ChemAxon, for further information see ESI,† Fig. S1). For the sake of conciseness, we will focus on the ammonium and sulfonate groups as main H-bond partners, as discussed below. For the other moieties the interested reader is referred to the ESI.†![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) = 1033 cm−1 (at 300 K), which represents the absorption arising from the symmetric stretching vibration of the SO3 group (νs(SO3)), (Fig. 1, Fig. S6, ESI† and Table 1).45–47 With decreasing temperature this peak is reversibly shifted to higher frequencies (Fig. 2c). In addition, the shift exhibits a pronounced hysteresis which sets in between Tg/T = 1.10–1.05 (T = 196–206 K); a temperature which matches well with the glass transition temperature of the repeat unit (RU, comprising one monomer and one cation) (TRUg = 199 K, Tg/TRUg = 1.09).35 The glass transition temperature of the polymer, instead, is higher than that of the repeat unit (Tpolg = 216–225 K, Tg/Tpolg = 1.00–0.96)31,35 and lies inbetween the commencement of the hysteresis and the temperature of its maximum value. Please note, the calorimetric glass transition temperature of Tg = 216 K determined by means of differential scanning calorimetry (DSC) has been used throughout this work to scale the diagrams. Other methods as BDS or AC-chip calorimetry lead to slightly different values of Tg,31 which explains the range of values for Tg/Tpolg provided above.
= 1033 cm−1 (at 300 K), which represents the absorption arising from the symmetric stretching vibration of the SO3 group (νs(SO3)), (Fig. 1, Fig. S6, ESI† and Table 1).45–47 With decreasing temperature this peak is reversibly shifted to higher frequencies (Fig. 2c). In addition, the shift exhibits a pronounced hysteresis which sets in between Tg/T = 1.10–1.05 (T = 196–206 K); a temperature which matches well with the glass transition temperature of the repeat unit (RU, comprising one monomer and one cation) (TRUg = 199 K, Tg/TRUg = 1.09).35 The glass transition temperature of the polymer, instead, is higher than that of the repeat unit (Tpolg = 216–225 K, Tg/Tpolg = 1.00–0.96)31,35 and lies inbetween the commencement of the hysteresis and the temperature of its maximum value. Please note, the calorimetric glass transition temperature of Tg = 216 K determined by means of differential scanning calorimetry (DSC) has been used throughout this work to scale the diagrams. Other methods as BDS or AC-chip calorimetry lead to slightly different values of Tg,31 which explains the range of values for Tg/Tpolg provided above.
From the chemical structure it is evident that the sulfonate part is negatively charged with oxygen as a standard hydrogen bond acceptor (Fig. S1, ESI†). Consequently, we expect that the sulfonate group is an H-bond acceptor. In general, when a stretching vibration undergoes hydrogen bonding, the respective peak frequency is reduced (red shift) due to weakening of covalent bonds, whereas the band intensity is enhanced.55 However, in the particular case of νs(SO3) the band intensity increases during hydrogen bonding while the frequency exhibits a blue shift (instead of a red shift). This indicates binding of one N–H group to one oxygen atom of the sulfonate group as described by Huang et al. (monodentate ion pairs as well as bi- and tridentate bridges are causing a blue shift, while bi- and tridentate ion pairs are causing a red shift).48 A blue shift arising from hydrogen bonding is also found for νs(SO3) in ethyl sulfate.56 Additionally, this 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 donor
1 donor![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acceptor ratio can also be found in the case of the proIL ethylammonium hydrogen sulfate exhibiting a similar chemical structure of donor and acceptor.57
acceptor ratio can also be found in the case of the proIL ethylammonium hydrogen sulfate exhibiting a similar chemical structure of donor and acceptor.57
Furthermore, the temperature of the maximum hysteresis of the IR blue shift coincides with the maximum of Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(σ′) (eqn (5), inset in Fig. 2b). Thus, the onset of the hysteresis at TRUg indicates that already at this temperature the polymer side chains are mobile enough for structural reorganization. In addition, the maximum of the hysteresis and its concordance with the most reduced conductivity at a particular temperature indicate that in PAAPS, hydrogen bonding hinders charge transport.
log(σ′) (eqn (5), inset in Fig. 2b). Thus, the onset of the hysteresis at TRUg indicates that already at this temperature the polymer side chains are mobile enough for structural reorganization. In addition, the maximum of the hysteresis and its concordance with the most reduced conductivity at a particular temperature indicate that in PAAPS, hydrogen bonding hinders charge transport.
We want to emphasize that this pronounced hysteresis is observed despite of the very small effective cooling/heating rate of 0.012 K s−1 throughout the whole measurement. At this rate it takes 100 s to change the temperature by about 1 K, which is accepted as the rate of structural relaxations at the dynamic glass transition temperature.31,32 This means that at any temperature above Tg the system can easily equilibrate and effects of thermal or dynamic inertia are excluded.
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) = 3600–3250 cm−1, Fig. 1, Fig. S7, ESI† and Table 1), which is a combination of peaks indicative of hydrogen bonding.58
= 3600–3250 cm−1, Fig. 1, Fig. S7, ESI† and Table 1), which is a combination of peaks indicative of hydrogen bonding.58
In order to unravel the temperature dependence of the hydrogen bonding of the of N–H moiety, 4 Gaussian (plus 1 for the adjacent band at the low wavenumber side) are fitted to this band and their integrated absorbance (Aint) measured by the area under the curve (AuC) is recorded (Fig. 3 and Fig. S7, S8, ESI†). When the temperature is decreased to 170 K, the cumulative AuC (sum of the AuCs of the particular peaks) increases up to the 8.6-fold of the initial value at 300 K, which quantifies the increase of the number density of hydrogen bonds. (The cumulative AuC is chosen, because this is the most reliable measure. Due to the minor structure of this band, individual peak positions may vary and hence the individual AuCs are affected.) During the subsequent heating the number density increases even further to the 10.3-fold at Tg/T = 0.90 (240 K). Only then, further heating leads to a reduction of the hydrogen bond density and eventually the initial value at 300 K is recovered. In order to exclude that the variation in the occupation of states causes the altered band intensity, we estimate the populations via a Boltzmann distribution. We find that for all peaks the ratio of the population in the first excited state to the population of the ground state is ≤3 × 10−7 at 300 K, and ≤3 × 10−12 at 170 K. Thus, already at 300 K the first (and any higher excited state) is effectively unoccupied and the absorption is not affected by the variation in the population numbers.
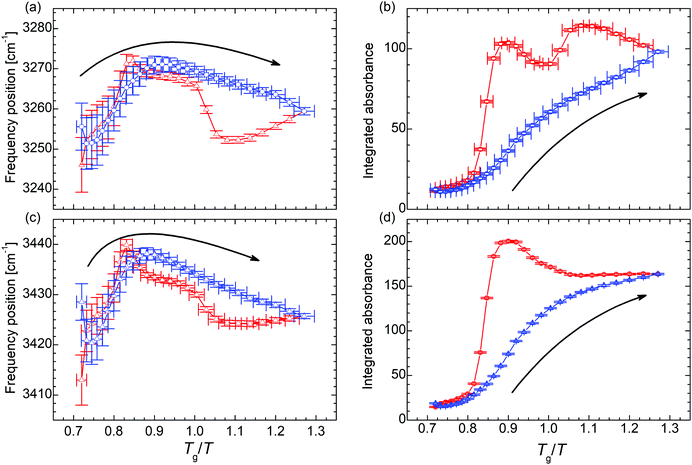 | ||
| Fig. 3 (a) and (c) Temperature dependence of the frequency position and (b) and (d) integrated absorbance of the N–H stretching vibration ν(N–H). The blue symbols denote data points recorded during the cooling run, the red symbols during the subsequent heating run. The arrows indicate the direction of the initial cooling. The analysis of the remaining N–H stretching peaks can be found in the ESI.† | ||
In the trajectory of the AuC two kinds of traces can be identified in the set of absorption peaks assigned to the N–H stretching vibration. On the one hand, there are peaks undergoing a two-step hysteresis during heating (Fig. 3b and Fig. S8b, d, ESI†). In the case of these peaks, the hysteresis sets in immediately after the lowest temperature of 170 K has been passed and the sample is heated (Fig. 3b). This clearly indicates remaining molecular mobility, even though the system is at 46 K below the macroscopic glass transition temperature Tg.31,35 On the other hand, there are peaks undergoing a one-step hysteresis during heating (Fig. 3d and Fig. S8f, h, ESI†), similar to the frequency position of νs(SO3) (Fig. 2c). For these peaks, the hysteresis does not start right with the beginning of the heating run at 170 K but still before Tg is reached, namely at TRUg as in the case of νas(SO3).
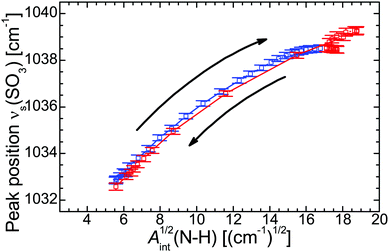
![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) (SO3) vs. Aint(N–H)1/2, Fig. 4) the individual data points represent different temperatures during the cooling and heating run and form a fairly straight line. The strong correlation suggests that the H-bonds are mainly formed between the SO3 moiety of the polymer side chain and the N–H group of the cation. Even the hysteresis during the heating run evident as point cloud at Aint1/2 ≈ 18 cm−1/2 coincides with the approximately linear correlation. Other significant interactions with the N–H group, for example with the C–O–C moiety, can be excluded on the basis of the according correlation plots (see ESI†).
(SO3) vs. Aint(N–H)1/2, Fig. 4) the individual data points represent different temperatures during the cooling and heating run and form a fairly straight line. The strong correlation suggests that the H-bonds are mainly formed between the SO3 moiety of the polymer side chain and the N–H group of the cation. Even the hysteresis during the heating run evident as point cloud at Aint1/2 ≈ 18 cm−1/2 coincides with the approximately linear correlation. Other significant interactions with the N–H group, for example with the C–O–C moiety, can be excluded on the basis of the according correlation plots (see ESI†).
4 Discussion
4.1 Proton Transfer
One measure to discern between ILs and a mixture of ionic and neutral species is the difference between the aqueous pKa values of the base and the acid,| ΔpKa = pKa(base) − pKa(acid). | (7) |
Davidowski et al.63 employed NMR spectroscopy in order to characterize the ionicity and transport properties of a series of proILs formed by protonation of diethylmethylamine. The charged center of this molecule is fairly comparable with that of the cation in PAAPS. From the 1H chemical shift, the authors deduced the affinity of the proton to the base. For PAAPS and AAPS we found a chemical shift of 9.3 and 9.1 ppm (Fig. S13 in the ESI†), respectively. On the basis of the calibration line elaborated by Davidowski et al. (Fig. 3 in ref. 63), we further calculate a proton affinity of 318 kcal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol−1 (13.8 eV) and 317 kcal
mol−1 (13.8 eV) and 317 kcal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mo−1 (13.8 eV), respectively. In addition Davidowski et al. derived a correlation between the 1H chemical shift and ΔpKa (Fig. 2 in ref. 63). According to this correlation the ΔpKa values for PAAPS and AAPS are supposed to amount to 12.0 and 12.5, respectively. However, Davidowski et al. stated that the proton chemical shift is a better predictor for the proton transfer than the frequently used ΔpKa values.
mo−1 (13.8 eV), respectively. In addition Davidowski et al. derived a correlation between the 1H chemical shift and ΔpKa (Fig. 2 in ref. 63). According to this correlation the ΔpKa values for PAAPS and AAPS are supposed to amount to 12.0 and 12.5, respectively. However, Davidowski et al. stated that the proton chemical shift is a better predictor for the proton transfer than the frequently used ΔpKa values.
In the following discussion we will show that these values of the chemical shift correspond to a partial proton transfer. This means, the proton is neither completely at the donor, nor at the acceptor site; it is bridging both moieties.63
With regard to Nakamoto et al. the different N–H bond distances can be approximated from the particular ![[small nu, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ce.gif) (N–H).64 On the basis of the derived parameters for the different peaks, the values of the N–H⋯O bond length are between 2.9 and 3.2 Å, whereas each bond does not change by more than 0.02 Å during the temperature cycle. Thus, we treat this distance as constant during the measurement. This is corroborated by DFT simulations (ORCA program system, B3LYP/6-31G(d) and B3LYP/6-31G(2d,2p)65–69) yielding a distance of 2.6 Å (d(N–H) = 1.1 Å
(N–H).64 On the basis of the derived parameters for the different peaks, the values of the N–H⋯O bond length are between 2.9 and 3.2 Å, whereas each bond does not change by more than 0.02 Å during the temperature cycle. Thus, we treat this distance as constant during the measurement. This is corroborated by DFT simulations (ORCA program system, B3LYP/6-31G(d) and B3LYP/6-31G(2d,2p)65–69) yielding a distance of 2.6 Å (d(N–H) = 1.1 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) and d(H⋯O) = 1.5 Å; literature, Hayes et al. d(H⋯O) = 1.6 Å
and d(H⋯O) = 1.5 Å; literature, Hayes et al. d(H⋯O) = 1.6 Å![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57) for the relaxed structure of one repeat unit and one anion in vacuo. Further repeat units and additional anions may introduce structural constraints and increase the bond distance.
57) for the relaxed structure of one repeat unit and one anion in vacuo. Further repeat units and additional anions may introduce structural constraints and increase the bond distance.
4.2 Charge transfer mechanism
The chemical structure of the H-bonding moieties of PAAPS (center of the cation and sulfate group at the outermost position at the polymer side chain) is similar to that in DEMA-MS (mixture of diethylmethylamine with methanesulfonic acid), a sample studied by Davidowski et al.63 Interestingly, both PAAPS as well as DEMA-MS show a comparable chemical shift of the exchangeable proton (9.3/9.1 vs. 9.5 ppm), and thus a comparable proton affinity to the base. In addition, 15N pulsed-field gradient NMR spectroscopy on DEMA-MS revealed that anion, cation, and exchangeable proton diffuse with the same rates, which is why the authors presumed a “hydrogen bonded ion pair”.63 On the basis of our IR spectroscopy results and the similar chemical structures of the hydrogen bond donor and acceptor in the cases of PAAPS/AAPS and DEMA-MS, we validate the existence of an extended hydrogen bond network. Moreover, the comparable diffusion constants of anion, cation, and exchangeable proton as determined by Davidowski et al.63 corroborate our findings of a correlation between the rates of structural fluctuation (α-relaxation) and charge transport (ωc) as determined by Frenzel et al.31 Thus, the mechanism of charge transport can indubitably be specified as a hopping mechanism strongly influenced through the glassy nature of the polymeric system (known as glass transition assisted hopping conduction).27,31,32,70 This means, hopping depends on the thermally activated fluctuations of molecules, which are drastically slowed down at the dynamic glass transition. Thus, the dynamic behavior of the glass building polymer influences molecular mobility and hence the events of hopping.27,70Further verification of the glass transition assisted hopping conduction mechanism is provided by the thermal response of PAAPS. Therefor, we divide the evolution of H-bonding and DC-conductivity during the temperature cycle into 4 steps (Fig. 5); first, cooling from 300 K to 240 K (Tg/T = 0.90), the latter of which is the temperature of the maximum hysteresis; second, cooling from 240 K to 170 K (Tg/T = 1.27) i.e. the lowest recorded temperature; and third and fourth, subsequent heating to 240 K and further to 300 K, respectively.
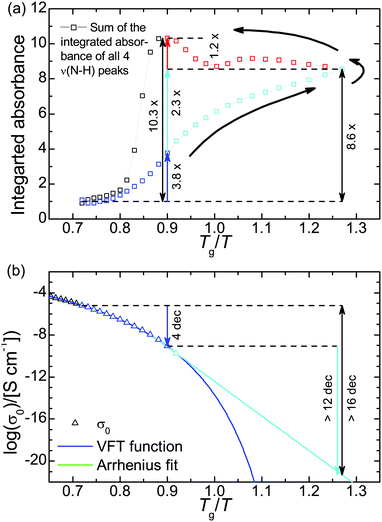 | ||
Fig. 5 (a) Cumulative integrated absorbance of ν(N–H) and (b) DC-conductivity. The DC-conductivity during heating is not shown since the hysteresis (Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(σ′) = −0.10, eqn (5)) is too small to be visible in this plot. Please note, the integrated absorbance is normalized to 1 at 300 K. The relative uncertainty is equal or less than 2% and hence smaller than the symbol size. The logarithm in panel b is to base 10. log(σ′) = −0.10, eqn (5)) is too small to be visible in this plot. Please note, the integrated absorbance is normalized to 1 at 300 K. The relative uncertainty is equal or less than 2% and hence smaller than the symbol size. The logarithm in panel b is to base 10. | ||
During step 1, the number density of H-bonds increases by a factor of 3.8. At the same time the DC-conductivity is reduced by 4 orders of magnitude (Fig. 5). In step 2, the DC-conductivity decreases further by more than 12 orders of magnitude (extrapolated from a conservative Arrhenius fit), while the H-bond density increases only to the 8.6-fold of the initial value or by a factor of 2.3 compared to the value at 240 K. Already at this position within the temperature cycle it is evident that the increase in H-bond density during the first step (factor 3.8) is bigger than during the second one (factor 2.3), whereas the change in DC-conductivity is bigger during the second temperature change (4 orders of magnitude vs. 12). This finding further supports the perception of glassy dynamics assisted hopping. We note, that the chosen Arrhenius dependence for extrapolating the thermal activation of the DC-conductivity marks a very upper limit of σ0; most likely, its value will be much lower leading to a much bigger reduction of σ0 during step 2. In general, the thermal activation of the conductivity in polyILs changes from a Vogel–Fulcher–Tammann- (VFT) into an Arrhenius-dependence at a particular temperature Tσ0, which is frequently reported to coincide with Tg21,22 but can be very distinct as recently published.32
During step 3, the number density of H-bonds increases further to the 10.3-fold of the initial value (a factor of 1.2 more than compared to their density at 170 K); the DC-conductivity, instead, increases approximately by about the same amount as it was reduced during step 2, except for a residue of 20% (Δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10(σ′) = −0.10, eqn (5)).
log10(σ′) = −0.10, eqn (5)).
At the first glance, the heating run increases the H-bond density even further, whereas the conductivity rises as well. Obviously, the conductivity is generally dominated by the thermal activation of molecular fluctuations, rather than by H-bonding.
In a more detailed view, the conductivity rises (because of thermal activation) but does not reach the values which were evident during the cooling run at the same temperatures. Because the thermal activation of molecular fluctuations is identical at the same absolute temperatures, reduced conductivity in step 3 must arise from the increased H-bond density (as evidenced by means of IR spectroscopy). We can conclude for the particular case of PAAPS that H-bonding hinders molecular fluctuations and hence charge transport hopping.
We are aware that the current results contradict the frequently published concept of fast proton hopping within hydrogen bond networks, which is believed to be faster than structural fluctuations.17,18,36 One indication for fast proton or synonymously superionic conduction is the DC-conductivity at Tg with the limit of 10−15 S cm−1.18,36 In the case of the polyIL PAAPS, σ0 amounts 2.1 × 10−14 S cm−1 at Tg, which is comparable with recently published low molecular weight proton conductors as lidocaine-hemisuccinate or lidocaine-dihydrogen citrate (σ0 = 3.7 × 10−14 or 1.6 × 10−13 S cm−1, respectively).36 However, the combination of IR spectroscopy and BDS together with temperature cycling provides findings that object the concept of fast proton hopping. The results by Davidowski et al.63 as well as the one by FTIR and NMR spectroscopy and DFT simulations corroborate the non-complete ionization state of donor and acceptor, which is believed to be favorable for proton conduction.36
In addition, FTIR spectroscopy reveals that the number density of H-bonds is drastically increased during cooling and even further increased during subsequent heating (hysteresis in Fig. 5a). Since a higher H-bond density is believed to favor proton conductivity,36 in the hypothetical case of fast proton conduction the DC-conductivity would be expected to be greater, when the H-bond density is increased at the same particular temperature. This is not the case for PAAPS; at the same temperature the DC-conductivity is reduced with increased H-bond density.
Even though PAAPS fulfills the prerequisites for fast proton hopping, such as sufficiently high ΔpKa for proton transfer but delocalized protons and an increased H-bond density,36 we have to conclude that for our protic polyIL the charge transport is mediated through a hopping mechanism which is not dominated by fast proton hopping. Instead, the hopping mechanism is governed by structural fluctuations, which obey glassy dynamics and are hindered through H-bonding (Fig. 6).
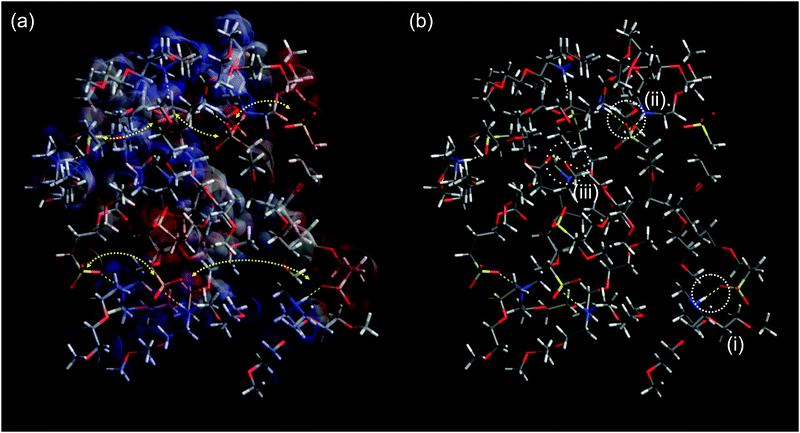 | ||
| Fig. 6 (a) Surface charge of a PAAPS oligomer (8 repeat units) surrounded by 8 cations (blue: positive; red: negative; gray: neutral) and schematic representation of hopping conduction of transient dipole moments between ammonium moieties of the cations and sulfonate groups at the outermost ends of the polymer side chains. Because the fluctuations of transient dipole moments are dominated by the thermally activated fluctuations of the molecular moieties as described in the framework of glass transition-assisted hopping, the conductivity obeys a VFT-dependence.31 Moreover, hydrogen bonding hinders the molecular mobility which becomes evident in a reduced conductivity at the same temperature but increased H-bond density (Fig. 2b); (b) hydrogen bonding scenarios as recorded via FTIR spectroscopy: (i) H-bond between one oxygen atom of the sulfonate group and one ammonium part or (ii) between two different oxygen atoms of one sulfonate group and two different ammonium parts, as indicated by the measured spectral blue shift (Fig. 2c) and the blue shift in simulations from Huang et al.48 (iii) H-bond formation between carboxyl and ammonium groups might be possible; however, the carboxyl group is effectively screened from interactions and only 11% of all groups undergo inter- as well as intra-molecular interactions (cf. ESI†). Please note this structure is for visualization purposes only. The system was constructed by adding 8 monomers forming one main chain and 8 cations in arbitrary order and allowed to relax without any constraints in accord to the Merck molecular force field 94 (MMFF94)71 following the steepest decent in Avogadro molecule editor program.72 | ||
5 Conclusion
On the basis of IR spectroscopy, we prove the formation of an extended H-bond network in the protic polymerized ionic liquid PAAPS. This network is in accordance with 1H chemical shift, which indicates an intermediate bound state of the proton between donor and acceptor unit, as stated by Davidowski et al.63 Moreover, when the sample is heated after previous cooling during the temperature cycle, the network becomes even more strengthened giving rise to a pronounced hysteresis. Because of the extremely low cooling/heating rate of 0.012 K s−1, which corresponds approximately to the structural relaxation rate at Tg of 102 s,31,32 the system is able to follow temperature changes above Tg; a too fast cooling/heating as cause for this hysteresis is excluded.On the basis of broadband dielectric spectroscopy (BDS), we record the conductivity during the temperature cycles and determine two attributes. First, cooling and heating affect the DC-conductivity by several orders of magnitude, as frequently observed for hopping transport.25,31,32,73 Second, at the same temperature σ0 differs for different H-bond densities; a (by a factor of 3) greater density results in (20%) lower conductivity. Thus, for the particular case of PAAPS it is demonstrated that the thermal activation of molecular fluctuations affects the charge transport to a much greater extent than H-bonding. Furthermore, at the identical temperature and identical thermal activation an increased H-bond density reduces the conductivity.
This very first study combining FTIR spectroscopic and BDS measurements during temperature cycling in order to investigate H-bond formation in protic polyILs provides detailed results about moiety-specific H-bonding and macroscopic conductivity as well as their interrelation. The sample under study provides the second highest published DC-conductivity at 300 K for anhydrous polyIL;31 interestingly, the anhydrous polyIL with the highest published DC-conductivity at 300 K has similar elements in its chemical structure.37 Thus, in the frame of these results the concept of charge transport in this class of materials may need to be reshaped. The DC-conductivity might be adjusted via Tg reduction, whereas mechanical properties can be customized via H-bond density on a much less expense of conductivity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. M. A. thanks the Deutsche Forschungsgemeinschaft (DFG) for financial support of project AN 1523/1-1, A. M. A. and F. K. for granting project B08 within the framework of SFB/TRR 102, F. F. and F. K. for support of project KR 1138/24-1. M. T. is grateful to the DFG for granting project B15 within the framework of SFB/TRR 102 as well as to the Alexander von Humboldt foundation for granting his Feodor-Lynen postdoc fellowship. J. Y. is grateful for financial support from the ERC Starting Grant NAPOLI-639720, the Swedish Research Council (Project No. 2018-05351), and the Wallenberg Academy Fellow program (KAW 2017.0166).References
- X. Wang, Y. Chi and T. Mu, J. Mol. Liq., 2014, 193, 262–266 CrossRef CAS.
- S. Aparicio, M. Atilhan and F. Karadas, Ind. Eng. Chem. Res., 2010, 49, 9580–9595 CrossRef CAS.
- M. Armand, F. Endres, D. R. MacFarlane, H. Ohno and B. Scrosati, Nat. Mater., 2009, 8, 621–629 CrossRef CAS PubMed.
- K. Ghandi, Green Sustainable Chem., 2014, 4, 44–53 CrossRef CAS.
- H. Ohno and K. Ito, Chem. Lett., 1998, 751–752 CrossRef CAS.
- H. Ohno, M. Yoshizawa-Fujita and Y. Kohno, Bull. Chem. Soc. Jpn., 2019, 92, 852–868 CrossRef CAS.
- P. G. Jessop, D. J. Heldebrant, X. Li, C. A. Eckert and C. L. Liotta, Nature, 2005, 436, 1102 CrossRef CAS PubMed.
- S. G. Cull, J. D. Holbrey, V. Vargas-Mora, K. R. Seddon and G. J. Lye, Biotechnol. Bioeng., 2000, 69, 227–233 CrossRef CAS.
- D. Langevin, Q. T. Nguyen, S. Marais, S. Karademir, J.-Y. Sanchez, C. Iojoiu, M. Martinez, R. Mercier, P. Judeinstein and C. Chappey, J. Phys. Chem. C, 2013, 117, 15552–15561 CrossRef CAS.
- M. Forsyth, L. Porcarelli, X. Wang, N. Goujon and D. Mecerreyes, Acc. Chem. Res., 2019, 52, 686–694 CrossRef CAS PubMed.
- S. Menne, J. Pires, M. Anouti and A. Balducci, Electrochem. Commun., 2013, 31, 39–41 CrossRef CAS.
- S. Schneider, T. Hawkins, Y. Ahmed, M. Rosander, L. Hudgens and J. Mills, Angew. Chem., Int. Ed., 2011, 50, 5886–5888 CrossRef CAS PubMed.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2008, 108, 206–237 CrossRef CAS PubMed.
- A. Bagno, C. Butts, C. Chiappe, F. D’Amico, J. C. D. Lord, D. Pieraccini and F. Rastrelli, Org. Biomol. Chem., 2005, 3, 1624–1630 RSC.
- J. A. Widegren, A. Laesecke and J. W. Magee, Chem. Commun., 2005, 1610–1612 RSC.
- M. Anouti, A. Vigeant, J. Jacquemin, C. Brigouleix and D. Lemordant, J. Chem. Thermodyn., 2010, 42, 834–845 CrossRef CAS.
- Z. Wojnarowska, H. Feng, M. Diaz, A. Ortiz, I. Ortiz, J. Knapik-Kowalczuk, M. Vilas, P. Verdia, E. Tojo, T. Saito, E. W. Stacy, N.-G. Kang, J. W. Mays, D. Kruk, P. Wlodarczyk, A. P. Sokolov, V. Bocharova and M. Paluch, Chem. Mater., 2017, 29, 8082–8092 CrossRef CAS.
- Z. Wojnarowska, J. Knapik, M. Díaz, A. Ortiz, I. Ortiz and M. Paluch, Macromolecules, 2014, 47, 4056–4065 CrossRef CAS.
- J. R. Nykaza, Y. Ye, R. L. Nelson, A. C. Jackson, F. L. Beyer, E. M. Davis, K. Page, S. Sharick, K. I. Winey and Y. A. Elabd, Soft Matter, 2016, 12, 1133–1144 RSC.
- M. H. Allen, S. Wang, S. T. Hemp, Y. Chen, L. A. Madsen, K. I. Winey and T. E. Long, Macromolecules, 2013, 46, 3037–3045 CrossRef CAS.
- U. H. Choi, Y. Ye, D. S. de la Cruz, W. Liu, K. I. Winey, Y. A. Elabd, J. Runt and R. H. Colby, Macromolecules, 2014, 47, 777–790 CrossRef CAS.
- C. Iacob, A. Matsumoto, M. Brennan, H. Liu, S. J. Paddison, O. Urakawa, T. Inoue, J. Sangoro and J. Runt, ACS Macro Lett., 2017, 6, 941–946 CrossRef CAS.
- C. Tracy, A. M. Adler, A. Nguyen, R. D. Johnson and K. M. Miller, ACS Omega, 2018, 3, 13442–13453 CrossRef CAS PubMed.
- E. Mapesa, M. Chen, M. F. Heres, M. A. Harris, T. Kinsey, Y. Wang, T. E. Long, B. S. Lokitz and J. R. Sangoro, Macromolecules, 2019, 52, 620–628 CrossRef CAS.
- F. Frenzel, W. H. Binder, J. R. Sangoro and F. Kremer, in Dielectric Properties of Ionic Liquids, ed. M. Paluch, Springer International Publishing, 2016, ch. Glassy Dynamics and Charge Transport in Polymeric Ionic Liquids, pp. 115–129 Search PubMed.
- J. R. Sangoro and F. Kremer, Acc. Chem. Res., 2012, 45, 525–532 CrossRef CAS PubMed.
- J. R. Sangoro, C. Iacob, A. L. Agapov, Y. Wang, S. Berdzinski, H. Rexhausen, V. Strehmel, C. Friedrich, A. P. Sokolov and F. Kremer, Soft Matter, 2014, 10, 3536–3540 RSC.
- J. R. Sangoro, C. Iacob, W. K. Kipnusu, M. Jasiurkowska, R. Valiullin, C. Friedrich, J. Kärger and F. Kremer, Soft Matter, 2011, 7, 10565–10568 RSC.
- J. R. Sangoro, C. Iacob, S. Naumov, R. Valiullin, H. Rexhausen, J. Hunger, R. Buchner, V. Strehmel, J. Kärger and F. Kremer, Soft Matter, 2011, 7, 1678–1681 RSC.
- J. R. Sangoro, M. Mierzwa, C. Iacob, M. Paluch and F. Kremer, RSC Adv., 2012, 2, 5047–5050 RSC.
- F. Frenzel, R. Guterman, A. M. Anton, J. Yuan and F. Kremer, Macromolecules, 2017, 50, 4022–4029 CrossRef CAS.
- F. Frenzel, P. Borchert, A. M. Anton, V. Strehmel and F. Kremer, Soft Matter, 2019, 15, 1605–1618 RSC.
- C. Gainaru, E. W. Stacy, V. Bocharova, M. Gobet, A. P. Holt, T. Saito, S. Greenbaum and A. P. Sokolov, J. Phys. Chem. B, 2016, 120, 11074–11083 CrossRef CAS PubMed.
- E. W. Stacy, C. P. Gainaru, M. Gobet, Z. Wojnarowska, V. Bocharova, S. G. Greenbaum and A. P. Sokolov, Macromolecules, 2018, 51, 8637–8645 CrossRef CAS.
- S. Prescher, F. Polzer, Y. Yang, M. Siebenbürger, M. Ballauff and J. Yuan, J. Am. Chem. Soc., 2014, 136, 12–15 CrossRef CAS PubMed.
- Z. Wojnarowska, K. J. Paluch, E. Shoifet, C. Schick, L. Tajber, J. Knapik, P. Wlodarczyk, K. Grzybowska, S. Hensel-Bielowka, S. P. Verevkin and M. Paluch, J. Am. Chem. Soc., 2015, 137, 1157–1164 CrossRef CAS PubMed.
- A. Jourdain, A. Serghei and E. Drockenmuller, ACS Macro Lett., 2016, 5, 1283–1286 CrossRef CAS.
- J. C. Dyre, J. Appl. Phys., 1988, 64, 2456–2468 CrossRef.
- T. B. Schröder and J. C. Dyre, Phys. Rev. Lett., 2000, 84, 310–313 CrossRef PubMed.
- Broadband Dielectric Spectroscopy, ed. F. Kremer and A. Schönhals, Springer-Verlag Berlin Heidelberg GmbH, Berlin Heidelberg New York, 1st edn, 2003 Search PubMed.
- W. H. T. Davison, J. Chem. Soc., 1955, 3270–3274 RSC.
- T. Miyazawa, K. Fukushima and Y. Ideguchi, J. Chem. Phys., 1962, 37, 2764–2776 CrossRef CAS.
- K.-J. Liu and J. L. Parsons, Macromolecules, 1969, 2, 529–533 CrossRef CAS.
- M. A. K. L. Dissanayake and R. Frech, Macromolecules, 1995, 28, 5312–5319 CrossRef CAS.
- D. H. Johnston and D. F. Shriver, Inorg. Chem., 1993, 32, 1045–1047 CrossRef CAS.
- A. G. Bishop, D. R. MacFarlane, D. McNaughton and M. Forsyth, J. Phys. Chem., 1996, 100, 2237–2243 CrossRef CAS.
- R. Frech, S. Chintapalli, P. G. Bruce and C. A. Vincent, Macromolecules, 1999, 32, 808–813 CrossRef CAS.
- W. Huang, R. Frech and R. A. Wheeler, J. Phys. Chem., 1994, 98, 100–110 CrossRef CAS.
- K. Haupa, A. Bil and Z. Mielke, J. Phys. Chem. A, 2015, 119, 10724–10734 CrossRef CAS PubMed.
- V. H. Paschoal, L. F. O. Faria and M. C. C. Ribeiro, Chem. Rev., 2017, 117, 7053–7112 CrossRef CAS PubMed.
- H. Matsuura and T. Miyazawa, Bull. Chem. Soc. Jpn., 1967, 40, 85–94 CrossRef CAS.
- R. Pruthtikul, M. M. Coleman, P. C. Painter and N. B. Tan, Macromolecules, 2001, 34, 4145–4150 CrossRef CAS.
- Y. Mikhaylova, G. Adam, L. Häussler, K.-J. Eichhorn and B. Voit, J. Mol. Struct., 2006, 788, 80–88 CrossRef CAS.
- G. Socrates, Infrared and Raman Characteristic Group Frequencies: Tables and Chartes, John Wiley & Sons, Ltd, Chichester, 3rd edn, 2004 Search PubMed.
- G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond In Structural Chemistry and Biology, Oxford University Press, Oxford New York, 1st edn, 2001 Search PubMed.
- Q.-G. Zhang, N.-N. Wang and Z.-W. Yu, J. Phys. Chem. B, 2010, 114, 4747–4754 CrossRef CAS PubMed.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Angew. Chem., Int. Ed., 2013, 52, 4623–4627 CrossRef CAS PubMed.
- A. V. Iogansen, Spectrochim. Acta, Part A, 1999, 55, 1585–1612 CrossRef.
- A. D. Sherry and K. F. Purcell, J. Am. Chem. Soc., 1972, 94, 1848–1853 CrossRef CAS.
- Z. Wojnarowska and M. Paluch, J. Phys.: Condens. Matter, 2015, 27, 073202 CrossRef PubMed.
- J.-P. Belieres and C. A. Angell, J. Phys. Chem. B, 2007, 111, 4926–4937 CrossRef CAS PubMed.
- D. R. MacFarlane, J. M. Pringle, K. M. Johansson, S. A. Forsyth and M. Forsyth, Chem. Commun., 2006, 1905–1917 RSC.
- S. K. Davidowski, F. Thompson, W. Huang, M. Hasani, S. A. Amin, C. A. Angell and J. L. Yarger, J. Phys. Chem. B, 2016, 120, 4279–4285 CrossRef CAS PubMed.
- K. Nakamoto, M. Margoshes and R. E. Rundle, J. Am. Chem. Soc., 1955, 77, 6480–6486 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, J. Chem. Phys., 1982, 77, 3654–3665 CrossRef CAS.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- F. Neese, M. Atanasov, G. Bistoni, D. Maganas and S. Ye, J. Am. Chem. Soc., 2019, 141, 2814–2824 CrossRef CAS PubMed.
- J. R. Sangoro, C. Iacob, A. Serghei, C. Friedrich and F. Kremer, Phys. Chem. Chem. Phys., 2009, 11, 913–916 RSC.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- F. Frenzel, M. Y. Folikumah, M. Schulz, A. M. Anton, W. H. Binder and F. Kremer, Macromolecules, 2016, 49, 2868–2875 CrossRef CAS.
Footnote |
† Electronic supplementary information (ESI) available: Analysis of possible H-bond sites, hysteresis of σ′ for a wider frequency range, FTIR spectra of additional samples for comparison measurements and peak assignments, FTIR spectra of νas((SO3)), FTIR spectra and further analysis of ν((N–H)), FTIR spectra and analysis of ν((C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)), FTIR spectra and analysis of ρgauche((CH3)), νtrans-gauche((CH3)) and νas((C–O–C)), correlation between the different analyzed vibrational modes and 1H NMR spectra of the polyIL PAAPS and the monomer AAPS. See DOI: 10.1039/d0sm00337a O)), FTIR spectra and analysis of ρgauche((CH3)), νtrans-gauche((CH3)) and νas((C–O–C)), correlation between the different analyzed vibrational modes and 1H NMR spectra of the polyIL PAAPS and the monomer AAPS. See DOI: 10.1039/d0sm00337a |
| This journal is © The Royal Society of Chemistry 2020 |