Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theory of droplet ripening in stiffness gradients†
Estefania
Vidal-Henriquez
 * and
David
Zwicker
* and
David
Zwicker
 *
*
Max-Planck Institute for Dynamics and Self-Organization, Am Faβberg 17, 37077 Göttingen, Germany. E-mail: estefania.vidal@ds.mpg.de; david.zwicker@ds.mpg.de
First published on 8th June 2020
Abstract
Liquid droplets embedded in soft solids are a new composite material whose properties are not very well explored. In particular, it is unclear how the elastic properties of the matrix affect the dynamics of the droplets. Here, we study theoretically how stiffness gradients influence droplet growth and arrangement. We show that stiffness gradients imply concentration gradients in the dilute phase, which transport droplet material from stiff to soft regions. Consequently, droplets dissolve in the stiff region, creating a dissolution front. Using a mean-field theory, we predict that the front emerges where the curvature of the elasticity profile is large and that it propagates diffusively. This elastic ripening can occur at much higher rates than classical Ostwald ripening, thus driving the dynamics. Our work shows how gradients in elastic properties control the arrangement of droplets, which has potential applications in soft matter physics and biological cells.
1 Introduction
Phase separation has recently been established as a crucial mechanism for organizing membrane-less organelles in biological cells.1–4 These membrane-less organelles, or biomolecular condensates, often posses properties of liquid-like droplets, like internal rearrangement, spherical shapes, and monomer exchange with their surroundings. However, these droplets exist in complex environments that cannot be described as simple liquids. For example, the cytoskeleton in the cytosol5,6 as well as the chromatin in the nucleoplasm7 have solid-like properties, which could affect droplets. Indeed, recent experiments showed that droplets typically form in chromatin-poor regions in the nucleus.8 This suggests that the elastic properties of chromatin suppress droplet formation. However, it is difficult to disentangle the effect of the elastic surroundings from other potential processes that could affect droplet formation in the complex case of a living cell.Physical experiments with synthetic materials can help to understand how an elastic environment affects droplet growth. For instance, oil droplets growing in a homogeneous PDMS gel form mono-disperse emulsions and the stiffness of the gel controls droplet size.9 There are several advantages of these experiments: first, the system is not driven, implying it relaxes toward equilibrium after preparation. Second, the gel is strongly cross-linked, so it does not spontaneously rearrange on the time scale of the experiments.10 Viscous relaxation is thus negligible. Third, droplets are large compared to the mesh size, implying that the gel can be described by a continuum theory. Taken together, these properties allow to isolate the effects of an elastic environment on droplets.
The aim of the present paper is to understand how spatially varying stiffnesses affect droplet dynamics. This is motivated by recent experiments showing that stiffness gradients lead to elastic ripening, where droplets dissolve in stiffer regions.11 Moreover, these experiments revealed a dissolution front invading stiffer regions, while the material of the dissolving droplets accumulated in softer regions. We already developed a theoretical description of the situation, which is based on the assumption that the gel exerts a pressure onto droplets that is proportional to the local stiffness.11 Numerical simulations of this theory showed excellent agreement with the measured data. In the present paper, we analyze this model numerically and analytically to understand the details of elastic ripening. In particular, we use a simplified, coarse-grained version to derive scaling laws for where and when the dissolution front starts and how it evolves in time. These simple equations allow us to predict how the model parameters affect elastic ripening in more complex situations, e.g., when the elasticity profile varies in all spatial dimensions.
2 Elasticity gradients produce dissolution fronts
We aim at understanding the dynamics of an emulsion embedded in a gel with spatially varying stiffness. Motivated by elastic ripening experiments,11 we focus on the case where the gel is strongly cross-linked and behaves as an elastic material. Moreover, the droplets are well separated and deform the gel only locally, so they only interact by exchanging material via the dilute phase. This exchange is driven by the difference between the concentration in the dilute phase and the concentration right outside a droplet's surface. We determine the latter by considering a single droplet in an homogeneous elastic environment.2.1 Thermodynamics of isolated droplets
Motivated by recent experimental results,11 we describe a three-component system of two liquids and a network of cross-linked polymers. At high temperatures, the two liquids are miscible and form a homogeneous gel with the polymer network. When the temperature is lowered, one liquid forms droplets by segregating from the other two components. Therefore, this phase separation can effectively be described as a binary system; droplets with a high volume fraction ϕin of the segregating liquid coexist with a dilute gel phase of lower volume fraction ϕ. In the case of thermodynamically large phases, these equilibrium volume fractions can be determined by minimizing the total free energy of the system using the Maxwell construction;12 see ESI.† In particular, the equilibrium conditions imply that the pressures and chemical potentials are identical in both phases.In the case of a single spherical droplet of radius R embedded in an isotropic elastic matrix, the droplet exhibits an additional pressure P due to both surface tension and elastic effects. In the simple case of a dense droplet phase and an ideal dilute phase, the resulting equilibrium volume fraction in the dilute phase can be approximated as
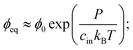 | (1) |
The pressure P on a single spherical droplet of radius R embedded in an elastic gel is
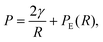 | (2) |
To see whether surface tension γ is important in the ripening experiments, we next estimate the relevant pressure differences between droplets. The pressure difference generated by surface tension is roughly γΔR/R2, where R is the mean droplet radius and ΔR denotes the difference in the radii. Conversely, the pressure difference created by the external gel can be estimated by the typical stiffness difference ΔE. Surface tension is thus negligible if the ratio
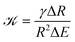 | (3) |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) ≈ 3 × 10−4, so that Ostwald ripening is indeed negligible. Taken together, the equilibrium volume fraction ϕeq can thus be approximated by
≈ 3 × 10−4, so that Ostwald ripening is indeed negligible. Taken together, the equilibrium volume fraction ϕeq can thus be approximated by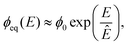 | (4) |
2.2 Dynamical equations of emulsions
We now consider an emulsion of droplets embedded in a gel with spatially varying stiffness E(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ). We describe the system by the droplet radii Ri and their positions
). We describe the system by the droplet radii Ri and their positions ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i, as well as the volume fraction ϕ(
i, as well as the volume fraction ϕ(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) in the dilute phase. The thermodynamics discussed in the previous section imply that the equilibrium volume fraction ϕeq right outside each droplet depends on its position. The difference between ϕeq and ϕ drives a diffusive flux between the droplet and the dilute phase. Since we are only interested in dynamics on length scales larger than the droplet radii, we evaluate all involved quantities at the droplet position
) in the dilute phase. The thermodynamics discussed in the previous section imply that the equilibrium volume fraction ϕeq right outside each droplet depends on its position. The difference between ϕeq and ϕ drives a diffusive flux between the droplet and the dilute phase. Since we are only interested in dynamics on length scales larger than the droplet radii, we evaluate all involved quantities at the droplet position ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i. Consequently, the material efflux Ji integrated over the droplet surface can be expressed as Ji = 4πDRi[ϕeq(
i. Consequently, the material efflux Ji integrated over the droplet surface can be expressed as Ji = 4πDRi[ϕeq(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i) − ϕ(
i) − ϕ(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i)], where D is the molecular diffusivity.12 This flux drives changes in droplet radius,
i)], where D is the molecular diffusivity.12 This flux drives changes in droplet radius,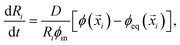 | (5) |
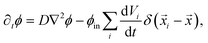 | (6) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) i are constant, since the elastic gel restricts the motion of the droplets. In principle, our model allows overlapping droplets, but since they do not move and their initial positions are far apart, overlapping does not occur in practice. Consequently, eqn (5) and (6) fully describe how an emulsion of droplets evolves over time.
i are constant, since the elastic gel restricts the motion of the droplets. In principle, our model allows overlapping droplets, but since they do not move and their initial positions are far apart, overlapping does not occur in practice. Consequently, eqn (5) and (6) fully describe how an emulsion of droplets evolves over time.
The dynamics of the system is governed by two diffusive fluxes that act on different length scales. Locally, material is exchanged between the droplets and the dilute phase by the flux Ji. Conversely, transport on longer length scales only happens in the dilute phase by the redistribution flux −D∇ϕ.
2.3 Numerical simulations show dissolution fronts
We simulated eqn (5) and (6) to understand the effects of an elasticity gradient on the emulsion dynamics. Motivated by elastic ripening experiments,11 we consider a system consisting of two regions of different stiffness Esoft and Estiff. When the two regions are put side-by-side, a transition region emerges. To capture this, we model the stiffness profile in the entire system by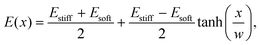 | (7) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) in the dilute phase.
) in the dilute phase.
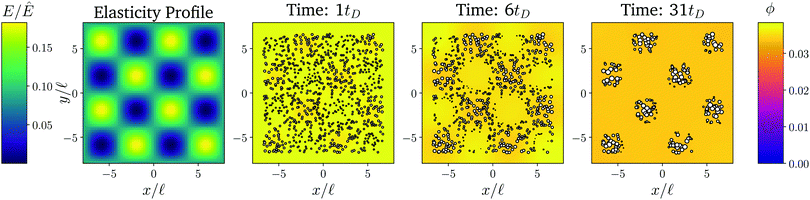
Fig. 1 shows the time course of a typical simulation. Starting from the homogeneous initial condition, the system quickly forms two separate regions aligned with the stiffness profile (upper panel). Here, the stiff side exhibits smaller droplets and larger volume fractions in the dilute phase compared to the soft side. Droplets then start dissolving in the transition region and a dissolution front moves into the stiff side. Simultaneously, droplets grow on the soft side of the transition region while droplets far into the soft side remain unchanged. The exact same dynamics have been observed in the elastic ripening experiments;11 see Fig. 2. These dynamics can be understood qualitatively by considering the diffusive fluxes in the system.
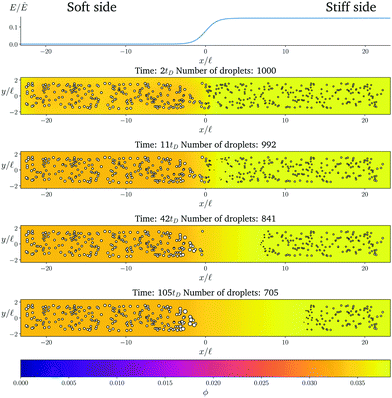 | ||
Fig. 1 Numerical simulation showing a dissolution front invading the stiff region defined by a sigmoidal elasticity profile (upper panel). Subsequent images show projections of 3-dimensional simulations (obtained by solving eqn (5) and (6) of the droplets (symbols) and the volume fraction ϕ in the dilute phase (density plot with color bar at the bottom) at the indicated times. The model parameters are ϕ0 = 0.033, ϕin = 1, Estiff = 0.15Ê, Esoft = 10−4Ê, and w = 1.45![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . Here, . Here, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = (Vsys/Ndrop)1/3 is a typical droplet separation with associated diffusive time tD = = (Vsys/Ndrop)1/3 is a typical droplet separation with associated diffusive time tD = ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2/D, where Vsys is the system's volume and Ndrop is the total number of droplets. The mean droplet radius on the stiff side is 0.08 2/D, where Vsys is the system's volume and Ndrop is the total number of droplets. The mean droplet radius on the stiff side is 0.08![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . . | ||
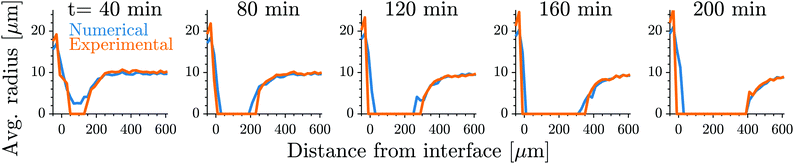 | ||
Fig. 2 Our model quantitatively captures the dynamics of dissolution fronts in the elastic ripening experiments.11 Shown are the experimental and numerical mean droplet radii as a function of the distance from the interface on the stiff side for five different time points. The model parameters are Estiff = 0.0341Ê, Esoft = 3.2 × 10−4Ê, w = 0.37![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) , and the mean droplet radius on the stiff side is 0.09 , and the mean droplet radius on the stiff side is 0.09![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ; see ESI,† for further details on the comparison. ; see ESI,† for further details on the comparison. | ||
In the initial stage, the system is supersaturated everywhere, ϕ > ϕeq. Consequently, material is transferred from the dilute phase to the droplets until a local equilibrium is reached, ϕ = ϕeq. Eqn (4) implies that ϕeq is smaller for softer regions, so more material is absorbed by the droplets. We thus observe larger droplets in softer regions (see Fig. 1), consistent with experimental observations.9
After the initial, local equilibration, material redistribution on longer length scales sets in. Since the stiffer side exhibits larger volume fractions ϕ in the dilute phase, material is transported to the soft side. Consequently, on the stiff side, ϕ drops below the local equilibrium volume fraction ϕeq, droplets shrink, and eventually dissolve. This process starts close to the transition region, since the redistribution flux is driven by gradients in ϕ, which do not exist further away. Once droplets start disappearing in the transition region, droplets further away begin to be affected and a dissolution front forms that invades the stiff side. All the material redistributed from the stiff side is absorbed by the droplets on the soft side close to the transition region, which effectively shield all the other droplets on the soft side.
3 A coarse-grained model explains the dissolution dynamics
To understand the front's dynamics quantitatively, we next consider a simplified version of our model. Here, we do not describe the dynamics of individual droplets, but rather focus on the fractions of material in droplets and in the dilute phase. We thus introduce the coarse-grained volume fraction ψ of material contained in droplets,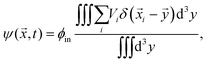 | (8) |
![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) . Note that the discretization volume needs to be large enough to contain multiple droplets, but also small compared to the characteristic length scales of the elasticity gradient. Introducing the local mean droplet volume V(
. Note that the discretization volume needs to be large enough to contain multiple droplets, but also small compared to the characteristic length scales of the elasticity gradient. Introducing the local mean droplet volume V(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t), we can express ψ as ψ = ϕinnV, where n is the local droplet number density. Motivated by the elastic ripening experiments and our numerical simulations, we consider the case where the volume of individual droplets does not deviate substantially from the local mean volume V. In this case, the volume fractions ϕ and ψ, characterizing the amount of material in the dilute phase and droplets, respectively, are sufficient to describe the system's state.
,t), we can express ψ as ψ = ϕinnV, where n is the local droplet number density. Motivated by the elastic ripening experiments and our numerical simulations, we consider the case where the volume of individual droplets does not deviate substantially from the local mean volume V. In this case, the volume fractions ϕ and ψ, characterizing the amount of material in the dilute phase and droplets, respectively, are sufficient to describe the system's state.
The dynamics of the coarse-grained system follow from eqn (5) and (6). We show in the ESI,† that the dynamical equations are
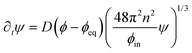 | (9a) |
| ∂tϕ = D∇2ϕ − ∂tψ. | (9b) |
Fig. 3 shows that the results of the numerical simulation of the coarse-grained model are virtually indistinguishable from that of the detailed model. Therefore, the coarse-grained model captures the essential features of the elastic ripening process. In particular, the dynamics of the dissolution front are governed by the material distribution, while individual droplets are irrelevant.
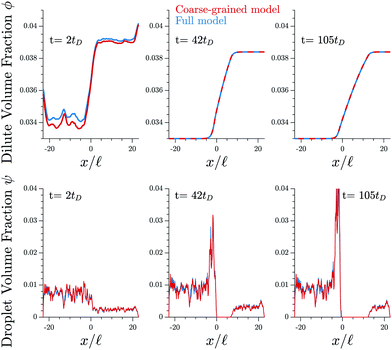 | ||
| Fig. 3 The coarse-grained model (red lines, eqn (9)) captures the detailed dynamics of the full model (blue lines, eqn (5) and (6)). Shown are the profiles of the volume fractions ϕ in the dilute phase (upper panels) and the fraction ψ contained in droplets (lower panels) for three different time points t. The model parameters are given in Fig. 1. | ||
3.1 Dissolution starts at high curvatures of the elasticity profile
We now use the coarse-grained model to understand where and when the dissolution front appears, i.e., when droplets first disappear. In the numerical simulations, we observe that ϕ quickly approaches ϕeq by local equilibration between the droplets and the dilute phase. Assuming that the system is initialized with ϕ = ϕinit and ψ = ψinit, the volume fractions approach ϕ ≈ ϕeq and ψ = ψ0 with ψ0 ≈ ψinit + ϕinit − ϕeq after this initial stage. Consequently, the volume fraction ϕ in the dilute phase is controlled by the stiffness profile E(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ), while the remaining material is absorbed in the droplets.
), while the remaining material is absorbed in the droplets.
After the initial equilibration stage, the inhomogeneities in E, and thus in ϕ, drive diffusive fluxes toward the soft side. However, we observe that these fluxes mostly affect ψ and hardly change ϕ before the first droplets disappear. To understand the dynamics in this stage, we approximate eqn (9b) by ∂tψ ≈ D∇2ϕeq. Consequently, ψ evolves as
ψ(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ,t) ≈ ψ0( ,t) ≈ ψ0(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) + tD∇2ϕeq ) + tD∇2ϕeq | (10) |
We can use eqn (10) to estimate the time and position of the start of the dissolution front. In particular, droplets dissolve after a time τ*(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) ≈ −ψ0(
) ≈ −ψ0(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) )/(D∇2ϕeq), when all material is removed from the droplet phase. The dissolution front starts at the earliest of these time points, τstart = min
)/(D∇2ϕeq), when all material is removed from the droplet phase. The dissolution front starts at the earliest of these time points, τstart = min![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) (τ*|τ* ≥ 0), which is given by
(τ*|τ* ≥ 0), which is given by
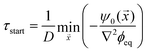 | (11) |
The starting time τstart can be estimated for the simple stiffness profile given by eqn (7). In particular, the droplet volume fraction ψ0 will be close to the value ψstiff deep into the stiff side; the curvature is approximately ∇2ϕeq ∼ Δϕ/w2, where Δϕ = ϕeq(Estiff) − ϕeq(Esoft) denotes the difference in the equilibrium volume fractions between the two sides and w is the width of the transition region. Using these estimates, eqn (11) suggests a time scale
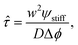 | (12) |
We test the prediction of eqn (11) and the scaling discussed above by comparing to numerical simulations of the full model; see Fig. 4. The collapse of the starting times shown in the left panel indicates that ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) is the relevant time scale for this process. Moreover, the actual prediction τstart given in eqn (11) is within a factor of two of the measured data. This analysis shows that the front appears earlier for larger stiffness differences (larger Δϕ) between the two sides, for narrower transitions regions (smaller w), as well as when there is less material in the droplet phase (small ψstiff). Fig. 4b shows the corresponding starting positions, which clearly are determined by the width w of the transition region. The data collapse indicates that neither the absolute stiffnesses nor the droplet size affects where the front appears.
is the relevant time scale for this process. Moreover, the actual prediction τstart given in eqn (11) is within a factor of two of the measured data. This analysis shows that the front appears earlier for larger stiffness differences (larger Δϕ) between the two sides, for narrower transitions regions (smaller w), as well as when there is less material in the droplet phase (small ψstiff). Fig. 4b shows the corresponding starting positions, which clearly are determined by the width w of the transition region. The data collapse indicates that neither the absolute stiffnesses nor the droplet size affects where the front appears.
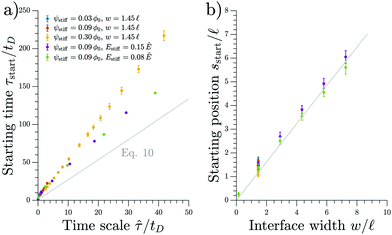 | ||
Fig. 4 The starting time τstart and position sstart of the front scale with the predicted time and length scales, respectively. Results from numerical simulations of the full model (dots) for various parameters are compared to the theoretical predictions from the coarse-grained model (gray line). The time point τstart of the first dissolving droplet is shown in panel (a) as a function of the predicted associated time scale ![[small tau, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b8.gif) given in eqn (12). The theoretical prediction given by eqn (11) is shown for ψ = 0.09ϕ0 and w = 1.45 given in eqn (12). The theoretical prediction given by eqn (11) is shown for ψ = 0.09ϕ0 and w = 1.45![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) . Panel (b) shows the associated starting position sstart together with the equivalent prediction following from eqn (11), which is shown for ψ = 0.09ϕ0 and Estiff = 0.15Ê. The remaining parameters are Esoft = 10−4Ê and ϕin = 1. . Panel (b) shows the associated starting position sstart together with the equivalent prediction following from eqn (11), which is shown for ψ = 0.09ϕ0 and Estiff = 0.15Ê. The remaining parameters are Esoft = 10−4Ê and ϕin = 1. | ||
3.2 Two fronts move in opposite direction initially
Shortly after the first droplets dissolved, the surrounding droplets continue to shrink and disappear. Consequently, the region devoid of droplets expands in all directions. The material of the shrinking droplets is transported toward the soft side by diffusive fluxes. Initially, the material will accumulate where the equilibrium field ϕeq has the largest positive curvature (maximal ∇2ϕeq); see eqn (10). The accumulating material is absorbed by the droplets in this region, which thus grow; see Fig. 1. The fact that droplets grow on the soft side implies that the front moving from sstart toward this side slows down. Conversely, the front moving in the opposite direction can continue invading the stiff side.3.3 Dissolution front moves diffusively at late times
We next analyze the late time dynamics of the front invading the stiff side. Specifically, we consider the case where the width L of the region devoid of droplets is large compared to the width w of the transition region (L ≫ w). At this stage, the front moving toward the soft side is virtually stationary. We can thus understand the dynamics of the front invading the stiff side by analyzing the width L of the region devoid of droplets (where ψ = 0). The dynamics in this region are governed by a simple diffusion equation of the volume fraction ϕ in the dilute phase; see eqn (9b). At the stiff side of this region, the dissolving droplets impose the equilibrium fraction ϕeq(Estiff) as a boundary condition for the diffusion equation. The corresponding boundary condition at the soft side can be approximated by ϕeq(Esoft). For simplicity, we focus on slow fronts where the diffusion equation is in a stationary state, so the fraction ϕ in the region devoid of droplets is governed by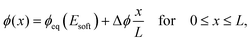 | (13) |
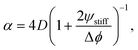 | (14) |
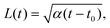 | (15) |
We test the theoretical prediction given in eqn (15) by comparing to numerical simulations of the full model. Fig. 5 shows the recorded times and positions when droplets dissolved (gray symbols), thus marking the dissolution fronts. The fronts start in the transition region on the stiff side and then move in opposite directions. The front moving toward the soft side slows down and comes to a halt on the soft side of the transition region, as predicted in the previous section. Conversely, the front invading the stiff side is quicker and does not stop. We measure its speed by fitting eqn (15) to the front positions deep into the stiff side to extract α and t0; see Fig. 5a. Since the model explains the measured data at late times, we conclude that the front moves diffusively.
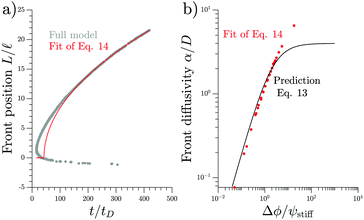 | ||
| Fig. 5 Dissolution fronts move diffusively. (a) Position and time points of dissolving droplets in a simulation of the full model (dots) are compared to a fit (red line) of the theoretical prediction given in eqn (15). Model parameters are Estiff = 0.09Ê and ψ = 0.09ϕ0. Remaining parameters are given in Fig. 1. (b) The front diffusivity α (dots) determined from fitting to numerical simulations is compared to the prediction (line) given by eqn (14). Simulations were done for ψstiff/ϕ0 = 0.03, 0.09, 0.30 for various Estiff, while the remaining parameters are the same as in panel (a). | ||
The fitted front diffusivity α is presented in Fig. 5b as a function of the relevant non-dimensional parameter Δϕ/ψstiff. This parameter compares the strength Δϕ of the elastic ripening to the fraction ψstiff of material that needs to be removed from the droplets. Consequently, the front is faster for larger Δϕ/ψstiff. The theoretical prediction for α, given in eqn (14), matches the data well for α < 2D. The fact that the front diffusivity α needs to be smaller than or comparable to the molecular diffusivity D is not surprising since we assumed that the front is slow enough for the region devoid of droplets to be in a stationary state; see eqn (13). Consequently, our theory predicts a maximal front diffusivity of 4D while the simulations indicate that faster fronts are possible.
4 Elasticity profiles spatially control droplets
So far, we considered elasticity profiles that only vary in one direction. However, our full model (eqn (5) and (6)) and the coarse-grained model (eqn (9)) are more general. In particular, eqn (11) implies that droplets first disappear in regions of strongly negative curvature ∇2ϕeq. Then, a front of dissolving droplets moves in all directions. The material of the dissolving droplets accumulates in regions of large positive curvature ∇2ϕeq, where droplets grow and remain for a long time. Consequently, where droplets grow or shrink is governed by ϕeq(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ) and thus the elasticity profile E(
) and thus the elasticity profile E(![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) ).
).
Fig. 6 shows a numerical simulation of the full model for a two-dimensional elasticity profile (left panel). A detailed simulation of a similar pattern has already identified that droplets accumulate in the soft valleys8 and the time course shown in the right panels of Fig. 6 confirms that droplets follow the dynamics described above. A movie of this simulation, as well as one for a more complex elasticity profile, can be found in the ESI.† Taken together, this shows that we can engineer elasticity profiles to locate droplets in precise arrangements.
5 Conclusions
We presented a theoretical description of elastic ripening, which agrees quantitatively with experimental data.11 Therefore, our theory identifies the driving mechanism of elastic ripening: the elastic matrix exerts a pressure onto droplets that raises the equilibrium concentration in their surroundings; gradients in this concentration then lead to diffusive material transport in the system. Surprisingly, the droplets do not start to dissolve in regions where the stiffness is maximal nor where its gradient is largest. In fact, our coarse-grained model reveals that droplets initially shrink faster where the curvature of stiffness is larger. However, at late times droplets only remain in the softest regions. Taken together, we find complex dissolution dynamics, where for instance two fronts move in opposite directions, as in the experiments.11 In particular, we derived scaling laws for the time when the first droplets disappear (eqn (12)) and for the late-stage dynamics of the dissolution front (eqn (15)). Taken together, these laws can be used to predict the effect of elastic ripening for various setups.Elastic ripening competes with Ostwald ripening since both effects are driven by pressure differences between droplets. Their relative importance is quantified by ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) , given by eqn (3), when ΔE is the relevant stiffness difference in the droplets' surroundings. For instance, although elastic ripening dominates initially in the simulation shown in Fig. 6, Ostwald ripening will eventually occur between the remaining islands because they have the same elastic properties (ΔE ≈ 0). A similar situation occurs in heterogeneous elastic materials, where ΔE corresponds to local stiffness variations. Thus, both elastic ripening and Ostwald ripening can happen in the same system, on different length- and time-scales.
, given by eqn (3), when ΔE is the relevant stiffness difference in the droplets' surroundings. For instance, although elastic ripening dominates initially in the simulation shown in Fig. 6, Ostwald ripening will eventually occur between the remaining islands because they have the same elastic properties (ΔE ≈ 0). A similar situation occurs in heterogeneous elastic materials, where ΔE corresponds to local stiffness variations. Thus, both elastic ripening and Ostwald ripening can happen in the same system, on different length- and time-scales.
The elastic ripening in stiffness gradients is similar to other droplet coarsening dynamics in gradient systems. For instance, concentration gradients, e.g., of regulating species that compete for mRNA binding,16 have been shown to bias droplet locations in experimental1 and theoretical studies.17–19 Similarly, other external fields, like temperature gradients created by local heating20,21 or even gravity22 could be used to control droplet arrangements. Such systems can be analyzed using approaches that are similar to the ones presented here.
We showed that elastic ripening allows to control droplet arrangements, which could for instance be used in technical applications for micropatterning or for creating structural color. Moreover, our theory can help to understand the localization of biomolecular condensates in biological cells. For instance, elastic ripening explains experiments where droplets have been induced in the stiff regions of heterochromatin, but moved into softer regions immediately.8 We expect that similar processes happen in the cytosol, where biomolecular condensates should be less likely where the cytoskeleton is dense. Interestingly, there are counterexamples, like centrosomes that localize to regions of high microtubule density23–25 or ZO-1 clusters that concentrate in the acto-myosin cortex.26,27 This seems to contradict elastic ripening, but in both examples the condensates interact with the elastic matrix: centrosomes bind the tubulin of microtubules28 and the ZO-1 protein interacts with the F-actin of the cortex.29 Consequently, there are two competing gradients in this situation: droplets are repelled by the stiffness of the surrounding matrix but are attracted by its molecular components. Indeed, when the actin-binding domain of ZO-1 is removed, the clusters do not accumulate in the cortex anymore, but are more broadly distributed,26 as predicted by elastic ripening.
Our theoretical description of elastic ripening can be naturally extended to include other effects. In fact, the dynamics described by eqn (5) and (6) already include surface tension effects when the pressure given by eqn (2) is used. Although we did not analyze the impact of surface tension since it is negligible in the experiments, it will become important on longer timescales or when surface tensions are large. Moreover, the elastic properties of the matrix might be more complex than considered here. For instance, the cytoskeleton can shown strain-stiffening, which might arrest droplet growth, as well as visco-elastic effects, which allow to relax elastic stresses.6 The latter effect can be captured by the theory of viscoelastic phase separation, which affects the coarsening behavior.30,31 This stress-relaxation, as well as the reduced stress due to hysteresis effects,15 could slow down elastic ripening. Finally, the droplets themselves can possess elastic properties. This is particularly true in biological condensates,32 which sometimes even form solid-like aggregates33 that potentially cause diseases.4 All these effects might be crucial for understanding the behavior of biomolecular condensates in cells.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
We thank Tal Cohen, Eric Dufresne, Frank Jülicher, Peter Olmsted, Kathryn A. Rosowski, Pierre Ronceray, and Robert W. Style for helpful discussions. Open Access funding provided by the Max Planck Society.References
- C. P. Brangwynne, C. R. Eckmann, D. S. Courson, A. Rybarska, C. Hoege, J. Gharakhani, F. Jülicher and A. A. Hyman, Science, 2009, 324, 1729–1732 CrossRef CAS PubMed.
- J. Berry, C. Brangwynne and M. P. Haataja, Rep. Prog. Phys., 2018, 81, 046601 CrossRef PubMed.
- S. Boeynaems, S. Alberti, N. L. Fawzi, T. Mittag, M. Polymenidou, F. Rousseau, J. Schymkowitz, J. Shorter, B. Wolozin, L. Van Den Bosch, P. Tompa and M. Fuxreiter, Trends Cell Biol., 2018, 28, 420–435 CrossRef CAS PubMed.
- S. Alberti and D. Dormann, Annu. Rev. Genet., 2019, 53, 171–194 CrossRef CAS PubMed.
- A. F. Pegoraro, P. Janmey and D. A. Weitz, Cold Spring Harbor Perspect. Biol., 2017, 9, a022038 CrossRef PubMed.
- M. L. Gardel, K. E. Kasza, C. P. Brangwynne, J. Liu and D. A. Weitz, Methods Cell Biol., 2008, 89, 487–519 CAS.
- F. Erdel, M. Baum and K. Rippe, J. Phys.: Condens. Matter, 2015, 27, 064115 CrossRef PubMed.
- Y. Shin, Y.-C. Chang, D. S. Lee, J. Berry, D. W. Sanders, P. Ronceray, N. S. Wingreen, M. Haataja and C. P. Brangwynne, Cell, 2018, 175, 1481–1491 CrossRef CAS PubMed.
- R. W. Style, T. Sai, N. Fanelli, M. Ijavi, K. Smith-Mannschott, Q. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. X, 2018, 8, 011028 CAS.
- R. W. Style, R. Boltyanskiy, G. K. German, C. Hyland, C. W. MacMinn, A. F. Mertz, L. A. Wilen, Y. Xu and E. R. Dufresne, Soft Matter, 2014, 10, 4047–4055 RSC.
- K. A. Rosowski, T. Sai, E. Vidal-Henriquez, D. Zwicker, R. W. Style and E. R. Dufresne, Nat. Phys., 2020, 16, 422–425 Search PubMed.
- C. A. Weber, D. Zwicker, F. Jülicher and C. F. Lee, Rep. Prog. Phys., 2019, 82, 064601 CrossRef CAS PubMed.
- R. S. Rivlin, Proc. R. Soc. London, Ser. A, 1948, 193, 260–281 Search PubMed.
- R. S. Rivlin and D. Saunders, Philos. Trans. R. Soc., A, 1951, 243, 251–288 CrossRef.
- J. Y. Kim, Z. Liu, B. M. Weon, T. Cohen, C.-Y. Hui, E. R. Dufresne and R. W. Style, Sci. Adv., 2020, 6, eaaz0418 CrossRef PubMed.
- S. Saha, C. A. Weber, M. Nousch, O. Adame-Arana, C. Hoege, M. Y. Hein, E. Osborne-Nishimura, J. Mahamid, M. Jahnel, L. Jawerth, A. Pozniakovski, C. R. Eckmann, F. Jülicher and A. A. Hyman, Cell, 2016, 166, 1572–1584 CrossRef CAS PubMed.
- C. F. Lee, C. P. Brangwynne, J. Gharakhani, A. A. Hyman and F. Jülicher, Phys. Rev. Lett., 2013, 111, 088101 CrossRef PubMed.
- C. A. Weber, C. F. Lee and F. Jülicher, New J. Phys., 2017, 19, 053021 CrossRef.
- S. Krüger, C. A. Weber, J.-U. Sommer and F. Jülicher, New J. Phys., 2018, 20, 075009 CrossRef.
- O. Y. Antonova, O. Y. Kochetkova, L. Shabarchina and V. Zeeb, Biophysics, 2017, 62, 769–777 CrossRef CAS.
- J. Choi, H. Zhou, R. Landig, H.-Y. Wu, X. Yu, S. V. Stetina, G. Kucsko, S. Mango, D. Needleman, A. D. T. Samuel, P. Maurer, H. Park and M. D. Lukin, Probing and manipulating embryogenesis via nanoscale thermometry and temperature control, 2020 Search PubMed.
- M. Feric and C. P. Brangwynne, Nat. Cell Biol., 2013, 15, 1253–1259 CrossRef CAS PubMed.
- D. Zwicker, M. Decker, S. Jaensch, A. A. Hyman and F. Jülicher, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E2636–E2645 CrossRef CAS.
- S. Redemann, J. Baumgart, N. Lindow, M. Shelley, E. Nazockdast, A. Kratz, S. Prohaska, J. Brugués, S. Fürthauer and T. Müller-Reichert, Nat. Commun., 2017, 8, 15288 CrossRef PubMed.
- D. Zwicker, J. Baumgart, S. Redemann, T. Müller-Reichert, A. A. Hyman and F. Jülicher, Phys. Rev. Lett., 2018, 121, 158102 CrossRef CAS PubMed.
- C. Schwayer, S. Shamipour, K. Pranjic-Ferscha, A. Schauer, M. Balda, M. Tada, K. Matter and C.-P. Heisenberg, Cell, 2019, 179, 937–952 CrossRef CAS PubMed.
- O. Beutel, R. Maraspini, K. Pombo-Garca, C. Martin-Lemaitre and A. Honigmann, Cell, 2019, 179, 923–936 CrossRef CAS PubMed.
- J. Baumgart, M. Kirchner, S. Redemann, A. Bond, J. Woodruff, J.-M. Verbavatz, F. Jülicher, T. Müller-Reichert, A. A. Hyman and J. Brugués, J. Cell Biol., 2019, 218, 3977–3985 CrossRef CAS PubMed.
- A. S. Fanning, T. Y. Ma and J. M. Anderson, FASEB J., 2002, 16, 1835–1837 CrossRef CAS PubMed.
- H. Tanaka, J. Phys.: Condens. Matter, 2000, 12, R207–R264 CrossRef CAS.
- H. Tanaka and Y. Nishikawa, Phys. Rev. Lett., 2005, 95, 078103 CrossRef PubMed.
- L. M. Jawerth, M. Ijavi, M. Ruer, S. Saha, M. Jahnel, A. A. Hyman, F. Jülicher and E. Fischer-Friedrich, Phys. Rev. Lett., 2018, 121, 258101 CrossRef CAS.
- A. Patel, H. O. Lee, L. Jawerth, S. Maharana, M. Jahnel, M. Y. Hein, S. Stoynov, J. Mahamid, S. Saha and T. M. Franzmann, et al. , Cell, 2015, 162, 1066–1077 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm00182a |
| This journal is © The Royal Society of Chemistry 2020 |