Grand canonical inverse design of multicomponent colloidal crystals†
Abstract
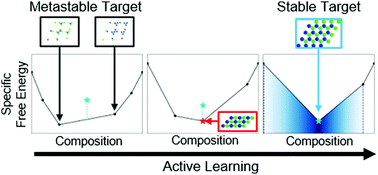
Inverse design methods are powerful computational approaches for creating colloidal systems which self-assemble into a target morphology by reverse engineering the Hamiltonian of the system. Despite this, these optimization procedures tend to yield Hamiltonians which are too complex to be experimentally realized. An alternative route to complex structures involves the use of several different components, however, conventional inverse design methods do not explicitly account for the possibility of phase separation into compositionally distinct structures. Here, we present an inverse design scheme for multicomponent colloidal systems by combining active learning with a method to directly compute their ground state phase diagrams. This explicitly accounts for phase separation and can locate stable regions of Hamiltonian parameter space which grid-based surveys are prone to miss. Using this we design low-density, binary structures with Lennard-Jones-like pairwise interactions that are simpler than in the single component case and potentially realizable in an experimental setting. This reinforces the concept that ground states of simple, multicomponent systems might be rich with previously unappreciated diversity, enabling the assembly of non-trivial structures with only few simple components instead of a single complex one.


 Please wait while we load your content...
Please wait while we load your content...