Biofilms at interfaces: microbial distribution in floating films
Abstract
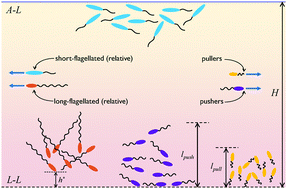
Cellular motility is a key function guiding microbial adhesion to interfaces, which is the first step in the formation of biofilms. The close association of biofilms and bioremediation has prompted extensive research aimed at comprehending the physics of microbial locomotion near interfaces. We study the dynamics and statistics of microorganisms in a ‘floating biofilm’, i.e., a confinement with an air–liquid interface on one side and a liquid–liquid interface on the other. We use a very general mathematical model, based on a multipole representation and probabilistic simulations, to ascertain the spatial distribution of microorganisms in films of different viscosities. Our results reveal that microorganisms can be distributed symmetrically or asymmetrically across the height of the film, depending on their morphology and the ratio of the film's viscosity to that of the fluid substrate. Long-flagellated, elongated bacteria exhibit stable swimming parallel to the liquid–liquid interface when the bacterial film is less viscous than the underlying fluid. Bacteria with shorter flagella on the other hand, swim away from the liquid–liquid interface and accumulate at the free surface. We also analyze microorganism dynamics in a flowing film and show how a microorganism's ability to resist ‘flow-induced-erosion’ from interfaces is affected by its elongation and mode of propulsion. Our study generalizes past efforts on understanding microorganism dynamics under confinement by interfaces and provides key insights on biofilm initiation at liquid–liquid interfaces.


 Please wait while we load your content...
Please wait while we load your content...
