Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Simple sugars shape giant vesicles into multispheres with many membrane necks†
Tripta
Bhatia
 ,
Simon
Christ
,
Simon
Christ
 ,
Jan
Steinkühler
,
Jan
Steinkühler
 ,
Rumiana
Dimova
,
Rumiana
Dimova
 and
Reinhard
Lipowsky
and
Reinhard
Lipowsky
 *
*
Theory and Bio-Systems, Max Planck Institute of Colloids and Interfaces, 14424 Potsdam, Germany. E-mail: lipowsky@mpikg.mpg.de; Fax: +49 331 5679602; Tel: +49 331 5679600
First published on 16th December 2019
Abstract
Simple sugars such as glucose and sucrose are ubiquitous in all organisms. One remarkable property of these small solutes is their ability to protect biomembranes against dehydration damage. This property, which reflects the underlying sugar–lipid interactions, has been intensely studied for lipid bilayers interacting with a single sugar at low hydration. Here, we use giant vesicles to investigate fully hydrated lipid membranes in contact with two sugars, glucose and sucrose. The vesicles were osmotically balanced, with the same total sugar concentration in the interior and exterior aqueous solutions. However, the two solutions differed in their composition: the interior solution contained only sucrose whereas the exterior one contained primarily glucose. This sugar asymmetry generated a striking variety of multispherical or “multi-balloon” vesicle shapes. Each multisphere involved only a single membrane that formed several spherical segments, which were connected by narrow, hourglass-shaped membrane necks. These morphologies revealed that the sugar–lipid interactions generated a significant spontaneous curvature with a magnitude of about 1 μm−1. Such a spontaneous curvature can be generated both by depletion and by adsorption layers of the sugar molecules arising from effectively repulsive and attractive sugar–lipid interactions. All multispherical shapes are stable over a wide range of parameters, with a substantial overlap between the different stability regimes, reflecting the rugged free energy landscape in shape space. One challenge for future studies is to identify pathways within this landscape that allow us to open and close the membrane necks of these shapes in a controlled and reliable manner. We will then be able to apply these multispheres as metamorphic chambers for chemical reactions and nanoparticle growth.
1 Introduction
Simple sugars such as glucose and sucrose are ubiquitous in the living world. Glucose is the most important source of energy in all organisms,1 with a particularly high consumption in the human brain.2 Sucrose is the end product of photosynthesis and the primary sugar transported in most plants.3,4 One remarkable property of simple sugars is their ability to protect biomembranes against damage by dehydration arising from dessication and freezing.5,6 This property allows many organisms to survive in a strongly dehydrated state of cryptobiosis, in which their metabolism has reversibly come to a standstill.7,8 Even though this bioprotective property of simple sugars is well documented, the underlying molecular mechanisms is still controversial.It is generally believed that hydrogen bonds between waters, sugars, and lipid head groups make an important contribution to sugar–lipid interactions. However, the resulting hydrogen bond network involves different types of hydrogen bonds and one controversial aspect of the ongoing debate about sugar–lipid interactions is which hydrogen bonds are the dominant ones. Some experimental studies support the view that the lipids prefer to form hydrogen bonds with the water and not with the sugar molecules. As a consequence, the sugars experience effectively repulsive interactions with the lipids and are partially excluded from the hydration shells of the membranes.9–14 Other experimental studies provide evidence that the lipids prefer to form hydrogen bonds with the sugar molecules, which then experience effectively attractive interactions towards the membranes.15–21 These opposing views have been reconciliated by the proposal that the sugar–lipid interactions depend on the bulk concentration of the sugar, being attractive for low concentrations and repulsive for high concentrations.18
The interactions between lipid bilayers and sugar molecules have also been investigated by molecular dynamics (MD) simulations.21–25 In several simulation studies, the sugar molecules were observed to form multiple hydrogen bonds with the lipid head groups, thereby replacing a couple of water molecules.21–23 Some simulation results for the disaccharide trehalose were interpreted in terms of a glassy sugar layer,24 alluding to the so-called vitrification hypothesis.26 In addition, MD simulations were also used to demonstrate that sucrose strongly affects the phase separation within lipid bilayers by shifting the binodal lines and dissolving liquid-ordered domains.25
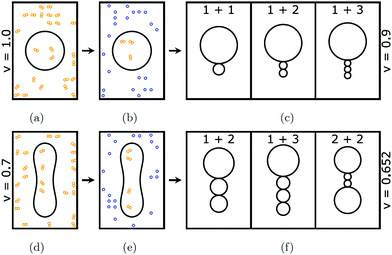
The experimental studies in ref. 9–21 addressed the interactions between lipid bilayers and a single sugar species. In contrast, in the present paper, we consider lipid vesicles exposed to two types of simple sugars, glucose and sucrose. Our experimental procedure involved several steps as schematically shown in Fig. 1. First, the vesicles were prepared in aqueous solutions that contained only sucrose. After this preparation step, both leaflets of the vesicle membrane were exposed to the same sucrose concentration. Subsequently, a small amount of the vesicle-sucrose solution was transferred into the observation chamber and added to a much larger amount of aqueous glucose solution. Thus, after this transfer step, the inner leaflet of each vesicle membranes was still exposed to sucrose whereas the outer leaflet was now exposed to an exterior solution that contained primarily glucose. Furthermore, immediately after transfer, the vesicles had the same volume and the same sucrose concentration as before. However, because the total sugar concentration in the exterior solution was typically larger than in the interior solutions, water started to permeate through the membrane and the vesicle volume decreased until both solutions were osmotically balanced. The resulting asymmetry between the two bilayer leaflets created a striking variety of multispherical or “multi-balloon” vesicles, consisting of a variable number of large and small spheres connected by very narrow, hourglass-shaped membrane necks, in accordance with the theory of curvature elasticity.27 Analogous necks are also formed by cellular membranes, e.g., during endocytosis or cell division.28 These necks have a diameter of about 10 nm, corresponding to twice the bilayer thickness.
To make the vesicle shapes accessible to optical microscopy, we used giant unilamellar vesicles (GUVs), a versatile research tool for membrane science as demonstrated in many previous studies.28–31 The multispherical shapes of the GUVs had several remarkable properties. First, for each such shape, the radii of the individual spheres could attain at most two different values. Thus, the multispherical shapes were either composed of large and small spheres with two different radii or, alternatively, of several equally sized spheres. This morphological feature implies that all spherical membrane segments experienced the same mechanical tension and that the whole multisphere was formed by a single bilayer membrane. Second, each multisphere is stable for a wide range of parameters as we show by a detailed comparison between theory and experiment. Third, the stability regimes for the different multispheres have a significant overlap which implies that GUVs with the same membrane area and the same initial volume can attain many different multispherical shapes even though they are exposed to the same sugar asymmetry, as illustrated in Fig. 1. Finally, we discuss possible molecular mechanisms for the sugar-induced membrane curvature and show that this curvature can arise from repulsive or attractive interactions between the sugars and the lipid head groups.
2 Results and discussion
2.1 GUV membranes exposed to asymmetric sugar solutions
The GUVs were prepared from a binary lipid mixture of 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and 10 mol% cholesterol in aqueous sucrose solutions. Cholesterol was added to the GUV membranes to ensure that the curvature-elastic behavior of these bilayer membranes is adequately described by the spontaneous curvature model.27 In contrast to POPC, cholesterol undergoes frequent flip-flops between the two leaflets of the bilayers on the typical time scales of the experiments. In the absence of cholesterol, we would have to take into account that the number of POPC molecules is separately conserved in each leaflet. In fact, the detailed comparison between experiment and theory as provided in the present paper directly demonstrates that the observed multitude of multisphere shapes is in full agreement with the spontaneous curvature model.To balance the osmotic pressure arising from the exterior sucrose solution, the vesicles changed their volume until the interior solutions contained the same sucrose concentration as the exterior one and the two leaflets of the bilayer membrane were exposed to identical aqueous environments. Therefore, this preparation procedure led to symmetric bilayers with zero spontaneous curvature. Two examples for such osmotically balanced vesicles with symmetric bilayers are displayed in Fig. 1(a and d). Next, a small aliquot of the prepared sucrose-GUV solution was transferred into the observation chamber and added to a larger aqueous droplet that contained only glucose or an excess of glucose, with a glucose or glucose–sucrose concentration that exceeded the sucrose concentration in the aliquot. This transfer or dilution step led to the reduction of the vesicle volume by osmotic deflation and, at the same time, to the generation of bilayer asymmetry and spontaneous curvature. Immediately after transfer, the vesicles retained their volume as in Fig. 1(b and e) until the higher osmotic pressure in the exterior glucose solution started to reduce these volumes by water permeation across the membranes, thereby increasing the sucrose concentration in the interior solution. The latter process continued until the interior sucrose concentration was equal to the total sugar concentration in the exterior solution.
When we reduce the volume of a GUV, we always create excess area of the vesicle membrane that allows the GUV to undergo a variety of shape transformations. One example for such a transformation process is displayed in Fig. 2. In this case, the GUV was prepared in 172 mM sucrose and transferred into an observation chamber with 200 mM glucose. The resulting water permeation led to a reduction of the vesicle volume and to an increase of the interior sucrose concentration until this latter concentration was equal to 200 mM as well. As a result, the inner leaflet of the GUV membrane was exposed to 200 mM sucrose whereas the outer leaflet of this membrane was in contact with 200 mM glucose. This bilayer asymmetry led to a shape transformation of the GUV, from the pear shape in the first snapshot of Fig. 2 to the dumbbell shape in the last snapshot of this figure. The dumbbell shape consisted of two spheres, a large and a small one that did not separate from each other. Furthermore, the time evolution in Fig. 2 and Movie 1 (ESI†) also shows that the morphological transformation from a pear to a two-sphere shape was quite fast and completed within about 15 s. The resulting two-sphere morphology represents a stable shape of the GUV that remained unchanged for many hours.
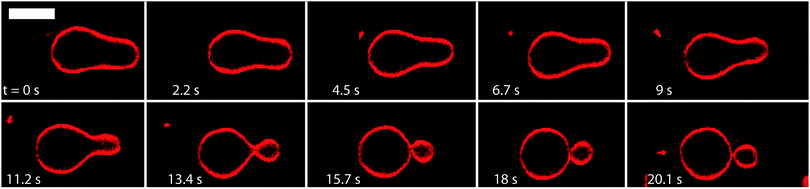 | ||
| Fig. 2 Morphological transformation of a GUV with an initial pear-like shape: time evolution of shape with selected images from Movie 1 (ESI†). The first image shown here defines time t = 0 s and corresponds to about 38 min after the aliquot of sucrose-GUV solution was transferred to the observation chamber. Within 15 s, the GUV transforms into a two-sphere morphology consisting of a large and a small sphere which are connected by a membrane neck. The GUV was prepared in 172 mM sucrose and then transferred into an observation chamber filled with 200 mM glucose. The osmotic imbalance reduces the volume of the GUV until the interior solution reaches a concentration of 200 mM sucrose. The scale bar is 5 μm. | ||
2.2 Striking diversity of stable multispherical morphologies
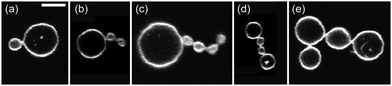
The two-sphere morphology in Fig. 2 represents the simplest example for a stable multispherical shape. In general, many more complex multispherical morphologies can be formed and remain stable for hours, provided we exposed the inner and the outer leaflets of the GUV membranes to different sugar solutions. Indeed, control experiments in which we used one sugar species and exposed both leaflets to the same sugar, either sucrose or glucose, did not generate multispherical vesicles, see Methods section.Any multispherical morphology that is formed by a uniform membrane can involve at most two different sphere radii as shown in the Methods section. Vice versa, the observation of such a multispherical shape provides direct evidence that all spherical membrane segments experience the same mechanical tension and that the whole multisphere is formed by a single bilayer membrane. Thus, we can observe a variety of (Nl + Ns)-spheres that are built up from a variable number Nl of large spheres and a variable number Ns of small spheres. Several examples for these morphologies, which have the form of necklaces and linear or branched chains, are displayed in Fig. 3 and 4. In addition, multispherical shapes with N* equally sized spheres are also possible, see Fig. 5. Because the necklaces and chains of multispheres undergo thermal fluctuations, the individual spheres move in and out of optical focus which implies that their apparent radii in the confocal image change. The true radii are obtained from equatorial cross sections which can be determined by adjusting the focus for each sphere separately but can be rarely seen for all spheres on the same image. Thus, the images in Fig. 3–5 have been selected in such a way that the visible cross sections provide good approximations to the equatorial cross sections.
 | ||
| Fig. 3 Multispherical shapes with a total number of up to four spheres, as observed for various sugar concentrations: (a) one large and one small sphere as in Fig. 2; (b and c) multispheres consisting of one large and two small spheres, the latter forming a 2-sphere chain and two separate buds, respectively; (d) a small sphere in between two large spheres; (e) one large sphere connected to a linear chain of three small spheres; (f and g) two large spheres and two small spheres forming two distinct necklaces; and (h) three large (l) spheres and one small (s) sphere arranged in an (llsl)-necklace. The scale bar in (a) is 10 μm and applies to all panels. | ||
 | ||
| Fig. 5 Multispherical shapes consisting of N* equally sized spheres as observed for different sugar concentrations: (a) branched chain with N* = 14. Twelve of these spheres are clearly visible. In addition, one sphere, located at the right chain end, is out of focus and another one, connected to the second sphere from the left, is hardly visible, see Movie 3 (ESI†); (b) branched chain with N* = 15; (c) branched chain with N* = 15. Fourteen of these spheres are visible, another one is hidden behind the bottom sphere, see Movie 4 (ESI†); (d) linear chain with N* = 24; and (e) branched chain with N* = 39. Various sugar concentrations; the scale bar in (a) is 10 μm and applies to all panels. | ||
The multispherical shapes shown in Fig. 3 are composed of up to four spheres. Apart from the (1 + 1)-sphere consisting of one large and one small sphere, this figure displays three different multispherical shapes with N = 3 and four distinct multispheres with N = 4. The two (1 + 2)-spheres in Fig. 3(b and c) consist of one large and two small spheres but differ in the necklace arrangement of the spheres: in Fig. 3(b), the two small spheres form a short chain, in Fig. 3(c), they form two separate buds. Thus, in Fig. 3(b), the three spheres are linked into the linear arrangement large–small–small whereas they form the linear arrangement small–large–small in Fig. 3(c). We will call these two arrangements an (lss)-necklace and an (sls)-necklace, respectively. Likewise, for N = 4, Fig. 3 displays a (1 + 3)-sphere that forms a (lsss)-necklace, two distinct (2 + 2)-spheres corresponding to an (lssl)-necklace and an (lsls)-necklace, as well as a (3 + 1)-sphere arranged as a (llsl)-necklace.
Another type of multispheres is shown in Fig. 4. The latter shapes consist of one large sphere and Ns ≥ 4 small spheres that form a single chain, which may be linear or branched. A chain with a larger Ns-value is more likely to be branched. In fact, as a result of thermal fluctuations, the small spheres are surprisingly mobile: individual spheres can move along the chains, thereby transforming linear chains into branched ones and vice versa, an example is shown in Movie 2 (ESI†). Furthermore, in Fig. 5 as well as in Movies 3 and 4 (ESI†), we display several examples for multispherical shapes consisting of N* equally sized spheres.
The time-dependent relaxation process towards the final multispherical shape with a chain of Ns small spheres can proceed via a transient shape that resembles a capped unduloid with open necks. One example with Ns = 5 is displayed in Movie 5 (ESI†). In this example, the transformation from open to closed necks is completed within about two minutes. Two additional examples that further illustrate the time-dependent formation of closed membrane necks are provided by Movies 6 and 7 (ESI†). The initial frame of Movie 6 (ESI†) displays a shape that resembles a thick letter ‘C’ which then develops two constrictions and three bellies as well as a spherical bud connected to the belly in the middle. After about 78 s, the GUV has been transformed into a multispherical shape consisting of three large and two small spheres, arranged as an linear (lslsl)-necklace connected by four ls-necks. The initial frame of Movie 7 (ESI†) displays a shape that resembles a three-armed starfish. This shape transforms into a (3 + 1)-sphere, for which the three large spheres are all connected to the small sphere in the middle, resembling a three-leaved trefoil. The latter process leads to the formation of three ls-necks and takes about 60 s.
The multisphere images displayed in Fig. 3–5 have been observed for a variety of sugar concentrations. The (3 + 1)-sphere in Fig. 3h and the (1 + 5)-sphere in Fig. 4(b), for example, were observed after adding the GUVs to a 180 mM glucose solution in the observation chamber whereas the (1 + 3)-shape in Fig. 3(e) was observed after adding them to a 326 mM glucose solution. In fact, we observed multispherical shapes after adding the GUVs to even much lower glucose concentrations, down to 60 mM. In order to elucidate the interrelations of the GUV morphologies and the sugar concentrations, we will now analyze the multispherical shapes in a systematic manner. This analysis will proceed in several steps. First, we describe the geometry of the multispherical shapes and show that this geometry is completely determined by a single dimensionless parameter, the “reduced volume” or volume-to-area ratio v, see next subsection. Second, we discuss two general stability conditions for multispheres, one for the stability of closed membrane necks against neck opening and another one for the stability of the individual spheres against prolate deformations.27 Third, we use the stability conditions to estimate the numerical values of the spontaneous curvature for two specific sugar asymmetries. Finally, we discuss the overall morphology diagram, which depends on two dimensionless parameters, and show that the experimentally observed multispherical shapes belong to the theoretically predicted stability regimes.
2.3 Geometry of multispherical shapes
The shape of a laterally uniform membrane depends only on three parameters: the vesicle volume V, the membrane area A, and the spontaneous curvature m.32 For all multispherical morphologies described here, the vesicle membranes bulged towards their outer leaflets, from which we can directly conclude that all membranes had a positive spontaneous curvature, m > 0.27 Furthermore, it is convenient to use the vesicle size as defined by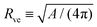 | (1) |
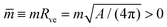 | (2) |
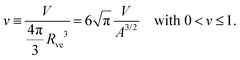 | (3) |
The parameter space or morphology diagram is now defined by the (![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ,v)-plane with
,v)-plane with ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) > 0 and 0 < v ≤ 1. The largest possible volume-to-area ratio v = 1 corresponds to a single sphere.
> 0 and 0 < v ≤ 1. The largest possible volume-to-area ratio v = 1 corresponds to a single sphere.
Now, let us consider a (Nl + Ns)-sphere consisting of Nl large and Ns small spheres. Using the basic length scale Rve, we introduce the dimensionless sphere radii
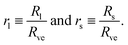 | (4) |
| Nlrl2 + Nsrs2 = 1 and v = Nlrl3 + Nsrs3. | (5) |
The first equation is equivalent to the condition that the total area of all large and small spheres must be equal to A and the second equation to the condition that the total volume of all spheres must be V. For given values of the sphere numbers Nl and Ns, these two equations determine the two radii rl and rs in terms of the volume-to-area ratio v. In other words, the geometry of any (Nl + Ns)-sphere is completely determined by the volume parameter v. As a consequence, this geometry does not depend on any other parameter such as, e.g., the spontaneous curvature.
A multisphere consisting of Nl large and Ns small spheres can only be formed if the volume parameter v exceeds a certain minimal value. This lowest possible v-value is provided by N* = Nl + Ns spheres of equal size. For equal sphere radii rl = rs = r*, the two relations in eqn (5) lead to the unique solution
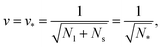 | (6) |
2.4 Stability of multispherical shapes
Next, we must examine the stability of the multispherical shapes, which is primarily determined by the stability of the closed membrane necks with respect to neck opening. The latter stability depends on two parameters. First, it depends on the spontaneous curvature that provides a quantitative measure for the bilayer asymmetry arising from the different sugar solutions on the two sides of the membranes. Second, the neck stability depends on the geometry of the closed neck, which we will characterize in terms of a certain neck curvature. In general, we have to distinguish different types of necks. First, a multisphere typically exhibits at least one ls-neck between a large and a small sphere. Such ls-necks can be seen in all images of Fig. 3 and 4. Second, we observe ss-necks between two small spheres as in panels b, e, and f of Fig. 3 and in all images of Fig. 4. Occasionally, we also observed ll-necks, one example is shown in Fig. 3h.Each neck is governed by a simple stability condition that depends on the curvature radii of the spherical segments adjacent to the neck. These sphere radii can be directly measured from the optical images. For the sake of generality, we will first denote these two radii by Ra and Rb. As we move across a closed neck, the mean curvature of the membrane changes abruptly from the value Ra−1 to the value Rb−1. It is then useful to define the neck curvature
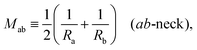 | (7) |
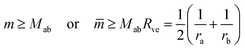 | (8) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = mRve is sufficiently large. More precisely, a closed membrane neck with neck curvature Mab is only stably closed if the spontaneous curvature m exceeds Mab. The equality Mab = m represents a boundary case because the neck remains closed for m > Mab but opens up for m < Mab. Vice versa, the neck closes continuously as we increase the spontaneous curvature from m<Mab to m = Mab. Therefore, the equality Mab = m represents the closure condition for the ab-neck. Note that the stability condition for the closed membrane neck as given by eqn (8) provides a local relation between the spontaneous curvature m, which is a curvature-elastic material parameter, and the neck curvature Mab as defined by eqn (7), which is a purely geometric quantity. The neck curvature can be directly deduced from the optical micrographs, provided the curvature radii Ra and Rb of the two membrane segments adjacent to the neck can be optically resolved.
= mRve is sufficiently large. More precisely, a closed membrane neck with neck curvature Mab is only stably closed if the spontaneous curvature m exceeds Mab. The equality Mab = m represents a boundary case because the neck remains closed for m > Mab but opens up for m < Mab. Vice versa, the neck closes continuously as we increase the spontaneous curvature from m<Mab to m = Mab. Therefore, the equality Mab = m represents the closure condition for the ab-neck. Note that the stability condition for the closed membrane neck as given by eqn (8) provides a local relation between the spontaneous curvature m, which is a curvature-elastic material parameter, and the neck curvature Mab as defined by eqn (7), which is a purely geometric quantity. The neck curvature can be directly deduced from the optical micrographs, provided the curvature radii Ra and Rb of the two membrane segments adjacent to the neck can be optically resolved.
The stability condition as given by eqn (8) can be applied to the different types of necks that have been observed in Fig. 3–5. For an ls-neck, we identify ab in eqn (8) with ls and conclude that the spontaneous curvature m satisfies the inequality 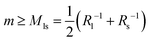 . Likewise, the observation of a stable ss- or ll-neck implies that m ≥ Mss = Rs−1 and m ≥ Mll = Rl−1. When a multispherical shape exhibits several types of membrane necks, this shape is only stable if all of its necks are stable against neck opening. In practice, we typically encounter two different cases. The first case corresponds to multispheres that involve only ls-necks, see the images in the panels a, c, d, and g of Fig. 3. The second case is provided by multispheres that involve at least one ss-neck, see all images in Fig. 4 and 5.
. Likewise, the observation of a stable ss- or ll-neck implies that m ≥ Mss = Rs−1 and m ≥ Mll = Rl−1. When a multispherical shape exhibits several types of membrane necks, this shape is only stable if all of its necks are stable against neck opening. In practice, we typically encounter two different cases. The first case corresponds to multispheres that involve only ls-necks, see the images in the panels a, c, d, and g of Fig. 3. The second case is provided by multispheres that involve at least one ss-neck, see all images in Fig. 4 and 5.
In addition to the stability against neck opening, multispherical shapes must also be stable against prolate deformations of the individual spheres. As shown in the Methods section, the large sphere is always stable whereas the stability of the small sphere requires that the spontaneous curvature m satisfies the inequality
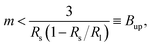 | (9) |
2.5 Estimating the magnitude of the spontaneous curvature
We will now use the stability conditions for the multispherical shapes as described in the previous paragraphs to estimate the magnitude of the spontaneous curvature m. First, we consider a certain membrane neck and measure the corresponding sphere radii Ra and Rb from which we deduce the neck curvature Mab as defined by eqn (7), with ab replaced by the corresponding neck type. According to eqn (8), the neck curvature Mab of each neck provides a lower bound for the spontaneous curvature. In order to improve this bound, we studied whole populations of GUVs, all exposed to the same sugar asymmetry. For each sugar asymmetry, we examined about 100 GUV shapes with at least one membrane neck. We performed confocal z-stacks for each of these shapes and determined the corresponding cross sections of both large and small membrane segments, using the software ImageJ-Analysis. We then selected those shapes for which these largest cross sections were circular to a very good approximation and thus provided the equatorial cross sections of large and small spheres. For sugar asymmetry I and II, this selection procedure led to 9 and 15 vesicles, respectively, for which we determined the radii Rl and Rs as well as the neck curvatures Mne of the ls- and ss-necks as obtained from eqn (7), see Fig. 7 and 9. The strongest lower bound is then obtained by the largest neck curvature within the whole vesicle population. This largest lower bound also represents the best estimate for the spontaneous curvature m based on the observed neck curvatures.Likewise, we use the measured values for the radii Rl and Rs of the large and small spheres to determine the parameter Bup in eqn (9). We examine again the whole vesicle population exposed to the same sugar concentrations in the interior and exterior solution and determine the parameter Bup for each multisphere. The strongest upper bound is then obtained by the smallest value of Bup. This smallest upper bound provides the best estimate for the spontaneous curvature based on the stability of the individual spheres. We will now use the upper and lower bounds just described to estimate the spontaneous curvature for two specific sugar asymmetries.
2.6 Spontaneous curvature generated by sugar asymmetries
 | ||
| Fig. 6 Five multispheres from a vesicle population that was exposed to an interior solution of 234 mM sucrose and an exterior solution of 234 mM glucose. These concentrations define the sugar asymmetry I of the two leaflets of the bilayer membranes. Another multisphere obtained for this sugar asymmetry is the (39*)-sphere in Fig. 5e. The scale bar in (a) corresponds to 5 μm and applies to the images in (b–e) as well. | ||
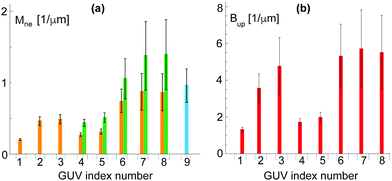 | ||
| Fig. 7 Analysis of nine multispherical vesicles, labeled from 1 to 9, that were observed for sugar asymmetry I: (a) Bar chart with neck curvatures Mne for all nine multispheres. The four vesicles with the index numbers 1 to 3 were (1 + 1)-spheres with a single ls-neck (orange). The corresponding neck curvature were obtained from eqn (7). The vesicles with the index numbers 4 to 8 involved both ls-necks (orange) and ss-necks (green). The neck curvature Mss of the ss-necks is equal to the inverse radius 1/Rs of the small spheres. The vesicle with index number 9 (blue) consisted of 39 equally sized spheres with radius R* = 1.03 ± 0.25 μm as shown in Fig. 6f; and (b) bar chart with parameters Bup as defined in eqn (9) for the vesicles with index numbers 1 to 8. The vesicle with index number 9 is not included in (b) because the parameter Bup becomes infinite for Rl = Rs = R*. For the index numbers 1 to 8, the two bar charts are supplemented by Table S1 (ESI†). | ||
Inspection of Fig. 7a shows that the largest neck curvatures are obtained for the ss-necks of the vesicles with index numbers 7 and 8. These neck curvatures are quite similar in size and have the value Mss = (1.4 ± 0.5) μm−1 which provides the best lower bound for the spontaneous curvature. The large uncertainty of this numerical value arises from the smallness of the small spheres which were only about 1.5 μm in diameter and thus only about three times the optical resolution. Furthermore, from the bar chart in Fig. 7b, the smallest value for the parameter Bup is found to be Bup = (1.3 ± 0.1) μm−1, corresponding to the vesicle with index number 1. This value of Bup provides the best upper bound for the spontaneous curvature. Combining the best lower bound Mss = (1.4 ± 0.5) μm−1 with the best upper bound Bup = (1.3 ± 0.1) μm−1, we estimate the spontaneous curvature m to be (1.3 ± 0.1) μm−1 for sugar asymmetry I.
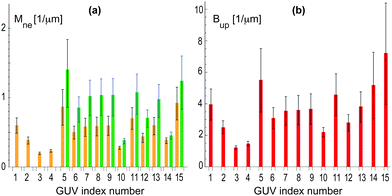 | ||
| Fig. 9 Analysis of 15 multispherical vesicles, labeled from 1 to 15, that were observed for sugar asymmetry II: (a) bar chart with neck curvatures Mne for all 16 multispheres. The four vesicles with index numbers 1 to 4 were (1 + 1)-spheres with a single ls-neck (orange). The corresponding neck curvature Mls were obtained from eqn (7). The vesicles with index numbers 5 to 15 involved both ls-necks (orange) and ss-necks (green). The neck curvature Mss of the ss-necks is equal to the inverse radius 1/Rs of the small spheres; and (b) bar chart with parameters Bup as defined in eqn (9) for all 15 multispheres. The two bar charts are supplemented by Table S2 (ESI†). | ||
As shown in Fig. 9a, the largest neck curvature is obtained for the vesicle with index number 5 which is displayed in Fig. 8b. This vesicle has a single ss-neck with neck curvature Mss = (1.4 ± 0.5) μm−1, which represents the strongest lower bound for the spontaneous curvature. The large uncertainty of the Mss-value again arises from the smallness of the small spheres which were only about three times as large as the optical resolution. Furthermore, from the bar chart in Fig. 9b, the smallest value for the parameter Bup is found for the vesicle with index number 3 which leads to Bup = (1.2 ± 0.1) μm−1 and represents the strongest upper bound for the spontaneous curvature. Combining the strongest lower bound Mss = (1.4 ± 0.5) μm−1 with the strongest upper bound Bup = (1.2 ± 0.1) μm−1, we estimate the spontaneous curvature m to be (1.2 ± 0.1) μm−1 for sugar asymmetry II.
2.7 Stability regimes for multispherical morphologies
Finally, we will use the estimated values for the spontaneous curvature m to show that the experimentally observed multispherical shapes belong to the stability regimes as predicted theoretically. To determine these stability regimes, we will return to the morphology diagram as defined by the (![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ,v)-plane with
,v)-plane with ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) > 0 and 0 < v ≤ 1 with
> 0 and 0 < v ≤ 1 with ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ≡ mRve. The morphology diagram allows us to obtain a global view of the space of multispherical shapes. Each multispherical shape is stable within a certain subregion of the (
≡ mRve. The morphology diagram allows us to obtain a global view of the space of multispherical shapes. Each multispherical shape is stable within a certain subregion of the (![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ,v)-plane. This subregion represents the stability regime of the respective multisphere. Inspection of Fig. 10 shows that all stability regimes are located between two boundary lines, one of which is horizontal while the other one is curved. The two boundary lines meet in a corner point.
,v)-plane. This subregion represents the stability regime of the respective multisphere. Inspection of Fig. 10 shows that all stability regimes are located between two boundary lines, one of which is horizontal while the other one is curved. The two boundary lines meet in a corner point.
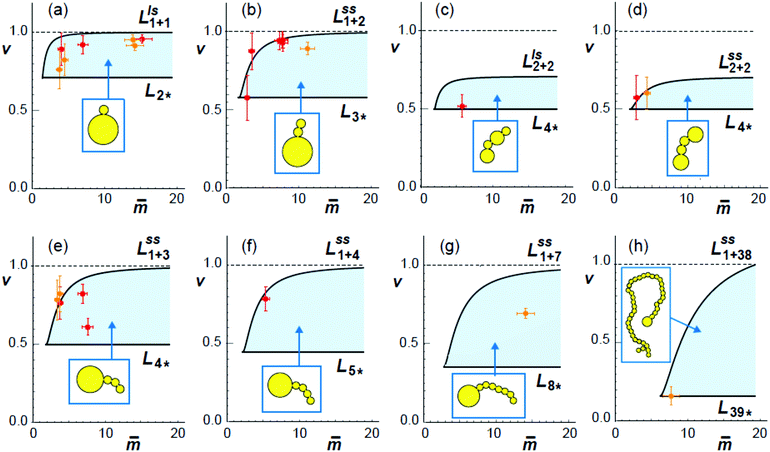 | ||
Fig. 10 Comparison between calculated stability regimes (light blue areas) and experimental data (orange and red crosses) for eight different multispherical shapes (yellow cartoons). The orange and red data were obtained for sugar asymmetry I and II, using the spontaneous curvature values estimated viaFig. 7 and 9. All stability regimes depend on two dimensionless parameters, the rescaled spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = mRve and the volume-to-area ratio v, and are located between two boundary lines. The horizontal boundary lines LN* correspond to the special shapes consisting of N* equally sized spheres, see examples in Fig. 5. The orange data point in (h) describes the 39*-sphere as shown in Fig. 5e. When we leave a stability regime by crossing one of the horizontal boundary lines, all membrane necks open up simultaneously. The second type of boundary lines, denoted by Llsn+n in (a and c) and = mRve and the volume-to-area ratio v, and are located between two boundary lines. The horizontal boundary lines LN* correspond to the special shapes consisting of N* equally sized spheres, see examples in Fig. 5. The orange data point in (h) describes the 39*-sphere as shown in Fig. 5e. When we leave a stability regime by crossing one of the horizontal boundary lines, all membrane necks open up simultaneously. The second type of boundary lines, denoted by Llsn+n in (a and c) and 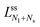 in (b) and (d)–(g), are curved and described by eqn (22) and (20), respectively. The superscripts ls and ss indicate which type of neck opens up when we cross one of the latter boundary lines. In all eight cases, the experimental data points for the observed multispheres lie within the calculated stability regimes, demonstrating the good agreement between theory and experiment. in (b) and (d)–(g), are curved and described by eqn (22) and (20), respectively. The superscripts ls and ss indicate which type of neck opens up when we cross one of the latter boundary lines. In all eight cases, the experimental data points for the observed multispheres lie within the calculated stability regimes, demonstrating the good agreement between theory and experiment. | ||
The shapes along the two boundary lines are limit shapes in the sense that they separate shapes with closed from those with open necks. The limit shapes LN* along the horizontal boundary line consist of N* = Nl + Ns equally sized spheres which have the volume-to-area ratio 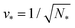 as given by eqn (6). For these multispheres, the stability of the closed **-necks also implies that
as given by eqn (6). For these multispheres, the stability of the closed **-necks also implies that ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ≥ r*−1 = v*−1 or
≥ r*−1 = v*−1 or
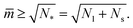 | (10) |
Therefore, multispheres with N* equally sized spheres are stable along the line LN* located at 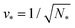 and
and 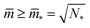 . In addition, the shape of a (N*)-sphere remains unchanged as we vary
. In addition, the shape of a (N*)-sphere remains unchanged as we vary ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) because this shape is uniquely determined by v* alone.
because this shape is uniquely determined by v* alone.
The second boundary line and the associated limit shapes depend on three features of the multispheres: on the number of large spheres, on the number of small spheres, and, in addition, on the types of membrane necks that connect the different spheres. Thus, the second boundary line is denoted by 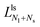 if the corresponding limit shapes involve only ls-necks connecting Nl large and Ns small spheres. Two examples for these latter lines are displayed in panels a and c of Fig. 10. On the other hand, if the (Nl + Ns)-spheres are connected by at least one ss-neck, we indicate this feature by the notation (Nl + Ns)ss and denote the corresponding line of limit shapes by
if the corresponding limit shapes involve only ls-necks connecting Nl large and Ns small spheres. Two examples for these latter lines are displayed in panels a and c of Fig. 10. On the other hand, if the (Nl + Ns)-spheres are connected by at least one ss-neck, we indicate this feature by the notation (Nl + Ns)ss and denote the corresponding line of limit shapes by 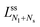 . Six examples for this latter case are displayed in panels b, d, e, f, g, and h of Fig. 10. All boundary lines displayed in Fig. 10 can be described by explicit functions of the form v = v(
. Six examples for this latter case are displayed in panels b, d, e, f, g, and h of Fig. 10. All boundary lines displayed in Fig. 10 can be described by explicit functions of the form v = v(![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ), see eqn (22) and (20) in the Methods section.
), see eqn (22) and (20) in the Methods section.
All stability regimes in Fig. 10 exhibit a corner point at which the second boundary line meets the horizontal line LN* of N* equally sized shapes with N* = Nl + Ns. These corner points are located at 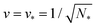 and
and 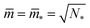 . Furthermore, the multispherical shape at any such corner point is characterized by zero bending energy27 and by the mechanical tension Σ = 2κm2, see eqn (15) in the Methods section.
. Furthermore, the multispherical shape at any such corner point is characterized by zero bending energy27 and by the mechanical tension Σ = 2κm2, see eqn (15) in the Methods section.
For all eight different types of multispherical shapes in Fig. 10, the experimental data points belong to the theoretically predicted stability regimes, within the accuracy of the measurements. This agreement provides strong evidence that the spontaneous curvature model used here does indeed describe the curvature elasticity of lipid membranes with one lipid species such as cholesterol that undergoes fast flip-flops on the time scale of the experiments.27 Inspection of Fig. 10 also reveals two remarkable properties of the stability regimes. On the one hand, the extension of the stability regime as described by the boundary lines is somewhat different for each type of multisphere. On the other hand, when we superimpose all eight stability regimes, we see that these regimes have substantial overlap. Therefore, when we consider a GUV with a certain volume and membrane area, exposed to a certain sugar asymmetry, leading to the same values of v and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) in the morphology diagram, this GUV can attain many distinct and stable multispherical shapes that differ in their numbers of large and small spheres as well as in the necklace arrangements of these spheres.
in the morphology diagram, this GUV can attain many distinct and stable multispherical shapes that differ in their numbers of large and small spheres as well as in the necklace arrangements of these spheres.
Two examples for this polymorphism are provided in the introductory Fig. 1. In panel c of this figure, we see three distinct multispherical shapes which can be formed when we deflate a spherical vesicle with v = 1 to v = 0.9 by exposing it to an exterior glucose solution, which generates a sufficiently large sugar asymmetry and spontaneous curvature as well. Likewise, panel f of Fig. 1 displays three distinct multispherical shapes, which can be obtained by deflating a prolate vesicle from v = 0.7 to v = 0.652 by exposing it to an exterior glucose solution, again creating, at the same time, a sufficiently large sugar asymmetry and spontaneous curvature. The stability regimes for the three multispherical shapes in Fig. 1c are shown in the three panels a, b, and e of Fig. 10. Likewise, the stability regimes of the three multispherical shapes in Fig. 1f are displayed in the three panels b, e, and d of Fig. 10. In both cases, a superposition of all three stability regimes reveals the minimal value of the rescaled spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = mRve for which all three multispherical shapes can coexist in the same batch of vesicles. Furthermore, all multispherical vesicles built up from different numbers of large and small spheres differ in the bending energy of their membranes whereas all vesicles with the same number of large and small spheres have the same bending energy. Therefore, the multispherical vesicles form a rugged energy landscape with many metastable states.27,28
= mRve for which all three multispherical shapes can coexist in the same batch of vesicles. Furthermore, all multispherical vesicles built up from different numbers of large and small spheres differ in the bending energy of their membranes whereas all vesicles with the same number of large and small spheres have the same bending energy. Therefore, the multispherical vesicles form a rugged energy landscape with many metastable states.27,28
2.8 Generation of membrane curvature by simple sugars
For all multispherical morphologies described in this paper, the vesicle membranes bulged towards their outer leaflets, from which we can directly conclude that all membranes had a positive spontaneous curvature. Thus, one robust conclusion that we can draw from our study is that an osmotically balanced vesicle membrane with its inner leaflet exposed to sucrose and its outer leaflet exposed to glucose acquires a positive spontaneous curvature. Furthermore, when we exposed the inner leaflet of the GUV membranes to glucose only and the outer leaflet to a sucrose-glucose solution, thereby reversing the sugar asymmetry, we observed inward-pointing buds and chains of small spheres, see Fig. S1 (ESI†), as predicted for negative spontaneous curvature.27 We will now focus on the case of positive spontaneous curvature and will show that this sugar-induced curvature can arise via two molecular mechanisms.Analytical theories and computer simulations have previously shown that small solutes in contact with lipid membranes can generate membrane curvature, both by forming adsorption and by forming depletion layers at the two sides of the membranes. For solute depletion, membrane curvature is generated by the loss of translational entropy of the solutes, arising from the inaccessibility of the other aqueous compartment. Because the larger solutes lose more entropy, the bilayer prefers to bulge towards the solution with the smaller solutes.34,35 Thus, if both glucose and sucrose were effectively repelled from the lipid head groups and formed depletion layers in front of the two leaflets, the membrane would bulge towards the glucose solution as observed experimentally. Furthermore, a simple but useful estimate for the magnitude of the sugar-induced curvature can be obtained if one takes the sugar molecules to be hard-core particles, with particle sizes that correspond to the hydrodynamic radii of the molecules. The hydrodynamic radius of glucose is 0.36 nm, the one of sucrose is 0.47 nm.36 Using the previously developed theory,35 one then finds that an interior sucrose solution of 234 mM and an exterior solution of 234 mM glucose generate a sugar-induced curvature of about 0.94 μm−1, which is in reasonable agreement with the value 1.3 μm−1 obtained from the experimental data in Fig. 7. It is quite remarkable that this agreement is obtained without any fit parameter.
For solute adsorption, on the other hand, we must distinguish two cases depending on whether or not the bilayer contains a lipid species that undergoes frequent flip-flops from one leaflet to the other. In the absence of flip-flops, the adsorption-induced curvature can be estimated in terms of the mechanical leaflet tensions.34,37,38 One then finds, in accordance with the Gibbs adsorption equation, that the bilayer bulges towards the leaflet with the larger coverage, i.e., with the larger number density of membrane-bound solutes. Alternatively, we may also consider the areas per lipid in the two leaflets, which leads to the conclusion that the bilayer bulges towards the leaflet with the larger average area per lipid. In the presence of a flip-flopping lipid species, the bilayer should relax towards a state in which both leaflets are tensionless as has been observed in MD simulations of lipid bilayers with compositional asymmetry.39 Relaxation towards tensionless leaflets implies that we can no longer use the leaflet tensions to estimate the adsorption-induced curvature. However, the study in ref. 39 also showed that a bilayer with tensionless leaflets can have a significant spontaneous curvature and that this curvature can be estimated by considering two leaflets with equal preferred areas. For different leaflet compositions, these equal leaflet areas contain different numbers of lipids and are thus characterized by different average areas per lipid. Therefore, even for tensionless leaflets, we could use the average lipid areas in the two leaflets to estimate the adsorption-induced curvature.
Unfortunately, it is notoriously difficult to determine the area per lipid experimentally and even more difficult to measure changes in this area. For simple sugars, only a few examples have been reported in the literature10,18,21 and these examples reveal that the sugar-induced changes in area per lipid are of the same order of magnitude as the area changes induced by typical membrane tensions. Furthermore, in these experiments, different membrane systems have been used – multilamellar vesicles,10 polydisperse liposome dispersions,18 and oriented bilayer stacks21 – without paying any attention to the tensions in these membranes. From an intuitive point of view, one may imagine that the adsorbing sugar molecules intercalate partially between the lipid head groups, a plausible view that has been repeatedly advocated.5,17,18,23,24 If both sucrose and glucose intercalated between the head groups of the respective leaflets, we might naively expect that the larger size of sucrose leads to a larger area increase per lipid compared to glucose. We would then conclude that the bilayer prefers to bulge towards the inner leaflet with adsorbed sucrose, in contrast to our experimental observations. However, the relevant quantities to compare are not the dimensions of the individual sugar molecules but rather the sugar coverage, i.e., the number density of membrane-bound sugar molecules on the two leaflets. These densities depend on the binding free energies between the sugars and the lipid bilayer. Therefore, the smaller size of the glucose could be overcompensated by a higher binding free energy of this molecule which would then lead to a positive sugar-induced curvature, in agreement with our experimental observations.
3 Conclusions
In summary, we have studied giant vesicles which were prepared in aqueous sucrose solutions and transferred into another aqueous solution that contained only glucose or a glucose–sucrose mixture with a much larger mole fraction of glucose. The osmotic balance between the two sugar solutions across the lipid membranes implied that both solutions contained the same total concentration of sugar. In this way, we prepared asymmetric bilayers, with the inner leaflet in contact with sucrose and the outer leaflet in contact with (primarily) glucose. This sugar asymmetry across the bilayer membranes created a striking diversity of multispherical vesicle shapes. One remarkable property of these shapes is that the individual spheres have either two different radii, Rl and Rs, corresponding to large and small spheres, or have all the same size, see Fig. 3–5. Vice versa, the observation of a multispherical shape that involves at most two different sphere radii provides direct evidence that all spherical membrane segments experience the same mechanical tension and that the whole multisphere is formed by a single bilayer membrane. Thus, we can conclude that all individual spheres of each multisphere were concatenated by very narrow, hourglass-shaped membrane necks even though these necks were below optical resolution. Such multispherical shapes were observed over a wide range of total sugar concentrations, from 60 mM to 326 mM.We performed a systematic analysis of the multispherical shapes which involved several steps. First, we showed that the geometry of any multisphere is completely determined by the numbers of large and small spheres as well as by the dimensionless volume-to-area ratio v defined in eqn (3). We then determined the overall stability of multispheres by deriving stability conditions both for the closed membrane necks against neck opening (eqn (8)) and for the individual spheres against prolate deformations (eqn (9)). These stability conditions can be used to derive lower and upper bounds for the sugar-induced spontaneous curvature of the vesicle membranes. By analyzing many multispheres for two specific sugar asymmetries, see Fig. 7 and 9, we obtained the values (1.3 ± 0.1) μm−1 and (1.2 ± 0.1) μm−1 for the corresponding spontaneous curvatures. The known magnitude of these curvatures allowed us to map the multispherical shapes into the global morphology diagram in Fig. 10 and to compare the experimental data with the theoretically determined stability regimes. This detailed comparison between experiment and theory directly shows that the shapes of lipid bilayers with a single flip-flopping species such as cholesterol are quantitatively described by the spontaneous curvature model. In addition, the strong overlap between the eight stability regimes shown in Fig. 10 also implies that the same sugar asymmetry can transform a GUV into many different multispherical shapes as schematically shown in Fig. 1c and f.
Last not least, we argued that the sugar-induced curvature observed here can arise via two molecular mechanisms. The first mechanism is based on effectively repulsive interactions between the sugar molecules and the lipid bilayers which lead to partial exclusion of the sugars from the lipid head groups and to the formation of two depletion layers adjacent to the two leaflets. Furthermore, a simple theoretical model for the mutual exclusion of sugars and head groups leads even to the correct order of magnitude for the sugar-induced curvature, without adjusting any fit parameter. The second mechanism by which sugar molecules can generate a positive spontaneous curvature are effectively attractive interactions between the sugars and the lipid bilayer, provided the number density of glucose molecules bound to the outer leaflet exceeds the number density of sucrose molecules bound to the inner leaflet. To distinguish these two mechanisms in a reliable way, it will be very valuable to determine the number density of membrane-bound sugar molecules and the associated binding free energies by atomistic MD simulations.
In this paper, we focused on the most basic properties of multispherical vesicles. Many interesting properties and processes remain to be investigated. Changing the vesicle volume by osmotic inflation or deflation, for example, we should be able to transform multispheres into other shapes via many different morphological pathways. Particularly entangled pathways should be obtained when we start from a multisphere with N* equally sized spheres as in Fig. 5. In the latter case, the multisphere can grow, via inflation, into many different multispheres with variable numbers of Nl large spheres and Ns = N* − Nl small spheres. Other intriguing aspects of multispheres that require further studies are their responses to mechanical forces arising from micropipette aspiration, adhesion to other surfaces, or compression by confining walls. In all of these cases, the applied forces will have to overcome certain threshold values to open up the different membrane necks. Once we know how to open and close the membrane necks in a controlled and reliable manner, we will be able to use these multispheres as metamorphic chambers for chemical reactions and nanoparticle growth. Another challenge for future studies is to couple the multispherical vesicles to membrane fission and fusion processes in order to change their topology.
4 Methods
4.1 Lipids and GUV preparation
GUVs were prepared by electroformation.31,40 We dissolved the phospholipid 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine, POPC (purchased from Avanti Polar Lipids, 850457C) and 10 mol% cholesterol (purchased from Sigma-Adrich C8667) in chloroform containing about 0.1 mol% Texas-Red DHPE (purchased from Fischer Scientific, T1395MP). About 10 μl of lipid solution were spread onto two indium tin oxide coated glass plates. The sample was kept covered inside a desiccator with little vacuum during 1–2 hours. Coated glass plates with dried sample were spaced using a Teflon spacer of about 2 mm thickness and clamped at the edges. Solvent was introduced between coverslips of sample cells through a tiny hole in the Teflon spacer using a syringe. The open hole was sealed using Teflon tape, immediately after the solvent filled the whole gap. A sinusoidal AC electric field at 10 Hz, 1.1 Vpp was applied for electroswelling the lipid films at room temperature (23 °C).4.2 Sugar solutions
We have prepared sucrose (Sigma) and glucose (Sigma) solutions in millipore water. The osmolality of the solutions was measured using Osmomat 3000 (freezing point osmometer, Gonotec). Osmolality is defined as the number of osmotically active solutes per kg water. The unit of osmolality is mosmol kg−1 for which we use the acronym mM. The osmometer measures the osmolality with an accuracy of ±2 mM for aqueous sugar solutions. It is important to notice that the overall osmotic pressure is the same for 234 mM sucrose, 234 mM glucose and an aqueous solution composed of 219 mM glucose plus 15 mM sucrose.4.3 Observation chamber
For GUVs observations, we prepared an observation chamber composed of two glass coverslips: the lateral dimensions of the bottom coverslip were 26 × 56 mm and its thickness was 0.17 ± 0.01 mm, the top coverslip had l 22 × 22 mm and thickness 0.17 ± 0.01 mm. 5 μl of GUVs solution was transferred in 50 μl of exterior aqueous solution on bottom coverslip and then sealed by the top coverslip with silica spacer in the middle. All the experiments are performed at room temperature. Before introduction of GUVs, the coverslips were coated with 2 mg ml−1 β-casein (Sigma) solution. After 30 min, the β-casein was washed with Millipore filtered water and dried in nitrogen stream. β-Casein prevents vesicle adhesion and rupture upon contact with the glass coverslips. Before use, the silica spacer was washed in water and ethanol and dried in nitrogen stream.4.4 GUV imaging
The vesicles in the sample cell were observed under a confocal microscope (Leica TCS-SP5) equipped with a 63× water immersion objective (HCX PL APO CS 1.2 N. A.). The objective has a working distance of 220 μm and xy-resolution of 0.163 μm. The optical section with pinhole of 1 AU is 1.25 μm. A thin 2D planar optical slice (or xy-section) of the GUVs is imaged in raster pattern. In order to build a 3D image, the confocal objective is moved via controlled step in the z-direction to image the consecutive 2D optical slice. Texas-red DHPE was excited with either a He–Ne laser at 594 nm or DPPS laser 561 nm and emission collected between (605–700) nm or (590–680) nm respectively. Experimental images shown in figures are the confocal section of GUVs as imaged in the red (membrane dye) channel. For display purpose only, we display most of the confocal images of GUVs (except Fig. 2) as black and white showing the best image contrast.4.5 Control experiments
We performed control experiments, in which the GUVs were exposed to only one type of sugar, either sucrose or glucose. GUVs were prepared as described in the previous paragraph on lipids and GUV preparation and then transferred into the observation chamber, see Fig. 1. The sucrose concentration used in these control experiments was between 60 and 326 mM, the glucose concentration was between 60 and 130 mM. After osmotic balance was reached, no multispherical vesicles were observed as expected. Indeed, when the exterior and the interior solution are osmotically balanced, these two solutions have the same sugar concentration, i.e., either the same sucrose or the same glucose concentration. As a consequence, both bilayer leaflets are exposed to identical concentrations of the same sugar molecules, which implies no sugar asymmetry and zero spontaneous curvature.4.6 Coexistence of large and small spheres
We consider a uniform membrane with bending rigidity κ and spontaneous curvature m. As in the main text, we take the spontaneous curvature m to be positive which implies that all spherical segments have positive mean curvatures. The membrane experiences the pressure difference ΔP = Pin − Pex between the interior and exterior solution and the mechanical tension Σ. The curvature radius Rsp of a spherical segment then satisfies the Euler–Lagrange or shape equation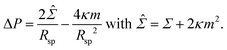 | (11) |
This equation is quadratic in the inverse curvature radius 1/Rsp which represents the mean curvature of the spherical segment. For ΔP < ![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e139.gif) 2/4κm, the quadratic equation has two solutions, Rsp = Ra and Rsp = Rb, but only one solution, Rsp = R*, for ΔP =
2/4κm, the quadratic equation has two solutions, Rsp = Ra and Rsp = Rb, but only one solution, Rsp = R*, for ΔP = ![[capital Sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e139.gif) 2/4κm. The two distinct solutions correspond to the formation of large and small spheres on the same vesicle whereas the degenerate solution with Rsp = R* corresponds to a multispherical shape consisting of several equally sized spheres.
2/4κm. The two distinct solutions correspond to the formation of large and small spheres on the same vesicle whereas the degenerate solution with Rsp = R* corresponds to a multispherical shape consisting of several equally sized spheres.
4.7 Mechanical tension and pressure difference for multispherical shapes
The two solutions Ra−1 and Rb−1 of the spherical shape equation can be used to obtain explicit expressions for the mechanical tension and the pressure difference in terms of the two radii.27 As a result, one obtains the mechanical tension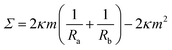 | (12) |
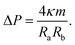 | (13) |
These two relationships allow us to calculate Σ and ΔP from the experimentally observed curvature radii Ra and Rb provided we know the bending rigidity κ and the spontaneous curvature m. It is instructive to rewrite the mechanical tension Σ as given by eqn (12) in terms of the neck curvature Mab as given by eqn (7) and of the spontaneous tension37
| σ ≡ 2κm2 | (14) |
which leads to
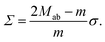 | (15) |
This relationship has several interesting consequences. First, apart from the special case m = 0, the spontaneous tension σ provides the basic tension scale for the mechanical tension Σ. Second, for those limit shapes, for which the least stable necks become marginally unstable, the corresponding neck closure condition m = Mab implies the positive mechanical tension Σ = σ = 2κm2 irrespective of the numbers Nl and Ns of large and small spheres. This tension value applies, in particular, at the corner points in the morphology diagrams of Fig. 10, corresponding to N* equally sized spheres with N* = Nl + Ns. At these corner points, the rescaled spontaneous curvature 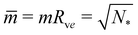 which implies Σ = 2κN*/Rve2. Third, the mechanical tension Σ vanishes for m = 2Mab. When we express the latter condition in terms of the rescaled curvatures
which implies Σ = 2κN*/Rve2. Third, the mechanical tension Σ vanishes for m = 2Mab. When we express the latter condition in terms of the rescaled curvatures ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) and
and ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ab ≡ MabRve, we obtain another set of lines within the different stability regimes in Fig. 10. The latter lines meet the horizontal lines LN* of N* equally sized spheres at
ab ≡ MabRve, we obtain another set of lines within the different stability regimes in Fig. 10. The latter lines meet the horizontal lines LN* of N* equally sized spheres at 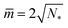 .
.
4.8 Stability of individual spheres
A single sphere with radius Rsp is stable for32,41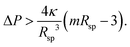 | (16) |
First, let us apply this stability criterion to the large spheres with radius Rsp = Rl which leads to
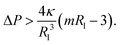 | (17) |
When we combine this relation with the pressure difference for the large and small spheres as given by eqn (13), we obtain
| 3 > mRl(1 − Rl/Rs). | (18) |
Because the large-sphere radius Rl is never smaller than the small-sphere radius Rs, the right hand side of this inequality is never positive and the inequality is always fulfilled. Therefore, the large spheres are always stable.
For the small spheres with radius Rsp = Rs, we obtain
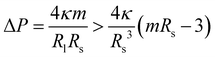 | (19) |
4.9 Boundary lines of limit shapes within the morphology diagram
The neck closure condition for an ss-neck has the form m = Mss = Rs−1. Therefore, the limit shapes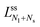 have the property that the small-sphere radius Rs = 1/m. It then follows that the dependence of the volume-to-area ratio v on the spontaneous curvature mRve ≡
have the property that the small-sphere radius Rs = 1/m. It then follows that the dependence of the volume-to-area ratio v on the spontaneous curvature mRve ≡ ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) has the explicit functional form
has the explicit functional form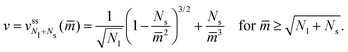 | (20) |
The line of limit shapes 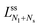 meets the horizontal line of limit shapes LN* at a corner point, which has the coordinates
meets the horizontal line of limit shapes LN* at a corner point, which has the coordinates 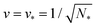 and
and 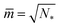 . Furthermore, the line
. Furthermore, the line 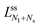 behaves as
behaves as
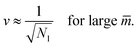 | (21) |
The latter v-value represents the volume of Nl equally sized spheres. Therefore, the line of limit shapes 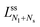 approaches the line of limit shapes LNl* for large spontaneous curvatures.
approaches the line of limit shapes LNl* for large spontaneous curvatures.
In the two panels a and c of Fig. 10, we display multispheres with only ls-necks which have the same number n of large and small spheres. The corresponding lines of limit shapes Llsn+n are described by
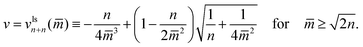 | (22) |
These lines behave as
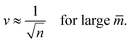 | (23) |
The latter v-value represents the volume of n equally sized spheres. Therefore, the line of limit shapes Llsn+n approaches the line of limit shapes Ln* for large spontaneous curvature.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support by the Max Planck Society and the Federal Ministry of Education and Research (BMBF) via the MaxSynBio consortium. Open Access funding provided by the Max Planck Society.Notes and references
- A. Lehninger, D. Nelson and M. Cox, Principles of biochemistry, Worth Publishers, New York, 2nd edn, 1993 Search PubMed.
- P. Mergenthaler, U. Lindauer, G. A. Dienel and A. Meisel, Trends Neurosci., 2013, 36, 587–597 CrossRef CAS PubMed.
- Y.-L. Ruan, Annu. Rev. Plant Biol., 2014, 65, 3367 CrossRef PubMed.
- D. M. Daloso, L. dos Anjos and A. R. Fernie, New Phytol., 2016, 211, 809–818 CrossRef CAS PubMed.
- J. H. Crowe, L. M. Crowe and D. Chapman, Science, 1984, 223, 701–703 CrossRef CAS PubMed.
- M. Caffrey, V. Fonesca and A. C. Leopold, Plant Physiol., 1988, 86, 754–758 CrossRef CAS PubMed.
- J. S. Clegg, Comp. Biochem. Physiol., Part B: Biochem. Mol. Biol., 2001, 128, 613–624 CrossRef CAS.
- E. P. Feofilova, Appl. Biochem. Microbiol., 2003, 29, 1–18 Search PubMed.
- B. Demé, M. Dubois and T. Zemb, Biophys. J., 2002, 82, 215–225 CrossRef.
- T. Söderlund, J.-M. I. Alakoskela, A. L. Pakkanen and P. K. J. Kinnunen, Biophys. J., 2003, 85, 2333–2341 CrossRef.
- T. Lenné, G. Bryant, C. J. Garvey, U. Keiderling and K. L. Koster, Physica B, 2006, 385-386, 862–864 CrossRef.
- P. Westh, Phys. Chem. Chem. Phys., 2008, 10, 4110–4112 RSC.
- C. J. Garvey, T. Lenné, K. L. Koster, B. Kent and G. Bryant, Int. J. Mol. Sci., 2013, 14, 8148–8163 CrossRef PubMed.
- B. Kent, T. Hauß, B. Demé, V. Cristiglio, T. Darwish, T. Hunt, G. Bryant and C. J. Garvey, Langmuir, 2015, 31, 9134–9141 CrossRef CAS PubMed.
- G. Strauss, P. Schurtenberger and H. Hauser, Biochim. Biophys. Acta, 1986, 858, 169–180 CrossRef CAS.
- C. Lambruschini, A. Relini, A. Ridi, L. Cordone and A. Gliozzi, Langmuir, 2000, 16, 5467–5470 CrossRef CAS.
- M. D. C. Luzardo, F. Amalfa, A. M. Nuñez, S. Daz, A. C. B. de Lopez and E. A. Disalvo, Biophys. J., 2000, 78, 2452–2458 CrossRef CAS PubMed.
- H. D. Andersen, C. Wang, L. Arlethc, G. H. Peters and P. Westh, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1874–1878 CrossRef CAS PubMed.
- K. B. Konov, D. V. Leonov, N. P. Isaev, K. Y. Fedotov, V. K. Voronkova and S. A. Dzuba, J. Phys. Chem., 2015, 119, 10261–10266 CrossRef CAS PubMed.
- M. I. Morandi, M. Sommer, M. Kluzek, F. Thalmann, A. P. Schroder and C. M. Marques, Biophys. J., 2018, 114, 2165–2173 CrossRef CAS PubMed.
- A. Dhaliwal, A. Khondker, R. Alsop and M. C. Rheinstädter, Membranes, 2019, 9, 15 CrossRef.
- A. K. Sum, R. Faller and J. J. de Pablo, Biophys. J., 2003, 85, 2830–2844 CrossRef CAS.
- C. S. Pereira and P. H. Hünenberger, J. Phys. Chem. B, 2006, 110, 15572–15581 CrossRef CAS PubMed.
- J. Kapla, J. Wohlert, B. Stevensson, O. Engström, G. Widmalm and A. Maliniak, J. Phys. Chem. B, 2013, 117, 6667–6673 CrossRef CAS PubMed.
- G. Moiset, C. A. López, R. Bartelds, L. Syga, E. Rijpkema, A. Cukkemane, M. Baldus, B. Poolman and S. J. Marrink, J. Am. Chem. Soc., 2014, 136, 16167–16175 CrossRef CAS PubMed.
- W. Q. Sun and A. C. Leopold, Comp. Biochem. Physiol., Part A: Mol. Integr. Physiol., 1997, 117, 327–333 CrossRef.
- R. Lipowsky, The Giant Vesicle Book, ed. R. Dimova and C. Marques, Taylor & Francis, 2019, ch. 5 Search PubMed.
- P. Bassereau, R. Jin, T. Baumgart, M. Deserno, R. Dimova, V. A. Frolov, P. V. Baskirov, H. Grubmüller, R. Jahn, H. J. Risselada, L. Johannes, M. M. Kozlov, R. Lipowsky, T. J. Pucadyil, W. F. Zeno, J. C. Stachowiak, D. Stamou, A. Breuer, L. Lauritsen, C. Simon, C. Sykes, G. A. Voth and T. R. Weikl, J. Phys. D: Appl. Phys., 2018, 51, 343001 CrossRef PubMed.
- Y. Liu, J. Agudo-Canalejo, A. Grafmüller, R. Dimova and R. Lipowsky, ACS Nano, 2016, 10, 463–474 CrossRef CAS PubMed.
- T. Bhatia, J. Agudo-Canalejo, R. Dimova and R. Lipowsky, ACS Nano, 2018, 12, 4478–4485 CrossRef CAS.
- R. Dimova, Annu. Rev. Biophys., 2019, 48, 93–119 CrossRef CAS PubMed.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1182–1202 CrossRef CAS.
- B. Fourcade, L. Miao, M. Rao, M. Wortis and R. Zia, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5276–5286 CrossRef CAS.
- R. Lipowsky and H. G. Döbereiner, Europhys. Lett., 1998, 43, 219–225 CrossRef CAS.
- B. Różycki and R. Lipowsky, J. Chem. Phys., 2016, 145, 074117 CrossRef PubMed.
- A. C. F. Ribeiro, O. Ortona, S. M. N. Simões, C. I. A. V. Santos, P. M. R. A. Prazeres, A. J. M. Valente, V. M. M. Lobo and H. D. Burrows, J. Chem. Eng. Data, 2006, 51, 1836–1840 CrossRef CAS.
- R. Lipowsky, Faraday Discuss., 2013, 161, 305–331 RSC.
- B. Różycki and R. Lipowsky, J. Chem. Phys., 2015, 142, 054101 CrossRef PubMed.
- M. Miettinen and R. Lipowsky, Nano Lett., 2019, 19, 5011–5016 CrossRef CAS PubMed.
- M. Angelova and D. Dimitrov, Faraday Discuss. Chem. Soc., 1986, 81, 303–311 RSC.
- Z.-C. Ou-Yang and W. Helfrich, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 5280–5288 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tables S1 and S2 with parameter values for bar charts in Fig. 7 and 9; Fig. S1 with multisphere shapes for reversed sugar asymmetries; movie captions for seven movies, Movies 1–7. See DOI: 10.1039/c9sm01890e |
| This journal is © The Royal Society of Chemistry 2020 |