Computer simulations of colloidal gels: how hindered particle rotation affects structure and rheology
Hong T.
Nguyen
 *a,
Alan L.
Graham
b,
Peter H.
Koenig
*a,
Alan L.
Graham
b,
Peter H.
Koenig
 c and
Lev D.
Gelb
c and
Lev D.
Gelb
 a
a
aDepartment of Materials Science and Engineering, University of Texas at Dallas, Richardson, Texas 75080, USA. E-mail: hong.nguyen@utdallas.edu
bDepartment of Mechanical Engineering, University of Colorado – Denver, Denver, CO, USA
cBeauty Care Modeling and Simulation, Mason Business Center, 8700 Mason-Montgomery Rd, Mason, OH 45040, USA
First published on 22nd November 2019
Abstract
The effects of particle roughness and short-ranged non-central forces on colloidal gels are studied using computer simulations in which particles experience a sinusoidal variation in energy as they rotate. The number of minima n and energy scale K are the key parameters; for large K and n, particle rotation is strongly hindered, but for small K and n particle rotation is nearly free. A series of systems are simulated and characterized using fractal dimensions, structure factors, coordination number distributions, bond-angle distributions and linear rheology. When particles rotate easily, clusters restructure to favor dense packings. This leads to longer gelation times and gels with strand-like morphology. The elastic moduli of such gels scale as G′ ∝ ω0.5 at high shear frequencies ω. In contrast, hindered particle rotation inhibits restructuring and leads to rapid gelation and diffuse morphology. Such gels are stiffer, with G′ ∝ ω0.35. The viscous moduli G′′ in the low-barrier and high-barrier regimes scale according to exponents 0.53 and 0.5, respectively. The crossover frequency between elastic and viscous behaviors generally increases with the barrier to rotation. These findings agree qualitatively with some recent experiments on heterogeneously-surface particles and with studies of DLCA-type gels and gels of smooth spheres.
I. Introduction
A particle gel is a heterogeneous stress-bearing space-spanning network of interacting particles. Particle gels can be found in a wide array of practical applications, ranging from tissue engineering1 to drug delivery2 to biomaterials3 to consumer products.4 A suspension of colloids can aggregate to form such a network via gelation, a process in which the colloid volume fraction ϕ and the inter-particle attraction strength U and range Δ are among the most important factors. In many cases, the resulting network is self-similar and is characterized by a mass fractal dimension df. Even though df does not fully determine all gel properties, it is still a critical metric and controls the scaling of many properties with volume fraction.Colloid gelation has been studied computationally and theoretically using a variety of methods. Many models have been developed to explore the microstructure and mechanics of particle aggregates, which can be divided into two families: hard-potential and soft-potential-based models. In hard-potential models only contact forces are present. Hard-potential simulations typically make use of Monte Carlo methods, in which particles or aggregates (clusters of bonded particles) are stochastically displaced, avoiding overlapping configurations, and bond irreversibly and rigidly upon collision. Such simulations may be performed either on an discrete underlying lattice5–8 or continuously (off-lattice).9–13 Some off-lattice simulations use Brownian dynamics (BD) instead of Monte Carlo14–18 in which realistic diffusive dynamics are included via a Langevin type equation. Studies of hard-potential models have been instrumental in understanding the kinetics of aggregation, fractal properties and cluster structures. Nearly all work to date has focused on spherical particles.
Studies of hard-sphere aggregation models have generally focused on one of two kinetic limits: diffusion-limited cluster aggregation (DLCA),19 in which colliding particles always stick together, and reaction-limited cluster aggregation (RLCA)20 in which particles bond only with a (low) probability upon collision. DLCA is considered a realistic model for colloidal systems with very strong interparticle attractions (U ≫ kBT), such as gold19 or silica nanoparticles.21 RLCA describes systems in which particles must cross an energy barrier before bonding, most often a solvent-induced repulsive force.22 By introducing a parameter controlling the probability of bond formation upon collision23 both DLCA and RLCA simulations can be performed with the same computer code. The fractal dimensions of DLCA and RLCA gels are different; 1.78 for DLCA and 2.1 for RLCA.5
Hard-sphere simulations have certain limitations. First, the bonding in such models is irreversible (bonds never break once formed). This fails to describe many technologically important cases with low and intermediate U. Second, the aggregates formed are rigid; the energy of the system is not a continuous function of the volume or simulation cell parameters, and so one cannot directly extract moduli and rheological information from such simulations. Some MC-type simulations have been augmented with loop-deflection and related “moves”24–26 which allow for a limited degree of gel restructuring, but overall such models are unsuitable for studies of long-time aging or mechanical deformation. Finally, hard-sphere simulations can form gels at arbitrarily low volume fractions, which is generally not observed in experimental systems (although real gels with volume fraction below 0.001 have been prepared in some cases).27–29
More realistic simulation models allow for restructuring, e.g. effect of cluster deformation, bond extension, rotation about bonds, and intra-cluster cluster motion.23 The development of reversible models with breakable bonds allowed for closer agreement between simulation and experiment.30 Stochastic bond breakage can be included in MC simulations via a breakage probability,31 or bond lifetime.32 In BD simulations, bonds break when their length exceeds a (preset) maximum value.15,33,34 Such modifications allowed for investigation of systems with lower U and improved description of the gel network structure and dynamics. They have explained the fractal dimension changes observed in experiment.35
Models based on soft potentials have continuous forces and can be used to study long-time evolution, rheology and flow behavior in gels. Soft potentials can be either central (acting only on particle centers) or non-central. In studies dealing with central interactions,18,36,37 there is no resistance to angular rotation38 because the energy only depends on inter-particle separations. Depletion interactions are an example of a central potential.39 Central interactions are appropriate for smooth spherical particles without site-specific bonding. Such interactions typically produce gels with coarse structures, which may or may not be fractal, and which exhibit significant aging and time-dependent rheology.29,36,40
Noncentral interactions may arise from particle anisotropy41 or from close contacts between rough-surfaced or chemically inhomogeneous particles. In some computational studies, non-central bonding forces are included through bonds acting between specific points on particle surfaces, which are created dynamically when particles collide. These bonds may be freely orienting16,34,42 or govered by angular and torsional terms.33 In such simulations the surface points at which the bond acts remain fixed, unless the bond is broken and a new bond is formed. Models of this type are more computationally complex than central-force models, both because of the data-management associated with the dynamic creation and removal of bonds, and because the bond forces in the simulation now act on particle surfaces, introducing torques and complicating the calculation of stresses and other quantities. This class of model has been successfully used to study gels in which the bonds are due to specific chemical interactions33 or due to the interaction of surface-bonded polymers.16,42 This approach is less suitable for rough-surfaced particles, in which it may be possible for one particle to “roll” around on the surface of another without losing contact.
Another approach to incorporating non-central interactions is the use of “patchy” models,43 in which each particle's surface is decorated with interaction sites at fixed positions.44 Wang et al.45 recently studied such a model, where each particle had 42 randomly arranged interaction sites. This surface heterogeneity shifted the gel point away from that predicted by Baxter's isotropic model,46 and increased the elastic modulus of the colloidal suspension. Because of their complex structure, only small systems of 500 particles were simulated. In an alternative approach, Del Gado et al. introduced non-central forces by adding a three-body bending term with a preferred angle.47–49 However, it is difficult to physically justify the use of a preferred three-body angle in terms of microscopic interparticle interactions. The results obtained are only reasonable descriptions of gels of low coordination number, and it is not clear how to extend this approach to systems with larger contact numbers as is commonly seen in experiments.
Recently, Pantina and Furst experimentally measured tangential forces between particles in isolated colloidal aggregates, demonstrating the relevance of contact interactions in the rheology and dynamics of DLCA gels.50,51 Laxton and Berg likewise used bending of linear aggregates to probe the rigidity of interparticle bonds.52 Many experimental systems composed of rough-surfaced particles53,54 have been synthesized and characterized; such work has been reviewed recently by Hsiao and Pradeep.55 Those results emphasize the important role of particle surface chemistry and anisotropy in aggregation kinetics, restructuring and rheology.
In this paper, we study a simple model for non-central surface-type interactions that can be applied to particles varying from very smooth to very rough. Barriers to the rotational motion of bonded particles are accounted for by introducing a sinusoidally varying two-body angular potential Ua with two parameters: the barrier height (energy scale) K and the number of energy minima n explored as one particle completes a rotation. We show that for appropriate choices of K and n the model produces stable gel structures at low volume fractions. The gels obtained are fractal, with df ∼ 1.99–2.16. The dynamics, network structure and linear rheology of systems at various K, n, and ϕ are characterized and compared. The gel time is found to be decreasing with increasing K and n. For low barrier height K, particles are nearly free to rotate and the resulting colloidal networks resemble the coarse, strand-like structures obtained in simulations of soft central-force models. The scaling exponent of the elastic moduli G′ and the frequency is ∼0.5, as in colloidal suspensions of smooth spheres without hydrodynamic interactions. For higher barrier heights and large numbers of minima, particle rotation is restricted, leading to much less intracluster restructuring and more diffuse networks. The rheology for higher barrier heights is also different; the low-frequency limit of the modulus is well-defined and increases with increasing n, and at high frequency the scaling exponent is reduced to 0.35. Transitions from solid-like to liquid-like frequency response are shifted to higher frequencies relative to the low-barrier case and are also n-dependent. The power-law exponent describing the viscous frequency-dependent moduli G′′ varies only weakly with K.
II. Model and methods
The model gel consists of monodisperse spherical particles which interact through both a non-bonding pair-wise potential and interactions between bonded particles. The parameters chosen and approximations made are appropriate to the case of short, stiff bonds which do not break over the course of the simulation. The non-bonding interaction is a truncated-and-shifted Lennard-Jones (LJ) potential: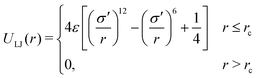 | (1) |
Inter-particle bonds are created dynamically over the course of the simulation. A new bond is made when two particles which are not bonded to each other approach to a separation shorter than the equilibrium bond length l0 = rc. The interaction potential has no energetic barrier to bond formation which will result in diffusion-limited cluster aggregation. The stretching of interparticle bonds is modeled with a harmonic potential:
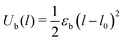 | (2) |
Bond breakage, which is important in nonlinear processes such as large-amplitude shear34 and gel collapse,57 is not considered here; once formed, bonds remain active for the duration of the simulation. This approximation is reasonable in cases where the bond energy is large, such that bonds do not break during the gelation process or during small-amplitude shear. Many real colloidal systems fall into this category. When the bond energy is much smaller than the thermal energy, this is not the case, and the assumption of unbreakable bonds would restrict the states accessible to the gel over long time-scales. The use of an unbreakable harmonic potential will obviously lead to unphysical results under large strains, since it results in ideal-spring behavior for arbitrarily large deformations.
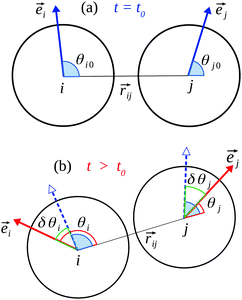
In real gels particles may experience site-specific interactions when they come into contact. These may be due to inhomogeneity of the particle surfaces; particles may not be perfectly smooth or spherical, and their surfaces may also be chemically inhomogeneous (e.g., hydrogen-bonding sites may be non-uniformly distributed). Such effects are likely to be more significant for small (nanoscale) particles. In such systems, the angular (tangential) motion of one particle relative to its near (bonded) neighbors will cause a change in potential energy, even though the interparticle distance does not change. We model this variation with a sinusoidal term Urot(δθ) = K[1 − cos(nδθ)] (see Fig. 1), where δθ is the angular displacement. Here K and n control the magnitude and frequency of the oscillation, such that as a particle completes a rotation the energy goes through n minima separated by barriers of height 2K. A similar oscillatory term is applied to torsional motion around the interparticle bond.
The specifics of the implementation are as follows. Each particle i is assigned an internal orientation ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) i fixed in the particle frame of reference. The orientational configuration of a pair of bonded particles i, j is then a triad Γij(t) = {θi(t), θj(t), γij(t)}, where θi = cos−1[
i fixed in the particle frame of reference. The orientational configuration of a pair of bonded particles i, j is then a triad Γij(t) = {θi(t), θj(t), γij(t)}, where θi = cos−1[![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) i·
i·![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij/(|
ij/(|![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) i|·|
i|·|![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij|)] is the angle between the internal vector of particle i and the interparticle direction
ij|)] is the angle between the internal vector of particle i and the interparticle direction ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij; similar expressions are applied for particle j. Torsional orientation is defined by the angle between the two orientational vectors
ij; similar expressions are applied for particle j. Torsional orientation is defined by the angle between the two orientational vectors ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) i and
i and ![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) j, γij = cos−1[
j, γij = cos−1[![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) i·
i·![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) j/(|
j/(|![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) i|·|
i|·|![[e with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0065_20d1.gif) j|)]. Suppose that a bond is formed between particles i and j at time t0. As time progresses, the triad will deviate from its initial value {θi0, θj0, γij0}. The bond energy Ua between the particles is then a sum of three oscillatory terms as described above, one each for the angular displacements and one for the torsion, with all K and n parameters taken to be the same for simplicity:
j|)]. Suppose that a bond is formed between particles i and j at time t0. As time progresses, the triad will deviate from its initial value {θi0, θj0, γij0}. The bond energy Ua between the particles is then a sum of three oscillatory terms as described above, one each for the angular displacements and one for the torsion, with all K and n parameters taken to be the same for simplicity:
| Ua(θi, θj, γij) = K[3 − cos(nδθi) − cos(nδθj) − cos(nδγij)]. | (3) |
In principle K should vary with the interparticle distance l; as particles are moved apart the effect of surface inhomogeneities on their interactions should decrease.33,48 However, since for the stiff bonds considered here l will not vary very far from l0, it is reasonable to assume K is independent of interparticle distance. Likewise, there is no a priori reason for the energy scale parameter K to be identical for the torsional and angular terms; this choice is made to reduce the size of the parameter space to be explored.
A. Simulation protocol
The initial state of the system contains N particles randomly placed in a cubic box, avoiding any overlap. Periodic conditions are applied in all directions. We choose to ignore hydrodynamics, as is common in simulations of this type; we note in this regard that De Graaf et al. simulated a simple colloid model with only central forces and found that ignoring hydrodynamics did affect gelation dynamics but did not change the structures produced.58 The particle motion is thus described by Langevin dynamics14,59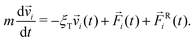 | (4) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i is the velocity of particle i, and
i is the velocity of particle i, and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) i is the total pair-wise force on particle i.
i is the total pair-wise force on particle i. ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Ri(t) is a random force satisfying condition 〈FRi,α(t)FRj,β(t′)〉 = 2ξTkBTδijδαβδ(t − t′), where α, β = x, y, z are Cartesian components, T is temperature, and kB is Boltzmann's constant.
Ri(t) is a random force satisfying condition 〈FRi,α(t)FRj,β(t′)〉 = 2ξTkBTδijδαβδ(t − t′), where α, β = x, y, z are Cartesian components, T is temperature, and kB is Boltzmann's constant. ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) Ri simulates fluctuating forces exerted on gel particles by the solvent. In the absence of hydrodynamic interactions there is no coupling between rotational and translational motion.14 Rigid-body rotational motion is described by15
Ri simulates fluctuating forces exerted on gel particles by the solvent. In the absence of hydrodynamic interactions there is no coupling between rotational and translational motion.14 Rigid-body rotational motion is described by15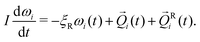 | (5) |
![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) i,
i, ![[Q with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0051_20d1.gif) Ri are the total and random torques on particle i, ξR = πησ3 is the rotational friction coefficient and I is the particle's moment of inertia, which is a scalar for spherical particles. The random torque satisfies 〈QRi(t)QRi(t′)〉 = 2ξRkBTδijδ(t − t′). The rotational and translational friction coefficients ξR and ξT are related by the identity ξT = 3σ−2ξR.
Ri are the total and random torques on particle i, ξR = πησ3 is the rotational friction coefficient and I is the particle's moment of inertia, which is a scalar for spherical particles. The random torque satisfies 〈QRi(t)QRi(t′)〉 = 2ξRkBTδijδ(t − t′). The rotational and translational friction coefficients ξR and ξT are related by the identity ξT = 3σ−2ξR.
Key simulation parameters are summarized in Table 1. Because the particles are monodisperse, they all have the same mass m. All quantities are reported in reduced units, with temperature scaled by ε, and distance scaled by the particle diameter σ. The reduced unit for time is 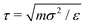 , but a more useful choice is the Brownian relaxation time τR = σ2ξT/4kBT, which is the time taken for a particle to move a distance equal to its own diameter;15 most temporal quantities are therefore reported in units of τR. ξT is set to 10.0 mτ−1 (thus, ξR = 10/3 mτ−1σ2) in all simulations, which is in the range commonly seen in the gel simulation literature.47,58 The integration time step is 25 × 10−4τ in simulations of gelation or low-frequency shear, and 1 × 10−4τ in simulations of high-frequency shear, discussed further below. The real times corresponding to these simulated times depend on the properties of the particles simulated. For near-buoyant 100 nm particles in water at ambient conditions, for instance, τR corresponds to 5.06 × 10−4 seconds. The simulation cell edge length is L = 60σ, which is substantially larger than the characteristic length scale of the simulated gels at all volume fractions considered. This ensures that the cell periodicity does not influence the gel structures or rheological results presented below. To confirm that the finite size of the simulation cells does not affect material properties, selected calculations were repeated in L = 40σ and L = 100σ simulation cells (data not shown); the results were found to agree to within statistical uncertainties.
, but a more useful choice is the Brownian relaxation time τR = σ2ξT/4kBT, which is the time taken for a particle to move a distance equal to its own diameter;15 most temporal quantities are therefore reported in units of τR. ξT is set to 10.0 mτ−1 (thus, ξR = 10/3 mτ−1σ2) in all simulations, which is in the range commonly seen in the gel simulation literature.47,58 The integration time step is 25 × 10−4τ in simulations of gelation or low-frequency shear, and 1 × 10−4τ in simulations of high-frequency shear, discussed further below. The real times corresponding to these simulated times depend on the properties of the particles simulated. For near-buoyant 100 nm particles in water at ambient conditions, for instance, τR corresponds to 5.06 × 10−4 seconds. The simulation cell edge length is L = 60σ, which is substantially larger than the characteristic length scale of the simulated gels at all volume fractions considered. This ensures that the cell periodicity does not influence the gel structures or rheological results presented below. To confirm that the finite size of the simulation cells does not affect material properties, selected calculations were repeated in L = 40σ and L = 100σ simulation cells (data not shown); the results were found to agree to within statistical uncertainties.
| System size | L | 60σ |
| LJ length parameter | σ′ | 0.90872σ |
| System temperature | T | 0.2ε |
| Equilibrium bond length | l 0 | 1.02σ |
| Volume fraction | ϕ | 0.02–0.075 |
| Time step | δt | 25 × 10−4 or 10−4τ |
| Translational friction coefficient | ξ T | 10 mτ−1 |
| Bond energy | ε b | 400ε |
| Duration of gelation simulations | 2 × 102–2 × 104τR |
All simulation are performed using a modified version of LAMMPS60 that implements the Ua potential described above. Implementation of Ua within LAMMPS is not straightforward because the triad Γ0ij = {θi0, θj0, γij0} is only determined at the moment that a bond between two particles is created. Keeping track of Γij for each bond must therefore be carried out “on the fly”, which is accomplished with new data fields added within LAMMPS's base classes. Furthermore, interprocess communication routines were modified so as to keep all processors updated with the Γij values during the simulation.
B. Characterization of simulated gel structures
| ζ ∼ ϕ−1/(3−df). | (6) |
The structure factor S(q) is also computed from g(r) through
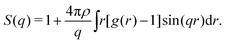 | (7) |
Where ρ is particle density. In fractal gels S(q) ∼ q−df in the intermediate range of wave vector q corresponding to the real-space intermediate scale defined above. One can therefore determine df from the slope of log[S(q)] vs. log[q] in the appropriate range of q.
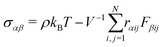 | (8) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ij and
ij and ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) ij are the center-to-center vector and total pair-wise force between particles i and j as defined above. In this method the gel is subjected to a sinusoidal shear of amplitude γ0 and frequency ω in the xy plane: γ(t) = γ0
ij are the center-to-center vector and total pair-wise force between particles i and j as defined above. In this method the gel is subjected to a sinusoidal shear of amplitude γ0 and frequency ω in the xy plane: γ(t) = γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt). Because the x-dimension remains fixed, this deformation protocol preserves the system volume. After running the simulation for m cycles of shear, the storage G′(ω) and loss G′′(ω) are calculated from
sin(ωt). Because the x-dimension remains fixed, this deformation protocol preserves the system volume. After running the simulation for m cycles of shear, the storage G′(ω) and loss G′′(ω) are calculated from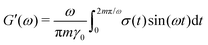 | (9) |
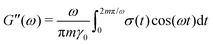 | (10) |
To reduce statistical noise, many cycles are simulated. For α < 10 (low frequencies), 10 cycles and a time step of 25 × 10−4τ were found to give good results. For 10 < α, 50 cycles were sufficient, and a time step of 1 × 10−4τ was used in order to accomodate the higher strain rate.
III. Results
Simulations were performed for models with a range of bond potential parameters K and n at several volume fractions. In each case two types of simulation were performed: gelation and oscillatory shearing. The gelation simulations were all run up to 2 × 104τR, which is well past the point of complete aggregation in each case. In the following discussion we first analyze a particular system in detail and then explore how changes in the bonding potential affect gel properties.A. Gelation dynamics and gel structure at K = 1 and n = 1
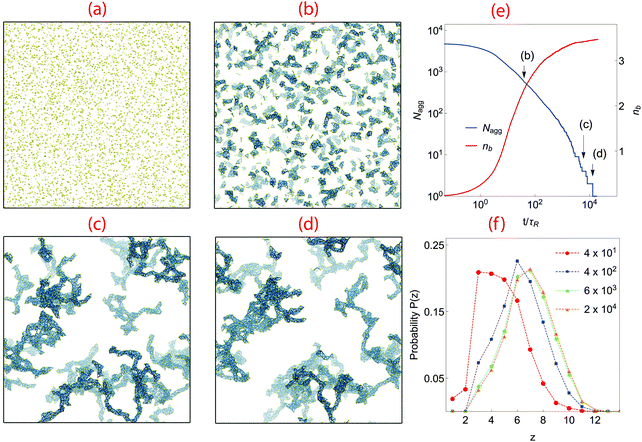
We begin with an analysis of gelation dynamics in a system with volume fraction ϕ = 0.02, K = 0.1 and n = 1, in which the barrier to particle rotation is very small. A series of snapshots from the gelation simulation and several quantities describing the bond network are shown in Fig. 2. In the initial state particles are randomly scattered, Fig. 2(a). As they collide, they bond and form clusters, Fig. 2(b). As clusters grow the dynamics slows because the cluster diffusion constant is inversely proportional to its diameter. The clusters also slowly become more compact. This occurs because the particles can move about within each cluster (as long as no bonds are broken) and form new bonds with other particles in the cluster; the cluster interior becomes denser and locally trapped in this way.When clusters meet they merge into larger clusters as bonds are formed between particles near their surfaces. At tgel ∼ 6 × 103τR, in Fig. 2(c), the largest cluster spans the simulation box, although there are many smaller clusters still present. Aggregation continues with the attachment of smaller structures to the spanning network while cluster densification is still taking place. Full aggregation is reached at tc ∼ 1.3 × 104τR, Fig. 2(d).
Fig. 2(e) shows the time evolution of the number of clusters present (Nagg) and the number of bonds per particle, nb. At early times (t < 6τR) the kinetics of aggregation is governed by the particle–particle collision rate, and nb increases according to a power law. At t ∼ 6τR the supply of monomers is largely exhausted and cluster–cluster aggregation becomes the dominant growth mechanism. In this region Nagg decays according a power law. nb is growing but no longer according to a power-law; it reaches a plateau at around t ∼ 8 × 102τR after which it only increases a very small amount for the remainder of the simulation. This behavior suggests that all possible intra-cluster relaxations have occurred by this time; further bond formation only occurs between clusters. The system-spanning network does not form until tgel = 6 × 103τR. There are still  clusters present at tgel; the Nagg plot exhibits large steps after this time as the remaining clusters very slowly collide and merge. The final structure contains an average of nb ∼ 3.5 bonds per atom, indicating a much denser packing than in DLCA networks which have 2.0 bonds per particle.10,11 Note that because bonds cannot be broken in these simulations, the degree to which the gel structure can evolve over long times is limited; in particular, spinodal-decomposition type coarsening is not possible because such large-scale restructuring necessarily involves breaking bonds.
clusters present at tgel; the Nagg plot exhibits large steps after this time as the remaining clusters very slowly collide and merge. The final structure contains an average of nb ∼ 3.5 bonds per atom, indicating a much denser packing than in DLCA networks which have 2.0 bonds per particle.10,11 Note that because bonds cannot be broken in these simulations, the degree to which the gel structure can evolve over long times is limited; in particular, spinodal-decomposition type coarsening is not possible because such large-scale restructuring necessarily involves breaking bonds.
Fig. 2(f) shows P(z), the distribution of contact number z made by a particle, at various times. z strongly affects the rigidity and mechanical response of the gel.36,40 In simulations of colloidal gel aging Zia et al.36 showed that particles on the surface of network strands adopt 1 ≤ z ≤ 3, while particles in the interior have z ≥ 8. As time progresses, the peak zmax of P(z) clearly shifts to higher z, suggesting network coarsening by additional bond formation. At t = 4 × 101τR, P(z) has a maximum at z = 3, implying most particles are near cluster surfaces. At t = 4 × 102τR the maximum in P(z) shifts to the isostatic value ziso = 6,40 consistent with the thickening of network strands visible in Fig. 2(c) and (d). This trend persists until the gel point, at which the maximum of P(z) occurs at z = 7, consistent with the final value of nb ∼ 3.5 found in Fig. 2(e). There is no further significant change in P(z) over the remainder of the simulation.
B. Effects of n and K on dynamics and gel structure
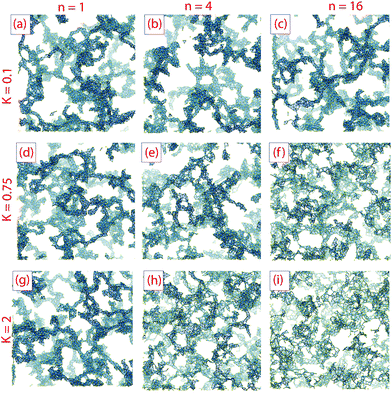
Both local structure and overall gel morphology can be tuned by adjusting the parameters K and n. Fig. 3 shows final gel structures from simulations with low K = 0.1 (K/kBT = 0.5), moderately high K = 0.75 (K/kBT = 3.75) and very high K = 2 (K/kBT = 10), for each of n = 1, 4 and 16; each structure shown is that observed at the time of complete aggregation, rather than at the end of the gelation simulation.With K = 0.1, varying n has very little effect on gel structure. This is as expected; when the barrier height K is smaller than thermal activation kBT, particles easily move between minima, and so changing the number of minima is unlikely to have a significant effect. In other words, when the angular potential Ua is small compared with the bonding potential Ub, we recover behavior typical of models with strong short-range attraction but without angular rotation, viz.ref. 36 and 37.
With K = 0.75 there is a visible change in the texture of the gel with increasing n. At low n the gel strands are thick (coarse) and very similar to those in the K = 0.1 gels, but at high n the gel has thinner strands and a finer texture. At small n the local minima in the orientational potential are much broader than at high n, so that even though escape from a minimum is kinetically limited there is still the possibility of significant orientational motion and intra-cluster restructuring. As a result, small clusters become compact before aggregation and the gel texture resembles that obtained at low K. For higher n the minima in the orientational energy are narrow and prevent intra-cluster restructuring, so clusters do not become compact before they aggregate.
At K = 2 the possibility of thermal escape from an orientational potential minimum is extremely small. The effect of n on the gel structure is similar to that observed at K = 0.75 but more pronounced; at small n some local restructuring can still occur, resulting in relatively thick strands, but at n = 4 and especially at n = 16 much finer textures are obtained. In particular, at n = 16 there is almost no compaction into strands and the structure closely resembles the DLCA models produced in stochastic simulations of aggregating hard spheres.62
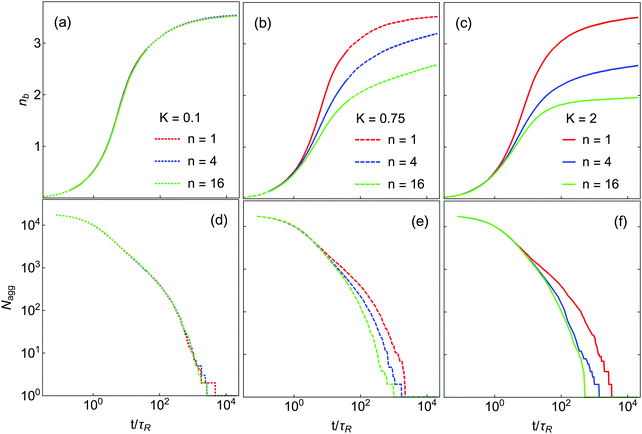
The kinetics of gelation and compaction are likewise influenced by K and n. Fig. 4(a–c) show the time evolution of nb for the systems in Fig. 3. For K = 0.1, nb(t) is essentially independent of n, while at higher K this is not the case. The bond creation rate at short times is almost independent of K and n, as it is controlled primarily by the diffusion rate of monomers and very small clusters (dimers, trimers, etc.) for which internal restructuring is largely irrelevant. For K = 0.75, nb reaches a plateau for the n = 1 system, but slow restructuring is still occuring at the longest times simulated n = 4 and n = 16. In these systems the probability of thermal escape from orientational local minima is small but not extremely so, which means that restructuring can still occur over long time scales. For K = 2.0 such restructuring is much slower. In this case, only the n = 1 and n = 4 systems are still creating small numbers of new bonds at the end of the simulation. At K = 2.0 and n = 16 the nb(t) curve is quite flat and nearly equal to 2.0 at late times, implying DLCA-type structure.10,11
The aggregation dynamics as quantified by Nagg are shown in Fig. 4(d–f). Nagg decays slowly at short times, crosses a ‘shoulder’ at intermediate time and then approaches 1 at late times. Nagg(t) is independent of K and n at short time (t < 2τR) where particle–particle aggregation dominates, similar to nb(t). As in the case of nb, with K = 1 the Nagg(t) is independent of n at all times. At higher K, Nagg decreases faster for higher n. This occurs because in these systems clusters and aggregates are more diffuse (highly branched) at higher n (see Fig. 3), which makes them larger and more likely to come into contact with each other. As a result, the aggregation kinetics are faster in these systems. (Equivalently, if clusters can restructure to become more compact, they will be smaller and less likely to collide, which slows down the aggregation process.) These effects result in a substantial dependence of the gel time tgel on n, which is shown in Fig. 5; the gel time decreases with n in all cases, but most dramatically at high K. At intermediate K = 0.75, further increase in n may still affect gelation kinetics, while at K = 2 further increases in n seem unlikely to substantially reduce the gel time. More generally, these data suggest that any substantial degree of surface roughness will substantially decrease the gel time.
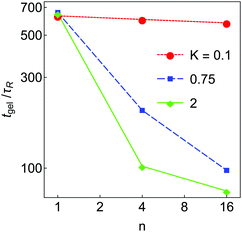 | ||
| Fig. 5 Gel time tgel as a function of n for the simulated systems in Fig. 3, plotted on a log–log scale. Each data point is an average taken over 8 independent simulations, with a relative standard error of less than 10%. Lines are included only as guides to the eye. | ||
We now discuss qualitative analyses of the structures of the final gel states displayed in Fig. 4 and how they depend on K and n. Fig. 6(a–c) show the angular deviation distributions P(δθ;K,n), and Fig. 6(d–f) show the contact number distributions. The angular term Ua has n minima located at ±m360°/n (with m = 0,1,2…n/2), independent of K. Depending on K, some of these minima are well-populated in the gel structure, resulting in peaks in P(δθ;K,n). In particular, many such peaks are visible for K = 0.1 and 0.75, but only the m = 0 peak is visible for the K = 2 systems. Overall, the m = 0 maximum is the most intense in all cases, because this is the minimum corresponding to the initial orientation at which each bond is formed; peaks at larger m are populated only through orientational motion of the bonded particles.
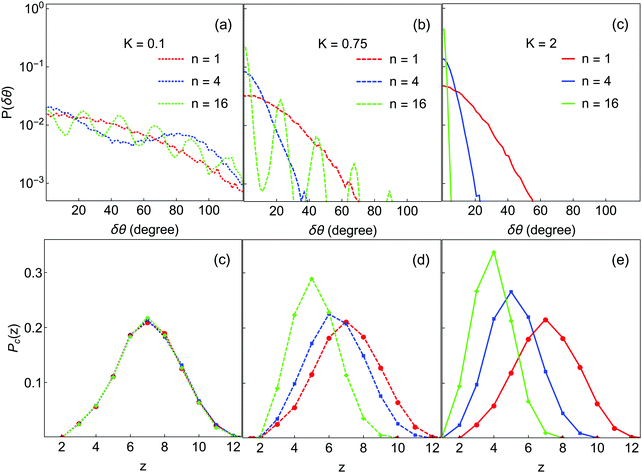 | ||
| Fig. 6 Bond angle and contact number distributions in the final gel states from Fig. 3. Colors are the same as in Fig. 4. Top row: Distributions of angular deviation; only δθ ≥ 0 is shown because of symmetry. Bottom row: Contact number distributions. | ||
At K = 0.1, all the minima are well-populated for each of n = 1, 4 and 16, consistent with a large degree of restructuring in these systems. In each case, the intensity of peaks at larger m decays logarithmically with m. Even for n = 1, where there is only a single minimum, the angular distribution is quite broad, indicating that particles have substantially re-oriented within that minimum. For K = 0.75, at n = 1 and n = 4 only a single peak is visible (and narrower than for the K = 0.1 cases), while at n = 16 only a few peaks at small m have high intensity, corresponding to population only of minima near to the orientation at bond formation. In other words, large deviations from initial contact angle (δθ ≳ 100°) are not observed at K = 0.75. At K = 2.0, only the m = 0 minimum is populated for each n; the particles are clearly unable to rotate into neighboring minima.
These results can be understood in term of diffusion. After a new bond is created, δθ starts to deviate from its initial value of zero due to thermal motion and the forces exerted by other particles. For each bond, a particle can explore its m = 0 minimum or it can hop over the potential barrier into neighboring minima, and from there into other minima. The hopping rate is proportional to the barrier height and width, i.e. ∝n−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−K/kBT). Thus, as K rises the probability to cross the barrier decreases, resulting in a narrower achievable range of δθ. It is clear from these data that the significant restructuring and densification noted earlier for low K and n is made possible by a large degree of rotational motion of particles within clusters; conversely, large K and n values prevent rotational motion within clusters and lead to more diffuse local structure.
exp(−K/kBT). Thus, as K rises the probability to cross the barrier decreases, resulting in a narrower achievable range of δθ. It is clear from these data that the significant restructuring and densification noted earlier for low K and n is made possible by a large degree of rotational motion of particles within clusters; conversely, large K and n values prevent rotational motion within clusters and lead to more diffuse local structure.
The effect of n and K on cluster densification are also reflected in the contact number distribution Pc(z). As n and K are increased the maxima in Pc(z) are shifted to lower values, consistent with lower-coordinated, less-compact structures. For K = 0.1, Pz(c) is independent of n and symmetrically distributed about z = 7. A significant portion of particles have z > 8, implying thick and close-packed network strands.36 At higher K, the effect of increasing n is to reduce the number of high-z particles and increase the number of low-z particles, making Pc(z) asymmetric. This effect is stronger for higher K. For example, with K = 2 and n = 16, more than 70% of particles have ≤4 contacts, consistent with highly branched and diffuse fractal structures as observed in Fig. 3(f). The variation of Pc(z) with different K and n seems to match with experiment63 on dilute colloid–polymer mixtures with tunable depletion attractions. Even though these interactions are central in nature, the grafted layer of polymer on colloids may have introduced some resistance to rotation, making the experimentally-measured Pc(z) depend on the strength and range of depletion attractions.
Fig. 7(a–c) shows the radial distribution function g(r) for the final gel states for K and n as in Fig. 6. All samples have a sharp peak at r ∼ 1.0 corresponding to the first-nearest neighbor contact. For K = 0.1 (panel (a)), there is only a very weak dependence on n. Peaks are observed at r = 1.41, 1.73, 2.5, 3, 3.35, 4 and 4.2; these positions are present in face-centered close-packed structures. This behavior is consistent with the compacted appearance of all K = 0.1 samples observed earlier. At K = 0.75 and K = 2.0, the g(r) curves vary with n. At these K values, the intensity of almost all structure in g(r) is diminished with increasing n. The exception to this behavior is at r = 1.41, where the intensity of g(r) increases with increasing n. This r corresponds to the second-nearest neighbor distance in a square-planar configuration of particles, which is a more open structure than the tetrahedral packing signified by the r = 1.73 peak. This behavior is thus consistent with the development of more diffuse gels with increasing barriers to local restructuring.
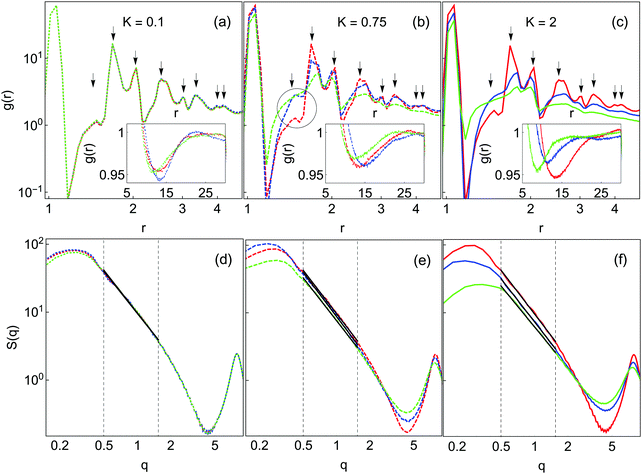 | ||
| Fig. 7 Spatial distribution functions in the final gel states from Fig. 3. Colors are the same as in Fig. 4. Top row (a–c): radial distribution functions, g(r), with peak positions indicated by solid arrows. Bottom row (d–f): static structure factors S(q). Insets in (a–c) highlight the minima in g(r) at large r. The solid lines are fits to the fractal region as used to obtain df. The dashed vertical lines indicate the fitting region. g(r) and S(q) curves are averages over 8 independent simulations. The circle in panel (b) highlights the r = 1.41 peak. | ||
The corresponding static structure factors are shown in Fig. 7(d–f). All curves have a strong peak at low wavevector q. For K = 0.1, the data for different n are essentially identical, while at higher K there is some n-dependence. As n is increased the intensities of the low-q peak and the oscillation at high q are reduced, suggesting a more homogeneous mass distribution corresponding to a more diffuse gel structure.
The dependence of df on K and n is reported in Table 2, where df is extracted from the slope of the linear portion of the plot S(q) vs. q on log–log scale. In general, df depends only weakly on n for K = 0.1 and 0.75. At high K, df decreases slightly with increasing n, consistent with the finer structure observed in many other ways. That such a trend in df is only observed at high K even though there are clearly changes in gel structure with n at lower K supports the notion that df is not an unique measure that fully characterizes the gel structure. For the largest K and n considered df = 1.99, which, while lower than the fractal dimensions obtained under all other conditions, is still significantly higher than the commonly quoted value of df = 1.78 for DLCA gels.20,21 This suggests that even under these conditions local restructuring still has some effect on gel structure. We have repeated these simulations and analysis at ϕ = 0.025 and obtained fractal dimensions in quantitative agreement with those given in Table 2 (data not shown).
| K | d f,n=1 | d f,n=4 | d f,n=16 |
|---|---|---|---|
| 0.1 | 2.05 ± 0.02 | 2.05 ± 0.01 | 2.08 ± 0.02 |
| 0.75 | 2.12 ± 0.01 | 2.16 ± 0.02 | 2.10 ± 0.02 |
| 2.0 | 2.13 ± 0.03 | 2.10 ± 0.02 | 1.99 ± 0.02 |
C. Effects of K and n on rheology
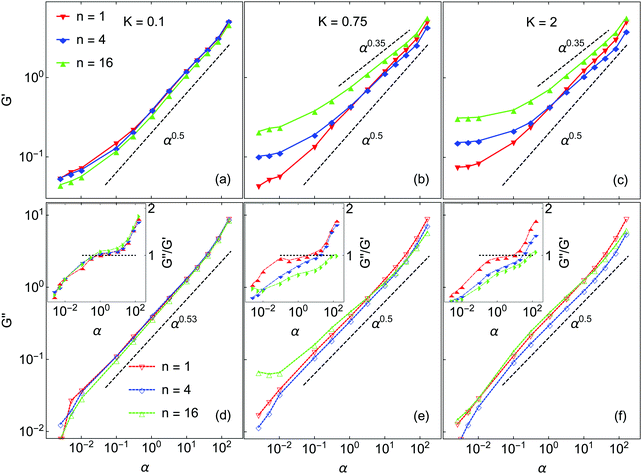
Next we turn to the rheological behavior of the model gels. The data presented is taken at volume fraction ϕ = 0.075, which is higher than the ϕ = 0.045 systems discussed in the preceding section. Selected simulations performed at ϕ = 0.045 did show the same general trends and scaling behavior as those at ϕ = 0.075, but the results were quite noisy. Increasing the volume fraction to ϕ = 0.075 raises both the storage and loss moduli by approximately one order of magnitude, which greatly improves the statistical quality of these data. For 100 nm near-buoyant colloidal particles, the unitless frequency range from 0.003 to 200 corresponds to a real frequency range of ω = 5.93 to 3.94 × 105 s−1.As noted earlier, results are reported in terms of the dimensionless frequency α = ωτR. The elastic modulus G′(α) and the loss modulus G′′(α) are measured over the frequency range 3 × 10−3 < α < 2 × 102. The results are shown in Fig. 8 and all show the following features commonly observed in experiments on DLCA-like colloidal gels.39,64 At low α (<10−1), G′ approaches a frequency-independent limiting value, G0′, which here depends on both n and K. The loss modulus G′′ is likewise smaller than the elastic modulus G′; all these systems behave as elastic solids. As α increases, G′′ increases faster than G′. Finally, both G′ and G′′ exhibit a power-law scaling with exponents that depend on both K and n.
For K = 0.1, varying n has no effect on G′ except at the lowest frequencies studied, where there is a small change in the limiting value. At high α, G′ scales as α0.5 in all cases, in accord with the findings of Zia et al. in simulations of gels of attractive hard-sphere colloids,36 albeit at rather higher volume fraction. We note that the same scaling α0.5 has elsewhere been reported for short-ranged attractive colloidal suspensions in the “free draining limit” of negligible hydrodynamic interactions.65–68 Because the same exponent is observed in the gel networks here, it suggests that the network backbone of K = 0.1 systems plays a secondary role in transmitting the stress, i.e. the stress correlation length scale is short-ranged.
There are two limiting regimes of rheological behavior, separated by the frequency αc such that G′(αc) = G′′(αc). At low α gels are elastic-dominated or solid-like, and at high α they are viscous-dominated or liquid-like. At K = 0.1 these systems have nearly identical αc ∼ 1, independent of n (see inset in Fig. 8(d)), such that the crossover occurs when the rate of perturbation is comparable with the Brownian relaxation time. G′′ varies with α as α0.53, except at very low and very high frequencies where there are small deviations.
Markedly different rheological behaviors arise at higher K. At K = 0.75 the high-α elastic responses for n = 4 and n = 16 deviate from the α0.5 law; their scaling exponents are 0.4 and 0.35, respectively. These are significantly weaker than the n = 1 system which still follows the α0.5 power law. This weaker dependence on frequency signals the network structure becoming more rigid and more particles moving in response to the external perturbation. The crossover frequencies are well separated and increase with n, with αc ∼ 3, 15 and 76 for n = 1, 4, and 16, respectively. At K = 2, the scaling exponent 0.35 is seen for both n = 4 and n = 16. As for K = 0.75, the crossover frequency increases with increasing n, αc ∼ 6, 28 and 66 for n = 1, 4 and 16 respectively. A well-defined low-frequency plateau of G′ is clearly observed for all systems at K = 2, while for lower K this is not the case. The low-frequency limit of G′ for K = 2.0 varies with n; these systems become stiffer with increasing n.
The power-law scaling of G′′ is only weakly dependent on n and K. It varies from 0.53 for K = 0.1 to 0.5 for higher K, independent of n. In all but one case, only small deviations from power-law scaling are observed over the entire range of frequency studied. However, for K = 0.75 and n = 16, G′′ appears to be almost frequency-independent at low α. This appears to be due to the gel aging during the shear simulations,18,29 even though the creation of new bonds is suppressed.15 At this K and n, the barriers to rotational motion are not very high and are narrow enough that some particles jump to neighboring minima and do not return to the original state at the end of each shear cycle. This is confirmed by calculating G′′ values from individual successive shear cycles, which increase systematically. In all the other systems studied, there was no significant variation of rheological properties over the duration of the shearing simulations.
The results in Fig. 8 demonstrate that gels stiffen as the resistance to inter-particle rotation increases, even though the gel texture becomes finer and there are fewer total bonds formed. As n and K increase, the network connectivity increasingly becomes more important in the elastic response, while the stress correlation length grows. It is interesting to note that the same stiffening has recently been observed in experiments on colloid suspensions.54 High-frequency rheology was used to investigate the effect of heterogeneous particle surfaces controlled by varying the thickness of the stabilizing layer on particle surfaces. That study found scaling with α0.5 for smooth particles in the intermediate frequency range 100 < α < 103. However, for higher surface heterogenities the elastic responses showed a weaker power-law dependence, in agreement with our findings.
The data in Fig. 8(a) suggests that for K = 0.1 and K = 0.75 a much lower probing frequency is required in order to obtain the low frequency limit G0. However, this is problematic because the shear cycle simulation time becomes substantially larger than tgel, such that it is possible for significant evolution of the gel structure to occur during the shear simulation. This is especially true for K = 0.1. This aging effect will complicate the interpretation of the rheological response.36
IV. Summary and discussion
To recap, both K and n have a significant impact on the dynamics of aggregation and gelation and the morphology of the gels formed. At low K particles are nearly free to rotate, and consequently gel properties are mostly independent of number of local minima n. The clusters formed under such conditions are compact, and they aggregate to form coarse networks with thick strands and relatively high average coordination number. At higher K and n, significant, barriers to particle rotation hinder the densification and restructuring of clusters. This results in highly branched clusters which aggregate to form more diffuse space-spanning networks with lower coordination numbers, especially at higher n. The dynamics of gelation is governed by the competition between coarsening/densification and cluster–cluster aggregation. Low K and n favor densification and result in longer gelation times, while high K and n lead to lower-density clusters and shorter aggregation times.Quantitative metrics including the structure factor, radial distribution, distribution of the number of bonds per particle, distributions of deviation from initial contact angle at bonding, and fractal dimensions were used to assess gel structure. Gelation dynamics were likewise probed by measuring the mean number of bonds per particle and the number of clusters remaining as a functions of time. At low K, all these metrics were largely independent of n. A large degree of restructuring is indicated by a broad distribution of changes in bond angles δθ, and structure in the radial distribution function at small length scales consistent with dense packing. The number of bonds formed per particle at the end of the gelation simulations was 3.5 under the conditions studied, again independent of n.
At high K, barriers to particle rotation hinder cluster densification and restructuring, increasingly so as n is increased. In the bond angle distributions at high K only the energy minimum corresponding to the initial contact angle is populated, indicating that particles do not escape from this potential well on the timescales simulated. The mean number of bonds per particle decreases with increasing K and n, and is as low as 2.0 for K = 2.0 and n = 16, similar to that observed in hard-sphere-type DLCA simulations. At K = 2.0 the characteristic length scale ζ decreases with increasing n, though such a dependence is not observed at K = 0.75. The gelation time decreases systematically with increased hinderance to particle rotation; at K = 2.0 and high n gelation occurs approximately one order of magnitude faster than at n = 1. This suggests that particle roughness is a significant variable for processing of commercial gel-based products.
The mass fractal dimension df was found to be only weakly dependent on K and n. df was found in the range 2.05–2.16 for all systems except at K = 2.0 and n = 16, for which df = 1.99. This quantity therefore appears to be insensitive to small changes in the potential Ua, though for large changes in the potential there are clearly effects. At K = 2.0 df decreases monotonically with increasing n, though a large change is only observed between n = 4 and n = 16. This suggests that yet higher values of n (and possibly K) are required in order to obtain fractal dimensions close to the df = 1.78 obtained in DLCA models that do not allow any restructuring.
Mechanical properties of the simulated gels were measured using non-equilibrium oscillatory shear simulations over a frequency range spanning the transition from elastic to viscous-dominated response. Two trends were observed. First, for higher K and n the gel networks become stiffer and the frequency dependence of the elastic moduli G′ become weaker. Second, higher K and n increase the crossover frequency from elastic to viscous-dominated behavior. G′′ was found to scale according to either α0.5 or α0.53, with only small deviations observed at high and low frequencies. At frequencies above crossover, G′ scaled with a power law exponent in the range 0.35–0.5, depending on K and n; the lower exponent was observed for higher K and n, where rotation is strongly hindered. At high K, the crossover frequency from solid-like to liquid-like behavior shifts to higher frequency and is strongly n-dependent. The low-K scaling exponent of 0.5 is consistent with both previous simulation studies of systems without rotational barriers. The dependence of the high-frequency scaling exponent on Ua suggests that linear rheology measurements of this type can be a sensitive tool for characterizing non-central bonding interactions. Our findings of the frequency-dependent G′ agree with recent experiments on how suspension rheology varies with surface characteristics.54
Aging can affect the mechanical properties of particle gels both before and during mechanical tests. The rheology data in this study was extracted for systems at the same ‘waiting time’ tw (all gelation simulations were of the same duration). We have tested with different tw and confirmed that the reported results are qualitatively insensitive to the waiting time. To reduce the effects of aging, new-bond formation was suppressed during shear simulations. Structural and rheological analysis of per-cycle data indicated that only in the system with K = 0.75 and n = 16 was there any appreciable effect of aging over the frequency range studied. Finally, at K = 0.1 and K = 0.75 the frequency range studied did not extend low enough to obtain the low-frequency limit of the modulus; aging effects may also prevent this limit from being achieved in these systems even if much longer simulations at lower frequencies were attempted.
In real systems, DLCA-like behavior corresponding to the high-K-and-n conditions simulated here is more often observed in colloids of very small particles (such as gold or silica nanoparticles19,28). This is consistent, because such particles have high surface roughness (relative to their diameter), while the nearly-barrierless conditions are typical of gels of large spherical particles such as polystyrene that form through depletion interactions.39,40,69 Mapping of real particle properties to the model parameters K and n is a nontrivial problem but could be approached either by empirical fitting to experimental rheological data or by using detailed atomistic simulations to study interparticle interactions and then coarse-graining.
Several additional interesting questions remain open. In fractal particle gels many quantities scale with volume fraction. How those scalings change with K and n was not considered in the current study. The “gel point” (lowest ϕ at which connected structures form) was also not determined,27 which is of practical concern in applications where gels are used to stabilize consumer products, among others.70 Future work will (i) examine gels formed via RLCA kinetics, which have more compact clusters than the DLCA-type systems studied here, (ii) incorporate breakable bonds in the model and investigate their impact on gelation, structure and rheology, and (iii) explore how the rotational relaxation time in the gel state varies with volume fraction and interparticle interactions, and how this impacts rheological properties. These studies are expected to elucidate the link between non-central bonding interactions and non-linear responses, e.g. large-amplitude shear40 or two-step yielding.69
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Procter and Gamble Company provided funding for this project.References
- Q. Wang, L. Wang, M. S. Detamore and C. Berkland, Biodegradable Colloidal Gels as Moldable Tissue Engineering Scaffolds, Adv. Mater., 2008, 20(2), 236–239 CrossRef CAS.
- X. Xia, Z. Hu and M. Marquez, Physically bonded nanoparticle networks: a novel drug delivery system, J. Controlled Release, 2005, 103(1), 21–30 CrossRef CAS.
- M. Guvendiren, H. D. Lu and J. A. Burdick, Shear-thinning hydrogels for biomedical applications, Soft Matter, 2012, 8(2), 260–272 RSC.
- C. Gallegos and J. M. Franco, Rheology of food, cosmetics and pharmaceuticals, Curr. Opin. Colloid Interface Sci., 1999, 4(4), 288–293 CrossRef CAS.
- P. Meakin, Formation of fractal clusters and networks by irreversible diffusion-limited aggregation, Phys. Rev. Lett., 1983, 51(13), 1119–1122 CrossRef.
- J. C. Gimel, T. Nicolai and D. Durand, 3D Monte Carlo simulations of diffusion limited cluster aggregation up to the sol-gel transition: structure and kinetics, J. Sol-Gel Sci. Technol., 1999, 15(2), 129–136 CrossRef CAS.
- M. Kolb, R. Botet and R. Jullien, Scaling of Kinetically Growing Clusters, Phys. Rev. Lett., 1983, 51(13), 1123 CrossRef.
- J. C. Gimel, D. Durand and T. Nicolai, Transition between flocculation and percolation of a diffusion-limited cluster–cluster aggregation process using three-dimensional Monte Carlo simulation, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51(17), 11348–11357, DOI:10.1103/PhysRevB.51.11348.
- D. Fry, T. Sintes, A. Chakrabarti and C. M. Sorensen, Enhanced Kinetics and Free-Volume Universality in Dense Aggregating Systems, Phys. Rev. Lett., 2002, 89(14), 148301, DOI:10.1103/PhysRevLett.89.148301.
- A. Hasmy, E. Anglaret, M. Foret, J. Pelous and R. Jullien, Small-angle neutron-scattering investigation of long-range correlations in silica aerogels: Simulations and experiments, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(9), 6006 CrossRef CAS.
- A. Hasmy, M. Foret, J. Pelous and R. Jullien, Small-angle neutron-scattering investigation of short-range correlations in fractal aerogels: Simulations and experiments, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(13), 9345 CrossRef CAS.
- F. Pierce, C. M. Sorensen and A. Chakrabarti, Computer simulation of diffusion-limited cluster–cluster aggregation with an Epstein drag force, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021411 CrossRef CAS.
- M. Rottereau, J. C. Gimel, T. Nicolai and D. Durand, Monte Carlo simulation of particle aggregation and gelation: I. Growth, structure and size distribution of the clusters, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 15, 133–140, DOI:10.1140/epje/i2004-10044-x.
- B. H. Bijsterbosch, M. T. A. Bos, E. Dickinson, J. H. J. Van Opheusden and P. Walstra, Brownian dynamics simulation of particle gel formation: From argon to yoghurt, Faraday Discuss., 1995, 101, 51–64 RSC.
- M. Whittle and E. Dickinson, Brownian dynamics simulation of gelation in soft sphere systems with irreversible bond formation, Mol. Phys., 1997, 90(5), 739–758 CrossRef CAS.
- M. Whittle and E. Dickinson, Stress overshoot in a model particle gel, J. Chem. Phys., 1997, 107(23), 10191–10200, DOI:10.1063/1.474155.
- A. A. Rzepiela, J. H. J. Van Opheusden and T. van Vliet, Large shear deformation of particle gels studied by Brownian dynamics simulations, Comput. Phys. Commun., 2002, 147, 303–306 CrossRef.
- R. J. M. D'Arjuzon, W. Frith and J. R. Melrose, Brownian dynamics simulations of aging colloidal gels, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 061404 CrossRef.
- D. A. Weitz and M. Oliveria, Fractal structures formed by kinetic aggregation of aqueous gold colloids, Phys. Rev. Lett., 1984, 52(16), 1433–1436 CrossRef CAS.
- D. A. Weitz, Limits of the Fractal Dimension for Irreversible Kinetic Aggregation of Gold Colloids, Phys. Rev. Lett., 1985, 54(13), 1416–1419 CrossRef CAS.
- M. Y. Lin, H. M. Lindsay, D. A. Weitz, R. C. Ball, R. Klein and P. Meakin, Universality in colloid aggregation, Nature, 1989, 339(1), 360–362 CrossRef CAS . Available from: http://weitzlab.seas.harvard.edu/publications/lin.nature.1989.pdf{\%}5Cnhttp://www.weitzlab.seas.harvard.edu/publications/lin.nature.1989.pdf.
- J. M. Jin, K. Parbhakar, L. H. Dao and K. H. Lee, Gel formation by reversible cluster–cluster aggregation, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54(1), 997–1000 CrossRef CAS.
- P. Meakin, Models For Colloidal Aggregation, Annu. Rev. Phys. Chem., 1988, 39, 237–267 CrossRef CAS.
- R. Jullien, A. Hasmy and E. Anglaret, Effect of cluster deformations in the DLCA modeling of the sol-gel process, J. Sol-Gel Sci. Technol., 1997, 8, 819–824, DOI:10.1007/BF02436944.
- H. S. Ma, J. H. Prévost, R. Jullien and G. W. Scherer, Computer simulation of mechanical structure-property relationship of aerogels, J. Non-Cryst. Solids, 2001, 285, 216–221 CrossRef CAS.
- H. S. Ma, J. H. Prévost and G. W. Scherer, Elasticity of DLCA model gels with loops, Int. J. Solids Struct., 2002, 39, 4605–4614 CrossRef.
- S. Manley, L. Cipelletti, V. Trappe, A. E. Bailey, R. J. Christianson and U. Gasser, et al., Limits to Gelation in Colloidal Aggregation, Phys. Rev. Lett., 2004, 93(10), 2–5 CrossRef.
- S. Manley, B. Davidovitch, N. R. Davies, L. Cipelletti, A. E. Bailey and R. J. Christianson, et al., Time-dependent strength of colloidal gels, Phys. Rev. Lett., 2005, 95, 048302 CrossRef CAS.
- L. Cipelletti, S. Manley, R. C. Ball and D. A. Weitz, Universal Aging Features in the Restructuring of Fractal Colloidal Gels, Phys. Rev. Lett., 2000, 84(10), 2275–2278, DOI:10.1103/PhysRevLett.84.2275.
- M. Kolb, Reversible diffusion-limited cluster aggregation, J. Phys. A: Math. Gen., 1986, 19(5), L263 CrossRef.
- W. Y. Shih, I. A. Aksay and R. Kikuchi, Reversible-growth model: cluster–cluster aggregation with finite binding energies, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36(10), 5015–5020, DOI:10.1103/PhysRevA.36.5015.
- E. Del Gado, A. Fierro, L. de Arcangelis and A. Coniglio, Slow dynamics in gelation phenomena: From chemical gels to colloidal glasses, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69(5), 051103 CrossRef.
- L. D. Gelb, Simulating silica aerogels with a coarse-grained flexible model and Langevin dynamics, J. Phys. Chem. C, 2007, 111(43), 15792–15802 CrossRef CAS.
- J. D. Park, K. H. Ahn and S. J. Lee, Structural change and dynamics of colloidal gels under oscillatory shear flow, Soft Matter, 2015, 11(48), 9262–9272, 10.1039/C5SM01651G.
- J. Liu, W. Y. Shih, M. Sarikaya and I. A. Aksay, Fractal colloidal aggregates with finite interparticle interactions: Energy dependence of the fractal dimension, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41(6), 3206–3213 CrossRef CAS.
- R. N. Zia, B. J. Landrum and W. B. Russel, A micro-mechanical study of coarsening and rheology of colloidal gels: Cage building, cage hopping, and Smoluchowski's ratchet, J. Rheol., 2014, 58(5), 1121–1157 CrossRef CAS.
- S. Griffiths, F. Turci and C. P. Royall, Local structure of percolating gels at very low volume fractions, J. Chem. Phys., 2017, 146(1), 1–8, DOI:10.1063/1.4973351.
- A. A. Potanin, R. De Rooij, D. Van Den Ende and J. Mellema, Microrheological modeling of weakly aggregated dispersions, J. Chem. Phys., 1995, 102(14), 5845–5853, DOI:10.1063/1.469317.
- V. Prasad, V. Trappe, A. D. Dinsmore, P. N. Segre, L. Cipelletti and D. A. Weitz, Universal features of the fluid to solid transition for attractive colloidal particles, Faraday Discuss., 2003, 123, 1–12 RSC.
- L. C. Hsiao, R. S. Newman, S. C. Glotzer and M. J. Solomon, Role of isostaticity and load-bearing microstructure in the elasticity of yielded colloidal gels, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(40), 16029–16034 CrossRef CAS.
- A. Mohraz and M. J. Solomon, Orientation and rupture of fractal colloidal gels during start-up of steady shear flow, J. Rheol., 2005, 49(3), 657–681 CrossRef CAS.
- E. Dickinson, Computer Simulation of Particle Gel Formation, J. Chem. Soc., 1994, 90, 1 Search PubMed.
- N. Kern and D. Frenkel, Fluid–fluid coexistence in colloidal systems with short-ranged strongly directional attraction, J. Chem. Phys., 2003, 118(21), 9882–9889, DOI:10.1063/1.1569473.
- E. Zaccarelli, Colloidal gels: Equilibrium and non-equilibrium routes, J. Phys.: Condens. Matter, 2007, 19(32), 323101 CrossRef.
- G. Wang and J. W. Swan, Surface heterogeneity affects percolation and gelation of colloids: dynamic simulations with random patchy spheres, Soft Matter, 2019, 15, 5094–5108 RSC.
- R. J. Baxter, Percus–Yevick Equation for Hard Spheres with Surface Adhesion, J. Chem. Phys., 1968, 49(6), 2770–2774, DOI:10.1063/1.1670482.
- M. Bouzid and E. Del Gado, Network Topology in Soft Gels: Hardening and Softening Materials, Langmuir, 2018, 34, 773–781 CrossRef CAS.
- J. Colombo, A. Widmer-Cooper and E. Del Gado, Microscopic picture of cooperative processes in restructuring gel networks, Phys. Rev. Lett., 2013, 110, 198301 CrossRef.
- J. Colombo and E. Del Gado, Stress localization, stiffening and yielding in a model colloidal gel, J. Rheol., 2014, 58, 1089, DOI:10.1122/1.4882021.
- J. P. Pantina and E. M. Furst, Elasticity and critical bending moment of model colloidal aggregates, Phys. Rev. Lett., 2005, 94(13), 8–11 CrossRef.
- E. M. Furst and J. P. Pantina, Yielding in colloidal gels due to nonlinear microstructure bending mechanics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75(5), 1–4 CrossRef.
- P. B. Laxton and J. C. Berg, Investigation of the link between micromechanical interparticle bond rigidity measurements and macroscopic shear moduli of colloidal gels, Colloids Surf., A, 2007, 301(1–3), 137–140 CrossRef CAS.
- L. C. Hsiao, S. Jamali, E. Glynos, P. F. Green, R. G. Larson and M. J. Solomon, Rheological State Diagrams for Rough Colloids in Shear Flow, Phys. Rev. Lett., 2017, 119(15), 1–6 CrossRef PubMed.
- B. Schroyen, C. P. Hsu, L. Isa, P. Van Puyvelde and J. Vermant, Stress Contributions in Colloidal Suspensions: The Smooth, the Rough, and the Hairy, Phys. Rev. Lett., 2019, 122(21), 218001 CrossRef CAS.
- L. C. Hsiao and S. Pradeep, Experimental synthesis and characterization of rough particles for colloidal and granular rheology, Curr. Opin. Colloid Interface Sci., 2019, 43, 94–112 CrossRef CAS.
- W. C. K. Poon and M. D. Haw, Mesoscopic structure formation in colloidal aggregation and gelation, Adv. Colloid Interface Sci., 1997, 73, 71–126 CrossRef CAS.
- R. Buscall, T. H. Choudhury, M. A. Faers, J. W. Goodwin, P. A. Luckham and S. J. Partridge, Towards rationalising collapse times for the delayed sedimentation of weakly-aggregated colloidal gels, Soft Matter, 2009, 5(7), 1345–1349 RSC.
- J. De Graaf, W. C. K. Poon, M. J. Haughey and M. Hermes, Hydrodynamics strongly affect the dynamics of colloidal gelation but not gel structure, Soft Matter, 2019, 15, 10–16 RSC.
- T. Schneider and E. Stoll, Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 17(3), 1302–1322 CrossRef CAS.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- A. W. Lees and S. F. Edwards, The computer study of transport processes under extreme conditions, J. Phys. C: Solid State Phys., 1972, 5(15), 1921–1928 CrossRef , Available from: http://stacks.iop.org/0022-3719/5/i=15/a=006?key=crossref.e594e5cd0b6eb0d5dc9f68b23ee836be.
- L. D. Gelb, A. L. Graham, A. M. Mertz and P. H. Koenig, On the permeability of colloidal gels, Phys. Fluids, 2019, 31(2), 021210 CrossRef.
- B. Rajaram and A. Mohraz, Steady shear microstructure in dilute colloid–polymer mixtures, Soft Matter, 2012, 8(29), 7699 RSC , Available from: http://xlink.rsc.org/?DOI=c2sm25936b.
- V. Trappe and D. A. Weitz, Scaling of the viscoelasticity of weakly attractive particles, Phys. Rev. Lett., 2000, 85(2), 449–452 CrossRef CAS.
- R. A. Lionberger and W. B. Russel, High frequency modulus of hard sphere colloids, J. Rheol., 1994, 38(6), 1885–1908 CrossRef CAS.
- J. W. Swan, E. M. Furst and N. J. Wagner, The medium amplitude oscillatory shear of semi-dilute colloidal dispersions. Part I: Linear response and normal stress differences, J. Rheol., 2014, 58(2), 307–337, DOI:10.1122/1.4861071.
- Z. Varga and J. W. Swan, Linear viscoelasticity of attractive colloidal dispersions, J. Rheol., 2015, 59(5), 1271–1298, DOI:10.1122/1.4928951.
- S. L. Elliott and W. B. Russel, High frequency shear modulus of polymerically stabilized colloids, J. Rheol., 1998, 42(2), 361–378, DOI:10.1122/1.550940.
- H. K. Chan and A. Mohraz, Two-step yielding and directional strain-induced strengthening in dilute colloidal gels, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85(4), 1–6 CrossRef PubMed.
- P. Burey, B. R. Bhandari, T. Howes and M. J. Gidley, Hydrocolloid Gel Particles: Formation, Characterization, and Application, Crit. Rev. Food Sci. Nutr., 2008, 48(5), 361–377, DOI:10.1080/10408390701347801.
| This journal is © The Royal Society of Chemistry 2020 |