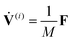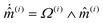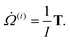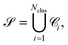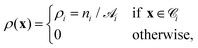DOI:
10.1039/C8SM01831F
(Paper)
Soft Matter, 2020,
16, 8893-8903
Unravelling the role of phoretic and hydrodynamic interactions in active colloidal suspensions
Received
7th September 2018
, Accepted 6th August 2020
First published on 7th August 2020
Abstract
Active fluids comprise a variety of systems composed of elements immersed in a fluid environment which can convert some form of energy into directed motion; as such they are intrinsically out-of-equilibrium in the absence of any external force. A fundamental problem in the physics of active matter concerns the understanding of how the characteristics of autonomous propulsion and agent–agent interactions determine the collective dynamics of the system. We study numerically the suspensions of self-propelled diffusiophoretic colloids, in (quasi)-2d configurations, accounting for both dynamically resolved solute-mediated phoretic interactions and solvent-mediated hydrodynamic interactions. Our results show that the system displays different scenarios at changing the colloid–solute affinity and it develops a cluster phase in the chemoattractive case. We study the statistics of cluster sizes and cluster morphologies for different magnitudes of colloidal activity. Finally, we provide evidences that hydrodynamics plays a relevant role in the aggregation kinetics and cluster morphology, significantly hindering cluster growth.
1 Introduction
Collective behaviour is widespread in Nature: fish schools, insects swarms, bacterial colonies, and plankton blooms are but a few examples. Collective phenomena in active matter are characterised by long-ranged correlations, large density fluctuations,1,2 complex pattern-formation,3 and non-equilibrium changes of state, such as a flocking,4–6 clustering,7 or mobility induced phase separation.8,9 Answering key questions on how individuals interact and communicate goes even beyond the fundamental goal of unravelling the physical mechanisms at the basis of self-organisation in living systems. This will help in the design of micro- and nano-scale self-propelled objects,10–17 with the aim of generating motion in miniaturised devices and developping biomimetic environments.18–21 Although most of these natural and artificial particles move in a fluid medium, the role played by particle-motion induced hydrodynamic correlations has been essentially overlooked so far. Here we present a numerical study on a suspension of non-Brownian colloids which move responding to gradients of a self-generated concentration field;22–25 the latter determines, dynamically by diffusion and advection, the means of interaction/communication among the active particles. In analogy to typical experimental setups,9,26–29 we consider the dynamics of a layer of self-propelled colloids (SPCs) on a flat wall, under the action of gravity, embedded in a liquid medium. We find that the system develops two distinct dynamic regimes, forming large scale clusters when the interaction of the colloidal particles with solute is of “chemoattractive” type. We characterise the transition between the two observed non-equilibrium regimes and focus on the morphology and dynamics of the cluster phase. With respect to previous studies, we quantitatively single out, for the first time, the impact of solvent hydrodynamics on the collective dynamics of suspensions of active self-diffusiophoretic Janus colloids.
2 Theory and numerical model
2.1 Hydrodynamic model for the solvent–solute mixture
The 3d Navier–Stokes equations for the fluid velocity field u| | 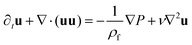 | (1) |
are numerically evolved by means of the lattice Boltzmann (LB) method.30,31 The dynamics of the solute concentration field C is described by an advection–diffusion–reaction equation| | ∂tC + ∇·(uC) = D∇2C + ![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) C − kdC, C − kdC, | (2) |
which is integrated numerically by means of a finite difference scheme.32–36 In eqn (1), ρf is the fluid density (assumed to be constant, since the flow regime is close to incompressible, the maximum Mach number being Ma ≈ 10−2), P is the pressure field, and ν is the kinematic viscosity.
In eqn (2), D is the solute diffusivity and ![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) C is a source field that represents the production of solute by the colloidal activity and it is localised at particle surfaces, i.e. it has the form
C is a source field that represents the production of solute by the colloidal activity and it is localised at particle surfaces, i.e. it has the form
| | 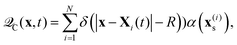 | (3) |
where the sum runs over all colloids (of radius
R), whose positions are
Xi(
t). The function
α(
x(i)s) is a prescribed activity profile over the surface (see
Fig. 1 and the discussion in the next section).
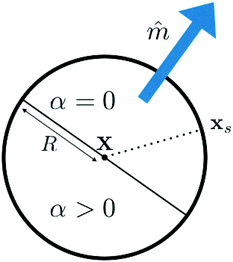 |
| | Fig. 1 Sketch of a spherical self-phoretic colloid of radius R. X is the position of the centre of mass, ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) is the particle characteristic vector, based on which we set the activity profile: α(xs) = α0 in the bottom hemisphere ( is the particle characteristic vector, based on which we set the activity profile: α(xs) = α0 in the bottom hemisphere (![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) · ·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) < 0) and α(xs) = 0 on top ( < 0) and α(xs) = 0 on top (![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) · ·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) > 0). > 0). | |
The local sink term −kdC models the degradation of products at rate kd (with associated characteristic screening length 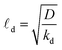 ). The velocities attained in our simulations are such that the typical particle Reynolds Re = VpR/ν and Péclet Pe = VpR/D numbers are always smaller than 10−1 (Vp is the self-propulsion speed), thus making the advection terms in eqn (1) and (2) negligible. The fluid is confined along the z-direction by two parallel walls, at which a no-slip boundary condition is imposed on the velocity field and a zero-flux condition applies for the equation for C. Periodic boundary conditions apply in the x and y directions. The boundary conditions at the particle surfaces need a deeper description that will be provided hereafter.
). The velocities attained in our simulations are such that the typical particle Reynolds Re = VpR/ν and Péclet Pe = VpR/D numbers are always smaller than 10−1 (Vp is the self-propulsion speed), thus making the advection terms in eqn (1) and (2) negligible. The fluid is confined along the z-direction by two parallel walls, at which a no-slip boundary condition is imposed on the velocity field and a zero-flux condition applies for the equation for C. Periodic boundary conditions apply in the x and y directions. The boundary conditions at the particle surfaces need a deeper description that will be provided hereafter.
2.2 Particle–solute coupling: self-diffusiophoresis
According to the theory of colloidal phoresis,37 a non-homogeneous concentration field C around a solid particle causes a pressure imbalance that, in turn, induces a flow within the solid–liquid interfacial layer. Such flow appears, on macroscopic length scales, as an effective slip boundary condition for the velocity. The interfacial layer thickness being much smaller than the typical particle size allows a lubrication theory analysis, which leads to the following effective slip velocity for the fluid velocity u at the particle surface Σ:| | vs = μ(xs)(1 − ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ⊗ ⊗ ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) )·∇C, )·∇C, | (4) |
where ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) is the normal to the surface in xs and μ(xs) is the phoretic mobility, xs ∈ Σ, which contains the molecular details of the colloid–solute interaction. For uniform phoretic mobility μ(xs) ≡ μ0, particles gain a net propulsion velocity Vp ∼ −μ0∇C, i.e. they perform positive diffusiophoresis for negative μ0 (“chemoattractive” colloids) and negative diffusiophoresis for positive μ0 (“chemorepulsive” colloids).
is the normal to the surface in xs and μ(xs) is the phoretic mobility, xs ∈ Σ, which contains the molecular details of the colloid–solute interaction. For uniform phoretic mobility μ(xs) ≡ μ0, particles gain a net propulsion velocity Vp ∼ −μ0∇C, i.e. they perform positive diffusiophoresis for negative μ0 (“chemoattractive” colloids) and negative diffusiophoresis for positive μ0 (“chemorepulsive” colloids).
Self-diffusiophoresis is realised by letting each particle produce solute C according to the prescribed activity profile α(xs). Although we may deal, in principle, with arbitrarily patchy38 (yet axisymmetric) active colloids, in the present study we will specialise in the case of Janus-like particles,39 that produce solute at a constant rate per unit surface α0, homogeneously over only one hemisphere, i.e.:
| | 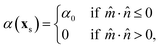 | (5) |
![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif)
being the particle characteristic unit vector (see the sketch in
Fig. 1). An isolated free Janus SPC with the activity profile
(5) and uniform phoretic mobility
μ0 performs a rectilinear motion with constant speed
Vp = |
μ0|
α0/(4
D).
22,23,40
2.3 Particle dynamics
SPCs are described as solid spheres of radius R, mass M and moment of inertia 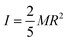 . The boundary condition for the velocity field at the particle surfaces is implemented via the bounce-back-on-links scheme for LB probability densities.41–44 Details of the method and on how to introduce in it the concentration-dependent effective slip velocity (4) are given in the Appendix.
. The boundary condition for the velocity field at the particle surfaces is implemented via the bounce-back-on-links scheme for LB probability densities.41–44 Details of the method and on how to introduce in it the concentration-dependent effective slip velocity (4) are given in the Appendix.
The Lagrangian dynamics for the position X(i) and velocity V(i) of the centre of mass of the i-th SPC (i = 1, 2,…, N), and for its intrinsic orientation ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) (i) and angular velocity Ω(i), is described by the following equations of motion:
(i) and angular velocity Ω(i), is described by the following equations of motion:
The total force and torque acting on the particle read:
| | | F = Fh − ζF·V − ΓF·Ω − Fp | (7) |
| | | T = Th − ζT·V − ΓT·Ω − Tp, | (8) |
where
ζF and
ζT are the friction matrices.
Fh and
Th are the force and torque exerted by the fluid on the particle, respectively, and depend on the global configuration of the velocity field
u, thus also including hydrodynamic interactions; whereas,
Fp and
Tp depend on the solute field configuration
C and mediate phoretic interactions.
Eqn (6) are solved numerically, time-marching first the positions and orientations vector by means of a forward-Euler scheme, and then the velocities and angular velocities by means of an implicit (backward-Euler) update.
2.4 Numerical details
We have performed numerical simulations of suspensions with N = 6400 SPCs of radius R = 2.5 lattice spacings (a value which is relatively small, such to allow simulations of many particle systems, but large enough to keep deviations from the expected physical behaviour, in terms, e.g., of the drag coefficient, below 10%42,45), on lattices of 1024 × 1024 × 24 grid points (≈410R × 410R × 10R) at a fixed area fraction ϕ ≈ 0.12. The values, in lattice Boltzmann units (lbu), of the parameters used in the simulations are summarised in Table 1. Particles are subjected to a gravity force Fb strong enough to prevent them from leaving the bottom wall (the limit fall velocity being five times larger than the self-propulsion speed corresponding to the maximum phoretic mobility considered, i.e.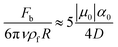 ). A soft-core particle–particle repulsion is introduced to prevent overlapping (further details on the treatment of close-to-contact particles are provided in the Appendix).
). A soft-core particle–particle repulsion is introduced to prevent overlapping (further details on the treatment of close-to-contact particles are provided in the Appendix).
Table 1 Parameters of the simulations and corresponding numerical values (in lbu)
| Parameter |
Symbol |
Value |
| Simulation box size |
L
x
× Ly × Lz |
1024 × 1024 × 24 |
| Fluid kinematic viscosity |
ν
|
0.167 |
| Fluid density |
ρ
f
|
1.0 |
| Solute diffusivity |
D
|
0.087 |
| Particle radius |
R
|
2.5 |
| Volume fraction |
ϕ
|
0.12 |
| Surface activity |
α
0
|
0.005 |
| Phoretic mobility |
|μ0| |
0.1–0.5 |
| Gravity force |
F
b
|
0.25 |
| Characteristic time |
τ
|
345–1725 |
| Run length |
T
run
|
2 × 106 |
The simulations are initialised with fluid velocity and concentration fields null everywhere and particles randomly distributed on the surface of the bottom wall, with random in-plane orientations and velocities equal to zero. We let each simulation run for 2 × 106 time steps, corresponding to approximately Trun ≈ 1200–5800τ, where the characteristic time τ is the time an isolated particle takes to displace by one radius, i.e. τ = R/Vp, and it varies in the range of ≈ 350–1700 lbu (depending on the value of |μ0|). It is worth noticing that, the typical experimental values of size and propulsion speed of SPCs are, respectively, on the order of few μm and few μm s−1,14,46,47 such that τ ∼ 1 s. This means that our run lengths are comparable with the duration of experiments which typically lasts few tens of minutes.9,26
3 Results and discussion
3.1 Dynamic scenarios controlled by the phoretic mobility
A number of experimental and numerical/theoretical studies on self-propelled particles in (quasi)-2d have given indication of the emergence of clustering,9,26–28,48–50 however the nature of the mechanisms determining the formation of aggregates lacks a consensual agreement and seems to be strongly system-dependent (see also ref. 16 for a recent review). In our simulations solvent and solute hydrodynamics is fully resolved, from the far field down to the distances on the order of the particle size (below which it is regularised by the lubrication interaction). We deal with spherical particles, which rules out the possibility of alignment-induced collective motion; instead, chemical production and diffusion mediate an effective interaction, analogously to the experimental system studied in ref. 26 and 28. While in the experiments it was surmised that active colloids experienced an attractive interaction, here we can tune the affinity of the particles for the solute via the phoretic mobility μ0, which can be regarded as an effective charge,51i.e. positive/negative values induce repulsive/attractive interactions, respectively. Indeed, while for μ0 < 0 our simulations confirm the formation of clusters, for μ0 > 0 such cluster phase disappears, with the average cluster size going to zero. Incidentally, let us remark that, in some respect, suspensions of SPCs may recall other systems of interacting microswimmers, as, for instance, attractive squirmers;52 there are however at least two major differences: for SPCs, unlike squirmers, the characteristic self-propulsion speed is constant only for an isolated swimmer, but in general it depends on the concentration field; the second and probably the most important one, from the point of view of collective dynamics, is that while in the case of squirmers particle–particle interactions are frozen (i.e. dictated by the interaction potential once for all), in a SPC suspension phoretic interactions are mediated by the solute field and are, therefore, dynamical, in the sense that they depend on the local (in space and time) field configuration. In other words, phoretic interactions are not pairwise additive but change as a function of the global dynamics and, as such, they give rise to a collective behaviour that is genuinely out-of-equilibrium. In what follows, the phoretic mobility will be expressed as μ ≡ μ0/|μ*|, where |μ*| is the absolute phoretic mobility for which an isolated particle of radius R would have unitary Péclet number. To address the impact of the chemical affinity on the collective dynamics quantitatively, we have performed a Voronoi tessellation analysis of the particle space configurations.†53,54
The bottom insets of Fig. 2 show the Voronoi diagrams for both the repulsive and cluster-forming regimes; as clearly visible to the naked eye, the geometries of the Voronoi cells for chemoattractive and chemorepellent active colloids are distinctively different. The standard deviation of the cell area distribution 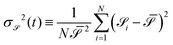 (normalised by the square of the mean value
(normalised by the square of the mean value 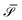 ) turns out to be a good indicator to distinguish the two types of dynamics. In the top inset of Fig. 2 we plot σ
) turns out to be a good indicator to distinguish the two types of dynamics. In the top inset of Fig. 2 we plot σ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) 2(t), as a function of time, for two cases with different sign of the phoretic mobility. In the attractive case, μ < 0, cluster formation induces the appearance of very small (and large) cells and, hence, the surface fluctuations grow and eventually saturate at long times. For positive μ, instead, colloids repel each other and tend to reach an optimal covering of the space, implying that σ
2(t), as a function of time, for two cases with different sign of the phoretic mobility. In the attractive case, μ < 0, cluster formation induces the appearance of very small (and large) cells and, hence, the surface fluctuations grow and eventually saturate at long times. For positive μ, instead, colloids repel each other and tend to reach an optimal covering of the space, implying that σ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) 2(t) attains a (lower) value which remains constant in time. Correspondingly, the dependence of
2(t) attains a (lower) value which remains constant in time. Correspondingly, the dependence of 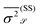 (the time average of
(the time average of 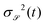 over the steady state) on μ discriminates between the two regimes: it is high for negatively large μ, decreases as μ approaches zero and then remains low and constant for μ > 0.
over the steady state) on μ discriminates between the two regimes: it is high for negatively large μ, decreases as μ approaches zero and then remains low and constant for μ > 0.
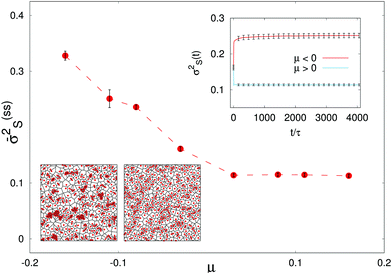 |
| | Fig. 2 Main panel: Steady state standard deviation of Voronoi cell areas as a function of the “coupling constant” (the phoretic mobility) μ. Top inset: σ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) 2(t) vs. time for two cases with positive and negative μ. Bottom insets: Snapshots of the colloid distributions and relative Voronoi diagrams in the attractive, μ = −0.11 (left), and repulsive, μ = +0.11 (right), case, respectively. 2(t) vs. time for two cases with positive and negative μ. Bottom insets: Snapshots of the colloid distributions and relative Voronoi diagrams in the attractive, μ = −0.11 (left), and repulsive, μ = +0.11 (right), case, respectively. | |
We will focus, in what follows, on the chemoattractive case, but before moving on we stress that the phase diagram for chemorepulsive self-phoretic colloids, as recently shown theoretically and numerically,55,56 is indeed rather complex and deserves further investigation.
3.2 Cluster statistics and morphology
We first characterise the cluster size distribution of chemoattractive SPCs, varying the colloid/solute coupling intensity, |μ|. We identify clusters according to a distance criterion. Two particles share a bond if their centres are at a distance equal to or less than a cutoff apart,‡ and we define clusters as groups of particles connected to each other through a bond. We compute probability density functions (PDFs) of cluster sizes over the steady state of each run. Fig. 3 shows such PDFs, which can be in all cases fitted to an exponential, ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (n) ∝ e−n/nc, over a wide range of sizes n.
(n) ∝ e−n/nc, over a wide range of sizes n.
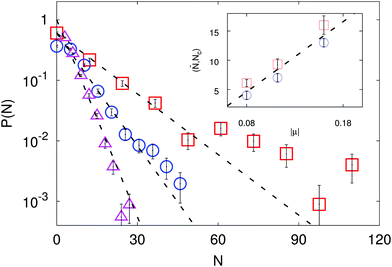 |
| | Fig. 3 Main panel: PDFs of cluster sizes for three values of the phoretic mobility: μ = −0.16 ( ), μ = −0.11 ( ), μ = −0.11 ( ) and μ = −0.08 ( ) and μ = −0.08 ( ); the dashed lines represent the exponential fit which are drawn to guide the eye. Inset: Characteristic (nc, ); the dashed lines represent the exponential fit which are drawn to guide the eye. Inset: Characteristic (nc,  ) and mean ( ) and mean (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , ,  ) cluster sizes as a function of |μ| ∝ Vp, the intrisic SPC velocity (the dashed line indicates a linear relation). ) cluster sizes as a function of |μ| ∝ Vp, the intrisic SPC velocity (the dashed line indicates a linear relation). | |
The characteristic value nc and the mean size 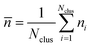 increase linearly with |μ| (see the inset of Fig. 3), hence with the velocity of an isolated particle, in agreement with experimental and numerical observations.9,26,50 The global attractor for the SPC dynamics is a set
increase linearly with |μ| (see the inset of Fig. 3), hence with the velocity of an isolated particle, in agreement with experimental and numerical observations.9,26,50 The global attractor for the SPC dynamics is a set
where
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) i
i is the region of plane occupied by the
i-th cluster of area
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) i
i and containing
ni SPCs. Correspondingly, the colloid number density reads
Since the colloid density fluctuations can be expressed as
σρ2 = 〈(
ρ(
x) − 〈
ρ〉)
2〉 (where 〈(…)〉 denotes a surface average), we can write
| | 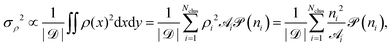 | (9) |
where |
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif)
| is the measure of the whole plane. The number of particles in a cluster
n is known to scale with the cluster gyration radius
Rg as
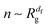
,
df being the fractal (Hausdorff) dimension;
57,58ni and
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) i
i are, then, related by
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) i
i ∼
Rg2 ∼
n2/df. Plugging the latter relation and
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif)
(
n) ∼ e
−n/nc into
(9), and approximating the sum with the integral, we finally get:
| | 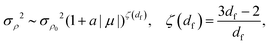 | (10) |
where
σρ02 stands for the fluctuations of an inactive (non-phoretic) particle and
a is a phenomenological parameter; to derive (10) we have also used the relation
nc ∼ |
μ|
§ (see the inset of
Fig. 3).
Fig. 4 shows the quantitative agreement of the predicted power law, with the correct scaling exponent, with the numerical observations.
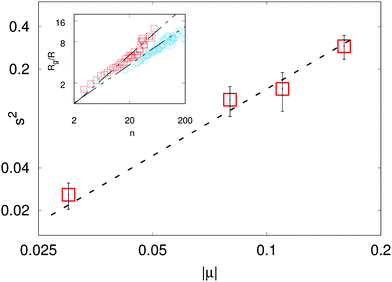 |
| | Fig. 4 Main panel: Deviation of the steady state SPC density fluctuations σρ2 from the value for inactive particles σρ02, normalised as 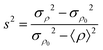 , vs. the coupling strength |μ| from LB (squares) and the phenomenological derivation (dashed line), eqn (10), with fractal dimension df = 1.4, as measured in the simulations. Inset: Mean gyration radius of clusters vs. number of particles with ( , vs. the coupling strength |μ| from LB (squares) and the phenomenological derivation (dashed line), eqn (10), with fractal dimension df = 1.4, as measured in the simulations. Inset: Mean gyration radius of clusters vs. number of particles with ( ) and without ( ) and without ( ) HI. The two dashed lines represent the power law Rg ∼ n1/df (df = 1.8 for no-HI). ) HI. The two dashed lines represent the power law Rg ∼ n1/df (df = 1.8 for no-HI). | |
3.3 Role of hydrodynamic interactions
Self-propelled colloids interact through both the chemicals they produce and the flows they induce. Understanding the relative magnitude and competition between these two sources of dynamic interactions remains challenging. The model put forward allows us to switch off the hydrodynamic interactions (HI), setting the fluid velocity to zero at each time step, yet keeping the self-phoretic mechanism and the correct translational and rotational hydrodynamic friction (see Appendix for more details). Interestingly, our study reveals that although different dynamic scenarios at changing the sign of the phoretic mobility are preserved even without HI (being mainly determined by the chemical interaction), HI have a profound effect on the kinetics of formation and morphology of the observed aggregates. In the absence of particle induced flows in the solvent, attractive SPCs (μ < 0) show an enhanced tendency to form clusters, as it appears in figure Fig. 5, where we compare the time evolution of the mean cluster size ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t), with and without HI (no-HI). In the no-HI case, clusters coarsen, with
(t), with and without HI (no-HI). In the no-HI case, clusters coarsen, with ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t) growing in time as t1/2 (top right inset), as for domains in the spinodal decomposition of fluid mixtures in two dimensions.75 The same behaviour (
(t) growing in time as t1/2 (top right inset), as for domains in the spinodal decomposition of fluid mixtures in two dimensions.75 The same behaviour (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t) ∼ t1/2) has been observed, indeed, in simulations of self-propelled Brownian particles interacting via a shifted-truncated Lennard–Jones potential.49,52 With HI, instead, coarsening is arrested, as observed in experiments.26 Simulations have suggested that in suspensions of attractive squirmers the emergence of continuous or arrested coarsening is selected depending on the form and intensity of the active stress (the coefficient B2 in the squirmer terminology);52 self-phoretic Janus colloids behave, in this respect, as squirmers with B2 = 0,59 for which, indeed, arrested coarsening was observed.52 Due to the non stationarity of the coarsening process, steady state PDFs of cluster sizes cannot be computed in the no-HI simulations. Nevertheless, we observe that istantaneous cluster size distributions F(n,t) (i.e. the number of clusters of size n at time t) tend to assume a self-preserving scaling form F(n,t) ∼ n−2f(n/
(t) ∼ t1/2) has been observed, indeed, in simulations of self-propelled Brownian particles interacting via a shifted-truncated Lennard–Jones potential.49,52 With HI, instead, coarsening is arrested, as observed in experiments.26 Simulations have suggested that in suspensions of attractive squirmers the emergence of continuous or arrested coarsening is selected depending on the form and intensity of the active stress (the coefficient B2 in the squirmer terminology);52 self-phoretic Janus colloids behave, in this respect, as squirmers with B2 = 0,59 for which, indeed, arrested coarsening was observed.52 Due to the non stationarity of the coarsening process, steady state PDFs of cluster sizes cannot be computed in the no-HI simulations. Nevertheless, we observe that istantaneous cluster size distributions F(n,t) (i.e. the number of clusters of size n at time t) tend to assume a self-preserving scaling form F(n,t) ∼ n−2f(n/![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t)), as it happens in the classical colloidal aggregation phenomenon for mass-conserving systems.60 This is shown in the top left inset of Fig. 5, where we plot n2F(n,t) vs. n/
(t)), as it happens in the classical colloidal aggregation phenomenon for mass-conserving systems.60 This is shown in the top left inset of Fig. 5, where we plot n2F(n,t) vs. n/![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t) and see that all sets of points for different t's in the coarsening regime where
(t) and see that all sets of points for different t's in the coarsening regime where ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ∼ t1/2, within error bars, collapse onto each other. The statement on the different dynamics, with and without HI, is corroborated by the inspection of the radial distribution functions (RDFs)61 (indicated as gHI(r,t) and gno-HI(r,t), respectively), defined as the probability of finding a particle between the distances r and r + dr from a reference particle (and averaged over all particles), i.e.
∼ t1/2, within error bars, collapse onto each other. The statement on the different dynamics, with and without HI, is corroborated by the inspection of the radial distribution functions (RDFs)61 (indicated as gHI(r,t) and gno-HI(r,t), respectively), defined as the probability of finding a particle between the distances r and r + dr from a reference particle (and averaged over all particles), i.e.| | 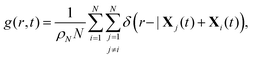 | (11) |
where ρN is the particle number density and δ(x) is the Dirac's delta. RDFs at different times are shown in Fig. 6: without HI (middle panel) the peaks are higher and decay more slowly, associated with the development of clusters larger than those formed when hydrodynamics is active. Besides, clusters appear substantially more compact, as appreciated in the snapshots (insets) and quantified by the measurement of a larger fractal dimension (d(HI)f ≈ 1.4 and d(no-HI)f ≈ 1.8, see Fig. 4). Hydrodynamics then hinders the colloidal aggregation process. Several complex mechanisms can be conjectured to cause this phenomenon: dynamically induced effective repulsion among particles, fluid flow generated disturbances in the chemical field distribution, etc. An effect, that we could clearly identify, is an enhanced tendency of SPCs to be oriented off-plane, when HI are present, not only when they hit a cluster (as, e.g., in the mechanism proposed in ref. 62) but also for isolated particles. This may be attributed to fluid motion close to the wall, giving rise to hydrodynamic torques that rotate the particles. Actually the roto-translational dynamics of self-diffusiophoretic colloids, at and close to interfaces, is an intricate problem:63–65 in highly confined situations, one might indeed expect even the opposite trend (clusterisation enhancement);62 the argument maintains, therefore, a qualitative character. Nevertheless, Fig. 6 (bottom panel) provides a quantitative insight into the picture. There, we show the PDF of the degree of alignment of the particle orientation with the bounding solid wall, m‖2 = mx2 + my2. When HI are present, indeed, the peak of the PDF around m‖2 ∼ 0 is more pronounced, i.e. there is a larger fraction of colloids pointing out of the plane. Accordingly, the self-propulsion speed is effectively reduced, thus limiting the in-plane mobility and diminisihing the capability of particles to gather and clusterise. Before concluding, we would like to remind that it is still an open question whether Janus particles can really have a homogeneous phoretic mobility; if the opposite is true, inhomogeneous μ(r) gives rise, in response to gradients of the concentration field, to chemical torques that can lead, themselves, to clustering inhibition.66,67,68 With hydrodynamic interactions, the dynamics is, of course, even more complicated, due to the competition of these effects, and it is the subject of ongoing research.
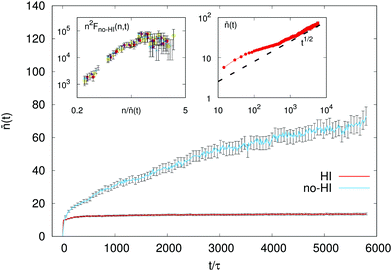 |
| | Fig. 5 Main panel: Mean cluster size ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) vs. time from simulations with (HI) and without (no-HI) hydrodynamic interactions (the values for the HI case are magnified by a factor two, for the sake of clarity of visualisation). Left inset: Cluster size distributions for μ = −0.16 and no-HI, at various times t ∈ [1500τ; 3000τ] during the coarsening process. Right inset: log–log plot of vs. time from simulations with (HI) and without (no-HI) hydrodynamic interactions (the values for the HI case are magnified by a factor two, for the sake of clarity of visualisation). Left inset: Cluster size distributions for μ = −0.16 and no-HI, at various times t ∈ [1500τ; 3000τ] during the coarsening process. Right inset: log–log plot of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) vs. t, without HI, highlighting the scaling t1/2 in the coarsening process. vs. t, without HI, highlighting the scaling t1/2 in the coarsening process. | |
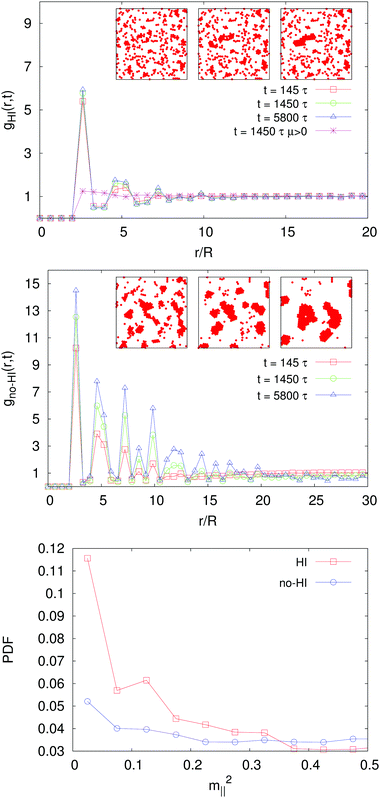 |
| | Fig. 6 Top panel: RDFs for μ = −0.16 at three different times and corresponding snapshots of the colloid distribution, indicating cluster formation, in a sub-system of size 256 × 256, located in the center of the box. Also the repulsive case μ = +0.16 (pink *) is reported for comparison. Middle panel: Same as in the top panel but without hydrodynamic interactions. Bottom panel: PDFs of m‖2, the square magnitude projection onto the {x,y}-plane of the colloid orientations, from simulations with (HI) and without (no-HI) hydrodynamics. | |
4 Conclusions
To conclude, we have used a mesoscopic numerical model of fully resolved spherical active colloids, propelled by self-generated gradients of a scalar field (e.g. a chemical product) where the self-induced hydrodynamic flows can be accounted for. We have identified the role of the phoretic mobility as the key controlling parameter that determines two distinct dynamic regimes and the onset of a cluster phase. By means of a Voronoi tessellation we have characterised the cluster state finding that the probability distribution of sizes decays exponentially with a mean size growing linearly with the particle activity, in agreement with experimental results.9,26 We have quantified the profound effect of hydrodynamics, which inhibits clustering for negative phoretic mobilities. We have identified the interplay between induced flows and particle reorientation as a possible explanation for the strong slowing down of cluster coarsening, however, it remains an open question, whether fluid–wall interactions dominate over particle–particle hydrodynamic correlations, which needs deeper analysis. This study shows that our novel numerical method is powerful and has some unique features, namely the explicit description of chemical signalling, through the production and diffusion of a solute concentration field and the solvent hydrodynamics, to simulate realistic systems. Moreover, it opens the way to address the dynamics of self-propelled colloids in general geometries and also for stronger activity (larger Pe), both in isotropic and unforced situations, where aggregation can lead to the formation of active colloidal gels, or under gravity as in the experimental sedimentation setup.
Conflicts of interest
There are no conflicts to declare.
5 Appendix
5.1 The lattice Boltzmann method (LBM)
The fundamental quantities, in the LBM, are the discrete single particle probability density functions (pdfs), fl(x,t), defined in such a way that fl(x,t)Δx3 is the probability of finding a fluid particle (of unit mass) in a small volume Δx3, centred at x, at time t, moving with the velocity cl; the index l runs over the set of discrete lattice velocities (nineteen in our case).31,69 The evolution equation for the fl's is the so called lattice BGK–Boltzmann equation:70| | 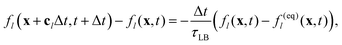 | (12) |
where Δx and Δt are the lattice spacing and time step, respectively, and τLB is the relaxation time. Algorithmically, eqn (12) consists of two steps: (i) streaming, where the pdfs move (“stream”) over the lattice and (ii) collisions, which induce relaxation on the local equilibrium distribution functions, f(eq)l(x,t). The latters depend on space and time only through their prescribed dependence on the hydrodynamic fields, density ρ(x,t) and velocity u(x,t). We adopt, for the f(eq)l's, a standard second order polynomial form,30 that is:| | 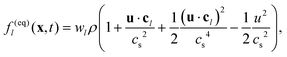 | (13) |
where wl and cs are constants (the lattice weights and speed of sound) characteristic of the particular lattice geometry and velocity scheme. The density and velocity fields are expressed, in terms of fl's, as:| | 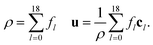 | (14) |
In the small Knudsen and Mach numbers limits, eqn (12)–(14) represent a numerical solver (second order accurate in space and time69,71) for the incompressible Navier–Stokes equations.
5.2 Fluid–solid coupling
Coupling the solvent dynamics with that of the suspended particles requires tackling a boundary condition at the solid–fluid interface. A solid particle is discretized on the lattice, so that its surface crosses the links between neighbouring lattice nodes. Let us assign a generic link the label j (j = 1,…, Nlinks) and denote the associated outer and inner node as xo and xi = xo + cljΔt, where clj is the corresponding lattice velocity (lj = 1,…, 18).¶ If a no-slip condition were to be enforced at the solid surface, the boundary probability density functions would be updated as follows:| | 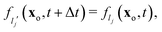 | (15) |
where the index lj′ is such that 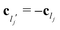 and flj is the post-collisional distribution. However, the boundary velocity at a given location on the particle surface will be in general non-zero (due to slip and/or particle motion). Rule (15) must be, then, modified accordingly as:41,42,44
and flj is the post-collisional distribution. However, the boundary velocity at a given location on the particle surface will be in general non-zero (due to slip and/or particle motion). Rule (15) must be, then, modified accordingly as:41,42,44| | 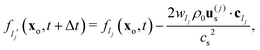 | (16) |
where ρ0 is the mean fluid density and u(j)s, the velocity at the particle surface location 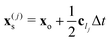 (the position of the boundary node is assumed to be in the middle of the link), depends on the particle linear V and angular Ω velocities and on the (local) slip velocity v(j)s as
(the position of the boundary node is assumed to be in the middle of the link), depends on the particle linear V and angular Ω velocities and on the (local) slip velocity v(j)s as| | | u(j)s = V + Ω∧ (x(j)s − X) + v(j)s, | (17) |
where X is the position of the particle centre of mass. The boundary conditions (16) and (17) induce a local fluid–particle momentum exchange (the total momentum being conserved) which entails a force at the boundary node x(j)s| | 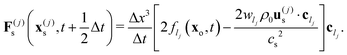 | (18) |
The total force and torque acting on the particle are, then, given by:| | 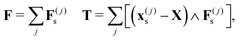 | (19) |
where the sum runs over all links constituting the particle surface. Let us notice that, because of (17) and (18), both force and torque can be split into four terms:44| | | F = Fh − ζF·V − ΓF·Ω − Fp | (20) |
| | | T = Th − ζT·V − ΓT·Ω − Tp; | (21) |
The expressions of Fh and Th are as follows:| | 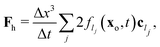 | (22) |
| | 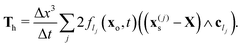 | (23) |
The latter equations provide the force and torque exerted by the fluid on the particle and as such they mediate also the hydrodynamic interactions. The friction matrices| | 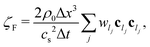 | (24) |
and| | 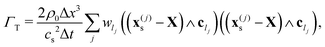 | (25) |
are diagonal, whereas| | 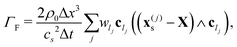 | (26) |
| | 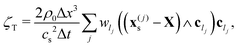 | (27) |
are null (apart from discretisation effects, coming from surface irregularities, which can be reduced by increasing the particle radius). In what we call the ‘no-HI’ case (without hydrodynamic interactions) the effect of the fluid enters, then, in the drag terms −ζF·V and −ΓT·Ω. The phoretic force Fp and torque Tp are given by:| | 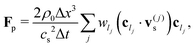 | (28) |
| | 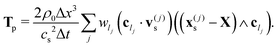 | (29) |
In order to get a better insight into the effect of these terms on the particle dynamics, we first consider the case of an axisymmetric configuration of the chemical field C(x) around the particle. This is the case, for instance, of the active Janus self-diffusiophoretic colloid we considered. The sum in (28), which runs over all links (or, equivalently, over all boundary nodes), can be split into two sums: a sum over the subset Ixo of links connecting a certain fluid node xo, proximal to the particle surface, to the corresponding solid nodes inside the particle,| | Ixo = {b|cb·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) < 0}, < 0}, | (30) |
and a sum over all such ‘outer’ fluid nodes, i.e.| | 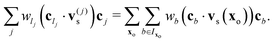 | (31) |
The particle surface is endowed with a spherical coordinate system, such that the generic point xo can be associated to the usual polar and azimuthal angles, (θ, ϕ), with respect to the symmetry axis identified by the particle director ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) (defined in the main text). For
(defined in the main text). For| | 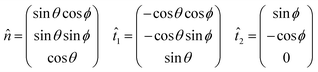 | (32) |
the triple of orthonormal vectors corresponding to the normal and the two tangential directions to the surface in xo,|| the following decomposition cb = (cb·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) )
)![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) + (cb·
+ (cb·![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 1)
1)![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 1 + (cb·
1 + (cb·![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 2)
2)![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 2 obviously holds for the lattice velocities, with b ∈ I(θ,ϕ) (we will use for xo its spherical coordinates from now on). We recall that the effective slip velocity, vs ∝ (1 −
2 obviously holds for the lattice velocities, with b ∈ I(θ,ϕ) (we will use for xo its spherical coordinates from now on). We recall that the effective slip velocity, vs ∝ (1 − ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ⊗
⊗ ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) )∇C, is, by definition, tangent to the surface, therefore:
)∇C, is, by definition, tangent to the surface, therefore:| | cb·vs = vs,1(θ)(cb·![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 1) + vs,2(θ)(cb· 1) + vs,2(θ)(cb·![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 2), 2), | (33) |
where vs,1(θ) and vs,2(θ) are the components of vs along the two tangent directions (polar and azimuthal), which depend only on θ owing to the axisymmetric character of the field C(θ). Using (31) and (33), the force (28) can be rewritten as:| | 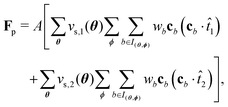 | (34) |
where 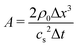 . Let us note, now, a property of the set of links: given xo = (θ, ϕ) on the sphere, and its associated I(θ,ϕ), there will be a xo′ = (θ′, ϕ′) (with θ′ = θ′ and ϕ′ = ϕ + π) such that for every b ∈ I(θ,ϕ) there exists a b′ ∈ I(θ′,ϕ′) fulfilling
. Let us note, now, a property of the set of links: given xo = (θ, ϕ) on the sphere, and its associated I(θ,ϕ), there will be a xo′ = (θ′, ϕ′) (with θ′ = θ′ and ϕ′ = ϕ + π) such that for every b ∈ I(θ,ϕ) there exists a b′ ∈ I(θ′,ϕ′) fulfilling| | 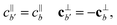 | (35) |
where the superscripts “‖” and “⊥” stand for the directions, respectively, parallel and orthogonal to the symmetry axis ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) . Such property follows from the definition of I(θ,ϕ), eqn (30): since, by symmetry, upon the shift ϕ → ϕ + π the normal to the surface
. Such property follows from the definition of I(θ,ϕ), eqn (30): since, by symmetry, upon the shift ϕ → ϕ + π the normal to the surface ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) changes as n′‖ = n‖ and n′⊥ = −n⊥ (see (32)), in order to preserve the condition cb′·
changes as n′‖ = n‖ and n′⊥ = −n⊥ (see (32)), in order to preserve the condition cb′·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ′ < 0, the velocities have to transform as in (35). Analogously,
′ < 0, the velocities have to transform as in (35). Analogously, 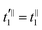 ,
, 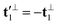 and t2′ = −t2. Therefore, in (34), upon summing on ϕ (i.e. on nodes all around the particle at a fixed latitude θ), only the component parallel to
and t2′ = −t2. Therefore, in (34), upon summing on ϕ (i.e. on nodes all around the particle at a fixed latitude θ), only the component parallel to ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) survives and reduces to:
survives and reduces to:| | 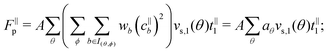 | (36) |
if the particle is large enough (R/Δx ≫ 1), so to minimise the discretisation errors, the coefficients are aθ ∝ 2πR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, such that the sum in (36) approximates the integral over the polar angle. So, basically, for a solute distribution around the particle which is axisymmetric, the bounce-back-on-links algorithm yields a phoretic force which is proportional to the surface integral of the effective slip velocity, i.e.:
θ, such that the sum in (36) approximates the integral over the polar angle. So, basically, for a solute distribution around the particle which is axisymmetric, the bounce-back-on-links algorithm yields a phoretic force which is proportional to the surface integral of the effective slip velocity, i.e.:| | 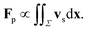 | (37) |
It is easy to verify, by similar symmetry arguments, that the torque in (29) is Tp = 0. In the general case it is not so straightforward to estimate such forces; however, we can grasp qualitatively what happens. We can always decompose the solute field C(x) around a (Janus) particle as the sum of the self-generated field (which is axisymmetric) and a background field (which will not be, in general, axisymmetric), C(x) = Caxisymm(x) + Cbackground(x). If we now assume that the background field does not vary significantly on the scale of the particle size (that is 〈C2〉1/2/||∇C(X)|| ≫ R), we can approximate it as C(x) ≈ C(X) + ∇C|X·(x − X). To leading order, then, the phoretic force Fp will also split into a self-propulsion contribution and in a term ![[F with combining tilde]](https://www.rsc.org/images/entities/b_char_0046_0303.gif) p ∝ ∇C|X; the latter represents a sort of chemotactic drift towards regions of high or low solute, depending on the sign of the phoretic mobility.
p ∝ ∇C|X; the latter represents a sort of chemotactic drift towards regions of high or low solute, depending on the sign of the phoretic mobility.
5.3 Switching off hydrodynamics
When assessing the dynamics where no hydrodynamic interactions are present (see Section 3.3), we set the fluid velocity field u(x,t) to zero everywhere. Consequently, the equation for the solute field C(x,t) reduces to a diffusion equation and the force Fh and torque Th are null. To understand this latter point, we have to first notice that what enters in the expressions (22) and (23) are the post-collisional distribution functions. For τLB = Δt (as it is in all our simulations), these coincide exactly with the equilibrium distributions, eqn (13), with u ≡ 0, that is fl(x,t) = wlρ, ∀l. This implies:| | 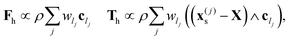 | (38) |
which, by symmetry, vanish (again, apart from small errors due to surface discretization) when summed over all boundary link velocities around the sphere. Let us remark that setting the fluid velocity to zero does not directly affect** the expression for the phoretic force, eqn (28), therefore the self-propulsion and phoretic interactions survive the operation of switching-off hydrodynamics. In this way we can decouple, in our mesoscopic framework, physical phenomena occurring at well separated scales: the fluid dynamic processes localised (on molecular scales) close to the particle (and effectively accounted for in the solute-field-dependent slip velocity) from macroscopic flows in the solvent (and associated hydrodynamic interactions).
5.4 Particles close to contact: lubrication corrections and short-range repulsion
For particles close to contact, lubrication corrections are introduced: the forces and torques acting on two particles approaching each other are calculated, in terms of particle velocities and angular velocities, according to a grand-resistance-matrix formulation.44,45,72 In particular, the lubrication correction takes the form of the difference between the lubrication force at a surface separation h and the force at a given cut-off separation hc; for two particles of radii R1 and R2 (the particle–wall interaction corresponds to the limit R2 → ∞) this reads:44| | 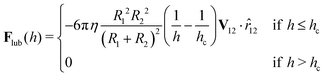 | (39) |
where r12 = X1 − X2 ≡ r12![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 12 is the particle centre–centre distance vector and h = r12 − R1 − R2; the cutoff distance is chosen to be hc = 0.67 lattice units, which is an optimal value to get good agreement with lubrication theory calculations, as shown in ref. 44. Lubrication forces may not be enough, though, to prevent particle overlap (as recognised also in ref. 73 and 74), especially when the particle density is large (even just locally, as, for instance, inside clusters). Therefore, we add also a short-range soft-sphere repulsion modelled by the force Fss ∝ ((hssc/h)3 − 1)
12 is the particle centre–centre distance vector and h = r12 − R1 − R2; the cutoff distance is chosen to be hc = 0.67 lattice units, which is an optimal value to get good agreement with lubrication theory calculations, as shown in ref. 44. Lubrication forces may not be enough, though, to prevent particle overlap (as recognised also in ref. 73 and 74), especially when the particle density is large (even just locally, as, for instance, inside clusters). Therefore, we add also a short-range soft-sphere repulsion modelled by the force Fss ∝ ((hssc/h)3 − 1)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 12, with cutoff (coinciding with the soft-sphere radius) hssc = 2hc.
12, with cutoff (coinciding with the soft-sphere radius) hssc = 2hc.
5.5 Numerical tests
In this section we present results from simulations of simple test cases in order to check to which extent our method agree, qualitatively and/or quantitatively, with the theoretical predictions. Firstly, we consider a single SPC with constant phoretic mobility, μ(xs) ≡ μ0 > 0, and a Janus activity profile| | 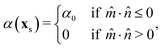 | (40) |
moving in a fully periodic tridimensional box. If the box side is much larger than the particle radius, such a particle is expected to perform a uniform rectilinear motion with speed23| | 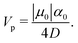 | (41) |
In Fig. 7 we report the coordinates of the position and the three velocity components (in lattice Boltzmann units) for an SPC of radius R = 2.5Δx in a cubic box of side L = 32Δx, initially located in X(0) = (L/2, L/2, L/2) with orientation ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) (0) = (0, 0, 1): the plot suggests that indeed the particle moves in a straight line, with director (0, 0, 1), at a constant speed (the oscillations are due to recomputation of the set of links, hence of the discretised surface, as the particle moves across the lattice), albeit about half of the theoretical value. Such a quantitative disagreement is not too surprising, given the small size of the particle. The quality of the numerical result improves, in fact, significantly with the resolution. This is shown in Fig. 8, where we plot the steady state z-component of the velocity, Vz, normalised by the expected Vp, eqn (41), as a function of the radius (the ratio R/L ≈ 0.08 is kept fixed over various runs). We see that the numerics (red dots) approximate better and better the theoretical prediction as the particle radius is increased, and eventually tend to converge to the value of ∼1.1 (i.e. the measured Vz is about 10% larger than Vp). This residual mismatch might be due to the fact that, as R grows, the Péclet number, Pe, approaches unity, whereas the prediction (41) is valid when Pe is strictly zero. For a smaller Pe ≈ 0.1 we find, indeed, a better agreement for the largest radius (blue square in Fig. 8), for which Vz/Vp ≈ 1.04.
(0) = (0, 0, 1): the plot suggests that indeed the particle moves in a straight line, with director (0, 0, 1), at a constant speed (the oscillations are due to recomputation of the set of links, hence of the discretised surface, as the particle moves across the lattice), albeit about half of the theoretical value. Such a quantitative disagreement is not too surprising, given the small size of the particle. The quality of the numerical result improves, in fact, significantly with the resolution. This is shown in Fig. 8, where we plot the steady state z-component of the velocity, Vz, normalised by the expected Vp, eqn (41), as a function of the radius (the ratio R/L ≈ 0.08 is kept fixed over various runs). We see that the numerics (red dots) approximate better and better the theoretical prediction as the particle radius is increased, and eventually tend to converge to the value of ∼1.1 (i.e. the measured Vz is about 10% larger than Vp). This residual mismatch might be due to the fact that, as R grows, the Péclet number, Pe, approaches unity, whereas the prediction (41) is valid when Pe is strictly zero. For a smaller Pe ≈ 0.1 we find, indeed, a better agreement for the largest radius (blue square in Fig. 8), for which Vz/Vp ≈ 1.04.
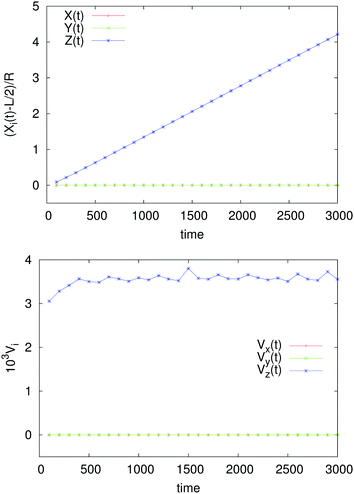 |
| | Fig. 7 Kinematics of a single self-phoretic Janus colloid in a periodic box: particle position (top panel) X(t) = (x(t), y(t), z(t)) and velocity V(t) = (Vx(t), Vy(t), Vz(t)) (bottom panel) vs. time (all quantities here are expressed in lattice Boltzmann units). | |
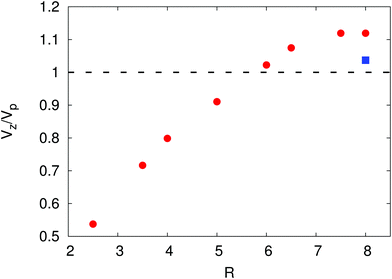 |
| | Fig. 8 Steady state z-component of the particle velocity (red dots), normalised by the theoretical prediction Vp (eqn (41)), for a single Janus SPC in a periodic box as a function of the particle radius (a dashed line at the value of 1 is plotted as a guide for the eye). | |
In the multi-particle case we decided to pay the price of a worse agreement with the single particle theoretical speed and adopted a smaller radius such to be able to simulate statistically significant systems at an affordable computational cost.
Acknowledgements
We acknowledge the Spanish MINECO and Generalitat de Catalunya DURSI for financial support under the projects FIS2015-67837-P and 2014SGR-922, respectively. I. P. acknowledges Generalitat de Catalunya under the Program Icrea Acadèmia. A. S. acknowledges the European Research Council under the European Union Horizon 2020 Framework Programme (No. FP/2014-2020)/ERC Grant Agreement No. 739964 (COPMAT). This work was possible, thanks to the access to the MareNostrum Supercomputer at Barcelona Supercomputing Center (BSC) and also through the Partnership for Advanced Computing in Europe (PRACE).
Notes and references
- M. Marchetti, J.-F. Joanny, S. Ramaswamy, T. Liverpool, J. Prost, M. Rao and R. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- E. Budrene and H. Berg, Nature, 1991, 349, 630–633 CrossRef CAS.
- T. Vicsek, T. Czirók, E. Ben-Jacob, I. Cohen and O. Shochet, Phys. Rev. Lett., 1995, 75, 1226–1229 CrossRef CAS.
- A. Cavagna and I. Giardina, Annu. Rev. Condens. Matter Phys., 2014, 5, 183–207 CrossRef CAS.
- F. Ginelli and H. Chaté, Phys. Rev. Lett., 2010, 105, 1681032 CrossRef.
- F. Peruani, A. Deutsch and M. Bär, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 030904 CrossRef.
- M. Cates, D. Marenduzzo, I. Pagonabarrga and J. Tailleur, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11715–11720 CrossRef CAS.
- I. Buttinoni, J. Bialké, F. Kümmel, H. Löwen, C. Bechinger and T. Speck, Phys. Rev. Lett., 2013, 110, 238301 CrossRef.
- W. Paxton, K. Kistler, C. Olmeda, A. Sen, S. K. S. Angelo, Y. Cao, T. Mallouk, P. Lammert and V. Crespi, J. Am. Chem. Soc., 2004, 126, 13424–13431 CrossRef CAS.
- R. Dreyfus, J. Baudry, M. Roper, M. Fermigier, H. Stone and J. Bibette, Nature, 2005, 437, 862–865 CrossRef CAS.
- J. Howse, R. Jones, A. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef.
- J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 105, 088304 CrossRef.
- S. Ebbens and J. Howse, Soft Matter, 2010, 6, 726–738 RSC.
- L. Giomi, N. Hawley-Weld and L. Mahadevan, Proc. R. Soc. A, 2013, 469, 20120637 Search PubMed.
- C. Bechinger, R. D. Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- S. Ebbens, Curr. Opin. Colloid Interface Sci., 2016, 21, 14–23 CrossRef CAS.
- A. Snezhko and I. Aranson, Nat. Mater., 2011, 10, 698–703 CrossRef CAS.
- A. Demirörs, F. Eichenseher, M. Loessner and A. Studart, Nat. Commun., 2017, 8, 1872 CrossRef.
- J. Gómez-Solano, S. Samin, C. Lozano, P. Ruedas-Batuecas, R. van Roij and C. Bechinger, Sci. Rep., 2017, 7, 14891 CrossRef.
- M. Popescu, M. Tasinkevych and S. Dietrich, Europhys. Lett., 2011, 95, 28004 CrossRef.
- R. Golestanian, T. Liverpool and A. Ajdari, Phys. Rev. Lett., 2005, 94, 220801 CrossRef.
- R. Golestanian, T. Liverpool and A. Ajdari, New J. Phys., 2007, 9, 126 CrossRef.
- M. Popescu, W. Uspal and S. Dietrich, Eur. Phys. J.: Spec. Top., 2016, 225, 2189–2206 CAS.
- G. Rückner and R. Kapral, Phys. Rev. Lett., 2007, 98, 150603 CrossRef.
- I. Theurkauff, C. Cottin-Bizonne, J. Palacci, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2012, 108, 268303 CrossRef CAS.
- J. Palacci, S. Sacanna, A. Steinberg, D. Pine and P. Chaikin, Science, 2013, 339, 936–940 CrossRef CAS.
- F. Ginot, I. Theurkauff, F. Detcheverry, C. Ybert and C. Cottin-Bizonne, Nat. Commun., 2018, 9, 696 CrossRef CAS.
- C. Maggi, J. Simmechen, F. Saglimbeni, M. Dipalo, F. D. Angelis, S. Sánchez and R. D. Leonardo, Small, 2015, 12, 446–451 CrossRef.
- R. Benzi, S. Succi and M. Vergassola, Phys. Rep., 1992, 222, 145–197 CrossRef.
-
D. Wolf-Gladrow, Lattice-gas cellular automata and lattice Boltzmann models: an introduction, Springer, 2000 Search PubMed.
- J.-C. Desplat, I. Pagonabarraga and P. Bladon, Comput. Phys. Commun., 2001, 134, 273–290 CrossRef CAS.
- K. Stratford, R. Adhikari, I. Pagonabarraga and J.-C. Desplat, J. Stat. Phys., 2005, 121, 163–178 CrossRef.
- K. Stratford and I. Pagonabarraga, Comput. Math. Appl., 2008, 55, 1585–1593 CrossRef.
- M. Swift, E. Orlandini, W. Osborn and J. Yeomans, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 54, 5041–5052 CrossRef CAS.
- V. Kendon, M. Cates, I. Pagonabarraga, J.-C. Desplat and P. Bladon, J. Fluid Mech., 2001, 440, 147–203 CrossRef CAS.
- J. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- F. Sciortino, A. Giacometti and G. Pastore, Phys. Rev. Lett., 2009, 103, 237801 CrossRef.
- A. Walther and A. Müller, Soft Matter, 2008, 4, 663–668 RSC.
- M. Popescu, S. Dietrich, M. Tasinkevych and J. Ralston, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 31, 351–367 CrossRef CAS.
- A. Ladd, J. Fluid Mech., 1994, 271, 285–309 CrossRef CAS.
- A. Ladd, J. Fluid Mech., 1994, 271, 311–339 CrossRef CAS.
- C. Aidun, Y. Lu and E.-J. Ding, J. Fluid Mech., 1998, 373, 287–311 CrossRef CAS.
- N.-Q. Nguyen and A. Ladd, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 046708 CrossRef.
-
F. Janoschek, J. Harting and F. Toschi, 2013, arXiv:1308.6482.
- S. Sánchez, L. Soler and J. Katuri, Angew. Chem., Int. Ed., 2014, 53, 2–33 CrossRef.
- L. Palacios, J. Katuri, I. Pagonabarraga and S. Sánchez, Soft Matter, 2019, 15, 6581–6588 RSC.
- Y. Fily and M. Marchetti, Phys. Rev. Lett., 2012, 108, 235702 CrossRef.
- G. Redner, M. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef.
- O. Pohl and H. Stark, Phys. Rev. Lett., 2014, 112, 238303 CrossRef.
- R. Soto and R. Golestanian, Phys. Rev. Lett., 2014, 112, 068301 CrossRef.
- F. Alarcón, C. Valeriani and I. Pagonabarraga, Soft Matter, 2017, 13, 814–826 RSC.
- G. Voronoi, J. Reine Angew. Math., 1908, 133, 97–102 Search PubMed.
- C. Rycroft, G. Grest, J. Landry and M. Bazant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021306 CrossRef.
- B. Liebchen, D. Marenduzzo, I. Pagonabarraga and M. Cates, Phys. Rev. Lett., 2015, 115, 258301 CrossRef.
- O. Pohl and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 93 CrossRef.
- T. Witten and L. Sander, Phys. Rev. Lett., 1981, 47, 140–1403 CrossRef.
- P. Meakin, Phys. Rev. Lett., 1983, 51, 1119–1122 CrossRef.
- M. Popescu, W. Uspal, Z. Eskandari, M. Tasinkevych and S. Dietrich, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 145 CrossRef CAS.
- P. Meakin, Rev. Geophys., 1991, 29, 317–354 CrossRef.
-
J.-P. Hansen and I. McDonald, Theory of simple liquids, Elsevier, 3rd edn, 2006 Search PubMed.
- A. Zöttl and H. Stark, Phys. Rev. Lett., 2014, 112, 118101 CrossRef.
- S. Das, A. Garg, A. Campbell, J. Howse, A. Sen, D. Velegol, R. Golestanian and S. Ebben, Nat. Commun., 2015, 6, 8999 CrossRef CAS.
- W. Uspal, M. Popescu, S. Dietrich and M. Tasinkevych, Soft Matter, 2015, 11, 434–438 RSC.
- A. Mozaffari, N. Sharifi-Mood, J. Koplik and C. Maldarelli, Phys. Fluids, 2016, 28, 053107 CrossRef.
- S. Saha, R. Golestanian and S. Ramaswamy, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 062316 CrossRef.
- T. Bickel, G. Zecua and A. Wurger, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 050303(R) CrossRef.
- B. Leibchen, D. Marenduzzo and M. Cates, Phys. Rev. Lett., 2017, 118, 268001 CrossRef.
-
S. Succi, The lattice Boltzmann equation for complex states of flowing matter, Oxford University Press, 2018 Search PubMed.
- P. Bhatnagar, E. Gross and M. Krook, Phys. Rev., 1954, 94, 511–525 CrossRef CAS.
-
T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva and E. Viggen, The lattice Boltzmann method: principles and practice, Springer, 2017 Search PubMed.
- J. Brady and G. Bossis, Annu. Rev. Fluid Mech., 1988, 20, 111–157 CrossRef.
- E. Yariv, Phys. Rev. Fluids, 2016, 1, 032101(R) CrossRef.
- A. Varma, T. Montenegro-Johnson and S. Michelin, Soft Matter, 2018, 14, 7155–7173 RSC.
- K. Binder and D. Stauffer, Phys. Rev. Lett., 1974, 33, 1006–1009 CrossRef.
Footnotes |
| † We follow the standard procedure of embedding each particle in a d-dimensional cell whose i-th edge (face) is set to be equally distant from the reference particle and its i-th nearest neighbour. |
| ‡ We set such cutoff to the value of Λ = 2R + h, h being the soft-sphere range of interaction (see Appendix). |
| § In principle there can be a dependence on μ also of the fractal dimension df; we assume here, however, that the change in μ affects only the characteristic cluster size and not its “compactness” (or fractality). |
| ¶ lj is a dummy index, in the sense that it is slaved to j. We introduced it just to clarify that it runs on a different set of possible values (the lattice velocity set, i.e. lj = 1,…, 18), whereas j runs over the number of links around the particles (j = 1,…, Nlinks), but for each link j there is only one lj. In other words, it represents a sort of map that associates a given link to a certain lattice velocity vector. |
|| The components are given with respect to the reference system constituted by the particle symmetry axis ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) and two directions orthogonal to it, that, without loss of generality, can be identified with z, and (x, y), respectively. and two directions orthogonal to it, that, without loss of generality, can be identified with z, and (x, y), respectively. |
| ** It affects it, of course, indirectly, since the dynamics of C(x,t) differs. |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab and
Ignacio
Pagonabarraga
*ab and
Ignacio
Pagonabarraga
 cde
cde
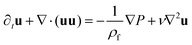
![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) C − kdC,
C − kdC,![[scr Q, script letter Q]](https://www.rsc.org/images/entities/char_e530.gif) C is a source field that represents the production of solute by the colloidal activity and it is localised at particle surfaces, i.e. it has the form
C is a source field that represents the production of solute by the colloidal activity and it is localised at particle surfaces, i.e. it has the form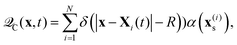
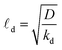 ). The velocities attained in our simulations are such that the typical particle Reynolds Re = VpR/ν and Péclet Pe = VpR/D numbers are always smaller than 10−1 (Vp is the self-propulsion speed), thus making the advection terms in eqn (1) and (2) negligible. The fluid is confined along the z-direction by two parallel walls, at which a no-slip boundary condition is imposed on the velocity field and a zero-flux condition applies for the equation for C. Periodic boundary conditions apply in the x and y directions. The boundary conditions at the particle surfaces need a deeper description that will be provided hereafter.
). The velocities attained in our simulations are such that the typical particle Reynolds Re = VpR/ν and Péclet Pe = VpR/D numbers are always smaller than 10−1 (Vp is the self-propulsion speed), thus making the advection terms in eqn (1) and (2) negligible. The fluid is confined along the z-direction by two parallel walls, at which a no-slip boundary condition is imposed on the velocity field and a zero-flux condition applies for the equation for C. Periodic boundary conditions apply in the x and y directions. The boundary conditions at the particle surfaces need a deeper description that will be provided hereafter.![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ⊗
⊗ ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) )·∇C,
)·∇C,![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) is the normal to the surface in xs and μ(xs) is the phoretic mobility, xs ∈ Σ, which contains the molecular details of the colloid–solute interaction. For uniform phoretic mobility μ(xs) ≡ μ0, particles gain a net propulsion velocity Vp ∼ −μ0∇C, i.e. they perform positive diffusiophoresis for negative μ0 (“chemoattractive” colloids) and negative diffusiophoresis for positive μ0 (“chemorepulsive” colloids).
is the normal to the surface in xs and μ(xs) is the phoretic mobility, xs ∈ Σ, which contains the molecular details of the colloid–solute interaction. For uniform phoretic mobility μ(xs) ≡ μ0, particles gain a net propulsion velocity Vp ∼ −μ0∇C, i.e. they perform positive diffusiophoresis for negative μ0 (“chemoattractive” colloids) and negative diffusiophoresis for positive μ0 (“chemorepulsive” colloids).
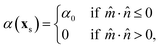
![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) being the particle characteristic unit vector (see the sketch in Fig. 1). An isolated free Janus SPC with the activity profile (5) and uniform phoretic mobility μ0 performs a rectilinear motion with constant speed Vp = |μ0|α0/(4D).22,23,40
being the particle characteristic unit vector (see the sketch in Fig. 1). An isolated free Janus SPC with the activity profile (5) and uniform phoretic mobility μ0 performs a rectilinear motion with constant speed Vp = |μ0|α0/(4D).22,23,40
 . The boundary condition for the velocity field at the particle surfaces is implemented via the bounce-back-on-links scheme for LB probability densities.41–44 Details of the method and on how to introduce in it the concentration-dependent effective slip velocity (4) are given in the Appendix.
. The boundary condition for the velocity field at the particle surfaces is implemented via the bounce-back-on-links scheme for LB probability densities.41–44 Details of the method and on how to introduce in it the concentration-dependent effective slip velocity (4) are given in the Appendix.
![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) (i) and angular velocity Ω(i), is described by the following equations of motion:
(i) and angular velocity Ω(i), is described by the following equations of motion: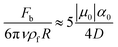 ). A soft-core particle–particle repulsion is introduced to prevent overlapping (further details on the treatment of close-to-contact particles are provided in the Appendix).
). A soft-core particle–particle repulsion is introduced to prevent overlapping (further details on the treatment of close-to-contact particles are provided in the Appendix).
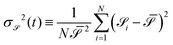 (normalised by the square of the mean value
(normalised by the square of the mean value 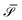 ) turns out to be a good indicator to distinguish the two types of dynamics. In the top inset of Fig. 2 we plot σ
) turns out to be a good indicator to distinguish the two types of dynamics. In the top inset of Fig. 2 we plot σ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) 2(t), as a function of time, for two cases with different sign of the phoretic mobility. In the attractive case, μ < 0, cluster formation induces the appearance of very small (and large) cells and, hence, the surface fluctuations grow and eventually saturate at long times. For positive μ, instead, colloids repel each other and tend to reach an optimal covering of the space, implying that σ
2(t), as a function of time, for two cases with different sign of the phoretic mobility. In the attractive case, μ < 0, cluster formation induces the appearance of very small (and large) cells and, hence, the surface fluctuations grow and eventually saturate at long times. For positive μ, instead, colloids repel each other and tend to reach an optimal covering of the space, implying that σ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) 2(t) attains a (lower) value which remains constant in time. Correspondingly, the dependence of
2(t) attains a (lower) value which remains constant in time. Correspondingly, the dependence of 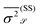 (the time average of
(the time average of 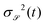 over the steady state) on μ discriminates between the two regimes: it is high for negatively large μ, decreases as μ approaches zero and then remains low and constant for μ > 0.
over the steady state) on μ discriminates between the two regimes: it is high for negatively large μ, decreases as μ approaches zero and then remains low and constant for μ > 0.![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (n) ∝ e−n/nc, over a wide range of sizes n.
(n) ∝ e−n/nc, over a wide range of sizes n.
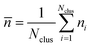 increase linearly with |μ| (see the inset of Fig. 3), hence with the velocity of an isolated particle, in agreement with experimental and numerical observations.9,26,50 The global attractor for the SPC dynamics is a set
increase linearly with |μ| (see the inset of Fig. 3), hence with the velocity of an isolated particle, in agreement with experimental and numerical observations.9,26,50 The global attractor for the SPC dynamics is a set![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) i is the region of plane occupied by the i-th cluster of area
i is the region of plane occupied by the i-th cluster of area ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) i and containing ni SPCs. Correspondingly, the colloid number density reads
i and containing ni SPCs. Correspondingly, the colloid number density reads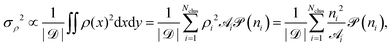
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) | is the measure of the whole plane. The number of particles in a cluster n is known to scale with the cluster gyration radius Rg as
| is the measure of the whole plane. The number of particles in a cluster n is known to scale with the cluster gyration radius Rg as 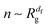 , df being the fractal (Hausdorff) dimension;57,58ni and
, df being the fractal (Hausdorff) dimension;57,58ni and ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) i are, then, related by
i are, then, related by ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) i ∼ Rg2 ∼ n2/df. Plugging the latter relation and
i ∼ Rg2 ∼ n2/df. Plugging the latter relation and ![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) (n) ∼ e−n/nc into (9), and approximating the sum with the integral, we finally get:
(n) ∼ e−n/nc into (9), and approximating the sum with the integral, we finally get: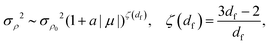

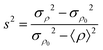 , vs. the coupling strength |μ| from LB (squares) and the phenomenological derivation (dashed line), eqn (10), with fractal dimension df = 1.4, as measured in the simulations. Inset: Mean gyration radius of clusters vs. number of particles with (
, vs. the coupling strength |μ| from LB (squares) and the phenomenological derivation (dashed line), eqn (10), with fractal dimension df = 1.4, as measured in the simulations. Inset: Mean gyration radius of clusters vs. number of particles with ( ) and without (
) and without ( ) HI. The two dashed lines represent the power law Rg ∼ n1/df (df = 1.8 for no-HI).
) HI. The two dashed lines represent the power law Rg ∼ n1/df (df = 1.8 for no-HI).![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t), with and without HI (no-HI). In the no-HI case, clusters coarsen, with
(t), with and without HI (no-HI). In the no-HI case, clusters coarsen, with ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t) growing in time as t1/2 (top right inset), as for domains in the spinodal decomposition of fluid mixtures in two dimensions.75 The same behaviour (
(t) growing in time as t1/2 (top right inset), as for domains in the spinodal decomposition of fluid mixtures in two dimensions.75 The same behaviour (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t) ∼ t1/2) has been observed, indeed, in simulations of self-propelled Brownian particles interacting via a shifted-truncated Lennard–Jones potential.49,52 With HI, instead, coarsening is arrested, as observed in experiments.26 Simulations have suggested that in suspensions of attractive squirmers the emergence of continuous or arrested coarsening is selected depending on the form and intensity of the active stress (the coefficient B2 in the squirmer terminology);52 self-phoretic Janus colloids behave, in this respect, as squirmers with B2 = 0,59 for which, indeed, arrested coarsening was observed.52 Due to the non stationarity of the coarsening process, steady state PDFs of cluster sizes cannot be computed in the no-HI simulations. Nevertheless, we observe that istantaneous cluster size distributions F(n,t) (i.e. the number of clusters of size n at time t) tend to assume a self-preserving scaling form F(n,t) ∼ n−2f(n/
(t) ∼ t1/2) has been observed, indeed, in simulations of self-propelled Brownian particles interacting via a shifted-truncated Lennard–Jones potential.49,52 With HI, instead, coarsening is arrested, as observed in experiments.26 Simulations have suggested that in suspensions of attractive squirmers the emergence of continuous or arrested coarsening is selected depending on the form and intensity of the active stress (the coefficient B2 in the squirmer terminology);52 self-phoretic Janus colloids behave, in this respect, as squirmers with B2 = 0,59 for which, indeed, arrested coarsening was observed.52 Due to the non stationarity of the coarsening process, steady state PDFs of cluster sizes cannot be computed in the no-HI simulations. Nevertheless, we observe that istantaneous cluster size distributions F(n,t) (i.e. the number of clusters of size n at time t) tend to assume a self-preserving scaling form F(n,t) ∼ n−2f(n/![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t)), as it happens in the classical colloidal aggregation phenomenon for mass-conserving systems.60 This is shown in the top left inset of Fig. 5, where we plot n2F(n,t) vs. n/
(t)), as it happens in the classical colloidal aggregation phenomenon for mass-conserving systems.60 This is shown in the top left inset of Fig. 5, where we plot n2F(n,t) vs. n/![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t) and see that all sets of points for different t's in the coarsening regime where
(t) and see that all sets of points for different t's in the coarsening regime where ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ∼ t1/2, within error bars, collapse onto each other. The statement on the different dynamics, with and without HI, is corroborated by the inspection of the radial distribution functions (RDFs)61 (indicated as gHI(r,t) and gno-HI(r,t), respectively), defined as the probability of finding a particle between the distances r and r + dr from a reference particle (and averaged over all particles), i.e.
∼ t1/2, within error bars, collapse onto each other. The statement on the different dynamics, with and without HI, is corroborated by the inspection of the radial distribution functions (RDFs)61 (indicated as gHI(r,t) and gno-HI(r,t), respectively), defined as the probability of finding a particle between the distances r and r + dr from a reference particle (and averaged over all particles), i.e.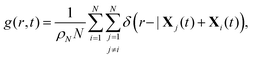
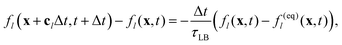
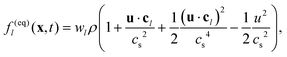
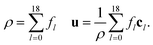
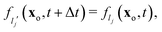
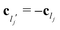 and flj is the post-collisional distribution. However, the boundary velocity at a given location on the particle surface will be in general non-zero (due to slip and/or particle motion). Rule (15) must be, then, modified accordingly as:41,42,44
and flj is the post-collisional distribution. However, the boundary velocity at a given location on the particle surface will be in general non-zero (due to slip and/or particle motion). Rule (15) must be, then, modified accordingly as:41,42,44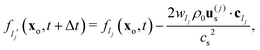
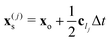 (the position of the boundary node is assumed to be in the middle of the link), depends on the particle linear V and angular Ω velocities and on the (local) slip velocity v(j)s as
(the position of the boundary node is assumed to be in the middle of the link), depends on the particle linear V and angular Ω velocities and on the (local) slip velocity v(j)s as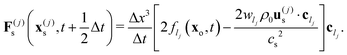
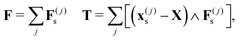
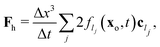
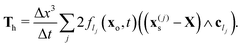
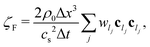
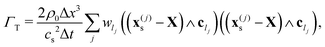
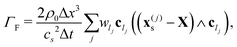
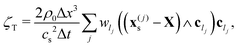
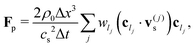
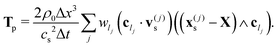
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) < 0},
< 0},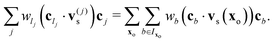
![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) (defined in the main text). For
(defined in the main text). For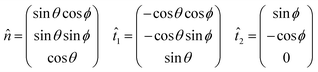
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) )
)![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) + (cb·
+ (cb·![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 1)
1)![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 1 + (cb·
1 + (cb·![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 2)
2)![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 2 obviously holds for the lattice velocities, with b ∈ I(θ,ϕ) (we will use for xo its spherical coordinates from now on). We recall that the effective slip velocity, vs ∝ (1 −
2 obviously holds for the lattice velocities, with b ∈ I(θ,ϕ) (we will use for xo its spherical coordinates from now on). We recall that the effective slip velocity, vs ∝ (1 − ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ⊗
⊗ ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) )∇C, is, by definition, tangent to the surface, therefore:
)∇C, is, by definition, tangent to the surface, therefore:![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 1) + vs,2(θ)(cb·
1) + vs,2(θ)(cb·![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) 2),
2),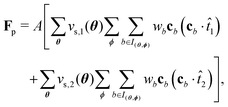
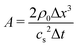 . Let us note, now, a property of the set of links: given xo = (θ, ϕ) on the sphere, and its associated I(θ,ϕ), there will be a xo′ = (θ′, ϕ′) (with θ′ = θ′ and ϕ′ = ϕ + π) such that for every b ∈ I(θ,ϕ) there exists a b′ ∈ I(θ′,ϕ′) fulfilling
. Let us note, now, a property of the set of links: given xo = (θ, ϕ) on the sphere, and its associated I(θ,ϕ), there will be a xo′ = (θ′, ϕ′) (with θ′ = θ′ and ϕ′ = ϕ + π) such that for every b ∈ I(θ,ϕ) there exists a b′ ∈ I(θ′,ϕ′) fulfilling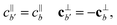
![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) . Such property follows from the definition of I(θ,ϕ), eqn (30): since, by symmetry, upon the shift ϕ → ϕ + π the normal to the surface
. Such property follows from the definition of I(θ,ϕ), eqn (30): since, by symmetry, upon the shift ϕ → ϕ + π the normal to the surface ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) changes as n′‖ = n‖ and n′⊥ = −n⊥ (see (32)), in order to preserve the condition cb′·
changes as n′‖ = n‖ and n′⊥ = −n⊥ (see (32)), in order to preserve the condition cb′·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ′ < 0, the velocities have to transform as in (35). Analogously,
′ < 0, the velocities have to transform as in (35). Analogously, 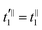 ,
, 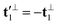 and t2′ = −t2. Therefore, in (34), upon summing on ϕ (i.e. on nodes all around the particle at a fixed latitude θ), only the component parallel to
and t2′ = −t2. Therefore, in (34), upon summing on ϕ (i.e. on nodes all around the particle at a fixed latitude θ), only the component parallel to ![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) survives and reduces to:
survives and reduces to: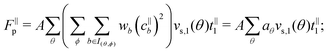
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, such that the sum in (36) approximates the integral over the polar angle. So, basically, for a solute distribution around the particle which is axisymmetric, the bounce-back-on-links algorithm yields a phoretic force which is proportional to the surface integral of the effective slip velocity, i.e.:
θ, such that the sum in (36) approximates the integral over the polar angle. So, basically, for a solute distribution around the particle which is axisymmetric, the bounce-back-on-links algorithm yields a phoretic force which is proportional to the surface integral of the effective slip velocity, i.e.: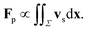
![[F with combining tilde]](https://www.rsc.org/images/entities/b_char_0046_0303.gif) p ∝ ∇C|X; the latter represents a sort of chemotactic drift towards regions of high or low solute, depending on the sign of the phoretic mobility.
p ∝ ∇C|X; the latter represents a sort of chemotactic drift towards regions of high or low solute, depending on the sign of the phoretic mobility.
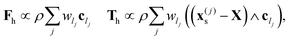
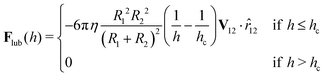
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 12 is the particle centre–centre distance vector and h = r12 − R1 − R2; the cutoff distance is chosen to be hc = 0.67 lattice units, which is an optimal value to get good agreement with lubrication theory calculations, as shown in ref. 44. Lubrication forces may not be enough, though, to prevent particle overlap (as recognised also in ref. 73 and 74), especially when the particle density is large (even just locally, as, for instance, inside clusters). Therefore, we add also a short-range soft-sphere repulsion modelled by the force Fss ∝ ((hssc/h)3 − 1)
12 is the particle centre–centre distance vector and h = r12 − R1 − R2; the cutoff distance is chosen to be hc = 0.67 lattice units, which is an optimal value to get good agreement with lubrication theory calculations, as shown in ref. 44. Lubrication forces may not be enough, though, to prevent particle overlap (as recognised also in ref. 73 and 74), especially when the particle density is large (even just locally, as, for instance, inside clusters). Therefore, we add also a short-range soft-sphere repulsion modelled by the force Fss ∝ ((hssc/h)3 − 1)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) 12, with cutoff (coinciding with the soft-sphere radius) hssc = 2hc.
12, with cutoff (coinciding with the soft-sphere radius) hssc = 2hc.
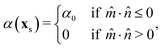
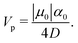
![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) (0) = (0, 0, 1): the plot suggests that indeed the particle moves in a straight line, with director (0, 0, 1), at a constant speed (the oscillations are due to recomputation of the set of links, hence of the discretised surface, as the particle moves across the lattice), albeit about half of the theoretical value. Such a quantitative disagreement is not too surprising, given the small size of the particle. The quality of the numerical result improves, in fact, significantly with the resolution. This is shown in Fig. 8, where we plot the steady state z-component of the velocity, Vz, normalised by the expected Vp, eqn (41), as a function of the radius (the ratio R/L ≈ 0.08 is kept fixed over various runs). We see that the numerics (red dots) approximate better and better the theoretical prediction as the particle radius is increased, and eventually tend to converge to the value of ∼1.1 (i.e. the measured Vz is about 10% larger than Vp). This residual mismatch might be due to the fact that, as R grows, the Péclet number, Pe, approaches unity, whereas the prediction (41) is valid when Pe is strictly zero. For a smaller Pe ≈ 0.1 we find, indeed, a better agreement for the largest radius (blue square in Fig. 8), for which Vz/Vp ≈ 1.04.
(0) = (0, 0, 1): the plot suggests that indeed the particle moves in a straight line, with director (0, 0, 1), at a constant speed (the oscillations are due to recomputation of the set of links, hence of the discretised surface, as the particle moves across the lattice), albeit about half of the theoretical value. Such a quantitative disagreement is not too surprising, given the small size of the particle. The quality of the numerical result improves, in fact, significantly with the resolution. This is shown in Fig. 8, where we plot the steady state z-component of the velocity, Vz, normalised by the expected Vp, eqn (41), as a function of the radius (the ratio R/L ≈ 0.08 is kept fixed over various runs). We see that the numerics (red dots) approximate better and better the theoretical prediction as the particle radius is increased, and eventually tend to converge to the value of ∼1.1 (i.e. the measured Vz is about 10% larger than Vp). This residual mismatch might be due to the fact that, as R grows, the Péclet number, Pe, approaches unity, whereas the prediction (41) is valid when Pe is strictly zero. For a smaller Pe ≈ 0.1 we find, indeed, a better agreement for the largest radius (blue square in Fig. 8), for which Vz/Vp ≈ 1.04.
![[m with combining circumflex]](https://www.rsc.org/images/entities/i_char_006d_0302.gif) and two directions orthogonal to it, that, without loss of generality, can be identified with z, and (x, y), respectively.
and two directions orthogonal to it, that, without loss of generality, can be identified with z, and (x, y), respectively.