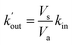Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Underlying mechanisms in microbial solar cells: how modeling can help†
Léna
Beauzamy
*a,
Frédéric
Lemaître
 a and
Julien
Derr
a and
Julien
Derr
 *b
*b
aPASTEUR, Département de Chimie, École Normale Supérieure, PSL University, Sorbonne Université, CNRS, 75005 Paris, France. E-mail: lena.beauzamy@gmail.com
bLaboratoire “Matière et Systèmes Complexes” (MSC), Université de Paris, UMR 7057 CNRS, 75013 Paris, France. E-mail: julien.derr@u-paris.fr
First published on 30th September 2020
Abstract
Solar cells using living micro-organisms often require the help of a redox mediator, a small molecule which carries the electrons from inside the organisms to the electrode. Ideally the mediator is able to cross biological membranes to access the source of electrons, without causing damage. The diffusion rate across membranes, reduction rate inside the micro-organism, and the absence of toxicity are key parameters. Here we use modeling, fit of fluorescence and electrochemical experimental data, and simulation to quantify the reaction rates of the main processes involved in the case of the micro-alga Chlamydomonas reinhardtii, in interaction with the redox mediator 2,6-dichloro-1,4-benzoquinone. We found that the photo-induced reduction inside algae is not the limiting process, but in contrast 10 times faster than the process of electron consumption at the electrode. The maximum current limitation is due to the slow outflow of the mediator out of algae: the molecule has a tendency to get trapped inside because of its lipophilicity. Additionally, it has an important toxicity, and we find that its mode of action is likely to cause a quasi-exponential decay of the number of active photosynthetic chains. This is consistent with known side effects of quinones (oxidative stress, electrophilic behaviour).
Introduction
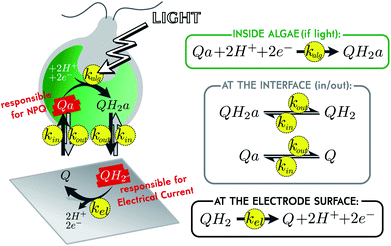
In the current energetic landscape, new energy sources, especially eco-friendly ones, are welcome. This is why oxygenic photosynthesis has been extensively studied as a promising way to produce bioelectricity for more than ten years. Many strategies rely on the use of the photosynthetic chain as a light converter in terms of isolated photosystems, thylakoid membranes or photosynthetic organisms.1–8 In this context, microbial solar cells are promising alternatives, especially because they involve living photosynthetic organisms, which have been naturally selected for their ability to harvest solar energy. Moreover, using living organisms is expected to provide robust biosystems for long-term approaches in order to reach photovoltaics performances in the future.9 In this case, one of the key points to enhance the electricity production is the use of a redox (soluble or immobilized) mediator to shuttle the photosynthetic electrons from the photosynthetic organism to the collecting electrode.5,6 To date, one of the most used exogenous redox carriers belongs to the family of quinones, because it may compete with endogenous plastoquinones involved in the electron transfer steps within the thylakoid membranes.10,11 It thus raises the question of the structure–activity relationship of quinones, i.e. the compromise between an electron harvesting behavior and no unwanted damage. In this way, we previously focused our work on the control case composed of the living micro-alga Chlamydomonas reinhardtii, in interaction with the redox mediator 2,6-dichloro-1,4-benzoquinone (shortly called “Q” in this document).12–14 This small molecule diffuses through biological membranes and can be reduced inside an illuminated alga, when in contact with a photosynthetic chain.15,16 The reduced molecule (shortly called “QH2”) eventually diffuses back to the solution and is re-oxidized at the surface of a polarized electrode, producing an electrical current (see Fig. 1). As mentioned above, such a system could theoretically work by itself for long periods of time, but there is currently a major limitation: the toxicity of the mediator.17,18 Efficient molecules are indeed toxic for living organisms, which may result in a drastic drop of current in less than an hour.19 To understand the mechanism of this toxicity is crucial, for being able to further develop sustainable microbial solar cells. In order to better analyze this lack of performances, we recently implemented a fluoroelectrochemical coupling to correlate the production of current and the status of photosynthetic chains. As a result, very relevant complementary data were recorded like the photochemical PSII yield or the “non-photochemical quenching” (NPQ, that reflects thermal losses, in opposition to the electron transfer along the photosynthetic chain which is sometimes called “photochemical quenching”). In this paper, we wish to use such coupled data to investigate and model the most commonly supposed mechanisms related to the current drop (quinones sequestered within cell compartments, photosynthetic chain degradation and screening-like effect due to quinone quenching). These modeling studies will help us quantify the kinetics of the different steps involved during the production of current (mediator diffusion, oxidation at the electrode surface, quinone reduction by the photosynthetic chain) and give a first overview of the possible reasons of current evolution in such biophotoelectrochemical systems.Modeling of the system
A previous study demonstrated how to access, by coupling chronoamperometry with chlorophyll fluorescence measurements, information about the metabolic state of algae during electrical current delivery.19 One of these additional pieces of information is the level of quenching experienced by the algal chlorophylls. A redox mediator such as Q indeed has quenching properties, and the NPQ it produces on chlorophylls can be monitored over time by fluorescence.15,20,21 Remarkably, the oxidized form Q is a quencher, but not its reduced form QH2. Inside algae Q is responsible for NPQ. Once reduced in QH2 and after diffusion out of the alga, it is responsible for electrical current (see Fig. 1). Both these signals can be monitored over time. By fitting such coupled data with the help of a model, we can extract the reaction rates of the different processes involved. A simple kinetic model of the system is presented in Fig. 1. All reactions are assumed to be first order, with associated reaction rates k. For inward and outward transport (kin and kout), the validity of this hypothesis relies on the assumption that the traveling molecules in the membrane correspond to a single transition state.22 Regarding the mediator molecule, we use the subscript “a” (which stands for “algae”) to differentiate molecules located inside algae, from those located outside (in the bulk solution). This highlights the phenomenon of diffusion across biological membranes, for which we will compare efficiency with the two other main phenomena. First of all, the reduction inside illuminated algae is characterized by its apparent reaction rate kalg that takes into account the ability of the photosynthetic chain to be oxidized by the mediator (the value of kalg depends on the available catalytic PSII sites, see below). Secondly, it is worth mentioning that the biophotoelectrochemical system considered here corresponds to electrolysis conditions, i.e. a quite large collecting electrode (A ∼ 1 cm2) for a low volume (2 mL) under continuous stirring.19 In this specific case, the re-oxidation at the electrode surface can be characterized by its reaction rate kel.17,23Transport across membranes is due to concentration gradients, but to consider more complex phenomena than just pure diffusion in the outer membrane, we assume specifically that kin and kout are a priori independent (which would not be the case if there was pure diffusion, see ESI eqn (11)†). This gives the model the possibility to take into account the lipophilic behavior of the mediator. If lipophilic, we expect the molecule to more easily enter algae, than leave them, because algae are rich in internal lipid membranes. But we do not discriminate between Q and QH2 in terms of lipophilicity (they both have the same set of kin and kout values). This is a reasonable assumption regarding the values of the partition coefficient “P”. P is the concentration ratio of a given molecule in a mixture of immiscible hydrophobic solvent (1-octanol for instance) and water. It somehow reflects the lipophilicity of the molecule, and experimental or calculated values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P for Q and QH2 are in the same order of magnitude (see ESI†).24
P for Q and QH2 are in the same order of magnitude (see ESI†).24
Taking into account the balance equations of Fig. 1, one can write the time evolution equations for the concentrations of the four species:
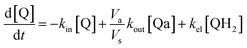 | (1) |
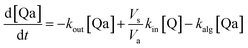 | (2) |
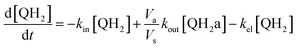 | (3) |
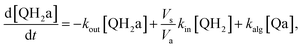 | (4) |
This system of four equations (1 to 4) enables us to solve for time dependent concentrations. In particular, it leads to the knowledge of the photocurrent given by
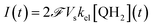 | (5) |
where 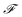 is the Faraday constant.
is the Faraday constant.
Experimental data
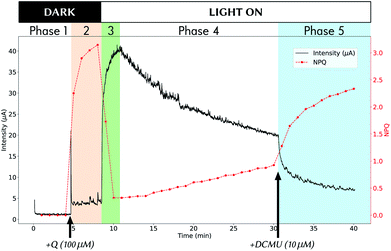
Fig. 2 shows an example of experimental data obtained during a 40 min experiment. Methods for obtaining such coupled data are detailed in a previous study.19 The experiment can be divided into 5 phases:• Phase 1 from t = 0 to t = 4.5 min: the experiment starts in the dark, with only algae in the electrochemical cell.
• Phase 2 (orange background) from t = 4.5 to t = 8.5 min: still in the dark, the mediator Q is added (100% of oxidized form) at t = 4.5 and diffuses inside algae, leading to NPQ rise. Only negligible current is detected at this stage (“dark current”).
• Phase 3 (green) from t = 8.5 to when the maximum current intensity is reached (∼11 min in Fig. 2): the light is switched ON at t = 8.5 min and we observe a rapid current rise accompanied by NPQ drastic drop, due to reduction of mediator molecules into their non-quencher QH2 form.
• Phase 4 from maximum current intensity to t = 30.5 min: the system is left evolving under light, and shows signs of “fatigue” imputed to mediator toxicity.
• Phase 5 (blue) from t = 30.5 min to the end of experiment: the photosynthesis is at arrest (here by adding DCMU which is an inhibitor of photosynthesis, but the same result is obtained by switching OFF the light), and the electrode slowly consumes already produced QH2 that exits algae.
Among these different phases we emphasize phases 2, 3 and 5. They are especially interesting because they represent specific conditions where our model can be simplified, and therefore the kinetic equations solved. During phase 2, by neglecting the residual “dark current”, we have a system only involving the oxidized form of the mediator, and therefore the NPQ rise shows the dynamics of its entry into algae. Phase 5 is also a simplified case because kalg = 0 due to the use of DCMU, but here both oxidized and reduced forms of the mediator are present. Phase 3 is a more complex case, but we can still neglect the effect of toxicity at this stage, at least for explaining the rapid changes observed.
Results and discussion
Reaction rate of diffusion across membranes: focus on phase 2
Phase 2 occurs in the dark, and therefore kalg = 0 (no photosynthesis). Since kalg = 0, no QH2 can be produced (except for the small “dark current” that we neglect here). Therefore, the observed NPQ rise is representative of Q diffusion dynamics alone: it consists of an exponential saturation with an effective rate K = kin + kout (see ESI† for details). NPQ is not strictly equal to the concentration of Q inside algae, but the two are proportional by a factor α. Overall the time increase of NPQ reads:| NPQ(t) = α × [Qa](t) = α × [Qa]∞ × (1 − e−Kt) | (6) |
| K = kin + kout = 2.1 × 10−2 ± 0.1 × 10−2 s−1 | (7) |
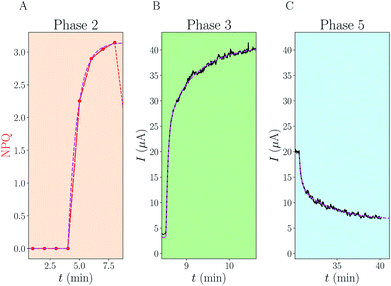 | ||
| Fig. 3 Analytical fits of experimental data. For each of the phases 2, 3 and 5 of Fig. 2, we have fitted the data (NPQ in red or electrical current in black) using analytical formulae derived in the ESI.† The fits are displayed using dotted magenta lines. (A) Phase 2: single exponential increase, with rate K. (C) Phase 5: sum of two exponentials with rate constants k+ and k−. (B) Phase 3: sum of three exponentials with rates combining K, k+, k− and kalg. The knowledge of (A) and (C) enables us to fit the last unknown kalg. | ||
Reaction rate of re-oxidation at the electrode: focus on phase 5
Because of photosynthesis arrest at t = 30.5 min, we also have kalg = 0 during phase 5. We observe the consumption of previously produced QH2. Because the dynamics of the current involves a true coupling between QH2 and QH2a concentrations, the dynamics is a superposition of two exponential decays: I(t) = c+e−k+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t + c−e−k−
t + c−e−k−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t. c+ and c− are constants linked to the boundary conditions, while k+ and k− are rate constants of these decays. The fast rate k+ is linked to the fast consumption of QH2 present in solution while the slow rate k− is mostly linked to the slow release of QH2a from algae. An example of data fitting is presented in Fig. 3C. We find that k+ ≈ kin + kout + kel and k− ≈ kout. The three pieces of information provided by the experimental values K, k+ and k− enable us to solve for the three unknowns kin, kout and kel. We provide in the SI the derivation as well as the exact formulation of the numerical system to solve eqn (S23)†. Applying this procedure to 4 experimental replicas gives:
t. c+ and c− are constants linked to the boundary conditions, while k+ and k− are rate constants of these decays. The fast rate k+ is linked to the fast consumption of QH2 present in solution while the slow rate k− is mostly linked to the slow release of QH2a from algae. An example of data fitting is presented in Fig. 3C. We find that k+ ≈ kin + kout + kel and k− ≈ kout. The three pieces of information provided by the experimental values K, k+ and k− enable us to solve for the three unknowns kin, kout and kel. We provide in the SI the derivation as well as the exact formulation of the numerical system to solve eqn (S23)†. Applying this procedure to 4 experimental replicas gives:| kin = 1.13 ± 0.32 × 10−2 s−1 | (8) |
| kout = 9.49 ± 0.9 × 10−3 s−1 | (9) |
| kel = 6.02 ± 0.85 × 10−2 s−1 | (10) |
As expected the kel value found is high, indicating that the re-oxidation process is faster than the diffusion across biological membranes. The ratio of kout to kin is interestingly low. Because the “out” volume (Vs) is 100 times bigger than the “in” volume (Va), we expect the 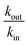 ratio to be 100 in the case of free diffusion across membranes. This is clearly not the case, as kout is even smaller than kin. This can be explained by a highly lipophilic behavior of the molecule, that tends to get trapped inside membranes. This is consistent with the quite high partition coefficient values for substituted methyl and chloroquinones (log
ratio to be 100 in the case of free diffusion across membranes. This is clearly not the case, as kout is even smaller than kin. This can be explained by a highly lipophilic behavior of the molecule, that tends to get trapped inside membranes. This is consistent with the quite high partition coefficient values for substituted methyl and chloroquinones (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ≥ 1; see ESI† and ref. 25), and especially for 2,6-DCBQ (log
P ≥ 1; see ESI† and ref. 25), and especially for 2,6-DCBQ (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 1.73). Such lipophilic behavior of the mediator plays an important role in the global shape of the experimental curves. As shown in Fig. 4E and F, simulations where kin and kout are chosen such as
P = 1.73). Such lipophilic behavior of the mediator plays an important role in the global shape of the experimental curves. As shown in Fig. 4E and F, simulations where kin and kout are chosen such as 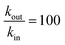 hardly resemble the experimental data.
hardly resemble the experimental data.
Reaction rate of photo-reduction inside algae: focus on phase 3
For phase 3, kalg is non zero. The time evolution of the system is more complex: it involves three different characteristic rate constants. We show in the ESI† the mathematical links between kalg and the three different rate constants observed. An example of fit is shown in Fig. 3B, and fitting the data over 4 replicas enables us to get a numerical value for kalg:| kalg = 0.63 ± 0.07 s−1 | (11) |
The kalg value is surprisingly 10 times bigger than kel, making the inner photo-reduction process the fastest occurring in the studied set-up. Overall the rate constants we estimate here depend on the experimental conditions, in particular kalg depends on parameters such as the light intensity or the algae concentration. This high value of kalg certainly plays an important role in the rapid current rise and NPQ decrease at the beginning of phase 3, but interestingly we show in ESI† that the fastest rate observed in the increase of intensity is mostly associated with the sum of the four rate constants kalg + kel + kin + kout.
Simulations
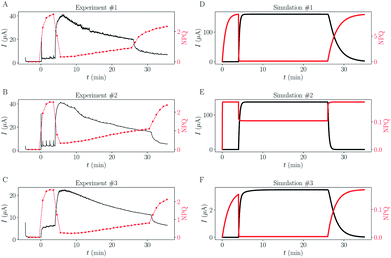
Rate constants deduced from the previous analytical fits allow us to run a numerical simulation of the experiment, using the model presented in Fig. 1. By changing the different rates and comparing the result of the simulation with experimental data we could gain a better understanding of the role of the different parameters in the global dynamics of the system. In this respect Fig. 4D shows the result of the simulation using the rate constants previously deduced, next to three experimental replicates (Fig. 4A–C), for comparison. Except for the slow current decrease and NPQ rise that we attribute to toxicity – for now absent from the model – the global shape of the experimental data is well reproduced. Interestingly, this is not true for simulations of cases where Q and QH2 are not lipophilic molecules (cases shown in Fig. 4E and F). For these simulations we changed the value of kout (Fig. 4E), or kin (Fig. 4F), such as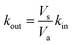 , which is expected in the case of free diffusion (balance of inward and outward diffusive fluxes, see ESI eqn (11).† In our experiments this prefactor is 100). Clearly, in the case of a higher kout (Fig. 4E), the simulation is non-realistic. All diffusion processes appear instantaneous, and the NPQ behavior, which drops experimentally almost to zero when the light is turned on, is especially not well reproduced in this case. This highlights the role of the mediator retention inside algae in the observed drastic drop of NPQ during the first minutes after turning on the light. In the second extreme case, when kin is lower (Fig. 4F), the global shape of the curves is not drastically changed, except for the NPQ rise in the dark, that does not have the time to reach its maximum plateau value before the light is turned on. Additionally to this shape discrepancy, both the current and NPQ intensities are at least one order of magnitude lower than the experimental data. Overall the good agreement between the simulation using previously deduced reaction rates and the experimental data, both in shape and intensities, validates our basic model and methodology.
, which is expected in the case of free diffusion (balance of inward and outward diffusive fluxes, see ESI eqn (11).† In our experiments this prefactor is 100). Clearly, in the case of a higher kout (Fig. 4E), the simulation is non-realistic. All diffusion processes appear instantaneous, and the NPQ behavior, which drops experimentally almost to zero when the light is turned on, is especially not well reproduced in this case. This highlights the role of the mediator retention inside algae in the observed drastic drop of NPQ during the first minutes after turning on the light. In the second extreme case, when kin is lower (Fig. 4F), the global shape of the curves is not drastically changed, except for the NPQ rise in the dark, that does not have the time to reach its maximum plateau value before the light is turned on. Additionally to this shape discrepancy, both the current and NPQ intensities are at least one order of magnitude lower than the experimental data. Overall the good agreement between the simulation using previously deduced reaction rates and the experimental data, both in shape and intensities, validates our basic model and methodology.
Discussion
If the simple model allows us to reproduce the global shape of the experimental data, it does not explain the observed slow current decrease under light. For this purpose we complexify the model by adding two possible mechanisms:• The trapping of mediator molecules in “inactive” cellular compartments (compartments invisible for the experimental set-up, such as mitochondrial membranes). This behavior was already observed in previous studies with a similar system where the added quinones are not all able to interact with the photosynthetic system.15 This will lead to an apparent decrease of the quantity of mediator molecules, and therefore cannot be distinguished in our model from the case of mediator degradation over time.
• The destruction of photosynthetic chains (PC) due to mediator toxicity. This is a common observation and assumption of the side effect of quinones in biological systems.26–28 In our case, it will reduce the photosynthetic activity of algae, and therefore kalg in the model.
Besides these two mechanisms, another case was also considered but rapidly discarded: the decrease of photosynthetic activity due to the quenching properties of Q (light-screening effect of the mediator). The mediator, by its quenching properties, could be responsible for the algae not having enough light to properly perform the photo-reduction of Q molecules. The mediator would therefore accumulate more in its quencher form and would make the phenomenon even worse. But this effect is actually very small and cannot explain the photo-current drop (see ESI Fig. 5b†).
The first mechanism, the trapping of Q and QH2 molecules, is implemented by considering the kinetic reactions Q → Qtrap and QH2 → QHtrap2, with reaction rate ktrap, and by defining a maximum trapping capacity Ktrap in the membrane. The corresponding evolution of trapped molecule concentration reads:
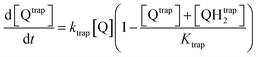 | (12) |
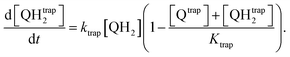 | (13) |
The second mechanism, mediator toxicity, is a well-known fact, but its mode of action is still debated and depends on the exact type of quinone.29–31 In a previous study we showed that the photosystem II efficiency (ΦPSII) of Chlamydomonas reinhardtii is drastically reduced in the presence of 2,6-DCBQ, indicating that the toxicity of this molecule could directly target the PC of the alga.19 So we implement the PC destruction over time, due to Q, with or without Q consumption depending on the scenario. The first one is related to a catalytic cycle between quinones and O2 that leads to Reactive Oxygen Species (ROS) and oxidative stress.31–33 The second scenario relies on the electrophilic behaviour of quinones (“Michael acceptor”) that makes them able to react with nucleophiles and leads to adducts.31,33,34 Beyond the possible photosynthetic chain impairing, such a pathway is expected to consume Q during the PC degradation.
We present here the second order kinetics oxidative stress mechanism although variations of this model like considering either a first order kinetics, or a Michael mechanism would not affect sensibly our results (see ESI Fig. 5†).
The fraction of photosynthetic chains fPC will decrease as follows:
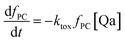 | (14) |
| keffalg = kalg(fPC + ϕra(1 − fPC)) | (15) |
The results of the simulations using this complexified model are shown in Fig. 5, on the right column (B–D). For reminder, one experimental dataset is shown in subpanel (A).
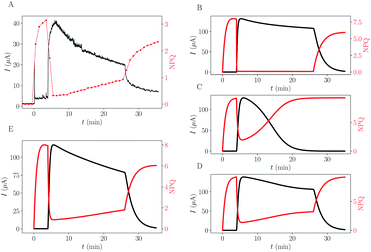 | ||
| Fig. 5 Comparison between experimental data and different trapping or toxicity scenarios simulated. (A) Typical experimental data. (B–E) Results of simulations using different scenarios (commonly fitted rate constants are the same as in Fig. 4). (B) Trapping ktrap = 1.9 × 10−3 s−1, Ktrap = 30 μM. (C) PC destruction, ktox = 2.5 × 10−6 s−1 μM−1. (D) PC destruction with remaining residual activity (ϕra = 2.3%). (E) Combination of all mechanisms: Trapping + PC destruction + residual activity. | ||
The trapping of quinone molecules is a phenomenon which can explain the decrease of the current as a function of time (B). It also explains why the final value of NPQ is a bit smaller than its maximum value. Still, this phenomenon does not explain the slow rise of the NPQ, associated with the current intensity shrink. The decay of active PC due to toxicity (C and D) is able to mimic the experimentally observed mirror-effect between current drop and NPQ rise over time, especially if algae maintain a basal activity different from zero (D). Without implementing this basal remaining photosynthetic activity (C), the current is already too low at the time point of DCMU injection (or light turned-off),19 and the changes can barely be noticed, unlike in experimental data.
The remarkable symmetric pattern of NPQ rise combined with current intensity shrink can be obtained through toxicity (D), but the convexity of the intensity peak is altered (it appears more concave than convex compared to the experimental data (A)). This qualitative feature was recovered on the trapping simulation (B). The simulation combining the two effects gets both the symmetric effect and the right convexity of the intensity peak (E) indicating that both phenomena are in play.
In conclusion, we have shown that simple kinematic modeling can capture the essence of the dynamics of mediator–micro-organism interactions. Of note, this model only applies for stirred algae suspension and cannot be directly extended to immobilized systems where other equations and parameters should be taken into account. Nevertheless, our results give some interesting trends for future interpretations and models. Beyond the fact that modeling is a helpful tool to discriminate between different hypothetical scenarios, our study suggests that the experimentally observed photo-current drop is mostly due to a decay of the photosynthetic activity evolving over time towards a non-zero basal level. This is consistent with the usual mode of action of quinone toxicity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported in part by CNRS (UMR 8640, UMR7141), Ecole Normale Supérieure, Faculté des Sciences et Ingénierie - Sorbonne Université and the “Initiative d'Excellence” program from the French State (Grant “DYNAMO”, ANR-11-LABX-0011-01).Notes and references
- J. Z. Zhang and E. Reisner, Nat. Rev. Chem., 2019, 1–16 Search PubMed.
- O. Yehezkeli, R. Tel-Vered, D. Michaeli, I. Willner and R. Nechushtai, Photosynth. Res., 2014, 120, 71–85 CrossRef CAS.
- J. Tschörtner, B. Lai and J. O. Krömer, Front. Microbiol., 2019, 10, 866 CrossRef.
- A. J. McCormick, P. Bombelli, R. W. Bradley, R. Thorne, T. Wenzel and C. J. Howe, Energy Environ. Sci., 2015, 8, 1092–1109 RSC.
- N. Sekar and R. P. Ramasamy, J. Photochem. Photobiol., C, 2015, 22, 19–33 CrossRef CAS.
- R. A. Voloshin, V. D. Kreslavski, S. K. Zharmukhamedov, V. S. Bedbenov, S. Ramakrishna and S. I. Allakhverdiev, Biofuel Res. J., 2015, 2, 227–235 CrossRef CAS.
- M. Kato, J. Z. Zhang, N. Paul and E. Reisner, Chem. Soc. Rev., 2014, 43, 6485–6497 RSC.
- D. Pankratov, G. Pankratova and L. Gorton, Curr. Opin. Electrochem., 2020, 19, 49–54 CrossRef CAS.
- K. L. Saar, P. Bombelli, D. J. Lea-smith, T. Call, E.-m. Aro, T. Müller, C. J. Howe and T. P. J. Knowles, Nat. Energy, 2018, 3, 75–81 CrossRef CAS.
- K. Hasan, Y. Dilgin, S. C. Emek, M. Tavahodi, H. E. Åkerlund, P. Å. Albertsson and L. Gorton, ChemElectroChem, 2014, 1, 131–139 CrossRef.
- M. Grattieri, Z. Rhodes, D. P. Hickey, K. Beaver and S. D. Minteer, ACS Catal., 2019, 9, 867–873 CrossRef CAS.
- H.-Y. Fu, D. Picot, Y. Choquet, G. Longatte, A. Sayegh, J. Delacotte, M. Guille-Collignon, F. Lemaître, F. Rappaport and F.-A. Wollman, Nat. Commun., 2017, 8, 15274 CrossRef.
- G. Longatte, F. Rappaport, F. A. Wollman, M. Guille-Collignon and F. Lemaître, Electrochim. Acta, 2017, 236, 337–342 CrossRef CAS.
- A. Sayegh, G. Longatte, O. Buriez, F.-A. Wollman, M. Guille-Collignon, E. Labbé, J. Delacotte and F. Lemaître, Electrochim. Acta, 2019, 304, 465–473 CrossRef CAS.
- G. Longatte, H.-Y. Fu, O. Buriez, E. Labbé, F.-A. Wollman, C. Amatore, F. Rappaport, M. Guille-Collignon and F. Lemaître, Biophys. Chem., 2015, 205, 1–8 CrossRef CAS.
- G. Longatte, F. Rappaport, F.-A. Wollman, M. Guille-Collignon and F. Lemaître, Photochem. Photobiol. Sci., 2016, 15, 969–979 RSC.
- G. Longatte, M. Guille-Collignon and F. Lemaître, ChemPhysChem, 2017, 18, 2643–2650 CrossRef CAS.
- G. Longatte, A. Sayegh, J. Delacotte, F. Rappaport, F.-A. Wollman, M. Guille-Collignon and F. Lemaître, Chem. Sci., 2018, 9, 8271–8281 RSC.
- L. Beauzamy, J. Delacotte, B. Bailleul, K. Tanaka, S. Nakanishi, F.-A. Wollman and F. Lemaître, Anal. Chem., 2020, 92, 7532–7539 CrossRef CAS.
- K. K. Karukstis, S. Boegeman, J. A. Fruetel, S. M. Gruber and M. H. Terris, Biochim. Biophys. Acta, Bioenerg., 1987, 891, 256–264 CrossRef CAS.
- N. G. Bukhov, G. Sridharan, E. A. Egorova and R. Carpentier, Biochim. Biophys. Acta, Bioenerg., 2003, 1604, 115–123 CrossRef CAS.
- K. J. Laidler, Theories of Chemical Reaction Rates, McGraw-Hill, 1969 Search PubMed.
- A. J. Bard and L. R. Faulkner, Fundamentals and Applications: Electrochemical Methods, Wiley, New York, 2001 Search PubMed.
- P. R. Rich and R. Harper, FEBS Lett., 1990, 269, 139–144 CrossRef CAS.
- A. G. Siraki, T. S. Chan and P. J. O'brien, Toxicol. Sci., 2004, 81, 148–159 CrossRef CAS.
- A. Brunmark and E. Cadenas, Free Radicals Biol. Med., 1989, 7, 435–477 CrossRef CAS.
- P. O’brien, Chem.-Biol. Interact., 1991, 80, 1–41 CrossRef.
- T. J. Monks, R. P. Hanzlik, G. M. Cohen, D. Ross and D. G. Graham, Toxicol. Appl. Pharmacol., 1992, 112, 2–16 CrossRef CAS.
- J. Imlay and I. Fridovich, Arch. Biochem. Biophys., 1992, 296, 337–346 CrossRef CAS.
- T. Henry and K. B. Wallace, SAR QSAR Environ. Res., 1995, 4, 97–108 CrossRef CAS.
- J. L. Bolton, M. A. Trush, T. M. Penning, G. Dryhurst and T. J. Monks, Chem. Res. Toxicol., 2000, 13, 135–160 Search PubMed.
- Y. Song and G. R. Buettner, Free Radicals Biol. Med., 2010, 49, 919–962 CrossRef CAS.
- J. L. Bolton and T. Dunlap, Chem. Res. Toxicol., 2017, 30, 13–37 Search PubMed.
- A. Brunmark and E. Cadenas, Chem.-Biol. Interact., 1988, 68, 273–298 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Beauzamy2020-supplemental.pdf. See DOI: 10.1039/d0se01304h |
| ‡ Such an exponential NPQ behaviour was already observed in independent fluorescence experiments.18 |
| This journal is © The Royal Society of Chemistry 2020 |