Open Access Article
Open Access ArticleData-powered augmented volcano plots for homogeneous catalysis†
Matthew D.
Wodrich‡
 a,
Alberto
Fabrizio‡
ac,
Benjamin
Meyer
ac and
Clemence
Corminboeuf
a,
Alberto
Fabrizio‡
ac,
Benjamin
Meyer
ac and
Clemence
Corminboeuf
 *abc
*abc
aLaboratory for Computational Molecular Design, Institute of Chemical Sciences and Engineering, Ecole Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland. E-mail: clemence.corminboeuf@epfl.ch
bNational Center for Competence in Research – Catalysis (NCCR-Catalysis), Ecole Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland
cNational Center for Computational Design and Discovery of Novel Materials (MARVEL), Ecole Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland
First published on 21st September 2020
Abstract
Given the computational resources available today, data-driven approaches can propel the next leap forward in catalyst design. Using a data-driven inspired workflow consisting of data generation, statistical analysis, and dimensionality reduction algorithms we explore trends surrounding the thermodynamics of a model hydroformylation reaction catalyzed by group 9 metals bearing phosphine ligands. Specifically, we introduce “augmented volcano plots” as a means to easily visualize the similarity of each catalyst's complete catalytic cycle energy profile to that of a hypothetical ideal reference profile without relying upon linear scaling relationships. In addition to quickly identifying catalysts that most closely match the ideal thermodynamic catalytic cycle energy profile, these maps also enable a more refined comparison of closely lying species in standard volcano plots. For the reaction studied here, they inherently uncover the presence of multiple sets of scaling relationships differentiated by metal type, where iridium catalysts follow distinct relationships from cobalt/rhodium catalysts and have profiles that more closely match the ideal thermodynamic profile. Reconstituted molecular volcano plots confirm the findings of the augmented volcanoes by showing that hydroformylation thermodynamics are governed by two distinct volcano shapes, one for iridium catalysts and a second for cobalt/rhodium species.
Introduction
Identifying and exploiting relationships between molecular structure, reactivity, and other experimental observables has long been a central pillar of chemical research.1–3 Some of the earliest and most celebrated examples, including the Brønsted catalysis equation,4 the Hammett equation,5 and the Bells–Evans–Polanyi principle6,7 are built upon simple, yet highly predictive, linear scaling relationships. Despite their uncomplicated construct, such relationships are often surprisingly robust and continue to find widespread use in, for example, understanding and predicting the behavior and activity of both heterogeneous8–12 and homogeneous13–15 catalysts. Often, this task is accomplished using volcano plots,16–19 which exploit the inherent linear relationships between the free energies of intermediates and transition states present in the catalytic cycle to discriminate active from non-active catalysts. In 2015 our research group demonstrated that the concept volcano plots, a cornerstone of computational research in heterogeneous and electrocatalysis, also provided a means to rationalize and predict the behavior of homogeneous species.13 Since that time, we have refined and honed these “molecular volcano plots” for various applications relevant to homogeneous catalysis,20 including inclusion of kinetic information,21 developing unified pictures of classes of reactions,22,23 direct prediction of theoretical turnover frequencies,24 estimations of reaction regioselectivity,25 and coupling these tools with machine-learning (ML).26–28Traditionally, volcano plots predict the energetics associated with a catalyst by linking the value of an easily determined descriptor variable (such as the relative free energy of one of the catalytic cycle intermediates) with the relative free energies of other intermediates and transition states through linear scaling relationships. The general volcano shape emerges by post-processing these relationships to establish the most difficult thermodynamic or kinetic reaction step (that appears on the volcano's y-axis) as a function of the value of descriptor variable (that appears on the x-axis). Prospective catalysts can then rapidly be analyzed by computing this descriptor variable, which returns an estimate of the largest energetic barrier that must be overcome in the catalytic cycle when placed onto the volcano plot. By definition, both the accuracy of the energetic predictions and the rationalization of chemical behavior is predicated on the existence of unambiguous linear scaling relationships that govern the energetics of the catalytic cycle. Often, these relationships are established by determining a complete energetic picture of the catalytic cycle for a small number of catalysts, frequently on the order of 10–50 species. After identifying a suitable descriptor variable, the corresponding energetic data for each individual catalytic cycle intermediate/transition state is “fit” to a single linear scaling relationship. Normally, this procedure provides linear scaling relationships of sufficient accuracy to distinguish energetically “good” from “bad” catalysts and pinpoint the fundamental chemical elements leading to more active species. Obviously, there is an inherent risk in assuming that relationships drawn from a small number of data points (i.e., catalysts) will continue to be valid for a much larger and more chemical diverse set of catalysts that will be subjected to screening. To this point, error analysis related to linear scaling relationships and its ultimate influence on catalysis prediction and screening continues to be an active research field.29–33
An alternative approach to predicting catalytic behavior that moves beyond linear scaling relationships would be to directly compute the complete catalytic cycles of all prospective catalysts. A volcano plot facsimile could then be established by directly plotting the (explicitly computed) energetically most costly catalytic cycle step for each catalyst as a function of a descriptor variable. These “reconstituted volcano plots” would not rely on any predefined linear scaling relationships and, particularly when coupled with larger data sets, may lead to an alternative, more refined, understanding of catalytic cycle energetics that would be entirely missed by using linear scaling relationships and volcano plots constructed in the typical fashion. While this process obviously is more computationally burdensome, it could exploit recent ML-based workflows to increase the speed at which new data can be acquired.
Here, we invoke a big-data inspired workflow (Scheme 1), which involves the generation of significant amounts of data through density functional computations and supervised ML. This data is subsequently subjected to statistical analysis and dimensionality reduction algorithms to create similarity maps. Specifically, we introduce and demonstrate the utility of a novel tool, the “augmented volcano plot”, that displays a one-dimensional similarity measure of the entire catalytic cycle free energy profile relative to a hypothetical ideal profile on the y-axis against the value of a descriptor variable on the x-axis. Note that these plots are a subcategory of a broader tool which we term energy profile similarity (EPSim) maps, where the overall shape resembles that of a conventional volcano curve.34,35 Ultimately, we come full circle by utilizing the results drawn from unsupervised learning to reexamine molecular volcano plots. These tasks are accomplished by studying a prototypical homogeneous catalytic reaction, olefin hydroformylation, an industrially important reaction that produces millions of tons of aldehydes per year.36 Overall, our augmented volcanoes visually demonstrate that the most similar profiles are often dominated by the same potential determining step, while also providing a more refined and holistic analysis of the catalytic cycle energetic similarities of related species. Additionally, they differentiate the thermodynamics of iridium as being distinct from cobalt and rhodium catalysts. In turn, this led to the discovery of two separate volcano curves, one for iridium catalysts and a second for cobalt/rhodium species that govern hydroformylation reaction thermodynamics. While this work focuses solely on the thermodynamic aspects of the catalytic cycle, the workflow and tools utilized would be equally valid when including kinetic aspects.
Results and discussion
Reaction details and free energy profiles
During hydroformylation an olefin reacts with H2 and CO to form an aldehyde (eqn (1)). Historically, group 9 metals were found to be excellent catalysts for this reaction, as first shown by Heck and Breslow with cobalt,37 and later with rhodium phosphine complexes as demonstrated by Wilkinson and coworkers,38,39 as well as iridium by Benzoni et al.40 Indeed, today numerous other transition metals have been shown to capably facilitate this reaction.41 For group 9 catalysts, the proposed catalytic cycle proceeds through a series of six intermediates (I2–I7), as illustrated in Scheme 2. Here, we use ethylene as a model olefin, which eliminates any issues surrounding the formation of different regioisomers.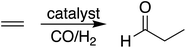 | (1) |
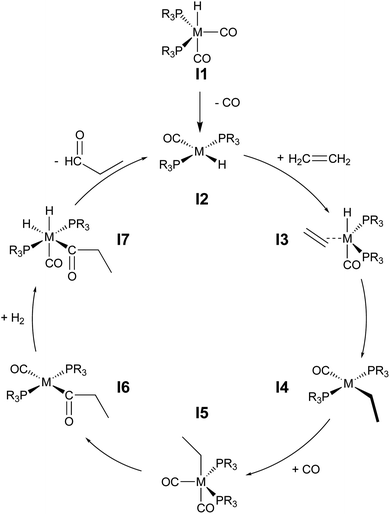 | ||
| Scheme 2 Catalytic cycle depicting key intermediates for olefin hydroformylation by a transition metal catalyst. | ||
We began by constructing an initial data set consisting of 1510 catalysts formed from combinations of three group 9 metal centers (Co, Rh, Ir) and two identical monodentate phosphine ligands created by combining 23 “R” groups (Scheme 3, 0–22) in a –P(R1)(R2)(R2) fashion. Each catalytic cycle intermediate (I2–17) was then computed for each of the metal/ligand combinations, which yielded the complete catalytic cycle thermodynamics for the 1510 catalysts. To supplement this data, a kernel based ML model was trained (see Computational details for additional information) to predict the catalytic cycle thermodynamics of an additional 491 catalysts (an exemplary number that could be increased) [the “out-of-sample” (OOS) data set consisting of using “R” groups 23–28 as the R1 component and 0–28 as the R2 component of –P(R1)(R2)(R2)]. Following training, this model was capable of predicting the relative free energies of catalytic cycle intermediates I3–I7 directly from the optimized geometry of I2 with a mean average error of under 3.5 kcal mol−1.
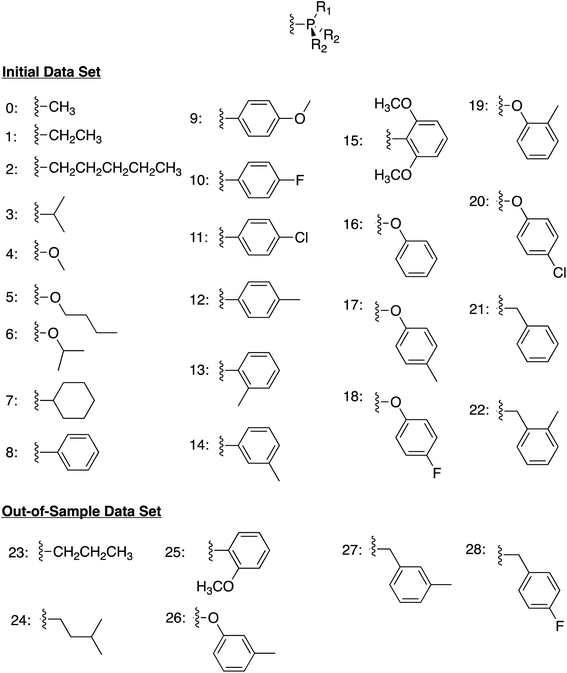 | ||
| Scheme 3 Ligand structure and “R” groups used to construct the phosphine ligands comprising the initial data set (0–22) and the out-of-sample data set (23–28). | ||
While examining the individual thermodynamic free energy profiles of over 2000 catalysts is clearly impractical, Fig. 1 provides an overview of the magnitude to which various metal/phosphine combinations influence the relative free energies of each of the catalytic cycle intermediates. Here, the reactant (I2) and product energies are defined from the overall reaction free energy of eqn (1) (zero for the reactant, −30.74 for the product), while each of the other intermediates has a large range of free energies (2σ values indicated by the vertical colors bars, whole range shown in the inset distribution plots). Interestingly, reaction steps that involve binding of a new molecule, specifically I3 (olefin binding), I5 (CO binding), and I7 (H2 binding) each have relative free energies that span a larger range than those reaction steps that involve only a structural rearrangement of existing components. Intuitively, one may consider that the larger span may arise from the greater influence of steric interactions in I3, I5 and I7, as each of these intermediates has either a five- (trigonal bipyramidal) or six-coordinate (octahedral) metal environment. Indeed, both intermediates I4 and I6 where the metal is in a four-coordinate environment with the various ligand/substrates arranged in a square planar environment possess narrow distributions. However, a more detailed examination (vide infra) reveals that the electronic influence caused by the metal center also play a large role in dictating the stability of the catalytic cycle intermediates (particularly I3, I5 and I7) seen in Fig. 1.
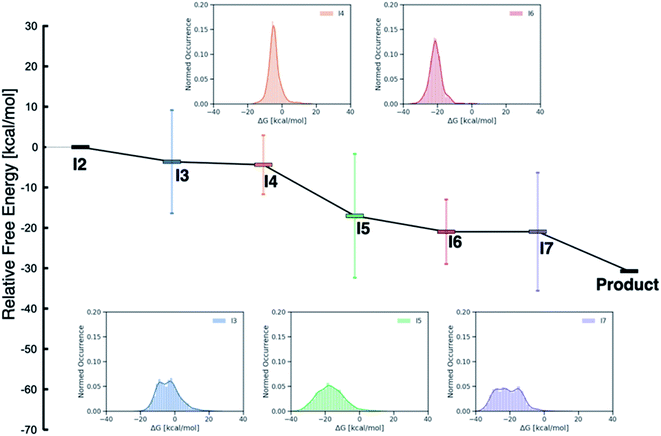 | ||
| Fig. 1 Overview of the free energy profiles of the catalysts in the original (DFT data) and out-of-sample (machine-learned data) data sets. The horizontal colored bars represent the average value (relative to I2) for each catalytic cycle intermediate over both data sets while the vertical colored bars show 2σ values (i.e., ∼97% of catalysts fall within this range of relative free energies). The insets show the distribution of values for each intermediate (I3–I7). Note that both I2 (0.0 kcal mol−1) and the product (−30.74 kcal mol−1) have fixed numeric values, as these points represent the reactants and products of the catalytic process that are governed by the energy associated with eqn (1). | ||
Breaking the relative energy distributions for each intermediate down based on the catalyst's metal center (Fig. 2) provides a more detailed picture of which reaction steps of the catalytic cycle may be the most difficult.42 For instance, Fig. 2a and b shows that intermediate I3 is quite stabilized with respect to I2 for cobalt and iridium species and less for rhodium catalysts, while intermediate I4 is roughly equally stable for all species. As a result, I3 → I4 will be thermodynamically costly for many cobalt and iridium catalysts, while being facile for rhodium species. Similarly, I5 → I6 is expected to a thermodynamically costly step for cobalt catalysts based on the fact that intermediate I5 is very stable (Fig. 2d). Finally, the clear separation of distributions based on metal type for intermediate I7 (Fig. 2e) indicates that I6 → I7 will be energetically costly for a large number of rhodium catalysts while the same reaction step will be facile for iridium species.
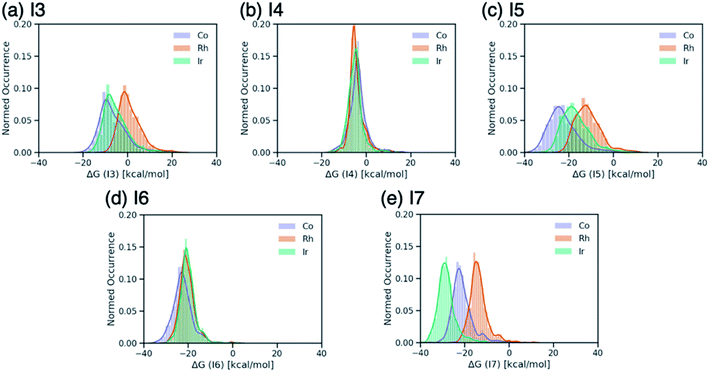 | ||
| Fig. 2 Distributions of ΔG values of intermediates (a) I3, (b) I4, (c) I5, (d) I6, and (e) I7 classified by metal center of the catalyst. ΔG values are relative to ΔG(I2). | ||
Dimensionality reduction and similarity maps
Fig. 1 and 2 allow us to compare the relative similarity of each catalytic cycle intermediate independently, but do not provide a measure of similarity regarding the entirety of the catalytic energy profile. To overcome this drawback, we created t-distributed stochastic neighbor embedding (t-SNE) maps, which is a dimensionality reduction technique that measures how closely the free energy profiles of the catalysts align in multi-dimensional space. Here, the t-SNE maps depict the five-dimensional space associated with the thermodynamic free energy profile (one dimension for each of the intermediate free energies I3–I7), but the same tool could describe equally well a kinetic free energy profile that includes intermediates and transition states. Two points that are close to one another on the t-SNE map, indicate similar free energy profiles in five-dimensional space. By coloring the t-SNE maps in different ways, various patterns emerge that relate catalyst makeup with the associated catalytic cycle energetics.Fig. 3a shows a t-SNE map with each of the catalysts colored based on a key element of the catalytic cycle and molecular volcano plots (the quantity generally displayed on the y-axis), the potential determining step (pds), as defined by eqn (2). The pds represents the most energetically costly thermodynamic step of the catalytic cycle (i.e., the step that is most energetically uphill, or least downhill if all reaction steps are exergonic). Since the hydroformylation of ethylene is exergonic an “ideal” catalyst will have a thermodynamic profile consisting of a series of equally exergonic steps before arriving at the products (i.e., the Sabatier ideal profile, see ESI Fig. S2† and ref. 13 for a detailed explanation). In reality, this ideal picture is rarely the case, as inevitable certain catalytic cycle intermediates will be overly stable, while others will be less stable. The coloring of Fig. 3a allows us to quickly visualize those catalysts having similar profiles that encounter their largest thermodynamic barriers in the same place of the catalytic cycle (i.e., those having the same pds).
| ΔG(pds) = max[ΔG(2 → 3), ΔG(3 → 4), ΔG(4 → 5), ΔG(5 → 6), ΔG(6 → 7), ΔG(7 → 2)] | (2) |
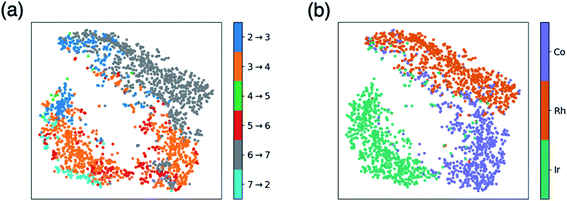 | ||
| Fig. 3 t-Distributed stochastic neighbor embedding (t-SNE) maps that depict overall similarity of the relative energies of the five catalytic cycle intermediates (I3–I7) for the set of 2001 catalysts (1510 from the initial set obtained from DFT computations and 491 from out-of-sample set obtained from machine-learning predictions) colored by (a) the potential determining step and (b) type of metal atom. Similar maps using the reaction energies of each step can be found in the ESI, Fig. S1.† | ||
Fig. 3a shows a considerable amount of clustering based on the nature of the pds. Here, it can quickly be seen that a majority of catalysts having similar profiles (i.e., lying close to each other in the plot) share the same pds and are thermodynamically controlled, specifically, by one of three key reaction steps that vary the most, H2 addition and splitting (I6 → I7, gray), olefin addition (I2 → I3, dark blue), and H-transfer and σ-complex formation (I3 → I4, orange). Each other reaction step: CO addition (I5 → I6, red), H-transfer and product release (I7 → I2, light blue) and particularly CO insertion into the metal–alkyl bond (I4 → I5, green) are characterized by a smaller number of scattered points in the map, indicating that they do not influence the profile similarity significantly. These reaction steps, at least for group 9 metal/phosphine catalysts play a diminished role in the overall thermodynamic picture of the catalytic cycle because they tend to be characterized by overall exergonic free energies (see Fig. 1). The Fig. 3a t-SNE map is complemented by t-SNE map shown in Fig. 3b, where individual points are colored according to the metal center of the catalyst (Co in purple, Rh in dark orange, Ir in blue green).
It is remarkable, albeit perhaps expected to see three well separated clusters in Fig. 3b that indicates the profile similarities are essentially dictated by the metal center. The most contiguous cluster of a single color (corresponding to a single pds) found in Fig. 3a (upper right of map) consists of rhodium catalysts (Fig. 3b) whose thermodynamics are governed by H2 addition/splitting (I6 → I7). The fact that I6 → I7 is the pds for nearly all rhodium species is consistent with the instability of I7 for rhodium seen in Fig. 2e. In contrast, both the cobalt (lower right) and iridium (lower left) clusters in Fig. 3b indicate a greater variety of potential determining steps are present (multiple colors for the same points in the Fig. 3a plot). Despite the greater pds variety for cobalt and iridium, the thermodynamics of a majority of these catalysts are governed by H-transfer and formation of the σ-bound alkyl complex from the π-olefin complex (I3 → I4, orange). For cobalt, there is also a spattering of catalysts that are governed either by H2 addition/splitting (I6 → I7) or by CO insertion into the metal–alkyl bond (I5 → I6). For iridium, a handful of catalysts also have olefin addition (I2 → I3) as the most thermodynamically difficult step. Notably, CO addition (I4 → I5) and H-transfer/product release (I7 → I2) appear as thermodynamically limiting step only for a very small number of catalysts, which is consistent with the average overall energies for these steps being exergonic, as shown in Fig. 1.
Energetic profile similarity maps and augmented volcano plots
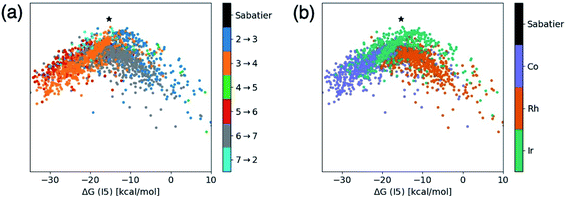
This brings us to a conceptually novel and powerful analytical tool that is related to the t-SNE maps shown in Fig. 3. In energetic profile similarity (EPSim) maps, we utilize an analogous dimensionality reduction concept that measures the similarity of the catalytic cycle energetic profile to a suitable reference on one axis (rather than in two axes as in the t-SNE maps) while imposing a physical meaning onto the second axis. An intuitive choice for the physically meaningful axis is the value of a descriptor variable used in molecular volcano plots, which gauges the strength of catalyst/substrate interactions present during the catalytic cycle. The y-axis is then used to measure the similarity of the catalytic cycle energetic profile to a reference species. Rather than choosing an actual catalyst (e.g., the catalyst found highest on the volcano plot), Sabatier's hypothetical ideal catalyst concept (see ESI Fig. S2†) can be employed as a reference species to which all “real” catalysts can be compared. By analyzing the similarity of each catalyst with this hypothetical ideal free energy profile, catalysts having the best thermodynamic profiles can quickly be identified and, ultimately, a better understanding of the underlying chemical process that govern the catalytic cycle energetics for different species extracted. While the unmistakable volcano shape seen here (vide infra) highlights a clear connection with molecular volcano plots, conceptually, these EPSim maps possess several intriguing novelties. First, EPSim maps do not rely on the existence of linear scaling relationships within the catalytic cycle energetics. As a result, these maps can be constructed for any catalytic process and used to readily identify species with the best thermodynamic profile (which will appear highest on the plot) by comparison with the Sabatier ideal reaction profile. Second, molecular volcano plots summarize the energetics of the catalytic cycle in terms of a single reaction step, the pds. However, more than one reaction step may contribute to overall catalytic activity. EPSim maps, where all of the energies of the catalytic cycle are explicitly considered, provide a more complete and accurate picture of a catalyst's thermodynamics (or kinetics). In particular, a catalyst appearing higher on the plot than another catalyst necessarily has a better overall profile, as the reaction steps are, globally, more similar to the ideal reference species (i.e., the Sabatier ideal profile). In traditional molecular volcano plots, there is no information included to differentiate two points lying close to one another in either the horizontal or vertical axis. In such cases, any reaction step other than the pds could negatively affect the global energetics of the catalyst, yet remain hidden (since the y-axis only provides the value of the pds). Thus, EPSim maps can be considered as an instrument both for obtaining a big picture type analysis of a large number of catalysts and for achieving refined comparison of candidates lying closely in conventional volcano plots.Fig. 4 shows the EPSim maps for the hydroformylation reaction, where ΔG(I5) is used as the descriptor variable (x-axis)21 and similarity to the Sabatier ideal reference profile43 is illustrated on the y-axis. The most noticeable feature of the two EPSim maps is their striking visual similarity to volcano plots, a feature that arises in spite of the fact that no explicit information regarding any linear scaling relationships were used during their creation. Thus, in this instance, the EPSim maps shown in Fig. 4 are part of a subcategory of EPSim maps which we call “augmented volcano plots”,34,35 which differ from traditional molecular volcanoes in both the nature of the y-axis and the manner in which they are constructed.
Despite the distinct nature of the augmented volcano plot, Fig. 4a clearly shows that the chemistry of these specific catalysts remains strongly linked to the underlying scaling relationships, as catalysts falling to the left and the right of the Sabatier ideal catalyst (i.e., the reference from which the similarity of the catalytic cycle of all other points is judged, shown in black) are clearly grouped based on their pds. This fact provides a strong indication that the pds is the key factor in the “similarity” measurement (indicated by changes in the value of the y-axis) that distinguishes the catalytic cycle energetics of different species. A closer examination of the plots shows that for catalysts with larger descriptor variables (i.e., those lying more right on the plot), that the pds is always associated with a molecular addition step (I2 → I3, I4 → I5, I6 → I7), while species with more exergonic descriptor variables (i.e., those lying more left of the plot) are governed by a structural rearrangement step involving a reduction in coordination number of the metal (I3 → I4, I5 → I6, I7 → I2). The presence of the different reaction steps to the left/right of the reference catalyst (black point) on the augmented volcano plots align closely with the location of the scaling relationships for the same reaction steps seen in our previous work.21 The fact that multiple potential determining steps appear on right/left sides of the reference catalyst in Fig. 4a (rather than a single pds for more positive and more negative descriptor values, as would be the case in a volcano plot) arises from the normal small deviations of individual species from the linear scaling relationships that are used to create volcano plots. Note that in the absence of any linear scaling relationships the EPSim maps would appear as an unordered cluster of points (and thus would no longer be considered to be augmented volcano plots), however those catalysts with the best energetic profiles would still be easily identifiable owing to their higher positions on the plot.
Fig. 4b shows the same augmented volcano as Fig. 4a, but now colored according to the catalyst's metal center. Here, clear definition between the behavior of the different metals appears. Most notably, iridium species are slightly set apart from cobalt/rhodium species and are located higher on the plot, indicating that iridium catalysts more closely match the ideal reference thermodynamic profile based on the similarity criterion.44 Even for catalysts with an ideal descriptor value (i.e., those with the same x-axis value as the black point), cobalt and rhodium catalysts show larger deviations than iridium catalysts from the ideal reference. A comparison of Fig. 4a and b reveals that rhodium catalysts tend to have more trouble binding the molecular components (i.e., CO/H2/olefin) required to complete the catalytic cycle, while cobalt has problems in traversing the reaction steps that require a structural rearrangement leading to a reduction in coordination number. Iridium is well-balanced, lying between rhodium and cobalt.
Reconstitution of molecular volcano plots
Generally, molecular volcano plots are formed from linear scaling relationships. In these plots, the x-axis is often taken as the stability of one intermediate present in the catalytic cycle (i.e., the descriptor variable) while the y-axis depicts the energy of the most difficult reaction step (i.e., the potential determining step) as a function of the value of the descriptor. Thus, the volcano is often divided into different regions based on which reaction step is the pds. However, by directly plotting the pds as a function of the descriptor variable a reconstituted molecular volcano that does not explicitly depend on any underlying linear scaling relationships can be obtained. Fig. 5a shows the resulting volcano plot analogue, which has been colored by the potential determining step for each catalyst. As in the augmented volcano plot (Fig. 4a), one of the first things that emerges is the unmistakable presence of linear scaling relationships that dictate the energies associated with the pds (i.e., catalysts with the same pds have a linear relationship between the value of descriptor variable and the quantitative value of the pds). Importantly, it is also clear that the vast majority of catalysts are governed by one of three key catalytic cycle reaction steps mentioned earlier: olefin addition (I2 → I3, dark blue), H-transfer and σ-complex formation (I3 → I4, orange), and H2 addition/splitting (I6 → I7, gray). Drawing best fit lines through those points having the same pds (see ESI Fig. S4† for correlations) reveals that the eqn (1) hydroformylation reaction is not governed by a single volcano, as would be expected, but alternatively by two volcanoes (Fig. 5b). A closer examination reveals that while the left side of both volcanoes is governed by H-transfer and σ-complex formation (I3 → I4), the right side of each volcano is governed by the free energy associated with a different reaction step, either olefin addition (I2 → I3) for catalysts that follow the taller volcano (peak 1) or H2 addition/splitting (I6 → I7) for catalysts belonging to the shorter volcano (peak 2).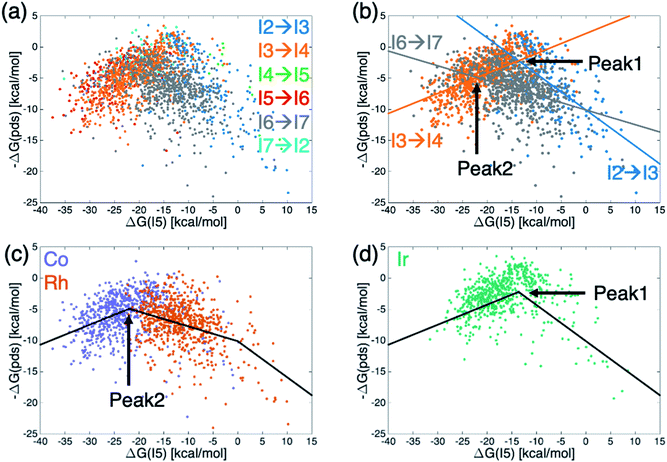 | ||
| Fig. 5 Volcano plots for the set of 2001 catalysts (1510 from the initial set obtained from DFT computations and 491 from out-of-sample set obtained from machine-learning predictions) colored by (a and b) potential determining step or (c and d) metal center. Fig. 4b shows the existence of two different volcanoes with different peaks within the data set. Coloring by type of metal center (c and d) shows that Co and Rh catalysts follow one set of scaling relationships that have the best thermodynamic profiles near peak 2, while Ir catalysts follow a different set of relationships that have their best thermodynamic profiles near peak 1. | ||
To distinguish which catalyst belongs to each of the two volcanoes, we recolored the same data points based on the catalyst's metal center (Fig. 5c and d), which confirmed that the constituent metal is the key factor that differentiates which volcano dictates the energetics of the catalytic cycle. Fig. 5 indicates that the shorter volcano (Fig. 5c) defines the thermodynamics for cobalt and rhodium catalysts, while the taller volcano (Fig. 5d) dictates the thermodynamics of iridium catalysts. Importantly, these findings provide the rationale behind the separate clustering of iridium from cobalt/rhodium catalysts in the t-SNE (Fig. 3b) and the enhanced similarity of iridium catalysts with the Sabatier ideal profile seen in the augmented volcano plot (Fig. 4b). The Fig. 5c and d thermodynamic plots show that cobalt and iridium catalysts lie at the top of their respective volcanoes, indicating that they have the best free energy profiles. On the other hand, experimentally employed rhodium catalysts fall along the right slope of the Fig. 5c volcano indicative of (generally) slightly worse thermodynamic (but not necessarily kinetic) profiles. Fig. 5d volcano indicates iridium catalysts generally have superior energy thermodynamic profiles relative to cobalt and rhodium catalysts.
An examination of the underlying scaling relationships (see ESI† for additional details) reveals the origin of the two separate volcano peaks. In essence, intermediate I7 is far more stable for iridium catalysts than for its cobalt and rhodium counterparts. This enhanced stability causes moving from I6 to I7 to be facile for iridium species, while it remains energetically costly for cobalt and rhodium catalysts. As a result, the I6 → I7 reaction seen in gray in Fig. 5b is shifted upwards for iridium catalysts and is no longer a pds for the iridium volcano plot (see ESI Fig. S3†). This finding is fully consistent with experimental observations regarding the generally enhanced stability of iridium catalysts used in hydroformylation,45–47 as well as additional ancillary evidence regarding the isolation of acyl dihydro iridium intermediates48,49 (i.e., I7) during the same process. It has been postulated that this extra stability arises from relativistic effects that stabilize the 6s electron level relative to the 5d level thereby inducing stronger bonding in third row relative to second row transition metals.50
Overall, it is important to reinforce the discovery of two volcanoes that dictate the thermodynamics of a single reaction would almost surely be missed if only a sparse amount of data were to be analyzed. In fact, using only a handful of catalysts with each metal center to establish volcano plots most likely would yield a hybrid of the two volcanoes, thereby furnishing a poorer quantitative picture of the catalytic cycle energetics and leading to a befuddled understanding of the underlying chemistry. Generally speaking, the incorporation of larger data sets, the removal of data fitting to preconceived models, and the application of concepts from big data analytics provides an alternative route to comprehending and predicting catalytic behavior. The systematic use of these techniques, especially augmented volcano plots/EPSim maps, provide an ameliorated route toward understanding and rationalizing catalytic cycle energetics that should lead to the development of novel strategies for designing more active and selective catalysts. Importantly, the general concept of EPSim maps/augmented volcano plots described here would be equally valid for studies involving a smaller number of data points (i.e., catalysts) as well as for examining heterogeneous and electrocatalytic processes.
Conclusions
In conclusion, we have introduced a novel conceptual tool, the augmented volcano plot/energetic profile similarity (EPSim) map, which compares the similarity of the entirely of a catalytic cycle energy profile for a large number of catalysts to that of an ideal reference species. These augmented volcano plots, similar in spirit to molecular volcanoes, are capable of identifying catalysts with the best energy profiles and recovering information regarding the existence of any linear scaling relationships. Importantly, the broader category of EPSim maps can also be used to identify the best catalysts even in the absence of linear scaling relationships while also discerning the most energetically superior catalyst among closely clustered species in conventional volcano plots. Application of the EPSim maps/augmented volcano plots to a model industrially important hydroformylation reaction indicates that iridium catalysts have reaction profiles that more closely match the ideal reference profile than cobalt/rhodium catalysts. A reexamination of a molecular volcano plot variant showed iridium catalysts are governed by a separate volcano curve than cobalt and rhodium species. Overall, the application of well-established tools, such as the volcano plot, in tandem with newly developed techniques, such as augmented volcano plots applied to larger data sets can reveal hidden trends that govern the underlying chemistry.Computational details
Generation of dimensionality reduction and energy similarity maps
The energy profile of each catalyst considered here spans either a five-dimensional (if the relative stability of intermediates I3–I7 are being considered) or a six-dimensional space (if the reaction energies between intermediates are being considered), where either the relative stability of each intermediate [i.e., ΔG(I3)] or each reaction energy [i.e., ΔG(I2 → I3)] represents one coordinate axis. Nonlinear dimensionality reduction algorithms, such as t-distributed stochastic neighbor embedding (t-SNE),51 facilitate the visualization and the identification of similarity patterns within the catalyst pool by embedding the six-dimensional data in a low-dimensional space. To obtain the two-dimensional t-SNE maps presented in this work (Fig. 3), we apply the t-SNE algorithm as implemented in the scikit-learn package,52 fixing the perplexity value at 50 and the maximum number of iteration for the minimization of the Kullback–Leibler divergence53 at 5000. While t-SNE provides a powerful tool to analyze the relationship between different catalysts, chemical patterns and trends can be only established qualitatively as the two axes of the map lack a well-defined physical meaning. The energy profile similarity (EPSim) maps define a two-dimensional space where each potential catalyst is represented by a chemically and physically meaningful quantity on the x-axis (e.g., the volcano plot descriptor variable) and a similarity measure between its reaction energy profile and the Sabatier's ideal on the y-axis. To obtain these maps, we first collect the reaction energies of each catalyst into a set of vectors, which is then standardized and compared to the Sabatier's ideal using the Euclidean norm of their difference as a metric. The final vertical axis is obtained by subtracting the normalized Euclidean distances to the unity. In this way, the catalysts with the closest energy profile to the Sabatier's ideal appear intuitively at the top of the map. A python code to compute the EPSim maps, as well as a practical example taken from this work, is available for download at https://github.com/lcmd-epfl/EPSim. All data can be found on the Materials Cloud website at DOI: 10.24435/materialscloud:s0-yx.Density functional computations
The initial data set of catalysts were formed from combinations of three group 9 metals (Co, Rh, Ir) along with 23 different “R” groups that were appended in a R1/R2/R2 fashion (0–22, see Scheme 2) to form each of the two monodentate phosphine ligands. Initial sets of Cartesian coordinates were obtained by converting SMILES strings54 for each catalyst into a three-dimensional structure using OpenBabel.55 Examination of the geometries created by invoking this procedure revealed that some structures contained overlapping “R” groups, which were corrected via manual manipulation of the structures. For some species, one of the ligands dissociated entirely from their metal center and these catalysts were removed from the data set. This procedure yielded a total of 1510 catalysts for which each of the catalytic cycle intermediates (I2–I7, Scheme 2) was optimized at PBE0 (ref. 56 and 57)-D3(BJ)58,59/def2-SVP60 level in Gaussian16.61 Subsequent single point optimizations were performed on the optimized gas phase geometries at the PBE0-D3(BJ)/def-TZVP level using the SMD solvation model for benzene. Free energy corrections (using the def2-SVP basis set) were determined using the rigid-rotor harmonic oscillator model62 as implemented in the GoodVibes program.63Training of the machine-learning models and out-of-sample predictions
The machine-learning models were trained and employed using the QMLCode64 quantum machine learning toolkit. Training of the ML models used the initial database of catalysts (Scheme 2) in order to predict the relative free energies of each of the catalytic cycle intermediates. This was accomplished by mapping these relative energies directly onto the molecular structure of I2 through use of a molecular representation. Three molecular representations were tested [the Coulomb Matrix (CM),65 the Bag of Bonds (BoB),66 and the Spectrum of London and Axilrod–Teller–Muto potential (SLATM)67] of which SLATM was found to yield the best results (see ESI† for detailed quantitative description of the results as well as the training procedure), consistently yielding errors smaller than 3 kcal mol−1 for the test set (ESI, Fig. S5†). Having shown that the ML models are capable of predicting to relative free energies of each of the catalytic cycle intermediates to an accuracy near or surpassing 3 kcal mol−1, we established the accuracy of out-of-sample (OOS) predictions for the 491 catalysts in OOS dataset. Our model yielded a mean average error of 2.99 (I3), 3.27 (I4), 3.13 (I5), 3.44 (I6), and 2.83 kcal mol−1 (I7) for the predictions of the relative free energies, which establishes it is a viable tool for predicting the catalytic cycle free energies of new group 9 metal/phosphine catalysts for the hydroformylation reaction (eqn (1)). These free energy profiles were then used to supplement the initial 1510 catalysts in Fig. 3–5. Thus, the total data set used here consists of 1510 catalytic cycles derived from DFT computations and 491 catalytic cycles derived from machine-learned profiles.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The EPFL and the National Centre of Competence in Research (NCCR) “Materials' Revolution: Computational Design and Discovery of Novel Materials (MARVEL)” of the Swiss National Science Foundation (SNSF) are acknowledged for financial support.References
- C. K. Ingold, Structure and Mechanism in Organic Chemistry, Cornell Univ. Press, Ithaca, NY, 1953 Search PubMed.
- C. D. Ritchie and W. F. Sager, Prog. Phys. Org. Chem., 1964, 2, 323–400 CAS.
- N. B. Chapman and J. Shorter, Correlation Analysis in Chemistry: Recent Advances, Plenum Press, New York, NY, 1978 Search PubMed.
- J. N. Brönsted and K. Pedersen, Z. Phys. Chem., 1924, 108, 185–235 Search PubMed.
- L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103 CrossRef CAS.
- R. P. Bell, Proc. R. Soc. London, Ser. A, 1936, 154, 414–429 Search PubMed.
- M. G. Evans and M. Polanyi, Trans. Faraday Soc., 1938, 34, 11–24 RSC.
- T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, J. Rossmeisl and M. T. M. Koper, Phys. Rev. Lett., 2012, 108, 116103 CrossRef CAS.
- F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410 CrossRef CAS.
- J. Pérez-Ramírez and N. López, Nat. Catal., 2019, 2, 971–976 CrossRef.
- M. Busch, M. D. Wodrich and C. Corminboeuf, Chem. Sci., 2015, 6, 6754–6761 RSC.
- Y. Wang, J. H. Montoya, C. Tsai, M. S. G. Ahlquist, J. K. Nørskov and F. Studt, Catal. Lett., 2016, 146, 304–308 CrossRef CAS.
- M. Anand and J. K. Nørskov, ACS Catal., 2020, 10, 336–345 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46 CrossRef.
- H. Dau, C. Limberg, T. Reier, M. Risch, S. Roggan and P. Strasser, ChemCatChem, 2010, 2, 724–761 CrossRef CAS.
- J. Greeley and N. M. Markovic, Energy Environ. Sci., 2012, 5, 9246–9256 RSC.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef.
- M. D. Wodrich, B. Sawatlon, M. Busch and C. Corminboeuf, ChemCatChem, 2018, 10, 1586–1591 CrossRef CAS.
- M. D. Wodrich, M. Busch and C. Corminboeuf, Chem. Sci., 2016, 7, 5723–5735 RSC.
- M. Busch, M. D. Wodrich and C. Corminboeuf, ACS Catal., 2017, 7, 5643–5653 CrossRef CAS.
- M. Busch, M. D. Wodrich and C. Corminboeuf, ChemCatChem, 2018, 10, 1592–1597 CrossRef CAS.
- M. D. Wodrich, B. Sawatlon, E. Solel, S. Kozuch and C. Corminboeuf, ACS Catal., 2019, 9, 5716–5725 CrossRef CAS.
- M. D. Wodrich, M. Busch and C. Corminboeuf, Helv. Chim. Acta, 2018, 101, e1800107 CrossRef.
- B. Meyer, B. Sawatlon, S. Heinen, O. A. von Lilienfeld and C. Corminboeuf, Chem. Sci., 2018, 9, 7069–7077 RSC.
- B. Sawatlon, M. D. Wodrich, B. Meyer, A. Fabrizio and C. Corminboeuf, ChemCatChem, 2019, 11, 4096–4107 CrossRef CAS.
- M. Cordova, M. D. Wodrich, B. Meyer, B. Sawatlon and C. Corminboeuf, ACS Catal., 2020, 10, 7021–7031 CrossRef CAS.
- A. J. Medford, J. Wellendorff, A. Vojvodic, F. Studt, F. Abild-Pedersen, K. W. Jacobsen, T. Bligaard and J. K. Nørskov, Science, 2014, 345, 197–200 CrossRef CAS.
- J. Zaffran, C. Michel, F. Auneau, F. Delbecq and P. Sautet, ACS Catal., 2014, 4, 464–468 CrossRef CAS.
- J. E. Sutton, W. Guo, M. A. Katsoulakis and D. G. Vlachos, Nat. Chem., 2016, 8, 331–337 CrossRef CAS.
- J. E. Sutton and D. G. Vlachos, J. Catal., 2016, 338, 273–283 CrossRef CAS.
- S. Matera, W. F. Schneider, A. Heyden and A. Savara, ACS Catal., 2019, 9, 6624–6647 CrossRef CAS.
- The broader category of energy profile similarity (EPSim) maps, also involve plotting a one-dimensional similarity measure of the entire catalytic cycle free energy profile relative to a hypothetical ideal reference profile on the y-axis against a descriptor variable on the x-axis. In some, but not all, cases the EPSim map falls into the augmented volcano plot subcategory when the volcano shape is observed. In other cases, a larger amount of scatter and no clear volcano shape exists. In such cases, catalysts with free energy profiles more similar to the ideal reference profile will still be located highest on the plot.
- While applied to relatively large set of data here, EPSim maps/augmented volcano plots can also be used with smaller data sets.
- R. Franke, D. Selent and A. Börner, Chem. Rev., 2012, 112, 5675–5732 CrossRef CAS.
- R. F. Heck and D. S. Breslow, J. Am. Chem. Soc., 1961, 83, 4023–4027 CrossRef.
- J. A. Osborn, G. Wilkinson and J. F. Young, Chem. Commun., 1965, 17 RSC.
- D. Evans, J. A. Osborn and G. Wilkinson, J. Chem. Soc. A, 1968, 3133–3142 RSC.
- L. Benzoni, A. Andreett, C. Zanzotte and M. Camia, Chim. Ind., 1966, 48, 1076 CAS.
- J. Pospech, I. Fleischer, R. Franke, S. Buchholz and M. Beller, Angew. Chem., Int. Ed., 2013, 52, 2852–2872 CrossRef CAS.
- In principle, distributions could also be made on the basis of ligand “R” groups in addition to the metal center. However, given that the metal is so strongly influential in dictating reaction energetics, such plots would have a wide range of distribution values and significant overlap. As such, we focus here solely on the influence of the metal.
- As we are considering only reaction thermodynamics, the catalytic cycle profile with the smallest pds is obtained by dividing the overall reaction energy (−30.74 kcal mol−1) by the number of reaction steps within the catalytic cycle (six, see ESI Fig. S2†). For this “Sabatier ideal catalyst” each reaction step will have a ΔG value of -5.12 kcal mol−1, thereby making the ΔG value of the pds −5.12 kcal mol−1. The descriptor value [ΔG(I5)] will then be 3x − 5.12 = −15.36 kcal mol−1 (since one must proceed through three reaction steps to arrive at intermediate I5).
- Since only thermodynamic, as opposed to kinetic, profiles are examined here, the fact that iridium catalysts more closely match the ideal reference profile than rhodium species does not indicate that these species would be more active catalysts.
- D. J. Fox, S. B. Duckett, C. Flaschenriem, W. W. Brennessel, J. Schneider, A. Gunay and R. Eisenberg, Inorg. Chem., 2006, 45, 7197–7209 CrossRef CAS.
- G. Abkai, S. Schmidt, T. Rosendahl, F. Rominger and P. Hofmann, Organometallics, 2014, 33, 3212–3214 CrossRef CAS.
- D. Guan, C. Godard, S. M. Polas, R. P. Tooze, A. C. Whitwood and S. B. Duckett, Dalton Trans., 2019, 48, 2664–2675 RSC.
- P. P. Deutsch and R. Eisenberg, Organometallics, 1990, 9, 709–718 CrossRef CAS.
- A. B. Permin and R. Eisenberg, J. Am. Chem. Soc., 2002, 124, 12406–12407 CrossRef CAS.
- G. C. Bond, J. Mol. Catal. A: Chem., 2000, 156, 1–20 CrossRef CAS.
- L. van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- S. Kullback and R. A. Leibler, Ann. Math. Stat., 1951, 22, 79–86 CrossRef.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1998, 110, 6158–6170 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- S. Grimme, Chem.–Eur. J., 2012, 18, 9955–9964 CrossRef CAS.
- I. Funes-Ardoiz and R. S. Paton, GoodVibes, version 2.0.3, 2018 Search PubMed.
- A. S. Christensen, F. A. Faber, B. Huang, L. A. Bratholm, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, QML: A Python Toolkit for Quantum Machine Learning, 2017 Search PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef.
- K. Hansen, F. Biegler, R. Ramakrishnan, W. Pronobis, O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, J. Phys. Chem. Lett., 2015, 6, 2326–2331 CrossRef CAS.
- F. A. Faber, A. S. Christensen, B. Huang and O. A. von Lilienfeld, J. Chem. Phys., 2018, 148, 241717 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc04289g |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |