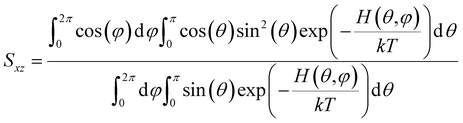Unequivocal structure confirmation of a breitfussin analog by anisotropic NMR measurements

Abstract

Structural features of proton-deficient heteroaromatic natural products, such as the breitfussins, can severely complicate their characterization by NMR spectroscopy. For the breitfussins in particular, the constitution of the five-membered oxazole central ring cannot be unequivocally established via conventional NMR methods when the 4′-position is halogenated. The level of difficulty is exacerbated by 4′-iodination, as the accuracy with which theoretical NMR parameters are determined relies extensively on computational treatment of the relativistic effects of the iodine atom. It is demonstrated in the present study, that the structure of a 4′-iodo breitfussin analog can be unequivocally established by anisotropic NMR methods, by adopting a reduced singular value decomposition (SVD) protocol that leverages the planar structures exhibited by its conformers.

---

Introduction

Proton-deficient heteroaromatic natural products such as the breitfussins¹ and cephalandole A² pose a significant challenge for structural characterization via conventional NMR methodologies. The situation can be further exacerbated by halogen substitutions on the heterocycles. Determining the structures of compounds with these molecular features has been accomplished in the past by a combination of experimental and theoretical approaches, such as using mass spectrometry (MS) to obtain the molecular formula, NMR spectroscopy^3,4 to identify ring structures and substituent configuration and to establish through-bond connectivities, computer-assisted structure elucidation (CASE)^5–8 to make structural proposals based on experimental data, and total synthesis for unequivocal verification of the proposed structures.⁹ Molecular mechanics and density functional theory (DFT) calculations^1,5,6,10 have also been utilized to obtain three-dimensional geometries and to calculate theoretical NMR parameters (chemical shifts and scalar coupling constants) for comparison with experimental data.^11,12 When the breitfussins were first isolated, three molecular fragments were identified by conventional NMR and mass spectrometric methods that defined the constituents of the molecule. The fragments included a bromoindole, a bromopyrrole and an iodo-substituted oxazole ring.¹ However, assembling the molecular structure was daunting due to the multiple permutational possibilities of the iodo-substituted oxazole. The position of the iodo-substitution was inferred from the 5′′-brominated des-iodo analog, breitfussin B (see Fig. S1† for structure), using HMBC correlations semi-qualitatively to differentiate ³J_CH and ^2/4J_CH correlations. The general problem with proton-deficient molecules is the difficulty of ruling out the existence of an unconsidered structure that satisfies the sparse and thus insufficient data constraints better than the suggested structure.¹³ Consequently, the proposed structures of breitfussins A and B were supported by CASE and GIAO-DFT chemical shift calculations, with experimental confirmation provided by novel, state-of-the-art Atomic Force Microscopy (AFM) technology.^1,2,10,14

Recent advances in our ability to measure and utilize Residual Chemical Shift Anisotropy (RCSA) data have further augmented the utility of Residual Dipolar Couplings (RDC) and anisotropic NMR methods for defining the constitution and configuration of small molecules.^15–22 In particular, anisotropic NMR methods generate additional experimental constraints that provide orthogonal validation of structural proposals in a manner that is not prone to investigator bias.^7,17,23,24 The simultaneous use of both RDC and RCSA data is highly desirable; the former establishes the relative orientations of different C–H bond vectors while the latter affords orientation information of chemical shielding tensors of both protonated and non-protonated carbons. This strategy generally provides a more robust and discriminative analysis of structural proposals than that provided by using either RDC or RCSA data alone. Although these anisotropic NMR data in conjunction with DFT calculations have been successfully applied to several highly complex natural products,^13,24,25 molecules like the breitfussins present still further challenges. First, iodo-substitution introduces significant relativistic effects that potentially decrease the accuracy of the theoretically calculated molecular geometries and chemical shielding tensors. Second, the nearly planar lowest energy conformation limits the out-of-plane orientational sampling of anisotropic NMR data and consequently their utility by conventional singular value decomposition (SVD) analysis. Finally, the two rotatable bonds (bold red bonds in Fig. 1) connecting the three aromatic moieties leads to conformational flexibility that complicates the interpretation of the anisotropic NMR data. However, we demonstrate that the structure of a breitfussin A analog can be unequivocally determined solely based on RDC and RCSA data through implementation of the single-tensor SVD method by making use of the unique alignment properties of its planar structures. To the best of our knowledge, this approach has not yet been used for natural product structural characterization, and applications will likely be limited to predominantly planar conformations.

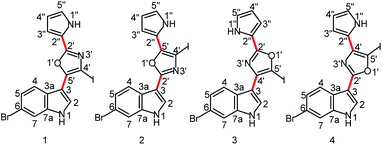Fig. 1 Four plausible constitutional isomers of a breitfussin A analog (see ESI† for the complete structural ensemble based on positional isomerism of the central aromatic ring). Red bonds denote rotatable bonds.

Results and discussion

The unambiguous characterization of breitfussin A analogs is problematic from both an experimental and a computational perspective due, in part, to the iodo-substitution of the oxazole. The problem is two-fold. First, there is the ambiguity associated with the possibility of positional isomerism of the oxazole moiety that is devoid of protons (Fig. 1). Although the constitution of the indole and pyrrole rings can be readily established from the usual ensemble of 2D NMR spectra (COSY, HSQC, HMBC), the same is not true for the substituted oxazole moiety – see Fig. S12† for all plausible oxazole and isoxazole isomers. Second, we found that the application of DFT techniques on the breitfussins did not lead to conclusive structural assignments, not least because of the large errors in computing accurate conformational energies and NMR chemical shifts for iodine-containing molecules. The impact of the relativistic effects of the heavy atoms, e.g. iodine and to a lesser extent bromine, on DFT calculation of energies and NMR parameters, including chemical shifts and spin–spin coupling constants must be taken into account.³⁶ For instance, in 1, a deviation of 42.3 ppm was observed for C4’ (the observed ¹³C chemical shift was 78.9 ppm for the iodo-bearing C4′ carbon) when the experimental chemical shift values were compared to the DFT-calculated chemical shift values (GIAO-mPW1PW91 ³⁷/6-311+G(2d,p)//M06-2X ³⁰/TZP-DKH ^33–35 for iodine and bromine and 6-31+G(d,p) for the other atoms) – see ESI† for the basis functions used on iodine and bromine. In comparison, the average ¹³C chemical shift for a series of six non-iodinated breitfussins analogs was 122.4 ppm.³⁸ In contrast, only a small difference of 0.5 ppm was observed for C5′.

Although the so-called heavy-atom–light-atom (HALA) relativistic effects³⁶ are primarily observed at the carbon nucleus directly attached to the heavy atom, their impact on conformer energies can be significant (Table 1). Geometry optimization of 1–4 at three levels of theory that are well validated for the modeling of organic molecules^26–35 revealed significant variations in the Boltzmann populations, relating to conformer energies.³⁹ The broad implications of this observation is that DFT-derived chemical shifts and other NMR parameters will likely be incorrectly weighted and could thus lead to unreliable comparisons with the experimental data. Specifically, the calculated Boltzmann population of conformer 1a, the major conformer of the correct constitutional isomer (vide infra), ranges from 79.1–48.5%, utilizing different DFT functionals/basis sets. The population of this conformer was, however, experimentally determined to be approximately 45% from ROESY measurements (see ESI† for details). Consequently, geometries and energies obtained with the contracted basis set for iodine and bromine (TZP-DKH^33–35) were used in all later comparisons, based on the assumption that the more accurate energy obtained for 1a indicates better suitability of this basis set for theoretical calculations on the other isomers as well.

Table 1 Boltzmann population distribution of the conformers of potential breitfussin A isomers, 1, 2, 3 and 4, computed with the electronic energies of the molecules derived from DFT calculations with selected functionals/basis sets shown (B3LYP,^26–29 M06-2X,³⁰ MIDI!,³¹ DGDZVP,³² TZP-DKH^33–35)

Isomers	Conformers	B3LYP/BS1^a^,^b(%)	M06-2X/BS2^a^,^b (%)	M06-2X/BS3^a (%)
a BS1: 6-31G* basis set on C, H, N, O and Br; MIDI!^31 basis set on I. BS2: 6-31+G** basis on C, H, N, O and Br; DZDZVP^32 basis on I. BS3: 6-31+G** basis on C, H, N and O; TZP-DKH^33–35 basis on Br and I. b Bracketed values were derived using electronic energies computed with Gaussian implementation of the Douglas-Kroll-Hess (DKH) Hamiltonian.
1	1a	79.1 (78.8)	61.8 (56.0)	48.5
	1b	3.0 (3.1)	19.6 (26.5)	33.8
	1c	17.9 (18.0)	14.0 (11.9)	10.1
	1d	0	4.6 (5.7)	7.7
2	2a	66 (67.1)	42.5 (46.3)	62.6
	2b	20.3 (20.7)	27.5 (24.0)	16.8
	2c	10.2 (9.2)	18.8 (20.4)	16.8
	2d	3.4 (3.1)	11.2 (9.4)	3.8
3	3a	76.7 (76.8)	61.0 (53.3)	39.3
	3b	2.4 (2.5)	20.4 (27.6)	43.9
	3c	20.9 (20.7)	13.6 (12.2)	9.1
	3d	0	5.0 (6.9)	7.7
4	4a	65.5 (65.2)	61 (59.4)	35.4
	4b	29.3 (29.1)	19.4 (18.6)	28.3
	4c	3.5 (3.9)	14.9 (16.9)	22.8
	4d	1.7 (1.8)	4.7 (5.1)	13.4

---

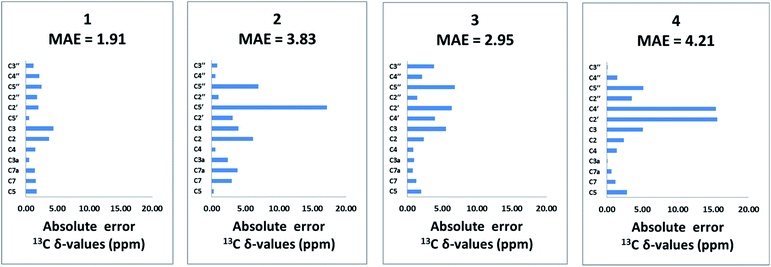
The population-averaged ¹³C chemical shifts calculated from DFT (mPW1PW91/TZP-DKH for iodine/bromine and mPW1PW91/6-311+G(2d,p) for other atoms) for 1–4 were compared to the experimental chemical shift values (chemical shift comparisons of the isoxazole analogs can be found in the ESI†). The mean absolute error (MAE) (excluding the halogen-bearing carbons) slightly favours 1 (1.91 ppm) over 2, 3 and 4 (3.83, 2.95, and 4.21 ppm, respectively). Bar charts of the absolute chemical shift errors for 1–4 are shown in Fig. 2. Although 2, 3 and 4 have slightly larger average errors than 1, unequivocal distinction of the isomers (especially between 1 and 3) is limited by possible errors in DFT-computed chemical shift values (see Fig. S13† for chemical shifts analysis of the isoxazole analogs). Clearly, further structural verification by orthogonal means, such as the utilization of RDC and RCSA data, is strongly justified.

Fig. 2 Bar charts of absolute errors of DFT-derived ¹³C chemical shift values for the non-halogenated carbons (mPW1PW91/6-311+G(2d,p)//M06-2X/TZP-DKH for iodine/bromine and mPW1PW91/6-311+G(2d,p)//M06-2X/6-31+G(d,p) for other atoms), compared to experimentally measured data for 1–4. The MAE of ¹³C chemical shifts is 1.91, 3.83, 2.95 and 4.21 ppm, respectively, for 1, 2, 3 and 4.

As shown in Table 1, the oxazole constitutional isomers can adopt at least two major conformations. Consequently, any meaningful interpretation of experimental RDC and RCSA data must account for this rotational exchange via comparisons with theoretical averages. The single-tensor singular-value decomposition (SVD) method was utilized to differentiate these isomers.^40–42 First, the coordinates and chemical shielding (CS) tensors of all conformers were superimposed to achieve the smallest RMSD for atomic positions through the principal axis frame (PAF) of their mass-weighted gyration tensors (Fig. 3). As Azurmendi, et al.⁴³ and Almond, et al.^44,45 have shown for biomolecules aligned in plane-like media, the principal axes of the mass-weighted gyration tensor, or the closely related moment of inertia tensor, coincide with those of the alignment tensor. For small molecules aligned in polymeric gels, this relationship cannot be assumed. As a result, we utilized only the gyration tensor PAF to provide a common frame for all conformations associated with each isomer thus setting the stage for single-tensor SVD analysis, following the proposal of Burnell and de Lange.⁴² As the gyration tensor has 4-fold symmetry, structural superposition was conducted by considering four possible orientations of each conformer relative to a reference conformer, and choosing the orientation that gave the lowest RMSD for pair-wise atomic positions. The Saupe order matrix in this common frame was assumed to be identical for all conformations and was determined by SVD using five free variables, specifically S_yy, S_zz, S_xy, S_yz, and S_xz, which were further used to back-calculate the theoretical averages of RDC and RCSA for each isomer.⁴⁶ The population of each conformation was optimized by the Nelder-Mead simplex procedure, which minimizes the Q-factor. This standard approach, the results of which are summarized in Table 2, is hereafter referred to as “Method A”. With the exception of 3, which exhibited a considerably higher Q-value of 0.154, the other isomers yielded very low Q-values: 0.050, 0.078 and 0.067, respectively, for 1, 2 and 4. This lack of differentiation clearly indicates that the available experimental data were insufficient for method A to unambiguously identify the correct isomer, and some degree of overfitting had likely occurred. It is worth pointing out that isomer 3, the closest isomer based on chemical shift MAE (2.95 vs. 1.91, Fig. 2), gives the largest Q-value of 0.154. The complementarity of chemical shifts and anisotropic NMR data, underscores the value of utilizing both approaches for structure elucidation of challenging molecules (similar observations have been made for a previously published study¹⁹). Due to conjugation, the conformers of the breitfussin A isomers, 1–4, were either nearly planar or have biaryl dihedral angles of <50° (see Fig. 3, S14 and S15† for details). Consequently, the out-of-plane orientation sampling in the anisotropic NMR data would be minimal. Although RCSA data for the aromatic carbons provide information on the orientation of the plane norm, this information is highly redundant for different carbons in a nearly flat conformation. To circumvent the potential problem of over-fitting by SVD analysis, we sought to impose additional constraints that leverages the planarity of conformers of these isomers.

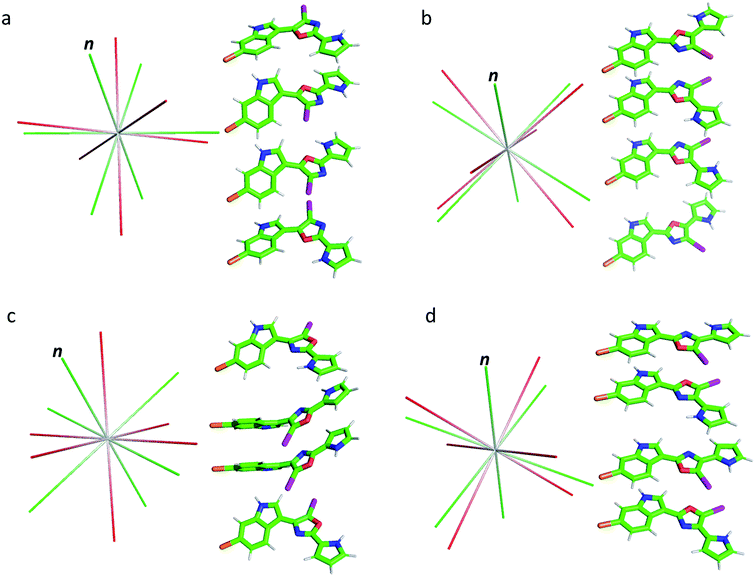Fig. 3 Conformations of isomers 1–4 (a–d) and their alignment tensor principal axes. Different conformations from the same isomer were initially superimposed through their mass-weighted gyration tensor PAF's and then separated vertically for better visualization (see alternative views in Fig. S14 and S15,† dihedral angles are collected in Table S5†). The alignment tensor principal axes determined from method A and B are coloured in red and green, respectively. The plane norm is indicated with “n”.

Table 2 Summary of results from the single-tensor SVD analysis of breitfussin A isomers 1–4

Isomers	Conformers	Population by DFT (%)	Optimized Population^a (%)	Q-factor (ensemble)^a, population is a variable	Optimized Population^b (%)	Q-factor (ensemble)^b, population is a variable	Q-factor (ensemble)^b, population fixed to DFT values
a Results obtained with method A. b Results obtained with method B.
1	1a	48.5	16	0.050	67	0.053	0.150
	1b	33.8	82.2		31.4
	1c	10.1	1.8		1.6
	1d	7.7	0		0
2	2a	62.6	0	0.078	0	0.095	0.744
	2b	16.8	0		0
	2c	16.8	0		43.1
	2d	3.8	100		56.9
3	3a	39.3	0	0.154	0	0.232	0.752
	3b	43.9	3.5		0
	3c	9.1	67.1		21
	3d	7.7	29.3		79
4	4a	35.4	0	0.067	0	0.126	0.802
	4b	28.3	0		0
	4c	22.8	92.3		100
	4d	13.4	7.8		0

---

Below we demonstrate that for a conformation of reflection symmetry, the mirror norm must be a principal axis of the alignment tensor when an achiral medium is used. To see this, we construct a molecular frame (MF) in which the mirror norm is along the z-axis; the x- and y-axes are within the mirror plane. The magnetic field B₀ has a zenith angle θ and azimuthal angle φ in this MF. To show that z is a principal axis of the alignment tensor, we prove that the off-diagonal Saupe order matrix elements S_xz and S_yz are zero. For instance, S_xz can be determined using the following equation:⁴⁷

where k and T are the Boltzmann constant and temperature, respectively, and H(θ,φ) is the energy of the molecule at a given orientation. In an achiral medium, including a new atactic poly-HEMA/MMA gel (for details of the gel preparation, which is a modification of the poly-HEMA gel reported by Gil, et al.⁴⁸ see ESI†), H(θ,φ) = H(π − θ,φ), which means that the interactions between a planar molecule and an achiral medium result in an energetically equivalent pair of microstates. Since sin(θ)is symmetric about π/2, i.e. 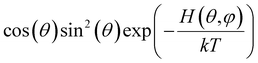sin(θ) = sin(π − θ), and cos(θ) is antisymmetric about π/2, the product will be antisymmetric about π/2. Consequently, the integral of the aforementioned expression from zero to π will be zero. The same conclusion is also derived for S_yz, proving that Z is a principal axis of alignment. It is worth noting that this relationship generally is not true for a chiral alignment medium, such as poly-γ-benzyl-L-glutamate (PBLG) lyotropic liquid crystalline phase.

In method B, we will impose the conclusion from the preceding paragraph on SVD analysis. If all conformations are transformed to a frame such that the plane norm is a Cartesian axis, e.g. the z-axis, then the off-diagonal elements of the Saupe order S_yz and S_xz, must be zero. Consequently, only three parameters, namely, S_yy, S_xx, and S_xy, need to be determined by SVD instead of five as this reduced SVD analysis now only needs to determine the orientation of the two in-plane principal axes. In practice, the implementation of this concept is quite simple based on the gyration tensor mentioned earlier. The approximate plane norm of a nearly flat conformation can be identified as the direction associated with the smallest principal moment of gyration (λ₁²). For a perfectly flat structure, λ₁² is zero. Therefore, the coordinates and CS tensors superimposed through the gyration tensor, as previously used in method A, can be directly used in method B, except that only three Saupe order matrix elements are used for SVD. The principal moments are listed in Table 3. The plane norm is associated with λ₁², which is zero or over five times smaller than λ₂² in all cases. It is also evident from Table 3 that different conformers of each constitutional isomer have very similar principal moments of gyration, and therefore the single-tensor approach is likely viable with the neutral poly-HEMA/MMA medium in which the alignment takes place mostly through steric interactions.

Table 3 The principal moments of gyration for all conformations of breitfussin A isomers, 1–4 (Ų)

Isomers	Conformers	λ 1 ^2	λ 2 ^2	λ 3 ^2
1	1a	0.0	6.1	13.3
	1b	0.6	3.9	14.8
	1c	0.6	4.1	14.6
	1d	0.1	6.1	13.1
2	2a	0.0	4.6	17.3
	2b	0.0	3.1	17.7
	2c	0.0	3.0	17.8
	2d	0.0	4.4	17.5
3	3a	0.2	5.9	13.6
	3b	0.7	3.8	15.0
	3c	0.7	3.6	15.1
	3d	0.1	5.7	13.9
4	4a	0.0	4.6	16.7
	4b	0.0	3.3	18.0
	4c	0.0	4.4	16.8
	4d	0.0	3.1	18.2

---

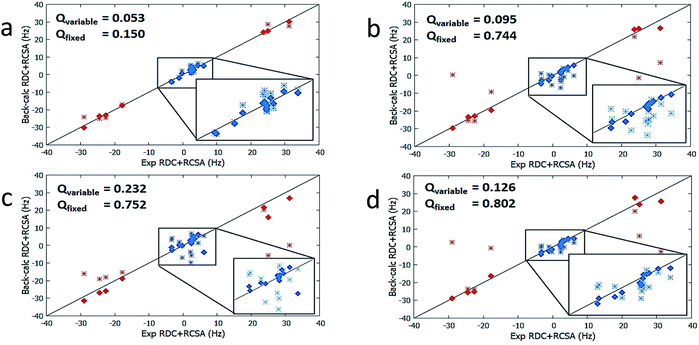
The results from method B are also summarized in Table 2. First, a reduced SVD analysis with variable conformational populations was performed. Clearly, 1 can be easily identified as the best match with a Q-factor of 0.053, with the second-best match 4 having a considerably larger Q-factor of 0.095. The correlation plots showing the agreement between experimental RDC and RCSA data and corresponding theoretical averaged values calculated using method B are displayed in Fig. 4. The correct structure, 1, is now clearly differentiated from its isomers. In Fig. 3, we displayed the alignment tensor PAF's from methods A (red) and B (green) side-by-side with the stacked conformers of the respective isomers, 1–4 (alternative top and side views of the various conformations of 1–4 are shown in Fig. S14 and S15†). The principal axis in method B that corresponds to the plane norm, n, is also indicated. Clearly, none of the principal axes from method A aligns with the plane norm or superimposes with the principal axes determined by method B, suggesting that method A generated physically unrealistic alignment tensor parameters for all isomers that led to artificially low Q-factors.

Fig. 4 Correlations between experimental RDC and RCSA measurements vs. theoretical averaged values calculated with method B for breitfussin A isomers 1–4 (a–d). Results from variable weight SVD analysis are plotted with diamond points whereas SVD analysis utilizing fixed Boltzmann populations (derived from DFT) are shown with double cross points. RDCs are denoted by red data points and RCSAs are denoted by blue data points.

It is also remarkable that amongst the four structure candidates 1–4, the optimized conformational distribution of 1, computed with method B, agrees reasonably well with DFT-computed Boltzmann distribution. In contrast, the optimized conformational distributions of 2, 3, and 4, also derived by SVD analysis with method B, favour conformations of higher DFT energies (see Table 2). This observation is further supported by a second reduced SVD analysis but with fixed conformer populations utilizing DFT-derived values as shown in Table 1 (M06-2X/BS3). As shown in Table 2, 1 is clearly distinguished as the correct isomer with the lowest Q-factor of 0.150 compared to the significantly higher Q-factors of 0.744, 0.752, and 0.802 for 2, 3, and 4, respectively. The enhanced isomeric differentiation using fixed Boltzmann populations underscores the benefit of obtaining accurate theoretical molecular energies in the ensemble-based analysis of flexible molecules.

Conclusions

Characterization of the structure of molecules like the breitfussins presents an enormous challenge utilizing traditional NMR methods. First, proton deficiency limits the number of HMBC correlations as well as the number of measurable RDCs. In the breitfussin A analog, only seven 1-bond ¹H–¹³C RDCs are available, and some of them are redundant, for instance C4–H4 and C7–H7, due to their parallel bonds. The data for the fourteen RCSAs were therefore critical for differentiating isomeric candidate structures. Second, the flat structural features limit out-of-plane orientation sampling of NMR anisotropic data. This potentially leads to incorrectly determined alignment tensor parameters and consequently seemingly good agreement can occur between experimental and back-calculated data for an incorrect isomer. In fact, for a perfect plane, there are only three independent in-plane RDCs and the plane norm orientation from RCSA is also redundant,^49,50 thus a SVD analysis with five free parameters is clearly problematic. In this work, we have shown that by imposing additional constraints on the alignment tensor based on molecular symmetry, such as the mirror symmetry/pseudo-symmetry inherent in the fairly flat conformations, the issue of orientation under-sampling can be successfully addressed. Indeed, making use of molecular symmetry has facilitated structural characterization of both biomolecules and small molecules.^{19,47,51–53} Third, conformational flexibility also complicates overall NMR analysis. For instance, reliable chemical shift-based structural differentiation of the isomers would require conformer Boltzmann populations to be calculated with reasonable accuracy to obtain correctly weighted average values. Conformational flexibility poses an even greater challenge for the interpretation of anisotropic NMR data and is most pronounced when internal molecular motions cannot be effectively decoupled from molecular re-orientation. Herein we have utilized the relatively simple single-tensor approach, leveraging the high similarity of the overall hydrodynamic properties of different conformers (Table 3), but more challenging cases certainly exist and would require further developments in experimental and computational methods. Finally, the presence of heavy atoms like iodine introduces substantial relativistic effects in DFT calculations that should be considered when working with such compounds.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

I. E. N. acknowledges support from the MRL Postdoctoral Research Program. S. K. P. also acknowledges the support of the Research Council of Norway (grant 224790/O30).

Notes and references

1. K. Ø. O. Hanssen, B. Schuler, A. J. Williams, T. B. Demissie, E. Hansen, J. H. Andersen, J. Svenson, K. Blinov, M. Repisky, F. Mohn, G. Meyer, J.-S. S. Svendsen, K. Ruud, M. Elyashberg, L. Gross, M. Jaspars and J. Isaksson, Angew. Chem., Int. Ed., 2012, 51, 12238–12241.
2. L. Gross, F. Mohn, N. Moll, G. Meyer, R. Ebel, W. M. Abdel-Mageed and M. Jaspars, Nat. Chem., 2010, 2, 821–825.
3. K. R. Gustafson, S. T. S. Chan and Y. Liu, in Modern NMR Approaches to the Structure Elucidation of Natural Products: Volume 2: Data Acquisition and Applications to Compound Classes, The Royal Society of Chemistry, 2017, vol. 2, pp. 39–70.
4. R. R. Gil and A. Navarro-Vázquez, in Modern NMR Approaches to the Structure Elucidation of Natural Products: Volume 2: Data Acquisition and Applications to Compound Classes, The Royal Society of Chemistry, 2017, vol. 2, pp. 1–38.
5. A. V. Buevich and M. E. Elyashberg, J. Nat. Prod., 2016, 79, 3105–3116.
6. A. V. Buevich and M. E. Elyashberg, Magn. Reson. Chem., 2018, 56, 493–504.
7. A. Navarro-Vázquez, R. R. Gil and K. Blinov, J. Nat. Prod., 2018, 81, 203–210.
8. M. R. M. Koos, A. Navarro-Vázquez, C. Anklin and R. R. Gil, Angew. Chem., Int. Ed., 2020, 59, 3938–3941.
9. S. K. Pandey, Y. Guttormsen, B. E. Haug, C. Hedberg and A. Bayer, Org. Lett., 2015, 17, 122–125.
10. B. Schuler, F. Mohn, L. Gross, G. Meyer and M. Jaspars, in Modern NMR Approaches to the Structure Elucidation of Natural Products, Volume 1: Instrumentation and Software, Royal Society of Chemistry, ed. D. R. Antony J. Williams and Gary E. Martin, 2016, pp. 306–320.
11. P. H. Willoughby, M. J. Jansma and T. R. Hoye, Nat. Protoc., 2014, 9, 643–660.
12. M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839–1862.
13. D. J. Milanowski, N. Oku, L. K. Cartner, H. R. Bokesch, R. T. Williamson, J. Saurí, Y. Liu, K. A. Blinov, Y. Ding, X.-C. Li, D. Ferreira, L. A. Walker, S. Khan, M. T. Davies-Coleman, J. A. Kelley, J. B. McMahon, G. E. Martin and K. R. Gustafson, Chem. Sci., 2018, 9, 307–314.
14. L. Gross, F. Mohn, N. Moll, P. Liljeroth and G. Meyer, Science, 2009, 325, 1110–1114.
15. F. Hallwass, M. Schmidt, H. Sun, A. Mazur, G. Kummerlöwe, B. Luy, A. Navarro-Vázquez, C. Griesinger and U. M. Reinscheid, Angew. Chem., Int. Ed., 2011, 50, 9487–9490.
16. N. Nath, M. Schmidt, R. R. Gil, R. T. Williamson, G. E. Martin, A. Navarro-Vázquez, C. Griesinger and Y. Liu, J. Am. Chem. Soc., 2016, 138, 9548–9556.
17. Y. Liu, J. Saurí, E. Mevers, M. W. Peczuh, H. Hiemstra, J. Clardy, G. E. Martin and R. T. Williamson, Science, 2017, 356, 5349.
18. Y. Liu, R. D. Cohen, K. R. Gustafson, G. E. Martin and R. T. Williamson, Chem. Commun., 2018, 54, 4254–4257.
19. I. E. Ndukwe, A. Brunskill, D. R. Gauthier, Y.-L. Zhong, G. E. Martin, R. T. Williamson, M. Reibarkh and Y. Liu, Org. Lett., 2019, 21, 4072–4076.
20. I. E. Ndukwe, X. Wang, I. Pelczer, M. Reibarkh, R. T. Williamson, Y. Liu and G. E. Martin, Chem. Commun., 2019, 55, 4327–4330.
21. A. Ibáñez de Opakua, F. Klama, I. E. Ndukwe, G. E. Martin, R. T. Williamson and M. Zweckstetter, Angew. Chem., Int. Ed., 2020, 59, 6172–6176.
22. X.-L. Li, L.-P. Chi, A. Navarro-Vázquez, S. Hwang, P. Schmieder, X.-M. Li, X. Li, S.-Q. Yang, X. Lei, B.-G. Wang and H. Sun, J. Am. Chem. Soc., 2020, 142, 2301–2309.
23. E. Troche-Pesqueira, C. Anklin, R. R. Gil and A. Navarro-Vázquez, Angew. Chem., Int. Ed., 2017, 56, 3660–3664.
24. I. E. Ndukwe, X. Wang, N. Y. S. Lam, K. Ermanis, K. L. Alexander, M. J. Bertin, G. E. Martin, G. Muir, I. Paterson, R. Britton, J. M. Goodman, E. J. N. Helfrich, J. Piel, W. H. Gerwick and R. T. Williamson, Chem. Commun., 2020, 56, 7565–7568.
25. E. Mevers, J. Saurí, Y. Liu, A. Moser, T. R. Ramadhar, M. Varlan, R. T. Williamson, G. E. Martin and J. Clardy, J. Am. Chem. Soc., 2016, 138, 12324–12327.
26. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
27. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
28. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
29. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
30. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
31. R. E. Easton, D. J. Giesen, A. Welch, C. J. Cramer and D. G. Truhlar, Theor. Chim. Acta, 1996, 93, 281–301.
32. C. Sosa, J. Andzelm, B. C. Elkin, E. Wimmer, K. D. Dobbs and D. A. Dixon, J. Phys. Chem., 1992, 96, 6630–6636.
33. C. T. Campos and F. E. Jorge, Mol. Phys., 2013, 111, 167–173.
34. K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052.
35. D. Feller, J. Comput. Chem., 1996, 17, 1571–1586.
36. T. B. Demissie, M. Repisky, S. Komorovsky, J. Isaksson, J. S. Svendsen, H. Dodziuk and K. Ruud, J. Phys. Org. Chem., 2013, 26, 679–687.
37. C. Adamo and V. Barone, J. Chem. Phys., 1998, 108, 664–675.
38. K. Ø. Hansen, J. H. Andersen, A. Bayer, S. K. Pandey, M. Lorentzen, K. B. Jørgensen, M. O. Sydnes, Y. Guttormsen, M. Baumann, U. Koch, B. Klebl, J. Eickhoff, B. E. Haug, J. Isaksson and E. H. Hansen, J. Med. Chem., 2019, 62, 10167–10181.
39. G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016, Gaussian, Inc., Wallingford CT.
40. C. M. Thiele, V. Schmidts, B. Böttcher, I. Louzao, R. Berger, A. Maliniak and B. Stevensson, Angew. Chem., Int. Ed., 2009, 48, 6708–6712.
41. V. M. Sánchez-Pedregal, R. Santamaría-Fernández and A. Navarro-Vázquez, Org. Lett., 2009, 11, 1471–1474.
42. E. Burnell and C. de Lange, J. Magn. Reson., 1980, 39, 461–480.
43. H. F. Azurmendi and C. A. Bush, J. Am. Chem. Soc., 2002, 124, 2426–2427.
44. A. Almond, J. Bunkenborg, T. Franch, C. H. Gotfredsen and J. Ø. Duus, J. Am. Chem. Soc., 2001, 123, 4792–4802.
45. A. Almond and J. B. Axelsen, J. Am. Chem. Soc., 2002, 124, 9986–9987.
46. J. A. Losonczi, M. Andrec, M. W. Fischer and J. H. Prestegard, J. Magn. Reson., 1999, 138, 334–342.
47. A. Saupe, Angew. Chem., Int. Ed. Engl., 1968, 7, 97–112.
48. L. F. Gil-Silva, R. Santamaría-Fernández, A. Navarro-Vázquez and R. R. Gil, Chem. - Eur. J., 2016, 22, 472–476.
49. D. L. Bryce and A. Bax, J. Biomol. NMR, 2004, 28, 273–287.
50. J. Boisbouvier, D. L. Bryce, E. O'Neil-Cabello, E. P. Nikonowicz and A. Bax, J. Biomol. NMR, 2004, 30, 287–301.
51. C. A. Bewley and G. M. Clore, J. Am. Chem. Soc., 2000, 122, 6009–6016.
52. H. M. Al-Hashimi, P. J. Bolon and J. H. Prestegard, J. Magn. Reson., 2000, 142, 153–158.
53. H. M. Al-Hashimi, A. Majumdar, A. Gorin, A. Kettani, E. Skripkin and D. J. Patel, J. Am. Chem. Soc., 2001, 123, 633–640.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc03664a

‡ Current address: Complex Carbohydrate Research Center, University of Georgia, 315 Riverbend Road, Athens, GA 30602.

§ Current address: Department of Chemistry and Biochemistry, University of North Carolina Wilmington, Wilmington, NC 28403.

¶ Current address: Analytical Research and Development, Pfizer Worldwide Research and Development, 445 Eastern Point Road, Groton, CT, 06340, USA.

|| Current address: Department of Chemistry and Biochemistry, Seton Hall University, South Orange, NJ 07079, USA.

---