Open Access Article
Open Access ArticleAcid–base chemistry at the single ion limit†
Vignesh
Sundaresan
 a and
Paul W.
Bohn
a and
Paul W.
Bohn
 *ab
*ab
aDepartment of Chemical and Biomolecular Engineering, University of Notre Dame, Notre Dame, IN 46556, USA. E-mail: pbohn@nd.edu
bDepartment of Chemistry and Biochemistry, University of Notre Dame, Notre Dame, IN 46556, USA
First published on 8th September 2020
Abstract
We present the results of acid–base experiments performed at the single ion (H+ or OH−) limit in ∼6 aL volume nanopores incorporating electrochemical zero-mode waveguides (E-ZMWs). At pH 3 each E-ZMW nanopore contains ca. 3600H+ ions, and application of a negative electrochemical potential to the gold working electrode/optical cladding layer reduces H+ to H2, thereby depleting H+ and increasing the local pH within the nanopore. The change in pH was quantified by tracking the intensity of fluorescein, a pH-responsive fluorophore whose intensity increases with pH. This behavior was translated to the single ion limit by changing the initial pH of the electrolyte solution to pH 6, at which the average pore occupancy 〈n〉pore ∼3.6H+/nanopore. Application of an electrochemical potential sufficiently negative to change the local pH to pH 7 reduces the proton nanopore occupancy to 〈n〉pore ∼0.36H+/nanopore, demonstrating that the approach is sensitive to single H+ manipulations, as evidenced by clear potential-dependent changes in fluorescein emission intensity. In addition, at high overpotential, the observed fluorescence intensity exceeded the value predicted from the fluorescence intensity-pH calibration, an observation attributed to the nucleation of H2 nanobubbles as confirmed both by calculations and the behavior of non-pH responsive Alexa 488 fluorophore. Apart from enhancing fundamental understanding, the approach described here opens the door to applications requiring ultrasensitive ion sensing, based on the optical detection of H+ population at the single ion limit.
Introduction
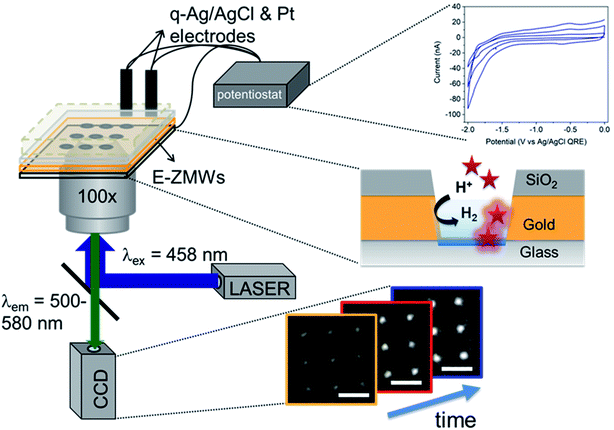
Electrochemistry of single entities in structures at the nanometer length scale has received much attention recently because it can reveal heterogeneity among entities that is hidden in ensemble/bulk measurements,1–4 thus providing a more nuanced picture of structure–property relationships than ensemble-average measurements.5–9 One of the growing areas in electrochemistry involves study of electron transfer reactions in small, confined volumes ranging from zeptoliters (1 zL = 10−21L = (10 nm)3) to femtoliters (1 fL = 10−15L = 1 μm3). Electrochemistry in these volumes is particularly attractive, because diffusive mass transport of the redox species is fast, iR drops are small so experiments can be implemented with two-electrode systems, and under proper electrolyte conditions, the entire volume resides within the electrical double layer.10–12 Exploiting these characteristics has produced unprecedented observations and capabilities. Bard and co-workers studied redox processes in attoliter volume emulsion droplets using the stochastic collision of single emulsion droplets on ultra-microelectrodes.13,14 Other groups have used this approach for electrodeposition of nanoparticles using nanoparticle precursor-filled emulsion droplets to achieve piece-by-piece construction.15–17 In addition, Unwin and co-workers developed scanning electrochemical cell microscopy (SECCM), where the electrolyte solution protruding from a nanopipette forms a localized electrochemical cell which can be scanned over an electrode surface to characterize the spatial distribution of electroactive sites.18,19In our laboratory, we have been interested in coupling zL/aL-volume electrochemistry with spectroscopic processes to achieve shot-noise limited electrochemical measurements. To achieve this, we developed a hybrid nano-electrochemical/nanophotonic structure – the electrochemical zero-mode waveguide (E-ZMW) – capable of addressing individual molecules, enzymes, and nanoparticles at volumes down to the zL scale by taking advantage of electrofluorogenic reactions.11,12,20–23 E-ZMWs are based on conical nanopores in a thin metal film (typically 100–200 nm thick Au) on an insulator (typically, fused silica). The bottom of the nanopore constitutes a sub-wavelength diameter aperture from the dielectric substrate into the (∼zL) fluid volume of the E-ZMW. When the ratio of the bottom diameter and metal thickness is beyond a cutoff value determined by the refractive index of the medium,24 far-field modes do not propagate. Under these conditions, the excitation radiation is confined within the conical nanopore, with the intensity decaying exponentially along the axial direction.20 E-ZMWs thus act as photonic nanobeakers with active volumes ∼10−18 L. It is straightforward to fabricate massively parallel arrays of such E-ZMW nanobeakers, and they can be efficiently monitored using optical techniques such as wide-field fluorescence microscopy, resulting in high throughput data collection. Time-sequence movies of the optical images can, for example, be used to follow the reactions occurring in each nanobeaker/E-ZMW and can be analyzed individually. In contrast, the electrochemical data is an ensemble measurement obtained from the whole array of E-ZMWs.
In this work, wide-field fluorescence microscopy was used to study the changes in local H+ concentration, Δ[H+], during electrochemical reduction of H+ in arrays of individual ∼6 aL-volume E-ZMWs. With aqueous electrolyte at pH 3, each E-ZMW nanopore initially contains ca. 3600H+ ions, 〈n〉pore ∼3600. The Pourbaix diagram predicts that direct H+ reduction dominates over H2O reduction to H2/OH− at acidic pH values, so applying a potential Eappl < −1.0 V vs. Ag/AgCl reduces H+ to H2, thereby decreasing the local [H+]. Changes in pH due to H+ reduction were monitored by adding sufficient pH-sensitive fluorophore fluorescein to achieve a 3 μM solution, corresponding to 〈n〉pore ∼10 fluorescein molecules per E-ZMW nanopore. Changes in fluorescence intensity during H+ reduction were then calibrated vs. pH, which allowed the pH in the E-ZMW to be determined to a local [H+] as low as 10−7 M (pH 7) which is equivalent to an average occupancy 〈n〉pore ∼0.36H+ per E-ZMW. In some instances, the fluorescence intensity during H+ reduction was found to significantly exceed the maximum intensity in the calibration curve, a behavior which is attributed to the generation of H2 nanobubbles within the E-ZMWs.
Results and discussion
Electrochemical zero-mode waveguide
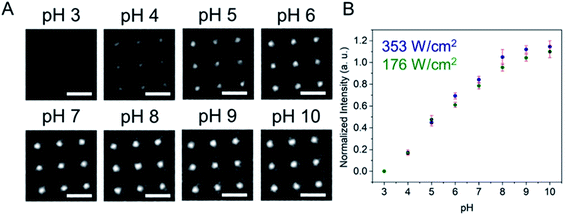
Fig. 1 shows a schematic diagram of the experimental apparatus (see ESI, Fig. S1 and S2,† for experimental details and procedures for fabrication of E-ZMW devices). Each E-ZMW nanopore is 300 nm thick (200 nm Au and 100 nm SiO2) with bottom and top diameters of ∼95 nm and ∼190 nm, respectively (Fig. S2†). The E-ZMW array was isolated in a polydimethylsiloxane (PDMS) well and mounted on an inverted epi-illumination fluorescence microscope equipped with a 100× oil-immersion objective, and the Au optical cladding layer of the E-ZMW was connected to a potentiostat, which ensures simultaneous electrical connection to all nine nanopores, and used as the working electrode. A platinum wire and a locally fabricated Ag/AgCl wire were placed in the PDMS well and used as counter and quasi-reference electrodes, respectively. A pH 3 solution containing 3 μM fluorescein and 0.2 M KNO3 supporting electrolyte was introduced into the PDMS well. When the potential was scanned to sufficiently negative potentials, the reduction of H+ to H2 produced a current which was integrated over the entire E-ZMW array by the potentiostat. At the same time, the sentinel fluorophores were excited at 458 nm in the E-ZMW configuration, as shown in Fig. 1, and the corresponding fluorescence was collected by the microscope objective, transmitted through a dichroic/cutoff filter, and imaged onto the active area of an EM-CCD camera with an image pixel size of 140 nm. Fluorescein is a pH-sensitive dye whose fluorescence increases with pH, as the weakly emissive monoanion, Fl−, is converted into the much more emissive dianion, Fl2−.25 Thus, in principle, the electrochemical reduction of H+ to H2 should deplete the local concentration of H+, shifting the Fl−/Fl2− equilibrium, and leading to an increase in ZMW emission, as shown schematically in Fig. 1.26First, a calibration curve was created relating the fluorescence intensity to the pH of the electrolyte solution in aL-volume solutions. The pH of a 0.2 M KNO3 electrolyte solution containing 3 μM fluorescein was adjusted to obtain solutions ranging from pH 3 to 10, and contrast-adjusted optical images, Fig. 2A, were obtained. The mean fluorescence intensity of each E-ZMW was measured by averaging the intensity over a 10 × 10 pixel region of interest. Then, the mean intensity of each E-ZMW at pH X was scaled to the mean intensity at pH 3 using,
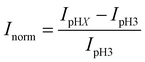 | (1) |
pH-dependent spectroelectrochemistry
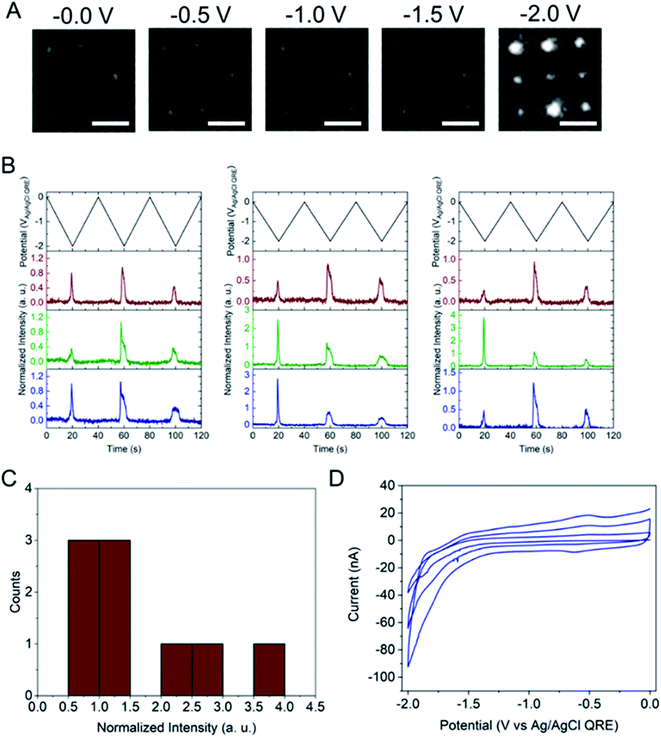
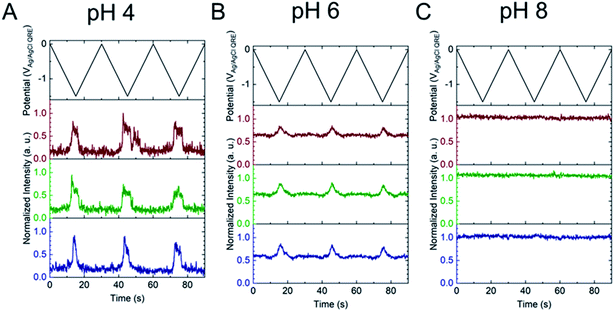
Next, the E-ZMW fluorescence intensity changes were tracked during potential sweeps in the range 0.0 V > Eappl > −2.0 V at pH 3. Fig. 3A shows series of optical images obtained from a 3 × 3 array of E-ZMW nanopores at different applied potentials, showing an increase in intensity at the most negative potential, −2.0 V (video available in ESI†). The intensity changes of all nine E-ZMW nanopores were then quantified and the normalized intensity displayed as a function of time/potential in Fig. 3B. In all three cycles of the potential sweep, the intensity remains low until the potential is within a few hundred mV of −2.0 V, at which point the fluorescence peaks sharply. However, the peak normalized intensity values vary from cycle to cycle for a given E-ZMW and also from nanopore to nanopore at the same point in a given cycle. These variation are likely due to the axial position at which fluorescein protonation occurs as well as variations in the nascent formation of nanobubbles (vide infra). Interestingly, some E-ZMW nanopores, e.g. green traces in the middle and right panel in Fig. 3B, show Inorm values substantially above the maximum, Inorm ∼1.2 shown in the calibration curve in Fig. 2B. The distribution of maximum values is summarized in Fig. 3C. Because the calibration curve for Inorm plateaus at ∼1.2 after pH 8, even if the local pH rises above 8, intensity values significantly exceeding 1.2 cannot be explained by pH alone. In addition, even though Inorm exceeds the expected maximum, the corresponding cyclic voltammogram, Fig. 3D, shows a response typical of the hydrogen evolution reaction (HER). The small peak observed in the range ∼ −0.5 to −0.7 V on the first CV cycle can be assigned to the electrochemical reduction of surface oxide formed on the titanium adhesion layer. The charge, ∼3 nC, associated with this small feature is ca. 100-fold smaller than that from direct H+ reduction and so is ignored in the analysis. Furthermore, the increase in current with the CV scans is attributed to an increase in the exposed electrochemical surface area caused by electrochemical reduction/cleaning of the gold electrode.There are two revealing observations in these potential sweep experiments: (a) the increase in emission intensity at the negative end of the potential range, and (b) the anomalously large maximum Inorm values observed in some experiments. In order to probe the dependence of the emission on pH, we characterized the luminescence resulting from pH changes produced during potential sweeps conducted at initial pH values of 4, 6 and 8. The results in Fig. 4 show several interesting points. As expected, the background fluorescence level increases with pH. Furthermore, similar to the behavior at the negative end of the potential sweep in Fig. 3B, Inorm remains constant until the negative end of the potential range is reached, at which point it increases. However, there are differences depending on the initial pH. When starting at pH 4, which corresponds to 〈n〉pore = 360H+, the intensity maximizes at Inorm = 0.7 ± 0.1 corresponding to an equivalent pH 6.57 ± 0.53 and 〈n〉pore = 1.53 ± 1.59. At a starting pH of 6, 〈n〉pore = 3.6H+, the observed changes in Inorm indicate pH 7.10 ± 0.27 and 〈n〉pore = 0.32 ± 0.19. Finally, at initial pH 8 solution (〈n〉pore = 0.036H+), no change in Inorm is observed due to change in the proton concentration given that pH 8 significantly exceeds the pKa of fluorescein (∼6.4). To complement these observations, control experiments were performed using buffered solutions at pH 4, 6 and 8, Fig. S3.† Interestingly, these experiments show no change in normalized intensity during potential sweep, as expected, due to buffer action.
It is important to interpret the observed electrochemically-induced fluorescence changes in the context of the shifting Fl−/Fl2− equilibrium, which can also be influenced by E-ZMW properties. Three factors are important. (1) Ion migration and ion accumulation. It is well known that nanopores are permselective, although this effect can be minimized by employing high concentration electrolyte (0.2 M KNO3).27 Negatively charged silica, in particular can accumulate positively charged ions/redox species.27,28 In the present experiment, we did not observe significant permselectivity effects, as shown by the calibration curve, Fig. 2B. Inorm increases linearly with pH due to the increase in Fl2− concentration, suggesting that the negatively charged silica layer does not substantially hinder transport of Fl−/Fl2− into the E-ZMW nanopores. (2) Optical field distribution. The optical field decays exponentially along the axial direction within the nanopore such that the estimated volume of the optical field, ca. 1 aL, is 6 times smaller than the geometric volume (∼6 aL).20 This indicates that under conditions used in these experiments only 〈n〉opt,pore ∼1.7 fluorescein molecules per E-ZMW are present in the effective optical volume. Although any given nanopore contains an integer number of molecules at a given time, fluctuations in occupancy do not affect the observed intensity, because images are integrated over 0.1 s, while fluorescein diffuses, 〈τ〉opt,pore ∼50 μs,22 into and out of the effective optical volume ∼2 × 103 times during the integration period, producing the uniform intensity values observed in Fig. 2A; (3) statistical fluctuations in E-ZMW nanopore population. The number of Fl− and Fl2− molecules in the E-ZMW excitation region can alter the observed intensity due to the difference in their fluorescence quantum yield. To help elucidate the effect of Fl−/Fl2− distribution we performed a Monte Carlo simulation at pH 6, because it close to the pKa (6.4) of fluorescein, Fig. S4.† Even though the ratio of Fl2−/Fl− is 0.40 at pH 6 based on Henderson–Hasselbalch equation, the Monte Carlo simulation provides an integer number distribution of Fl2−/Fl− within the E-ZMW. Based on 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations, the distributions in Fig. S4C and D† show the number of Fl− and Fl2− to be 7 ± 1 and 3 ± 1, respectively for single E-ZMW with an average capacity of 10 molecules. Thus, the expected Fl2−/Fl− ratio under these conditions is 0.43 ± 0.15 in good agreement with the equilibrium calculation. The simulation emphasizes that the observed fluorescence intensity at the single ion limit results from a time-averaged combination of three stochastic phenomena: (a) the presence of H+ ions and the propensity for them to be transported to - and reduced at – the working electrode, (b) the presence of the Fl2−/Fl− within the optical excitation volume, and (c) the Fl2−/Fl− equilibrium. The 100 ms time constant of the image acquisition smooths out the individual fluctuations, as shown in Fig. S4,† in all three phenomena and recovers the steady-state-like E-ZMW fluorescence signal observed experimentally.
000 iterations, the distributions in Fig. S4C and D† show the number of Fl− and Fl2− to be 7 ± 1 and 3 ± 1, respectively for single E-ZMW with an average capacity of 10 molecules. Thus, the expected Fl2−/Fl− ratio under these conditions is 0.43 ± 0.15 in good agreement with the equilibrium calculation. The simulation emphasizes that the observed fluorescence intensity at the single ion limit results from a time-averaged combination of three stochastic phenomena: (a) the presence of H+ ions and the propensity for them to be transported to - and reduced at – the working electrode, (b) the presence of the Fl2−/Fl− within the optical excitation volume, and (c) the Fl2−/Fl− equilibrium. The 100 ms time constant of the image acquisition smooths out the individual fluctuations, as shown in Fig. S4,† in all three phenomena and recovers the steady-state-like E-ZMW fluorescence signal observed experimentally.
H2 nanobubble formation
The other key observation from Fig. 3 concerns the anomalous maximum Inorm values. To further elucidate this observation, the experiment was repeated using another E-ZMW structure and scanned over a more limited range, 0.0 V > Eappl > −1.5 V, Fig. S5.† These abbreviated scan experiments were performed: (1) to test whether applying large negative potentials is solely responsible for the observation of substantially elevated Inorm values in Fig. 3, and (2) to control for any possible electrodeposition of Pt ions (oxidized from the counterelectrode) at the Au electrode/optical cladding layer of the E-ZMW. As shown in Fig. S5,† even scanning the potential to −1.5 V produces Inorm values exceeding the maximum normalized intensity value at ≥ pH 8 in Fig. 2. Furthermore, Fig. S5B† clearly indicates that the electrochemistry does not vary appreciably between scans, even though the maximum Inorm values vary significantly. Repeating this experiment multiple times with different substrates, a histogram of maximum normalized value from 50 individual E-ZMWs is obtained. Fig. S6,† shows that, far from being an anomalous observation, the majority (∼90%) of E-ZMWs exhibit Inorm values exceeding the pH 8 value.Next, the experiment was repeated in 0.1 M pH 3 phosphate buffer solution, as shown in Fig. S7,† and the results compared to those obtained from unbuffered solution. In the overwhelming majority [94% of 50 E-ZMWs] of cases, no changes in fluorescence intensity were observed, as exemplified by the brown and blue traces in Fig. S7.† The presence of the buffer clearly results in a very different electrofluorogenic luminescence behavior, indicating that the observation of anomalously high Inorm values in unbuffered solutions at the most negative potentials is not an artifact. In addition, these results inform the plausible mechanisms to explain the substantially increased maximum Inorm values. In particular, the calibration curve and the results of the potential sweep experiments in buffered solutions argue strongly that the large fluorescence spikes are not the result of altered Fl−/Fl2− ratios.
The electrochemical currents in Fig. 3D make it possible to calculate the total charge passed. Allowing for variation in maximum reduction currents among different cycles (40–90 nA), the estimated charge is ∼200 nC, corresponding to the reduction of 1.2 × 1012 H+ ions. This charge cannot be accounted for solely by the initial population of H+ at pH 3. In the 9 nanopores over which the current is integrated, ∼3.2 × 104 protons initially reside in the nanopores – or somewhat more, if permselectivity is taken into account. There are two possible ways this apparent limit could be circumvented: (1) direct reduction of water by the HER, or (2) diffusion of H+ from bulk solution into the nanopores. After reduction of all the H+ ions initially in the nanopore (discounting impurities) direct reduction of water would be the only viable faradaic process. Thus, after the reduction of initially resident H+ ions faradaic current would have to be supported by a combination of H+ replenished by diffusion from bulk solution or by direct HER of water. Ignoring activity effects, the last H+ ion left in a nanopore would represent a local pH ∼6.5, further supporting the conclusion that the non-canonical Inorm values are not due to acid–base chemistry of Fl−/Fl2−. If H+ were able to diffuse to the E-ZMW array from a hemispherical volume, taking the diffusion coefficient of H+ in H2O at 300 K to be ∼1 × 10−4 cm2 s−1, and estimating the time window of reduction to be 4 s total, the diffusive boundary hemisphere would be ∼0.25 μL, which at pH 3 would encompass ∼250 pmol, or ∼1.5 × 1014 H+ ions. Thus, the diffusive replacement mechanism would be able to replenish H+ ions reduced to H2 within the nanopores. Obviously the mass transport problem for bulk H2O is even less restrictive. Thus, a combination of H+ diffusion and direct HER is certainly feasible.
If direct acid–base chemistry is not likely responsible for the anomalously large fluorescence spikes, what is? An intriguing possibility is the formation of H2 nanobubbles, which could alter the fluorescence emission intensity in at least two ways, as shown schematically in Fig. S8.† First, fluorescein molecules can adsorb at the H2-solution interface, which can increase the fluorescence intensity substantially by allowing additional fluorescein to diffuse into the E-ZMW and, as previously reported, fluorescence at the air–water interface is 60 times stronger than in the bulk.29–31 Furthermore, the presence of the nanobubble changes the effective dielectric response function of the E-ZMW nanopore, thereby altering the outcoupling efficiency for emitted radiation.
To determine if the H2 nanobubble hypothesis is plausible, we first determined the bubble parameters based on observed electrochemical currents and nanopore geometry. Bubble formation is determined by the rate at which H2 is generated electrochemically, which in turn is governed by the observed currents. The maximum observed current in Fig. 3D, 90 nA, corresponds to 10 nA per nanopore. The current at a recessed disk electrode is related to the concentration of H2 generated by,
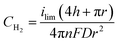 | (2) |
| PH2 = CH2/KH | (3) |
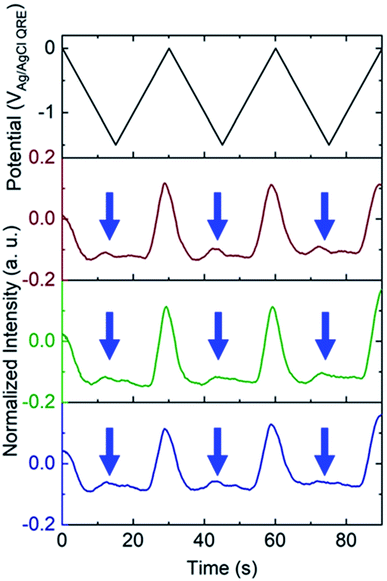
To test the nanobubble hypothesis further, we conducted two sets of experiments. First, the calibration, Fig. S9,† and potential sweep, Fig. S10,† experiments were repeated using a Pt-based E-ZMW instead of Au. Although the calibration curve is very similar to that observed with Au, Fig. 2B, Inorm values exceeding the maximum from the calibration curve (Inorm > 1.2) were also observed, Fig. S10,† confirming that the anomalous emission intensity phenomenon is independent of electrode material. Second, the pH-insensitive Alexa 488 fluorophore was employed, and a decrease in fluorescence intensity was observed over most of the potential range with the exception of the region near −1.5 V, where a small but reproducible increase was observed over multiple cycles and multiple pores, indicated by blue arrows in Fig. 5. Gooding and co-workers have documented the electrochemical reduction of Alexa 488 and accompanying fluorescence quenching over most of the negative portions of the potential range explored here.32 We attribute the modest increase in emission intensity observed at the most negative potentials in Fig. 5 to a small population of unreacted Alexa 488 whose intensity is enhanced by interaction with an H2 nanobubble, thus supporting the formation of nanobubbles even under these conditions, which mitigate against fluorescence.
White and co-workers identified a critical concentration of H2 (0.23 M) for the formation of nanobubbles, whereas in the present experiments a lower H+ concentration (pH 3) is observed to produce H2 nanobubbles.33–35 However, the nanobubbles observed here form randomly and are unstable. For example, the green trace in the middle panel of Fig. 3B, exhibits an Inorm above 1.2 for the first potential cycle, consistent with nanobubble formation, whereas in the second and third cycle no evidence of nanobubbles is observed. The distribution of maximum Inorm values shown in Fig. S6† also makes it clear that the formation of nanobubble nuclei with resulting anomalous (Inorm > 1.2) maximum fluorescence intensities is frequently, but not uniformly, observed. This is confirmed by the typical data in Fig. S11A,† where the modest increase in emission intensity is observed in the third cycle, but not in the first two. It is likely that the confined environment of the annular nanoband electrode in the E-ZMW affects nanobubble formation, but further experiments are required to better understand the role of E-ZMW geometry and materials. It is also worth noting that White and co-workers observed a characteristic decrease in the current due to blockage of the electroactive area by the nanobubble for electrodes with r < 50 nm. In the current experiments, we used nanocylindrical ring electrodes with substantially larger surface area, and measured current integrated over an ensemble of 9 nanopores, so we did not observe any blockage-related current features.
In conclusion, electrochemical-fluorescence microscopy with pH-responsive fluorescein was used to study redox-modulated acid–base chemistry inside attoliter volume E-ZMW nanopores under conditions that encompass the single ion limit. The overarching behavior of these structures involves the local depletion of H+ and concomitant formation of H2 inside the nanopore at the most negative potentials. The local pH was measured through the normalized fluorescence emission, which depends on the ratio Fl2−/Fl− which in turn depends on [H+]. Near pH 7 these measurements involve a small discrete number of protons interacting with a small population of fluorescein molecules. Averaging over large times (relative to diffusive transport into and out of the E-ZMW nanopores) produces fluorescence intensities that smooth out fluctuations in (a) H+ population, (b) the presence of the Fl2−/Fl− within the optical excitation volume, and (c) the Fl2−/Fl− equilibrium.
In addition, in a plurality of cases, anomalously large fluorescence intensities were observed at the most negative potentials. Based on a consideration of the limiting currents, nanopore geometries, and intensity distributions we attribute the higher intensity to the formation of H2 nanobubbles, which both traps fluorophores at the H2-water interface thereby enhancing the fluorescence intensity and also alters radiative outcoupling. Together these observations enable optical studies of the HER at the single entity level, making it possible to better understand nanobubble formation at the electrode–electrolyte interface. In addition, they may open the door to new diagnostics applications, such as DNA sequencing, by optical measurement of H+ release or consumption.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by NIH through grant 5R21GM126246-02. The authors thank the University of Notre Dame Nanofabrication Facility and Notre Dame Integrated Imaging Facility for their assistance and training.References
- L. A. Baker, J. Am. Chem. Soc., 2018, 140, 15549–15559 CrossRef CAS.
- T. Hersbach, J. MacPherson, O. Magnussen, R. Crooks, S. Higgins, D. Fermin, F. Kanoufi, W. Schuhmann, R. Nichols, S. Mitra, W. Schmickler, K. Tschulik, P. Bartlett, S. Faez, W. Nogala, M. Eikerling, C. Kranz, P. Unwin, M. Koper, S. Lemay, A. Mount, A. Ewing, Z. Tian, H. White, S. Chen, J. Clausmeyer and K. Krischer, Faraday Discuss., 2016, 193, 265–292 RSC.
- T. Albrecht, J. MacPherson, O. Magnussen, D. Fermin, R. Crooks, J. Gooding, T. Hersbach, F. Kanoufi, W. Schuhmann, C. Bentley, N. Tao, S. Mitra, K. Krischer, K. Tschulik, S. Faez, W. Nogala, P. Unwin, Y. Long, M. Koper, Z. Tian, M. A. Alpuche-Aviles, H. White, V. Brasiliense, C. Kranz, W. Schmickler, K. Stevenson, C. Jing and M. Edwards, Faraday Discuss., 2016, 193, 387–413 RSC.
- J. Gooding, O. Magnussen, D. Fermin, R. Crooks, F. Kanoufi, W. Schuhmann, R. Nichols, W. Schmickler, N. Tao, S. Chen, P. Actis, A. Page, K. Tschulik, S. Faez, M. Edwards, R. Johnson, W. Nogala, C. Kranz, M. Eikerling, P. Unwin, B. Thomas, V. Prabhakaran, J. Clausmeyer, K. Vincent, M. Koper, Z. Tian, A. Mount, M. A. Alpuche-Aviles, H. White, A. Ewing, S. Higgins, L. Baker, D. Zhan, J. Ulstrup, P. W. Bohn and S. Lemay, Faraday Discuss., 2016, 193, 141–170 RSC.
- V. Sundaresan, J. W. Monaghan and K. A. Willets, J. Phys. Chem. C, 2018, 122, 3138–3145 CrossRef CAS.
- F. T. Patrice, K. Qiu, Y.-L. Ying and Y.-T. Long, Annu. Rev. Anal. Chem., 2019, 12, 347–370 CrossRef.
- V. Sundaresan, J. W. Monaghan and K. A. Willets, ChemElectroChem, 2018, 5, 3052–3058 CrossRef CAS.
- K. Wonner, M. V. Evers and K. Tschulik, J. Am. Chem. Soc., 2018, 140, 12658–12661 CrossRef CAS.
- C. L. Bentley, M. Kang and P. R. Unwin, J. Am. Chem. Soc., 2019, 141, 2179–2193 CrossRef CAS.
- H. Alzahrani, C. Antoine, L. Baker, S. Balme, G. Bhattacharya, P. W. Bohn, Q. Cai, C. Chikere, R. M. Crooks, N. Das, M. Edwards, C. Ehi-Eromosele, N. Ermann, L. Jiang, F. Kanoufi, C. Kranz, Y. Long, J. MacPherson, K. McKelvey, M. Mirkin, R. Nichols, W. Nogala, J. Pelta, H. Ren, J. Rudd, W. Schuhmann, Z. Siwy, Z. Tian, P. Unwin, L. Wen, H. White, K. Willets, Y. Wu and Y. Ying, Faraday Discuss., 2018, 210, 145–171 RSC.
- K. Fu, S.-R. Kwon, D. Han and P. W. Bohn, Acc. Chem. Res., 2020, 53, 719–728 CrossRef CAS.
- K. Fu and P. W. Bohn, ACS Cent. Sci., 2018, 4, 20–29 CrossRef CAS.
- B.-K. Kim, A. Boika, J. Kim, J. E. Dick and A. J. Bard, J. Am. Chem. Soc., 2014, 136, 4849–4852 CrossRef CAS.
- B.-K. Kim, J. Kim and A. J. Bard, J. Am. Chem. Soc., 2015, 137, 2343–2349 CrossRef CAS.
- M. W. Glasscott and J. E. Dick, ACS Nano, 2019, 13, 4572–4581 CrossRef CAS.
- M. V. Evers, M. Bernal, B. R. Cuenya and K. Tschulik, Angew. Chem., Int. Ed., 2019, 58, 8221–8225 CrossRef CAS.
- Y. E. Jeun, B. Baek, M. W. Lee and H. S. Ahn, Chem. Commun., 2018, 54, 10052–10055 RSC.
- C. L. Bentley, M. Kang and P. R. Unwin, J. Am. Chem. Soc., 2017, 139, 16813–16821 CrossRef CAS.
- C. L. Bentley, M. Kang, F. M. Maddar, F. Li, M. Walker, J. Zhang and P. R. Unwin, Chem. Sci., 2017, 8, 6583–6593 RSC.
- D. Han, G. M. Crouch, K. Fu, L. P. Zaino III and P. W Bohn, Chem. Sci., 2017, 8, 5345–5355 RSC.
- L. P. Zaino III, D. A. Grismer, D. Han, G. M. Crouch and P. W. Bohn, Faraday Discuss., 2015, 184, 101–115 RSC.
- J. Zhao, L. P. Zaino III and P. W. Bohn, Faraday Discuss., 2013, 164, 57–69 RSC.
- J. Zhao, S. P. Branagan and P. W. Bohn, Appl. Spectrosc., 2012, 66, 163–169 CrossRef CAS.
- M. J. Levene, J. Korlach, S. W. Turner, M. Foquet, H. G. Craighead and W. W. Webb, Science, 2003, 299, 682–686 CrossRef CAS.
- H. Diehl and R. Markuszewski, Talanta, 1985, 32, 159–165 CrossRef CAS.
- N. C. Rudd, S. Cannan, E. Bitziou, I. Ciani, A. L. Whitworth and P. R. Unwin, Anal. Chem., 2005, 77, 6205–6217 CrossRef CAS.
- C. Ma, W. Xu, W. R. A. Wichert and P. W. Bohn, ACS Nano, 2016, 10, 3658–3664 CrossRef CAS.
- K. Fu, D. Han, C. Ma and P. W. Bohn, Nanoscale, 2017, 9, 5164–5171 RSC.
- X.-Y. Zheng, A. Harata and T. Ogawa, Spectrochim. Acta, Part A, 2001, 57, 315–322 CrossRef CAS.
- A. K. Dutta and C. Salesse, Langmuir, 1997, 13, 5401–5408 CrossRef CAS.
- R. Hao, Y. Fan, M. D. Howard, J. C. Vaughan and B. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5878–5883 CrossRef CAS.
- S. Fan, J. E. A. Webb, Y. Yang, D. J. Nieves, V. R. Gonçales, J. Tran, G. Hilzenrat, M. Kahram, R. D. Tilley, K. Gaus and J. J. Gooding, Angew. Chem., Int. Ed., 2019, 58, 14495–14498 CrossRef CAS.
- L. Luo and H. S. White, Langmuir, 2013, 29, 11169–11175 CrossRef CAS.
- Q. Chen, L. Luo, H. Faraji, S. W. Feldberg and H. S. White, J. Phys. Chem. Lett., 2014, 5, 3539–3544 CrossRef CAS.
- S. R. German, M. A. Edwards, H. Ren and H. S. White, J. Am. Chem. Soc., 2018, 140, 4047–4053 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: A detailed experimental section including fabrication of E-ZMW devices and spectroelectrochemical experimental apparatus, structural characterization of E-ZMWs, tracking pH changes during potential scan up to −1.5 V, statistics of the maximum normalized intensity value of 50 individual E-ZMWs, pH changes during the potential scan with pH 3 buffered solution, calibration curve and pH changes using Pt-based E-ZMWs, tracking pH changes during the potential scan with different buffed pH solution. Video (5.6 × 5.6 μm2) showing an increase in fluorescence intensity in E-ZMWs during electrochemical proton reduction (three potential sweep cycles). Video playing at 100 frames per second. See DOI: 10.1039/d0sc03756g |
| This journal is © The Royal Society of Chemistry 2020 |