Open Access Article
Open Access ArticleChallenging the Ostwald rule of stages in mechanochemical cocrystallisation†‡
Luzia S.
Germann
 *ab,
Mihails
Arhangelskis
*ab,
Mihails
Arhangelskis
 bc,
Martin
Etter
bc,
Martin
Etter
 d,
Robert E.
Dinnebier
d,
Robert E.
Dinnebier
 a and
Tomislav
Friščić
a and
Tomislav
Friščić
 *b
*b
aMax Planck Institute for Solid State Research, Heisenbergstr. 1, 70569 Stuttgart, Germany
bDepartment of Chemistry, McGill University, 801 Sherbrooke St. W., H3A 0B8 Montreal, Canada. E-mail: luzia.germann@mail.mcgill.ca; tomislav.friscic@mcgill.ca
cFaculty of Chemistry, University of Warsaw, 1 Pasteura Street, 02-109 Warsaw, Poland
dDeutsches Elektronen Synchrotron (DESY), Notkestraße 85, 22607 Hamburg, Germany
First published on 12th August 2020
Abstract
Mechanochemistry provides an efficient, but still poorly understood route to synthesize and screen for polymorphs of organic solids. We present a hitherto unexplored effect of the milling assembly on the polymorphic outcome of mechanochemical cocrystallisation, tentatively related to the efficiency of mechanical energy transfer to the milled sample. Previous work on mechanochemical cocrystallisation has established that introducing liquid or polymer additives to milling systems can be used to direct polymorphic behavior, leading to extensive studies how the amount and nature of grinding additive affect reaction outcome and polymorphism. Here, focusing on a model pharmaceutical cocrystal of nicotinamide and adipic acid, we demonstrate that changes to the choice of milling media (i.e. number and material of milling balls) and/or the choice of milling assembly (i.e. jar material) can be used to direct polymorphism of mechanochemical cocrystallisation, enabling the selective synthesis, and even reversible and repeatable interconversion of cocrystal polymorphs. While real-time mechanistic studies of mechanochemical transformations of metal–organic materials have previously suggested that reactions follow a path described by Ostwald's rule of stages, i.e. from metastable to increasingly more stable product structures, the herein presented systematic study presents an exception to that rule, revealing that modification of energy input in the mechanochemical system, combined with a small energy difference between polymorphs, permits the selective synthesis of either the more stable room temperature form, or the new metastable high-temperature form, of the target cocrystal.
Introduction
Mechanochemistry, i.e. the application of mechanical agitation as a way to conduct chemical transformations, is rapidly emerging as a cornerstone of greener, sustainable solvent-free strategies for molecular and materials synthesis,1,2 ranging from covalent3,4 and metal–organic frameworks (COFs and MOFs, respectively),5 coordination polymers,6 nanoparticle systems,7 to molecular cages,8 small molecules,9,10 and cocrystals.11,12 It has been shown that mechanochemistry is not only efficient for the synthesis of new metastable solid phases, but also a superior technique for polymorph and cocrystal screening, enabling the discovery of previously not observed thermodynamically stable phases even in well-studied systems.13Mechanochemical reactions are often performed by direct grinding or milling of reactants alone (neat grinding), or in presence of additives, as in liquid-assisted grinding (LAG)14 or polymer-assisted grinding (POLAG).15 The choice16–19 or amount of liquid additive16 in LAG, measured through the η-parameter14 (liquid-to-solid ratio in μL mg−1), can strongly influence mechanochemical reactions, and has been shown to enable modification of mechanochemical reaction mechanism,20 leading to different intermediates,21 or diverse product polymorphs.16–19,22 However, the factors that direct product formation in mechanochemistry remain poorly understood. Monitoring the progress of mechanochemical transformations in situ and ex situ has given evidence for complex reaction mechanisms, with multiple crystalline phases appearing as intermediates en route to the final product.5a,20,21 At least in the context of MOF formation,23a,b theoretical and experimental studies have indicated that such reaction sequences can be explained by Ostwald's rule of stages, i.e. relaxation of a system from a high energy state into the thermodynamically stable form via a series of increasingly stable intermediates.23c Whereas such thermodynamic considerations may suggest a route to predict the course of mechanochemical reactions,12b,23d it remains unclear whether mechanochemical reactions of organic and metal–organic materials generally conform to Ostwald's rule of stages. While it is well established that milling frequency,24–26 reaction jar filling,26,27a,28 size or mass of milling media26,27b,30–32 all affect rates of product formation, there are only a handful of reports discussing the influence of energy input,26,27,31,33,34 mixing properties, or design of the milling assembly in organic mechanochemistry.26,31,34–37 In fact, the latter appears to have remained unexplored in the context of polymorphism in mechanochemical reactions.37
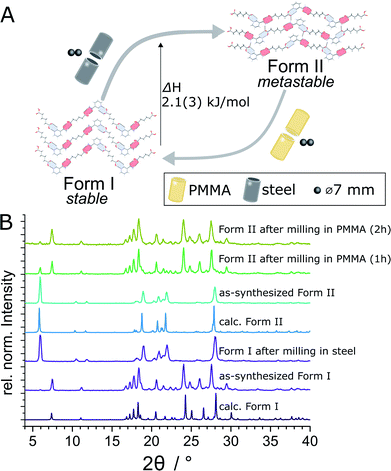
Here, we demonstrate a hitherto unexplored effect of the milling assembly, specifically the choice and material of milling jar and balls, on the polymorphism in mechanochemical cocrystallization (Fig. 1). This effect has resulted in the discovery of a previously not known metastable polymorph of a known model pharmaceutical cocrystal simply by changing the kind of milling balls or jar material. Moreover, changing the jar material enabled the reliable and repeatable interconversion between two cocrystal polymorphs simply by using different jar materials, e.g. stainless steel (ss) vs. poly(methyl methacrylate) (PMMA). While prior work suggested that mechanochemical reactions are likely to follow Ostwald's rule of phases, the herein presented reversible mechanochemical polymorph conversion contrasts such studies, and shows that different choices of the milling assembly can permit the selective formation of either thermodynamically more stable or metastable polymorphs of an organic cocrystal, independent of any external liquid or polymer additives.
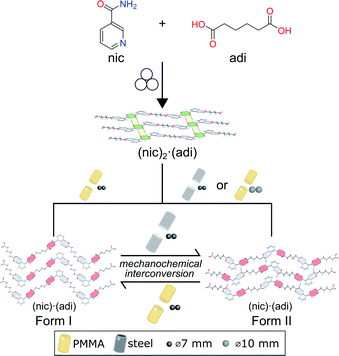 | ||
| Fig. 1 Schematic representation of the herein presented work, revealing that mechanochemical cocrystallisation of nic and adi can produce different, enantiotropically-related polymorphs Form I and Form II of the cocrystal (nic)·(adi), depending on the choice of the milling assembly. Similarly, milling the pre-made cocrystal polymorphs in either a PMMA or a ss milling jar enables the selective formation of either thermodynamicaly more stable Form I, or the metastable Form II, respectively. Sign for mechanochemistry (three balls) adapted from Rightmire and Hanusa.29 | ||
Results and discussion
Mechanochemical discovery of new polymorph
As the model system we used cocrystallisation of the active pharmaceutical ingredient (API) nicotinamide (nic) with the cocrystal former (coformer) adipic acid (adi). While the two are known to form cocrystals of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 respective stoichiometries,38 this work also led to the discovery and characterisation of a new, metastable (nic)·(adi) cocrystal polymorph (see section on evaluation of polymorph stability). Milling of nic and adi in a 1
1 respective stoichiometries,38 this work also led to the discovery and characterisation of a new, metastable (nic)·(adi) cocrystal polymorph (see section on evaluation of polymorph stability). Milling of nic and adi in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
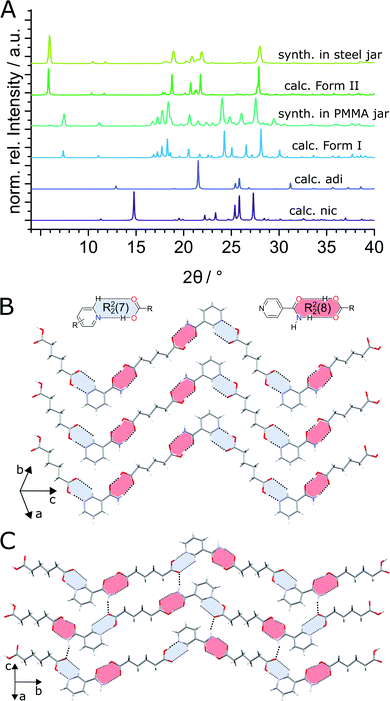
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio in the presence of acetonitrile (ACN) as liquid additive (η = 0.125 μL mg−1) and two stainless steel (ss) balls of 7 mm diameter (1.4 g each) in PMMA jars led to the formation of the previously known (nic)·(adi) cocrystal (CSD code NUKYIC), herein termed Form I (Fig. 2A and B). Comparison of measured and calculated X-ray powder diffraction (XRPD) patterns indicated that reaction was complete, with Form I (nic)·(adi) being the only crystalline phase in the reaction mixture, after ca. 60–90 min of milling (Fig. 2B). Surprisingly, repeating the reaction in ss jars under otherwise identical conditions led to the formation of a different material – a hitherto unknown (nic)·(adi) polymorph,‡ herein designated as Form II (Fig. 2A). Form II was found to be the enantiotropically related high-temperature phase of the thermodynamically more stable Form I (see section “Experimental and theoretical evaluation of polymorph stability”). The crystal structure of Form II was established from a combined XRPD and solid-state nuclear magnetic resonance (ssNMR) spectroscopy analysis (Fig. 2C, S1, S2B and S14–S18 in ESI‡). Both polymorphs consist of hydrogen-bonded zig-zag chains of alternating nic and adi molecules, connected by R22(7) pyridine-acid and R22(8) amide-acid heterosynthons (Fig. 2B and S2‡). Importantly, adi molecules in Form I lie on a centre of inversion, with each molecule involved in either two R22(7) or two R22(8) synthons (Fig. 2B). In contrast, each molecule of adi in Form II is involved in both a R22(7) and a R22(8) motif (Fig. 2B, C and S2‡).
1 molar ratio in the presence of acetonitrile (ACN) as liquid additive (η = 0.125 μL mg−1) and two stainless steel (ss) balls of 7 mm diameter (1.4 g each) in PMMA jars led to the formation of the previously known (nic)·(adi) cocrystal (CSD code NUKYIC), herein termed Form I (Fig. 2A and B). Comparison of measured and calculated X-ray powder diffraction (XRPD) patterns indicated that reaction was complete, with Form I (nic)·(adi) being the only crystalline phase in the reaction mixture, after ca. 60–90 min of milling (Fig. 2B). Surprisingly, repeating the reaction in ss jars under otherwise identical conditions led to the formation of a different material – a hitherto unknown (nic)·(adi) polymorph,‡ herein designated as Form II (Fig. 2A). Form II was found to be the enantiotropically related high-temperature phase of the thermodynamically more stable Form I (see section “Experimental and theoretical evaluation of polymorph stability”). The crystal structure of Form II was established from a combined XRPD and solid-state nuclear magnetic resonance (ssNMR) spectroscopy analysis (Fig. 2C, S1, S2B and S14–S18 in ESI‡). Both polymorphs consist of hydrogen-bonded zig-zag chains of alternating nic and adi molecules, connected by R22(7) pyridine-acid and R22(8) amide-acid heterosynthons (Fig. 2B and S2‡). Importantly, adi molecules in Form I lie on a centre of inversion, with each molecule involved in either two R22(7) or two R22(8) synthons (Fig. 2B). In contrast, each molecule of adi in Form II is involved in both a R22(7) and a R22(8) motif (Fig. 2B, C and S2‡).
In order to verify whether the observed difference in polymorphic outcome of the reaction is indeed associated with the choice of milling jar material, we compared products of milling nic and adi either neat, or by LAG in the presence of different liquid additives (H2O, MeOH, MeNO2, at a constant η value of 0.125 μL mg−1), in either PMMA or ss jars. All explored LAG reactions produced a different outcome depending whether the reactions were conducted in ss or PMMA jars (Fig. S3‡). While the thermodynamically more stable Form I was preferably formed in PMMA jars, reactions in ss jars tended to produce the metastable Form II. This confirms a profound effect of the milling jar material on the reaction outcome, regardless of the choice of milling additive.
Reactions by neat grinding in either ss or PMMA jars, as well as LAG with water in a ss jar, were found to be slower and incomplete,§ producing mixtures of Forms I and II or (nic)·(adi) with or without the stoichiometrically different (nic)2·(adi) cocrystal (CSD code NUKYOI). The (nic)2·(adi) cocrystal was subsequently identified as the first reaction intermediate by in situ monitoring (see In situ X-ray powder diffraction section).
While previous studies of LAG cocrystallisation have focused on the choice and/or amount of liquid additive as the principal factor controlling product polymorphism, these experiments clearly show a strong effect of the composition of the milling assembly on polymorphism in cocrystallisation.
Mechanochemical polymorph interconversion
The evident influence of jar material on mechanochemical cocrystallisation can be used to control the polymorphic form of the resulting cocrystal through post-synthetic interconversion (Fig. 3A). This was evidenced by milling a sample of mechanochemically prepared Form I in a ss jar, using a pair of ss balls (7 mm diameter each) in the presence of ACN (η = 0.125 μL mg−1). Milling produced phase-pure Form II within 60 minutes. Conversely, Form II prepared by this mechanochemical process was found to transform into Form I upon milling in a PMMA jar under otherwise identical conditions. The conversion of Form II into Form I was slower than the opposite process, as evidenced by a weak diffraction signal corresponding to small amounts of residual Form II after 2 hours milling (Fig. 3B). To the best of our knowledge, the described results represent the first demonstration of reversible mechanochemical polymorph interconversion between stable and metastable phases, achieved simply by modification of the milling assembly.In situ X-ray powder diffraction
We further explored mechanochemical cocrystallisation of nic and adi by monitoring the reaction through in situ synchrotron XRPD. Reaction monitoring was performed at the Powder Diffraction and Total Scattering beamline P02.1 of the Deutsches Elektronen-Synchrotron (DESY). All experiments were conducted using an in-house modified Retsch MM400 mill operating at 30 Hz,39 in 15 mL volume PMMA jars, with ACN as the liquid additive (η = 0.125 μL mg−1). X-ray transparent PMMA jars were used exclusively in order to minimise intrinsic X-ray absorption and scattering arising from the milling jars. Milling experiments were performed using either two (experiment A) or four (experiment B) ss balls of 7 mm diameter (1.4 g each), or two zirconia (ZrO2) balls of 10 mm diameter (2.9 g each, experiment C), leading to a total ball weight of 2.8, 5.6, and 5.8 g, respectively. In all cases, in situ observation revealed an initial formation of (nic)2·(adi) as the (first) reaction intermediate (Fig. 4 and 5A).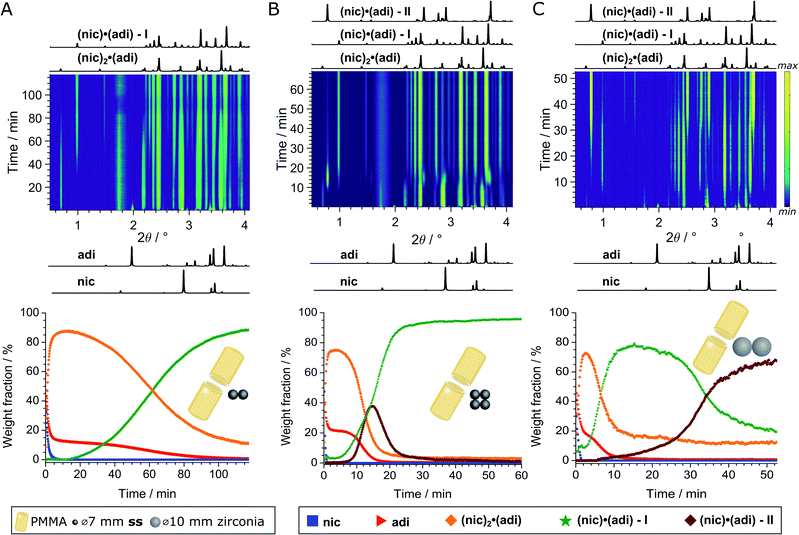 | ||
| Fig. 4 Top: In situ monitoring of the LAG reaction with ACN (η = 0.125 μL mg−1) with bottom the corresponding reaction profiles derived from quantitative phase via sequential Rietveld refinement for the reaction using (A) two 1.4 g ss, (B) four 1.4 g ss, and (C) two 2.9 g zirconia balls. Calculated XRPD patterns (λ = 0.207 Å) of reactants and cocrystals are shown below and above the 2D plots. The weight fractions of nic (blue squares), adi (red triangles), (nic)2·(adi) (orange diamond), (nic)·(adi) – I (green star), and (nic)·(adi) – II (burgundy diamond) are colored identical in (A)-(C). The weight fraction of (nic)2·(adi) cocrystal is intrinsically overestimated in (A and C), see ESI.‡ | ||
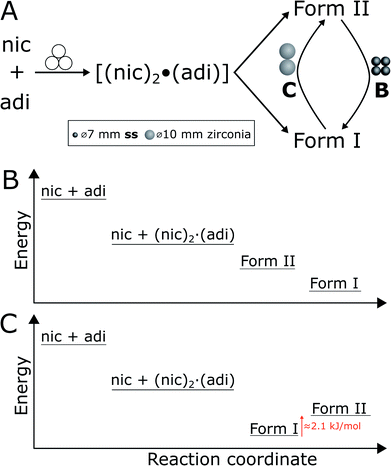
In experiment A, milling with two ss balls led to gradual conversion of (nic)2·(adi) into the known Form I (nic)·(adi) as the final product, with the reaction reaching completion after ca. 85 minutes milling (Fig. 4A). Next, we monitored the mechanochemical cocrystallisation using four ss balls of 1.4 g weight each (total balls weight 5.6 g), effectively doubling the total ball mass. Increasing the weight of milling media in experiment B corresponds to an increase in energy delivered to the reaction system, and is anticipated to lead to an increase in reaction rate.32 Such an increase was indeed observed, along with the transient appearance of Form II of the (nic)·(adi) cocrystal. Forms I and II appeared concomitantly and their content increased almost simultaneously, indicating the conversion of the intermediate (nic)2·(adi)via two competing pathways. However, the content of Form II reaches a maximum after ca. 15 minutes milling and is depleted soon after, while the amount of Form I steadily increases. This can be explained by most of the reaction mixture being converted to a mixture of Forms I and II after ca. 15 minutes, making apparent the process of mechanochemical conversion of Form II into Form I, which remains the final product after reaching a steady-state within ca. 40 min (Fig. 4B). Overall, in situ monitoring of experiment B reveals that milling under harsher reaction conditions, accomplished by increasing the overall weight of milling media from 2.8 g to 5.6 g, enabled the observation of a metastable intermediate. Such behavior is consistent with Ostwald's rule of stages that anticipates the appearance of metastable, high-energy intermediate phases, as the system is developing towards the thermodynamically preferred phase.
In experiment C (Fig. 4C), the reaction was repeated under identical conditions, but using two 10 mm ZrO2 balls (2.9 grams each), of approximately the same weight (total of 5.8 grams) as the four ss balls used in experiment B. This enabled conducting a mechanochemical reaction in which the energy being brought to the milling assembly is nearly identical to that in experiment B, but distributed in a different way. This led to a further acceleration of the first reaction step with the initial formation of (nic)2·(adi) being complete after ca. 2.5 minutes. While both Form I and II (nic)·(adi) again appeared concomitantly, under these conditions the growth of Form I was significantly faster than for Form II. As a result, after 15 minutes the reaction mixture was composed mostly of Form I (nic)·(adi). Further milling leads to the process opposite to that seen in experiment B, i.e. direct conversion of Form I into Form II. Considering that Form I is the thermodynamically more stable form of the (nic)·(adi) cocrystal until the transition point temperature measured to be ca. 85–90 °C, these observations that the mechanochemical formation of the metastable polymorph (Form II) proceeds via the thermodynamically more stable phase (Form I) are in contrast to Ostwald's rule of stages (Fig. 5B).
Experimental and theoretical evaluation of polymorph stability
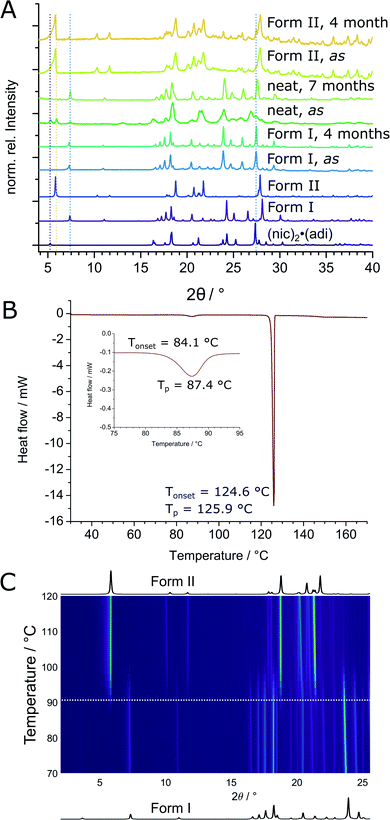
The thermodynamic relationship between two (nic)·(adi) polymorphs was investigated experimentally and by theoretical periodic density functional theory (DFT) calculations. Experimental studies were conducted by solvent-mediated phase transformation40 in a static system, in a slurry, by long-term stability measurements, and by thermal analysis. Solvent-mediated experiments under static conditions, starting with a physical mixture of both polymorphs, led to the disappearance of Form II (Fig. S4‡) with Form I remaining as the main crystalline phase. Slurry experiments were more difficult to interpret since, independent of the starting composition, some of the mixtures eventually transformed into (nic)2·(adi) with release of pure adi (Fig. S5‡). Several long-term stability measurements revealed on one hand a slow transformation of Form II into Form I over a couple of months in air at room temperature, as evidenced by the appearance of Bragg reflections of Form I in a previously phase-pure sample of Form II (Fig. 6A and S6‡). On the other hand, complete transformation of a reaction mixture of (nic)2·(adi), (nic)·(adi) Form I and Form II, as well as adi into Form I was observed within 7 months upon storage (Fig. 6A and S6‡). These results are consistent with Form I being the thermodynamically preferred one in this system. Thermal behavior of both polymorphs was investigated in detail by thermal analysis and variable temperature XRPD (VT-XRPD) measurements. A combined differential scanning calorimetry and thermogravimetric analysis (DSC-TGA) of Form II showed a sharp endothermic signal with an onset at ca. 124 °C upon heating, corresponding to melting. Crystallisation upon cooling took place at ca. 100 °C, without any notable changes in sample weight throughout the experiment (Fig. S10‡). In contrast, two distinct endothermic signals appeared in the DSC thermograms of Form I upon heating, starting at ca. 84 °C and 124 °C, again with no change in sample weight (Fig. 6B, S9 and S11–S13‡). The first signal was attributed to the transformation of Form I into Form II, as confirmed by VT-XRPD measurements which revealed a transition taking place in the range 85–100 °C (Fig. 6C and S7‡). The second DSC signal is assigned to melting of Form II, with crystallisation occurring upon cooling at ca. 106 °C (Fig. S9‡). No transformation of Form II into Form I was observed by VT-XRPD experiments upon cooling to −180 °C (Fig. S8‡). The crystallographic calculated density of Form II is somewhat lower (1.32 g cm−3) compared to Form I (1.36 g cm−3). In conclusion, Form I is the thermodynamically more stable form at ambient condition, with Form II as the enantiotropically-related high temperature polymorph. This is in excellent agreement with crystallographic calculated densities, different long-term stability, as well as VT-XRPD, and thermal measurements.The transition enthalpy for the polymorphic transformation of Form I into Form II was calculated based on the integrated area of the endothermic signal in DSC measurements (see ESI‡). The enthalpy for the transformation of Form I to Form II is ca. 1.6(2) kJ mol−1 at the transition temperature (ca. 90 °C), which translates to 2.1(3) kJ mol−1 at the temperature of mechanochemical milling (estimated to be ca. 35 °C), based on the molar heat capacity of Form I evaluated from DSC measurements (see ESI, Tables S2–S4, Fig. S10, and S11–S13‡).
The relative stability of (nic)·(adi) polymorphs was also explored by periodic DFT calculations, using the plane-wave DFT code CASTEP.41 Crystal structures of all the cocrystals as well as nic and adi reactants were geometry-optimised using the Perdew–Burke–Ernzerhof (PBE)42 functional combined with many-body dispersion (MBD*)43–45 correction scheme. In these calculations, the geometries of observed phases, i.e. atomic coordinates and lattice parameters, were fully optimised to yield the total electronic energies. The calculated energy of (nic)2·(adi) cocrystal with respect to the starting reactant mixture for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 reaction was −8.5 kJ mol−1. The corresponding relative energies for (nic)·(adi) Form I and (nic)·(adi) Form II were −7.5 kJ mol−1 and −10.2 kJ mol−1, respectively (Table S5‡). While calculations indicate that cocrystallisation of nic and adi is thermodynamically favourable, the calculated energies for all three cocrystals differ by less than 3 kJ mol−1, which is comparable to the experimentally determined transition enthalpy. This, however, also means that the relative energy ranking of the three cocrystals cannot be reliably established by herein explored periodic DFT calculations.46,47
1 reaction was −8.5 kJ mol−1. The corresponding relative energies for (nic)·(adi) Form I and (nic)·(adi) Form II were −7.5 kJ mol−1 and −10.2 kJ mol−1, respectively (Table S5‡). While calculations indicate that cocrystallisation of nic and adi is thermodynamically favourable, the calculated energies for all three cocrystals differ by less than 3 kJ mol−1, which is comparable to the experimentally determined transition enthalpy. This, however, also means that the relative energy ranking of the three cocrystals cannot be reliably established by herein explored periodic DFT calculations.46,47
Discussion
The described milling experiments demonstrate that the course and polymorphic outcome of mechanochemical cocrystallisation can strongly be affected by choice of material from which the milling media or the entire milling assembly are made. Whereas mechanochemical reactions of metal–organic materials were recently shown to follow Ostwald's rule of stages,23a the herein explored cocrystal of nic and adi exhibits significantly different behavior. In particular, our study shows that either the high temperature Form II or the room temperature Form I of the (nic)·(adi) cocrystal is obtained, depending on choice of milling assembly. While the observed appearance of Form II as an intermediate in the mechanochemical formation of the more stable Form I is not surprising (Fig. 4 and 5B), the ability to also obtain Form II as the final product, via the thermodynamically more stable Form I as an intermediate, is in clear contrast with Ostwald's rule of stages (Fig. 5C). Moreover, our study shows that the two forms can even readily interconvert depending on the choice of milling assembly, i.e. milling jars and balls.We tentatively explain such behavior, unprecedented in mechanochemical cocrystallisation, by the small energy difference between the two cocrystal polymorphs. Specifically, we propose that the difference in stability of Forms I and II is sufficiently small that minor changes in the mechanical energy input during milling can lead to preferred formation of either one or the other polymorph. This scenario is somewhat reminiscent of the proposal made over 120 years ago by M. Carey Lea, the “father of mechanochemistry”, who suggested that mechanochemical reactions can enable the formation of metastable products in systems that “…possessed an equilibrium so singularly balanced as to be affected by the slightest action…”.48 The herein presented system belongs to this category, with a ΔH between Forms I and II of only 2.1(3) kJ mol−1 (at the transition temperature, ca. 90 °C). We propose that the observed selectivity for either Form I or Form II is related to a difference in the efficiency of transfer of mechanical energy from the milling assembly to the sample (Fig. 5A). Specifically, formation of Form II, and transformation of Form I to Form II, was achieved by milling in ss jars, while the opposite processes were observed upon milling in PMMA jars. As the jar volume,¶ sample amount and choice of milling media were identical in those experiments, we relate the difference in reaction outcome to a more efficient transfer of mechanical energy using a ss jar of higher elastic properties compared to PMMA, evidenced by respective Young's moduli of 208 GPa![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 (for 440C ss jar material) to ca. 3–5 GPa.50
49 (for 440C ss jar material) to ca. 3–5 GPa.50
The importance of energy input in order to overcome the energy threshold for the formation of Form II is also evidenced by in situ monitoring studies, which were all conducted in PMMA jars of identical volume and weight. In this case, the appearance of Form II was first induced by increasing the number of ss media and their overall weight. Previous studies indicate that such changes result in a higher energy input in a mechanochemical reaction and, under these conditions, Form II was as observed as a metastable, short-lived intermediate consistent with Ostwald's rule of stages. However, more efficient energy transfer has also enabled the formation of Form II as the final reaction product in PMMA jars. This was observed by switching from ss media to those based on the more elastic material zirconia, with Young's modulus ∼221–223 GPa.51 By replacing four ss (total weight 5.6 grams) balls with two zirconia balls (total weight 5.8 grams), it was possible to conduct the experiment with almost identical weight of milling media. As there was no significant change in overall sample weight or choice of milling jars between these experiments, the observed difference in reactivity can be related to more efficient energy transfer due to choice of material. It is, however, important to note that energy input could also be affected by differences in motion and impact of individual balls.26b,27b
While we cannot fully exclude the importance of changes in additional factors such as particle size,52 frictional properties of the mixture, and/or temperature, we are confident that the observed results are not associated to seeding and surface templating effects, as the same set of PMMA jars was used for the mechanosynthesis of both polymorphs. Previous studies of mechanochemical organic reactions have indicated that the choice of milling media and/or jars can have a significant impact on temperature and frictional properties of the milled reaction mixture.25,30,33b We attempted to measure the temperature of reaction mixture using an infrared probe immediately after milling, but did not observe any significant differences between reactions in PMMA or ss jars. Indeed, the evolution of temperature in a mechanochemical reaction is difficult to establish with certainty,53 and surface temperature measurements are not expected to be highly reliable, as Kubota et al. have shown that the temperature can vary significantly (ca. 10 °C) across the jar surface.54
Conclusions
In conclusion, we have demonstrated that the formation and interconversion of polymorphs during mechanochemical cocrystallisation is strongly affected, and can be controlled, by the choice of milling assembly. While milling reactions have previously been shown to follow the Ostwald's rule of stages,23a our results demonstrate that exceptions can be observed for systems in which different products exhibit only a small difference in energy. This is the case for the herein described polymorphs of the cocrystal of nicotinamide and adipic acid, exhibiting a ∼2 kJ mol−1 difference in stability, whose selective formation can be accomplished by changes to the milling assembly leading to different energy inputs. While this represents the first experimental report of polymorphs that can mechanochemically interconvert by modification of the milling assembly, similar behaviour might be observable for other enantiotropically related polymorphic systems that are sufficiently close in energy.55 Moreover, while previous work focused solely on the choice and amount of liquid additive to control and explore polymorphism in mechanochemical cocrystallisation, our work shows that the choice of milling assembly itself can also play a crucial role in mechanochemical polymorph selection and, indeed, be used to interconvert between cocrystal polymorphs.To the best of our knowledge, this work represents the first demonstration of how a mechanochemical reaction can be directed to produce either thermodynamically stable or metastable cocrystal polymorphs, only by changes to the milling jar and/or balls. We believe that further studies of how the choice of milling assembly affects product polymorphism might provide a means to design more reliable mechanochemical synthesis procedures and avoid potential obstacles in mechanochemical solid form development, such as the recently discussed “disappearing polymorph”56,57 or “hidden cocrystal”58 phenomena.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Drs Sandra Kaabel and Dritan Hasa for valuable scientific discussions. Dr Robin S. Stein is acknowledged for collecting ssNMR spectra and scientific discussions. We thank Dr Hatem M. Titi for help with DSC measurements. L. S. G acknowledges financial support from the Swiss National Science Foundation (Grant P2SKP2_187638). M. A. acknowledges the financial support of the National Science Center of Poland (Grant 2018/31/D/ST5/03619). T. F. acknowledges the financial support of the NSERC Discovery Grant (RGPIN-2017-06467), NSERC Discovery Accelerator award (RGPAS 507837-17), and the NSERC E. W. R. Steacie Memorial Fellowship (SMFSU 507347-17). This article is based upon work from COST Action CA18112 (https://www.mechsustind.eu) supported by COST (European Cooperation in Science and Technology, https://www.cost.eu). This research was enabled in part by support provided by Calcul Québec (https://www.calculquebec.ca) and Compute Canada (https://www.computecanada.ca).Notes and references
- (a) T. Friščić, C. Mottillo and H. M. Titi, Angew. Chem., Int. Ed., 2020, 59, 1018–1029 CrossRef PubMed; (b) E. Colacino, A. Porcheddu, C. Charnay and F. Delogu, React. Chem. Eng., 2019, 4, 1179–1188 RSC; (c) W. Pickhardt, S. Grätz and L. Borchardt, Chem.–Eur. J., 2020 DOI:10.1002/chem.202001177; (d) G.-W. Wang, Chem. Soc. Rev., 2013, 42, 7668–7700 RSC; (e) J. L Howard, Q. Cao and D. L. Browne, Chem. Sci., 2018, 9, 3080–3094 RSC.
- (a) S. L. James, C. J. Adams, C. Bolm, D. Braga, P. Collier, T. Friščić, F. Grepioni, K. D. M. Harris, G. Hyett, W. Jones, A. Krebs, J. Mack, L. Maini, A. G. Orpen, I. P. Parkin, W. C. Shearouse, J. W. Steed and D. C. Waddell, Chem. Soc. Rev., 2011, 41, 413–447 RSC; (b) T. K. Achar, A. Bose and P. Mal, Beilstein J. Org. Chem., 2017, 13, 1907–1931 CrossRef CAS PubMed; (c) J. G. Hernández and C. Bolm, J. Org. Chem., 2017, 82, 4007–4019 CrossRef PubMed; (d) E. Colacino, G. Dayaker, A. Morere and T. Friščić, J. Chem. Educ., 2019, 96, 766–771 CrossRef CAS; (e) L. Konnert, F. Lamaty, J. Martinez and E. Colacino, Chem. Rev., 2017, 117, 13757–13809 CrossRef CAS PubMed; (f) K. Kubota, Y. Pang, A. Miura and H. Ito, Science, 2019, 366, 1500–1504 CrossRef CAS PubMed.
- B. P. Biswal, S. Chandra, S. Kandambeth, B. Lukose, T. Heine and R. Banerjee, J. Am. Chem. Soc., 2013, 135, 5328–5331 CrossRef CAS PubMed.
- S. Chandra, S. Kandambeth, B. P. Biswal, B. Lukose, S. M. Kunjir, M. Chaudhary, R. Babarao, T. Heine and R. Banerjee, J. Am. Chem. Soc., 2013, 135, 17853–17861 CrossRef CAS PubMed.
- (a) A. D. Katsenis, A. Puškarić, V. Štrukil, C. Mottillo, P. A. Julien, K. Užarević, M.-H. Pham, T.-O. Do, S. A. J. Kimber, P. Lazić, O. Magdysyuk, R. E. Dinnebier, I. Halasz and T. Friščić, Nat. Commun., 2015, 6, 6662 CrossRef CAS PubMed; (b) D. Prochowicz, J. Nawrocki, M. Terlecki, W. Marynowski and J. Lewiński, Inorg. Chem., 2018, 57, 13437–13442 CrossRef CAS PubMed.
- C. Cappuccino, F. Farinella, D. Braga and L. Maini, Cryst. Growth Des., 2019, 19, 4395–4403 CrossRef CAS.
- (a) P. Baláž, M. Achimovičová, M. Baláž, P. Billik, Z. Cherkezova-Zheleva, J. M. Criado, F. Delogu, E. Dutková, E. Gaffet, F. J. Gotor, R. Kumar, I. Mitov, T. Rojac, M. Senna, A. Streletskii and K. Wieczorek-Ciurowa, Chem. Soc. Rev., 2013, 42, 7571–7637 RSC; (b) H. Schreyer, R. Eckert, S. Immohr, J. de Bellis, M. Feldehoff and F. Schüth, Angew. Chem., Int. Ed., 2019, 58, 11262–11265 CrossRef CAS PubMed.
- M. Leonardi, M. Villacampa and J. C. Menéndez, Chem. Sci., 2018, 9, 2042–2064 RSC.
- G.-W. Wang, Chem. Soc. Rev., 2013, 42, 7668–7700 RSC.
- A. Bruckmann, A. Krebs and C. Bolm, Green Chem., 2008, 10, 1131–1141 RSC.
- (a) D. Hasa and W. Jones, Adv. Drug Delivery Rev., 2017, 117, 147–161 CrossRef CAS PubMed; (b) D. Braga, L. Maini and F. Grepioni, Chem. Soc. Rev., 2013, 42, 7638–7648 RSC; (c) D.-K. Bučar, S. Filip, M. Arhangelskis, G. O Lloyd and W. Jones, CrystEngComm, 2013, 15, 6289–6291 RSC.
- (a) S. A. Ross, D. A. Lamprou and D. Douroumis, Chem. Commun., 2016, 52, 8772–8786 RSC; (b) S. Lukin, I. Lončarić, M. Tireli, T. Stolar, M. V. Blanco, P. Lazić, K. Užarević and I. Halasz, Cryst. Growth Des., 2018, 18, 1539–1547 CrossRef CAS.
- I. R. Speight, I. Huskić, M. Arhangelskis, H. M. Titi, R. S. Stein, T. P. Hanusa and T. Friščić, Chem.–Eur. J., 2020, 26, 1811–1818 CrossRef CAS PubMed.
- T. Friščić, S. L. Childs, S. A. A. Rizvi and W. Jones, CrystEngComm, 2009, 11, 418–426 RSC.
- D. Hasa, G. Schneider Rauber, D. Voinovich and W. Jones, Angew. Chem., Int. Ed., 2015, 54, 7371–7375 CrossRef CAS PubMed.
- D. Hasa, E. Miniussi and W. Jones, Cryst. Growth Des., 2016, 16, 4582–4588 CrossRef CAS.
- T. Friščić and W. Jones, Cryst. Growth Des., 2009, 9, 1621–1637 CrossRef.
- A. V. Trask, W. D. S. Motherwell and W. Jones, Chem. Commun., 2004, 890–891 RSC.
- A. V. Trask, N. Shan, W. D. S. Motherwell, W. Jones, S. Feng, R. B. H. Tan and K. J. Carpenter, Chem. Commun., 2005, 880–882 RSC.
- P. A. Julien, K. Užarević, A. D. Katsenis, S. A. J. Kimber, T. Wang, O. K. Farha, Y. Zhang, J. Casaban, L. S. Germann, M. Etter, R. E. Dinnebier, S. L. James, I. Halasz and T. Friščić, J. Am. Chem. Soc., 2016, 138, 2929–2932 CrossRef CAS PubMed.
- I. Halasz, A. Puškarić, S. A. J. Kimber, P. J. Beldon, A. M. Belenguer, F. Adams, V. Honkimäki, R. E. Dinnebier, B. Patel, W. Jones, V. Štrukil and T. Friščić, Angew. Chem., Int. Ed., 2013, 52, 11538–11541 CrossRef CAS PubMed.
- S. H. Lapidus, A. Naik, A. Wixtrom, N. E. Massa, V. Ta Phuoc, L. del Campo, S. Lebègue, J. G. Ángyán, T. Abdel-Fattah and S. Pagola, Cryst. Growth Des., 2014, 14, 91–100 CrossRef CAS.
- (a) Z. Akimbekov, A. D. Katsenis, G. P. Nagabhushana, G. Ayoub, M. Arhangelskis, A. J. Morris, T. Friščić and A. Navrotsky, J. Am. Chem. Soc., 2017, 139, 7952–7957 CrossRef CAS PubMed; (b) M. Arhangelskis, A. D. Katsenis, N. Novendra, Z. Akimbekov, D. Gandrath, J. M. Marrett, G. Ayoub, A. J. Morris, O. K. Farha, T. Friščić and A. Navrotsky, Chem. Mater., 2019, 31, 3777–3783 CrossRef CAS; (c) J. C. Burley, M. J. Duer, R. S. Stein and R. M. Vrcelj, Eur. J. Pharm. Sci., 2007, 31, 271–276 CrossRef CAS PubMed; (d) M. Arhangelskis, F. Topić, P. Hindle, R. Tran, A. J. Morris, D. Cinčić and T. Friščić, Chem. Commun., 2020, 56, 8293–8296 RSC.
- P. A. Julien, I. Malvestiti and T. Friščić, Beilstein J. Org. Chem., 2017, 13, 2160–2168 CrossRef CAS PubMed.
- X. Ma, W. Yuan, S. E. J. Bell and S. L. James, Chem. Commun., 2014, 50, 1585–1587 RSC.
- (a) R. Schmidt, H. M. Scholze and A. Stolle, Int. J. Ind. Chem., 2016, 7, 181–186 CrossRef; (b) R. Schmidt, C. F. Burmeister, M. Baláž, A. Kwade and A. Stolle, Org. Process Res. Dev., 2015, 19, 427–436 CrossRef CAS; (c) A. Stolle, R. Schmidt and K. Jacob, Faraday Discuss., 2014, 170, 267–286 RSC.
- (a) H. Kulla, F. Fischer, S. Benemann, K. Rademann and F. Emmerling, CrystEngComm, 2017, 19, 3902–3907 RSC; (b) F. Fischer, N. Fendel, S. Greiser, K. Rademann and F. Emmerling, Org. Process Res. Dev., 2017, 21, 655–659 CrossRef CAS.
- Mechanochemical cocrystallization of caffeine and trifluoroacetic acid can lead to different polymorphic outcomes, depending on the total amount of material in the jar, and independent of reaction time: A. V. Trask, J. van de Streek, W. D. S. Motherwell and W. Jones, Cryst. Growth Des., 2005, 5, 2233–2241 CrossRef CAS.
- N. R. Rightmire and T. P. Hanusa, Dalton Trans., 2016, 45, 2352–2362 RSC.
- A. A. L. Michalchuk, I. A. Tumanov and E. V. Boldyreva, J. Mater. Sci., 2018, 53, 13380–13389 CrossRef CAS PubMed.
- K. S. McKissic, J. T. Caruso, R. G. Blair and J. Mack, Green Chem., 2014, 16, 1628–1632 RSC.
- A. A. L. Michalchuk, I. A. Tumanov and E. V. Boldyreva, CrystEngComm, 2019, 21, 2174–2179 RSC.
- (a) M. Carta, S. L. James and F. Delogu, Molecules, 2019, 24, 3600–3613 CrossRef CAS PubMed; (b) I. A. Tumanov, A. F. Achkasov, E. V. Boldyreva and V. V. Boldyrev, CrystEngComm, 2011, 13, 2213–2216 RSC.
- (a) J. Andersen and J. Mack, Angew. Chem., Int. Ed., 2018, 57, 13062–13065 CrossRef CAS PubMed; (b) J. M. Andersen and J. Mack, Chem. Sci., 2017, 8, 5447–5453 RSC.
- M. Broseghini, M. D'Incau, L. Gelisio, N. M. Pugno and P. Scardi, Materials & Design, 2016, 110, 365–374 CrossRef CAS.
- L. Takacs and V. Šepelák, J. Mater. Sci., 2004, 39, 5487–5489 CrossRef CAS.
- Kulla et al. recently reported the increased polymorphic stability of dimorphic cocrystals based on the used jar material, see: H. Kulla, C. Becker, A. A. L. Michalchuk, K. Linberg, B. Paulus and F. Emmerling, Cryst. Growth Des., 2019, 19, 7271–7279 CrossRef CAS.
- S. Karki, T. Friščić and W. Jones, CrystEngComm, 2009, 11, 470–481 RSC.
- (a) T. Friščić, I. Halasz, P. J. Beldon, A. M. Belenguer, F. Adams, S. A. J. Kimber, V. Honkimäki and R. E. Dinnebier, Nat. Chem., 2013, 5, 66–73 CrossRef PubMed; (b) I. Halasz, S. A. J. Kimber, P. J. Beldon, A. M. Belenguer, F. Adams, V. Honkimäki, R. C. Nightingale, R. E. Dinnebier and T. Friščić, Nat. Protoc., 2013, 8, 1718–1729 CrossRef PubMed.
- G. G. Z. Zhang, R. F. Henry, T. B. Borchardt and X. Lou, J. Pharm. Sci., 2007, 96, 990–995 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. M. Reilly and A. Tkatchenko, Chem. Sci., 2015, 6, 3289–3301 RSC.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- C. R. Taylor and G. M. Day, Cryst. Growth Des., 2018, 18, 892–904 CrossRef CAS PubMed.
- E. Schur, J. Bernstein, L. S. Price, R. Guo, S. L. Price, S. H. Lapidus and P. W. Stephens, Cryst. Growth Des., 2019, 19, 4884–4893 CrossRef CAS.
- M. C. Lea, Am. J. Sci., 1892, 34, 527–531 CrossRef.
- H. M. Ledbetter, N. V. Frederick and M. W. Austin, J. Appl. Phys., 1980, 51, 305–309 CrossRef CAS.
- (a) G. Wei and B. Bhushan, J. Vac. Sci. Technol., 2005, A23, 811–819 CrossRef; (b) C. Ishiyama and Y. Higo, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 460–465 CrossRef CAS.
- J. W. Adams, R. Ruh and K. S. Mazdiyasni, J. Am. Ceram. Soc., 1997, 80(4), 903–908 CrossRef CAS.
- A. M. Belenguer, G. I. Lampronti, A. J. Cruz-Cabeza, C. A. Hunter and J. K. M. Sanders, Chem. Sci., 2016, 7, 6617–6627 RSC.
- K. Užarević, N. Ferdelji, T. Mrla, P. A. Julien, B. Halasz, T. Friščić and I. Halasz, Chem. Sci., 2018, 9, 2525–2532 RSC.
- K. Kubota, Y. Pang, A. Miura and H. Ito, Science, 2019, 366, 1500–1504 CrossRef CAS PubMed.
- (a) J. Nyman and G. M. Day, CrystEngComm, 2015, 17, 5154–5165 RSC; (b) R. M. Bhardwaj, J. A. McMahon, J. Nyman, L. S. Price, S. Konar, I. D. H. Oswald, C. R. Pulham, S. L. Price and S. M. Reutzel-Edens, J. Am. Chem. Soc., 2019, 141, 13887–13897 CrossRef CAS PubMed.
- J. D. Dunitz and J. Bernstein, Acc. Chem. Res., 1995, 28, 193–200 CrossRef CAS.
- D. Hasa, M. Marosa, D.-K. Bučar, M. K. Corpinot, D. Amin, B. Patel and W. Jones, Cryst. Growth Des., 2020, 20, 1119–1129 CrossRef CAS.
- D.-K. Bučar, G. M. Day, I. Halasz, G. G. Z. Zhang, J. R. G. Sander, D. G. Reid, L. R. MacGillivray, M. J. Duer and W. Jones, Chem. Sci., 2013, 4, 4417–4425 RSC.
Footnotes |
| † This work is dedicated to Prof. Joel Bernstein (1941–2019). |
| ‡ Electronic supplementary information (ESI) available. CCDC 1981453. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc03629c |
| § Reactions by neat milling are generally expected to be slower compared to LAG reactions, see for example: N. Shan, F. Toda and W. Jones, Chem. Commun., 2002, 2372–2373. |
| ¶ Whereas the jar volume was different during synthesis for PMMA (15 mL) and ss jars (Retsch, 10 mL), it was identical for the interconversion reaction using 15 mL ss jars, see ESI.‡ |
| This journal is © The Royal Society of Chemistry 2020 |