Hierarchical two-dimensional molecular assembly through dynamic combination of conformational states at the liquid/solid interface

Abstract

Self-sorting of multiple building blocks for correctly positioning molecules through orthogonal recognition is a promising strategy for construction of a hierarchical self-assembled molecular network (SAMN) on a surface. Herein we report that a trigonal molecule, dehydrobenzo[12]annulene (DBA) derivative having three tetradecyloxy chains and three hydroxy groups in an alternating manner, forms hierarchical triangular clusters of different sizes ranging from 2.4 to 16.4 nm, consisting of 3 to 78 molecules, respectively, at the liquid/graphite interface. The key is the dynamic combination of three different conformational states, which is solvent and concentration dependent. The present knowledge extends design strategies for production of sophisticated hierarchical SAMNs using a single component at the liquid/solid interface.

---

Introduction

Self-assembled molecular networks (SAMNs)¹ spontaneously formed by organic molecules through self-assembly on solid surfaces are a subject of keen interest because of their prospect of application in the fields of nanoscience and nanotechnology.^2–6 Sophisticated structural control of SAMNs based on new design principles may lead to complexity as seen in biological systems, thereby enriching their potential for applications. One of the major challenges in this field of research is the construction of hierarchical structures that extend several tens of nanometers or even sub-micrometers in size.^2–8 However, the structural periodicities in the known SAMNs using small molecular building blocks are typically limited to several nanometers.^9,10 SAMNs with a periodicity of more than 100 nm could be fabricated only using large DNA molecules.¹¹ Therefore, there is a need for formulating clear design principles for the formation of hierarchical SAMNs with a long-range periodicity using small molecular building blocks.^12,13

The most common strategy to construct large hierarchical structures is the use of building blocks of C₃ or D_3h symmetry capable of assembling through strong non-covalent interactions such as hydrogen bonding and metal coordination, and they are typically prepared under ultrahigh vacuum (UHV) conditions.^14–17 Under these conditions, the size of unit cells can be modified by surface coverage. By fully exploiting this approach, a hierarchical structure with a large unit cell of 45 nm was reported recently.¹⁸ Another strategy for the construction of hierarchical SAMNs with long-range periodicity is to optimize multiple intermolecular interactions using elaborated building blocks or multi-component building block(s).^19–24 Such experiments are typically undertaken at the liquid/solid interfaces or occasionally in air.²⁵ Compared to UHV conditions, the unit cell size and the number of building blocks for constructing such hierarchical structures are limited, because the presence of a supernatant solvent renders the self-assembly and system complicated. Solvation and surface wetting compete with intermolecular and molecule–substrate interactions, and solvent molecules are often co-adsorbed in SAMNs.^26–28

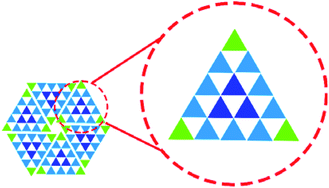
In hierarchical superstructures, the constituent clusters consist of three different parts, i.e., vertices, edges and internal core, each bearing different coordination numbers (Fig. 1). In most cases, a single building block forms these different parts by adapting the modes of intermolecular interactions as enforced by an external factor, i.e., surface density. Such self-assembly behavior may be regarded as a kind of self-sorting, even though this term is defined as “mutual recognition of complementary components in artificial self-assembly”.^29–31 On a surface, there exists only one example of such self-sorting through dynamic combination of conformational states of a single molecular building block, yet the structural controlling factors were not discussed in detail.³²

Fig. 1 Schematic representation of a hierarchical hexagonal structure of a triangular cluster which consists of three different parts (color codes for three different trigonal disks classified by their positions: blue; at an internal core, green; at vertices, cyan; at edges).

Here, we extend the above concept to produce hierarchical SAMNs using a C_3h-symmetric building block with orthogonal coordination sites for van der Waals interaction and hydrogen bonding. By changing its conformation on the surface depending on the solvent polarity, the building block self-assembles to form hierarchical structures made of triangular clusters with size ranging from 2.4 to 16.4 nm, and consisting of 3 to 78 molecules, respectively. The molecules form the vertices, edges and core positions of the clusters as well, thanks to balanced orthogonal intermolecular interactions. Each triangular cluster comprises the feature of Pascal's triangle which is a triangular array of binomial coefficients in mathematics. Scanning tunneling microscopy (STM) is our method of choice, since it provides high quality structural information in real space of SAMNs on atomically flat conductive surfaces such as graphite, even at the liquid/solid interface.^33,34

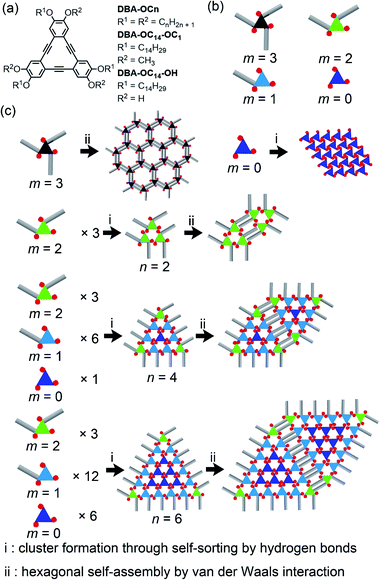
Over the past decade, we studied the self-assembly of dehydrobenzo[12]annulene derivatives DBA-OCns having six long alkoxy groups at the liquid/graphite interfaces (Fig. 2a).³⁵DBA-OCns form low density porous structures and high density non-porous structures. The length of the alkoxy groups, solute concentration and temperature determine the relative abundance of the polymorphs.³⁶ The main driving forces for the formation of these SAMNs are the intermolecular interaction through van der Waals interactions between the alkoxy groups and molecule–substrate interactions between the alkoxy groups and graphite. Of further relevance is the fact that in the non-porous structures, four alkoxy groups are physisorbed on the surface while the remaining two are probably solvated, whereas in the porous SAMNs all six alkoxy groups are adsorbed.

Fig. 2 (a) Chemical structures of DBA-OCn, DBA-OC14-OC1 and DBA-OC14-OH. (b) Schematic models of four DBA-OC14-OH geometries with different m numbers. m refers to the number of physisorbed alkoxy groups per DBA molecule (color code for the triangular π-core, blue; m = 0 at an internal core, cyan; m = 1 at edges, green; m = 2 at vertices, and dark gray; m = 3: color code for other parts, grey; tetradecyloxy (OC14) chain, and red; hydroxy group). (c) Conceived hierarchical self-assembly by clustering DBA-OC14-OH molecules in a triangular manner through hydrogen bonding interactions between the hydroxy groups and hexagonal packing of the clusters (n = 2, 4, and 6: n refers to the number of DBA-OC14-OH molecules forming each edge of the triangular cluster) through van der Waals interaction between the alkoxy groups. The alkoxy groups that orient to the solution phase are omitted in this model.

To further extend the self-assembling ability of DBA derivatives for the formation of various 2D patterns, we reduced the symmetry of the building blocks from D_3h to C_3h, thereby rendering them more flexible. Indeed, we found that DBA-OC14-OC1 having three long alkoxy groups and three methoxy groups in an alternating manner exhibits a rich structural polymorphism due to the increased mobility of the alkoxy groups and the variable number of physisorbed alkoxy groups (hereby denoted as m: m = 3–1). This structural variety depended on the type of solvent and solute concentration.³⁷ This led us to hypothesize that by dynamic self-sorting, based on the ability of the molecule to adsorb with a different number of alkoxy chains (m) in contact with the surface, in combination with extending the type and number of intermolecular interactions, it may become possible to assemble a C_3h-symmetric DBA molecule in a hierarchical manner. Therefore, we designed DBA-OC14-OH bearing three OC14 and three hydroxy groups in alternating positions on the DBA core (Fig. 2a and b). Indeed, we found that (i) this DBA derivative forms hierarchical patterns, consisting of triangular clusters ranging from 2.4 (3 molecules) to 16.4 nm (78 molecules) in size, (ii) each cluster is formed by hydrogen bonding through self-sorting of DBA conformers, (iii) clusters are connected via van der Waals driven alkyl chain interactions, and (iv) the size of the cluster could be modulated by changing the solvent polarity, demonstrating the dynamic feature of the self-sorting process (Fig. 2c: see Fig. S1† for more details).

Results and discussion

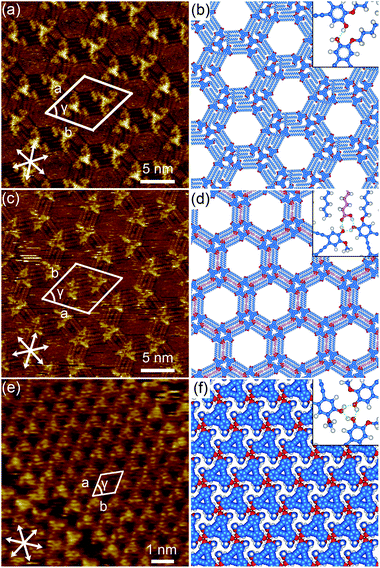
The synthesis of DBA-OC14-OH was reported previously.³⁸ As solvents, we chose 1,2,4-trichlorobenzene (TCB) and 1-hexanoic acid (HA) representing nonpolar and polar solvents,^2,39 respectively, to modify the solvation of DBA-OC14-OH, and thereby also the adsorption probability on graphite. We also expected hydrogen bond formation between the carboxy group of HA with the hydroxy groups of the DBA,⁴⁰ and potential co-adsorption of both solvents.⁴¹ Firstly, the self-assembly behavior of DBA-OC14-OH in a pure solvent was examined. To investigate the concentration dependent structural polymorphism, DBA solutions were prepared ranging from 3.0 × 10⁻⁶ to 1.0 × 10⁻⁴ M. The solution (40 μL) was poured into a liquid cell placed on a freshly cleaved surface of highly oriented pyrolytic graphite (HOPG). Reaching equilibrium was facilitated by annealing the liquid/graphite interface at 80 °C for 3 h.^38,42 After the annealing treatment, the cell was allowed to cool to room temperature, prior to STM imaging at the liquid/graphite interface.

At the TCB/graphite interface, DBA-OC14-OH exclusively forms a hexagonal porous structure with four bright triangles at each vertex of the hexagonal pore at all concentrations examined (Fig. 3a and S2†). Since π-conjugated cores are typically resolved as bright features in the STM images because of their relatively higher tunneling efficiency,⁴³ the bright triangle is assigned to a tetramer of DBA-OC14-OH with three physisorbed alkoxy groups (m = 3) forming the triangular shape by both van der Waals and hydrogen bonding interactions. The neighboring tetramers are connected by seven alkyl chains (Fig. S3†).⁴⁴ A molecular model optimized by molecular mechanics (MM) simulation (COMPASS force field) is shown in Fig. 3b. The mean O⋯H distance of the hydroxy groups between the central and surrounding DBA-OC14-OH molecules is 2.2 ± 0.2 Å, supporting the hypothesis that the molecules are clustered through hydrogen bonding interactions (Fig. 3b).^45,46 The presence of enantiomorphous domains was identified by the orientations of the alkyl chains located at the rims of the pore (Fig. S4–S9†). The details of the chirality aspects both at single and supramolecular levels are described in the ESI.†

Fig. 3 SAMNs formed by DBA-OC14-OH at the liquid/graphite interface. (a) STM image of a hexagonal porous structure at the TCB/graphite interface (1.0 × 10⁻⁴ M, I_set = 200 pA, and V_bias = −0.39 V) and (b) corresponding molecular models optimized by MM calculation. The unit cell parameters of the hexagonal porous structure are a = b = 7.2 ± 0.2 nm and γ = 60 ± 1°. (c) STM image of a triangular cluster (n = 2) at the HA/graphite interface (6.0 × 10⁻⁶ M, I_set = 250 pA, and V_bias = −0.39 V) and (d) corresponding molecular models optimized by MM calculation. The unit cell parameters of the triangular cluster (n = 2) are a = b = 6.4 ± 0.2 nm and γ = 60 ± 1°. (e) STM image of a dense structure at the HA/graphite interface (1.0 × 10⁻⁴ M, I_set = 200 pA, and V_bias = −1.20 V) and (f) corresponding molecular models optimized by MM calculation. The unit cell parameters of the dense structure are a = b = 1.37 ± 0.05 nm and γ = 60 ± 1°. For models (d) and (f), one or three OC14 group(s) are replaced by methoxy group(s) to represent the alkoxy group oriented to the solution phase. Color codes in (b, d, and f): blue; carbon atoms of the DBA-OC14-OH molecule, magenta; carbon atoms of the co-adsorbed HA molecule, red; oxygen atoms, and white; hydrogen atoms. The green dotted lines in insets of (b, d, and f) indicate hydrogen bonding interactions between the hydroxy groups of DBA-OC14-OH molecules and those including HA in the inset of (d).

In contrast to the results in TCB, the self-assembly of DBA-OC14-OH at the HA/graphite interface exhibits a sharp concentration dependence. At 6.0 × 10⁻⁶ M, a hexagonal assembly of triangular clusters consisting of three molecules of DBA (n = 2: n refers to the number of DBA-OC14-OH molecules forming each edge of the triangular cluster) with two physisorbed alkyl groups (m = 2) was exclusively observed (Fig. 3c and S10†). The total number of DBA-OC14-OH molecules (N) per cluster, represented by N = n(n + 1)/2, is three in this case. Based on the unit cell parameters and the STM image, it is safe to conclude that the triangular cluster is formed by hydrogen bonding mediated by one HA molecule per adjacent DBA pair. The triangular clusters are bridged by four interdigitated alkyl chains of DBA-OC14-OH. Note that two HA molecules stick in between the interdigitated alkoxy groups (Fig. 3d). In the model, the mean O⋯H atomic distances between the hydroxy group of DBA-OC14-OH and the carboxy group of HA measure 1.70 ± 0.02 and 1.75 ± 0.01 Å, respectively, suggesting the presence of hydrogen bonding interactions (Fig. S11†). Similar to the hexagonal porous structure, there are both antipodal domains differentiated by the alkyl chain orientations located at the rims of the hexagonal pore (Fig S12 and S13†). Again, the details are discussed in the ESI.†

By increasing the concentration to 1.0 × 10⁻⁵ M, in addition to small domains of the triangular cluster (n = 2), irregular areas consisting of triangular clusters of various sizes (n = 2 up to 6) and a densely packed phase cover the surface (Fig. S14†). Further increase of the concentration to 1.0 × 10⁻⁴ M led to the formation of a dense structure consisting of DBA-OC14-OH without physisorbed alkoxy groups (m = 0); all alkoxy groups orient to the solution phase (Fig. 3e, S15 and S16†). There exist two chiral domains of the dense structure, which could be differentiated by the molecular orientations with respect to the substrate axes. In the molecular model, all intermolecular O⋯H distances between DBA-OC14-OH are 2.0 Å, indicating hydrogen bonding (Fig. 3f). Thus, at the HA/graphite interface, though several hierarchical structures of n = 2 to 6 emerged, concentration control over the formation of clusters of specific size was not achieved.

Next, we examined the effect of solvent polarity by changing the ratio of TCB and HA in the solvent mixture on the size control of the hierarchical triangular clusters.⁴⁷ To compare the affinity of the solvents to DBA-OC14-OH, its solvation energies in TCB and HA are estimated by molecular dynamics (MD) simulations to be −54.22 and −0.26 kcal mol⁻¹, respectively (see the ESI†). The larger negative value in TCB indicates smaller adsorption probability than in HA, which is consistent with the favorable formation of the low density hexagonal porous network by the DBA with three physisorbed alkoxy groups (m = 3). In contrast, the less favorable solvation in HA is consistent with the formation of the densely packed structure by the DBA with none of the alkoxy groups (m = 0) physisorbed at high concentration. By varying the ratio of these two extreme solvents, we hypothesized that the distribution of the DBA molecules with a different number of physisorbed alkoxy groups m may be controlled to form triangular clusters of a specific size. Based on this hypothesis, solutions of mixtures of TCB and HA at different molar fractions (X_HA; 0.020–0.50 and X_TCB; 0.98–0.50) were prepared keeping the total DBA concentration constant (1.0 × 10⁻⁴ M), and the resulting SAMNs were analyzed. The overall results are summarized in Table 1.

Table 1 On-surface distributions of the triangular clusters with different sizes for solvent mixtures of TCB and HA at different molar fractions

a The surface coverages and standard deviations were determined from more than 20 images in three independent experimental sessions. b Collapsed triangular clusters. c The relative ratios of different clusters at an XHA of 0.20 are listed in Table 2. d The error was not determined due to its small area ratio.
X HA	Hexagonal porous structure^a (%)	Triangular clusters^a (%)					Dense structure^a (%)
		Defects^b	n = 2	n = 4	4 < n < 10	9 < n < 21
0.020	56.2 ± 6.9	0.7 ± 0.1	43.1 ± 6.8	0.0	0.0	0.0	0.0
0.049	0.5^d	2.9 ± 0.8	96.6 ± 0.4	0.0	0.0	0.0	0.0
0.066	0.5^d	2.7 ± 0.7	96.6 ± 0.7	0.2^d	0.0	0.0	0.0
0.070	1.1 ± 0.7	1.5 ± 0.5	84.6 ± 13.2	22.1 ± 12.5	0.0	0.0	0.0
0.076	0.0	1.0 ± 0.8	54.8 ± 6.7	44.3 ± 7.4	0.0	0.0	0.0
0.082	0.0	0.3 ± 0.2	44.7 ± 13.6	55.0 ± 13.6	0.0	0.0	0.0
0.090	0.0	0.7 ± 0.4	45.1 ± 3.7	23.7 ± 4.8	2.8 ± 1.7	27.6 ± 5.9	0.0
0.20^c	0.0	0.0	0.0	0.1^d	9.8 ± 1.1	90.2 ± 2.5	0.0
0.50	0.0	0.0	0.0	0.0	0.0	0.0	100

---

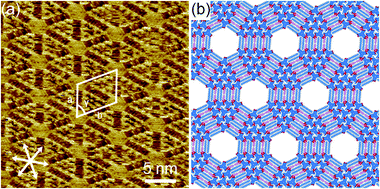
At X_HA = 0.020, both a hexagonal porous structure and a triangular cluster co-exist (n = 2, Fig. S17a†). At the mixing ratio X_HA ranging from 0.049 to 0.066, DBA-OC14-OH mainly forms the triangular cluster of n = 2, similar to the conditions in the pure HA solution of low concentration (Fig. S17b†). Upon increasing X_HA to 0.070–0.082, the n = 4 cluster appears and its surface coverage increases up to about 50% with increasing X_HA (Fig. 4a, S17c, d and S19†), reaching a maximum at X_HA = 0.082, forming large domains over 80 × 80 nm² (Fig. S18d†). The cluster of n = 4 consists of DBAs in three different conformational states (three of m = 2, six of m = 1, and one of m = 0) and 9 molecules of HA attached to the edges linked by hydrogen bonding interactions (Fig. 4b and S20†). The surrounding six DBA molecules are bound to the central core DBA of m = 0 via hydrogen bonds. The adjacent clusters are connected by van der Waals interactions between interdigitated alkoxy groups of DBA-OC14-OH with HA molecules stuck in between. We were unable to find clusters of n = 3.

Fig. 4 (a) STM image of a triangular cluster (n = 4) at X_HA = 0.076 (I_set = 200 pA, and V_bias = −1.20 V) and (b) corresponding molecular models optimized by MM calculation. The unit cell parameters of the triangular cluster (n = 4) structure are a = b = 9.2 ± 0.2 nm and γ = 60 ± 1°. In the model, one to three OC14 group(s) is/are replaced by methoxy group(s) to represent the alkoxy group oriented to the solution phase. Color codes in (b): blue; carbon atoms of the DBA-OC14-OH molecule, magenta; carbon atoms of the co-adsorbed HA molecule, red; oxygen atoms, and white; hydrogen atoms.

Hierarchical structures consisting of larger triangular clusters emerge upon further increasing X_HA to 0.090 (Fig. S21†). At an X_HA of 0.20, DBA-OC14-OH produces a mixed phase of hierarchical clusters containing the n = 12 cluster as the major component (ca. 27%) together with other clusters of similar sizes (n = 10, 11, 13 and 14, Fig. 5 and Table 2). Note that the length of the edge of the cluster of n = 12 reaches 16.4 nm and the cluster is composed of 78 DBA molecules (three DBAs of m = 2, 30 DBAs of m = 1, and 45 DBAs of m = 0). In the hexagonal assembly of the large clusters, even if the sizes of the triangular clusters are not all uniform, the hexagonal packing is sustained by small gaps (Δn) in between adjacent clusters (typically Δn is smaller than or equal to 2) by distorting the central hexagonal pore. When the size difference (Δn) becomes larger than 2, the triangular clusters are often chipped out from the vertex to maintain the overall hexagonal packing (triangles with red numbers in Fig. 5). These domains are stable against STM tip scanning. Moreover, a longer annealing period from 3 to 6 h led to no notable structural change and the hierarchical structure remains even after 1 day at room temperature, indicating that the hierarchical structure is thermodynamically stable. The formation of the triangular clusters rather than other clusters with different shapes, i.e. hexagonal shape clusters would be related to the favored intermolecular interactions (Fig. S25†).⁴⁸

Fig. 5 STM images of a hierarchical triangular cluster packing observed at X_HA = 0.20. (a) Triangular clusters of n = 10–15 (I_set = 200 pA and V_bias = −0.40 V). (b) The same STM image as (a), in which the sizes (n) of the triangular clusters are marked by white or red numbers. The clusters with the red numbers partially collapse due to large size mismatches with the adjacent clusters. (c) Enlarged image of the hexagonal packing of large clusters (I_set = 200 pA and V_bias = −0.40 V).

Table 2 Distributions of the triangular clusters at X_HA = 0.20

Cluster size	Ratio^a (%)	Cluster size	Ratio^a (%)
a 22 large area STM images (80 × 80 nm^2 or larger) obtained in three independent experimental sessions were used. Some imperfect triangular clusters in which the number of missing DBA molecules is less than 10% are included in the statistics. b The error was not determined due to its small occurrence.
n = 4	0.05^b	n = 13	12.0 ± 2.1
n = 5	0.22 ± 0.14	n = 14	15.1 ± 6.7
n = 6	0.77 ± 0.56	n = 15	5.2 ± 1.3
n = 7	0.88 ± 0.74	n = 16	4.3 ± 1.7
n = 8	3.2 ± 1.9	n = 17	0.20 ± 0.10
n = 9	4.7 ± 3.3	n = 18	0.43^b
n = 10	13.2 ± 4.3	n = 19	0.05^b
n = 11	13.1 ± 5.2	n = 20	0.05^b
n = 12	26.7 ± 4.9	—	—

---

We emphasize that each n = 12 cluster is formed by 78 molecules through a dynamic combination of its three different conformational states, each being a part of vertices, edges and core, even though the control is not perfect probably due to thermal fluctuations. This process can be regarded as a dynamic version at the solid/liquid interface of integrative self-sorting, which is a new aspect of self-assembly mainly observed in solution and in crystals.^29–31 Jester and Höger reported a related preliminary case in which a six-alkyl-bearing building block capable of adopting several conformations with a different coordination number at the solvent/graphite interface is a part of vertices, edges and core, forming a hierarchical structure of variable sizes.³² In our case, the hierarchical structures are formed through orthogonal van der Waals and hydrogen bond interactions not only between the DBA molecules but also between the DBA and solvent molecules. Moreover, the cluster size, namely the number of different dynamic conformers can be modulated to some extent by changing the degree of solvation. The present work improves the design strategy for the construction of hierarchical SAMNs.

Further increase of X_HA to 0.50 leads to the dense structure exclusively covering the whole surface (Fig. S23†). At all mixing ratios, domains of n with small odd numbers of 3 or 5 were never or scarcely observed. Though this may be related to the epitaxy with the substrate lattice^4–17 or formation mechanism of the clusters (vide infra), it is not understood yet. In contrast, both odd and even clusters coexist for the larger clusters (n = 10–14), which is attributed to the small differences in size and molecular density among these large clusters. To shed light on the formation mechanism of the clusters, monolayers formed without annealing treatments were observed. At X_HA = 0.076, the surface is covered with the hexagonal porous structure and the smallest triangular cluster (n = 2, Fig. S24a†), implying that the triangular cluster of n = 4 is formed by the lateral replacement of the smallest triangular clusters through the annealing treatment. This may also account for the absence of the triangular cluster of n = 3. At X_HA = 0.20, the DBA molecules form a disordered (non-uniform) structure consisting of incomplete large triangular clusters and smaller clusters of n = 2 and 4 (Fig. S24b†), implying that the larger triangular clusters are grown from the smaller clusters by the ripening process.

Conclusions

In conclusion, we demonstrated the formation of hierarchical hexagonal assemblies of DBA-OC14-OH consisting of triangular clusters of different sizes ranging from 2.4 to 16.4 nm at the solution/graphite interface. By modulating the polarity of the solvent by changing the ratio of nonpolar solvent (TCB) and polar solvent (HA), the size of the clusters was controlled to some extent. The n = 2 cluster containing two DBA molecules on the triangular edge was exclusively formed and the clusters of n = 4 and n = 12 were produced as the major components among clusters of similar sizes. Each cluster consisted of a discrete number of the DBA molecules with a different number of physisorbed alkyl groups m = 2–0, and its formation involved hydrogen bonding and co-adsorption of solvent molecules. A key element for the hierarchical pattern formation is the dynamic combination of three different conformational states of the building block. This result conceptually expands the scope of molecular self-assembly and may be useful for constructing self-assembled patterns of enhanced complexity.

Experimental

STM experiments

All the experiments were performed at 20–26 °C using a Nanoscope IIID or V (Bruker AXS) with an external pulse/function generator (Agilent 33220A or TEXIO FGX-295) with a negative sample bias. STM tips were mechanically cut from Pt/Ir wire (80%/20%, diameter 0.25 mm). All STM images were taken in a quasi-constant current mode. For preparation of the sample solution, commercially available 1,2,4-trichlorobenzene (TCB, purchased from Nacalai Tesque) and 1-hexanoic acid (HA, purchased from Wako) were used as the solvent after distillation. A drop of this solution (40 μL) was poured into a homemade liquid cell placed on a freshly cleaved basal plane of a 1 cm² piece of highly oriented pyrolytic graphite (HOPG, grade ZYB, Momentive Performance Material Quartz Inc., Strongsville, OH). The liquid cell was employed to minimize the effect of solvent evaporation by using a large amount of the sample solution (40 μL). Moreover, this liquid cell was covered with a stainless lid in an oven. The proportion of the solvent loss was estimated by weighing the liquid cell system to be 7% after annealing at 80 °C for 3 hours. After annealing treatment, the substrate was naturally cooled to room temperature. All STM images were taken within 3 hours after annealing treatment to minimize the concentration changes due to solvent evaporation during the observation. By changing the bias voltage applied to the substrate, the SAMNs of DBA-OC14-OH and the graphite substrate surface could be observed at low and high voltages, respectively. The distortion of the image due to the thermal drift effects was corrected by using the STM image of the underlying graphite surface. Such image correction was performed using SPIP software (Scanning Probe Image Processor, SPIP, version 4.0.6 or 6.0.13, Image Metrology A/S, Hørsholm, Denmark). In the STM images, the white arrows and the line indicate the directions of the main symmetric axes of graphite and the scale bar, respectively. For each concentration, more than 10 large area STM images (image sizes: 50 nm × 50 nm or larger) were acquired per session. Three independent sessions were performed at each concentration and mixing ratio to confirm reproducibility. The unit cell and its parameters were determined using over 50 experimental data points from at least five calibrated STM images (image sizes: 30 × 30 nm² or smaller). The surface coverages of SAMNs in the weighted average values with the standard deviations were determined from more than 20 images in three independent experimental sessions.

The average height profiles (11 lines, width of each line is one pixel) of the alkyl chains and DBA cores were measured from more than three different calibrated images (typically 30 × 30 nm², 512 pixels) by the use of SPIP software. In each cross section of the hexagonal porous structure, two structurally inequivalent DBA cores in the tetramer were included because the apparent height of the DBA core is slightly different depending on its position. The apparent heights of the central DBA core parts and the surrounding DBA core parts were averaged.

The triangular cluster sizes and its distribution were statistically analyzed at a HA molar fraction (X_HA) of 0.20. The size of triangular clusters is classified by the number of DBA-OC14-OH molecules (n) at each triangular side. To determine size distribution statistically, 22 large area images (80 × 80 nm² or larger) were used. There were also imperfect triangular clusters as defects. Some imperfect triangular clusters in which the number of missing DBA molecules was less than 10% were included in the statistics. In the case where the side lengths of the triangular clusters were different, the number of DBA-OC14-OH molecules at the longest side was used as n.

Molecular mechanics simulation

The initial geometry of DBA-OC14-OH was built from the respective molecular model optimized by the semiempirical PM3 method.⁴⁹ Then the orientation of the alkyl chains relative to the π system was adjusted based on that observed in the STM images. All MM/MD simulations were performed with Materials Studio 2017 R2 using the Forcite module with the COMPASS force field. The molecules were placed 0.350 nm above the first layer of a two-layer sheet of graphene (interlayer distance is 0.355 nm) which represents graphite. Experimentally derived unit cell parameters are used as periodic boundary conditions (PBCs). This double layer graphene flake was frozen during the simulations, and a cutoff of 2.0 nm was applied for the van der Waals interactions (Lennard-Jones type).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by JSPS KAKENHI Grant Numbers JP17K19130 and JP20H02553, and by the Higher Education Sprout Project of National Chiao Tung University and the Ministry of Education (MOE), Taiwan. S. D. F. thanks Research Foundation – Flanders (FWO) and Internal Funds – KU Leuven. M. M. and K. T. would like to thank prof. Tomoko Fukazawa (Meiji university) for a fruitful discussion.

Notes and references

1. D. P. Goronzy, M. Ebrahimi, F. Rosei, Arramel, Y. Fang, S. De Feyter, S. L. Tait, C. Wang, P. H. Beton, A. T. S. Wee, P. S. Weiss and D. F. Perepichka, ACS Nano, 2018, 12, 7445–7481.
2. M. Lackinger and W. M. Heckl, Langmuir, 2009, 25, 11307–11321.
3. J. A. A. W. Elemans, S. Lei and S. De Feyter, Angew. Chem., Int. Ed., 2009, 48, 7298–7332.
4. C.-A. Palma and P. Samorì, Nat. Chem., 2011, 3, 431–436.
5. D. Cui, J. M. MacLeod and F. Rosei, Chem. Commun., 2018, 54, 10527–10539.
6. J. V. Barth, Annu. Rev. Phys. Chem., 2007, 58, 375–407.
7. J. V. Barth, G. Costantini and K. Kern, Nature, 2005, 437, 671–679.
8. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421.
9. Y. L. Yang and C. Wang, Chem. Soc. Rev., 2009, 38, 2576–2589.
10. B. A. Hermann, C. Rohr, M. Balbás Gambra, A. Malecki, M. S. Malarek, E. Frey and T. Franosch, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 165451–165456.
11. G. Tikhomirov, P. Petersen and L. Qian, J. Am. Chem. Soc., 2018, 140, 17361–17364.
12. G. M. Whitesides, J. P. Mathias and C. T. Seto, Science, 1991, 254, 1312–1319.
13. I. Destoop and S. De Feyter, Chirality at the Solution/Solid-State Interface, in Chirality in Supramolecular Assemblies, ed. F. Richard Keene, John Wiley & Sons Ltd, Chichester, UK, 2017, pp. 257–284.
14. S. Clair, M. Abel and L. Porte, Angew. Chem., Int. Ed., 2010, 49, 8237–8239.
15. Y. Ye, W. Sun, Y. Wang, X. Shao, X. Xu, F. Cheng, J. Li and K. Wu, J. Phys. Chem. C, 2007, 111, 10138–10141.
16. W. Xiao, X. Feng, P. Ruffieux, O. Gröning, K. Müllen and R. Fasel, J. Am. Chem. Soc., 2008, 130, 8910–8912.
17. J. Zhang, B. Li, X. Cui, B. Wang, J. Yang and J. G. Hou, J. Am. Chem. Soc., 2009, 131, 5885–5890.
18. T. Jasper-Toennies, M. Gruber, S. Ulrich, R. Herges and R. Berndt, Angew. Chem., Int. Ed., 2020, 59, 7008–7017.
19. K. Tahara, K. Nakatani, K. Iritani, S. De Feyter and Y. Tobe, ACS Nano, 2016, 10, 2113–2120.
20. T. Balandina, K. Tahara, N. Sändig, M. O. Blunt, J. Adisoejoso, S. B. Lei, F. Zerbetto, Y. Tobe and S. De Feyter, ACS Nano, 2012, 6, 8381–8389.
21. S. Ahn and A. J. Matzger, J. Am. Chem. Soc., 2010, 132, 11364–11371.
22. J. Liu, T. Chen, X. Deng, D. Wang, J. Pei and L. J. Wan, J. Am. Chem. Soc., 2011, 133, 21010–21015.
23. Y. Xue and M. B. Zimmt, J. Am. Chem. Soc., 2012, 134, 4513–4516.
24. K. S. Mali, B. Van Averbeke, T. Bhinde, A. Y. Brewer, T. Arnold, R. Lazzaroni, S. M. Clarke and S. De Feyter, ACS Nano, 2011, 5, 9122–9137.
25. L.-M. Wang, J.-Y. Yue, Q.-Y. Zheng and D. Wang, J. Phys. Chem. C, 2019, 123, 13775–13781.
26. Y. Yang and C. Wang, Curr. Opin. Colloid Interface Sci., 2009, 14, 135–147.
27. W. Song, N. Martsinovich, W. M. Heckl and M. Lackinger, J. Am. Chem. Soc., 2013, 135, 14854–14862.
28. T. Sirtl, W. Song, G. Eder, S. Neogi, M. Schmittel, W. M. Heckl and M. Lackinger, ACS Nano, 2013, 7, 6711–6718.
29. M. Lal Saha and M. Schmittel, Org. Biomol. Chem., 2012, 10, 4651–4684.
30. M. M. Safont-Sempere, G. Fernández and F. Würthner, Chem. Rev., 2011, 111, 5784–5814.
31. Z. He, W. Jiang and C. A. Schalley, Chem. Soc. Rev., 2015, 44, 779–789.
32. S. S. Jester, E. Sigmund, L. M. Röck and S. Höger, Angew. Chem., Int. Ed., 2012, 51, 8555–8559.
33. J. P. Rabe and S. Buchholz, Science, 1991, 253, 424–427.
34. S. De Feyter and F. C. De Schryver, Chem. Soc. Rev., 2003, 32, 139–150.
35. K. Tahara, S. Furukawa, H. Uji-i, T. Uchino, T. Ichikawa, J. Zhang, W. Mamdouh, M. Sonoda, F. C. De Schryver, S. De Feyter and Y. Tobe, J. Am. Chem. Soc., 2006, 128, 16613–16625.
36. M. O. Blunt, J. Adisoejoso, K. Tahara, K. Katayama, M. Van der Auweraer, Y. Tobe and S. De Feyter, J. Am. Chem. Soc., 2013, 135, 12068–12075.
37. K. Tahara, R. Nakayama, M. Maeda, S. De Feyter and Y. Tobe, J. Phys. Chem. C, 2019, 123, 27020–27029.
38. K. Tahara, K. Inukai, J. Adisoejoso, H. Yamaga, T. Balandina, M. O. Blunt, S. De Feyter and Y. Tobe, Angew. Chem., Int. Ed., 2013, 52, 8373–8376.
39. G. M. Florio, B. Ilan, T. Müller, T. A. Baker, A. Rothman, T. L. Werblowsky, B. J. Berne and G. W. Flynn, J. Phys. Chem. C, 2009, 113, 3631–3640.
40. D. C. Y. Nguyen, L. Smykalla, T. N. H. Nguyen, T. Rüffer and M. Hietschold, J. Phys. Chem. C, 2016, 120, 11027–11036.
41. X. Zhang, Q. Chen, G. Deng, Q. Fan and L. J. Wan, J. Phys. Chem. C, 2009, 113, 16193–16198.
42. U. Mazur and K. W. Hipps, Chem. Commun., 2015, 51, 4737–4749.
43. R. Lazzaroni, A. Calderone, G. Lambin, J. P. Rabe and J. L. Brédas, Synth. Met., 1991, 41, 525–528.
44. T. Yang, S. Berber, J. F. Liu, G. P. Miller and D. Tománek, J. Chem. Phys., 2008, 128, 124709–124718.
45. R. Zangi, J. Phys. Chem. C, 2019, 123, 16902–16910.
46. L. K. Thomas, A. Kühnle, S. Rode, U. Beginn and M. Reichling, J. Phys. Chem. C, 2010, 114, 18919–18924.
47. H. D. Castillo, J. Yang, S. Debnath, J. R. Dobscha, C. Q. Trainor, R. D. Mortensen, K. Raghavachari, A. H. Flood, P. J. Ortoleva and S. L. Tait, J. Phys. Chem. C, 2020, 124, 6689–6699.
48. X. Zhang, N. Li, G.-C. Gu, H. Wang, D. Nieckarz, P. Szabelski, Y. He, Y. Wang, C. Xie, Z.-Y. Shen, J.-T. Lü, H. Tang, L.-M. Peng, S.-M. Hou, K. Wu and Y.-F. Wang, ACS Nano, 2015, 9, 11909–11915.
49. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, additional STM images, and details of MM simulations. See DOI: 10.1039/d0sc03163a

---