Photon echoes and two dimensional spectra of the amide I band of proteins measured by femtosecond IR – Raman spectroscopy

Abstract

Infrared (IR) and Raman spectroscopy are fundamental techniques in chemistry, allowing the convenient determination of bond specific chemical composition and structure. Over the last decades, ultrafast multidimensional IR approaches using sequences of femtosecond IR pulses have begun to provide a new means of gaining additional information on molecular vibrational couplings, distributions of molecular structures and ultrafast molecular structural dynamics. In this contribution, new approaches to measuring multidimensional spectra involving IR and Raman processes are presented and applied to the study of the amide I band of proteins. Rephasing of the amide I band is observed using dispersed IR-Raman photon echoes and frequency domain 2D-IR-Raman spectra are measured by use of a mid-IR pulse shaper or over a broader spectral range using a tuneable picosecond laser. A simple pulse shaping approach to performing heterodyned time-domain Fourier Transform 2D-IR-Raman spectroscopy is introduced, revealing that the 2D-IR-Raman spectra distinguish homogeneous and inhomogeneous broadening in the same way as the well-established methods of 2D-IR spectroscopy. Across all datasets, the unique dependence of the amide I data on the IR and Raman strengths, vibrational anharmonicities and inhomogeneous broadening provides a fascinating spectroscopic view of the amide I band.

---

Introduction

The amide I IR absorption and Raman scattering of a protein backbone provides a simple but deep spectroscopic connection to the structure and behaviour of proteins. Due to the relatively strong excitonic transition dipole coupling of neighbouring carbonyl group vibrations,¹ it has long been known that amide I spectra of alpha helical and beta sheet secondary structures are markedly different to one another.^2–4 As well as providing a useful bioanalytical metric for assays and imaging, the structure and complexity of the amide I band makes it interesting and rewarding for spectroscopic technique development, simulation and fundamental studies. Indeed, as the subject of this paper, pulsed laser two dimensional (2D) vibrational spectroscopy (the vibrational equivalent of 2D-NMR) was first demonstrated through a 2D-IR study on the amide I band of peptides.⁵

2D-IR spectroscopy offers the means to measure ultrafast structural dynamics, vibrational couplings, energy transfer, structural broadening mechanisms and simplified views of complex linear absorption spectra. A dramatic early illustration of this was the observation of the ultrafast unfolding of a peptide,⁶ where amide I 2D-IR provided sufficient structural constraints for the data to be considered a true molecular movie. 2D-IR spectra of the isotope labelled amide I band have been shown to contain sufficient constraints to solve the structure of a large peptide⁷ and although such comprehensive global structural determinations are best achieved by X-ray or NMR techniques, isotope labelled amide I 2D-IR is a unique site-specific probe of equilibrium protein structure and dynamics,⁸ with applications demonstrated testing ion channel filter mechanisms⁹ and amyloid aggregation.¹⁰ For 2D-IR analysis of the amide I band of unlabelled proteins,^11,12 secondary structure determination ability is comparable to ultraviolet circular dichroism¹³ and there is recent evidence of utility to this end in the analysis of blood serum samples¹⁴ and eye cataracts.¹⁵

In this paper, 2D spectra of the amide I band of proteins are measured using alternative laser pulse sequences involving IR and Raman processes. The approaches presented readily allow the observation of the amide I signal as a dispersed echo, and as homodyne and heterodyne detected 2D-IR-Raman spectra. These data reveal very clearly the spectroscopic differences between alpha and beta sheet proteins, and owing to their different spectroscopic origins compared with 2D-IR spectroscopy offer an alternative viewpoint of the lineshape and molecular coupling information contained in the amide I band. Not only is the view of the amide I band uncovered interesting, the approaches outlined show promise for more general spectroscopic investigations on other types of molecular species.

The 2D-IR-Raman methods presented here build on a picosecond (ps) laser approach developed by John Wright and co-workers known as ‘Doubly Vibrationally Enhanced’ (DOVE) 2D-IR,^16–20 or ‘Electron–Vibration–Vibration’ (EVV) 2D-IR.²¹ Numerous practical applications of DOVE-EVV spectroscopy were explored by David Klug and co-workers, investigating the technique as a spectroscopic probe of simple liquids,^21,22 intermolecular interaction geometries^23,24 and peptide and protein amino acid side-chains.^25,26 An application to tissue imaging was reported²⁷ and later work explored the detection of post-translational modification and protein–drug binding.^28,29 In another early work, a related spectroscopic approach was proposed in a theoretical study by Minhaeng Cho.³⁰ Termed ‘IR–IR-Visible Difference Frequency Generation’ (IIV-DFG), Cho predicted and simulated the IR – Raman overtone rephasing (photon echo) of an inhomogeneously broadened vibrational transition – an important step towards understanding lineshape origins and measuring ultrafast dynamics of a ground-state ensemble. The IR-Raman work presented here experimentally demonstrates these echoes and can be seen to fit into a family of related femtosecond techniques incorporating IR, THz and Raman transitions. Examples include IR-Raman spectroscopy of vibronic couplings,³¹ THz-IR-Raman³² and THz-Raman spectroscopies^33,34 examining structural dynamics in liquids.

The Feynman and wave mixing diagrams of the IR-Raman processes of interest in this paper are shown in Fig. 1.^16,35 Whereas 2D-IR methods are based on IR-pump IR-probe and IR transient grating spectroscopy of excited vibrational populations,³⁵ the 2D-IR-Raman methods discussed here are based on wave mixing processes that do not involve any intermediate vibrational populations, and owing to a Raman interaction generating the observed signal, are in a practical sense reminiscent of techniques such as Coherent Anti-Stokes Raman Spectroscopy (CARS) and vibrational surface-sum-frequency generation (VSFG). Despite apparent differences, it will become clear in this work that the IR-Raman pathways of Fig. 1 also have a deep connection to 2D-IR spectroscopy.

Fig. 1 Feynman and wave-mixing diagrams of DOVE-IR-Raman processes for a three level anharmonic oscillator. IR and visible frequencies are labelled in ascending order α, β (IR) and γ (Vis). The visible signal is labelled δ. The Raman process proceeds via ‘virtual’ electronic state e. The transition dipole products are shown next to each diagram. Coupled two-level ‘combination band’ cross-peak diagrams are very similar and laid out in ESI Section 7.†

The DOVE-EVV IR-Raman approach of Wright and co-workers uses a relatively uncommon configuration of three narrowband picosecond (ps) pulsed laser sources and single-wavelength detection to collect frequency domain 2D spectra.¹⁸ These are recorded by scanning the centre-frequencies of the two ps IR lasers across the resonances of pairs of coupled vibrational states, one state being a fundamental vibrational mode and the other a related overtone or combination band (Fig. 1 and S14 ESI†). A third ps visible pulse induces Raman emission from the vibrational coherent state, illuminating a single-channel detector. For vibrational modes narrower in linewidth than the laser pulses used, the ‘ps–ps–ps’ DOVE laser pulse sequence (shown in Fig. 2a) is an interesting and unique means of measuring electrical and mechanical vibrational anharmonic coupling strengths^21,22,36 and of fingerprinting congested spectra.^25,26 Owing to the intrinsic spectral and temporal resolution limits of the DOVE technique however, as well as the large backgrounds that occur at temporal overlap of the excitation pulses, very few labs have adopted the approach. It is difficult to apply the DOVE technique to vibrational bands broader in linewidth than the narrow laser pulses used, to lineshape analysis and to the study of ultrafast dynamical processes. It is shown in this paper how sequences of broadband femtosecond (fs) and narrowband ps pulses (‘fs–fs–ps’ and ‘ps–fs–ps’, Fig. 2b–d) transform the acquisition of 2D-IR-Raman spectra, overcoming these issues and revealing deeper connections to the more widespread techniques of 2D-IR spectroscopy. Despite involving weak overtone or combination bands, IR-Raman spectra are shown to be readily detectable from thin films or solutions, and the methods reported provide an experimental route to 2D-IR-Raman spectroscopy accessible to laboratories with femtosecond light sources.

Fig. 2 Pulse sequences for 2D-IR-Raman spectroscopy. (a) is the original ps DOVE-EVV sequence. (b)–(d) are IR-Raman sequences incorporating fs pulses.

Experimental

There are numerous possible permutations of laser pulses and observable signal frequencies in IR-Raman experiments.¹⁶ The signal of interest in the present work has frequency:

ω_δ = ω_β − ω_α + ω_γ (1)

Interpulse delays are labelled T_αγ and T_βγ (Fig. 2). The signal is generated by focusing time-synchronized laser pulses of centre frequency ω_α and ω_β (mid-IR) and ω_γ (visible or near-IR) into a sample, and analysing the broadband field at frequency ω_δ radiated by the induced nonlinear polarization in the sample. In a similar manner to VSFG and ordinary Raman spectroscopy, a spectrometer equipped with a CCD camera is introduced to disperse the signal (Fig. 3a), which is then plotted with the Raman excitation frequency ω_γ subtracted, yielding a difference frequency axis ω_β − ω_α. 2D-IR-Raman spectra for resonant vibrational modes i, j and k and their overtones/combination bands take the form shown in Fig. 3b. Differences in the appearance of these dispersed spectra and earlier DOVE-EVV 2D spectra^16–29 are discussed in ESI Section 1.†

Fig. 3 (a) Simplified optical scheme and (b) schematic 2D spectra for the IR-Raman spectroscopy experiments discussed in the text.

Experiments for generating and detecting IR-Raman signals using the pulse sequences in Fig. 2b–d were built via access to the LIFEtime^37,38 and Ultra A³⁹ lasers of the UK Central Laser Facility. Detailed descriptions of these experiments are found in ESI Section 2.† Both used broadband fs ω_β light. For the LIFEtime experiments, the ω_α light was generated from a broadband fs IR source passed through an acousto-optic pulse-shaper (Phasetech Spectroscopy). In the Ultra A experiment, the ω_α light was generated from a bright, tuneable narrowband ps amplifier synchronized to the broadband fs β and γ sources. In both cases, narrowband ps γ light was generated from the broadband light sources via a Fabry–Perot etalon (12.5 cm⁻¹ transmission width), determining the spectral resolution of the nonlinear signal. The spectrometers used had better resolution than this (5–6 cm⁻¹) and a 2 cm⁻¹ pixel spacing. The laser pulses were all ‘P’ polarised. Further details regarding the laser pulse parameters are noted in later sections. Discussion and simulations of the effect of the shape of the γ pulse on the optical response can be found in ESI Section 3.†

Bovine Serum Albumin (BSA, a 65% alpha helical protein⁴⁰), Concanavilin A (ConA, a 50–60% beta-sheet protein⁴¹) and other common proteins were purchased from Sigma-Aldrich and used without further purification. Owing to nonresonant background signals from the windows and solvent of solution infrared cells, previous DOVE-EVV work on proteins studied them as thin films on glass substrates.²⁶ For simplicity, the spectroscopy presented here was also mostly conducted on films, though a discussion of data in support of solution phase work is presented in the final section of the paper. Films of protein were prepared by drop-casting aqueous (H₂O) protein solutions onto 150 μm thick borosilicate microscope coverslips and drying them in a dessicator prior to placing them in the N₂ purged spectrometer. The protein films dried reproducibly into rings. Their position in the laser beams was adjusted to optimize signal generation. This tended to be inside and not on the ring. IR microscopy confirmed that the optical density of the amide I band and amide A regions was typically 0.1–0.3 within the rings for the samples studied, corresponding to a thickness of about 1 μm.⁴⁰ Infrared spectra of the films as deposited on CaF₂ windows at ambient humidity are shown in Fig. 4. Brief studies of preparations of films and solutions from D₂O confirmed that contributions to the IR-Raman signal from the NH stretch ‘Amide A’ band were not significant and that the observed signals were mostly amide I and its overtone.

Fig. 4 FT-IR spectra of drop-cast BSA and ConA films on CaF₂ substrates. (a) The amide I spectral region and (b) the amide A and amide I overtone spectral region.

Results and discussion

IR-Raman amide I photon echoes

The inhomogeneous broadening of a protein's amide I band is due to multiple structural and solvation environments, which in turn give rise to a broad range of individual and excitonically coupled amide I carbonyl absorption frequencies.¹² The ∼60 cm⁻¹ width of the BSA absorption spectrum of Fig. 4a is roughly five times the approximate 12 cm⁻¹ homogeneous width.⁵ Upon coherent excitation of the amide I band via an α laser pulse, despite the fact that individual groups of carbonyls may oscillate for picoseconds, the coherent oscillations of different amide groups across the band will become out of phase with one another within a few hundred femtoseconds. This destructive interference renders IR-Raman emission of the inhomogeneously broadened ensemble zero on a timescale proportional to the inverse of the inhomogeneous bandwidth excited.

The IR-Raman diagrams in Fig. 1 all involve the difference frequency ω_β − ω_α. The consequence of this is that the coherent oscillations of vibrational states driven by the β and α fields evolve with opposite sign (or phase) in time. The inhomogeneous broadening of fundamental and overtone bands are often well correlated and so for diagram 1 of Fig. 1 the β pulse reverses in time the direction of the oscillation of the inhomogeneously broadened nonlinear polarization. This causes the ensemble of emitters in the sample to rephase, giving an increase in emission of IR-Raman δ signal generated by pulse γ. An overtone oscillates at roughly double the frequency of the fundamental, so the correct timing of the α, β and γ pulses for rephasing is therefore:

T_αγ = 2T_βγ (2)

In other words, the β pulse induced rephasing requires only half the time to ‘undo’ the α pulse induced dephasing. This type of time dependent signal revival is a ‘photon echo’⁴² – a phenomenon of central importance in the development of condensed phase ultrafast spectroscopy.^43–45 Photon echoes and rephasing play a key role in distinguishing line broadening mechanisms that are slow on the timescale of the echo generation (inhomogeneous) from processes which occur on a faster timescale (homogenous). The identification of the influence of rephasing and echoes on the shape of 2D-IR spectra,^46,47 and the development of optimum procedures for using rephasing and nonrephasing processes to construct a 2D-IR spectrum^48–50 were key in the development of 2D-IR spectroscopy.

Here we explore the IR-Raman rephasing of the amide I band at around ∼1650 cm⁻¹ with its overtone at around ∼3285 cm⁻¹via diagram 1 (Fig. 1). Owing to the fact that ω_β is greater in frequency than ω_α, no time delay exists where the α pulse can rephase the β driven components of the polarization. Thus, diagrams 2 and 3 in Fig. 1 are both nonrephasing. It is straightforward to isolate rephasing diagram 1 from the other two diagrams using time ordered pulses.

Experiments were conducted using the pulse sequence of Fig. 2b and the pulse-shaped LIFEtime spectrometer (ESI Section 2†). The α, β and γ pulse centre frequencies (and half maximum bandwidths, durations and pulse energies) were ω_α ∼1640 cm⁻¹ (∼80 cm⁻¹, 280 fs and 0.3 μJ), ω_β ∼3280 cm⁻¹ (∼125 cm⁻¹, 180 fs and 0.3 μJ) and ω_γ ∼9670 cm⁻¹ (12 cm⁻¹, ∼0.6 ps (1/e) single-sided exponential and 0.7 μJ). These were optimal for excitation of the amide I band (Fig. 4a) and the amide I overtone, which is buried under the broader NH stretch (amide A) absorption in the IR spectra of Fig. 4b.⁵¹ The narrow-bandwidth of the γ pulse maintains spectral resolution in the Raman signal, whilst having a fast rising edge, helping to achieve a minimal instrument response.⁵²

Fig. 5 shows a plot of the IR-Raman signal of the amide I band of a thin film of BSA at two different detection frequencies measured as a function of the delays T_αγ and T_βγ. At detection frequencies far from that expected for amide I emission, instrument response (nonresonant background) is observed (Fig. 5a). Around the peak of the amide I emission (Fig. 5b), a very clear rephasing of signal along the diagonal line of interpulse delays satisfying eqn (2) is observed.

Fig. 5 An amide I IR-Raman photon echo from the protein BSA is generated around inter-pulse delays T_αγ = 2T_βγ. (a) The instrument response signal. (b) The IR-Raman signal at an emission wavelength close to the centre of the amide I band. A 0.2 s signal average per time point and a spacing of 20 fs per time point was used in the data acquisition.

The possibility of observing the rephasing of fully correlated inhomogeneously broadened fundamental and overtone vibrational modes in the diagram 1 IR-Raman pulse sequence was proposed and modelled theoretically by Cho.³⁰ In ref. 30, T_βγ is denoted ‘T’ and T_αγ is ‘T + τ’. For a single inhomogeneously broadened oscillator under the Markovian approximation, diagonal cuts of the IR-Raman echo signal as a function of either T_βγ or T_αγ/2 are exponentially decaying in intensity with a rate Γ which follows:³⁰

Γ/2 = 2γ₁₀ + γ₂₀ (3)

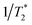γ₂₀ and γ₁₀ are the pure (homogeneous, 1/T₂) dephasing rates of the overtone and fundamental states respectively, each consisting of the sum of vibrational population relaxation 1/(2T₁) and transition frequency modulation rate (pure dephasing). The latter can be assumed similar for 0 → 1 and 0 → 2 transitions. For an isolated vibrational mode, 2 → 1 T₁ population relaxation occurs twice as fast as 1 → 0 T₁ relaxation and therefore γ₂₀ > γ₁₀.³⁵ For an excitonically coupled system comprising coupled amide I modes, the individual 1 → 0 amide I population relaxation rates are shared across all exciton state levels, resulting in γ₂₀ = γ₁₀.⁵

Spectrally dispersed plots of the diagonal IR-Raman echo cuts as a function of T_βγ are shown for BSA and ConA in Fig. 6a and b. Dephasing rates calculated from fitting exponential decays to these echo cuts are shown in the plots as a function of the detection frequency. Assuming that the whole amide I band is excited by the α pulse, the spectrum comprises all overtones and combination bands excited by the β pulse involving the common fundamental amide I, with its frequency ω₀₁ subtracted (see ESI Section 1†). The emission frequencies are shifted by mechanical anharmonicity, observed here to be ∼15 cm⁻¹ for BSA. In Fig. 6a, BSA's alpha helical/random coil rephasing spectrum peaks at around 1635 cm⁻¹ in ω_β − ω_α emission frequency. This is substantially different to ConA (Fig. 6b), which shows a distinct spectrum corresponding to its ‘bright’ (low frequency, 1620 cm⁻¹) and ‘dark’ (high frequency, ∼1660 cm⁻¹) beta-sheet states. A shoulder in both datasets indicates a further rephasing band at 1680 cm⁻¹. Absorption in this part of the spectrum is often ascribed to ‘turns’,⁵³ with 2D-IR-Raman spectra in the following sections indicating that the signal is actually a cross peak involving the main amide I band.

Fig. 6 Plots along the IR-Raman echo diagonal line T_αγ = 2T_βγ as a function of detection frequency and T_βγ for (a) BSA and (b) ConA. Shown above are single exponential fitted rates. The relative fit error is plotted in red. The regions greyed out gave poor fits (indicating non-exponential decay) or were at the extrema of the emission spectrum.

The BSA echo diagonal cuts fit well to single exponential decays along T_βγ and T_αγ/2. To eliminate instrument response, fits were made for delays >300 fs. The fitted rate Γ/2 (eqn (3)) has a maximum value of 3.8 ± 0.2 ps⁻¹ at around 1610 ± 10 cm⁻¹ emission frequency. Under the assumption of excitonic coupling (γ₂₀ = γ₁₀), for this dephasing rate eqn (3) gives γ₁₀ = 1.3 ± 0.2 ps⁻¹. This is not dissimilar to the value of 1.4 ps⁻¹ determined by Hamm et al. for a solvated helical peptide using the stimulated IR photon echo technique.⁵⁴ Interestingly, the observed IR-Raman rate Γ/2 appears to steadily diminish across the amide I emission range (Fig. 6a), continuing to fall to around 2.5 ± 0.2 ps⁻¹ by 1675 cm⁻¹. A possible explanation for this drop in decay rate is that higher emission frequencies correspond to blue-shifted excitonic states which are less hydrogen bonded and therefore have lower relaxation and dephasing rates.⁵³ The BSA studied here was in the form of a dehydrated film, with much less water hydrogen bonding to individual carbonyls than when solvated,⁴⁰ possibly increasing this effect.

The ConA echo diagonal data fits well to a single exponential decay at 1600–1620 cm⁻¹ in emission frequency. Compared with BSA, over this range a slightly lower dephasing rate (Γ/2) of 3–3.5 ps⁻¹ was observed. At higher emission frequencies, highly non-exponential behaviour occurs.

To better understand the behaviour of the amide I IR-Raman dispersed echo signals, plots of signal vs. ω_β − ω_αvs. T_βγ for fixed values of T_αγ are highly informative, as shown in Fig. 7. The rephasing time T_αγ = 2T_βγ is shown as a dotted black line. From left to right, echoes that peak along T_βγ tracking the increase in T_αγ are clear for the BSA and ConA states identified in Fig. 6. The 1650 cm⁻¹ ConA and 1680 cm⁻¹ BSA and ConA signals do not exactly track the echo line. 2D measurements (next Section) reveal that these contain a combination band cross peak signal. The total 1650 cm⁻¹ ConA signal decays with T_αγ more rapidly than the 1620 cm⁻¹ emission signal, consistent with Fig. 6b. Data at later times (see ESI Fig. S11†) indicates that the 1650 cm⁻¹ ConA signal is however oscillatory – a common effect for overlapping signals in homodyne techniques. In Fig. 7, the solid black lines indicates when T_αγ = T_βγ. Beyond this line, the pulse time ordering is reversed and diagrams 2 and 3 of Fig. 1 generate signal, which being nonrephasing is shorter-lived. The 1650 cm⁻¹ emission of ConA contains more signal from diagrams 2 and 3 than the other bands of ConA and BSA. These observations combined explain the poorer fit of this part of the ConA rephasing spectrum to a single exponential in Fig. 6b. Equivalent plots reversing the role of T_αγ and T_βγ also offer useful insights and are shown in ESI Section 4.†

Fig. 7 Amide I IR-Raman echoes from BSA (top row) and ConA (bottom row) viewed by plotting emission spectra as a function of T_βγ for fixed T_αγ. The dotted line is the spectrum of theoretical maximum rephasing time value, T_αγ = 2T_βγ. The solid line marks the T_αγ = T_βγ point, at which all three diagrams contributing to the signal are selected (Fig. 1). For T_βγ delays earlier than this line, pathway 1 is selected. For T_βγ delays later than this line, pathways 2 and 3 are selected. A 0.2 s average per time point and a spacing of 20 fs per time point was used for the data acquisition.

Amide I homodyne 2D-IR-Raman spectroscopy

In the previous section, use of a dispersed echo pulse sequence enabled the measurement of a single IR-Raman frequency axis (the emission frequency ω_β − ω_α) as a function of two interpulse delays, giving a detailed view of amide I IR-Raman rephasing and nonrephasing processes. The method is ‘homodyne’ meaning that the intensity of the IR-Raman emission is measured background free, as opposed to heterodyne detection, where the signal field is measured interferometrically using a reference beam. In the following sections, homodyne and heterodyne amide I spectra are presented where the ω_α frequency response is also determined, giving 2D-IR-Raman spectra that are functions of ω_α, ω_β − ω_α and one or both delays T_αγ and T_βγ. Through the use of mid-IR pulse-shaping on the α pulse train, the same experiment and samples used to collect the echo data of Fig. 5–7 were also used to collect these 2D-IR-Raman spectra. In this section, the homodyne frequency domain approach is presented.

Whereas the dispersed echo pulse sequence (Fig. 2b) uses the full bandwidth of the α pulses, a frequency domain 2D-IR-Raman approach is realised by using the pulse shaper to frequency-narrow the α pulses. The ω_α frequency is then stepped to record emission spectra as a function of ω_α at fixed pulse delays. The pulse sequence in Fig. 2c shows the approach. Reverse and forward single-sided exponential pulse shapes of width 10 and 12 cm⁻¹ were used on the α and γ pulses to reduce the nonresonant background.⁵⁵ The broadband β pulse (125 cm⁻¹ FWHM/180 fs) was the same as for the echo measurements.

Homodyne 2D-IR-Raman spectra of BSA and ConA as a function of T_αγ and T_βγ are shown in Fig. 8 and 9. The BSA spectra are dominated by a single alpha-helical feature, which appears diagonally elongated and almost identically shaped in the 2D spectra at rephasing pulse timings (T_αγ = 2T_βγ, top row of Fig. 8), but owing to improper rephasing dramatically distort at longer T_αγ delays (middle row of Fig. 8). As T_αγ is made smaller than the optimal rephasing time, the homodyne frequency domain 2D-IR Raman spectra narrow. This is also the case for the reverse (non-rephasing) pulse ordering (bottom row of Fig. 8), which isolates nonrephasing diagrams 2 and 3. In these, a very weak peak at ω_α ∼ 1620 cm⁻¹ is observed. This is possibly IR-Raman diagram 3, which is shifted along ω_α by the anharmonicity of the amide I band. Diagram 3 differs from the other two diagrams by its sign, dephasing factors and the transition dipole driven by ω_α (Fig. 1 and discussion in ESI Section 3†). It makes a subtle appearance in the BSA photon echo data of Fig. 7 (clearest in the T_αγ = 0.6 ps plot).

Fig. 8 2D-IR-Raman spectra of BSA as a function of T_αγ and T_βγ measured using homodyne detection of the dispersed emission ω_β − ω_α and frequency domain determination of the ω_α axis (5 cm⁻¹ steps). The peak CCD camera pixel signal count is shown in the top right of each spectrum for the 1 s accumulation time used at each ω_α step.

Fig. 9 2D-IR-Raman spectra of ConA as a function of T_αγ and T_βγ measured using homodyne detection of the dispersed emission ω_β − ω_α and frequency domain determination of the ω_α axis (5 cm⁻¹ steps). The peak CCD camera pixel signal count is shown in the top right of each spectrum for the 1 s accumulation time used at each ω_α step.

The 2D-IR-Raman spectra of the beta sheet containing ConA (Fig. 9) are, like the photon echo data, dramatically different in appearance to BSA. The ‘correct’ (T_αγ = 2T_βγ) diagram 1 rephasing delays and the diagrams 2 and 3 nonrephasing spectra all indicate an elongated ‘diagonal’ (overtone) amide I distribution stretching over a broader and higher frequency range compared to BSA, consistent with the well-known character of beta sheet IR spectra. A strong cross peak between the bright beta sheet amide I states (ω_α ∼ 1620 cm⁻¹) and the dark states (ω_β − ω_α ∼1655 cm⁻¹) is present for both the rephasing and nonrephasing pulse orderings (e.g.Fig. 9, top left, dotted ring), consistent with the signals observed at this emission frequency in the echo data. The rephasing time-ordering 2D-IR-Raman spectra were extremely sensitive to the pulse delays used. ‘Incorrect’ delays gave rise to broadening/narrowing and also beating as a function of delay, as can be seen in the middle row of Fig. 9. Additional sensitivities significantly affecting the appearance of the spectra included the exact centre frequency of the α and β laser pulses and at long T_αγ delays the presence of even small amounts of water vapour in the optical delivery lines (see ESI Section 2†). Nevertheless, in Fig. 9, the trends are clear and supported by the heterodyne 2D-IR-Raman measurements described in the following Section.

As with IR, Raman, 2D-IR and UV-CD spectroscopy, the differences in the nature of the excitonic states of alpha and beta structured proteins feature clearly in the homodyne 2D-IR-Raman spectra observed here. A final basic illustration of this point is Fig. 10, which show fixed delay rephasing (diagram 1) and nonrephasing (diagrams 2 + 3) spectra of a series of proteins with a range of helical/beta contents. Myoglobin is alpha helical and the remaining proteins are ordered very approximately in increasing beta sheet content,⁵³ illustrating the presence of the beta sheet IR-Raman cross-peak as a function of protein measured.

Fig. 10 Homodyne frequency domain 2D-IR-Raman spectra of 6 proteins collected at a rephasing pulse delay (selecting diagram 1) and a nonrephasing pulse delay (selecting diagrams 2 and 3). BSA and myoglobin are exclusively alpha helical/random coil, whereas the other proteins contain varying amounts of beta sheet.

Amide I heterodyne FT-2D-IR-Raman spectroscopy

In this section, an approach to collecting Fourier-Transform (FT), heterodyne detected 2D-IR-Raman spectra is presented and applied to the amide I bands of BSA and ConA. The same experimental setup used for the IR-Raman frequency domain homodyne 2D and dispersed echo spectroscopy of the previous sections was again used for the following heterodyne FT approach, the only change being in the manner in which the pulse-shaper on the α beam is used and in the way in which the data is processed. The principles and advantages of heterodyne detection of a spectroscopic signal field (as opposed to a homodyne measurement of the signal intensity) have been discussed extensively in the VSFG and 2D-IR literature.^35,56 For 2D-IR-Raman spectroscopy, the advantages are also numerous. Firstly, the strong nonresonant background signal that occurs at pulse overlap is exactly subtractable though heterodyning. In the homodyne measurements presented so far, pulse delays of <200 fs gave spectra containing significant nonresonant background, interfering with the signals of interest. A second advantage is that the heterodyne signal is linear in analyte concentration and linear in the strength of each vibrational state, as opposed to quadratic for homodyne detection. The third advantage is that the different detected signals emitted at similar wavelengths interfere with the local oscillator field – and not with one another, resulting in spectra that are simpler to interpret and which do not feature confusing signal beatings with laser pulse delay.

In a heterodyne detected optical experiment, a stable reference light source (local oscillator, LO) illuminates the detector. The signal emission from the sample is overlapped with the LO field at the detector and if these two fields are phase coherent, of similar wavelength and similar timing, then interference is observed between them, both spatially and temporally. For a measured intensity, I, signal and LO fields E with time delay Δt and relative phase Δφ, assuming collinear beams, an optical frequency ω and then integrating over time, the following equation commonly used to demonstrate the general principle of heterodyning is deduced:

I_total ∝ E_total² ∝ (E_LO + E_Sig)² ∝ E_LO² + E_Sig² + E_LOE_Sig cos(ωΔt + Δφ) (4)

The oscillatory dependence on ω, Δt and/or φ allows the heterodyne cross term E_LOE_Sig to be extracted from the homodyne (square) terms in the dispersed spectrum, constituting a direct measurement of the complex valued signal field of interest, as opposed to homodyne measurements, where the square of the signal field is detected alongside unwanted cross-terms of spectrally overlapping signals.

As noted earlier, the IR-Raman spectroscopy techniques introduced here resemble broadband VSFG spectroscopy in their detection scheme, but involve an additional IR field. A common means of heterodyne detection in VSFG is to use the excitation beams to first generate an LO field in a reference material, then optically relay the excitation beams and LO beam to the sample in a geometry ensuring phase stability and overlap of the LO and the SFG signal at the detector.⁵⁷ It is technically feasible to implement heterodyne detection this way for 2D-IR-Raman spectroscopy, however the required T_αγ and T_βγ pulse timing control (which is not necessary for VSFG) would have to be inserted after LO generation. Such an endeavour, along with 2D-IR-Raman spectroscopy being 3-beam as opposed to 2-beam for VSFG would require considerable optical design and alignment. Numerous other heterodyne schemes also exist,^32,58 but for similar reasons do not appear to be straightforward to implement in the present context.

The heterodyne scheme presented and explored here uses a mid-IR pulse-shaper to generate two identical collinear femtosecond α pulses with an adjustable delay – exactly as one would do in an FT pump-probe 2D-IR experiment,³⁵ but as will be described below, with quite different consequences. The pulse sequence is shown in Fig. 2d. The dual α pulse delay is defined as T_αα′, with α′ labelling the second replica pulse. The key point is that along with the β and γ fields, the two α pulses each generate separate nonlinear IR-Raman fields E_δ and . Setting T_αγ and T_βγ to zero results in E_δ mainly comprising nonresonant background, which acts as the fixed local oscillator. When the α′ pulse is scanned earlier in time, this causes the relative phase of IR-Raman fields E_δ and 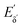to oscillate. These oscillations provide the means not only to extract the heterodyne signal (eqn (4)), but also to observe the free-induction decay initiated by the α′ interaction. This is then Fourier transformed to give the ω_α spectral coordinate of a 2D-IR-Raman spectrum. With modifications, the scheme is equally applicable to VSFG.

Fig. 11a shows a spectrally dispersed heterodyne IR-Raman signal as a function of the delay T_αα′ for a ConA film deposited on a glass coverslip. Cuts of this graph showing the interferogram at single detection frequencies are shown in Fig. 11b and the dispersed spectrum for T_αα′ = 0 is shown in Fig. 11c, where the heterodyne ConA signal can be seen negatively interfering with the larger nonresonant background. The Fourier Transform (FT) of Fig. 11a along T_αα′ is shown in Fig. 11d. This is a 2D-IR-Raman spectrum of the ConA signal overlaid on the nonresonant background. A spectrum of the glass coverslip only (Fig. 11e) provides a reference spectrum of the nonresonant background, which can be divided from the ConA spectrum to give the final heterodyned 2D-IR-Raman spectrum. The process is laid out mathematically in ESI Section 5.†

Fig. 11 Using two identical α pulses enables heterodyne detection of IR-Raman emission. (a) Shows a spectral interfergrom of a ConA film on glass as a function of the interpulse delay T_αα′. (b) Shows cuts of (a) for ω_β − ω_α = 1690 cm⁻¹ (black) and 1650 cm⁻¹ (red). (c) Shows a cut at T_αα′ = 0. The heterodyned IR-Raman emission is mix of resonant protein and nonresonant background signal. (d) Shows the 2D Fourier transformed IR-Raman spectrum of (a) along the T_αα′ coordinate. (e) Shows the 2D Fourier transformed spectrum for a sample of glass only.

Heterodyne detected FT 2D-IR-Raman spectra of the amide I band of BSA and ConA are shown in Fig. 12. The alpha helical BSA spectra are, just like the homodyne frequency domain data of Fig. 8, simple in shape, however they have a more clearly defined broad diagonal and narrow anti-diagonal width of ∼60 × ∼20 cm⁻¹. The time ordering of the pulses means that the signals are exclusively pathway 1. On comparing the Feynman diagrams and response functions of pathway 1 IR-Raman to 2D-IR spectroscopy, it can be concluded that the diagonal and anti-diagonal widths of heterodyne FT 2D-IR-Raman spectra report on inhomogeneous and homogeneous broadening in exactly the same way that conventional FT 2D-IR measurements do. This is further described in ESI Section 3.† The spectra of Fig. 12 are analogous to the rephasing component of ‘excited state’ absorption diagonal peak in a 2D-IR spectrum, except that the IR-Raman signal does not contain an interfering ground state bleach/stimulated emission signal.

Fig. 12 Heterodyne detected Fourier-Transform 2D-IR-Raman spectra of BSA and ConA. The ω_α spectral coordinate is Fourier Transformed from T_αα′ scans of 0 to 3 ps in steps of 20 fs (2× undersampling). The data are an average of 10 scans with 1 s averaging per time point.

The ConA Heterodyne 2D-IR-Raman spectrum of Fig. 12b is qualitatively similar along the diagonal to the ConA FT-IR absorption spectrum of Fig. 4a. The triangular-shaped 2D spectrum contains a strong cross peak involving the ‘bright’ and ‘dark’ beta sheet amide I exciton-state combinations (indicated in Fig. 12b by a white ring), as was also observed in the homodyne 2D-IR-Raman data (Fig. 9). In Fig. 12b, the heterodyned cross peak is similar in strength to the diagonal signal. Compared with the homodyne 2D-IR-Raman data, an important advantage of the heterodyne 2D spectra is that they are properly normalised regarding the ω_β and ω_α laser intensity distributions and linear in molecular response. In solution phase ConA 2D-IR spectra reported by Baiz et al., the intensity of the strongest beta sheet cross peak relative to the diagonal signal was ∼12–15%, a value obtained using perpendicularly polarised pump and probe pulses, which enhances 2D-IR cross-peak contrast.¹³ Although the physical states of the proteins are different, this is unlikely to account for such a large difference between the 2D-IR and 2D-IR-Raman cross peak sizes relative to the diagonal signal. The origin of the strong cross peak is likely to be due to the Raman strengths of the beta sheet amide I exciton states being reversed compared to that of the IR extinction coefficients i.e. the Raman cross section of the higher frequency beta sheet states are much larger than the Raman cross sections of the lower states.³ Diagram 1 for a combination band (ESI Section 7†) shows that a cross-peak always involves an α-driven IR transition for one of the two vibrational states and a γ-driven Raman transition for the other state. The absence of any ‘mirrored’ cross peak at ω_α ∼1660 cm⁻¹ further supports this. For this cross peak, both the IR and Raman strengths are weak.

On increasing the T_βγ delay to 300 fs, the ConA data (Fig. 12d) shows a loss of diagonal and cross peak ConA signal at ω_α ∼1620 cm⁻¹. Although homodyne 2D-IR-Raman rephasing measurements corroborate this observation, it is hard to infer this from the dispersed echo measurements (where this loss of signal occurs across the entire emission range). The homodyne nonrephasing measurements, which go out to longer T_βγ delays (Fig. 9) indicate that the cross peak signal does have long-lived components in these parts of the spectrum.

Maximising spectral coverage and signal size in 2D-IR-Raman spectroscopy

The ps-fs-ps frequency domain homodyne IR-Raman 2D-IR data measurements presented in Fig. 8 and 9 were collected at a laser repetition rate of 50 kHz, giving amide I signals of order 10⁶ photons per second per pixel at the smallest feasible inter-pulse delays. This level of signal allowed each 2D spectrum to be recorded in less than a minute. The ps α pulse was generated by spectrally narrowing a 300 fs mid-IR pulse (80 cm⁻¹ FWHM) to 5–10 cm⁻¹ with an acousto-optic pulse shaper. This reduced the α pulse energy by 10–20× and constrained the α-pulse frequency range to around ±80 cm⁻¹ about the laser centre frequency. Shifting this range required time consuming shaper/spectrometer realignment and re-calibration.

Many vibrational bands are <20 cm⁻¹ in width, and concentrating the energy of the α and β pulses into this bandwidth gives the largest signal sizes.⁵⁹ Combined with a large frequency tuning range, it is for this reason that the frequency domain ps–ps–ps DOVE-EVV 2D approach¹⁸ (Fig. 2a) is attractive. Nevertheless, incorporating a broadband β pulse, (as in the ps–fs–ps frequency domain scheme of Fig. 2c), is potentially advantageous when both the improved nonresonant background suppression, time resolution and multiplex advantage are accounted for.

To generate larger signals across a broader spectral range, IR-Raman experiments were conducted using a laser system incorporating a spectrally bright tunable ps laser to generate the α-pulses (CLF-Ultra A,³⁹ for experimental details, see ESI Section 2†). Here, the α-pulses were roughly 20 cm⁻¹ bandwidth and 1.5 ps duration with an energy at the sample of 0.2–0.5 μJ across a range of 1200–2000 cm⁻¹. The β-pulse was also spectrally broader compared with the pulse-shaped experiment (∼300 cm⁻¹ FWHM, 50 fs, 3300 cm⁻¹, ∼0.4 μJ at sample). Fig. 13 shows a ps-fs-ps homodyne 2D-IR-Raman spectrum of BSA at two intensity magnifications collected using the ‘bright α-pulse’ Ultra A setup. The same detector used in the pulse-shaped experiments measured a ∼20–30× increase in early-delay amide I signal size in the bright α pulse experiment, amounting to 10⁷ to 10⁸ photons per second per pixel. Many parameters were different between the two experiments, such as emission wavelengths, spectrometers used, focal spot sizes, repetition rate, pulse–widths/shapes etc. Accounting for emission wavelength, repetition rate and spot sizes, the gain from the change in pulse shapes and α spectral brightness is an impressive ∼40–60×.

Fig. 13 2D-IR-Raman spectra of protein BSA measured using homodyne detection of the dispersed emission ω_β − ω_α and frequency domain determination of the ω_α axis via a bright, tuneable ps laser (10 cm⁻¹ steps, 5 s average/step). Delays of T_αγ ∼1200 fs and T_βγ ∼600 fs (diagram 1, rephasing) were used to remove broader signals and reveal the aliphatic and aromatic peaks. (a) and (b) are the same 2D-IR-Raman spectrum shown at different z-scale maxima.

The bright α pulse 2D-IR-Raman spectrum of Fig. 13b reveals the weaker aliphatic scissor overtone (ω_β − ω_α ∼ 1450, ω_α ∼ 1450 cm⁻¹) and aromatic cross peaks that were identified by Klug and co-workers in peptides and proteins (e.g. tyrosine – ω_β − ω_α ∼1625 cm⁻¹, ω_α ∼ 1550 cm⁻¹ and phenylalanine – line of peaks at ω_α ∼ 1515 cm⁻¹).^25,26 The observed signals in Fig. 13 were at the level of 10² to 10³ photons per second per pixel. The delays used to collect this data were T_αγ ∼1.2 ps and T_βγ ∼0.6 ps, reducing the competing amide I signal somewhat. The aliphatic overtone signal was used as an intensity standard in previous work,²⁷ and signal levels from this band increased by roughly 10× when the β-pulse centre frequency was tuned from 3300 to 2900 cm⁻¹. With each CCD pixel spaced by 2 cm⁻¹, integrating the signal along ω_β − ω_α, across the band around 10⁵ photons per second were collected from the aliphatic overtone peak of a protein film sample. It can be concluded that the bright α pulse 2D-IR-Raman approach is clearly a viable option for studying weaker IR chromophores across a wide spectral range.

Solution-phase IR-Raman spectroscopy

Given that the data presented in the paper are from protein films, an important question is to what extent the methods presented are appropriate for solution phase studies. BSA solutions in the range of 50 mg ml⁻¹ BSA (in D₂O) were examined (equivalent to 0.5 M peptide bond concentration) in cells of 50 μm pathlength using 1 mm thick CaF₂ windows. These gave homodyne 2D-IR-Raman amide I spectra in exactly the same signal size range as the thin films (see ESI Section 6†). The instrument response increased only by ∼100 fs due to the increased nonresonant background from the solvent/windows. Given that IR-Raman dispersed echo signals are even stronger in size (owing to the use of the full bandwidth of the α pulse) there is clearly scope for applying both homodyne IR-Raman echo and 2D-IR-Raman spectroscopy to solutions of strong IR chromophores such as amide I in the hundreds of millimolar range.

The homodyne methods presented here necessarily suffer from a quadratic dependence of signal size on concentration, pathlength, IR transition moments and Raman polarisability.¹⁹ This is not so for heterodyne methods. The heterodyne method described uses pulse shaping to generate a local oscillator from the sample nonresonant background. The key aspect of heterodyne detection in the strong signal limit is maintaining I_LO ≫ I_sig. In the weak signal limit, it is capturing both I_LO and E_LOE_sig within the dynamic range of the detector. It is important to recognize that if the homodyne signal is shot (photon) noise limited at the detector, the heterodyne signal is also,⁶⁰ so attenuation of I_LO and E_LOE_sig does not make sense when observing low concentrations. For the protein films, owing to the zero delay homodyne amide I IR-Raman signal I_sig typically being comparable or greater in size to the nonresonant background I_LO, to achieve a signal mainly comprising I_LO and E_LOE_sig, it was actually necessary to reduce I_sig by translating the film to regions where the protein was 3–5× thinner than optimal in the homodyne measurements. Brief experimental tests on solution-phase liquid cells were conducted and the problem was found to be the opposite – the nonresonant background generated at T_βγ = 0 to be used as the LO saturated the detector. There are a number of approaches to investigate in future for controlling this. One is increasing the T_βγ delay to reduce the LO size, using lasers with shorter pulses to reduce the required T_βγ delay. Another is liquid jets, which have previously been used in THz-Raman methods, removing entirely the nonresonant response of the windows.^33,34

Conclusions

In this work, dispersed echo, homodyne and heterodyne 2D-IR-Raman pulse sequences are shown to be an interesting way of measuring 2D spectra. With the increased temporal and spectral resolution of these new approaches compared with earlier methods, application of the techniques to the amide I band of proteins is shown to be possible. The large ratio of inhomogeneous to homogeneous broadening results in amide I IR-Raman photon echoes, which, alongside nonrephasing processes and the unique excitonic nature of alpha and beta protein amide I bands yield interesting, yet tractable dispersed echo spectra as a function of the laser pulse delays. In spectral regions where the signal is purely overtone rephasing, quantification of homogeneous dephasing rates is straightforward. 2D spectra of the IR-Raman response reveal how cross peaks and nonrephasing signals enter the amide I echo data, causing nonexponential decay of the rephasing signal. The deep formal connection between rephasing 2D-IR-Raman and 2D-IR excited state absorption spectra is revealed by the heterodyne detected FT-2D-IR-Raman amide I spectrum of alpha helical BSA, which shows inhomogeneous and homogeneous broadening clearly separated along the diagonal and anti-diagonal of the spectrum.

Across all datasets, it is remarkable how different the beta sheet amide I 2D-IR-Raman spectra are compared with those of alpha helical proteins. Relative to the diagonal overtone intensity, the beta sheet cross peak appears in the 2D-IR-Raman spectra at a much higher intensity compared to that observed for 2D-IR spectra. Taking the ConA heterodyne 2D data as the standard, the beta sheet cross peak was observed to be roughly equal in amplitude to the diagonal overtone intensity. This strong cross peak strength observed is likely due to the Raman and IR intensities of the beta sheet states being reversed, providing a good example as to how 2D-IR-Raman might complement 2D-IR spectroscopy. Another area where IR-Raman methods are clearly interesting is in the study of IR-optically dense and spatially heterogeneous samples. Absorption of the IR beams or scattering of all the beams does not interfere with the detection of the visible IR-Raman signal in the same way as for 2D-IR spectroscopy, where the detector can be blinded by scattered or collinear pump light. Early EVV 2D-IR-Raman images of tissue sections provide a good example of this advantage.²⁷ There are also no interfering ground-state bleach and stimulated emission processes in the IR-Raman data, so it is possible to observe overtone or cross peak rephasing spectra in situations where small mechanical anharmonicities cause spectral overlap and attenuation in 2D-IR spectra. This feature appears to allow for high densities of cross peaks in protein EVV 2D-IR-Raman spectra.²⁹

There is ample scope for improvement and variation of the experimental approaches reported here and numerous possibilities for alternative permutations of the driving fields, such as 2D IR-Raman sum frequency generation,^30,61 heterodyne FT measurements of the nonrephasing pathways, or 2D-IR-resonance Raman.^27,61 Of the two experimental approaches presented, the mid-IR pulse-shaped femtosecond experiment offers the greatest flexibility in performing dispersed echo, frequency domain homodyne and time domain heterodyne 2D-IR-Raman spectroscopy with highest spectral resolution. For studies of weaker chromophores, this flexibility can be sacrificed for signal size and spectral range by replacing the pulse-shaped IR source with a bright, tuneable narrow linewidth laser. In future, emerging chirped pulse optical parametric amplification laser technologies may allow the infrared bandwidth to be tuned at constant pulse energy between the femtosecond and picosecond range – uniting the two approaches.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author gratefully acknowledges Mike Towrie and the CLF-Ultra team for helpful discussions and technical assistance, Mark Frogley and Gianfelice Cinque (Diamond Light Source) for access to an IR microscope, Chris Middleton (Phasetech Spectroscopy) for providing pulse-shaper Labview code and David Klug and his team (Imperial College London) for interest and support in the CLF provision of IR-Raman 2D-IR methods. This work was made possible through STFC-funded access to the CLF-LIFEtime facility (BBSRC grant BB/L014335/1) and CLF-Ultra A facility (STFC – BBSRC ST/501784) and through a UKRI Future Leaders Fellowship grant (MR/S015574/1).

Notes and references

1. S. Krimm and J. Bandekar, Adv. Protein Chem., 1986, 38, 181–364.
2. A. Elliott and E. J. Ambrose, Nature, 1950, 165, 921–922.
3. T. Yu, J. L. Lippert and W. L. Peticolas, Biopolymers, 1973, 12, 2161–2176.
4. J. L. Lippert, D. Tyminski and P. J. Desmeules, J. Am. Chem. Soc., 1976, 98, 7075–7080.
5. P. Hamm, M. Lim and R. M. Hochstrasser, J. Phys. Chem. B, 1998, 102, 6123–6138.
6. C. Kolano, J. Helbing, M. Kozinski, W. Sander and P. Hamm, Nature, 2006, 444, 469–472.
7. A. Remorino, I. V. Korendovych, Y. Wu, W. F. DeGrado and R. M. Hochstrasser, Science, 2011, 332, 1206–1209.
8. P. Mukherjee, I. Kass, I. Arkin and M. T. Zanni, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 3528–3533.
9. H. T. Kratochvil, J. K. Carr, K. Matulef, A. W. Annen, H. Li, M. Maj, J. Ostmeyer, A. L. Serrano, H. Raghuraman, S. D. Moran, J. L. Skinner, E. Perozo, B. Roux, F. I. Valiyaveetil and M. T. Zanni, Science, 2016, 353, 1040–1044.
10. M. Maj, J. P. Lomont, K. L. Rich, A. M. Alperstein and M. T. Zanni, Chem. Sci., 2018, 9, 463–474.
11. N. Demirdöven, C. M. Cheatum, H. S. Chung, M. Khalil, J. Knoester and A. Tokmakoff, J. Am. Chem. Soc., 2004, 126, 7981–7990.
12. Z. Ganim, S. C. Hoi, A. W. Smith, L. P. Deflores, K. C. Jones and A. Tokmakoff, Acc. Chem. Res., 2008, 41, 432–441.
13. C. R. Baiz, C. S. Peng, M. E. Reppert, K. C. Jones and A. Tokmakoff, Analyst, 2012, 137, 1793–1799.
14. S. Hume, G. Hithell, G. M. Greetham, P. M. Donaldson, M. Towrie, A. W. Parker, M. J. Baker and N. T. Hunt, Chem. Sci., 2019, 10, 6448–6456.
15. A. M. Alperstein, J. S. Ostrander, T. O. Zhang and M. T. Zanni, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 6602–6607.
16. J. C. Wright, P. C. Chen, J. P. Hamilton, A. Zilian and M. J. Labuda, Appl. Spectrosc., 1997, 51, 949–958.
17. W. Zhao and J. C. Wright, J. Am. Chem. Soc., 1999, 121, 10994–10998.
18. W. Zhao and J. C. Wright, Phys. Rev. Lett., 2000, 84, 1411–1414.
19. K. A. Meyer and J. C. Wright, Anal. Chem., 2001, 73, 5020–5025.
20. K. A. Meyer and J. C. Wright, J. Phys. Chem. A, 2003, 107, 8388–8395.
21. P. M. Donaldson, R. Guo, F. Fournier, E. M. Gardner, I. R. Gould and D. R. Klug, Chem. Phys., 2008, 350, 201–211.
22. P. M. Donaldson, R. Guo, F. Fournier, E. M. Gardner, L. M. C. Barter, C. J. Barnett, I. R. Gould, D. R. Klug, D. J. Palmer and K. R. Willison, J. Chem. Phys., 2007, 127, 114513.
23. R. Guo, F. Fournier, P. M. Donaldson, E. M. Gardner, I. R. Gould and D. R. Klug, Phys. Chem. Chem. Phys., 2009, 11, 8417–8421.
24. R. Guo, S. Mukamel and D. R. Klug, Phys. Chem. Chem. Phys., 2012, 14, 14023–14033.
25. F. Fournier, E. M. Gardner, R. Guo, P. M. Donaldson, L. M. C. Barter, D. J. Palmer, C. J. Barnett, K. R. Willison, I. R. Gould and D. R. Klug, Anal. Biochem., 2008, 374, 358–365.
26. F. Fournier, E. M. Gardner, D. A. Kedra, P. M. Donaldson, R. Guo, S. A. Butcher, I. R. Gould, K. R. Willison and D. R. Klug, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 15352–15357.
27. F. Fournier, R. Guo, E. M. Gardner, P. M. Donaldson, C. Loeffeld, I. R. Gould, K. R. Willison and D. R. Klug, Acc. Chem. Res., 2009, 42, 1322–1331.
28. L. Rezende Valim, J. A. Davies, K. Tveen Jensen, R. Guo, K. R. Willison, C. M. Spickett, A. R. Pitt and D. R. Klug, J. Phys. Chem. B, 2014, 118, 12855–12864.
29. H. Sowley, Z. Liu, J. Davies, R. Peach, R. Guo, S. Sim, F. Long, G. Holdgate, K. Willison, W. Zhuang and D. R. Klug, J. Phys. Chem. B, 2019, 123, 3598–3606.
30. M. Cho, J. Chem. Phys., 1999, 111, 10587–10594.
31. T. L. Courtney, Z. W. Fox, L. Estergreen and M. Khalil, J. Phys. Chem. Lett., 2015, 6, 1286–1292.
32. M. Grechko, T. Hasegawa, F. D'Angelo, H. Ito, D. Turchinovich, Y. Nagata and M. Bonn, Nat. Commun., 2018, 9, 885.
33. J. Savolainen, S. Ahmed and P. Hamm, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20402–20407.
34. A. Shalit, S. Ahmed, J. Savolainen and P. Hamm, Nat. Chem., 2017, 9, 273–278.
35. P. Hamm and M. Zanni, Concepts and methods of 2D infrared spectroscopy, Cambridge University Press, 2011, vol. 9781107000056.
36. K. Kwak, S. Cha, M. Cho and J. C. Wright, J. Chem. Phys., 2002, 117, 5675–5687.
37. P. M. Donaldson, G. M. Greetham, D. J. Shaw, A. W. Parker and M. Towrie, J. Phys. Chem. A, 2018, 122, 780–787.
38. G. M. Greetham, P. M. Donaldson, C. Nation, I. V. Sazanovich, I. P. Clark, D. J. Shaw, A. W. Parker and M. Towrie, Appl. Spectrosc., 2016, 70, 645–653.
39. G. M. Greetham, P. Burgos, C. Qian, I. P. Clark, P. S. Codd, R. C. Farrow, M. W. George, M. Kogimtzis, P. Matousek, A. W. Parker, M. R. Pollard, D. A. Robinson, X. Zhi-Jun and M. Towrie, Appl. Spectrosc., 2010, 64, 1311–1319.
40. J. Grdadolnik and Y. Maréchal, Biopolymers, 2001, 62, 54–67.
41. U. Novak and J. Grdadolnik, J. Mol. Struct., 2017, 1135, 138–143.
42. N. A. Kurnit, I. D. Abella and S. R. Hartmann, Phys. Rev. Lett., 1964, 13, 567–568.
43. R. F. Loring and S. Mukamel, J. Chem. Phys., 1985, 83, 2116–2128.
44. D. Zimdars, A. Tokmakoff, S. Chen, S. R. Greenfield, M. D. Fayer, T. I. Smith and H. A. Schwettman, Phys. Rev. Lett., 1993, 70, 2718–2721.
45. W. P. de Boeij, M. S. Pshenichnikov and D. A. Wiersma, Chem. Phys. Lett., 1995, 238, 1–8.
46. M. C. Asplund, M. T. Zanni and R. M. Hochstrasser, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 8219–8224.
47. A. Tokmakoff, J. Phys. Chem. A, 2000, 104, 4247–4255.
48. J. D. Hybl, A. A. Ferro and D. M. Jonas, J. Chem. Phys., 2001, 115, 6606–6622.
49. M. Khalil, N. Demirdöven and A. Tokmakoff, Phys. Rev. Lett., 2003, 90, 4.
50. V. Cervetto, J. Helbing, J. Bredenbeck and P. Hamm, J. Chem. Phys., 2004, 121, 5935–5942.
51. S. Lee, N. G. Mirkin and S. Krimm, Biopolymers, 1999, 49, 195–207.
52. A. Lagutchev, S. A. Hambir and D. D. Dlott, J. Phys. Chem. C, 2007, 111, 13645–13647.
53. C. T. Middleton, L. E. Buchanan, E. B. Dunkelberger and M. T. Zanni, J. Phys. Chem. Lett., 2011, 2, 2357–2361.
54. P. Hamm, M. Lim, W. F. DeGrado and R. M. Hochstrasser, J. Phys. Chem. A, 1999, 103, 10049–10053.
55. P. M. Donaldson, PhD thesis, Imperial College London, 2007.
56. I. V. Stiopkin, H. D. Jayathilake, A. N. Bordenyuk and A. V. Benderskii, J. Am. Chem. Soc., 2008, 130, 2271–2275.
57. H. Vanselous and P. B. Petersen, J. Phys. Chem. C, 2016, 120, 8175–8184.
58. H. Wang, T. Gao and W. Xiong, ACS Photonics, 2017, 4, 1839–1845.
59. J. C. Wright, J. Phys. Chem. Lett., 2019, 10, 2767–2774.
60. C. C. Davis, in Lasers and Electro-optics, Cambridge University Press, Cambridge, 2014, pp. 684–735.
61. E. S. Boyle, N. A. Neff-Mallon and J. C. Wright, J. Phys. Chem. A, 2013, 117, 12401–12408.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc02978e

---