Lilypad aggregation: localised self-assembly and metal sequestration at a liquid–vapour interface

Abstract

Spatially resolved soft materials, such as vesicles and microgels, have shown promise as selective adsorbents and microscale reaction vessels. However, spatiotemporal control of aggregation can be difficult to achieve. In this study, nickel(II) chloride and a dipyridyl oligo(urea) ligand were combined in a vapour-diffusion setup to produce a localised spheroidal aggregate at the liquid–vapour interface. This aggregate forms via the self-assembly and fusion of monodisperse colloids and grows until its weight is no longer counterbalanced by surface tension. A simple physical model reveals that this process, termed lilypad aggregation, is possible only for surface energies that favour neither bulk aggregation nor the growth of an interfacial film. These surface energies dictate the final size and shape of the aggregate and may be estimated through visual monitoring of its changing morphology. Lilypad aggregates sequester metal from the surrounding sol and can be collected manually from the surface of the liquid.

---

Introduction

Soft materials are a key component of biological tissues and play important roles in a wide variety of technological applications. They typically consist of a bulk liquid supporting a colloidal network of particles or fibres, which allow the materials to be moulded and reduce their tendency to flow. Due to the combined presence of mobile solutes and an internal scaffold of deformable aggregates, the materials can perform effectively as electrolytes, reaction media and flexible mechanical supports.¹ In many of these systems, it is preferable for aggregation to occur rapidly and in a localised fashion, so that the liquid phase is immobilised only as required. Targeted coagulation of biological fluids allows for the selective entrapment of pathogens and sealing of wounds,² and synthetic soft materials may be similarly designed to form exclusively in the vicinity of a specific stimulus. For example, oleophilic compounds may be used to immobilise the organic phase in an oil–water emulsion, aiding the purification of wastewater and decontamination of oil spills.^3,4

Many studies of spatially controlled aggregation focus on the formation of a gel, a viscoelastic soft material that is almost fully resistant to flow.⁵ For gelation to occur in a non-uniform fashion, the rate of aggregation must exceed the rate of mixing.⁶ Furthermore, the gel must form under non-equilibrium conditions, such as a temperature or concentration gradient.⁷ Low-molecular-weight gelators (LMWGs) are of particular interest since they interact dynamically via supramolecular motifs, which rapidly form or disassemble as stimuli are applied.^8–10 Localised gelation is commonly achieved by functionalising an LMWG with photoswitchable groups, such as stilbenes and azobenzenes, and partially illuminating the gelator sol.¹¹ For pH-sensitive gelation processes, spatial resolution can also be controlled by varying the concentration of a proton source, such as glucono-δ-lactone,¹² irradiating selected regions of a photoacid solution^13–15 or carrying out electrochemical reactions on the surface of an electrode.¹⁶ Likewise, gels may be confined to the interface of two immiscible phases¹⁷ or shaped by the gradual mixing of co-gelator solutions.¹⁸ Inducing sol–gel transitions at specific locations can provide exquisite control over mass transport processes, including molecular diffusion, bacterial motility and enzyme activity.¹⁹

Spatiotemporal control of a sol–gel transition offers access to aggregates with uniform sizes and well-defined morphologies. Rapid gelation of liquid droplets may give rise to monodisperse spheroidal microgels, which can further self-assemble into a close-packed lattice.²⁰ Microgels are useful as microscale reaction vessels,²¹ adsorbents,²² crystallisation media²³ and drug delivery devices,²⁴ and their assemblies can function as structural colourants for chemical sensors and electrochromic displays.²⁵ It is interesting to note that many such technologies possess analogues in the natural world, wherein clusters of cells give rise to similar microstructures and rheological properties. Indeed, microgels have been studied as model cells for simulating the communication and differentiation pathways of biological tissues.^26,27

The self-assembly of microgels and other colloidal aggregates is often controlled using physical stimuli, such as photoirradiation or magnetic fields.²⁸ However, such processes may also occur passively in response to surface tension and density gradients, causing the suspended particles to separate spontaneously from a liquid medium.²⁹ For example, gels incorporating water-immiscible solvents may be dispersed into an aqueous solution, allowed to bind and absorb a dissolved species, then manually retrieved from the liquid surface. This strategy has been used to sequester a range of common pollutants, including organic dyes and heavy metal ions.^30–32

Self-assembly processes have been observed at a variety of solid–liquid, liquid–liquid and liquid–vapour interfaces.^33–35 Colloidal particles can pack together to form symmetrical clusters and two-dimensional lattices,³⁶ while polymers and hydrogen-bonding oligomers are often incorporated into fibrous membranes.³⁷ Surface aggregates may prolong the lifetime of metastable phase mixtures, such as foams, emulsions and bicontinuous fluids.^38–40 In addition, one self-assembled material can template the formation of another, such that successive stages of aggregation give rise to complex hierarchical structures.⁴¹ At the macroscopic scale, spatiotemporal control is typically achieved through layering, emulsification or dropwise addition of precursor solutions.^41–45 Aggregation is thus localised to the initial liquid–liquid interfaces or droplet boundaries, where critical reagents such as solvents, gelators, acids and metal ions are most readily mixed.

An alternative method for generating interfacial aggregates is to identify a liquid in which the material is insoluble and diffuse the vapour of this antisolvent into the precursor sol. Vapour diffusion is a popular strategy for crystal growth and has also been used to control bulk gel formation and colloidal self-assembly.^46,47 A benefit of this approach is that a concentration gradient is established uniformly and reproducibly, without the local variations produced by manual reagent additions.⁴⁸ Furthermore, introducing the antisolvent passively minimises turbulent mixing and deformation of the interface. Thus, the formation of spatially resolved materials depends solely on interparticle interactions²⁹ and the composition of the sol, ensuring that the key physical properties of the system can be reliably assessed.

In this investigation, a vapour diffusion method was used to generate interfacial aggregates of nickel(II) chloride and pyridyl-functionalised oligo(urea)s 1 and 2 (Fig. 1).⁴⁹ To the best of our knowledge, this is the first demonstration of metal sequestration through in situ aggregation at a liquid–vapour interface. Aggregates were observed exclusively at the base of the solvent meniscus and formed in a hierarchical fashion, via the self-assembly and coalescence of monodisperse colloids. Compounds 1 and 2 were chosen for this study because they are simple oligomers which, like film-forming peptides,⁵⁰ feature multiple binding sites for both self-association and metal complexation. Urea groups are known to form robust, linear arrays of hydrogen bonds known as α-tape motifs, making them well suited to the growth of fibrous aggregates.⁵¹ Moreover, the self-assembly of α-tapes may be promoted or disrupted by other supramolecular processes, allowing aggregation to be triggered or reversed by strongly binding guests.⁵²

Fig. 1 (a) Structure of oligo(urea)s 1 and 2 and (b) schematic illustration of the vapour-diffusion strategy used to generate interfacial aggregates.

It has previously been shown that compound 1 forms solid precipitates above its solubility limit, while 2 self-assembles into gel fibres with interesting braided and helical morphologies.⁴⁹ Addition of nickel(II) chloride to the oligo(urea) solutions below their solubility limits does not result in visible precipitation. However, the use of a vapour-diffusion setup causes the metal to be sequestered into a localised spheroidal aggregate. We have termed this phenomenon lilypad aggregation, noting that the materials resemble the aquatic plants in that they grow at a liquid–air interface while supported by surface tension. It is proposed that lilypad aggregation represents an unusual but highly general pathway for non-equilibrium self-assembly, which arises when neither bulk aggregates nor interfacial films are energetically favoured. Because lilypad aggregates are isolated and well-defined, they serve as convenient packages for target solutes, which can be lifted manually from the liquid surface without filtering or evaporating the parent sol.

Experimental section

Materials

All solvents and reagents were purchased from commercial suppliers and used without further purification. Compounds 1 and 2 were synthesised and characterised as previously reported.⁴⁹

Aggregation experiments

Solutions of 1 (0.50% w/v, 9.8 mM) and 2 (0.20% w/v, 2.5 mM) were prepared by sonicating and vigorously heating suspensions of the compounds in dimethylformamide (DMF). Nickel(II) chloride hexahydrate (4.8 mg, 20 μmol) was added to the solution (2 cm³) and dissolved with gentle heating. The resulting mixture was placed in an open 7 cm³ vial and immersed in a 28 cm³ vial of diethyl ether (2 cm³) sealed with vacuum grease and a microscope slide. Lilypad aggregation typically took place over 8 hours at room temperature and was monitored intermittently under an optical microscope. The density of the sol, ρ_sol, was measured at the end of the experiment by weighing 0.1 cm³ aliquots extracted from the surface of the liquid using a micropipette. The aggregate density, ρ_agg, was determined by weighing the wet material and measuring the average spherical radius by optical microscopy.

Material characterisation

FT-IR spectra were measured using a PerkinElmer Spectrum Two spectrometer with an attenuated total reflection (ATR) accessory. For analysis of the aggregate composition and morphology, samples were spread over silicon wafers and dried in air at room temperature for two weeks. Scanning electron microscopy (SEM) images of the dried materials were obtained after coating the samples in 2 nm platinum with a Cressington 328 EM Coating System, while pyrolysates were imaged without coating. Imaging was performed using a FEI Helios NanoLab DualBeam microscope, with beam settings of 1.5 kV and 0.17 nA. X-ray photoelectron (XPS) spectra were obtained under ultrahigh-vacuum conditions (base pressure 4 × 10⁻¹⁰ mbar) using a Kratos Axis Supra with charge neutralisation (0.18 A filament current, 1.3 V bias, 4.2 V charge balance) and a monochromated Al K-α X-ray source. A gun voltage of 15 kV and filament current of 25 mA were used, with a 500 meV step size and pass energies of 80 and 20 eV for the wide and narrow scans, respectively. Spectra were analysed in CasaXPS 2.3.18, using Shirley background fits for narrow scans and the sp² C 1s signal at 284.5 eV for energy calibration.⁵³ The Ni 2p region was fitted with GL(30) peak shapes, a fixed doublet separation of 17.3 eV and equal full width at half maximum (FWHM) values for all core signals eV.⁵⁴

Pyrolysis experiments

Wet aggregates were pyrolysed under nitrogen during thermogravimetric analysis, using a TA Instruments TGA Q500 with a sample gas flow rate of 60 mL min⁻¹. The mass of non-coordinated solvent was measured with a 25 °C min⁻¹ ramp to 150 °C, followed by isothermal heating until no further mass loss was detected. Pyrolysis was subsequently achieved by increasing the temperature to 900 °C at a rate of 2 °C min⁻¹. The pyrolysate was analysed by powder X-ray diffraction (PXRD) at 20 °C, using a PANalytical Empyrean diffractometer operated at 40 kV and 40 mA (unsplit Cu Kα1 + Kα2 doublet, mean wavelength λ = 154.19 pm) with a PIXcel 1D scanning line detector and step size of 0.02626°. The instrument was fitted with a 1/8° fixed divergence slit, 1/4° antiscatter slit and 10 mm mask in the primary beam, a Ni filter and 7.5 mm antiscatter slit in the diffracted beam, and 0.04 rad Soller slots in both beam paths. Inductively coupled plasma mass spectrometry (ICP-MS) data for samples before and after pyrolysis were obtained using a Thermo Scientific X-Series spectrometer, previously optimised for Ni isotopes 58, 60, 61 and 62 to maximise sensitivity and minimise oxide interference. Samples corresponding to approximately 2 mg of wet material were transferred to PFA vials, dried under vacuum for 24 hours and dissolved in concentrated analytical grade nitric acid (Romil) over 24 hours at 20 °C. The solutions were diluted 100-fold in 3% nitric acid prior to analysis. Measurements were calibrated against standards made from a 1000 ppm Ni reference solution (Romil). The close agreement between isotopes confirmed the absence of significant spectral interference, while analysis of procedural blanks indicated that no Ni was present in the reagents used.

Conformational analysis

Density functional theory (DFT) calculations were performed in Gaussian 16 with the B3LYP functional.⁵⁵ Geometries were optimised in the 6-31+G* basis set⁵⁶ from estimated starting configurations and refined in the larger basis sets 6-31++G**, aug-cc-pVDZ⁵⁷ and def2-TZVP.⁵⁸ The intramolecular hydrogen bonding energy of 1 was calculated as the difference in energy between the folded and extended conformations. For comparison, the interaction energy of a related mono(urea) was determined by subtracting the energy of its hydrogen bonded dimer from that of two non-interacting molecules. Finally, the reaction profile for intramolecular hydrogen bond formation was modelled by extending the urea–urea distance of the folded tris(urea) in 0.4 Å increments (or 0.1 Å near the transition state) and reoptimising the structure after each scan step. The activation energy for folding was calculated as the difference in energy between the estimated transition state and most stable extended geometry.

Results and discussion

Aggregation pathway

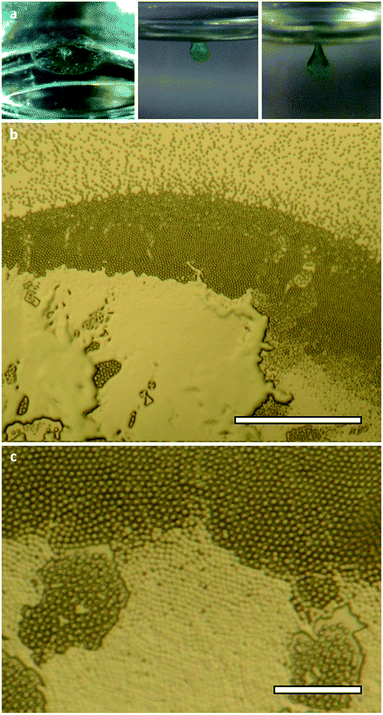
The synthesis and aggregation properties of oligo(urea)s 1 and 2 have been described previously.⁴⁹ The compounds exhibit solubility limits in DMF of approximately 1.0% w/v (20 mM) and 0.2% w/v (2.5 mM), respectively. Mixing DMF solutions of the compounds with transition metal chlorides yields only clear solutions or microcrystalline precipitates. However, when a solution of 1 (0.50% w/v, 9.8 mM) or 2 (0.20% w/v, 2.5 mM) and nickel(II) chloride (0.24% w/v, 1 eq.) is exposed to diethyl ether vapour at room temperature, a circular membrane is formed at the liquid–vapour interface (Fig. 2a and S1, ESI†). The membrane develops over 4–8 hours into a spheroidal green aggregate, which grows to a well-defined threshold size (Fig. S2, ESI†). For 2, the material cannot exceed a final volume of approximately 0.15 mm³ due to the limited solubility of the oligo(urea). By contrast, an aggregate of 1 may develop until its weight is equal to its surface tension, whereupon even slight mechanical inputs may cause it to sink. The aggregation process is comparable to the growth of lilypads and other floating plants, which expand over air–water interfaces and are prevented from sinking by surface tension.⁵⁹

Fig. 2 (a) Typical stages of aggregation during the slow diffusion of diethyl ether vapour into a DMF solution of 1 and nickel(II) chloride; (b) optical micrograph of a particle raft and aggregate after 1 hour (scale bar 500 μm); (c) close-packed lattice of monodisperse particles fusing to form a uniform material (scale bar 100 μm).

Compounds 1 and 2 do not differ significantly in their initial lilypad aggregation behaviour. However, given that 1 can ultimately give rise larger and more clearly defined aggregates, this system was selected for further investigation. Optical micrographs reveal three main stages in the aggregation process (Fig. 2b, c and S3, ESI†). Firstly, microparticles 5–10 μm in diameter self-assemble into a membrane-like particle raft that can be lifted intact from the liquid surface.⁶⁰ The hexagonal close-packed structure of the membrane is attributed to the “Cheerios effect”, whereby particles on a liquid surface are drawn together by the tension of the meniscus between them.⁶¹ In the second stage, the particles gradually fuse⁶² into a continuous aggregate, which adopts a spherical cap morphology to minimise surface energy. Finally, the aggregate reaches a threshold volume, V_end, of 1.3–1.8 mm³ and, being denser than the underlying sol, sinks from the interface. Due to the small quantity of aggregate generated by this process and the variability introduced by drying, we were unable to obtain reliable rheological data for the material. Nonetheless, it should be noted that the aggregate sometimes remains connected to the surface by a 2–3 mm ligament, which persists for several minutes before yielding takes place. This stalling is evidence of viscoelasticity, as extension of the metastable ligament would continue if it were not opposed by a significant increase in elastic potential energy.⁶³

Model of aggregate growth

A key aim of this investigation is to identify the necessary conditions for lilypad aggregation, so that the process may be harnessed and optimised for practical applications. We have thus sought to develop a simple mathematical framework for quantifying the physical properties of lilypad aggregates. These materials offer unique insight into the criteria governing interfacial self-assembly since they grow continuously and symmetrically without manual intervention. By contrast, aggregates formed by dropping reagents onto an interface may exhibit different shapes depending on the drop diameter and fall height,⁶⁴ limiting the reliability of surface energy measurements.

The evolving shape and size of a lilypad aggregate may be rationalised via a simple geometric model of the aggregation process (Fig. 3 and S4, ESI†). The sol is represented as a homogeneous liquid of density ρ_sol, with a planar interface intersecting a uniform aggregate of density ρ_agg > ρ_sol. The aggregate represents a spherical cap with radius R and a centre located a perpendicular distance fR from the sol–vapour interface, where −1 < f < 1. At each stage of growth, the observed value of f corresponds to a local minimum in the potential energy, E. The assumption of a spherical cap geometry prevents consideration of elastic deformation processes, such as the formation of a ligament at the end of aggregate growth. Nonetheless, this simple model reproduces the key features of the aggregation process and avoids some of the difficulties of classical force-based models, which often require the geometry of the interfacial phase boundaries to be precisely known.^60,65

Fig. 3 Geometric model of a lilypad aggregate, from which general expressions for the pattern of growth may be derived.

It can be shown that:

where ρ = (ρ_agg − ρ_sol), g is the acceleration due to gravity and γ_sol and γ_vap are the surface energies of the aggregate-sol and aggregate-vapour interfaces, respectively (Section 2, ESI†). The sol–vapour surface energy is not addressed explicitly in eqn (1) since any growth of the aggregate-vapour interface reduces the area of the sol–vapour interface by an equal amount. Thus, γ_vap corresponds to the difference between these two interfaces, rather than the absolute surface energy of the lilypad aggregate.

Eqn (1) is not applicable to aggregates that are close to sinking, as changes in elastic potential energy are not accounted for. Nonetheless, the model accurately describes materials in the earlier stages of growth, where a lack of deformation away from spherical cap morphologies suggests these elastic contributions are small. Indeed, for realistic values of ρ, γ_sol and γ_vap, the value of E in eqn (1) is overwhelmingly dependent on the surface energy terms (Fig. S5, ESI†). It may be deduced that the Bond number⁶⁵ of the aggregate is significantly less than unity, causing it to adopt a spherical cap morphology to minimise its surface area. Closer examination of eqn (1) reveals that lilypad aggregation is made possible by the term in γ_sol, as this is the only contribution that passes through a local minimum with varying f at constant V. By contrast, the term in γ_vap remains small and relatively fixed as V increases. Aggregate-vapour interactions are therefore energetically important only in the initial stages of aggregate growth.

The lilypad aggregate becomes localised at the base of the liquid meniscus to minimise the gravitational potential energy, given by the first term in eqn (1). For each value of V, the material adopts a morphology with the most favourable balance of aggregate-sol and aggregate-vapour surface energies. This optimal value of f is determined by minimising E at constant V:

Rearranging eqn (2) reveals a linear relationship between γ_sol and γ_vap:

Physical values of V and f are only possible if γ_sol > 0 and |γ_vap| < γ_sol. In a plot of γ_sol against γ_vap, a combination of γ_sol and γ_vap is allowed if it lies in the quadrant bounded by γ_vap = γ_sol and γ_vap = −γ_sol and bisected by the positive x-axis (Fig. S6, ESI†). This observation offers a partial explanation for the rarity of lilypad aggregates: though the aggregate-vapour surface energy is only weakly constrained, interactions between the aggregate and sol must be unfavourable. Consequently, in addition to reducing the solubility of the precursors, an antisolvent may promote lilypad aggregation by destabilising aggregates within the bulk of the solvent.

Although the above results do not account for elasticity or local variations in ρ, γ_sol and γ_vap, they nonetheless provide realistic estimates for the physical properties of a lilypad aggregate. Eqn (3) may be used to predict the growth of a material with known surface characteristics or deduce the values of γ_sol and γ_vap from the aggregate geometry. In a plot of γ_vap against γ_sol, straight lines intersect combinations of surface energies which, for a given value of f, produce the same value of V (Fig. 4a). The gradient of the line connecting the origin and the point (γ_sol, γ_vap) is given by the ratio γ_vap/γ_sol and equal to the value of f at the beginning of aggregate growth. Likewise, the intercept of the line with gradient f = 1 that passes through (γ_sol, γ_vap) may be used to calculate V when the material is fully spherical. If γ_vap ≥ 0, this volume defines the maximum size the aggregate can reach before sinking. For aggregates with γ_vap < 0, however, there is a critical value of f, f_end, beyond which the energy of the system, E, exhibits no local minimum (Fig. S7 and S8,† ESI). These aggregates become unstable and sink before attaining a spherical geometry.

Fig. 4 The surface energies of a lilypad aggregate may be estimated by plotting the possible surface energies for three aggregate geometries (shown in blue) and identifying the area of intersection (red) (a). Side (b) and top-down (c) views are shown for a typical lilypad aggregate, where f = −0.66, R = 1.34 mm and V = 0.77 mm³. Scale bars represent 5 mm in both images. The aggregate occupies a fraction of a sphere, the full circumference of which is delineated in red.

In the case γ_vap < 0, an expression for f_end is obtained by maximising V with respect to f:

The maximum aggregate volume, V_end, may be calculated by substituting this expression into eqn (3). Coordinates of constant f_end are specified by straight lines in the surface energy plot, while V_end and the corresponding radii R_end form curved contours (Fig. S9, ESI†). Marking the intersection of these lines may allow γ_sol and γ_vap to be estimated in situations where only the final aggregate geometry can be accurately observed. It should be noted that aggregates approaching f_end may display significant extension under gravity, necessitating the consideration of elastic potential energy and prolate spheroid geometries. At the cost of increasing the complexity of the model, such corrections could aid our understanding of ligament formation and enable a more predictive description of aggregates in the final stages of growth.

Surface energy measurements

Eqn (1)–(4) were applied to a lilypad aggregate generated from an 0.5% w/v DMF solution of 1 and equimolar nickel(II) chloride. Values of R were measured from side-on visual observations, while mean values of f were obtained from top-down micrographs of the growing material (Fig. 4b, c and S11, ESI†). According to eqn (4), f_end depends only on the ratio γ_vap/γ_sol. The final aggregate geometry can therefore be used to estimate the signs and relative values of the surface energies, even if no other physical parameters are known. Measurements at the end of aggregate growth indicate that R_end = 0.76 ± 0.06 mm and f_end = 0.50 ± 0.07, suggesting that γ_vap is negative and 38 ± 7% smaller than γ_sol.

To obtain absolute values for γ_vap and γ_sol, additional measurements are required. The value of ρ was estimated after eight hours of growth by weighing the aggregate and a 0.100 cm³ sample of sol from close to the interface. Averaging the results of three experiments reveals that ρ_sol = 0.82 ± 0.02 g cm⁻³ and ρ_agg = 1.00 ± 0.05 g cm⁻³, meaning that ρ = ρ_agg − ρ_sol = 0.18 ± 0.05 g cm⁻³. The error of approximately 30% in ρ affects the intercept in eqn (3) to produce errors of equal magnitude in the estimated surface energies. The irregular shape of the aggregate in the early stages of growth adds to these uncertainties by limiting the precision with which f and R can be monitored. Nonetheless, the intersection of three observations in a surface energy plot yields realistic surface energies of γ_sol = 0.25 ± 0.11 mJ m⁻² and γ_vap = −0.20 ± 0.07 mJ m⁻². Although the errors in these results are large, the signs of the surface energies and their orders of magnitude may be reliably determined.

It should be noted that γ_vap and γ_sol correspond to the changes in surface energy when solution at the interface is displaced by the lilypad aggregate. The measured energies are therefore much smaller than values typically reported for liquid–vapour and solid–liquid interfaces (15–30 mJ m⁻² for organic solvents under air⁶⁶ and 5–50 mJ m⁻² for water on organic polymers⁶⁷), which denote the absolute energies for surface formation. Indeed, comparable surface energies below 1.0 mJ m⁻² have been measured at the interfaces of liquid phases.⁶⁸ Interfacial aggregation occurs because aggregate-sol interactions are slightly weaker than interactions between the solvent molecules themselves (γ_sol > 0), whereas replacing solvent–vapour interactions with an aggregate-vapour interface is energetically favourable (γ_vap < 0).

Lilypad aggregation is an example of a Rayleigh–Taylor instability, in which layers of immiscible fluids interpenetrate due to the greater density of the upper phase.⁶⁹ As the radius of a lilypad aggregate approaches R_end, sinking may occur spontaneously and unpredictably in response to mechanical disturbances or other minor physical inputs. For systems in which γ_vap < 0, this observation may be rationalised by the presence of a local maximum in E at a value of f > f_end. The energy needed to deform beyond this value of f, E_a, decreases in magnitude as the aggregate grows larger. Thus, lilypad aggregates with f > 0 and γ_vap < 0 are metastable, meaning that they may relax into a spherical geometry and detach from the interface. For a typical aggregate in this study, E_a is approximately 50 pJ at f = −0.2, but decreases to 12 pJ at f = 0.0 and just 0.6 pJ at f = 0.2 (Fig. S12, ESI†). The sharp reduction in E_a on approaching f_end = 0.50 ± 0.07 greatly increases the probability of sinking, as even small perturbations can provide the energy required.

Analysing the surface energies of a lilypad aggregate provides insight into the factors underlying this unusual physical phenomenon. The values of γ_sol and γ_vap are likely to depend on the ligand structure and aggregation conditions. It is possible that modifying these parameters will enable rational tuning of the aggregate process, to generate larger aggregates incorporating a higher percentage of the dissolved metal salt. A key aim of future investigations will be to use surface energy measurements to rationalise the design of lilypad aggregate systems and target more efficient and versatile metal-sequestration agents.

Criteria for lilypad aggregation

According to our model, materials displaying certain values of γ_vap and γ_sol cannot form through lilypad aggregation. If γ_sol < 0 or γ_vap > γ_sol > 0, it is energetically favourable for aggregates to form in the bulk of the liquid, perhaps giving rise to a precipitate, colloidal suspension or homogeneous gel (Fig. S10, ESI†). Conversely, materials with γ_sol > 0 and γ_vap < −γ_sol will spread over the interface as a continuous film, such that relatively unfavourable liquid–vapour interactions are minimised. Lilypad aggregation is a general phenomenon occurring at the boundary between these two behaviours, when the developing material is strongly stabilised by neither the surface nor the bulk of the parent sol. Given that both gels⁵ and interfacial aggregates³³ are frequently observed, we expect that lilypad aggregation is feasible for a variety of compounds, with or without coordinating metals, under a range of non-equilibrium conditions.⁷

Interestingly, if DMF is replaced with dimethylacetamide or a different metal halide or antisolvent is used, lilypad aggregation does not occur (Table S1 and Fig. S13, ESI†). However, lilypad aggregates are formed if the concentration of 1 is reduced, albeit more slowly and with smaller final volumes (Fig. S14, ESI†). It may be concluded that the experimental outcome is highly sensitive to the choice of metal and solvent system but relatively weakly affected by changes in ligand concentration. To optimise the process for practical applications, it would be useful to measure the effect of these and other physical parameters, such as the temperature and container geometry, on the rate of aggregation.⁴⁸ Obtaining such kinetic data will be a key objective of future investigations.

In the absence of metal ions, the oligo(urea)s used in this study display very different aggregation behaviours. Tris(urea) 1 gives rise to microcrystalline precipitates in DMF while pentakis(urea) 2 forms braided networks of helical gel fibres.⁴⁹ In both cases, however, diffraction and modelling studies suggest that the aggregates consist of molecules in extended conformations. By contrast, many other linear oligo(urea)s have been shown to form foldamer structures through intramolecular hydrogen bonding⁷⁰ or anion complexation.⁷¹ It is proposed that 1 and 2 do not exhibit interactions of this type due to the relative rigidity of the p-benzyl spacers between urea groups. When the compounds are incorporated into labile⁷² nickel(II) complexes, conformational strain could similarly favour coordination polymers over discrete chelate structures, generating a flexible cross-linked network as the thermodynamic product.

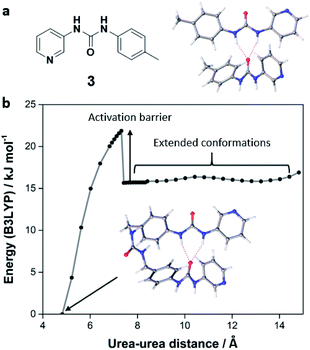
To assess the potential for folded conformations, we optimised the geometry of compound 1 in Gaussian 16 with the DFT functional B3LYP, using the 6-31+G* basis set for initial calculations and a range of larger basis sets for subsequent refinements. The tris(urea) was modelled both as an extended molecule and in a C-shaped geometry stabilised by intramolecular hydrogen bonds (Fig. S15, ESI†). The strength of this motif was calculated by subtracting the energy of the folded tris(urea) from that of the extended molecule. For comparison, we also calculated the interaction energy of mono(urea) 3, which can form intermolecular hydrogen bonds with little conformational strain (Fig. 5a). Finally, the activation energy for intramolecular hydrogen bonding was estimated by incrementally separating the terminal urea groups of the folded conformation of 1 and optimising the remainder of the structure after each scan step (Fig. 5b).

Fig. 5 (a) Hydrogen bonded dimer of mono(urea) 3, optimised with the DFT functional B3LYP in the basis set 6-31++G**; (b) optimised geometries of 1 for increasing urea–urea distances, measured between the carbonyl carbon atoms of the interacting groups. The geometry scan was performed in the basis set 6-31+G* and larger basis sets were used for refinements of local energy minima, including a folded conformation stabilised by intramolecular hydrogen bonding (inset).

The results of our DFT analysis indicate that the backbone of 1 is moderately flexible (Table S2, ESI†). For urea–urea distances greater than 7.5 Å, the molecule can adopt a range of conformations with similar energies. However, intramolecular hydrogen bonding requires the molecule to access less favourable geometries, producing an activation barrier of approximately 6 kJ mol⁻¹ (Fig. S16, ESI†). This conformational strain weakens the intramolecular hydrogen bond by 19–20 kJ mol⁻¹ (58–62%) relative to the dimer of 3. The stability of the folded geometry may be further reduced by the loss of conformational freedom, which is not accounted for in DFT calculations.⁷³ Indeed, studies of ring closure reactions suggest that the six fully rotatable bonds between terminal urea groups are significantly constrained, resulting in a total entropic cost of approximately 7 kJ mol⁻¹ at 298 K.⁷⁴

Despite the impact of conformational strain, folding of the tris(urea) molecule significantly lowers the energy of the system. Intramolecular hydrogen bonds may also be kinetically favoured due to the high effective molarities of the interacting groups.⁷⁴ However, the greater stabilities of motifs involving extended tris(urea) molecules, represented by the hydrogen bonded dimer of mono(urea) 3, likely leads to a preference for these structures at thermodynamic equilibrium. The p-benzyl linkages of 1 and 2 may promote the self-assembly of soft materials because they are compatible with supramolecular polymerisation but sufficiently flexible to inhibit crystallisation pathways. More versatile lilypad aggregation processes could be developed by incorporating similar spacers into alternative bidentate ligands, using metrics such as interaction plots to achieve optimal metal binding in aqueous solvent systems.^75–77

Metal sequestration

Supramolecular gels have been used as selective absorbents for a range of dissolved pollutants.⁷⁸ The formation of aggregates at a liquid–vapour interface could be similarly exploited for metal sequestration. Lilypad aggregation processes may offer greater convenience than preformed adsorbents since they are initiated with an antisolvent vapour and dissolved ligand, which are readily dispersed into the target metal solution. Furthermore, lilypad aggregates self-localise in response to surface tension, so can be collected more easily than a continuous interfacial film. While aqueous lilypad aggregates would be of greater practical use, our model system illustrates the advantages of this approach as well as the parameters to be optimised for future applications.

To assess the efficiency of metal sequestration, lilypad aggregates were prepared from DMF solutions of 1 (0.50% w/v, 9.8 mM) and nickel(II) chloride hexahydrate (0.24% w/v, 1 eq.) and analysed by a variety of techniques. The FT-IR spectrum of the wet aggregate indicates a high concentration of 1, but the characteristic signals of this species differ significantly from those of the pure compound (Fig. S17, ESI†). In particular, shifting of the amide I band from 1654 cm⁻¹ to 1710 cm⁻¹ suggests that the urea carbonyl interacts more weakly in the aggregate,⁷⁹ and aggregation is likely driven by the formation of a nickel(II) complex. X-ray photoelectron spectroscopy (XPS) measurements on the surface of the vacuum-dried aggregate support this conclusion, as the presence of shake-up peaks in the Ni 2p region are diagnostic of a paramagnetic octahedral complex (Fig. 6 and S18 and S19,† ESI).⁵⁴ Scanning electron microscopy (SEM) images of the coated aggregate reveal a lack of discernible microstructure at the surface of the material. However, fibrous structures are visible within desiccation cracks (Fig. 7a and S20, ESI†), suggesting that the nickel(II) complexes give rise to polymeric assemblies that densely entangle to form a homogeneous material.

Fig. 6 Background-subtracted XPS spectra in the Ni 2p region, revealing the similar coordination geometries in a powdered equimolar mixture of 1 and nickel(II) chloride hexahydrate and vacuum-dried lilypad aggregate prepared from 1 and nickel(II) chloride. Raw data are shown in blue, components in grey and envelope fits in red.

Fig. 7 (a) SEM micrograph of fibres in desiccation cracks of a typical dried lilypad aggregate coated in 2 nm platinum (scale bar 1 μm); (b) TGA thermogram for a lilypad aggregate undergoing pyrolysis in nitrogen; (c) SEM micrograph of an uncoated lilypad aggregate pyrolysate (scale bar 1 μm).

The composition of the lilypad aggregate was analysed by inductively coupled plasma mass spectrometry (ICP-MS). After drying under vacuum, the material displayed a nickel content of 5.4 ± 0.1% w/w (Table S3, ESI†). This value closely matches the expected value of 5.1% w/w for a 1 : 2 nickel(II)–tris(urea) complex. It is concluded that the tris(urea) accounts for most of the organic component of the aggregate, and occupies four of the six coordination sites of the octahedral nickel(II) complexes.

Further compositional information was obtained through thermogravimetric analysis (TGA) of the wet, as-synthesised material under a nitrogen atmosphere (Fig. 7b). An initial mass loss of 41% below 150 °C is attributed to the removal of weakly bound solvent, while a subsequent decrease of 47% between 150 and 900 °C corresponds to decomposition of the metal complexes. The measured solvent content is at least one order of magnitude lower than in comparable soft materials, such as supramolecular gels, and consistent with the high aggregate density observed at the surface of the material. SEM images of the black pyrolysate powder display a uniform arrangement of pores, 100–300 nm in diameter (Fig. 7c and S21, ESI†), on the particle surfaces. It may be concluded that the organic solvent occupies narrow voids and is homogeneously distributed in the original material.

After a lilypad aggregate is pyrolysed, its metal content may be usefully recovered from the solid residue. Powder X-ray diffraction (PXRD) analysis of a pyrolysate sample reveals peaks at 2θ = 44.5 and 51.9°, matching the (111) and (200) reflections of elemental nickel (Fig. S22, ESI†).⁸⁰ However, studies of pyrolysed elastomer-metal halide mixtures have shown that carbonaceous material often accounts for 20–40% of the residue mass.⁸¹ ICP-MS experiments reveal a total nickel concentration of 35.5 ± 0.3% w/w in the pyrolysed aggregate, suggesting that the material incorporates just 6% of the nickel in the parent sol (Table S3, ESI†). Nonetheless, formation of the aggregate may aid recovery of the metal, as the material exceeds the nickel concentration of the original DMF solution by 40–80 times (Table S4, ESI†) and may be harvested manually from the surface of the liquid. Future studies will focus on improving the efficiency and versatility of this metal sequestration and modifying the properties of aqueous film-forming ligands, such as peptides,⁵⁰ to target similar lilypad aggregation pathways.

Conclusions

Lilypad aggregation is a non-equilibrium process involving the localised formation of soft materials at a liquid–vapour interface. This phenomenon has been observed, for the first time, upon slow diffusion of an antisolvent into sols of nickel(II) chloride and an oligo(urea) ligand. It has been shown that localised interfacial aggregation occurs only when neither bulk aggregates nor continuous films are energetically favoured. Thus, the materials form within a restricted range of aggregate-sol and aggregate-vapour surface energies, which dictate the shape and size of the developing aggregate and may be estimated from simple geometric measurements. Optical micrographs reveal that lilypad aggregates are formed via the self-assembly and fusion of colloidal particles, growing in a predictable fashion until their weight is no longer counterbalanced by surface tension. The process can be used to recover substantial quantities of a dissolved metal salt, packaging the material into a discrete structure that is easily harvested from the surrounding solution. Our results may inform further studies into non-equilibrium aggregation and guide the development of more water-compatible systems for mineral processing, metal recycling and wastewater remediation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the Engineering and Physical Sciences Research Council for funding this work via a Doctoral Training Studentship awarded to CDJ. We would also like to acknowledge the assistance provided by Swansea University College of Engineering AIM Facility, which was funded in part by the EPSRC (EP/M028267/1).

Notes and references

1. N. J. Hogrebe, J. W. Reinhardt and K. J. Gooch, J. Biomed. Mater. Res., 2017, 105, 640–661.
2. P. Fratzl and R. Weinkamer, Prog. Mater. Sci., 2007, 52, 1263–1334.
3. J. Y. C. Lim, S. S. Goh, S. S. Liow, K. Xue and X. J. Loh, J. Mater. Chem. A, 2019, 7, 18759–18791.
4. S. Bhattacharya and Y. Krishnan-Ghosh, Chem. Commun., 2001, 185–186.
5. N. M. Sangeetha and U. Maitra, Chem. Soc. Rev., 2005, 34, 821–836.
6. P. R. A. Chivers and D. K. Smith, Nat. Rev. Mater., 2019, 4, 463–478.
7. A. Sorrenti, J. Leira-Iglesias, A. J. Markvoort, T. F. A. de Greef and T. M. Hermans, Chem. Soc. Rev., 2017, 46, 5476–5490.
8. C. D. Jones and J. W. Steed, Chem. Soc. Rev., 2016, 45, 6546–6596.
9. M. O. M. Piepenbrock, G. O. Lloyd, N. Clarke and J. W. Steed, Chem. Rev., 2010, 110, 1960–2004.
10. P. Terech and R. G. Weiss, Chem. Rev., 1997, 97, 3133–3159.
11. J. J. D. de Jong, P. R. Hania, A. Pugžlys, L. N. Lucas, M. de Loos, R. M. Kellogg, B. L. Feringa, K. Duppen and J. H. van Esch, Angew. Chem., Int. Ed., 2005, 44, 2373–2376.
12. D. J. Adams, M. F. Butler, W. J. Frith, M. Kirkland, L. Mullen and P. Sanderson, Soft Matter, 2009, 5, 1856–1862.
13. X. Li, J. Fei, Y. Xu, D. Li, T. Yuan, G. Li, C. Wang and J. Li, Angew. Chem., Int. Ed., 2018, 57, 1903–1907.
14. C. Maity, W. E. Hendriksen, J. H. van Esch and R. Eelkema, Angew. Chem., Int. Ed., 2015, 54, 998–1001.
15. J. Raeburn, T. O. McDonald and D. J. Adams, Chem. Commun., 2012, 48, 9355–9357.
16. C. Vigier-Carrière, F. Boulmedais, P. Schaaf and L. Jierry, Angew. Chem., Int. Ed., 2018, 57, 1448–1456.
17. V. Calabrese, M. A. da Silva, J. Schmitt, K. M. Z. Hossain, J. L. Scott and K. J. Edler, Soft Matter, 2020, 16, 357–365.
18. M. Lovrak, W. E. J. Hendriksen, C. Maity, S. Mytnyk, V. van Steijn, R. Eelkema and J. H. van Esch, Nat. Commun., 2017, 8, 15317.
19. S. Matsumoto, S. Yamaguchi, S. Ueno, H. Komatsu, M. Ikeda, K. Ishizuka, Y. Iko, K. V. Tabata, H. Aoki, S. Ito, H. Noji and I. Hamachi, Chem. - Eur. J., 2008, 14, 3977–3986.
20. S. Sacanna, D. J. Pine and G.-R. Yi, Soft Matter, 2013, 9, 8096–8106.
21. S. Matsumoto, S. Yamaguchi, A. Wada, T. Matsui, M. Ikeda and I. Hamachi, Chem. Commun., 2008, 1545–1547.
22. N. Khalida, F. Zahoor Hussain, R. Muhammad Zia Ur, R. Muhammad Atiq Ur and G. Maida, Rev. Chem. Eng., 2019, 35, 285–309.
23. R. Muñoz-Espí, Y. Mastai, S. Gross and K. Landfester, CrystEngComm, 2013, 15, 2175–2191.
24. N. M. B. Smeets and T. Hoare, J. Polym. Sci., Part A: Polym. Chem., 2013, 51, 3027–3043.
25. A. A. Shah, M. Ganesan, J. Jocz and M. J. Solomon, ACS Nano, 2014, 8, 8095–8103.
26. E. Guermani, H. Shaki, S. Mohanty, M. Mehrali, A. Arpanaei, A. K. Gaharwar and A. Dolatshahi-Pirouz, Sci. Rep., 2016, 6, 30445.
27. N. Tompkins, N. Li, C. Girabawe, M. Heymann, G. B. Ermentrout, I. R. Epstein and S. Fraden, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 4397–4402.
28. M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, ACS Nano, 2010, 4, 3591–3605.
29. P. A. Kralchevsky and N. D. Denkov, Curr. Opin. Colloid Interface Sci., 2001, 6, 383–401.
30. J. Yan, J. Liu, H. Lei, Y. Kang, C. Zhao and Y. Fang, J. Colloid Interface Sci., 2015, 448, 374–379.
31. J. Lu, Y. Gao, J. Wu and Y. Ju, RSC Adv., 2013, 3, 23548–23552.
32. S. Dutta, D. Das, A. Dasgupta and P. K. Das, Chem. - Eur. J., 2010, 16, 1493–1505.
33. A. Mohraz, Curr. Opin. Colloid Interface Sci., 2016, 25, 89–97.
34. R. McGorty, J. Fung, D. Kaz and V. N. Manoharan, Mater. Today, 2010, 13, 34–42.
35. A. Böker, J. He, T. Emrick and T. P. Russell, Soft Matter, 2007, 3, 1231–1248.
36. M. A. Boles, M. Engel and D. V. Talapin, Chem. Rev., 2016, 116, 11220–11289.
37. P. van Rijn, M. Tutus, C. Kathrein, L. Zhu, M. Wessling, U. Schwaneberg and A. Böker, Chem. Soc. Rev., 2013, 42, 6578–6592.
38. T. Li, F. Nudelman, J. W. Tavacoli, H. Vass, D. J. Adams, A. Lips and P. S. Clegg, Adv. Mater. Interfaces, 2016, 3, 1500601.
39. S. Bai, C. Pappas, S. Debnath, P. W. J. M. Frederix, J. Leckie, S. Fleming and R. V. Ulijn, ACS Nano, 2014, 8, 7005–7013.
40. M. E. Cates and P. S. Clegg, Soft Matter, 2008, 4, 2132–2138.
41. R. M. Capito, H. S. Azevedo, Y. S. Velichko, A. Mata and S. I. Stupp, Science, 2008, 319, 1812–1816.
42. Y. Nishida, A. Tanaka, S. Yamamoto, Y. Tominaga, N. Kunikata, M. Mizuhata and T. Maruyama, Angew. Chem., Int. Ed., 2017, 56, 9410–9414.
43. T. Li, M. Kalloudis, A. Z. Cardoso, D. J. Adams and P. S. Clegg, Langmuir, 2014, 30, 13854–13860.
44. D. I. Rożkiewicz, B. D. Myers and S. I. Stupp, Angew. Chem., Int. Ed., 2011, 50, 6324–6327.
45. E. Sanz, K. A. White, P. S. Clegg and M. E. Cates, Phys. Rev. Lett., 2009, 103, 255502.
46. A. Venault, Y. Chang, D.-M. Wang and D. Bouyer, Polym. Rev., 2013, 53, 568–626.
47. K. Kimura and T. Pradeep, Phys. Chem. Chem. Phys., 2011, 13, 19214–19225.
48. M. J. Wen, M. T. Jackson and C. M. Garner, Dalton Trans., 2019, 48, 11575–11582.
49. C. D. Jones, H. T. D. Simmons, K. E. Horner, K. Liu, R. L. Thompson and J. W. Steed, Nat. Chem., 2019, 11, 375–381.
50. A. F. Dexter and A. P. J. Middelberg, J. Phys. Chem. C, 2007, 111, 10484–10492.
51. M. de Loos, A. Friggeri, J. van Esch, R. M. Kellogg and B. L. Feringa, Org. Biomol. Chem., 2005, 3, 1631–1639.
52. J. A. Foster, M. O. M. Piepenbrock, G. O. Lloyd, N. Clarke, J. A. K. Howard and J. W. Steed, Nat. Chem., 2010, 2, 1037–1043.
53. T. L. Barr and S. Seal, J. Vac. Sci. Technol., A, 1995, 13, 1239–1246.
54. J. Matienzo, L. I. Yin, S. O. Grim and W. E. Swartz, Inorg. Chem., 1973, 12, 2762–2769.
55. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
56. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
57. D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371.
58. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
59. P. M. Reis, J. Hure, S. Jung, J. W. M. Bush and C. Clanet, Soft Matter, 2010, 6, 5705–5708.
60. M. Abkarian, S. Protière, J. M. Aristoff and H. A. Stone, Nat. Commun., 2013, 4, 1895.
61. D. Vella and L. Mahadevan, Am. J. Phys., 2005, 73, 817–825.
62. P. Dahiya, A. DeBenedictis, T. J. Atherton, M. Caggioni, S. W. Prescott, R. W. Hartel and P. T. Spicer, Soft Matter, 2017, 13, 2686–2697.
63. L. B. Smolka and A. Belmonte, J. Non-Newtonian Fluid Mech., 2003, 115, 1–25.
64. G. Xie, J. Forth, S. Zhu, B. A. Helms, P. D. Ashby, H. C. Shum and T. P. Russell, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 8360–8365.
65. S. G. Jones, N. Abbasi, A. Ahuja, V. Truong and S. S. H. Tsai, Phys. Fluids, 2015, 27, 072102.
66. N. A. Lange and J. A. Dean, Lange's Handbook of Chemistry, McGraw-Hill, 1967.
67. D. K. Owens and R. C. Wendt, J. Appl. Polym. Sci., 1969, 13, 1741–1747.
68. C. A. Grattoni, R. A. Dawe, C. Y. Seah and J. D. Gray, J. Chem. Eng. Data, 1993, 38, 516–519.
69. H. J. Kull, Phys. Rep., 1991, 206, 197–325.
70. D. J. Hill, M. J. Mio, R. B. Prince, T. S. Hughes and J. S. Moore, Chem. Rev., 2001, 101, 3893–4012.
71. E. A. John, C. J. Massena and O. B. Berryman, Chem. Rev., 2020, 120, 2759–2782.
72. H. P. Bennetto and E. F. Caldin, J. Chem. Soc. A, 1971, 2198–2207.
73. T. A. Hubbard, A. J. Brown, I. A. W. Bell and S. L. Cockroft, J. Am. Chem. Soc., 2016, 138, 15114–15117.
74. C. Galli and L. Mandolini, Eur. J. Org. Chem., 2000, 2000, 3117–3125.
75. M. D. Driver, M. J. Williamson, J. L. Cook and C. A. Hunter, Chem. Sci., 2020, 11, 4456–4466.
76. P. G. Argudo, R. Contreras-Montoya, L. Álvarez de Cienfuegos, J. M. Cuerva, M. Cano, D. Alba-Molina, M. T. Martín-Romero, L. Camacho and J. J. Giner-Casares, Soft Matter, 2018, 14, 9343–9350.
77. Y. Lan, M. G. Corradini, R. G. Weiss, S. R. Raghavan and M. A. Rogers, Chem. Soc. Rev., 2015, 44, 6035–6058.
78. B. O. Okesola and D. K. Smith, Chem. Soc. Rev., 2016, 45, 4226–4251.
79. R. Le Parc, V. T. Freitas, P. Hermet, A. M. Cojocariu, X. Cattoën, H. Wadepohl, D. Maurin, C. H. Tse, J. R. Bartlett, R. A. S. Ferreira, L. D. Carlos, M. Wong Chi Man and J.-L. Bantignies, Phys. Chem. Chem. Phys., 2019, 21, 3310–3317.
80. V. D. Jović, V. Maksimović, M. G. Pavlović and K. I. Popov, J. Solid State Electrochem., 2006, 10, 373–379.
81. M. Berger and T. A. Manuel, J. Polym. Sci., Part B: Polym. Lett., 1964, 2, 873–876.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc02190c. The underlying research data for this paper is available in accordance with RCUK open data policy from DOI: 10.15128/r1ms35t8650.

---