Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Amination of the Gd@C82 endohedral fullerene: tunable substitution effect on quantum coherence behaviors†
Zheng
Liu‡
a,
Huan
Huang‡
d,
Ye-Xin
Wang
a,
Bo-Wei
Dong
a,
Bao-Yun
Sun
 *d,
Shang-Da
Jiang
*d,
Shang-Da
Jiang
 *ab and
Song
Gao
*ab and
Song
Gao
 *abc
*abc
aBeijing National Laboratory of Molecular Science, Beijing Key Laboratory of Magnetoelectric Materials and Devices, College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, China. E-mail: jiangsd@pku.edu.cn; gaosong@pku.edu.cn
bSchool of Chemistry and Chemical Engineering, South China University of Technology, Guangzhou 510640, China
cBeijing Academy of Quantum Information Sciences, West Bld. #3, No. 10 Xibeiwang East Rd., Haidian District, Beijing 100193, P. R. China
dCAS Key Lab for Biomedical Effects of Nanomaterials and Nanosafety, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China. E-mail: sunby@ihep.ac.cn
First published on 28th May 2020
Abstract
The core–shell structure of endohedral fullerene-based anisotropic magnetic molecules of high spin with long coherence time could help scale up quantum systems. In this research, by amination of Gd@C82 with morpholine, three derivatives are functionalized with 5, 7 and 9 morpholine groups providing an interesting model to investigate the relationship between the quantum coherence and the spin environment. The original radical located on the carbon cage is successfully quenched, affording a quantum phase memory times (TM) over 5 μs at 5 K. By increasing the number of substitution groups, spin–lattice relaxation times (T1) also show significant enhancement due to the interaction variation between the molecules and the environments. We found that the TM of the three molecules show no obvious difference below 10 K, while they are limited by T1 at higher temperatures. In this work, the variable functional groups are able to tune both T1 and TM, offering the possibility for application of high-spin magnetic molecules in the field of quantum information processing.
Introduction
Endohedral fullerenes with encapsulated metal atoms, ions or clusters in the carbon cage have shown lots of distinctive properties compared to the hollow ones due to the electron transfer between the inner core and the outer shell. Plenty of applications of endohedral fullerenes have been investigated including in chemistry,1 electronics2 and reactions.3 Additionally, paramagnetic endohedral fullerenes containing well protected unpaired electron spins show unique characteristics compared to radicals and complexes. The various paramagnetic properties can be applied in dynamic nuclear polarization (DNP),4 magnetic resonance imaging (MRI) contrast agents,5,6 molecular magnets7 and biomedicines.8,9Recently, quantum information processing (QIP) has been proved to be able to provide efficient solutions in cryptography10,11 and database searching.12 Molecular spins, being much more versatile as building blocks, are becoming the competitive one in the area of QIP.13 The high spin state of molecular magnet-based “qudits” fits the requirements for Grover's algorithm proposed by Leuenberger and Loss.14 This proposal requires the spin system to possess non-equidistant energy levels and long enough quantum phase memory time. The design of magnetic coordination complexes will give us a chance in fine controlling the quantum coherence and building quantum gates.15 However, there is a significant contradiction between these conditions since the quantum coherence of an anisotropic high-spin system can be easily destroyed due to its strong coupling to the environment. One possible protocol to solve this problem is to employ rare earth ions of high spin ground state with small anisotropy. The core–shell structures of endohedral fullerenes could fulfill the requirements in QIP,16,17 and show even better properties compared to other molecule-based qubits. Various paramagnetic endohedral fullerenes show some particular phenomena including the qubit crossover phenomenon18 and diverse Rabi cycles.19
However, most investigations of paramagnetic endohedral fullerenes are limited to pristine molecules. Functionalization of fullerenes can precisely tune the spin environment,20,21 helping us understand the spin dynamics. Gd@C82 is a well-known endohedral fullerene with the paramagnetic metal ion Gd3+ of S = 7/2 for the inner core and C823− acting as a radical located at the outer shell. The antiferromagnetic coupling between Gd3+ and the radical makes an S = 3 ground state.22 Since the electron cloud of the radical is largely scattered among the outer shell with lack of protection, the properties of the spin system are largely influenced by the environment. This phenomenon is a disadvantage because the uncontrollable interactions will largely reduce the performance of endohedral fullerenes in QIP. The distribution of the electron cloud could enhance the influence of the environment and largely reduce the quantum coherence time. Herein, to overcome this disadvantage, we successfully quench the unwanted shell-radical by amination of the fullerene cage, obtaining three derivatives Gd@C82(morpholine)n (marked as Gd-n, n = 5, 7 and 9).
Results & discussion
In our previous studies,23,24 the amination of Gd@C82 with morpholine and N-fluorobenzenesulfonimide (NFSI) resulted in the selective formation of three derivatives, Gd-5, Gd-7 and Gd-9. The structure of Gd-7 has been confirmed by X-ray crystallographic analysis in the previous report. The evidence including UV-Vis-NIR spectroscopy, electrochemical analysis and continuous wave electron paramagnetic resonance (cw-EPR) demonstrated that this series of Gd-n derivative compounds are functionalized with an odd number of morpholine groups. Different from the original endohedral fullerene Gd@C82, the absence of the radical leads to a relatively independent environment with controllable differences. The comparison of this series of molecules provides a very interesting model to investigate the quantum coherence behavior with a tunable environment influence. In this work, we move forward to the different behaviors of the spin–lattice relaxation time (T1) and quantum phase memory time (TM).To evidence the quenching of the radical, the magnetizations of Gd-7 were measured at 2 K up to 5 T on a magnetometer as shown in Fig. S2-1.† The field-dependent magnetization curve and the saturation value fit best to the S = 7/2 model of the Brillouin function. These results confirm the disappearance of the radical in Gd-n molecules (ESI†).
cw-EPR characterization
In the previous research, the spin system of the Gd@C82 endohedral fullerene was considered as the combination of one high spin Gd3+ center of S = 7/2 and one radical of S = 1/2 delocalized on the carbon cage. The two spins were antiferromagnetically coupled as an S = 3 system according to high-frequency EPR measurements.22 However, the radical at the carbon cage reduces the protection of the spin system efficiently, which can be certified from measurements under different conditions. Such influence will also lead to poor quantum coherence properties.With the shell radical quenched, the Gd3+ ion is the only electron spin carrier in the molecules. Even though the first order orbit angular momentum of the Gd3+ ion is fully quenched, a slight magnetic anisotropy can still be observed due to the second order spin–orbit coupling in the existence of broken environmental symmetry. Gd@C82 and the three derivative compounds were resolved in a d8-toluene solution with relatively low concentrations from 5 K to 150 K as reported in a previous study. The X-band cw-EPR offers us a way to probe the crystal field effect with various chemical modifications on the fullerene cage. Therefore, the spin Hamiltonian of Gd-n is considered as
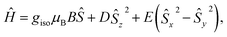 | (1) |
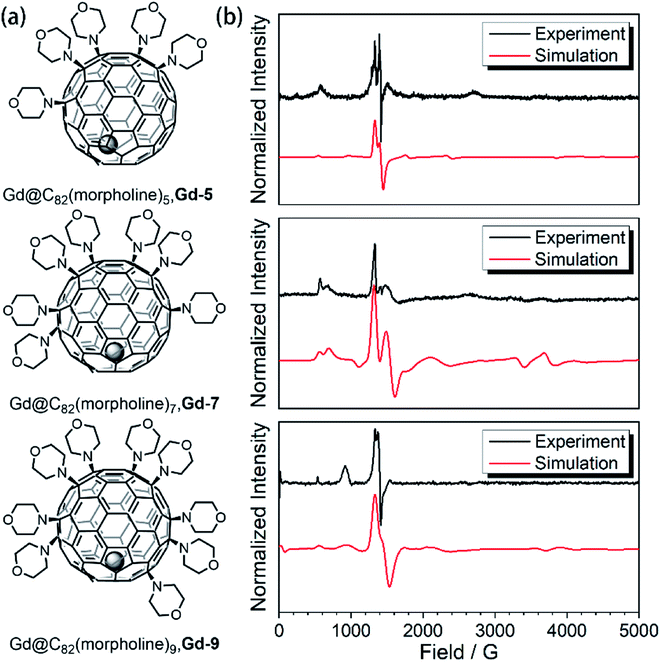 | ||
| Fig. 1 (a) Aminated derivatives of Gd@C82 with different numbers of morpholine groups. (b) The cw-EPR measurements for the Gd-n derivatives (black) and the best simulation results (red). | ||
Quantum coherence properties
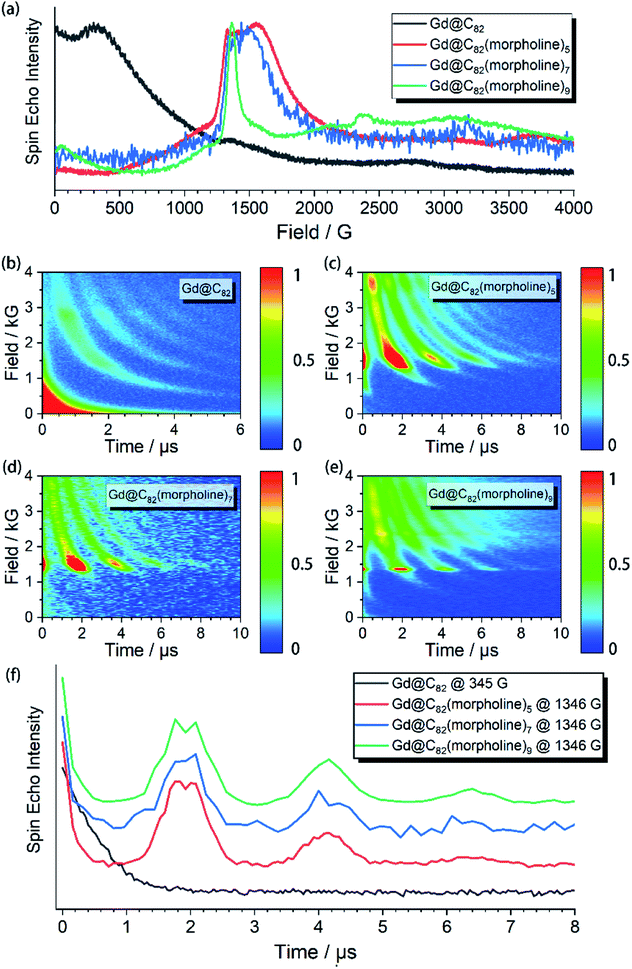
The aforementioned results illustrated that the Gd3+ electronic structures can be varied by chemical modification on the outer shell. The protocol for the quantum searching algorithm with molecular magnets proposed by Leuenberger and Loss requires non-equidistant energy levels. The present approach of modifying electronic structures of paramagnetic ions makes the employment of Gd-n as a qudit (d = 8) possible.25,26 Now we move to study how the substitution groups affect the spin dynamics behaviors. According to the simulations of the cw-EPR spectra of the three derivatives, the D values (0.2–0.3 cm−1) are comparable to the microwave frequency (∼9.3 GHz) used in an X-band EPR spectrometer. Only several transitions were observed in the experiments. In the echo-detected field swept (EDFS) experiments, the standard Hahn echo pulse sequence (π/2–τ–π–τ–echo with π/2- and π-pulses of 16 and 32 ns, respectively) was used to record the electron spin echo intensities from 1 to 4000 G for Gd-n at 5 K.As shown in Fig. 2a, several transitions at different magnetic fields can be observed. In the measurements of electron spin TM at 5 K, one can observe that the TM values strongly depend on the external magnetic field (B0) as shown in Fig. 2b–e. It can be clearly seen that Gd@C82 shows a different pattern compared to the three derivatives. These patterns are mainly influenced by the electronic structures and the surrounding environments. Peaks in the vertical cuts indicate the resonance magnetic fields, representing the transitions which can be calculated from the spin Hamiltonian parameters. In a certain applied magnetic field, the decay of the spin echo is modulated at frequencies that depend on the field, which is attributed to the electron-spin echo envelope modulation (ESEEM) effect. The horizontal cuts of all the compounds show the modulations shown in Fig. 2f. By choosing the same B0, the spin echoes oscillate at the same frequency, which represents the same influences from the surrounding nuclear spins. The Fourier transformations of the pattern of Gd-5 are shown in Fig. 3b. The slope of 6.59 MHz T−1 indicates that the electron spin is coupled to the deuterium nuclei from the solvent (γD = 6.5359 MHz T−1).
The temperature dependence of electron spin quantum coherence properties was investigated at the B0 field that gave the biggest transition probabilities and therefore the strongest signals. Based on the determined spin Hamiltonian parameters, the transition assignment at various magnetic fields can be easily calculated. For Gd@C82, the transition between |−1/2〉 and |+1/2〉 at 345 G was selected, and for the three derivative compounds, the transitions between |+1/2〉 and |+3/2〉 at around 1400 G were selected.
Quantum coherence behaviors
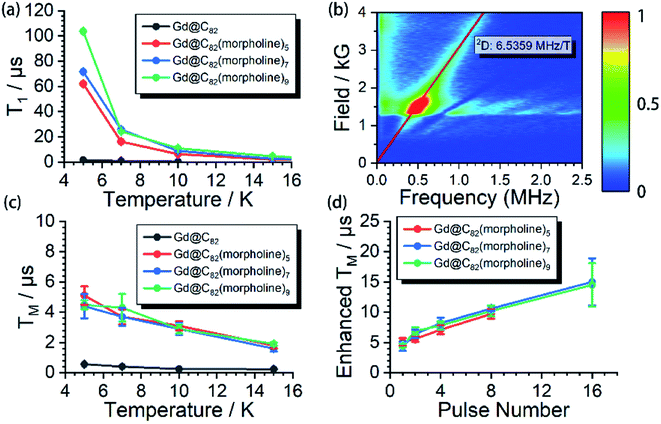
The spin echo can be observed up to 40 K for the three derivatives. T1 and TM at different temperatures are shown in Fig. 3. It can be clearly seen that both T1 and TM show clear response to the environment temperature. The T1 of Gd@C82 is two orders of magnitude smaller than that of Gd-n. The delocalized radical efficiently enhances the interaction between the electron spin and the environment. As a result, the thermally activated spin–lattice relaxation is therefore largely accelerated via the strong exchange of phonons between the cage and the environment. However in contrast, the phonon exchange between the inner magnetic ion and the environment is much less efficient, affording longer spin–lattice relaxation times in the derivatives due to the isolated spin environment. At a lower temperature of 5 K, T1 values of all Gd-n derivatives are around 100 μs and decrease to less than 1 μs upon warming to 40 K. Within the three analogs, T1 increases obviously with more substitution groups. This is probably due to the tougher restrictions imposed on the molecular tumbling. Fullerenes with more substitutions would have slower molecular tumbling rates,27 which influence the rate of the vertical relaxation.28 In our experiments, this effect of having more substitution groups appears to slow down the spin–lattice relaxation.The quantum coherence properties of these endohedral fullerenes are also distinguishable. Due to the strong coupling with the environment arising from the radical of the outer shell, the TM of only 1.4 μs was observed for Gd@C82 at 5 K and dropped below 1 μs upon warming. Nevertheless, the TM of the high spin derivatives with quenched radicals can be enhanced to more than 5 μs, which are even better than those of VO2+ (S = 1/2) and Cr3+ (S = 3/2) based low spin molecules.29–31 The temperature dependence of the quantum phase memory time shows a different trend compared to the spin–lattice relaxation time. Upon warming from 5 K to 10 K, TM decreases slightly for the three analogs. Different from the strong relation between T1 and temperature, the decoherence of the electron spin superposition state is caused by additional sources, including the dipolar interaction between the investigated electron spin and the environmental nuclear or electron spins.32,33 The molecular concentrations in these experiments were low enough to consider that the electron spin dipolar–dipolar interaction was a minor effect that resulted in the decoherence path here.34 The aforementioned ESEEM effects indicate that the electron spin of Gd3+ is effectively coupled to the environment nuclei. Based on these analyses, we confirm that the hyperfine coupling of the nuclear spins dominates the decoherence of the electron spin superposition states in the three derivatives at relatively low temperatures from 5 to 10 K. By warming up the spin system above 10 K, TM decreases with the same trend as T1. The T1 of each molecule is around twice of TM, and even closer at higher temperatures. Therefore, the thermal process becomes the main decoherence path above 10 K. It is also interesting to compare the quantum coherence time of the three derivatives. The molecule with the least number of substituted morpholine groups shows the longest phase memory time at 5 K. While upon warming, the TM of Gd-5 drops more rapidly than that of the other two. This is mainly due to the T1 limitation, indicating that the molecules with a longer spin–lattice relaxation time are less limited at relatively higher temperatures.
Dynamic decoupling
The nuclear spins around the electron spin can generate the local Overhauser field which oscillates at Larmor frequencies. As discussed previously, these nuclear spins acted as the major decoherence path in our experiment at relatively low temperatures. This unwanted environment effect can be decoupled by employing a train of refocusing pulses before the detection of the spin echo.35 Here, the CPMG-n pulse sequence was applied to the three derivatives at 5 K, where n represents the number of the inversion pulses. This dynamic decoupling pulse sequence exhibits very efficient enhancement of TM. By applying up to 16 inversion pulses, the phase memory times were successfully extended to nearly 20 μs, which is 4 fold higher compared to the original phase memory times. These dynamic decoupling experiments suggest that by employing refocusing pulses, the interactions between electrons and surrounding nuclear spins are successfully decoupled. It is also worth noting that TM can be further extended with more than 16 refocusing pulses; however, the detection is limited by the weak signals.Conclusions
In summary, the quantum coherence behaviors of the three derivative compounds of the endohedral fullerene Gd@C82 with an odd number of morpholine groups, Gd@C82(morpholine)n (n = 5, 7 and 9), have been investigated using pulse-EPR. By quenching the radical located at the carbon cage, the electronic structures become largely different from those of the original Gd@C82. The quantum phase memory times (TM) can be enhanced to more than 5 μs at 5 K which are even better compared to that of low spin molecules. While, with the increasing number of substitution groups, spin–lattice relaxation times (T1) also show significant enhancement due to the interaction variation between the molecules and environment. Besides, it is also worth noting that TM show no obvious difference below 10 K, while they are limited by T1 at higher temperatures. Gd3+ based endohedral fullerenes have been widely used in interesting studies including medical development and quantum information processing, and precisely controlling the quantum coherence properties are required for better applications. In this work, Gd-n derivative compounds can act as an appropriate model to investigate the quantum coherence behaviors with tunable environmental influences. We successfully find the relationship between the molecule structures and quantum coherence behaviors and give suggestions on designing particular molecules for certain applications. By taking advantage of paramagnetic endohedral fullerenes, we believe such chemical engineering can enrich the interests in molecular design.Experimental
Synthesis and isolation
The samples were synthesized and purified as described in our previous work.23,24EPR measurements
Gd@C82 and the three derivatives were dissolved in d8-toluene for EPR experiments with a spin concentration of 0.012 mmol L−1 determined by the spin counting method. The cw-EPR spectra were measured on a Bruker Elexsys E580 spectrometer with a superhigh sensitivity probehead (ω = 9.36 GHz). Pulsed EPR data were collected on the same system using an MS-3 cavity (ω = 9.33 GHz). The low-temperature environment was achieved using Oxford Instruments liquid helium cryostats (ESR900 for cw and CF935 for pulse). The cw-EPR spectra were simulated using an EasySpin36 toolbox (http://www.easyspin.org/) based on MATLAB. The signals of the pulsed-EPR experiments were collected by integrating the Hahn echo (π/2–τ–π–τ–echo) with τ = 200 ns. The T1 values were measured by the inversion recovery method (π–T–π/2–τ–π–τ–echo) with 4-step phase cycling. The TM values were obtained by increasing the τ value of the Hahn echo sequence with 4-step phase cycling. The ESEEM measurements were carried out using the 2p ESEEM sequence (π/2–τ–π–τ–echo) with 4-step phase cycling. The dynamic decoupling measurements were carried out using the CPMG-n sequence (π/2x–(τ–πy–τ)n–echo) with 4-step phase cycling. The π/2 and π pulse lengths in EDFS, T1 and TM measurements were 16 and 32 ns with 9 dB attenuation of the microwave power of 300 W, respectively.Magnetic measurements
The powder samples of Gd-7 with exact mass for DC magnetic measurements were wrapped in parafilm and fixed in a capsule. DC experiments were performed on a Quantum Design MPMS XL-5 SQUID magnetometer. Magnetic data were corrected for the paramagnetism from the parafilm and capsule, and the diamagnetic contribution of the sample was calculated from Pascal's constants. The magnetization and magnetic susceptibility data were simulated using an EasySpin toolbox36 (http://www.easyspin.org/) based on MATLAB.Author contributions
Z. L. performed the EPR and magnetic measurements, assisted by B.-W. D. H. H. and B.-Y. S. prepared and purified the sample for measurements. Z. L. processed and analyzed the EPR and magnetic data. The project was conceived by S. G. and S.-D. J. Z. L. and S.-D. J. designed the experiments and wrote the manuscript. All the authors revised the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This research was supported by the National Natural Science Foundation of China (21822301, 21971242, and 11705211), National Basic Research Program of China (2018YFA0306003, 2017YFA0204903, 2016YFA0203200 and 2018YFA0703504), Beijing Academy of Quantum Information Sciences (Y18G23) and Young Scientist Innovative Foundation of IHEP (E05469U2, and Y95461C).References
- P. Jin, Y. Li, S. Magagula and Z. Chen, Coord. Chem. Rev., 2019, 388, 406–439 CrossRef CAS.
- T. Wang and C. Wang, Small, 2019, 15, 1901522 CrossRef CAS PubMed.
- W. Cai, C.-H. Chen, N. Chen and L. Echegoyen, Acc. Chem. Res., 2019, 52, 1824–1833 CrossRef CAS PubMed.
- G. Liu, S.-H. Liou, N. Enkin, I. Tkach and M. Bennati, Phys. Chem. Chem. Phys., 2017, 19, 31823–31829 RSC.
- K. B. Ghiassi, M. M. Olmstead and A. L. Balch, Dalton Trans., 2014, 43, 7346–7358 RSC.
- H. Kato, K. Suenaga, M. Mikawa, M. Okumura, N. Miwa, A. Yashiro, H. Fujimura, A. Mizuno, Y. Nishida, K. Kobayashi and H. Shinohara, Chem. Phys. Lett., 2000, 324, 255–259 CrossRef CAS.
- L. Spree and A. A. Popov, Dalton Trans., 2019, 48, 2861–2871 RSC.
- I. Rašović, Mater. Sci. Technol., 2017, 33, 777–794 CrossRef.
- W. Zhang, B. Sun, L. Zhang, B. Zhao, G. Nie and Y. Zhao, Nanoscale, 2011, 3, 2636 RSC.
- P. W. Shor, in Proceedings 35th Annual Symposium on Foundations of Computer Science, IEEE Comput. Soc. Press, Santa Fe, NM, USA, 1994, pp. 124–134 Search PubMed.
- L. M. K. Vandersypen, M. Steffen, G. Breyta, C. S. Yannoni, M. H. Sherwood and I. L. Chuang, Nature, 2001, 414, 883–887 CrossRef CAS PubMed.
- V. L. Ermakov and B. M. Fung, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 042310 CrossRef.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed.
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793 CrossRef CAS PubMed.
- G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546 RSC.
- J. J. L. Morton, A. M. Tyryshkin, A. Ardavan, K. Porfyrakis, S. A. Lyon and G. A. D. Briggs, J. Chem. Phys., 2006, 124, 014508 CrossRef PubMed.
- R. M. Brown, Y. Ito, J. H. Warner, A. Ardavan, H. Shinohara, G. A. D. Briggs and J. J. L. Morton, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 033410 CrossRef.
- Z. Liu, B.-W. Dong, H.-B. Meng, M.-X. Xu, T.-S. Wang, B.-W. Wang, C.-R. Wang, S.-D. Jiang and S. Gao, Chem. Sci., 2018, 9, 457–462 RSC.
- Z. Hu, B.-W. Dong, Z. Liu, J.-J. Liu, J. Su, C. Yu, J. Xiong, D.-E. Shi, Y. Wang, B.-W. Wang, A. Ardavan, Z. Shi, S.-D. Jiang and S. Gao, J. Am. Chem. Soc., 2018, 140, 1123–1130 CrossRef CAS PubMed.
- S. Zhou, I. Rašović, G. A. D. Briggs and K. Porfyrakis, Chem. Commun., 2015, 51, 7096–7099 RSC.
- S. Zhou, M. Yamamoto, G. A. D. Briggs, H. Imahori and K. Porfyrakis, J. Am. Chem. Soc., 2016, 138, 1313–1319 CrossRef CAS PubMed.
- K. Furukawa, S. Okubo, H. Kato, H. Shinohara and T. Kato, J. Phys. Chem. A, 2003, 107, 10933–10937 CrossRef CAS.
- H. Huang, L. Zhang, X. J. Gao, X. Guo, R. Cui, B. Xu, J. Dong, Y. Li, L. Gan, F. Chang, X. Gao and B. Sun, Chem. Mater., 2018, 30, 64–68 CrossRef CAS.
- H. Huang, Z. Liu, L. Zhang, X. Guo, R. Cui, J. Dong, F. Chang, S. Jiang, S. Gao and B. Sun, Carbon, 2020, 158, 320–326 CrossRef CAS.
- M. D. Jenkins, Y. Duan, B. Diosdado, J. J. García-Ripoll, A. Gaita-Ariño, C. Giménez-Saiz, P. J. Alonso, E. Coronado and F. Luis, Phys. Rev. B, 2017, 95, 064423 CrossRef.
- E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513 RSC.
- G. Liu, M. d. C. Gimenez-Lopez, M. Jevric, A. N. Khlobystov, G. A. D. Briggs and K. Porfyrakis, J. Phys. Chem. B, 2013, 117, 5925–5931 CrossRef CAS.
- The essential physics of medical imaging, ed. J. T. Bushberg, Wolters Kluwer Health/Lippincott Williams & Wilkins, Philadelphia, 3rd edn, 2012 Search PubMed.
- M. J. Graham, J. M. Zadrozny, M. Shiddiq, J. S. Anderson, M. S. Fataftah, S. Hill and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 7623–7626 CrossRef CAS PubMed.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 15841–15844 CrossRef CAS PubMed.
- M. S. Fataftah, J. M. Zadrozny, S. C. Coste, M. J. Graham, D. M. Rogers and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 1344–1348 CrossRef CAS PubMed.
- W. Wernsdorfer, Nat. Mater., 2007, 6, 174–176 CrossRef CAS PubMed.
- A. Morello, P. C. E. Stamp and I. S. Tupitsyn, Phys. Rev. Lett., 2006, 97, 207206 CrossRef PubMed.
- A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201 CrossRef PubMed.
- S. Meiboom and D. Gill, Rev. Sci. Instrum., 1958, 29, 688–691 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc02182b |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2020 |