Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fulvalene as a platform for the synthesis of a dimetallic dysprosocenium single-molecule magnet†
Mian
He
 a,
Fu-Sheng
Guo
a,
Fu-Sheng
Guo
 a,
Jinkui
Tang
a,
Jinkui
Tang
 *b,
Akseli
Mansikkamäki
*b,
Akseli
Mansikkamäki
 *c and
Richard A.
Layfield
*c and
Richard A.
Layfield
 *a
*a
aDepartment of Chemistry, School of Life Sciences, University of Sussex, Brighton, BN1 9QR, UK. E-mail: R.Layfield@sussex.ac.uk
bChangchun Institute of Applied Chemistry, Chinese Academy of Sciences, Renmin Street 5626, 130022 Changchun, China. E-mail: tang@ciac.ac.cn
cNMR Research Unit, University of Oulu, P.O. Box 8000, FI-90014, Finland. E-mail: Akseli.Mansikkamaki@oulu.fi
First published on 18th May 2020
Abstract
The dinucleating fulvalenyl ligand [1,1′,3,3′-(C5tBu2H2)2]2− (Fvtttt) was used to synthesize the dimetallic dysprosocenium cation [{Dy(η5-Cp*)}2(μ-BH4)(η5:η5-Fvtttt)]+ (3) as the salt of [B(C6F5)4]− (Cp* = C5Me5). Compound [3][B(C6F5)4] was obtained using a method in which the double half-sandwich complex [{Dy(BH4)2(THF)}2(Fvtttt)] (1) was reacted with KCp* to give the double metallocene [{Dy(Cp*)(μ-BH4)}2(Fvtttt)] (2), followed by removal of a bridging borohydride ligand upon addition of [(Et3Si)2(μ-H)][B(C6F5)4]. The dimetallic fulvalenyl complexes 1–3 give rise to single-molecule magnet (SMM) behaviour in zero applied field, with the effective energy barriers of 154(15) cm−1, 252(4) cm−1 and 384(18) cm−1, respectively, revealing a significant improvement in performance across the series. The magnetic properties are interpreted with the aid of ab initio calculations, which show substantial increases in the axiality of the crystal field from 1 to 2 to 3 as a consequence of the increasingly dominant role of the Fvtttt and Cp* ligands, with the barrier height and hysteresis properties being attenuated by the equatorial borohydride ligands. The experimental and theoretical results described in this study furnish a blueprint for the design and synthesis of poly-cationic dysprosocenium SMMs with properties that may surpass those of benchmark systems.
Introduction
Observations of magnetic bistability in structurally well-defined, monodisperse nanomaterials have stimulated considerable interest in technology based on the quantum properties of atoms and molecules. For example, the demonstration of magnetic memory in single holmium atoms on surfaces has introduced potential for the fabrication of data storage devices with capacities surpassing those of conventional technology.1,2 Molecule-based magnetic materials offer similar opportunities, accompanied by the advantage that their electronic structure can be tuned using imaginative synthetic chemistry. Recent advances include magnetic molecules incorporated into spintronic devices or used as the basis of quantum algorithm operations.3–5The magnetic hysteresis properties of single-molecule magnets (SMMs) have also been acclaimed as a possible source of novel data storage materials and, while such applications may eventually be possible, certain obstacles must first be overcome.6–10 Challenges to the implementation of SMM-based technology include that: (1) all known systems require cooling with cryogens in order to show hysteresis; (2) uniform nano-structuring of SMMs on surfaces is difficult, and; (3) the chemical stability of SMMs throughout surface deposition processes and, subsequently, in a device environment is not guaranteed, regardless of whether or not the bulk material itself is air-sensitive. However, encouraging progress has been made, such as the discovery of magnetic hysteresis in an SMM at 80 K,11i.e. above the boiling point of liquid nitrogen, and elegant surface studies of some SMMs have demonstrated the single-molecule origins of the hysteresis.12
The advances made to date strengthen the motivation for further research into SMMs, particularly the exploration of new synthetic strategies that aim to increase the temperatures at which these materials function. Considerable effort has been invested into maximizing the effective energy barrier to reversal of the magnetization (Ueff) and the magnetic blocking temperature (TB). A few highly anisotropic metal ions have proven to be important as the basic ingredient in an SMM, with dysprosium being the most popular and terbium, erbium and cobalt(II) also playing prominent roles.13–21 In the case of Dy3+, a 4f9 ion with oblate spheroidal electron density, successful SMM synthesis strategies tend to produce compounds in which the metal occupies a coordination environment with a strong and highly axial crystal field.22–24 This approach partly explains why the highest-performing SMMs are based on metallocene cations of the type [Dy(η5-CpR)2]+, where the bulky cyclopentadienyl ligands [CpR]− provide the strong, axial crystal field whilst also blocking the formation of any deleterious equatorial crystal field.6,11,25–29
Previous work on sandwich SMMs constructed with erbium-COT (COT = cyclo-octatetraenyl)30,31 and terbium-phthalocyanine32,33 building blocks has shown that the parameters Ueff and TB increase when two or more blocks are linked to form multi-decker sandwich complexes. We therefore reasoned that improvements in the SMM properties of dysprosocenium cations might be possible if closely related polymetallic versions could be synthesized. To investigate this idea, we targeted the synthesis of a dimetallic dysprosocenium cation by replacing a cyclopentadienyl ligand with a bicyclopentadienyl ligand, also known as fulvalenyl or pentafulvalenyl, in which two cyclopentadienyl rings share an exocyclic carbon–carbon bond.34 Dinucleating fulvalenyl ligands have been used extensively in transition metal sandwich chemistry,35 with recent examples including macrocyclic poly(ferrocenyl) compounds with potential applications as molecular electronic materials.36,37 In contrast, the use of such ligands in f-element chemistry is uncommon, and in the case of the lanthanides was, hitherto, limited to the dimetallic divalent compounds [M(THF)(η5:η5-Fvtttt)]2 with M = Sm, Eu or Yb.38
Results and discussion
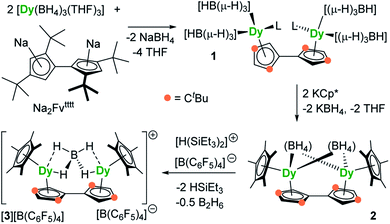
The reaction of the di-sodium salt of 1,1′,3,3′-tetra-tert-butylpentafulvalenyl, Na2Fvtttt, with two equivalents of [Dy(BH4)3(THF)3] produced the dimetallic complex [{Dy(BH4)2(THF)}2(η5:η5-Fvtttt)] (1), with the two half-sandwich units linked via the fulvalenyl ligand, as shown in Scheme 1. Subsequently, compound 1 was reacted with two equivalents of potassium pentamethylcyclopentadienide (KCp*) to give the double metallocene [{Dy(η5-Cp*)(μ-BH4)}2(η5:η5-Fvtttt)] (2) in which the dysprosium centres are bridged by both borohydride ligands. Finally, addition of one equivalent of the super-electrophile [(Et3Si)2(μ-H)][B(C6F5)4] to compound 2 produced the separated ion-pair [{Dy(η5-Cp*)}2(μ-BH4)(η5:η5-Fvtttt)][B(C6F5)4] ([3][B(C6F5)4]), containing the target dimetallic dysprosocenium cation 3, with the two sandwich units bridged by a single borohydride ligand.The molecular structures of all three compounds were determined by single-crystal X-ray diffraction (Fig. 1 and Table S1†). The structure of 1 consists of two similar half-sandwich units in which each dysprosium is ligated by one cyclopentadienyl unit of the Fvtttt ligand in an η5-manner, with additional coordination by two κ3-borohydride ligands and a THF ligand (Fig. 1). The Dy1–C distances are in the range 2.607(4)–2.698(4) Å and the distance from Dy1 to the fulvalenyl C5 centroid is 2.361(1) Å; the analogous distances for Dy2 are essentially the same (Table S2†). Appreciable twisting of the two halves of the molecule about the central Fvtttt carbon–carbon bond is evident from the C2–C1–C6–C7 torsional angle of 95.3(6)°, resulting in an intramolecular Dy⋯Dy separation of 5.443(1) Å. Diagnostic absorptions in the FTIR spectrum of compound 1 occur at ![[small upsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e131.gif) = 2127–2467 cm−1 for the terminal and bridging B–H groups (Fig. S1†).
= 2127–2467 cm−1 for the terminal and bridging B–H groups (Fig. S1†).
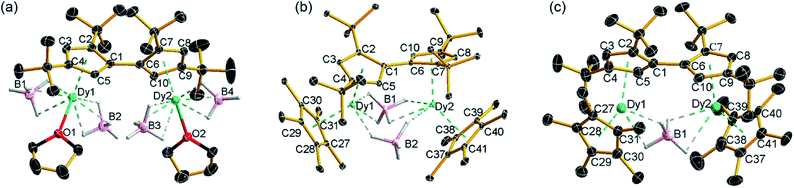 | ||
| Fig. 1 Thermal ellipsoid representations (30% probability) of the structures of: (a) 1, (b) 2 and (c) 3. For clarity, hydrogen atoms are omitted except those in the [BH4]− ligands. | ||
In compound 2, the two unique halves of the molecule each consist of a dysprosium centre sandwiched between an η5-Cp* ligand and an η5-Fvtttt ligand, with bridges between the metal atoms occurring via both borohydride ligands. The change in the bonding mode of the borohydride ligands in 2 as compared to those in 1 is presumably a consequence of the spatial demands of the Cp* ligands. For Dy1, the bond distances to the Cp* ligand are in the range 2.643(3)–2.667(2) Å and those to the fulvalenyl ligand are 2.630(2)–2.704(4) Å, with associated Dy1–centroid distances of 2.362(1) Å and 2.378(1) Å, respectively; the corresponding distances involving Dy2 are not significantly different (Table S3†). The metallocene bending angles subtended at Dy1 and Dy2 are 137.913(1)° and 139.143(1)°, respectively. The bridging borohydride ligands in 2 greatly reduce the extent of twisting between the two halves of the Fvtttt ligand relative to 1, as shown in the C2–C1–C6–C7 torsional angle of 30.0(4)°. The Dy⋯Dy separation is, at 4.148(1) Å, also markedly shorter than that in 1. The IR absorptions for the borohydride ligands occur in the range ![[small upsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e131.gif) = 2124–2473 cm−1 (Fig. S2†).
= 2124–2473 cm−1 (Fig. S2†).
In the structure of compound 3, the bonding modes of the Cp*, Fvtttt and borohydride ligands are similar to those in 2. Thus, the Dy1–C distances to the Cp* and Fvtttt ligands are in the range 2.594(7)–2.650(8) Å and 2.578(7)–2.742(8) Å, respectively, with associated Dy1–centroid distances of 2.348(1) Å and 2.355(1) Å, respectively. As in compounds 1 and 2, the geometric parameters for Dy2 are similar to those of Dy1 in compound 3 (Table S4†). However, the two metallocene components of 3 are markedly less bent than those in 2, with bending angles of 145.727(1)° and 146.246(1)° for Dy1 and Dy2, respectively. The fulvalene twist angle is 55.0(9)° and the Dy⋯Dy separation is 4.701(1) Å. The borohydride ligand adopts a κ2:κ2 bonding mode, with associated IR frequencies occurring as broad absorptions around ![[small upsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e131.gif) = 2230 cm−1 (Fig. S3†).
= 2230 cm−1 (Fig. S3†).
The synthesis of 1, 2 and [3][B(C6F5)4] demonstrates that fulvalenyl ligands can indeed form the structural basis of linked dysprosium metallocenes. In the next stage, our aim was to investigate how the changes in the crystal field environment experienced by the Dy3+ centres impact upon the SMM properties.
Magnetic properties
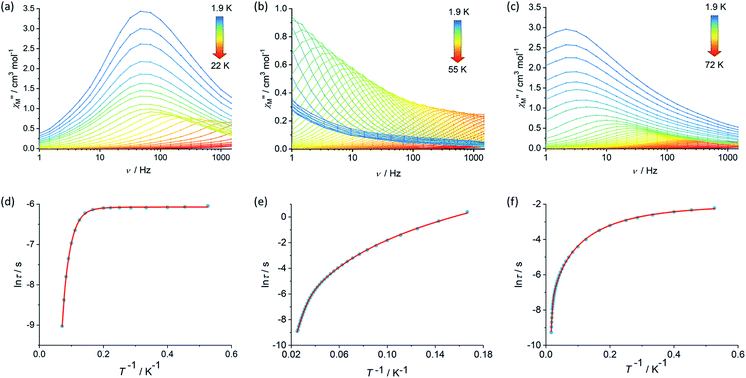
The magnetic properties of 1, 2 and [3][B(C6F5)4] were studied in static (DC) and dynamic (AC) magnetic fields using a Magnetic Property Measurement System. The temperature dependence of the product of the molar magnetic susceptibility and temperature, i.e. χMT(T), is consistent with the dimetallic composition of the three compounds. The values of χMT at 300 K are 27.3, 27.2 and 27.5 cm3 K mol−1 for 1, 2 and [3][B(C6F5)4], respectively, are close to the theoretical value of 28.2 cm3 K mol−1 for a complex containing two weakly interacting Dy3+ ions with 6H15/2 ground multiplets (Fig. S4, S6 and S8†).39 The decreases in χMT with temperature for 1 and [3][B(C6F5)4] are similar and gradual without featuring a sharp drop at lower temperatures, reaching values of 22.2 and 21.9 cm3 K mol−1 at 2.0 K. The decrease in χMT with temperature for 2 is similar in the high-temperature regime, however a much more pronounced decrease was observed below 20 K such that a value of 17.5 cm3 K mol−1 is reached at 2.0 K. The decrease in χMT(T) with decreasing temperature for all three compounds can be accounted for by gradual depopulation of the excited crystal field levels of the Dy3+ ions, which may occur concomitantly with antiferromagnetic exchange coupling becoming more prominent as thermal randomization effects diminish, particularly in compound 2. The isothermal field-dependence of the magnetization, M(H), for each compound also reflects the presence of two Dy3+ ions per complex, reaching values of 9.89, 10.11 and 9.60 Nβ at 7 T and 1.9 K for 1, 2 and [3][B(C6F5)4], respectively (Fig. S5, S7 and S9†).The real (χ′) and imaginary (χ′′) components of the AC magnetic susceptibility were measured for each compound as functions of temperature and AC frequency (ν) (Fig. 2, S10–S12, S15–S17, S20–S22†), using zero DC field and a small AC field of 3 Oe. The observation of well-defined maxima in the χ′′(T) and χ′′(ν) plots for 1, 2 and [3][B(C6F5)4] indicate slow relaxation of the magnetization without the need for an external DC field. For compound 1, maxima were observed in the χ′′(ν) plot from 1.9–14 K before the upper frequency limit of the measurement system is reached (Fig. 2). Up to 6 K, the position of the frequency maximum and, hence, the relaxation time (τ), varies only slightly with temperature, suggesting that relaxation via quantum tunnelling of the magnetization (QTM) is dominant in this regime. At higher temperatures, the frequency maximum becomes strongly temperature dependent, which is likely to reflect thermally activated relaxation becoming dominant. The relaxation times for each temperature were extracted and plotted as a function of T−1, revealing that the change from QTM to activated regimes is abrupt (Fig. 2). Fitting the data with the equation τ−1 = τ0−1e−Ueff/kBT + CTn + τQTM−1, where τ0−1 and Ueff denote the Orbach parameters, C and n denote the Raman parameters, and the rate of QTM is τQTM−1, gives an energy barrier of Ueff = 154(15) cm−1 with τ0 = 3.93(6) × 10−11 s, the Raman parameters are C = 8.16(3) × 10−4 s−1 K−n, n = 5.87(1) and τQTM = 2.31(1) × 10−3 s.
The AC susceptibility measurements on compounds 2 and [3][B(C6F5)4] revealed that slow relaxation of the magnetization occur across wider temperatures ranges of 1.9–55 K and 1.9–72 K, respectively, relative to 1 (Fig. 2). In the case of 2, the χ′′(ν) plot consists of well-defined maxima from 1.9 K up to 40 K, and for [3][B(C6F5)4] the maxima were observed from 1.9 K up to 60 K. The temperature dependence of the relaxation times for 2 revealed that the system does not cross to a purely temperature-independent regime even at the lowest measurement temperature (Fig. 2). Hence, it was possible to fit the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ vs. T−1 data for 2 without a QTM term, which produced Orbach parameters of Ueff = 252(4) cm−1, τ0 = 1.94(3) × 10−8 s and Raman parameters of C = 4.56 (2) × 10−4 s−1 K−n, n = 4.12(1). For [3][B(C6F5)4], after a strong dependence of ln
τ vs. T−1 data for 2 without a QTM term, which produced Orbach parameters of Ueff = 252(4) cm−1, τ0 = 1.94(3) × 10−8 s and Raman parameters of C = 4.56 (2) × 10−4 s−1 K−n, n = 4.12(1). For [3][B(C6F5)4], after a strong dependence of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ on T−1 in the high-temperature regime, the relaxation time is only weakly temperature-dependent below 5 K. A fit of the data for this compound gave Ueff = 384(18) cm−1, τ0 = 1.37(6) × 10−8 s, C = 6.55(4) × 10−1 s−1 K−n, n = 2.03(2) and τQTM = 1.39 (6) × 10−1 s.
τ on T−1 in the high-temperature regime, the relaxation time is only weakly temperature-dependent below 5 K. A fit of the data for this compound gave Ueff = 384(18) cm−1, τ0 = 1.37(6) × 10−8 s, C = 6.55(4) × 10−1 s−1 K−n, n = 2.03(2) and τQTM = 1.39 (6) × 10−1 s.
Comparing the Ueff parameters for 1, 2 and [3][B(C6F5)4] reveals substantial increases on moving through the series. This trend can be understood in a qualitative sense by considering how the composition and geometry of the crystal field experienced by each Dy3+ centre varies. Whilst the Dy3+ ions in all three compounds must experience a dominant axial crystal field to show any slow relaxation properties in zero DC field, this is clearly relatively weak in 1 and stronger in 3. The presence of only one cyclopentadienyl group per Dy3+ in 1 is sufficient to induce SMM behaviour by providing a relatively strong axial crystal field, but the two borohydride ligands and the THF ligand provide a competing equatorial field that limits the barrier height. In 2, the additional [Cp*]− ligands strengthen the axial component of the crystal field whilst simultaneously reducing the number of equatorial ligands, resulting in an increase in the barrier by approximately 100 cm−1 (60%) relative to 1. Upon forming 3, not only is another equatorial borohydride ligand removed from the coordination environment of both Dy3+ ions, the two metallocene units are also less bent by approximately 7°–8° and the individual cyclopentadienyl donor groups are slightly closer to the metal centres than in 2. Consequently, the barrier height in 3 is approximately 130 cm−1 (50%) greater than that in 2. Furthermore, the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ versus T−1 data are also consistent with the single-ion QTM being reduced by intramolecular exchange interactions between the Dy3+ ions. The Dy⋯Dy distances decrease in the order 1 > 3 > 2, hence the QTM should be slowest in 2, as observed.
τ versus T−1 data are also consistent with the single-ion QTM being reduced by intramolecular exchange interactions between the Dy3+ ions. The Dy⋯Dy distances decrease in the order 1 > 3 > 2, hence the QTM should be slowest in 2, as observed.
Compounds 1, 2 and [3][B(C6F5)4] further illustrate the magneto-structural correlation developed for dysprosium and terbium metallocene SMMs, in which the cyclopentadienyl ligands provide dominant axial crystal fields and the properties are attenuated by the equatorial ligands.28,40,41 In addition to accounting for the variation in energy barrier across the series, their hysteresis properties can also be interpreted in terms of the molecular structure. Thus, although the cyclopentadienyl ligands dominate the crystal field, the borohydride and THF ligands provide non-negligible equatorial components, which result in the magnetization versus field hysteresis occurring as narrow S-shaped curves at 1.9 K and various field in the range ±5 T with an average scan rate of 23 Oe s−1 for each compound (Fig. S14, S19 and S24†). There is essentially no hysteresis for 1, however the hysteresis for 2 displays narrow loops centred on field values of approximately ±1.3 kOe and ±5.0 kOe, respectively, and [3][B(C6F5)4] shows a loop around ±1.7 kOe. These subtle effects are presumably a consequence of exchange bias between the Dy3+ centres affecting the rate of relaxation via QTM, suggesting that the borohydride ligands are effective at transmitting exchange interactions.42 This proposal is consistent with a recent study of magnetic exchange in [Ln(BH4)3] (Ln = Gd–Tm), in which it was found that {HBH} bridges between the metal centres allow antiferro- or ferro-magnetic exchange, albeit with very small coupling constants.43
Theoretical analysis
The local magnetic properties of each individual Dy3+ ion in 1–3 were first studied. State-averaged complete active space self-consistent field (SA-CASSCF) calculations44–48 followed by restricted active space state interaction treatment of spin–orbit coupling (SO-RASSI)49 and calculation of local magnetic properties using the SINGLE_ANISO_OPEN module50,51 were carried out on each ion while the other Dy3+ ion in the complex was replaced by diamagnetic yttrium. The properties of the eight lowest Kramers doublets (KDs) of each ion are listed in Tables S8–S13.† In each case the ground Kramers doublet (KD) is characterized by a strongly axial g-tensor with small but non-vanishing transverse components. The direction of the principal magnetic axis of each ground KD is determined by an axial-type interaction with the Fvtttt and Cp* ligands (Fig. 3).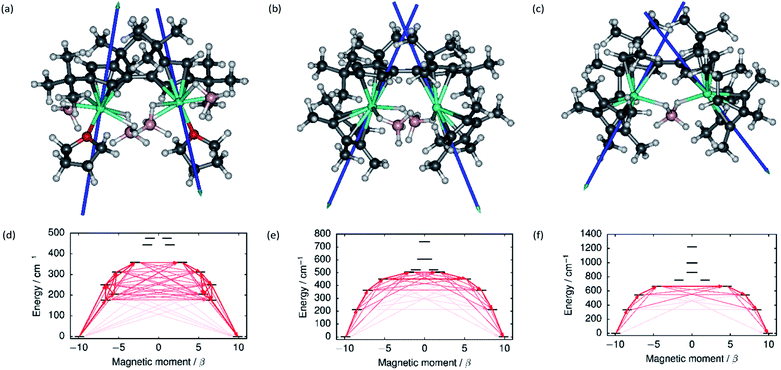 | ||
| Fig. 3 The principal magnetic axes of the ground KDs of the Dy3+ ions in (a) 1, (b) 2 and (c) 3. Calculated effective ab initio barriers for the relaxation of magnetization at the Dy1 ions (d) 1, (e) 2 and (f) 3. Stronger arrows indicate larger absolute value of the transition magnetic moment matrix elements between the respective states. Transitions involving higher-energy states not involved in the relaxation are omitted for clarity. The barriers for the Dy2 ions, which are similar to those of the Dy1 ions, are shown in ESI Fig. S25–S27.† | ||
The first-excited local KDs of the two Dy3+ ions in 1 lie 176 cm−1 and 181 cm−1 above the ground KD. The angles between the principal magnetic axes of the ground and first excited states are 41.3° and 43.0°, respectively. These relatively large angles should lead to an efficient Orbach mechanism via the first-excited KD, and an effective barrier corresponding to the energies of the first excited states. Indeed, the effective barrier height determined from the fits is 154 cm−1 which agrees well with the calculated values. A qualitative ab initio barrier for the relaxation of magnetization was constructed using a well-established methodology,52 where the relaxation pathway is traced by following large magnitudes of transition magnetic moment matrix elements between different states. The barriers for 1 are shown in Fig. 3 and the quantitative transition magnetic moment matrix elements are listed in Table S14.† Based on the calculated values, the barrier should be crossed earliest at the first-excited KD and latest at the fifth-excited KD. Based on the experimental barrier height, the most likely relaxation takes place via the first-excited KD.
In 2, the lowest four KDs on each Dy3+ ion have roughly collinear principal magnetic axes. The calculated transition magnetic moments (Fig. 3 and Table S15†) predict that the barrier becomes crossed either at the second- (364 cm−1 and 362 cm−1) or third-excited (452 cm−1 and 457 cm−1) local KDs. The experimentally determined barrier height (252 cm−1) is, however, closest to the energies of the first-excited local KD (214 cm−1 and 208 cm−1). The transition matrix elements for an Orbach process via the first excited KD are, however, not vanishingly small and this mechanism remains plausible. The first four KDs of Dy1 and the first three KDs of Dy2 in 3 are also roughly collinear. Based on the transition dipole moments (Fig. 3 and Table S16†) the barrier is most likely crossed at the second (546 cm−1 and 551 cm−1) or third excited KD (667 cm−1 and 666 cm−1). The experimentally determined barrier height (384 cm−1) is again closest to the energy of the first excited KD (336 cm−1 and 339 cm−1) and, again, an Orbach mechanism via the first excited KD has non-vanishing transition magnetic moment matrix elements and remains plausible.
Based on the energy of the first excited KD (which in all cases corresponds to the experimentally determined barrier height), the axiality of the crystal-field (CF) environments of the Dy3+ ions clearly increases from 1 to 3. Further to the qualitative analysis of this trend (see above), quantitative insight was obtained by calculating the ab initio CF parameters53 for each Dy3+ ion and the results are listed in Tables S17–S19† using the Iwahara–Chibotaru notation.54 The effect of the CF can be understood qualitatively by considering the second-rank parameters, summarized in Table 1. The axial B20 parameters clearly increase from 1 to 2 to 3, which is consistent with the increased axiality of the CF. The parameters should be compared to those calculated for the current benchmark SMM, i.e. the [(C5Me5)Dy(C5iPr5)]+ cation, which has an energy barrier of 1540 cm−1 and a blocking temperature of 80 K,11 also listed in Table 1. It is immediately clear that the axiality falls short of that in [(C5Me5)Dy(C5iPr5)]+ and the off-diagonal |B2±2| parameters of 1–3 are much larger. Thus, the equatorial borohydride ligands in 1–3, and the lack of axial Cp* ligands in 1, clearly lead to much reduced axiality.
| B 20 | |B2±1| | |B2±2| | ||
|---|---|---|---|---|
| 1 | Dy1 | −217.86 | 15.85 | 58.77 |
| Dy2 | −221.95 | 18.45 | 56.36 | |
| 2 | Dy1 | −375.17 | 18.19 | 81.70 |
| Dy2 | −384.52 | 21.80 | 57.93 | |
| 3 | Dy1 | −608.51 | 7.83 | 178.31 |
| Dy2 | −615.72 | 8.76 | 203.13 | |
| [(C5Me5)Dy(C5iPr5)]+ | −1195.31 | 17.70 | 30.23 |
The non-negligible off-diagonal CF parameters lead to significant mixing of the different local angular momentum eigenstates defined by some definite angular momentum projection M. This is evident from Tables S20–S25,† which give the projections of the ab initio CF eigenstates on angular momentum eigenstates. The states in the ground KDs have a large contribution from a state with some definite M, but in all cases even the states in the ground KD are significantly mixed. This is consistent with the effective barrier being crossed at the first excited local KD in each case.
The effect of intramolecular interaction between the two Dy3+ ions was studied by the Lines model55 and the magnetic point-dipole approximation as implemented in the POLY_ANISO module.51,56,57 The Lines model describes the exchange interaction in terms of a single phenomenological scalar parameter which was determined by minimizing the standard deviation between the measured and calculated magnetic susceptibilities. Due to the general lack of low-temperature features in the susceptibility of 1 and 3 (Fig. S4, S8 and S28†), the parameter could only be only reliably determined for 2. The eigenvalues of the Lines exchange operator and the dipolar coupling operator where mapped to an effective Ising-type Hamiltonian of the form:
Ĥ = −(Jex + Jdipolar)![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) z,1 z,1![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) z,2 = −Jtot z,2 = −Jtot![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) z,1 z,1![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) z,2 z,2 | (1) |
In eqn (1), the ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) = 1/2 pseudospin operators act on the ground KDs of the two Dy3+ ions. The dipolar coupling parameters Jdipolar are −0.9 cm−1, −2.5 cm−1 and −1.4 cm−1 for 1–3, respectively, which are consistent with variations in the Dy⋯Dy distance between the two ions. The exchange parameter Jex determined for 2 is −1.2 cm−1, hence the total exchange interaction is Jtot ≈ −3.7 cm−1. The absence of bridging borohydride ligands in 1 is likely to result in a vanishingly small Jex parameter relative to 2, which, combined with the smaller Jdipolar parameter, provides further support for the idea that the steps in the M(H) hysteresis in 2 and 3 occur as a consequence of exchange-bias effects.
= 1/2 pseudospin operators act on the ground KDs of the two Dy3+ ions. The dipolar coupling parameters Jdipolar are −0.9 cm−1, −2.5 cm−1 and −1.4 cm−1 for 1–3, respectively, which are consistent with variations in the Dy⋯Dy distance between the two ions. The exchange parameter Jex determined for 2 is −1.2 cm−1, hence the total exchange interaction is Jtot ≈ −3.7 cm−1. The absence of bridging borohydride ligands in 1 is likely to result in a vanishingly small Jex parameter relative to 2, which, combined with the smaller Jdipolar parameter, provides further support for the idea that the steps in the M(H) hysteresis in 2 and 3 occur as a consequence of exchange-bias effects.
Conclusions
In developing a stepwise route from the fulvalenyl double half-sandwich complex [{Dy(BH4)2(THF)}2(Fvtttt)] (1) via the double metallocene [{Dy(η5-Cp*)(μ-BH4)}2(Fvtttt)] (2) to ion-separated [{Dy(η5-Cp*)}2(μ-BH4)(Fvtttt)][B(C6F5)4] ([3][B(C6F5)4]), we have shown that a dimetallic dysprosocenium complex can be synthesized. All three fulvalenyl-supported compounds are SMMs in zero applied field and show appreciable increases in the effective energy barrier to reversal of the magnetization across the series, which more than doubles from 154(15) cm−1 in 1 to 384(18) cm−1 in 3. The improvements in the energy barrier are attributable to the increasingly dominant axial crystal field provided by the Fvtttt and Cp* ligands balanced against the influence of the equatorial borohydride ligands. Quantitative support for this magneto-structural correlation was obtained from ab initio calculations, which revealed marked increases in the axial B20 parameter across the series but also with appreciable non-axial parameters.It is instructive to consider these results in light of the SMM properties of [(C5Me5)Dy(C5iPr5)]+ and its precursors, i.e. the monometallic metallocene [(C5Me5)Dy(C5iPr5)(BH4)] and the half-sandwich [(C5iPr5)Dy(BH4)2(THF)]. In the case of [(C5Me5)Dy(C5iPr5)(BH4)], there many structural features in common with 2 and 3 and yet the energy barrier is a miniscule 7(1) cm−1 in zero field.11 This comparison further highlights how the strategy of combining metallocene building blocks to give a dimetallic dysprosocenium cation may improve SMM performance. In contrast, the barrier determined for [(C5iPr5)Dy(BH4)2(THF)] in zero field is 241(7) cm−1, which is markedly larger than the barrier of 154(15) cm−1 in 1. However, since the Dy–Cpcent distances in the two half-sandwich complexes are very similar, the different barriers are likely to originate from the influence of the THF ligands. The Dy–O distances in 1 are approximately 0.03–0.08 Å shorter than those in its monometallic counterpart, pointing towards a stronger equatorial component of the crystal field and, therefore, relaxation via an Orbach process with a lower barrier.
Looking forward, if a dimetallic dicationic dysprosocenium complex such as [{Dy(η5-Cp*)}2(η5:η5-Fvtttt)]2+ could be synthesized, substantial increases in the axial crystal field parameters and decreases in the non-axial parameters should combine with the beneficial effects of exchange coupling in a dimetallic complex. Whilst substituent-dependent geometric factors will clearly play an important role in determining the properties, a dimetallic dysprosocenium dication can reasonably be anticipated to display enhancements in the energy barrier and blocking temperature relative to the current benchmark SMM.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the University of Sussex, the ERC (CoG 646740), the EPSRC (EP/M022064/1), the National Natural Science Foundation of China (Grants 21525103 and 21871247) and the University of Oulu (Kvantum Institute). Computational resources were provided by CSC-IT Center for Science in Finland and the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533). JT and RAL also thank the Royal Society for a Newton Advanced Fellowship (NA160075).Notes and references
- F. D. Natterer, K. Yang, W. Paul, P. Willke, T. Choi, T. Greber, A. J. Heinrich and C. P. Lutz, Nature, 2017, 543, 226–228 CrossRef CAS PubMed.
- F. D. Natterer, F. Donati, F. Patthey and H. Brune, Phys. Rev. Lett., 2018, 121, 27201 CrossRef CAS PubMed.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348 CrossRef CAS PubMed.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed.
- E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513 RSC.
- Z. Zhu, M. Guo, X.-L. Li and J. Tang, Coord. Chem. Rev., 2019, 378, 350–364 CrossRef CAS.
- M. Feng and M.-L. Tong, Chem.–Eur. J., 2018, 24, 7574–7594 CrossRef CAS PubMed.
- J.-L. Liu, Y.-C. Chen and M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- F.-S. Guo, A. K. Bar and R. A. Layfield, Chem. Rev., 2019, 119, 8479–8505 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- F. Paschke, P. Erler, V. Enenkel, L. Gragnaniello and M. Fonin, ACS Nano, 2019, 13, 780–785 CrossRef CAS PubMed.
- T. P. Latendresse, V. Vieru, A. Upadhyay, N. S. Bhuvanesh, L. F. Chibotaru and M. Nippe, Chem. Sci., 2020, 11, 3936–3951 RSC.
- J. D. Hilgar, M. G. Bernbeck, B. S. Flores and J. D. Rinehart, Chem. Sci., 2018, 9, 7204–7209 RSC.
- J. D. Hilgar, M. G. Bernbeck and J. D. Rinehart, J. Am. Chem. Soc., 2019, 141, 1913–1917 CrossRef CAS PubMed.
- P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, eaat7319 CrossRef CAS PubMed.
- S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Commun., 2017, 8, 2144 CrossRef PubMed.
- F. Liu, L. Spree, D. S. Krylov, G. Velkos, S. M. Avdoshenko and A. A. Popov, Acc. Chem. Res., 2019, 52, 2981–2993 CrossRef CAS PubMed.
- X.-N. Yao, J.-Z. Du, Y.-Q. Zhang, X.-B. Leng, M.-W. Yang, S.-D. Jiang, Z.-X. Wang, Z.-W. Ouyang, L. Deng, B.-W. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373–380 CrossRef CAS PubMed.
- R. Collins, M. J. Heras Ojea, A. Mansikkamäki, J. Tang and R. A. Layfield, Inorg. Chem., 2020, 59, 642–647 CrossRef CAS PubMed.
- A. Chakraborty, B. M. Day, J. P. Durrant, M. He, J. Tang and R. A. Layfield, Organometallics, 2020, 39, 8–12 CrossRef CAS.
- K. L. M. Harriman, D. Errulat and M. Murugesu, Trends Chem., 2019, 1, 425–439 CrossRef.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- J. P. Durrant, J. Tang, A. Mansikkamäki and R. A. Layfield, Chem. Commun., 2020, 56, 4708–4711 RSC.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439 CrossRef CAS PubMed.
- K. Randall McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503 RSC.
- C. A. Gould, K. R. McClain, J. M. Yu, T. J. Groshens, F. Furche, B. G. Harvey and J. R. Long, J. Am. Chem. Soc., 2019, 141, 12967–12973 CrossRef CAS PubMed.
- B. M. Day, F.-S. Guo and R. A. Layfield, Acc. Chem. Res., 2018, 51, 1880–1889 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11145–11149 Search PubMed.
- S. I. Gorelsky, I. Korobkov, M. Jeletic, J. J. Le Roy, M. Murugesu, L. Ungur and L. F. Chibotaru, J. Am. Chem. Soc., 2013, 135, 3502–3510 CrossRef PubMed.
- K. L. M. Harriman and M. Murugesu, Acc. Chem. Res., 2016, 49, 1158–1167 CrossRef CAS PubMed.
- T. Morita, M. Damjanović, K. Katoh, Y. Kitagawa, N. Yasuda, Y. Lan, W. Wernsdorfer, B. K. Breedlove, M. Enders and M. Yamashita, J. Am. Chem. Soc., 2018, 140, 2995–3007 CrossRef CAS PubMed.
- K. Katoh, B. K. Breedlove and M. Yamashita, Chem. Sci., 2016, 7, 4329–4340 RSC.
- E. Solel and S. Kozuch, J. Org. Chem., 2018, 83, 10826–10834 CrossRef CAS PubMed.
- M. D. Walter and R. A. Andersen, Organometallics, 2019, 38, 3680–3687 CrossRef CAS.
- M. S. Inkpen, S. Scheerer, M. Linseis, A. J. P. White, R. F. Winter, T. Albrecht and N. J. Long, Nat. Chem., 2016, 8, 825 CrossRef CAS PubMed.
- L. E. Wilson, C. Hassenrück, R. F. Winter, A. J. P. White, T. Albrecht and N. J. Long, Angew. Chem., Int. Ed., 2017, 56, 6838–6842 CrossRef CAS PubMed.
- F. Nief and L. Ricard, J. Organomet. Chem., 1998, 553, 503–506 CrossRef CAS.
- C. Benelli and D. Gatteschi, in Introduction to Molecular Magnetism, John Wiley & Sons, Ltd, 2015, pp. 277–294 Search PubMed.
- T. Pugh, N. F. Chilton and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 11082–11085 CrossRef CAS PubMed.
- P. Evans, D. Reta, C. A. P. Goodwin, F. Ortu, N. F. Chilton and D. P. Mills, Chem. Commun., 2020 10.1039/C9CC08945D.
- E. M. Pineda, Y. Lan, O. Fuhr, W. Wernsdorfer and M. Ruben, Chem. Sci., 2017, 8, 1178–1185 RSC.
- W. Wegner, J. van Leusen, J. Majewski, W. Grochala and P. Kögerler, Eur. J. Inorg. Chem., 2019, 2019, 1776–1783 CrossRef CAS.
- B. O. Roos, in Advances in Chemical Physics: Ab Initio Methods in Quantum Chemistry II, ed. K. P. Lawley, Wiley, New York, NY, USA, 1987, vol. 69, pp. 399–455 Search PubMed.
- P. Siegbahn, A. Heiberg, B. Roos and B. Levy, Phys. Scr., 1980, 21, 323–327 CrossRef CAS.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- P. E. M. Siegbahn, J. Almlöf, A. Heiberg and B. O. Roos, J. Chem. Phys., 1981, 74, 2384–2396 CrossRef.
- B. O. Roos, R. Lindh, P. Å. Malmqvist, V. Veryazov and P.-O. Widmark, Multiconfigurational Quantum Chemistry, Wiley, Hoboken, NJ, USA, 2016 Search PubMed.
- P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 64112 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, in Lanthanides and Actinides in Molecular Magnetism, ed. R. A. Layfield and M. Murugesu, Wiley-VHC, Weinheim, Germany, 2015, pp. 153–184 Search PubMed.
- L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Inorg. Chem., 2013, 52, 6328–6337 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Chem.–Eur. J., 2017, 23, 3708–3718 CrossRef CAS PubMed.
- N. Iwahara and L. F. Chibotaru, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 174438 CrossRef.
- M. E. Lines, J. Chem. Phys., 1971, 55, 2977–2984 CrossRef CAS.
- L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126–4129 CrossRef CAS PubMed.
- L. Ungur, W. den Heuvel and L. F. Chibotaru, New J. Chem., 2009, 33, 1224–1230 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis details, spectroscopic characterization, X-ray crystallography, magnetic measurements and computational details. CCDC 1993006, 1993008 and 1993009. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc02033h |
| This journal is © The Royal Society of Chemistry 2020 |