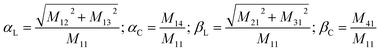Open Access Article
Open Access ArticleSafeguarding long-lived excitons from excimer traps in H-aggregated dye-assemblies†
Samaresh
Samanta
a,
Subir Kumar
Ray
 b,
Shubham
Deolka
b,
Shubham
Deolka
 a,
Sudipta
Saha
b,
Pradeep
K. R.
c,
Rohit
Bhowal
d,
Nirmalya
Ghosh
b and
Debangshu
Chaudhuri
a,
Sudipta
Saha
b,
Pradeep
K. R.
c,
Rohit
Bhowal
d,
Nirmalya
Ghosh
b and
Debangshu
Chaudhuri
 *a
*a
aDepartment of Chemical Sciences, Indian Institute of Science Education and Research (IISER) Kolkata, Mohanpur 741246, India. E-mail: dchaudhuri@iiserkol.ac.in
bDepartment of Physical Sciences, Indian Institute of Science Education and Research (IISER) Kolkata, Mohanpur 741246, India
cNew Chemistry Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Bengaluru 560064, India
dDepartment of Chemistry, Indian Institute of Science Education and Research (IISER) Bhopal, Bhopal 462066, India
First published on 21st May 2020
Abstract
The fate of perylene bisimide (PBI) H-aggregates as energy-harvesting materials depends on the ability to circumvent an extremely deleterious but efficient self-trapping process that scavenges the long-lived excitons to form deep excimeric traps. We present the first ever report of an ambient-stable, bright, steady-state photoluminescence (PL) from the long-lived exciton of an H-aggregated PBI crystal. The crystal structure reveals a rotationally displaced H-aggregated arrangement of PBI chromophores, in which transition from the lowest energy exciton state is partially allowed. Polarized absorption spectroscopy on single microcrystals confirms an unusually large exciton splitting of ∼1265 cm−1 that stabilizes the lower exciton state, and inhibits excimer formation. A PL Mueller matrix study shows an increase in the excited state polarization anisotropy, indicating a strong localization of the nascent exciton, which further safeguards it from the self-trapping process. Finally, the possibility of achieving excimer-free excitonic PL in solution self-assembly is also demonstrated.
Introduction
Long-range exciton diffusion is pivotal to a variety of applications involving organic semiconductors. In photovoltaics, it ensures that the photogenerated excitons are quantitatively transported to the heterojunction interface before they are lost to other relaxation pathways.1 Likewise, an artificial photosynthetic system requires the excitons to be efficiently channeled towards the reaction center.2 Even in PL quenching based sensors, excitons that are mobile can sample multiple analyte binding sites during their lifetime, resulting in improved sensitivity.3 Diffusion of singlet excitons is mediated by a Förster type process that necessitates strong interchromophoric interactions. To this end, aggregates of molecular chromophores are great candidates, and the nature of exciton coupling plays a crucial role in that process.4 In slip-stacked J-aggregates, the oscillator strength is transferred to the lowest energy exciton. Consequently, J-aggregates undergo fast radiative relaxation that competes with and limits exciton migration to a distance under 100 nm.5,6 Cofacial H-aggregates, on the other hand, have a symmetry-forbidden first excited state that has a longer lifetime, and can show extended mobility up to several microns.7,8 However, long-lived excited states are often susceptible to competing relaxation pathways. And nowhere is this problem more severe than in the H-type aggregates of PBI.As small-molecule chromophores with a very high optical absorption cross-section, an inherent tendency to self-assemble into strongly interacting H-type aggregates, and exceptional chemical and photochemical stability, PBI dyes make a great choice for energy harvesting applications. However, nearly all PBI based H-aggregates suffer from one serious limitation: an extremely fast self-trapping of the long-lived exciton into the excimer state.9,10 Excitons in H-aggregates are typically delocalized over several PBI units, and have an underlying molecular arrangement that is quite similar to that in the ground state. In contrast, excimer formation involves a significant structural reorganization of the excited aggregate that localizes it to a much smaller segment, presumably a dimer. This strong coupling of the excimer state to lattice deformation increases its effective mass, thus trapping it efficiently. Multiple studies based on femtosecond transient absorption11–14 and fluorescence upconversion15 spectroscopy have shown that excimer formation is triggered by an ultrafast mixing of the nascent exciton with charge-transfer (CT) states that takes place within 0.2–20 ps of photoexcitation. Consequently, the long-lived exciton of PBI H-aggregates has remained too elusive to be detected experimentally, and the H-aggregate photophysics is exclusively dominated by deep excimeric traps. Recently, we reported the suppression of excimer formation in H-aggregates of a flexible PBI dimer through an interplay of competing aggregation pathways.16 However, we found no direct evidence of the long-lived exciton. In this work, we present the first ever report of an ambient-stable, steady-state PL from long-lived excitons of a highly ordered H-aggregated PBI. As our subsequent investigations show, this unprecedented stability of the exciton against excimer traps is owed to an unusually large exciton splitting and an efficient localization of the exciton wavefunction.
Results and discussion
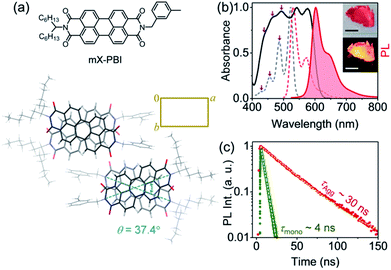
Fig. 1a presents the molecule under investigation, the unsymmetrically substituted mX-PBI. When crystallized from a 5% ethanol/CHCl3 mixture, mX-PBI yields long anisotropic crystals with a flat, belt-like morphology. Single crystal X-ray diffraction analysis shows that the molecule crystallizes in a monoclinic (P21/c) space group with cell parameters of a = 27.378(16) Å, b = 16.404(6) Å, c = 8.074(4) Å, α = γ = 90°, and β = 96.1(4)° (CCDC 1967792, Fig. 1a and Table S1†). The unit cell contains four mX-PBI molecules, arranged as a pair of identical π-stacked dimers, with an intra-stack torsion angle of 37.4° and an interplanar separation of 3.31 Å between two PBI units. Such rotationally displaced π-stacking is fairly common in PBI based H-aggregates. At an average separation of 11.2 Å, any dipolar coupling between adjacent PBI stacks can be ruled out. The electronic properties of the crystal are therefore largely dictated by the coupling between PBI chromophores within each stack. Fig. 1b presents the optical absorption spectrum of bulk mX-PBI crystals vis-à-vis the solution (CHCl3) spectrum. We first focus on the broad absorption feature that appears below 500 nm. Despite the broadening, one can identify the poorly resolved 0–1 and higher vibronic features at 493, 465 and 439 nm, respectively. We note a significant drop in the 0–1 to 0–2 absorbance ratio (A0–1/A0–2 = 1.08 vs. 2.63 in CHCl3), along with a diminished 0–0 absorbance at 520 nm. While a transfer of oscillator strength from 0–0 to higher vibronic peaks is reminiscent of an H-type coupling, the full complexity of the absorption spectrum cannot be adequately described within the framework of dipolar coupling. This becomes obvious from the two new red-shifted peaks that appear at 543 and 577 nm. The origin of these peaks becomes clear in the context of PL results discussed subsequently. Upon photoexcitation, mX-PBI crystals emit a bright PL at 602 nm with a fairly small Stokes shift of 720 cm−1, and an overall spectral width that is comparable to that of solution PL from monomeric mX-PBI (Fig. S5†). Most importantly, the crystal spectrum exhibits a pronounced vibronic structure, indicating that the PL transition is strongly coupled to the 1030 cm−1 vibrational mode. It is evident that the emissive state of the mX-PBI crystal could not be a structurally relaxed excimer that would otherwise feature a broad, structureless PL spectrum with a much larger Stokes shift (∼3100 cm−1).9,10 We therefore assert that the PL transition in the mX-PBI crystal happens from the lowest energy exciton, which, owing to the rotationally displaced H-aggregated structure, has a non-zero transition probability. This is also consistent with the PL lifetime, which is an order of magnitude longer (∼30 ns, Fig. 1c and S6†) than that of the solution-state monomeric PL. To the best of our knowledge, this is the first ever report of achieving a long-lived excitonic PL emission from PBI H-aggregates under ambient conditions.‡In order to account for the unprecedented stability of the long-lived exciton in the mX-PBI crystal against an otherwise efficient self-trapping process, we focussed on the relative energies of the different states involved. Fig. 2a presents a simplified energy level diagram of a rotationally displaced H-aggregate, where exciton coupling between chromophores lifts the excited state degeneracy to create an upper (E2) and a lower exciton (E1) state. We tentatively assign the lowest energy absorption peak (577 nm) in mX-PBI crystals (Fig. 1b) to the E1 state. The unusually large red-shift indicates that the E1 state is significantly stabilized. Likewise, comparing the PL peak energy of the crystals against the transient Frenkel exciton PL from two reported PBI H-aggregates15 confirms that the relaxed E1 state of the mX-PBI crystal is indeed ∼80–100 meV lower in energy. Can such a large stabilization of the lower exciton state explain the suppression of excimer formation in mX-PBI crystals? We address this question in light of Engel, Engels and co-workers’ model that presented a comprehensive description of excimer formation in PBI H-aggregates.17,18 Self-trapping of E1 into the excimeric state (Eex) is an energetically downhill process, one that goes through a transient charge-transfer state (ECT). This key non-adiabatic transition from E1 to ECT happens across an avoided crossing between the two states, which requires the relative energies and potential energy surfaces (PESs) of the two states to be optimally matched. We note that the typical energy spread of E1 and ECT states for a generic PBI dye in the vicinity of relevant nuclear coordinates is in the order of 100 meV.17§ In such a scenario, lowering of E1 energy by 80–100 meV can significantly jeopardize the self-trapping process.
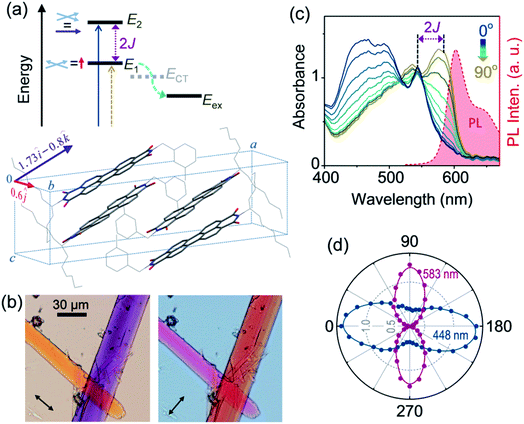
It is evident from Fig. 2a that the energy of the E1 state is directly linked to the magnitude of exciton splitting (2J) between two exciton states, and therefore to the strength of electronic coupling between chromophores. Though possible in principle, estimating 2J from the difference between E0 → E1 and E0 → E2 transition energies is not viable for most PBI H-aggregates, even when both exciton states are optically accessible. This is because the exciton bandwidth is often greater than 2J, which makes it difficult to resolve the two transitions in the optical absorption spectrum. However, it is possible to address these transitions individually by exploiting their polarization dependence. Fig. 2a also shows the transition dipole moments associated with E0 → E2 and E0 → E1 transitions, derived from the sum and difference of transition dipole moments of stacked PBI chromophores in the unit cell, respectively (Fig. S7†). We find that the transition to the lower exciton state is polarized exclusively along the b direction of the unit cell, while that to the upper exciton state has components along the a and c directions. A quick review of the noncovalent interactions further reveals that the a, b and c directions correspond to the thickness, width and length of the mX-PBI crystal, respectively (Fig. S8†). An interesting consequence of this is demonstrated in Fig. 2b, which presents two transmission optical micrographs of a pair of mX-PBI microcrystals using the white light of orthogonal polarizations. Since the light travelling through the crystal thickness (parallel to a axis) is polarized along either the b or the c direction, it interacts differently with the two crystals that are aligned approximately normal to each other, and transmits strikingly different colours. Specifically, the crystal with its long axis parallel to the electric field vector of light appears orange, while the one lying perpendicular to it is purple in colour. Quite remarkably, the two colours interchange once the polarization of light is switched by 90°. Such a large wavelength-dependent dichroism or pleochroism is of great interest in liquid crystal display applications. In the present context however, this observation clearly indicates that the two cross-polarized excitonic transitions absorb very different parts of the visible light, thus implying a large difference in their transition energies.
In order to quantify the observed pleochroism and estimate 2J, we carried out polarized absorption spectroscopy on a single mX-PBI microcrystal. As the polarization of incident light is rotated with respect to the crystal orientation, the absorption spectrum evolves in a manner consistent with the observed colour change (Fig. 2c). When the incident polarization is aligned with the long axis of the crystal (0°), a strong absorbance below 550 nm is seen. We note that the spectrum closely resembles the blue end of the unpolarized absorption spectrum for bulk crystals (Fig. 1b), with dominant peaks at 466 and 491 nm. One can additionally resolve the remnant of the 0–0 vibronic transition that appears as a considerably attenuated peak at 543 nm. In contrast, the spectrum measured with orthogonally polarized light (90°) is strongly red-shifted with peaks at 583 and 536 nm. As the polarization of light is rotated, the spectrum gradually changes from one to the other, with a quasi-isosbestic point at 518 nm. The distinct mirror-image relationship between the 90° absorption and crystal PL spectrum confirms that the same states are involved in the two transitions. From their respective energies and the knowledge of transition dipole moment orientations, we assign the 0° and 90° spectra to E0 → E2 and E0 → E1 transitions, respectively. That the two excitonic transitions are indeed cross-polarized is evident from the plot of their characteristic absorbances at 448 and 583 nm as a function of the polarization angle. We also note contrasting vibronic signatures for the two excitonic transitions. The E0 → E2 (0°) spectrum shows a strong H-type character with a considerably reduced A0–0/A0–1 ratio of 0.81, while the E0 → E1 (90°) spectrum has a relatively weaker H-character with a higher A0–0/A0–1 ratio of 1.15. Similar contrasting vibronic signatures have been reported in aggregates, where a combination of dominant long-range coulombic coupling and a relatively weaker short-range charge transfer interaction gives rise to an Hj-type coupling,19 as well as in systems where exciton-coupled chromophores are related through a C2 rotation.20 From the energy difference between the lowest-energy vibronic peaks of the two transitions at 543 and 583 nm, respectively, we estimate a 2J of ∼1265 cm−1. Such a large 2J is unprecedented among PBI aggregates, which typically feature a much smaller exciton splitting of 300 cm−1 or below.21 It is conceivable that a large splitting lowers the energy of the E1 state significantly, and renders the exciton self-trapping process ineffective. Recently, Spano and co-workers also reported a PBI crystal with a large exciton splitting of 1230 cm−1, albeit without any PL emission.22 A large exciton splitting results from a combination of short-range charge-transfer and long-range Coulomb interactions, a scenario that is also consistent with the Hj-type coupling discussed earlier.
It is worth noting that our conclusion about a large exciton splitting inhibiting excimer formation conflicts with the findings of Wasielewski and coworkers, who reported faster excimer formation kinetics in strongly coupled rigid PBI dimers.12,23 This apparent contradiction is presumably due to the fact that some of the rigid covalent dimers studied in their work have extremely low-lying excimer states (Eex ∼ 1.57–1.69 eV), unlike the majority of H-aggregated PBI self-assemblies where Eex is typically ∼1.95 eV. We believe that a coexistence of a very low energy excimer and exciton states on the same molecular unit makes the self-trapping process extremely efficient in dimers. Therefore, in the interest of suppressing exciton self-trapping and excimer formation, it seems reasonable to assume that an emissive exciton localized away from possible excimeric trap sites could offer some advantage. Our subsequent investigation into the intrinsic PL anisotropy of mX-PBI crystals indeed supports this idea.
In order to obtain a comprehensive description of various polarization effects associated with the PL of mX-PBI crystals, we recorded the full spectral PL Mueller matrix. The experiments were performed on a single mX-PBI microcrystal in exact backscattering collection geometry, following a method developed by Ghosh and coworkers.24,25 The elements of the 4 × 4 matrix were derived from sixteen separate measurements using different combinations of incident and emission polarization states (see the ESI† for details), and are presented in Fig. 3a. As opposed to the traditional PL anisotropy factor, PL Mueller matrix M allows one to separately account for the intrinsic and extrinsic contributions to the total anisotropy. This is possible because the PL Mueller matrix M can be empirically written as a direct product:26
| M = M1 × Md × M0 |
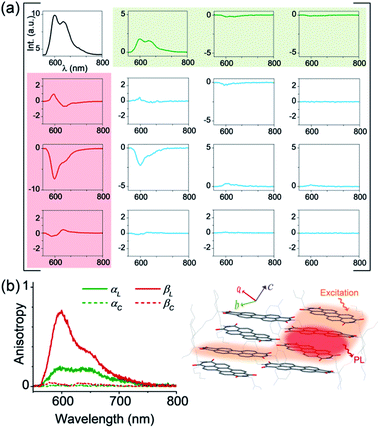 | ||
| Fig. 3 Intrinsic PL anisotropy. (a) Full spectral PL Mueller matrix (M) for a single mX-PBI crystal. The first row (shaded green) and first column (red) elements quantify ground (α) and excited state (β) anisotropies, respectively. The bottom-right 3 × 3 submatrix (blue curves) contains depolarization and phase retardation effects (see Fig. S9†). (b) The excited state linear anisotropy is significantly higher than that of the ground state (βL > αL), while βC and αC are ∼0. The schematic on the right illustrates the fate of the nascent exciton, which is initially delocalized over several PBIs along and across the π-stack (orange region), but eventually localizes to a much smaller (red) region from where the PL ensues. | ||
We note that the contributing terms to excitation and emission anisotropies are exclusively linear (αL, βL). A near-negligible magnitude of the circular anisotropy terms (αC, βC ∼ 0) is consistent with the lack of chirality in the crystal structure of mX-PBI. What is however striking is that the linear anisotropy in excitation is much smaller (αL ∼ 0.2) than what is expected for a single crystal with little or no orientational/organizational disorder. Interestingly, linear anisotropy in PL emission is significantly larger (βL ∼ 0.75). Since, the molecular arrangement does not change significantly upon photoexcitation, the observed increase in linear anisotropy may indicate a change in the degree of exciton delocalization. In the presence of strong interchromophoric coupling, the nascent exciton delocalizes over several molecular units. Within a strictly dipolar coupling picture (Kasha's model), the exciton wavefunction is expected to delocalize solely along the π-stack. However, taking into account the fact that PBI molecules from adjacent π-stacks in mX-PBI are as close as ∼3.2 Å apart (see Fig. S10†), there can be significant inter-stack charge-transfer interactions resulting from the overlap of their HOMO and LUMO.27,28 Such lateral interactions can further delocalize the exciton wavefunction and lower the polarization anisotropy of the excitation process (low αL). By the same argument, an increase in the emission anisotropy (high βL) would suggest a subsequent localization of the exciton wavefunction to a smaller and presumably a more linear segment of the aggregate, right before the onset of PL emission. Since the electronic transition in the mX-PBI crystal is strongly coupled to its vibrational mode, excitation is likely to cause a structural relaxation that can localize the exciton wavefunction. Such exciton self-localization processes are well documented in multichromophoric systems, including dye aggregates and conjugated polymers.29,30 We speculate that localized excitons are statistically less prone to encountering potential excimer trap sites, and are therefore more likely to participate in radiative recombination resulting in a long-lived PL.
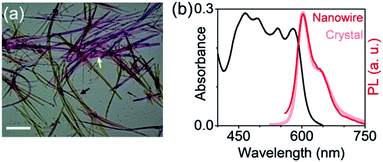
From a practical standpoint, stabilizing a long-lived exciton against excimer formation is far more relevant and desirable in solution-processed self-assemblies, than in molecular crystals. However, spontaneously assembled structures can be more disordered than slow-grown crystals, and thus more susceptible to self-trapping processes. It is therefore important to evaluate the emission characteristics of self-assembled mX-PBI. Fig. 4a presents a polarized optical micrograph of mX-PBI nanowires, assembled from a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v ethanol–CHCl3 mixture. Like the crystals, the wires too exhibit a strong pleochroism: orthogonally oriented wires show different colors in transmission. It is reasonable to infer that the molecular packing in wires is the same as that in the crystals, which allows a strong inter-PBI interaction, resulting in a large exciton splitting (2J). This is also supported by the absorption spectrum of nanowires (Fig. 4b), where transitions to lower and higher excitonic states can be clearly resolved. Finally, the narrow and vibronically resolved PL spectrum of the nanowires confirms that excimer formation is fully suppressed in the self-assembled mX-PBI.
1 v/v ethanol–CHCl3 mixture. Like the crystals, the wires too exhibit a strong pleochroism: orthogonally oriented wires show different colors in transmission. It is reasonable to infer that the molecular packing in wires is the same as that in the crystals, which allows a strong inter-PBI interaction, resulting in a large exciton splitting (2J). This is also supported by the absorption spectrum of nanowires (Fig. 4b), where transitions to lower and higher excitonic states can be clearly resolved. Finally, the narrow and vibronically resolved PL spectrum of the nanowires confirms that excimer formation is fully suppressed in the self-assembled mX-PBI.
Conclusions
In conclusion, we report a bright, ambient-stable and long-lived PL from the lowest energy exciton state of an H-aggregated PBI. The importance of this result can be judged in view of the fact that PBI H-aggregates are extremely vulnerable to a self-trapping process that rapidly depopulates their lowest excited state to form excimers. Our investigation unravels two critical factors that foil excimer formation in the present case, and provides a roadmap for future designs. An unusually large exciton splitting stabilizes the lowest energy exciton, thus preventing its crossover to the excimer state. In addition, the nascent exciton that is initially spread over several PBI units localizes rapidly to a smaller segment, and is thus shielded from possible trap sites. While both the factors are ultimately related to the molecular organization in the crystal, it is gratifying to note that achieving excimer free long-lived excitonic PL is not limited to carefully grown single crystals, but can also be realized in self-assembled nanowires grown from solution. Efforts to evaluate the performance of such long-lived excitons in transferring excitation energy over large distances are currently in progress.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge IISER Kolkata and the Department of Science and Technology (DST), India (Project: EMR/2014/000223) for financial support. We thank Dr R. Viswanatha (JNCASR) for PL lifetime measurements, Dr D. Haldar (IISER-K) for granting access to polarized optical microscope, and Niladri Modak and Nishkarsh Kumar (IISER-K) for additional PL Mueller matrix measurements. S. S. acknowledges the University Grants Commission (UGC) for providing a scholarship.Notes and references
- S. M. Menke, W. A. Luhman and R. J. Holmes, Nat. Mater., 2013, 12, 152 CrossRef CAS PubMed.
- G. D. Scholes, G. R. Fleming, A. Olaya-Castro and R. van Grondelle, Nat. Chem., 2011, 3, 763 CrossRef CAS PubMed.
- O. V. Mikhnenko, P. W. M. Blom and T.-C. Nguyen, Energy Environ. Sci., 2015, 8, 1867 RSC.
- T. Brixner, R. Hildner, J. Köhler, C. Lambert and F. Würthner, Adv. Energy Mater., 2017, 7, 1700236 CrossRef.
- H. Lin, R. Camacho, Y. Tian, T. E. Kaiser, F. Würthner and I. G. Scheblykin, Nano Lett., 2010, 10, 620 CrossRef CAS PubMed.
- K. A. Clark, E. L. Krueger and D. A. Vanden Bout, J. Phys. Chem. Lett., 2014, 5, 2274 CrossRef CAS PubMed.
- A. T. Haedler, K. Kreger, A. Issac, B. Wittmann, M. Kivala, N. Hammer, J. Köhler, H.-W. Schmidt and R. Hildner, Nature, 2015, 523, 196 CrossRef CAS PubMed.
- D. Chaudhuri, D. Li, Y. Che, E. Shafran, J. M. Gerton, L. Zang and J. M. Lupton, Nano Lett., 2011, 11, 488 CrossRef CAS PubMed.
- R. F. Fink, J. Seibt, V. Engel, M. Renz, M. Kaupp, S. Lochbrunner, H.-M. Zhao, J. Pfister, F. Würthner and B. Engels, J. Am. Chem. Soc., 2008, 130, 12858 CrossRef CAS PubMed.
- F. Würthner, C. R. Saha-Möller, B. Fimmel, S. Ogi, P. Leowanawat and D. Schmidt, Chem. Rev., 2016, 116, 962 CrossRef PubMed.
- J. M. Lim, P. Kim, M.-C. Yoon, J. Sung, V. Dehm, Z. Chen, F. Würthner and D. Kim, Chem. Sci., 2013, 4, 388 RSC.
- K. E. Brown, W. A. Salamant, L. E. Shoer, R. M. Young and M. R. Wasielewski, J. Phys. Chem. Lett., 2014, 5, 2588 CrossRef CAS PubMed.
- M. Son, K. H. Park, C. Shao, F. Würthner and D. Kim, J. Phys. Chem. Lett., 2014, 5, 3601 CrossRef CAS PubMed.
- R. J. Lindquist, K. M. Lefler, K. E. Brown, S. M. Dyar, E. A. Margulies, R. M. Young and M. R. Wasielewski, J. Am. Chem. Soc., 2014, 136, 14912 CrossRef CAS PubMed.
- J. Sung, P. Kim, B. Fimmel, F. Würthner and D. Kim, Nat. Commun., 2015, 6, 8646 CrossRef CAS PubMed.
- S. Samanta and D. Chaudhuri, J. Phys. Chem. Lett., 2017, 8, 3427 CrossRef CAS PubMed.
- A. Schubert, V. Settels, W. Liu, F. Würthner, C. Meier, R. F. Fink, S. Schindlbeck, S. Lochbrunner, B. Engels and V. Engel, J. Phys. Chem. Lett., 2013, 4, 792 CrossRef CAS PubMed.
- B. Engels and V. Engel, Phys. Chem. Chem. Phys., 2017, 19, 12604 RSC.
- A. Oleson, T. Zhu, I. S. Dunn, D. Bialas, Y. Bai, W. Zhang, M. Dai, D. R. Reichman, R. Tempelaar, L. Huang and F. C. Spano, J. Phys. Chem. C, 2019, 123, 20567 CrossRef CAS.
- K. A. Kistler, C. M. Pochas, H. Yamagata, S. Matsika and F. C. Spano, J. Phys. Chem. B, 2012, 116, 77 CrossRef CAS PubMed.
- J. Mizuguchi and K. Tojo, J. Phys. Chem. B, 2002, 106, 767 CrossRef CAS.
- A. Austin, N. J. Hestand, I. G. McKendry, C. Zhong, X. Zhu, M. J. Zdilla, F. C. Spano and J. M. Szarko, J. Phys. Chem. Lett., 2017, 8, 1118 CrossRef PubMed.
- J. M. Giaimo, J. V. Lockard, L. E. Sinks, A. M. Scott, T. M. Wilson and M. R. Wasielewski, J. Phys. Chem. A, 2008, 112, 2322 CrossRef CAS PubMed.
- S. Satapathy, J. Soni and N. Ghosh, Appl. Phys. Lett., 2014, 104, 131902 CrossRef.
- S. Saha, J. Soni, S. Chandel, U. Kumar and N. Ghosh, J. Biomed. Opt., 2015, 20, 085005 CrossRef PubMed.
- O. Arteaga, S. Nichols and B. Kahr, Opt. Lett., 2012, 37, 2835 CrossRef PubMed.
- F. Würthner, Chem. Commun., 2004, 1564 RSC.
- N. J. Hestand and F. C. Spano, Acc. Chem. Res., 2017, 50, 341 CrossRef CAS PubMed.
- S. Tretiak, A. Saxena, R. L. Martin and A. R. Bishop, Phys. Rev. Lett., 2002, 89, 097402 CrossRef CAS PubMed.
- K. Becker, E. Da Como, J. Feldmann, F. Scheliga, E. Thorn Csányi, S. Tretiak and J. M. Lupton, J. Phys. Chem. B, 2008, 112, 4859 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental methods, synthesis and characterization, additional figures and CIF. CCDC 1967792. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc01784a |
| ‡ Ref. 8 reported a long-lived excitonic PL in H-aggregated PBI, but at extremely low temperatures (∼4 K), and the origin of the excitonic PL was not investigated. |
| § The polarizable environment of larger PBI aggregates can increase the energy gap between E1 and CT states beyond 0.1 eV, as shown in ref. 18. However, the 0.1 eV energy gap obtained from the dimer model of ref. 17 agrees well with our results. |
| This journal is © The Royal Society of Chemistry 2020 |