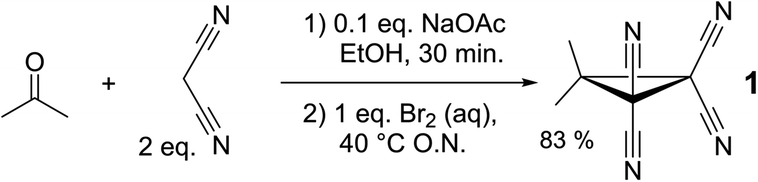Open Access Article
Open Access ArticleObservations of tetrel bonding between sp3-carbon and THF†
Victoria L.
Heywood
b,
Thomas P. J.
Alford
b,
Julius J.
Roeleveld
a,
Siebe J.
Lekanne Deprez
a,
Abraham
Verhoofstad
a,
Jarl Ivar
van der Vlugt
 ac,
Sérgio R.
Domingos
ac,
Sérgio R.
Domingos
 d,
Melanie
Schnell
d,
Melanie
Schnell
 de,
Anthony P.
Davis
de,
Anthony P.
Davis
 b and
Tiddo J.
Mooibroek
b and
Tiddo J.
Mooibroek
 *a
*a
avan 't Hoff Institute for Molecular Sciences, Universiteit van Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands. E-mail: t.j.mooibroek@uva.nl
bSchool of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK
cInstitute of Chemistry, Carl von Ossietzky University Oldenburg, Carl-von-Ossietzky-Straße 9-11, D-12629 Oldenburg, Germany
dDeutsches Elektronen-Synchrotron (DESY), Notkestraße 85, 22607 Hamburg, Germany
eInstitut für Physikalische Chemie, Christian-Albrechts-Universität zu Kiel, Max-Eyth-Str. 1, 24118 Kiel, Germany
First published on 7th May 2020
Abstract
We report the direct observation of tetrel bonding interactions between sp3-carbons of the supramolecular synthon 3,3-dimethyl-tetracyanocyclopropane (1) and tetrahydrofuran in the gas and crystalline phase. The intermolecular contact is established via σ-holes and is driven mainly by electrostatic forces. The complex manifests distinct binding geometries when captured in the crystalline phase and in the gas phase. We elucidate these binding trends using complementary gas phase quantum chemical calculations and find a total binding energy of −11.2 kcal mol−1 for the adduct. Our observations pave the way for novel strategies to engineer sp3-C centred non-covalent bonding schemes for supramolecular chemistry.
Introduction
Non-covalent interactions are key forces that drive phenomena such as host–guest chemistry, molecular aggregation, crystallization and protein folding.1,2 In recent years, important intermolecular interactions like hydrogen and halogen bonding1,3–7 have been contextualized as σ-hole interactions.8–10 A σ-hole can be seen as a Lewis acidic site along the vector of a covalent bond, the location of which coincides with the σ* orbital of that bond. The extreme outcome of a σ-hole interaction can be the breaking and/or making of a σ bond, such as in the formation of I3− from molecular I2 and I−.11,12 A similar rationale can be applied to so-called ‘π-hole interactions’ involving electron-deficient aromatic rings,13,14 or polarized double bonds with related covalent bond-forming chemistry such as in aldol-type reactions. In principle, σ- and π-hole interactions should be available with all the non-metallic elements of the periodic table. This includes carbon;15–17 an element of central importance to life and ubiquitous presence in synthetic chemistry.One might thus wonder to what extend carbon can be exploited as locus of Lewis acidity to establish ‘tetrel-bonding interactions’ (in analogy to halogen- and chalcogen-bonds).18 Such interactions are well-known for sp2-hybridized C-atoms in carbonyls19–26 and have recently been reported for the sp-hybridized C-atoms of (coordinated) acetonitrile,27 carbon monoxide28 and carbon dioxide.29–32 Non-covalent interactions with sp3-hybridized carbon atoms are implicated in the advent of canonical SN2 nucleophilic displacement reactions12,33–35 and can persist with methyl groups in crystal structures.36–38
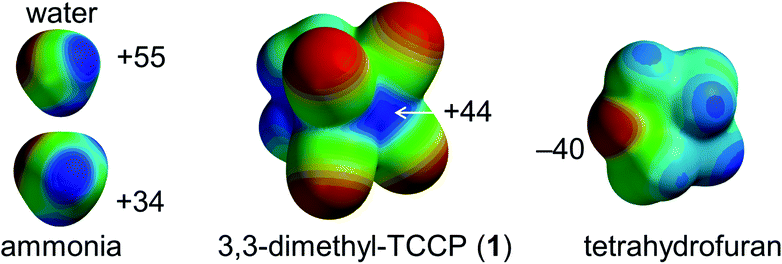
However, a supramolecular synthon to predictably generate directional tetrel-bonding interactions centred on sp3-C has not yet been experimentally disclosed. We envisaged that 1,1,2,2-tetracyanocyclopropane (TCCP) derivatives could fulfil this role.39,40 These rings are synthetically viable and contain a sterically accessible electrophilic site located roughly on the two sp3 C-atoms in the (NC)2C–C(CN)2 fragment. This is exemplified by the molecular electrostatic potential (MEP) map of 3,3-dimethyl-TCCP (1) shown in Fig. 1. The calculated σ-hole potential of +44 kcal mol−1 lies in-between the σ-holes of water (+55 kcal mol−1) and ammonia (+35 kcal mol−1), which are prototypical σ-hole (i.e. hydrogen bond) donors. The Lewis acidic site of 1 should thus be able to form a tetrel bonding interaction with an electron-rich partner such as the lone pair electron cloud on tetrahydrofuran (THF, estimated at −40 kcal mol−1).39–41 Here we report on the verification of this hypothesis by synthesizing 1 and showing that – as anticipated – 1 binds to THF via intermolecular sp3-C⋯O interactions, both in the crystalline state and in the gas phase.
Results and discussion
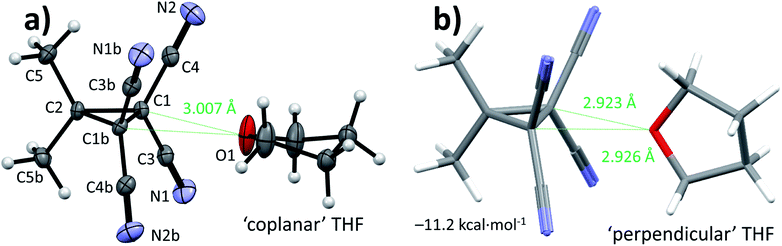
Cyclopropane 1 was readily prepared in a one-pot cascade reaction from acetone, malononitrile and molecular bromine (Scheme 1). Presumably, cyclization to 1 proceeds from an intermediate formed by the nucleophilic attack of in situ generated [BrC(CN)2]− on the Knoevenagel condensation product of acetone and malononitrile.42 The yield of our procedure (83%) is higher than obtained by previously reported methods42–48 (max. 72%).47 All literature procedures with a yield in excess of 50%42,43,45–48 (maximum 72%)47 use a two-step approach starting from an activated malononitrile derivative42,43,45–47 and/or use electrochemical synthesis.47,48Single crystals suitable for X-ray diffraction measurements (see ESI† for details) were obtained by slow evaporation of a solution of 1 in THF. The molecular model of [1⋯THF] resulting from the diffraction study is shown in Fig. 2a. All the intramolecular distances and angles within this structure can be considered as normal (not shown).49 The plane running through the O- and C-atoms of the THF molecule is roughly coplanar with the cyclopropane ring plane in 1 (∠plane–plane = 8.2°). Interestingly, the oxygen atom of the THF molecule is directed towards C1/C3/C4 of the cyclopropane ring in 1, with very short intermolecular distances, in particular sp3-C1⋯O1 of 3.007 Å (C3/C4 ⋯O1 = 3.1 Å, not shown). This is 0.213 Å within the van der Waals radii of O (1.52 Å) and C (1.70 Å) and thus consistent with a bonding interaction.12,27,39,40,50 Further stacking of [1⋯THF] in the crystal is aided by weak N1/N2⋯C1/C3/C4 interactions (max. 0.067 Å van der Waals overlap, see Fig. S3†).‡
A DFT optimization at the B3LYP51,52-D3(BJ)53/def2-TZVP54,55 level of theory of the atomic coordinates found in the crystal structure converged at a nearly identical structure (see Fig. S5†). The interaction energy (ΔE) was computed to be −10.1 kcal mol−1. This is much larger than interactions of dimethyl ether halogen bonded to I–C6F5 (−5.6 kcal mol−1) or hydrogen bonded to water (−6.7 kcal mol−1) at this same level of theory.37,56 Interestingly, the [1⋯THF] structure shown in Fig. 2b was found to be 1.1 kcal mol−1 more stable, representing the true energetic minimum with ΔE = −11.2 kcal mol−1 (see also Fig. S6†). The structure is similar to the crystal structure but with the THF oriented almost perpendicular to the cyclopropane plane, with ∠plane–plane = 83.8°. The distances between the THF-O and the two sp3 (NC)2C–C(CN)2 atoms display up to 0.297 Å van der Waals overlap, which is 0.084 Å more than observed in the crystal structure. This difference likely originates from the lack of any other interactions in the idealized gas phase computation versus various other potential weak interactions within the crystal of [1⋯THF].
Rotational spectroscopy is the technique to experimentally discriminate between the two relative orientations of [1⋯THF] (Fig. 2) that are so close in energy in the gas phase calculations (1.1 kcal mol−1). Thus, we conducted chirped pulse Fourier transform microwave (CP-FTMW) spectroscopy57,58 to assign the geometry of [1⋯THF] in the gas phase (see ESI† for details). Shown in Table 1 are spectroscopic parameters extracted from this experiment together with predicted values based on DFT calculations of [1⋯THF] with ‘coplanar’ or ‘perpendicular’ THF orientations. The experimental rotational constants (in particular B and C) provide a conclusive assignment of the [1⋯THF] complex in the ‘perpendicular’ orientation, which is also the DFT-energetic minimum (right-hand side of Fig. 2).
| Experimentb | DFTc | ||
|---|---|---|---|
| Coplanar | Perpendicular | ||
| a For the purpose of structure determination of the [1⋯THF] adduct in the gas phase, the hyperfine structure observed in the rotational spectrum has not been fitted entirely and only centre frequencies are used for the reported fit. As such the quadrupole coupling constants for the four nitrogen nuclei are not reported at this moment. This second layer of analysis of the spectrum goes beyond the scope of this work and will be reported later in a separate manuscript. b The errors for the measured values are standard errors. The experimental frequency accuracy is 25 kHz. c The predicted rotational constants were obtained from a DFT calculation at the B3LYP-D3(BJ)/def2-TZVP level of theory. ‘Coplanar’ and ‘perpendicular’ refer to the orientation of the THF ring relative to the cyclopropane ring in 1 (see also Fig. 1). d Number of lines included in the fit. e Standard deviation of the fit. | |||
| A/MHz | 632.927(43) | 633.88 | 635.59 |
| B/MHz | 342.56932(93) | 326.09 | 341.81 |
| C/MHz | 316.7863(10) | 325.50 | 317.89 |
| D J/kHz | 0.0135(35) | — | — |
| |μa|/D | Observed | 2.6 | 2.6 |
| |μb|/D | Not observed | 0.0 | 0.0 |
| |μc|/D | Not observed | 0.0 | 0.0 |
| N | 46 | — | — |
| σ/kHze | 22.1 | — | — |
| ΔE (kcal mol−1)c | — | +1.1 | 0 |
To date we were unable to quantify tetrel bonding interactions with 1 in solution, but we did observe a very large and unusual solvent dependency for the 1H and 13C NMR resonances of 1 (detailed in Fig. S7 and Table S4†). For example, the methyl protons of 1, which are γ to CN, span a range of 1.39 ppm passing from benzene through toluene, acetonitrile, methanol and chloroform, to acetone. In comparison, the ethoxy methyl protons in ethyl acetate and diethyl ether vary by just 0.34 and 0.12 ppm, despite being closer to functional groups.64 These results seem to suggest strong and geometrically specific interactions between 1 and most solvent molecules. Based on these preliminary observations, we anticipate that future studies will demonstrate that tetrel bonding interactions with tetracyanocyclopropane derivatives also persist in solution.
To gain more insight into the physical origins of the [1⋯THF] adduct, the ‘perpendicular’ structure was subjected to a Morokuma–Ziegler inspired energy decomposition,37,59–61 an ‘atoms-in-molecules’,62 and a non-covalent interaction analysis.63 The energy decomposition analysis revealed that the interaction is mainly electrostatic in origin (52.7%) followed by dispersion (30.7%) and orbital interactions (16.8%). Interestingly, orbital mixing occurred between the HOMO of THF and the LUMO of 1 (−3.86 kcal mol−1 stabilization) and between the HOMO−1 of THF and the HOMO of 1 (−4.80 kcal mol−1 stabilization, see Fig. S8† for details). The ‘atoms-in-molecules’ analysis of [1⋯THF] shown in Fig. 3a reveals several bond critical points (bcp's) between the N-atoms of 1 and several CH hydrogens of THF, indicating very weak hydrogen bonding interactions (ρ ≈ 0.005 a.u.). The densest bcp of ρ = 0.0115 a.u. is present between the THF O-atom and one of the sp3 (NC)2C–C(CN)2 atoms (highlighted in yellow).§ In line with these results, the NCI plot shown in Fig. 3b clearly reveals that there are two sp3-C⋯O interactions that are mainly electrostatic in origin (blue), and that the C–H⋯N interactions are mainly dispersive (yellow/green).
 | ||
| Fig. 3 Geometry optimized structures (B3LYP-D3/def2-TZVP) and ‘atoms-in-molecules’ analysis of [1⋯THF] (a, see also Fig. 2) and [1···cyclopentane] (c, obtained after in silico O → CH2 mutation and optimization). The bond densities of the intermolecular bond critical points are represented by small red spheres (ρ in a.u. ×100). (b) and (d) show a non-covalent interactions (NCI) analysis using NCIPLOT. Isolevel = 0.3 and regions in blue are mainly electrostatic interactions, in green are van der Waals dispersive forces and repulsions are in red. | ||
For comparison purposes, a cyclopentane adduct was calculated after in silico O → CH2 mutation and geometry optimization of structure [1⋯THF]. This resulted in the structurally similar [1···cyclopentane] adduct shown in Fig. 3c (see also Fig. S9†). The ‘atoms-in-molecules’ analysis of this adduct reveals only two C–H⋯C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bcp's (ρ ≈ 0.0055 a.u.). The adduct is also much less stable with ΔE = −4.0 kcal mol−1, which is mainly driven by dispersion (59.4%) followed by electrostatic interactions (22.2%). The NCI analysis of this adduct depicted in Fig. 3d clearly shows that this adduct is only held by dispersive C–H⋯N interactions (green).
N bcp's (ρ ≈ 0.0055 a.u.). The adduct is also much less stable with ΔE = −4.0 kcal mol−1, which is mainly driven by dispersion (59.4%) followed by electrostatic interactions (22.2%). The NCI analysis of this adduct depicted in Fig. 3d clearly shows that this adduct is only held by dispersive C–H⋯N interactions (green).
Summary and concluding remarks
In summary, it was shown that 1 can form [1⋯THF] complexes in the crystalline state and in the gas phase with a calculated interaction energy of up to −11.2 kcal mol−1. These complexes are held together by strong polar interactions between the de facto Lewis acidic site in between the sp3-hybridized C-atoms of 1 and the Lewis basic THF-O. These results demonstrate that tetrel-bonding interactions with sp3-carbon centres can indeed be used to engineer supramolecular complexes, thus paving the way for their exploration in other molecular disciplines, e.g. supramolecular chemistry, crystal engineering and medicine.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
TJM thanks NWO (VIDI project 723.015.006) and the EPSRC (EP/I028501/1) for funding. MS acknowledges financial support by the Deutsche Forschungsgemeinschaft in the context of the priority program SPP1807 (SCHN1280/4-2).Notes and references
- P. J. Cragg, Supramolecular Chemistry: From Biological Inspiration to Biomedical Applications, Springer, Dordrecht, 1 edn, 2010 Search PubMed.
- A. Bauza, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517 CrossRef CAS PubMed.
- H. J. Schneider, Supramolecular Systems in Biomedical Fields, RSC Publishing, Cambridge, UK, 1 edn, 2013 Search PubMed.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386–395 CrossRef CAS PubMed.
- Hydrogen Bonding: New Insights, ed. S. J. Grabowski, Springer, Heidelberg, 2006 Search PubMed.
- M. R. Scholfield, C. M. Vander Zanden, M. Carter and P. S. Ho, Protein Sci., 2013, 22, 139–152 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and P. Lane, Int. J. Quantum Chem., 2007, 107, 3046–3052 CrossRef CAS.
- S. J. Grabowski, Phys. Chem. Chem. Phys., 2013, 15, 7249–7259 RSC.
- S. Scheiner, Acc. Chem. Res., 2013, 46, 280–288 CrossRef CAS PubMed.
- R. H. Crabtree, Chem. Soc. Rev., 2017, 46, 1720–1729 RSC.
- A. Bauza, T. J. Mooibroek and A. Frontera, Chem. Rec., 2016, 16, 473–487 CrossRef CAS PubMed.
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- B. L. Schottel, H. T. Chifotides and K. R. Dunbar, Chem. Soc. Rev., 2008, 37, 68–83 RSC.
- S. J. Grabowski, Chem.–Eur. J., 2013, 19, 14600–14611 CrossRef CAS PubMed.
- J. S. Murray, P. Lane and P. Politzer, J. Mol. Model., 2009, 15, 723–729 CrossRef CAS PubMed.
- A. Bauza, T. J. Mooibroek and A. Frontera, ChemPhysChem, 2015, 16, 2496–2517 CrossRef CAS PubMed.
- C. B. Aakeroy, D. L. Bryce, G. Desiraju, A. Frontera, A. C. Legon, F. Nicotra, K. Rissanen, S. Scheiner, G. Terraneo, P. Metrangolo and G. Resnati, Pure Appl. Chem., 2019, 91, 1889–1892 CAS.
- P. Murrayrust, H. B. Burgi and J. D. Dunitz, J. Am. Chem. Soc., 1975, 97, 921–922 CrossRef CAS.
- H. B. Burgi, Angew. Chem., Int. Ed., 1975, 14, 460–473 CrossRef.
- M. Harder, B. Kuhn and F. Diederich, ChemMedChem, 2013, 8, 397–404 CrossRef CAS PubMed.
- G. J. Bartlett, A. Choudhary, R. T. Raines and D. N. Woolfson, Nat. Chem. Biol., 2010, 6, 615–620 CrossRef CAS PubMed.
- P. H. Maccallum, R. Poet and E. J. Milnerwhite, J. Mol. Biol., 1995, 248, 374–384 CAS.
- A. Choudhary, D. Gandla, G. R. Krow and R. T. Raines, J. Am. Chem. Soc., 2009, 131, 7244–7246 CrossRef CAS PubMed.
- R. W. Newberry, G. J. Bartlett, B. VanVeller, D. N. Woolfson and R. T. Raines, Protein Sci., 2014, 23, 284–288 CrossRef CAS PubMed.
- E. C. Vik, P. Li, P. J. Pellechia and K. D. Shimizu, J. Am. Chem. Soc., 2019, 141, 16579–16583 CrossRef CAS PubMed.
- A. R. van der Werve, Y. R. van Dijk and T. J. Mooibroek, Chem. Commun., 2018, 54, 10742–10745 RSC.
- M. T. Doppert, H. van Overeem and T. J. Mooibroek, Chem. Commun., 2018, 54, 12049–12052 RSC.
- Y. P. Zeng, S. W. Sharpe, S. K. Shin, C. Wittig and R. A. Beaudet, J. Chem. Phys., 1992, 97, 5392–5402 CrossRef CAS.
- A. C. Legon, Phys. Chem. Chem. Phys., 2017, 19, 14884–14896 RSC.
- S. Gao, D. A. Obenchain, J. C. Lei, G. Feng, S. Herbers, Q. Gou and J. U. Grabow, Phys. Chem. Chem. Phys., 2019, 21, 7016–7020 RSC.
- M. Juanes, R. T. Saragi, W. Caminati and A. Lesarri, Chem.–Eur. J., 2019, 25, 11402–11411 CrossRef CAS PubMed.
- J. Langer, S. Matejcik and E. Illenberger, Phys. Chem. Chem. Phys., 2000, 2, 1001–1005 RSC.
- J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Lourderaj, J. X. Zhang, W. L. Hase, M. Weidemuller and R. Wester, Science, 2008, 319, 183–186 CrossRef CAS PubMed.
- S. Pierrefixe, J. Poater, C. Im and F. M. Bickelhaupt, Chem.–Eur. J., 2008, 14, 6901–6911 CrossRef CAS PubMed.
- V. R. Mundlapati, D. K. Sahoo, S. Bhaumik, S. Jena, A. Chandrakar and H. S. Biswal, Angew. Chem., Int. Ed., 2018, 57, 16496–16500 CrossRef CAS PubMed.
- T. J. Mooibroek, Molecules, 2019, 24, 3370 CrossRef CAS PubMed.
- J. Dutta, D. Kumar Sahoo, S. Jena, K. D. Tulsiyan and H. S. Biswal, Phys. Chem. Chem. Phys., 2020, 22, 8988–8997 RSC.
- A. Bauza, A. Frontera and T. J. Mooibroek, Phys. Chem. Chem. Phys., 2016, 18, 1693–1698 RSC.
- A. Bauza, T. J. Mooibroek and A. Frontera, Chem.–Eur. J., 2014, 20, 10245–10248 CrossRef CAS PubMed.
- A. Bauza, T. J. Mooibroek and A. Frontera, Phys. Chem. Chem. Phys., 2014, 16, 19192–19197 RSC.
- A. N. Vereshchagin, M. N. Elinson, N. O. Stepanov and G. I. Nikishin, Mendeleev Commun., 2009, 19, 324–325 CrossRef CAS.
- R. Huisgen and G. Mloston, Heterocycles, 1990, 30, 737–740 CrossRef CAS.
- K. Kouno and Y. Ueda, Chem. Pharm. Bull., 1985, 33, 3998–4001 CrossRef CAS.
- H. Hart and Y. C. Kim, J. Org. Chem., 1966, 31, 2784–2789 CrossRef CAS.
- R. Huisgen, G. Mloston and E. Langhals, Helv. Chim. Acta, 2001, 84, 1805–1820 CrossRef CAS.
- M. N. Elinson, S. K. Feducovich, T. L. Lizunova and G. I. Nikishin, Tetrahedron, 2000, 56, 3063–3069 CrossRef CAS.
- G. I. Nikishin, M. N. Elinson, T. L. Lizunova and B. I. Ugrak, Tetrahedron Lett., 1991, 32, 2655–2656 CrossRef CAS.
- F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, J. Chem. Soc., Perkin Trans. 2, 1987, S1–S19 RSC.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–452 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- J. M. Hoffmann, A. K. Sadhoe and T. J. Mooibroek, Synthesis, 2020, 52, 521–528 CrossRef CAS.
- G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, Rev. Sci. Instrum., 2008, 79, 053103 CrossRef PubMed.
- S. R. Domingos, K. Martin, N. Avarvari and M. Schnell, Angew. Chem., Int. Ed., 2019, 58, 11257–11261 CrossRef CAS PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, Vol 15, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-Vch, Inc, New York, 2000, vol. 15, pp. 1–86 Search PubMed.
- S. C. C. van der Lubbe and C. F. Guerra, Chem.–Asian J., 2019, 14, 2760–2769 CAS.
- R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS.
- J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. T. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef CAS PubMed.
- G. R. Fulmer, A. J. M. Miller, N. H. Sherden, H. E. Gottlieb, A. Nudelman, B. M. Stoltz, J. E. Bercaw and K. I. Goldberg, Organometallics, 2010, 29, 2176–2179 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1983293. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc01559h |
| ‡ Attempts to co-crystallize 1 with various n-butylammonium salts were unsuccessful. However, cryospray ionization high resolution mass spectrometry of solutions of 1 and various n-butylammonium salts (Cl−, Br−, NO3−, PF6−) in CH2Cl2 unambiguously revealed the corresponding [M+anion]− ions (Fig. S4,† top). All four adducts were calculated to be energetically stable by about −13 to −24 kcal mol−1 (Fig. S4,† bottom). |
| § The bond path is actually directed in between the two sp3 C-atoms and only steeply curves to one of the C-atoms nearby the atoms. |
| This journal is © The Royal Society of Chemistry 2020 |