Open Access Article
Open Access ArticleTuning reactivity layer-by-layer: formic acid activation on Ag/Pd(111)†
Mustafa
Karatok
 a,
Kaining
Duanmu
a,
Kaining
Duanmu
 b,
Christopher R.
O'Connor
b,
Christopher R.
O'Connor
 a,
Jorge Anibal
Boscoboinik
a,
Jorge Anibal
Boscoboinik
 c,
Philippe
Sautet
c,
Philippe
Sautet
 bd,
Robert J.
Madix
bd,
Robert J.
Madix
 e and
Cynthia M.
Friend
e and
Cynthia M.
Friend
 *ae
*ae
aDepartment of Chemistry and Chemical Biology, Harvard University, Cambridge, MA 02138, USA. E-mail: friend@fas.harvard.edu
bDepartment of Chemical and Biomolecular Engineering, University of California, Los Angeles, California 90095, USA
cCenter for Functional Nanomaterials, Brookhaven National Laboratory, Upton, NY 11973, USA
dDepartment of Chemistry and Biochemistry, University of California, Los Angeles, California 90095, USA
eJohn A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138, USA
First published on 20th April 2020
Abstract
The potential for tuning the electronic structure of materials to control reactivity and selectivity in heterogenous catalysis has driven interest in ultrathin metal films which may differ from their bulk form. Herein, a 1-atomic layer Ag film on Pd(111) (Ag/Pd(111)) is demonstrated to have dramatically different reactivity towards formic acid compared to bulk Ag. Formic acid decomposition is of interest as a source of H2 for fuel cell applications and modification of Pd by Ag reduces poisoning by CO and increases the selectivity for H2 formation. Formic acid reacts below room temperature on the 1-atomic layer Ag film, whereas no reaction occurs on pristine bulk Ag. Notably, 2 monolayer films of Ag again become unreactive towards formic acid, indicating a reversion to bulk behavior. A combination of infrared reflection absorption spectroscopy (IRRAS), X-ray photoelectron spectroscopy (XPS) and density functional theory (DFT) was used to establish that the Ag monolayer is continuous and electronically modified compared to bulk Ag. The work establishes a demonstration of the altered electronic structure of Ag monolayers on Pd(111) and an associated change in reactivity. The effect on reactivity only persists for the first layer, demonstrating the need for precise control of materials to exploit the modification in electronic properties.
Introduction
Bimetallic catalysts often have different chemical properties to their individual parent metals, exhibiting enhanced reactivity, selectivity and stability for many reactions.1–4 Two main factors considered in describing the properties of bimetallic systems are so-called “ligand” and “strain” effects both of which alter the electronic structure of the catalyst material. A ligand effect refers to the modification of the local electronic structure due to bonding to the second metal. Strain effects arise because of differences in the bond lengths of the two atoms in bulk form, potentially leading to strain between dissimilar atoms. Both of these electronic effects can contribute to significant changes in bonding to reactants that can also alter chemical properties. These factors can play a role in determining chemical behaviour of bimetallic materials, including ultrathin films of one metal on another.Stimulated by the interest in tuning electronic properties, there has been tremendous effort to understand the nature of the electronic and chemical properties of ultrathin metal films.5–9 The electronic alteration of some of these metal films was demonstrated both experimentally,10,11 and theoretically12,13 and in some cases a strong correlation between the surface electronic structure and the binding energy of adsorbates was demonstrated.1 For example, the Pd 3d core level binding energies are shifted to higher binding energy by 0.3–0.9 eV for one layer of Pd on Ta, W, Re, and Ru relative to bulk Pd, indicating a change in electronic structure.1 The binding strength of CO on these structures decreases in concert with the increasing core level shift, likewise suggesting differences in the surface electronic structure of monolayer vs. bulk Pd.1 Changes in CO binding to transition metals has often been related to changes in the d-band centre due to both ligand and strain effects.14
Silver is an important material in catalytic reactions, especially for partial oxidation. Therefore, the surface chemistry of Ag has been extensively studied.15–17 Silver has a low inherent reactivity towards organic molecules, because of the low density of states near the Fermi level and the low d band center.12 At the same time, once reaction is initiated on Ag by, for example, adsorbed oxygen or by a second metal, selectivity is generally high.
The reactions of formic acid are a topic of current interest because it is a promising hydrogen storage material and a source of H2 for fuel cell applications and Ag shows promise for improvement of catalytic performance.18,19 Core–shell nanoparticles with a Ag core and Pd shell have specifically been shown to be excellent catalysts for H2 production from formic acid, selectively yielding H2 and CO2 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio with no CO formation.19 Carbon monoxide is formed via a dehydration pathway that decreases selectivity. It also strongly binding to and, therefore, poisons the catalyst.
1 ratio with no CO formation.19 Carbon monoxide is formed via a dehydration pathway that decreases selectivity. It also strongly binding to and, therefore, poisons the catalyst.
Previous theoretical studies of Pd layers on Ag(111) investigated changes in reaction selectivity once formate is formed for various structures.44 The selectivity for formation of CO2 and H2 relative to CO and H2O is strongly influenced by the number of Pd layers on the Ag due to changes in the electronic structure near the Fermi level as a consequence of both strain and ligand effects.
The previous DFT models did not allow for reconstruction of the Pd/Ag(111), which has been shown to facilely rearrange so that Ag caps the Pd.20 This raises questions about the potential for contributions of Ag-capped Pd structures to formic acid decomposition in the catalytic system. Formic acid does not react on pristine Ag; adsorbed O is required to initiate reaction. On the other hand, formic acid readily decomposes on clean Pd, yielding CO2, CO, H2O, and H2. The reactions of formic acid have been widely studied on transition metals,21–25 and formate is generally formed in the first step, including on Pd(111),24 and O-covered Ag.26
Herein, reaction of formic acid on a 1-layer thick continuous Ag film deposited on Pd(111) is demonstrated, indicating that the silver electronic structure is strongly influenced by the underlying Pd. A continuous, two-dimensional Ag layer forms on Pd(111) after deposition at room temperature, as previously reported,27 rendering this an ideal system for understanding nanoparticle performance. The modification of the electronic structure of the Ag monolayer is further indicated by a core level shift in the Ag 3d5/2 peak and by density functional theory (DFT) calculations. Interestingly, thicker Ag overlayers (2 monolayers or higher) exhibit no electronic alteration and are inert to reaction with formic acid. These results reveal a clear correlation between the surface electronic structure and reactivity of Ag for initiation of formic acid decomposition while also demonstrating that it is highly localized to one atomic layer.
Methods
Experimental methods
Temperature-programmed reaction spectroscopy (TPRS) experiments were performed in an ultrahigh vacuum (UHV) chamber with a background pressure <2.0 × 10−10 torr, equipped with a quadrupole mass spectrometer (QMS; Hiden RGA) and an Auger electron spectrometer (AES) (PHI, Model 15-155). The single crystal is radiatively heated using a thoriated tungsten filament located behind the sample. The heating rate was controlled using a proportional-integral-derivative (PID) controller (Eurotherm Controls Inc., Model 2404) so as to maintain a constant heating rate of 1 K s−1 in all temperature programmed experiments. The sample temperature was measured using a K-type thermocouple inserted into a pinhole near the edge of the Pd(111) single crystal.The Pd(111) single crystal (Surface Preparation Laboratory, 10 mm diameter × 1.7 mm thick disk, 6 N purity) was cleaned by several cycles of Ar+ sputtering (Ar(g), 99.9999% purity, Matheson; PHI, Model 161-5-251, 1.0 kV × 20 mA) followed by annealing to 950 K for 5 min. An electron beam evaporator (Omicron, EFM3) was used to deposit Ag (∼0.25 ML min−1) on the clean Pd(111) surface at 300 K using a silver rod (Surepure Chemetals Inc., 99.99% purity, 2.0 mm diameter). The amount of Ag deposited on the Pd(111) was estimated based on the Ag/Pd ratio measured by AES, as described in detail in the ESI.†
Formic acid (Sigma-Aldrich, purity ≥ 98%) was dried in a glass bulb with anhydrous CaSO4 and purified by several freeze–pump–thaw cycles prior to dosing via a leak valve. In all of the TPRS experiments, 0.03 L of formic acid exposure was used which was the lowest exposure to achieve a saturation coverage of formic acid on Pd(111). Formic acid purity was checked by the fragmentation signals in gas phase along with water signal (m/z = 18) via a quadrupole mass spectrometer.
X-ray photoelectron spectroscopy (XPS) and infrared reflection absorption spectroscopy (IRRAS) measurements were performed at the Center for Functional Nanomaterials (CFN) at Brookhaven National Laboratory using a UHV system with three interconnected chambers for AP-XPS, IRRAS, and sample preparation (metal deposition, ion sputtering and annealing), respectively. All X-ray photoelectron data were obtained at room temperature using a SPECS PHOIBOS NAP 150 hemispherical analyser and a monochromatic Al Kα X-ray source (1486.6 eV, ∼0.25 eV linewidth) focused on the sample surface to a spot size <300 mm (0.05 eV step, 5 scan, 0.1 s dwell time, 50 pass energy; FWHM for Ag 3d5/2 and Pd 3d5/2 is 0.95 and 1.26, respectively). The binding energies were all calibrated relative to the Fermi level.
The Ag(111) single crystal used in XPS measurements (Surface Preparation Laboratory, 10 mm diameter × 1.7 mm thick disk, 6 N purity) was cleaned by several cycles of Ar+ sputtering (Ar(g), 99.999% purity, Matheson; Specs IQE 11/35, 1.0 kV × 10 mA) followed by annealing to 750 K for 5 min. For Ag deposition in this system, an electron beam evaporator (SPECS EBE-4) with a silver rod (Surepure Chemetals Inc., 99.99% purity, 2.0 mm diameter) was used. Details for the Ag coverage quantification method based on XPS were provided in the ESI.†
Infrared data were obtained using a Bruker Vertex 80 V spectrometer with a motorized polarizer and an MCT detector (500 scans, 4 cm−1 resolution, ∼2 min acquisition time). The sample is located in a UHV chamber with KBr windows and the angle between the IR beam and the sample surface is set at ∼8°. The beam path between the light source and the chamber, and between the chamber and detector is evacuated to ∼1 torr.
Computational methods
Calculations are performed within density functional theory applied to periodic systems, using the PBE exchange correlation functional and the projector augmented wave method.28,29 The one-electron functions are developed on a basis set of plane waves using a 400 eV cut-off energy. K-space integration uses a 15 × 15 × 1 k-point mesh. The Ag/Pd(111) was modelled by using a 6-layer slab and 1 × 1 unit cell. The bottom 3 layers were fixed to the bulk geometry while the top 3 layers were fully optimized with a convergence threshold of 0.02 eV Å−1. Two separate calculations were performed using the Ag (4.14 Å) and Pd (3.94 Å) lattice constants for the slab, respectively, to model the Ag/Pd(111) system (Fig. S1 and S2†). In the first model, the Pd(111) surface is submitted to a tensile stain. The chemical potential calculated for Ag in the surface layer on Pd(111) is −3.05 eV when the Ag lattice constant is used compared to −2.97 eV for a model with the Pd lattice, indicating that the Ag layer is more stable for the Ag lattice constant. Therefore, the Ag lattice constant is used for the Ag/Pd(111) slab model in the paper unless indicated otherwise. The explicit modelling of a Ag layer at the Ag lattice constant on a Pd(111) slab at the Pd lattice constant requires a very large supercell, and cannot be accessed with DFT calculations.Core-level shifts (CLS) were calculated using the final state approximation and a half electron excitation. DFT-calculated CLS have been shown to agree well with XPS-measured values using this approximation with, for example, the O 1s and Ag 3d CLS in Ag(111)-p(4 × 4)-O.30,31 In this work, all Ag 3d CLS values are calculated with respect to bulk Ag, and the method was calibrated by calculating the surface core-level shift (SCLS) for Ag(111). The calculated SCLS is −0.08 eV, which is close to the experimental value of −0.1 eV, again justifying the selected method.32 The number of k-points was increased to 21 × 21 × 1 and the number of bands in calculation were increased by 25% for the density of states (DOS) calculations. All the calculations were performed with VASP.33,34
Results and discussion
Surface morphology and electronic structure of Ag/Pd(111)
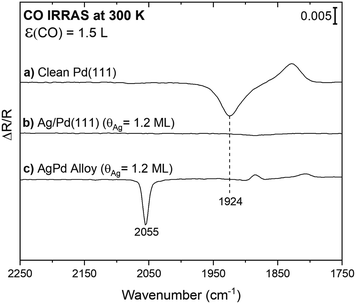
Infrared spectroscopy using CO as a probe molecule was used to establish that a continuous layer of Ag forms after deposition onto Pd(111) at room temperature, in agreement with prior work.27 The limited vibrational signature for CO on the surface after exposure of CO to a layer of Ag onto Pd(111) (Ag(θ = 1.2 ML)/Pd(111)) provides evidence that Ag forms a continuous film and that a limited fraction of Pd is exposed (Fig. 1b). This result is consistent with prior scanning tunnelling microscopy (STM),27,35 and two-photon photoemission36 studies that indicate that Ag grows as a uniform two-dimensional layer on Pd(111) at 300 K, starting at the palladium step-edges and expanding across the terraces until reaching a monolayer coverage. Prior STM images show only a small fraction of the Pd atoms remain uncovered, residing mainly at the step edges for a monolayer Ag deposited on Pd(111), consistent with the vibrational results (Fig. 1b).35 This structure is thermally stable up to ∼500 K.36Carbon monoxide (CO) was also used to probe the amount of exposed surface palladium following deposition of lower coverages of Ag onto Pd(111) at 300 K. Since CO does not appreciably adsorb on silver at 300 K,37 all CO signals can be attributed to adsorption on exposed Pd. For reference, a broad vibrational signal at 1924 cm−1 was obtained in the IR spectrum subsequent to 1.5 Langmuir (1 L = 10−6 torr s−1) of CO exposure on a clean Pd(111) single crystal at 300 K (Fig. 1a). This signal is attributed to CO adsorption on bridge sites as previously reported for moderate CO coverages.38 The CO coverage from 1.5 L of CO exposure is estimated as 0.45 ML (∼70% of a saturation), based on the CO stretch frequency in comparison to the literature.38 The binding site of CO on Pd depends on coverage, signified by a shift in the CO stretch frequency. A transition from threefold-hollow to bridge sites occurs with increasing CO coverage from <0.1 to 0.6 ML indicated by a shift from 1815 to 1944 cm−1.38,39 Thus, the positive signal at 1828 cm−1 observed in the spectrum for CO on clean Pd(111) is attributed to adsorption of background CO bound in threefold-hollow sites present in the spectrum used for background subtraction. Since the binding site changes to bridge sites upon exposure to 1.5 L CO, the background is not flat (Fig. S3†).
Notably, CO is detected after exposure of CO to a PdAg surface alloy formed by heating the Ag/Pd(111) surface to 750 K, where it is known that a surface alloy containing isolated Pd atoms forms (Fig. 1c).27 This result establishes that CO can be readily detected even when only a few Pd atoms are present. A sharp peak at 2055 cm−1 characteristic of on-top CO adsorption on palladium is observed after exposure of CO to the annealed surface at room temperature (Fig. 1c). For comparison, the frequency for high coverages of atop CO on Pd is 2097 cm−1.38 The frequency of this vibration is in the range anticipated for CO bound atop a single Pd, indicating that some Pd atoms emerge on the surface as a result of annealing and that Pd monomers are predominant, in agreement with STM.27 As discussed above, the small positive background at 1884 cm−1 and 1808 cm−1 are attributed to adventitious CO adsorption in the spectrum used for background subtraction.
The Ag 3d5/2 binding energies are different for Ag deposited at 300 K on Pd(111) compared to pristine Ag(111) measured in X-ray photoelectron spectra, providing evidence for alteration of the electronic properties of Ag in the Ag/Pd(111) (Fig. 2, Table 1). The Ag 3d5/2 binding energy of Ag deposited Pd(111) is 368.0 eV for Ag coverages of both 0.5 ML and 1.1 ML (Fig. 2a and b), compared to a binding energy of 368.3 eV for the surface layer of clean Ag(111) measured in the same instrument (Fig. 2d). The core-level shift (CLS) of −0.3 eV for the Ag mono- and half-layer compared to pristine Ag(111) indicates that 2D Ag islands are electronically altered by the underlying Pd atoms. In a recent study, a similar experimental CLS in the Ag 3d5/2 binding was reported for AgPd alloys formed from Pd deposition on Ag(111).20 The Ag 3d5/2 CLS values were linearly correlated with the number of Pd neighbours (i.e. changing from −0.1 to −0.5 eV for 1–8 Pd neighbours, respectively) in the prior studies of the alloy;20 hence, the constancy of the Ag 3d5/2 binding energies observed here for sub-ML Ag coverages (θAg = 0.5 ML vs. 1.1 ML) as well as the fact that the full width at half maximum (FWHM) for both coverages is 0.95 ± 0.01 eV, is evidence that the number of Pd neighbours does not change with the Ag coverage in the sub-ML regime. Together, these results provide further evidence for a uniform Ag growth on Pd(111) until the saturation of the first layer.
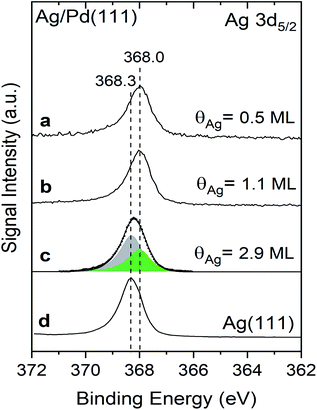 | ||
| Fig. 2 Shifts in the binding energy of the Ag 3d5/2 measured using X-ray photoelectron spectroscopy indicate that the first monolayer of Ag deposited on Pd(111) has different electronic properties than bulk Ag(111). X-ray photoelectron spectra (XPS) obtained after deposition of varying amounts of Ag onto Pd(111): (a) 0.5 ML of Ag; (b) 1.1 ML of Ag; and, (c) 2.9 ML. (d) Reference data for clean Ag(111). The spectrum in (c) is fit with two peaks at 368.0 (green) and 368.3 eV (grey) attributed to the first layer and multilayers of Ag, respectively. Spectra were obtained at 300 K and Ag was deposited at the same temperature. Details of the curve fitting procedure are provided in the ESI (Fig. S4†). | ||
| System | Theory (DFT) | Experiment (XPS-Ag 3d5/2) | ||
|---|---|---|---|---|
| μ Ag (eV) | Surface Ag 3d CLS (eV) | B. E. (eV) | CLS (eV) | |
| Ag(111) bulk | — | −0.08 | 368.3 | — |
| 1-Layer Ag/Pd(111) | −3.05 | −0.23 | 368.0 | −0.3 |
| 2-Layer Ag/Pd(111) | −2.91 | −0.05 | 368.3 (in multilayer) | 0.0 |
| 368.0 (in monolayer) | −0.3 | |||
The Ag 3d5/2 peak broadens and shifts slightly for thicker layers of Ag (θ = 2.9 ML) deposited on the Pd(111) at room temperature (Fig. 2c). Specifically, the peak maximum shifts to 368.2 eV and the FWHM increases to 1.0 eV for the Ag multilayer compared to a Ag 3d5/2 binding energy of 368.3 eV and FWHM of 0.95 eV, suggesting that the broad peak for the 2.9 ML Ag film is a convolution of multiple peaks (Table 1). The broad peak can be accurately fit with two features corresponding to the Ag monolayer (368.0 (green)) and for bulk Ag (368.3 eV (grey)) with FWHM of 0.95 eV (Fig. 2c and S4†). The integrated area of the signal attributed to the Ag monolayer in contact with Pd at 368.0 eV is 37% of the total Ag signal, in agreement with the layer-by-layer model used to quantify the total Ag coverage by XPS (Fig. S5†). The signal fraction of the first Ag layer for Ag (θ = 2.9 ML)/Pd(111) is calculated to be ∼30% in an ideal layer-by-layer model (Fig. S5†). The deviation is attributed to the deteriorated layer-by-layer growth for Ag multilayers that is shown in a previous study.35
Density functional calculations likewise indicate that the Ag in contact with Pd on the single layer film is significantly perturbed electronically, and that this effect is only present for the monolayer, not for Ag multilayers. The core level shift (CLS) for Ag on the surface of 1-layer of Ag on Pd(111) (Ag/Pd(111)) is calculated to be −0.23 eV relative to Ag atoms in the bulk of a Ag(111) slab when the Ag lattice constant is used for the Ag/Pd(111) slab model. This CLS is comparable to the experimental value of −0.30 eV for Ag monolayers on Pd(111) and significantly larger than that for surface Ag in Ag(111) (Table 1). If the Pd lattice constant is used for the slab, the CLS is increased slightly, by 0.08 eV, so that the trend is preserved (Table S3†).
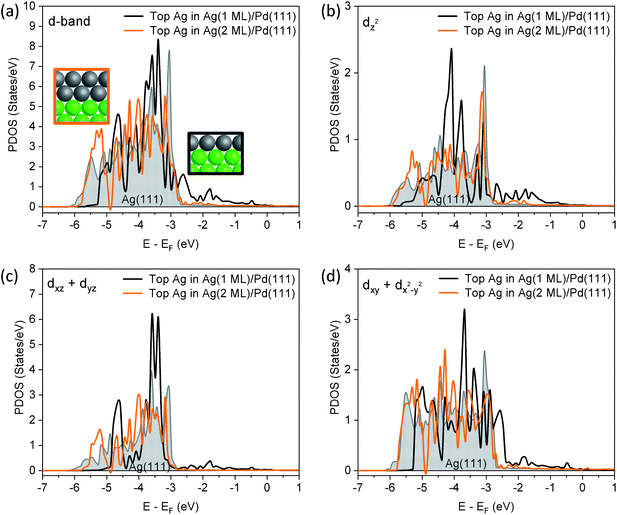
A more detailed analysis of the density of states (DOS) demonstrates that the 1 layer Ag/Pd(111) has a different valence band structure than bulk Ag(111) (Fig. 3). The edge of the d band for surface Ag in Ag(111) is located significantly below the Fermi level, as expected. For a 1-layer film of Ag on Pd(111), the Ag d band is narrowed, due to a smaller Ag–Ag coordination number. Furthermore, the d-band center of the Ag monolayer is shifted up by 0.2 eV relative to the top layer in Ag(111) (Table S4†). There is a significant contribution of Ag d states to the DOS in the energy interval between the Fermi level and −3 eV which is attributed to mixing of Ag and Pd d states. While the contribution to the valence band by the Ag monolayer cannot be quantitatively deconvoluted, experimental data obtained in the valence band region using XPS also indicates that there are Ag states between −3 eV and the Fermi energy due to mixing with Pd states (Fig. S6†).
Notably, the changes in the d band of Ag disappear for a 2 monolayer thick slab (Fig. 3a), demonstrating the extremely short-range nature of the perturbation of the electronic structure. First, the surface Ag 3d CLS is calculated at −0.05 eV for a 2-layer slab of Ag on Pd(111) (Table S3†), which is close to Ag(111) surface value (−0.08 eV), and in general agreement with the experimental value measured for 2.9 ML of Ag (Fig. 2). Furthermore, the states in the range of −3 eV–EF that are present in the DOS for the Ag monolayer are no longer present, nor are there significant changes in the projected orbital densities of states.
In order to show which orbitals contribute the most to the changing d band of surface Ag for the 1-layer film, orbital resolved density of states (ORDOS) are also shown in Fig. 3. Three main effects are seen. First, the d band narrows from loss of Ag–Ag contact in the monolayer compared to Ag(111). This effect is clearly more important for orbitals that point towards the missing neighbours (dxz + dyz and dz2) and it is not present for dxy + dx2−y2, since these orbitals only overlap with Ag atoms in the surface layer. Second, all ORDOS centers are shifted up in energy by approximately the same amount. This shift creates significant Ag d states above the Ag(111) band edge for the dxy + dx2−y2 components (states at −2.5 eV). Third, mixing between Ag and Pd d orbitals at the interface, also creates Ag contribution above the Ag(111) band edge and this effect is more important for dxz + dyz and dz2 orbitals that point towards Pd atoms in the substrate. The (dxz + dyz) orbitals are expected to contribute to bonding to species in hollow sites, as discussed below. In contrast to the above described changes in ORDOS for the 1 ML Ag film, all d orbital states change very little for the 2 ML Ag film (Fig. 3).
Formic acid reactivity on Ag/Pd(111)
The alteration in electronic structure of the Ag monolayer on Pd(111) manifests itself in the reactivity of formic acid. Formic acid reacts on 1 monolayer of Ag on Pd(111), yielding CO2 at 280 K in temperature programmed reaction experiments (Fig. 4). This result demonstrates that the 1-layer Ag film has different chemical properties than bulk Ag(111), since pristine silver requires adsorbed O to initiate reaction.40,41 The reactivity for the Ag monolayer is not due to exposed Pd based on the fact that the CO2 peak temperature of 280 K is substantially different than for Pd(111) and the lack of CO adsorption on the film (Fig. 1). Carbon dioxide forms from formic acid decomposition on Pd(111) at 190 K (Fig. 4), in agreement with the literature.24,42 Water is also evolved at 190 K along with some formic acid after adsorption of HCOOH on Pd(111) (Fig. S7†).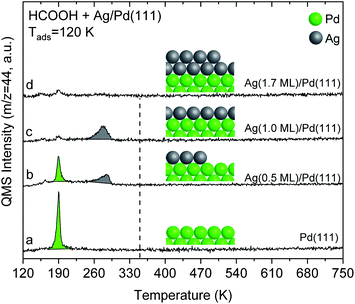 | ||
Fig. 4 Temperature programmed reaction of formic acid shows that a multilayer of Ag on Pd(111) is unreactive whereas a monolayer yields CO2 at 280 K. Spectra for CO2 production during temperature programmed reaction of HCOOH from: (a) pristine Pd(111), and after deposition of various amounts of Ag onto Pd(111): (b) 0.5 ML (c) 1.0 ML; and (d) 1.7 ML. Formic acid (0.03 L) was exposed at 120 K in all cases. All data are corrected by subtracting the 44 amu fragment of molecular formic acid (m/z = 44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 was ∼1 46 was ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2). The dashed-line indicates the temperature for CO2 production from formate decomposition on Ag(111) taken from the literature.41 The heating rate was constant and 1 K s−1 in all cases. 1.2). The dashed-line indicates the temperature for CO2 production from formate decomposition on Ag(111) taken from the literature.41 The heating rate was constant and 1 K s−1 in all cases. | ||
Temperature programmed reaction experiments for different Ag coverages also confirm that the CO2 produced at 280 K from formic acid reaction on the monolayer of Ag is not due to exposed Pd. Both the 190 K CO2 peak, attributed to reaction on exposed Pd, and the 280 K peak, attributed to the Ag monolayer, are observed at Ag coverages below one monolayer, e.g. 0.5 ML of Ag (Fig. 4). Furthermore, the 280 K CO2 feature increases as the 190 K peak diminishes with increasing Ag coverage, providing additional evidence that the 280 K peak is associated with the Ag layer.
Formic acid does not react on a multilayer Ag (1.7 ML) film on Pd(111) based on the lack of CO2 production during temperature programmed experiments (Fig. 4), which indicates that the 2 ML film reverts to chemical behaviour similar to bulk Ag. Instead, formic acid desorbs reversibly at 180 K. This behaviour is analogous to pristine silver which requires adsorbed O to activate formic acid. The lack of reactivity is also generally consistent with the DFT calculations that show a similar d-band structure for the top layer of Ag in Ag(111) and for Ag bilayers on Pd(111) (Fig. 3). The small CO2 signal obtained at 190 K for monolayer and multilayer Ag on Pd(111) structures is attributed to formic acid reaction on a small number of exposed Pd atoms at the step edges.
The other major product detected from reaction of formic acid on the Ag monolayer on Pd(111) is hydrogen, formed nearly coincident with the CO2 (Fig. S8†). Hydrogen is likewise evolved from formic acid reaction on Pd(111) at a similar temperature, 310 K (Fig. S8†). The hydrogen produced from formic acid was differentiated from background H2 in temperature programmed reaction experiments with DCOOD, which yielded HD (Fig. S8†). The temperature for hydrogen evolution is generally consistent with the decomposition of adsorbed formate on Ag/Pd(111). As noted above, pristine silver does not activate formic acid;40 however, reaction of formic acid with adsorbed oxygen on the pre-oxidized silver occurs to produce adsorbed formate, based on vibrational spectroscopy, which decomposes at 350 K on Ag(111)41 and at 400 K on Ag(110).26 The oxygen used to activate formic acid is removed as water through a stoichiometric reaction.
Carbon monoxide is also produced from reaction of formic acid on both the Ag monolayer on Pd(111) and on clean Pd(111) (Fig. S9†). The amount of CO produced for the Ag monolayer on Pd(111) is significantly lower than for pristine Pd(111) based on the amount of 13CO produced during temperature programmed reaction of H13COOH (Fig. S9†). The 13CO is produced at similar temperatures for both systems, ∼475 K (Fig. S9†). Since H13COOH produces 13CO and 13CO2, these experiments differentiate background CO from that produced via reaction. While there is clearly a lower 13CO signal for the Ag monolayer on Pd(111) (Fig. S9†), quantitative analysis is challenging because the H13COOH reacts on the chamber walls, leading to an increase in background 13CO over time.
Overall, there is clear evidence that the Ag monolayer on Pd(111) has a different electronic structure than pristine Ag, resulting in activation of formic acid on the Ag. While the intermediate formed from formic acid on the Ag monolayer has not been explicitly identified, formate has been widely identified as the intermediate formed on many surfaces, including Pd(111)24 and O-covered Ag.40,41 Hence, we infer that formate is formed from initial reaction on the Ag monolayer/Pd(111), suggesting that the alteration in the Ag electronic structure leads to O–H bond activation.
The activation energy for C–H bond rupture is also significantly different on the Ag monolayer/Pd(111) compared to clean Ag. The activation energy for CO2 production on the Ag monolayer/Pd(111) is estimated to be ∼90 kJ mol−1 compared to a value of 125 kJ mol−1 for formate decomposition on clean Ag(110),40 with the assumption of first-order kinetics43 and a constant pre-exponential factor of 8 × 1015 s−1.40 This comparison also provides evidence that the modified electronic structure of the Ag monolayer on Pd(111) enhances the activity of Ag for C–H bond breaking.
Previous theoretical studies of formic acid reactivity on one layer of Pd on Ag(111) also show that the electronic structure of one monolayer of metal is different than multilayers or than bulk Pd.44 Two or three layers of Pd on Ag(111) were similar to pure Pd(111). Therefore, the changes in the electronic structure of Pd/Ag(111) is restricted to one layer, similar to the results herein for the Ag/Pd(111) system.
While a detailed theoretical study of the bond activation processes in formic acid is beyond the scope of this work, the overall increase in the states near the Fermi level in the Ag monolayer due to bonding to the underlying Pd(111) is most likely the reason for the increase in reactivity of formic acid. Interestingly, the (dxz + dyz) states are most strongly affected by bonding of the Ag monolayer to Pd, suggesting that bonding to hollow sites is important in determining reactivity. More detailed studies are required to investigate this in more detail.
Conclusions
The electronic properties of a uniform, monolayer thick Ag film on Pd(111) are different than pristine Ag(111), leading to enhanced reactivity of the Ag towards formic acid. Alteration in the electronic structure of the Ag monolayer on Pd(111) is manifested by changes in the Pd 3d5/2 binding energy measured in X-ray photoelectron spectra and also in theoretical models studied using DFT. The changes in electronic properties and the corresponding changes in reactivity are not observed for thicker layers of Ag. Even a 2 monolayer thick film of Ag reverts to the electronic structure of bulk Ag(111). Furthermore, the 2 monolayers of Ag on Pd(111) are unreactive towards formic acid. These results are consistent with prior theoretical studies of Pd/Ag(111) that also show changes in electronic structure for the first monolayer but not for thicker layers.These results demonstrate that changes in electronic structure can be achieved for monolayer films of one metal on another, but that they do not persist for even two atomic layers. Hence, synthesis of nanomaterials for the purposes of changing reactivity requires atomic-scale control of layer thickness. These findings indicate that single layer Ag covered Pd core–shell nanoparticles have a potential for selective hydrogen production from formic acid which can also possibly be extrapolated to other selective catalytic processes.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Integrated Mesoscale Architectures for Sustainable Catalysis (IMASC), an Energy Frontier Research Center funded by the U. S. Department of Energy, Office of Science, Basic Energy Sciences under Award No. DE-SC0012573.References
- J. A. Rodriguez and D. W. Goodman, Science, 1992, 257, 897–903 CrossRef CAS PubMed.
- J. R. Kitchin, J. K. Nørskov, M. A. Barteau and J. G. Chen, J. Chem. Phys., 2004, 120, 10240–10246 CrossRef CAS PubMed.
- J. G. Chen, C. A. Menning and M. B. Zellner, Surf. Sci. Rep., 2008, 63, 201–254 CrossRef CAS.
- M. Sankar, N. Dimitratos, P. J. Miedziak, P. P. Wells, C. J. Kiely and G. J. Hutchings, Chem. Soc. Rev., 2012, 41, 8099–8139 RSC.
- J. E. Houston, C. H. F. Peden, D. S. Blair and D. W. Goodman, Surf. Sci., 1986, 167, 427–436 CrossRef CAS.
- P. J. Berlowitz and D. W. Goodman, Surf. Sci., 1987, 187, 463–480 CrossRef CAS.
- J. A. Rodriguez and D. W. Goodman, J. Phys. Chem., 1990, 94, 5342–5347 CrossRef CAS.
- J. W. He, W. L. Shea, X. Jiang and D. W. Goodman, J. Vac. Sci. Technol., A, 1990, 8, 2435–2444 CrossRef CAS.
- J. M. Heitzinger, S. C. Gebhard and B. E. Koel, J. Phys. Chem., 1993, 97, 5327–5332 CrossRef CAS.
- M. Walker, C. R. Parkinson, M. Draxler and C. F. McConville, Surf. Sci., 2005, 584, 153–160 CrossRef CAS.
- J. E. Houston, C. H. F. Peden, P. J. Feibelman and D. R. Hamann, Surf. Sci., 1987, 192, 457–474 CrossRef CAS.
- B. Hammer and J. K. Nørskov, Adv. Catal., 2000, 45, 71–129 CAS.
- F. C. H. Lim, J. Zhang, H. Jin, M. B. Sullivan and P. Wu, Appl. Catal., A, 2013, 451, 79–85 CrossRef CAS.
- B. Hammer, Y. Morikawa and J. K. Nørskov, Phys. Rev. Lett., 1996, 76, 2141–2144 CrossRef CAS PubMed.
- I. E. Wachs and R. J. Madix, Surf. Sci., 1978, 76, 531–558 CrossRef CAS.
- R. J. Madix, Science, 1986, 233, 1159–1166 CrossRef CAS PubMed.
- A. Nagy and G. Mestl, Appl. Catal., A, 1999, 188, 337–353 CrossRef CAS.
- X. Yu and P. G. Pickup, J. Power Sources, 2008, 182, 124–132 CrossRef CAS.
- K. Tedsree, T. Li, S. Jones, C. W. A. Chan, K. M. K. Yu, P. A. J. Bagot, E. A. Marquis, G. D. W. Smith and S. C. E. Tsang, Nat. Nanotechnol., 2011, 6, 302–307 CrossRef CAS PubMed.
- M. A. Van Spronsen, K. Daunmu, C. R. O'Connor, T. Egle, H. Kersell, J. Oliver-Meseguer, M. B. Salmeron, R. J. Madix, P. Sautet and C. M. Friend, J. Phys. Chem. C, 2019, 123, 8312–8323 CrossRef CAS.
- R. J. Madix, Adv. Catal., 1980, 29, 1–53 CAS.
- B. E. Hayden, K. Prince, D. P. Woodruff and A. M. Bradshaw, Surf. Sci., 1983, 133, 589–604 CrossRef CAS.
- C. Houtman and M. A. Barteau, Surf. Sci., 1991, 248, 57–76 CrossRef CAS.
- J. L. Davis and M. A. Barteau, Surf. Sci., 1991, 256, 50–66 CrossRef CAS.
- M. R. Columbia, A. M. Crabtree and P. A. Thiel, J. Am. Chem. Soc., 1992, 114, 1231–1237 CrossRef CAS.
- B. A. Sexton and R. J. Madix, Surf. Sci., 1981, 105, 177–195 CrossRef CAS.
- A. K. Engstfeld, H. E. Hoster and R. J. Behm, Phys. Chem. Chem. Phys., 2012, 14, 10754–10761 RSC.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- M. Schmid, A. Reicho, A. Stierle, I. Costina, J. Klikovits, P. Kostelnik, O. Dubay, G. Kresse, J. Gustafson, E. Lundgren, J. N. Andersen, H. Dosch and P. Varga, Phys. Rev. Lett., 2006, 96, 146102 CrossRef CAS PubMed.
- H. Grönbeck, S. Klacar, N. M. Martin, A. Hellman, E. Lundgren and J. N. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115445 CrossRef.
- J. N. Andersen, D. Hennig, E. Lundgren, M. Methfessel, R. Nyholm and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17525–17533 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- V. M. Trontl, I. Pletikosić, M. Milun, P. Pervan, P. Lazić, D. Šokčević and R. Brako, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 235418 CrossRef.
- T. Fauster, Appl. Phys. A: Solids Surf., 1994, 59, 479–486 CrossRef.
- W. Hansen, M. Bertolo and K. Jacobi, Surf. Sci., 1991, 253, 1–12 CrossRef CAS.
- Y. Ma, T. Diemant, J. Bansmann and R. J. Behm, Phys. Chem. Chem. Phys., 2011, 13, 10741–10754 RSC.
- A. M. Bradshaw and F. M. Hoffmann, Surf. Sci., 1978, 72, 513–535 CrossRef CAS.
- M. A. Barteau, M. Bowker and R. J. Madix, Surf. Sci., 1980, 94, 303–322 CrossRef CAS.
- W. S. Sim, P. Gardner and D. A. King, J. Phys. Chem., 1996, 100, 12509–12516 CrossRef CAS.
- B. Karakurt, Y. Kocak and E. Ozensoy, J. Phys. Chem. C, 2019, 123, 28777–28788 CrossRef.
- P. A. Redhead, Vacuum, 1962, 12, 203–211 CrossRef CAS.
- J. Cho, S. Lee, J. Han, S. P. Yoon, S. W. Nam, S. H. Choi, K. Y. Lee and H. C. Ham, J. Phys. Chem. C, 2014, 118, 22553–22560 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc01461c |
| This journal is © The Royal Society of Chemistry 2020 |