Al(OR^F)₃ (R^F = C(CF₃)₃) activated silica: a well-defined weakly coordinating surface anion

Abstract

Weakly Coordinating Anions (WCAs) containing electron deficient delocalized anionic fragments that are reasonably inert allow for the isolation of strong electrophiles. Perfluorinated borates, perfluorinated aluminum alkoxides, and halogenated carborane anions are a few families of WCAs that are commonly used in synthesis. Application of similar design strategies to oxide surfaces is challenging. This paper describes the reaction of Al(OR^F)₃*PhF (R^F = C(CF₃)₃) with silica partially dehydroxylated at 700 °C (SiO_2-700) to form the bridging silanol ≡Si–OH⋯Al(OR^F)₃ (1). DFT calculations using small clusters to model 1 show that the gas phase acidity (GPA) of the bridging silanol is 43.2 kcal mol⁻¹ lower than the GPA of H₂SO₄, but higher than the strongest carborane acids, suggesting that deprotonated 1 would be a WCA. Reactions of 1 with NOct₃ show that 1 forms weaker ion-pairs than classical WCAs, but stronger ion-pairs than carborane or borate anions. Though 1 forms stronger ion-pairs than these state-of-the-art WCAs, 1 reacts with alkylsilanes to form silylium type surface species. To the best of our knowledge, this is the first example of a silylium supported on derivatized silica.

---

Introduction

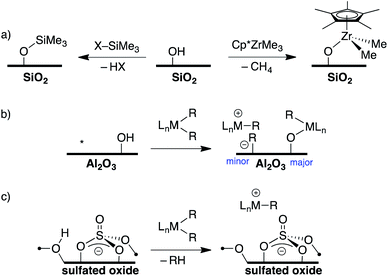
The development of inert Weakly Coordinating Anions (WCAs) was critical to isolate very reactive electrophilic species.¹ Studies of superacid media resulted in the first generation of WCAs (CF₃SO₃⁻, PF₆⁻, SbF₆⁻, etc., Fig. 1).² The first generation WCAs continue to find broad applications in the synthetic community, but these anions are too reactive or coordinating to stabilize highly reactive cations. For example, organometallic Zr(IV) cations, key 14-electron intermediates in the synthesis of polyolefins, are incompatible with first generation WCAs.³ These anions are also not sufficiently weakly coordinating to form R₃Si⁺ cations.⁴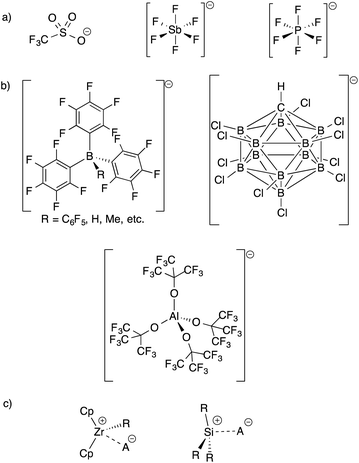

Fig. 1 Structures of first generation WCAs (a) and bulky inert WCAs (b); very strong electrophiles that are too reactive to form with first generation WCAs (c).

Fluorinated borates (e.g.⁻B(C₆F₅)₄, ⁻B(3,5-(CF₃)₂–C₆H₃)₄),⁵ aluminates (e.g.⁻Al(OC(CF₃)₃)₄),⁶ or carborane anions (e.g.⁻CHB₁₁H₆X₅, ⁻CHB₁₁X₁₁; X = halide),⁷ shown in Fig. 1, stabilize organometallic Zr(IV) cations or R₃Si⁺. The anions are designed to delocalize charge throughout the structure of the WCA, which results in low basicity. The conjugate acids of the WCAs shown in Fig. 1, when isolable, are the strongest known Brønsted acids.⁸ The strong C–F or B–X bonds in these WCAs also provide some degree of chemical inertness, which is important in reactions involving the strong electrophiles mentioned above.

Direct translation of these concepts to well-defined heterogeneous catalysts is more challenging. Well-defined heterogeneous catalysts are desirable because the molecular structure of a catalytically active site can be determined using spectroscopic methods,^9–11 which provides opportunities to optimize the properties of these catalysts based on the structure of the active site. The largest class of well-defined heterogeneous catalysts are supported on SiO₂ partially dehydroxylated at 700 °C. Well-defined sites supported on SiO₂ generally do not form ion-pairs but rather ≡SiO–ML_n. For example, the ²⁹Si Cross Polarization Magic Angle Spinning (CPMAS) NMR spectrum of alkylsilane functionalized silica (≡SiO–SiMe₃, Fig. 2a) contains a signal at 14 ppm for the alkylsilane fragment, which is inconsistent with formation of a Me₃Si⁺ species on the silica surface.^12–15 Similarly, Cp*ZrMe₃ (Cp* = pentamethylcyclopentadienyl) reacts with partially dehydroxylated SiO₂ to form ≡SiO–Zr(Cp*)Me₂ (Fig. 2a),¹⁶ which is inactive in the polymerization of ethylene. However, ≡SiO–Zr(Cp*)Me₂ does react with B(C₆F₅)₃ to form electrophilic ion-pairs that are active in the polymerization of ethylene.¹⁷ Silica surfaces can also form strong ion-pars with between surface siloxide anions and tetraalkylphosphonium groups.^18,19

Fig. 2 Formation of R₃Si–O_x and Cp*Zr(Me)₂–O_x (O_x = surface oxygen) on partially dehydroxylated SiO₂ (a); reaction of organometallics with partially dehydroxylated Al₂O₃ (* = Lewis acid site), minor product are ion-pairs (b); formation of electrophilic ion pairs on sulfated oxides (c).

Partially dehydroxylated Al₂O₃ contains a very small quantity of tri-coordinate Al Lewis-acid sites²⁰ that react with organometallic complexes to form electrophilic ion-pairs, Fig. 2b.^21,22 However, the surface coverage of the –OH sites is much higher than the surface coverage of Lewis sites, resulting in low active site loadings in these well-defined catalysts.²³

The trends in WCAs described above suggest that oxides containing more acidic –OH sites may be more weakly coordinating. Zeolites contain –OH sites that are more acidic than –OH sites on SiO₂, and can support organometallic species.²⁴ Studies of well-defined organometallics are limited to small molecules because SiO₂/Al₂O₃ zeolite materials have small pore sizes. Oxides treated with sulfuric acid, sulfated oxides, were claimed to contain superacid Brønsted acid sites.²⁵ This relates sulfated oxides to first generation WCAs, and several studies showed that sulfated oxides form electrophilic ion pairs with organometallics (Fig. 2c).^26–31 However, titrations of the –OH sites on sulfated oxides with phosphines are inconsistent with superacid –OH sites.³² This data is consistent with DFT calculations showing that sulfated oxides are weaker acids than zeolites.³³ Detailed studies showed that sulfated oxides also contain significant amounts of oxidative pyrosulfate sites, which can result in undesirable side reactions with organometallic substrates.³⁴

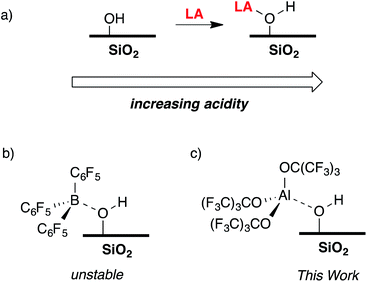
The reaction of a strong Lewis acid and a ≡Si–OH on partially dehydroxylated silica should form a strong Brønsted acid site (Fig. 3a).³⁵ Deprotonation of the strong Brønsted acid should result in a weakly coordinating anion that may stabilize electrophilic surface species that would not typically form on SiO₂ surfaces, and also translate solution WCA concepts to heterogeneous supports. Contacting dehydroxylated silica with AlCl₃ forms strong Brønsted acid sites, but also results in various side reactions leading to strong Lewis sites on the silica surface,³⁶ which is common in this class of functionalized oxides.³⁷ Redox inactive strong Lewis acids, such as B(C₆F₅)₃, are not sufficiently Lewis acidic to form stable bridging silanols with silica (Fig. 3b).³⁸ However, B(C₆F₅)₃ reacts with silica and aniline bases to form ion-pairs that are capable of activating organometallic species,^39,40 or with exogenous H₂O to form grafted species on the SiO₂ surface.⁴¹ This paper describes the reaction of Al(OR^F)₃*PhF (R = C(CF₃)₃)⁴² with silica partially dehydroxylated at 700 °C (SiO_2-700) to generate ≡Si–OH⋯Al(OR^F)₃ (1, Fig. 3c). Calculated gas phase acidity (GPA) of 1 shows that the activated silanols are very strong Brønsted acids. Reactions of 1 with silane reagents result in the formation of [R₃Si][≡Si–O⋯Al(OR^F)₃], a rare example of a silylium supported on SiO₂.

Fig. 3 The reaction of a Lewis acid with silica to form a bridging silanol (a); B(C₆F₅)₃ reacts with silica to form unstable bridging silanols (b); the focus of this work, generation of ≡Si–OH⋯Al(OR^F)₃ (c).

Results and discussion

Reaction of Al(OR^F)₃*PhF with partially dehydroxylated SiO₂

A perfluorohexane slurry of SiO_2-700 (0.26 mmol OH g⁻¹) reacts with Al(OR^F)₃*PhF to form ≡Si–OH⋯Al(OR^F)₃ (1, Fig. 4a). ICP-OES analysis shows that 0.24 mmol g⁻¹ is present in 1, indicating that most of the silanols in SiO_2-700 are coordinated to Al(OR^F)₃. The FTIR spectrum of 1, shown in Fig. 4b, contains a new red-shifted ν_OH at 3542 cm⁻¹ that is typical of bridging silanols in silica–alumina materials. This spectrum also contains a ν_OH corresponding to silanols that do not form adducts with Al(OR^F)₃. Weak sp²–ν_CH and ν_C=C are also present, suggesting that some fluorobenzene remains adsorbed to 1. Consistent with this observation, ¹⁹F{¹H} NMR measurements of 1 suspended in CD₃CN show that 0.045 ± 0.004 mmol g⁻¹ of PhF leaches off the silica surface (Fig. S19†).

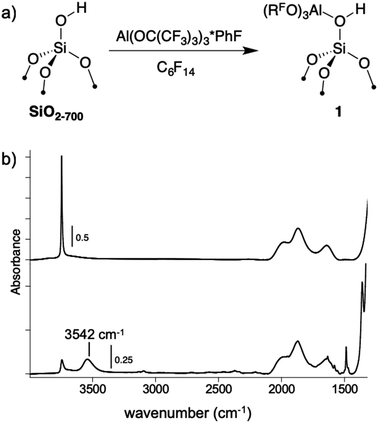Fig. 4 The reaction of Al(OR^F)₃*PhF with SiO_2-700 in perfluorohexane (a); FTIR spectra of SiO_2-700 (top) and 1 (bottom, b).

The static ²⁷Al NMR spectrum of 1 contains a typical quadrupolar powder pattern that can be simulated with a single site (Fig. 5a).⁴³ The isotropic chemical shift (δ_iso = 43 ppm) and large quadrupolar coupling constant (C_Q = 14.6 MHz) is consistent with a highly distorted tetrahedral Al coordination environment. These values are in agreement with those obtained from ²⁷Al MAS measurements of 1 (Fig. S4†). The ¹H magic angle spinning (MAS) NMR spectrum of 1 contains signals at 7.1 (adsorbed PhF), 5.0 (≡Si–OH⋯Al(OR^F)₃), and 2.3 (≡Si–OH) ppm (Fig. 5b, top trace). A ¹H dipolar double-quantum single-quantum (DQ-SQ) spectrum does not show crosspeaks between adsorbed PhF and the bridging silanol (see the ESI, Fig. S5†), suggesting that adsorbed PhF is distant from the acidic silanol in 1. A 2D ¹H{²⁷Al} D-RINEPT spectrum shows that the ²⁷Al signal in 1 correlates to the acidic silanol (≡Si–OH⋯Al(OR^F)₃) signal at 5.0 ppm (Fig. S7†), supporting these assignments.

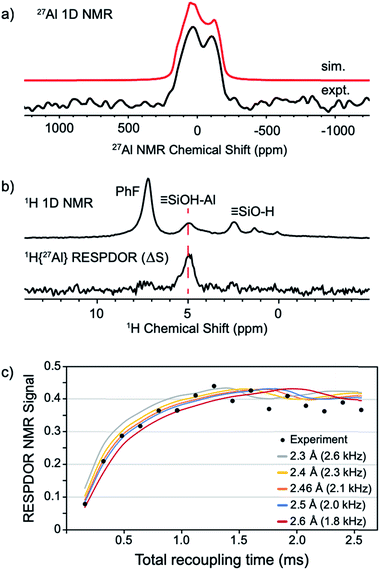Fig. 5 Static ²⁷Al solid-state NMR spectrum of 1 acquired at 14.1 T (a); solid-state 1D ¹H MAS NMR (top) and ¹H{²⁷Al} RESPDOR difference spectrum of 1 (middle, b); fit of RESPDOR dipolar dephasing curve to measure dipolar ¹H–²⁷Al dipolar coupling present in 1 (bottom, c). See the ESI† for Experimental details.

The ¹H{²⁷Al} Resonance-Echo Saturation-Pulse Double-Resonance (RESPDOR)^44,45 NMR experiment allows measurement of the dipolar coupling constant for ¹H and ²⁷Al spins. The ¹H–²⁷Al dipolar coupling constant is inversely proportional to the cube of the inter-atomic distance, so only ¹H and ²⁷Al spins that are in close spatial proximity (<5 Å) will be affected in this experiment. The ¹H{²⁷Al}-RESPDOR difference NMR spectrum (ΔS) is shown in Fig. 5b (bottom) and contains a single ¹H NMR signal at 5.0 ppm (≡Si–OH⋯Al(OR^F)₃). This result indicates that the bridging silanol is close to the aluminum in Al(OR^F)₃, and that the signals at 7.1 ppm (PhF) and 2.3 ppm (≡Si–OH) are from protons distant from aluminum, as expected. Variation of recoupling times in the ¹H{²⁷Al}-RESPDOR pulse sequence, and numerical simulation of the RESPDOR dipolar dephasing curve allows the ¹H–²⁷Al dipolar coupling constant to be determined. These data are given in Fig. 5c, and show that the ¹H–²⁷Al dipolar coupling is ∼2.0–2.3 kHz, which corresponds to Al–OH distances in the range of 2.4–2.5 Å. This distance is in good agreement with structural models predicted by DFT (see below).

DFT studies of small cluster models of 1

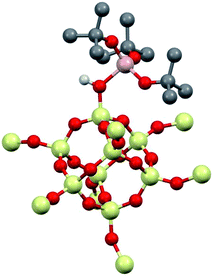
1 was modeled using Al(OR^F)₃ and the –SiH₃ capped polysesquisiloxane cluster⁴⁶ at the B3LYP/6-31G(d,p) level of theory. The cluster 1-DFT is shown in Fig. 6. Al(OR^F)₃ in 1-DFT coordinates to the isolated silanol in the cluster and not Si–O–Si bridges. The aluminum fragment in 1-DFT adopts a distorted tetrahedral geometry, and the Al–OH distance in 1-DFT is 1.91 Å. The terminal Si–O distance is 1.70 Å, slightly longer than the average Si–O distances (1.62 Å) in the cluster. These observations are similar to those obtained for alcohol adducts of Al(OR^F)₃.⁴⁷ The predicted Al–OH distance is 2.46 Å, and is in good agreement with an estimated Al–OH distances determined with the ¹H{²⁷Al} RESPDOR experiment.

Fig. 6 1-DFT with selected hydrogens and fluorines hidden for clarity. Selected distances (Å) and angles (deg.): O–H (0.98 Å), Al–OH (1.91 Å), Al–OH (2.46 Å) Al–OR^F (1.74 Å), Si–OH (1.70 Å), Si–O_cluster (1.60–1.63 Å), H–O–Al 113°, H–O–Si 116°, Si–O–Al 128°, O–Si–O(H) 105°.

The calculated IR spectrum of 1-DFT predicts a ν_OH at 3550 cm⁻¹ (expt. ν_OH = 3542 cm⁻¹). NMR calculations at the M06L/Al(6-311G(d,p)), 6-31G(d,p) level of theory predict that the acidic proton appears at 5.1 ppm, and that the ²⁷Al C_Q is 15.3 MHz. These values agree well with those obtained experimentally for 1, and are similar to those obtained for molecular H[Al(OC(CF₃)₃)₄].⁴⁷

Quantitative measurement of Brønsted acidity on oxides is challenging.^48–50 Gas-phase acidity (GPA) can be calculated using DFT methods, and is reasonably accurate for small molecules. Table 1 gives the GPA of various mineral acids at BP86/def2-TZVP to calibrate the accuracy of this level of theory. The GPA of HCl is 334.5 kcal mol⁻¹, which is very close to the experimental value (333.6 kcal mol⁻¹). In general, we find good agreement between experimental and calculated values. The calculated deprotonation energy of 1-DFT is 262.7 kcal mol⁻¹. For comparison, small clusters of ≡Si–OH⋯Al(OMe)₃, simplified models for bridging silanols in SiO₂/Al₂O₃, were also calculated at this level of theory and have deprotonation energy of 279–299 kcal mol⁻¹ (see the ESI† for details). These values are similar to those calculated for more complex models of zeolities,^51–54 indicating that 1-DFT is more acidic than bridging silanols in silica/aluminas. However, 1-DFT is clearly a weaker acid than H[Al(OC(CF₃)₃)₄] (GPA = 262.7 kcal mol⁻¹) or the H[CHB₁₁Cl₁₁] carborane acid (GPA = 239.0 kcal mol⁻¹). The strong Brønsted acidity of 1 suggests that the conjugate base of the bridging silanol may behave as a weakly coordinating anion.

Table 1 Calculated gas-phase acidity (GPA) in kcal mol⁻¹ at BP86/def2-TZVP level of theory

Acid	Expt. GPA (kcal mol^−1)	Calc'd GPA (kcal mol^−1)
HCl	336.2	334.5
HBr	318.3	321.6
HI	309.2	305.9
H2SO4	302.2	305.9
HSO3F	299.8	294.6
Zeolite	—	279–299
HSO3CF3	299.5	293.3
1-DFT	—	262.7
H[Al(OC(CF3)3)4]	—	248.8 (ref. 47)
H[CHB11Cl11]	—	239.1

---

Formation of ion-pairs with 1

The most common experimental method to assess the ion-pairing on a solid involves adsorption of a probe molecule to the solid and measuring the change in a spectroscopic observable, usually Δν by FTIR or Δδ by NMR spectroscopy. However, solution ¹⁹F{¹H} NMR studies indicate adsorption of common probes (pyridine or triethylphosphine oxide) or heteroatom containing solvents (CD₃CN, Et₂O, or CH₂Cl₂) to 1 results in desorption of solvated Al(OR^F)₃ from the silica surface.

Reed and co-workers described the properties of [Oct₃NH][X] contact ion pairs in CCl₄ solution.⁵⁵ The ν_NH stretch from FTIR measurements provides information about ion-pairing in [Oct₃NH][X]. In a H-bonded contact ion-pair, weaker NH⋯X interactions will result in higher ν_NH stretching frequencies. The ν_NH values for selected [Oct₃NH][X] contact ion pairs in CCl₄ solution are given in Table 2.

Table 2 ν _NH stretching frequencies for [Oct₃NH][X]

Anion	ν NH (cm^−1)
a Values from ref. 54. b This work.
B(C6F5)4	3223
[CHB11Cl11]	3163
[CH5B11Cl6]	3148
[CH5B11Br6]	3125
[CH5B11I6]	3097
2	3070^b
ClO4	3049
FSO3	2953
CF3SO3	2939

---

The reaction of 1 with 0.95 equiv NOct₃ in C₆H₁₂ at room temperature results in the formation of [Oct₃NH][(R^FO)₃Al–OSi≡] (2, eqn (1)). Solution ¹⁹F NMR spectra of this mixture indicates that desorption of Al(OR^F)₃ or decomposition of 1 does not occur under these conditions. 2 was characterized by multinuclear solid-state NMR spectroscopy (see the ESI† for details).

The FTIR spectrum of 2 shows ν_NH at 3070 cm⁻¹. This result indicates 2 forms a weaker ion pair than [Oct₃NH][SO₃CF₃] (ν_NH = 2939 cm⁻¹) or [Oct₃NH][ClO₄] (ν_NH = 3049 cm⁻¹), common first generation WCAs. This experimental data is consistent with the calculated GPA showing that 2 is a very strong Brønsted acid because strong acids form weak ion pairs. However, 2 forms stronger ion-pairs with [Oct₃NH] than carborane or [B(C₆F₅)₄] anions.

Formation of [ⁱPr₃Si][(R^FO)₃Al–OSi≡] (3)

As mentioned above, R₃Si⁺ ions are not stable in the presence of first generation WCAs because these WCAs either react or bind to the silylium ions. The characteristics of 1 suggest that R₃Si⁺ species may be stable on this surface. The reaction of allyltriisopropylsilane and 1 results in the formation of [ⁱPr₃Si][(R^FO)₃Al–OSi≡] and small amounts of ≡SiOSiⁱPr₃ (3, Fig. 7a). The FTIR of 3 lacks the strong ν_OH for the bridging silanol observed in 1 (Fig. 7b). The ²⁹Si CPMAS NMR spectrum of 3 contains a minor signal at 4.0 ppm, which is commonly observed in alkylsilane functionalized silica, and is consistent with the formation of ≡SiOSiⁱPr₃. The major signal in the ²⁹Si CPMAS NMR spectrum is at 70 ppm (Fig. 7c), and is assigned to 3. This chemical shift is typical of R₃Si⁺ fragments interacting with weak ligands. The ²⁹Si chemical shift of [ⁱPr₃Si(SO₂)][CH₆B₁₁Br₆] appears at 85 ppm,⁵⁶ and [Et₃Si(toluene)][B(C₆F₅)₄] appears at 94 ppm. Solvents that form stronger complexes with R₃Si⁺ fragments appear at lower chemical shift values. For example, the ²⁹Si chemical shift of [^tBu₃Si(OH₂)][CH₆B₁₁Br₆] is 46.7 ppm,⁵⁷ and [ⁱPr₃Si(NCCH₃)] [CH₆B₁₁Br₆] appears at 37.2 ppm.⁵⁸ These results suggest that the ⁱPr₃Si⁺ fragment in 3 is bound to a weaker ligand than MeCN or H₂O, but a stronger ligand than toluene or SO₂.

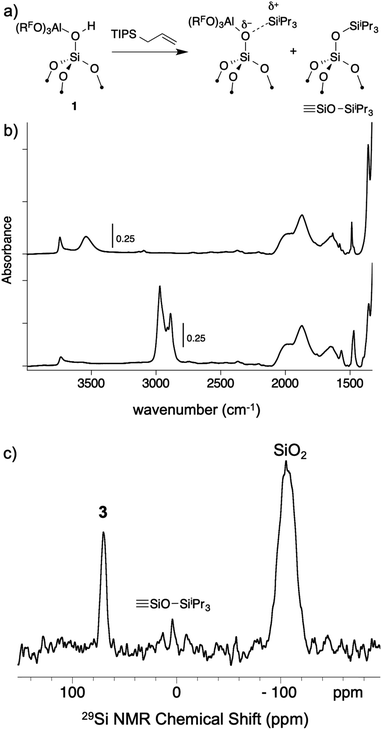Fig. 7 Reactivity of 1 with allyltriisopropylsilane to form 3 and small amounts of ≡SiOSiⁱPr₃ (a); FTIR spectrum of 1 (top) and 3 (bottom, b); ²⁹Si CPMAS NMR spectrum of 3 (c).

The structure of 3 was studied using DFT methods. The optimized structure of the [ⁱPr₃Si][(R^FO)₃Al–OSi≡] ion pair (3-DFT) at the B3LYP/6-31G(d,p) level of theory is shown in Fig. 8. The calculated ²⁹Si NMR chemical shift of 3-DFT at the M06L/Al(6-311G(d,p)),6-31G(d,p) level of theory is 67 ppm, in good agreement with experimental data. The ⁱPr₃Si⁺ fragment coordinates to the most sterically open ≡Si–O–Si≡ bridge in the polysesquisiloxane model, and does not interact with the C–F bonds on the anionic (R^FO)₃Al–OSi≡ fragment. The Si–O distance in 3-DFT is 1.86 Å, which is ∼0.1 Å longer than the Si–O bond in [^tBu₃Si(OH₂)][CH₆B₁₁Br₆].⁵⁷ The Si is displaced from the plane defined by the three carbon atoms by 0.57 Å, a larger value than typically observed for silylium ions containing carborane anions (∼0.3–0.4 Å).

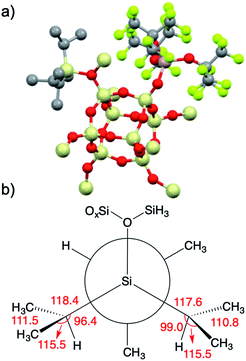Fig. 8 3-DFT with hydrogens hidden for clarity (a); Newman projection of the ⁱPr₃Si⁺ fragment in 3 (b). Selected angles (deg) are given in red and referred to in the text.

ⁱPr₃Si⁺ salts contain σ_C–H/3p hyperconjugation interactions between the methine C–H group of an isopropyl group and the empty 3p_z hybrid orbital on Si.⁵⁹ The presence of hyperconjugation results in bond angles that deviate from those expected for sp³ geometries. A Newman projection showing the [ⁱPr₃Si] fragment in 3 is shown in Fig. 8b. The Si–C–H bond angles in two of the ⁱPr units are 96.4° and 99.0°, respectively. These values are lower than the expected 109.5° expected for sp³ carbon, and is suggestive of σ_C–H/3p hyperconjugative interactions in 3-DFT. The sum of bond angles around these isopropyl carbons (Σ_C–C–X; X = C or Si) are 345.4° and 343.9°, respectively. Similar trends in bond angles were observed in the solid-state structure of [ⁱPr₃Si][CH₆B₁₁Br₆].⁵⁹ The third isopropyl has bond angles closer to those expected for sp³ carbon (Si–C–H = 103.4°; Σ_C–C–X = 339°).

A scale of ²⁹Si NMR chemical shift for selected ⁱPr₃Si–X species is shown in Fig. 9. The ²⁹Si NMR chemical shift of triisopropylsilane is 11 ppm, while triisopropylsilyltriflate has a chemical shift of 41 ppm. R₃Si⁺ salts containing carborane anions are more deshielded with respect to these species, appearing between 97 ppm for [ⁱPr₃Si][CH₆B₁₁I₆] and 115 ppm for [ⁱPr₃Si][CH₆B₁₁Cl₆].⁶⁰ [Me₃Si][EtCB₁₁F₁₁] contains a more weakly coordinating carborane anion and has a ²⁹Si NMR chemical shift of 138 ppm,⁶¹ similar to silylium zwitterions.⁶²

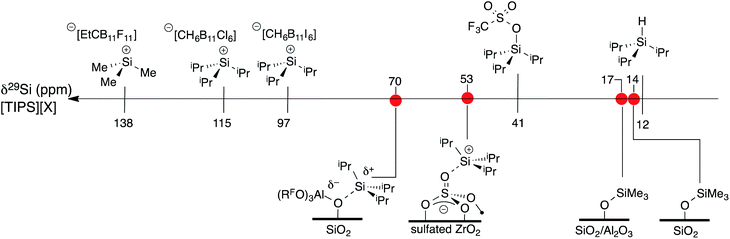Fig. 9 A scale relating buildup of positive charge on silicon to ²⁹Si NMR chemical shift for various WCAs and oxides.

Typical ²⁹Si NMR chemical shifts for alkylsilanes on oxides are also included in Fig. 9. The ²⁹Si CPMAS NMR spectrum of partially dehydroxylated silica containing –OSiMe₃ groups contains a ²⁹Si NMR signal at 14 ppm.^12–15 The ²⁹Si NMR chemical shift of trimethylsilyl functionalized zeolites appear at 17 ppm.⁶³ These results are inconsistent with a silylium character in these materials. To the best of our knowledge, the only [R₃Si][oxide] type species is ⁱPr₃Si⁺ supported on sulfated zirconia (δ²⁹Si = 53 ppm).⁶⁴ The ²⁹Si NMR chemical shift of 3 is 17 ppm more downfield than that of [ⁱPr₃Si][sulfated zirconia].

The data in Fig. 9 indicates that the isotropic ²⁹Si NMR chemical shift of R₃Si–X relate to the electronics at silicon.⁶⁰ A clear comparison is ⁱPr₃Si–OTf (δ²⁹Si = 41 ppm) and [ⁱPr₃Si][CH₆B₁₁Cl₆] (δ²⁹Si = 115 ppm). Triflate anions bind to ⁱPr₃Si fragments stronger than electron deficient carborane anions, which modulates the Lewis acidity of the ⁱPr₃Si-fragment in these compounds because silicon is more positively charged in carborane salts than triflates. This is also reflected in the geometry of the ⁱPr₃Si-fragment, which becomes more planar in carborane salts than typical sp³ organosilanes. Less clear was if this trend would also apply to alkylsilanes supported on oxides. The available ²⁹Si chemical shift values for R₃Si-supported on silica and silica–alumina suggested that alkylsilanes do not form R₃Si⁺ sites.^12–15,63 This is a result of formation of ≡SiO–SiR₃ sites on these material surfaces.

Sulfated zirconium oxide and 1 are more acidic than silica or silica alumina based on proton affinity calculations.³³ This suggests that these ⁱPr₃Si-functionalized materials would contain ²⁹Si NMR chemical shifts more downfield than R₃Si-functionalized silica or silica alumina. The ²⁹Si chemical shift of [ⁱPr₃Si][sulfated zirconia] (δ²⁹Si = 53 ppm) and 3 (δ²⁹Si = 70 ppm) are consistent with formation of species with R₃Si⁺ character. However, these chemical shifts are far from those of ⁱPr₃Si⁺ carborane salts. These data indicate that ²⁹Si NMR chemical shift trends for molecular R₃Si–X also apply to surface species. This implies that the ²⁹Si NMR chemical shift on R₃Si-functionalized surfaces gives information about ion-pairing on surfaces sites, which could be important in designing catalytic sites on these weakly coordinating surfaces.

Silylium ions are strong Lewis acids that catalyze or mediate numerous chemical reactions.^65–67 Silylium ions activate C–F bonds to form R₃Si–F and carbocation intermediates,^68–72 which are rapidly quenched in the presence of excess silane to form C–H bonds. 3 activates C–F bonds in 1-adamantylfluoride in the presence of Et₃SiH at 0 °C to give adamantane (TON = 18). This reactivity is consistent with silylium character in the ⁱPr₃Si⁺ fragment in 3. However, 3 is less stable than ⁱPr₃Si⁺ sites supported on sulfated zirconia, which gives 160 turnovers in this reaction.⁶⁴ Solution ¹⁹F NMR spectra monitored during the C–F bond activation reaction contain signals for Al(OR^F)₃ and HOC(CF₃)₃, indicating that the low stability of 3 is probably related to decomposition reactions of the surface aluminum anion under these conditions (Fig. S20†).

Conclusions

This study shows that design strategies for WCAs in solution can be applied to generate well-defined surface WCAs. The reaction of SiO_2-700 with Al(OR^F)₃*PhF in perfluorohexane forms ≡Si–OH⋯Al(OR^F)₃ (1) and contains strong Brønsted acid sites based on GPA calculations. Experimental evaluation of the ν_NH stretch in [Oct₃NH][(R^FO)₃Al–OSi≡)] (2) shows that this material forms weaker ion-pairs than typical first generation WCAs. 1 reacts with allyltriisopropylsilane to generate [ⁱPr₃Si][(R^FO)₃AlOSi≡] (3), a rare example of a silylium-like Lewis acid supported on an oxide, and to the best of our knowledge the only example supported on derivatized silica. Though the ν_NH stretch of 2 and ²⁹Si NMR chemical shift of 3 show that 1 does fulfill the prerequisites to form WCAs, these data also suggest that ion-pairing on these surface sites is stronger than carborane or [B(C₆F₅)₄] anions. Neutral Lewis acids stronger than Al(OR^F)₃ are necessary to form strong Brønsted acids with partially dehydroxylated silica to form weaker coordinating anions than 1.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. P. C. is a member of the UCR Center for Catalysis. This work was supported by NSF CHE-1800561 (M. P. C.). Solid-state NMR measurements were recorded on an instrument supported by NSF CHE-1626673. A. J. R. acknowledges the Donors of the American Chemical Society Petroleum Research Fund (58627-DNI6) for supporting solid-state NMR measurements. Computations were performed using the computer clusters and data storage resources of the HPCC at UC Riverside, which were funded by grants from NSF (MRI-1429826) and NIH (1S10OD016290-01A1).

References

1. I. Krossing and I. Raabe, Angew. Chem., Int. Ed., 2004, 43, 2066–2090.
2. G. A. Olah, G. K. Surya Prakash, Á. Molnár and J. Sommer, in Superacid Chemistry, John Wiley & Sons, Inc., 2008, ch. 1, pp. 1–34,  DOI:10.1002/9780470421604.
3. R. F. Jordan, W. E. Dasher and S. F. Echols, J. Am. Chem. Soc., 1986, 108, 1718–1719.
4. C. A. Reed, Acc. Chem. Res., 1998, 31, 325–332.
5. E. Y.-X. Chen and T. J. Marks, Chem. Rev., 2000, 100, 1391–1434.
6. A. B. A. Rupp and I. Krossing, Acc. Chem. Res., 2015, 48, 2537–2546.
7. C. A. Reed, Acc. Chem. Res., 2010, 43, 121–128.
8. C. A. Reed, Acc. Chem. Res., 2013, 46, 2567–2575.
9. C. Copéret, A. Comas-Vives, M. P. Conley, D. P. Estes, A. Fedorov, V. Mougel, H. Nagae, F. Núñez-Zarur and P. A. Zhizhko, Chem. Rev., 2016, 116, 323–421.
10. C. Copéret, M. Chabanas, R. Petroff Saint-Arroman and J.-M. Basset, Angew. Chem., Int. Ed., 2003, 42, 156–181.
11. S. L. Wegener, T. J. Marks and P. C. Stair, Acc. Chem. Res., 2011, 45, 206–214.
12. M. P. Conley, C. Copéret and C. Thieuleux, ACS Catal., 2014, 4, 1458–1469.
13. C. Zapilko, M. Widenmeyer, I. Nagl, F. Estler, R. Anwander, G. Raudaschl-Sieber, O. Groeger and G. Engelhardt, J. Am. Chem. Soc., 2006, 128, 16266–16276.
14. J. Bluemel, J. Am. Chem. Soc., 1995, 117, 2112–2113.
15. K. D. Behringer and J. Blümel, J. Liq. Chromatogr. Relat. Technol., 1996, 19, 2753–2765.
16. M. Jezequel, V. r. Dufaud, M. J. Ruiz-Garcia, F. Carrillo-Hermosilla, U. Neugebauer, G. P. Niccolai, F. d. r. Lefebvre, F. β. Bayard, J. Corker, S. Fiddy, J. Evans, J.-P. Broyer, J. Malinge and J.-M. Basset, J. Am. Chem. Soc., 2001, 123, 3520–3540.
17. N. Millot, S. Soignier, C. C. Santini, A. Baudouin and J.-M. Basset, J. Am. Chem. Soc., 2006, 128, 9361–9370.
18. Y. Yang, B. Beele and J. Blümel, J. Am. Chem. Soc., 2008, 130, 3771–3773.
19. J. Sommer, Y. Yang, D. Rambow and J. Blümel, Inorg. Chem., 2004, 43, 7561–7563.
20. R. Wischert, P. Laurent, C. Copéret, F. Delbecq and P. Sautet, J. Am. Chem. Soc., 2012, 134, 14430–14449.
21. J. Joubert, F. Delbecq, P. Sautet, E. L. Roux, M. Taoufik, C. Thieuleux, F. Blanc, C. Copéret, J. Thivolle-Cazat and J.-M. Basset, J. Am. Chem. Soc., 2006, 128, 9157–9169.
22. P. J. Toscano and T. J. Marks, J. Am. Chem. Soc., 1985, 107, 653–659.
23. T. J. Marks, Acc. Chem. Res., 1992, 25, 57–65.
24. J. Guzman and B. C. Gates, Dalton Trans., 2003, 3303–3318,  10.1039/b303285j.
25. M. Hino and K. Arata, J. Chem. Soc., Chem. Commun., 1980, 851–852,  10.1039/c39800000851.
26. D. B. Culver, H. Tafazolian and M. P. Conley, Organometallics, 2018, 37, 1001–1006.
27. H. Tafazolian, D. B. Culver and M. P. Conley, Organometallics, 2017, 36, 2385–2388.
28. D. M. Kaphan, R. C. Klet, F. A. Perras, M. Pruski, C. Yang, A. J. Kropf and M. Delferro, ACS Catal., 2018, 8, 5363–5373.
29. M. Stalzer, M. Delferro and T. Marks, Catal. Lett., 2015, 145, 3–14.
30. W. Gu, M. M. Stalzer, C. P. Nicholas, A. Bhattacharyya, A. Motta, J. R. Gallagher, G. Zhang, J. T. Miller, T. Kobayashi, M. Pruski, M. Delferro and T. J. Marks, J. Am. Chem. Soc., 2015, 137, 6770–6780.
31. Z. H. Syed, D. M. Kaphan, F. A. Perras, M. Pruski, M. S. Ferrandon, E. C. Wegener, G. Celik, J. Wen, C. Liu, F. Dogan, K. I. Goldberg and M. Delferro, J. Am. Chem. Soc., 2019, 141, 6325–6337.
32. J. Rodriguez, D. B. Culver and M. P. Conley, J. Am. Chem. Soc., 2019, 141, 1484–1488.
33. F. Haase and J. Sauer, J. Am. Chem. Soc., 1998, 120, 13503–13512.
34. R. C. Klet, D. M. Kaphan, C. Liu, C. Yang, A. J. Kropf, F. A. Perras, M. Pruski, A. S. Hock and M. Delferro, J. Am. Chem. Soc., 2018, 140, 6308–6316.
35. J. Sauer, J. Mol. Catal., 1989, 54, 312–323.
36. T. Xu, N. Kob, R. S. Drago, J. B. Nicholas and J. F. Haw, J. Am. Chem. Soc., 1997, 119, 12231–12239.
37. G. A. Olah, G. K. S. Prakash, J. Sommer and A. Molnar, Superacid Chemistry, John Wiley & Sons, 2009.
38. N. Millot, C. C. Santini, F. d. r. Lefebvre and J.-M. Basset, C. R. Chim., 2004, 7, 725–736.
39. J. F. Walzer, US Pat., 5,643,847, 1995.
40. N. Millot, C. C. Santini, A. Baudouin and J.-M. Basset, Chem. Commun., 2003, 2034–2035,  10.1039/b304047j.
41. Y.-J. Wanglee, J. Hu, R. E. White, M.-Y. Lee, S. M. Stewart, P. Perrotin and S. L. Scott, J. Am. Chem. Soc., 2012, 134, 355–366.
42. L. O. Müller, D. Himmel, J. Stauffer, G. Steinfeld, J. Slattery, G. Santiso-Quiñones, V. Brecht and I. Krossing, Angew. Chem., Int. Ed., 2008, 47, 7659–7663.
43. S. E. Ashbrook and S. Sneddon, J. Am. Chem. Soc., 2014, 136, 15440–15456.
44. Z. Gan, Chem. Commun., 2006, 4712–4714,  10.1039/b611447d.
45. L. Chen, Q. Wang, B. Hu, O. Lafon, J. Trébosc, F. Deng and J.-P. Amoureux, Phys. Chem. Chem. Phys., 2010, 12, 9395–9405.
46. I. Del Rosal, I. C. Gerber, R. Poteau and L. Maron, J. Phys. Chem. A, 2010, 114, 6322–6330.
47. A. Kraft, J. Beck, G. Steinfeld, H. Scherer, D. Himmel and I. Krossing, Organometallics, 2012, 31, 7485–7491.
48. W. E. Farneth and R. J. Gorte, Chem. Rev., 1995, 95, 615–635.
49. J. F. Haw, Phys. Chem. Chem. Phys., 2002, 4, 5431–5441.
50. A. Zheng, S.-B. Liu and F. Deng, Chem. Rev., 2017, 117, 12475–12531.
51. M. Rybicki and J. Sauer, Catal. Today, 2019, 323, 86–93.
52. A. J. Jones and E. Iglesia, ACS Catal., 2015, 5, 5741–5755.
53. H. Fang, A. Zheng, Y. Chu and F. Deng, J. Phys. Chem. C, 2010, 114, 12711–12718.
54. A. Zheng, H. Zhang, X. Lu, S.-B. Liu and F. Deng, J. Phys. Chem. B, 2008, 112, 4496–4505.
55. E. S. Stoyanov, K.-C. Kim and C. A. Reed, J. Am. Chem. Soc., 2006, 128, 8500–8508.
56. S. P. Hoffmann, T. Kato, F. S. Tham and C. A. Reed, Chem. Commun., 2006, 767–769,  10.1039/b511344j.
57. Z. Xie, R. Bau and C. A. Reed, J. Chem. Soc., Chem. Commun., 1994, 2519–2520,  10.1039/c39940002519.
58. Z. Xie, D. J. Liston, T. Jelínek, V. Mitro, R. Bau and C. A. Reed, J. Chem. Soc., Chem. Commun., 1993, 384–386,  10.1039/c39930000384.
59. Z. Xie, R. Bau, A. Benesi and C. A. Reed, Organometallics, 1995, 14, 3933–3941.
60. Z. Xie, J. Manning, R. W. Reed, R. Mathur, P. D. W. Boyd, A. Benesi and C. A. Reed, J. Am. Chem. Soc., 1996, 118, 2922–2928.
61. T. Küppers, E. Bernhardt, R. Eujen, H. Willner and C. W. Lehmann, Angew. Chem., Int. Ed., 2007, 46, 6346–6349.
62. R. Ramírez-Contreras, N. Bhuvanesh, J. Zhou and O. V. Ozerov, Angew. Chem., Int. Ed., 2013, 52, 10313–10315.
63. W. Song, D. M. Marcus, S. M. Abubakar, E. Jani and J. F. Haw, J. Am. Chem. Soc., 2003, 125, 13964–13965.
64. D. B. Culver and M. P. Conley, Angew. Chem., Int. Ed., 2018, 57, 14902–14905.
65. H. F. T. Klare, ACS Catal., 2017, 7, 6999–7002.
66. H. F. T. Klare and M. Oestreich, Dalton Trans., 2010, 39, 9176–9184.
67. Y. Seo and M. R. Gagné, ACS Catal., 2018, 8, 6993–6999.
68. C. Douvris, C. M. Nagaraja, C. H. Chen, B. M. Foxman and O. V. Ozerov, J. Am. Chem. Soc., 2010, 132, 4946–4953.
69. V. J. Scott, R. Celenligil-Cetin and O. V. Ozerov, J. Am. Chem. Soc., 2005, 127, 2852–2853.
70. C. Douvris and O. V. Ozerov, Science, 2008, 321, 1188–1190.
71. S. Duttwyler, C. Douvris, N. L. P. Fackler, F. S. Tham, C. A. Reed, K. K. Baldridge and J. S. Siegel, Angew. Chem., Int. Ed., 2010, 49, 7519–7522.
72. B. Shao, A. L. Bagdasarian, S. Popov and H. M. Nelson, Science, 2017, 355, 1403–1407.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc05904k

---