Open Access Article
Open Access ArticleNon-redox doping boosts oxygen evolution electrocatalysis on hematite†
Huu Chuong
Nguyën‡
 a,
Felipe Andrés
Garcés-Pineda‡
a,
Felipe Andrés
Garcés-Pineda‡
 a,
Mabel
de Fez-Febré
ab,
José Ramón
Galán-Mascarós
a,
Mabel
de Fez-Febré
ab,
José Ramón
Galán-Mascarós
 *ac and
Núria
López
*ac and
Núria
López
 *a
*a
aInstitute of Chemical Research of Catalonia (ICIQ), The Barcelona Institute of Science and Technology, Av. Països Catalans 16, Tarragona 43007, Spain. E-mail: nlopez@iciq.es; jrgalan@iciq.es
bDepartament de Quimica Fisica i Inorganica, Universitat Rovira i Virgili, Marcel.lí Domingo s/n, Tarragona, E-43007, Spain
cICREA, Passeig Lluis Companys, 23, Barcelona 08010, Spain
First published on 30th January 2020
Abstract
The oxygen evolution reaction (OER) is the major bottleneck to develop viable and cost-effective water electrolysis, a key process in the production of renewable fuels. Hematite, all iron α-Fe2O3, would be an ideal OER catalyst in alkaline media due to its abundance and easy processing. Despite its promising theoretical potential, it has demonstrated very poor OER activity under multiple experimental conditions, significantly worse than that of Co or Ni-based oxides. In the search for improving hematite performance, we have analysed the effect of doping with redox vs. non-redox active species (Ni or Zn). Our results indicate that Zn doping clearly outperforms Ni, commonly accepted as a preferred dopant. Zn-doped hematite exhibits catalytic performances close to the state-of-the-art for alkaline water splitting: reaching 10 mA cm−2 at just 350 mV overpotential (η) at pH 13, thus twenty times that of hematite. Such a catalytic enhancement can be traced back to a dramatic change in the reaction pathway. Incorporation of Ni, as previously suggested, decreases the energetic barrier for the OER on the available centres. In contrast, Zn facilitates the appearance of a dominant and faster alternative via a two-site reaction, where the four electron oxidation reaction starts on Fe, but is completed on Zn after thermodynamically favoured proton coupled electron transfer between adjacent metal centres. This unique behaviour is prompted by the non-redox character of Zn centres, which maintain the same charge during OER. Our results open an alternative role for dopants on oxide surfaces and provide a powerful approach for catalytic optimisation of oxides, including but not limited to highly preferred all-iron oxides.
Introduction
Artificial photosynthesis (AP), using solar energy to transform CO2 and H2O into fuels and O2, is the most promising approach to a carbon-neutral cycle and scalable energy storage.1,2 Electrocatalysis appears as an attractive option for AP, which could be extended to all intermittent renewable energy sources. Another advantage is the bifurcation of AP reactions into two electrochemical half-reactions: the CO2 reduction reaction (CO2RR) and oxygen evolution reaction (OER), that can be developed using different catalysts for optimal performance under ambient conditions.Earth abundant transition metal oxides are excellent OER catalysts under alkaline conditions.3–5 Among them, the most efficient are typically based on Ni or Co,6 with other metals incorporated at low concentrations, or as dopants7 to enhance performance. Although the role of iron is supposed to be fundamental for many of these OER catalysts, surprisingly, all-iron oxides have exhibited, until now, significantly poor performance, appearing as the worst OER catalysts in the series.8 This is the case for α-Fe2O3 (hematite, or most commonly known as “rust”), a low cost, highly stable, and non-toxic oxide.9–11 Extensive studies have been done on tuning hematite's electronic structure to improve its catalytic activity on water splitting. Among them, doping with metal12–17 and non-metal18–20 impurities has been specially addressed. In general, the incorporation of transition metals has been regarded as an effective approach to enhance the catalytic activity of α-Fe2O3.21–24 Unfortunately, results on hematite have been modest, when compared with the state-of-the-art. The best hematite-based OER electrocatalyst was obtained in 98%-hematite nano-sphericons doped with atomically dispersed Ce and Ni/NiO nanoparticles.25 Significantly, the introduction of close-shell (non-redox) active dopants has been overlooked in all these previous electrocatalytic studies.
In contrast, non-redox doping has been studied in detail in the corresponding hematite-based photoelectrodes. α-Fe2O3 is a semiconductor with a band gap of 2.0–2.2 eV, well-aligned for overall water splitting, with a theoretical conversion efficiency of 12%. Despite its promising features, experimental studies delivered moderate results due to its poor conductivity and high electron–hole recombination rates and to the large OER overpotential needed to carry out water oxidation on a hematite surface.9–11 Doping with non-redox cations such as Zn2+, Sn4+ or Ti4+ has been used to facilitate charge transport, enhancing electrical conductivity and photoelectrochemical performance. Zn2+ doping, for instance, transforms the weakly n-type hematite into a p-type semiconductor, as required for a successful photocathode.26,27 In comparison, Zn doping should be detrimental in the case of a photoanode. Interestingly, very recent studies have reported that, although anodic photocurrent decreases upon Zn doping when compared with a more suitable n-type dopant,28 Zn doping results in a significant decrease in the OER onset overpotential, even in the dark.29 From these surprising results, Ferapontova et al. suggested that Zn doping was directly enhancing the water oxidation catalysis on hematite surfaces, but the origin of this effect was not identified.30
This is precisely the aim of the present work, where we report a systematic study on OER catalysis promoted by α-Fe2O3, as modified with redox and non-redox active aliovalent dopants. In pure catalytic studies (in the dark), our results indicate that non-redox dopants promote a superior OER activity, thanks to the appearance of an alternative and faster multi-centre OER mechanism, only accessible upon the presence of such close-shell centres on the oxide surface. These findings obtained from the combination of experimental and computational data appear to be valid for other transition metal oxides as OER catalysts, opening alternative optimisation strategies into the complex and crucial problem of water splitting catalysis.
Results and discussion
Preparation and electrocatalysis
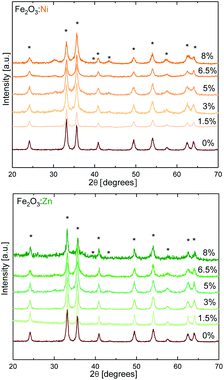
As model redox and non-redox dopants we selected Ni and Zn. Hematite catalysts with variable doping contents were synthesised by the combustion method,31 changing the concentration of the aliovalent (M2+ = Ni and Zn) dopants in the Fe2O3 structure up to 8%. The X-ray diffraction (XRD) powder patterns recorded for α-Fe2O3 Ni and Zn-doped α-Fe2O3 samples are shown in Fig. 1. The diffractograms for all compounds obtained are consistent with the α-Fe2O3 hematite crystal structure (ICSD code 15840), which confirms that doping is not altering the α-Fe2O3 phase, and that the doping at low ratios does not induce impurities. Doping above ≈8% induces a phase transition (Fig. S1†), and traces of spinel phases appear.32 Therefore, this was the doping limit for our experimental studies, since it is fundamental to maintain the pristine α-Fe2O3 structure to properly correlate and understand the experimental activity. The average crystallite sizes were calculated from XRD data using the Scherrer equation and the results are in agreement with previous reports on doped-hematite. A subtle reduction from 18 nm down to 14 nm between α-Fe2O3 and the 8% dopant content was found.33Then, we tested the OER activity by linear sweep voltammetry (LSV) in 0.1 M KOH solution (pH 13) (see Fig. 2a and S2†). The (Fe2O3:Ni) electrode activity in basic media increases with Ni doping, starting at very low Ni concentrations (<1%), until reaching a maximum OER activity at 3% doping, obtaining a current density of 5.6 mA cm−2 at 1.57 V vs. RHE when, under the same conditions, hematite only delivers 0.5 mA cm−2. Above 3% doping is not beneficial, and performance is essentially constant up to 8% doping (Fig. 2b).
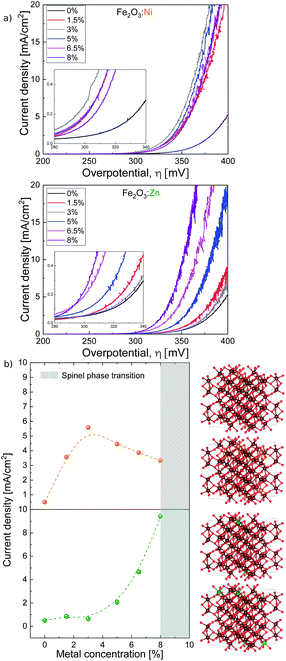 | ||
| Fig. 2 (a) Ni and Zn doped hematite current density vs. overpotential. (b, left) Current density vs. metal concentration taken at 350 mV overpotential and (b, right) most stable structures from DFT (from top to bottom) 5% Ni:Fe2O3, 10% Ni:Fe2O3, 5% Zn:Fe2O3, and 10% ZnFe2O3. Notice that Ni dopants sit in lower layers when concentration is increased but Zn dopants always prefer to be on top. The same color code as in Fig. 1. | ||
On the other hand, the activity of Zn-doped hematite (Fe2O3:Zn) follows a different trend. Very low Zn concentration shows a negligible effect on catalytic performance. However, above 4% Zn, OER activity progressively improves reaching a current density over 9 mA cm−2 at 1.57 V vs. RHE (350 mV overpotential) at maximum doping. This is approximately twenty times higher than that of undoped hematite α-Fe2O3, and significantly higher also in comparison with the Ni-doped samples.
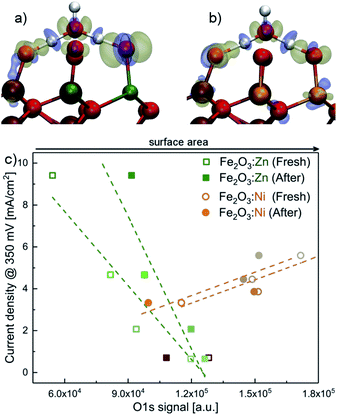
In order to determine if the apparently different catalytic activity could be due to physicochemical modifications of the material upon doping, and not directly related to an enhanced catalytic activity, we carried out several additional characterisation experiments. First, it is important to note that all electrochemical measurements were iR-compensated, so conductivity improvement could not explain the OER current boost. We also looked into the effect of doping on the preferential growth of active crystalline faces. Analysis of the XRD data indicates that only Ni doping induces some variations in the texture of the crystallites, whereas Zn doping has no effect (Fig. S3†). We also performed nitrogen adsorption/desorption analysis that confirms that the exposed surface area is barely affected by doping (Fig. S4†). The same conclusion was found from double layer capacitance data for all materials. Capacitance, proportional to the surface density of active sites, shows very minor changes and follows the same trend upon doping for both, Ni and Zn (Fig. S5†). Finally, although ZnO is highly soluble in alkaline media, we did not find significant Zn leaching during OER experiments with Zn:Fe2O3. Less than 0.05% of the total Zn content (Table S1†) was found in the electrolyte solution after 2 hour water electrolysis at 10 mA cm−2 in KOH (0.1 M). This small Zn leaching was also observed in the XPS analysis, where the Zn+2/Fe+3 ratio decreases slightly after electrochemical performance (Fig. S6†). This negligible leaching evidences that the incorporated Zn in the hematite structure is chemically stable. In summary, all data indicate that indirect effects, such as improved charge transport or larger surface area, cannot justify the enhanced electrocatalytic performance observed, suggesting that the origin should be associated with an improved catalytic mechanism.
This is also hinted by the Tafel plots (Fig. S7†). Upon Ni doping, the Tafel slope remains almost constant at 36 ± 2 mV dec−1. In contrast, upon Zn doping, the slope drops very fast, down to 26 ± 2 mV dec−1. Since the Tafel slope is directly related to the rate limiting step during the reaction, this change suggests a change in the reaction mechanism upon Zn doping.
Computational modeling
To unravel the origin for this different effect on the catalytic properties we performed computational studies with the PBE+U functional.34 The α-Fe2O3 bulk parameters obtained with Quantum Espresso35,36 (Table S2†) are similar to those in the literature.37–40To first explain the behaviour observed in Fig. 2b, we have computed the stability of the structure doped with Ni and Fe. Our results from DFT show that the first Ni dopants prefer to be on the top layer, making them available to participate in the catalytic process. However, as the dopant concentration increases, the next dopants prefer to be on the second layer, with a detrimental effect on OER catalysis (Table S7†). For the Zn doping, our DFR results show that Zn always prefers to stay on the top layer up to even 10% doping. These results are in accordance with the experimental measurements.
The aliovalent doped hematite was represented by a slab of the lowest energy surface (0001) and a (2 × 2) supercell containing 5% (Zn and Ni) and 10% as an approximation for the 8% Zn-doped hematite. Initially, the dopants replace Fe ions in the lattice and an extensive configurational search (1466 structures)41 to localise the lowest energy distribution was performed with PBE+U. An exact 8% computational doping would have increased the number of possible configurations to sample and requires enormous supercells; therefore the 10% was considered instead (see the ESI and Fig. S8† for more details).
The effect of the dopants in the mechanism of electrocatalytic water oxidation on hematite electrodes can be very complex.42 There are two main OER mechanisms in the literature: water nucleophilic attack (WNA) and interaction of two M–O units (I2M).43–45 However, ab initio molecular dynamics simulations have shown that the WNA is energetically more favorable on the (0001) surface of hematite.46 Rossmeisl et al.47,48 showed that alkaline and acidic models for the OER have equivalent intermediates during the reaction cycles and mostly the resting state of the surface under reaction conditions is different.49 In alkaline solutions, the WNA is a four-step process48 with the following reaction network:
| OH− + * ⇌ *OH + e− | (1) |
| *OH + OH− ⇌ *O + H2O(l) + e− | (2) |
| *O + OH− ⇌ *OOH + e− | (3) |
| *OOH + OH− ⇌ * + O2(g) + H2O(l) + e− | (4) |
For each step involving the (*OH, *O, and *OOH) intermediates we computed the corresponding free energy ΔG using the computational hydrogen electrode.49–51 The OER potential UOER = max[ΔG1, ΔG2, ΔG3, ΔG4] was determined for the pure Fe2O3 system, and Fe2O3:M (M = Ni, Zn and 5–10%). The simplest OER path would be one in which all the intermediates interact with only one type of active site (either Fe or the dopant M).
Our results in Table 1 show that the second process, i.e. the oxidation of the *OH species to *O with the release of a proton and an electron (ΔG2), is a very energy demanding step in all cases (Fig. S9†). The Ni-doped system would exhibit the best OER activity at any doping level if no other paths were possible, despite (i) appearing to be the worst for ΔG1 and ΔG4, and (ii) the Zn-doped system being the best for ΔG3. In the same line, the limited effect of Ni doping that reaches a maximum at just 3% is consistent with the DFT model, since the first Ni dopants prefer to be on the surface, but additional Ni atoms go preferably into the lower layer when the concentration increases (see Table S7†). Thus, increasing the doping level beyond a given threshold may not improve the activity.
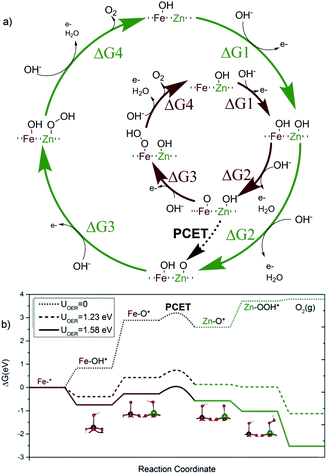
Thus, the superior effect on catalytic performance observed for the Zn-doped system must arise from a different mechanism. One plausible possibility is the appearance of a multi-center model, where the initial reaction steps take place on the Fe sites, but with the reaction concluding on an adjacent Zn site. In this alternative model, the OER starts on an iron site for steps 1 and 2, reaching the Fe–*O state, previous to the nucleophilic attack (Fig. 3b). Then, the reaction continues on an adjacent Zn center, with steps 3 and 4, as compiled in Fig. 3a. This alternative appears to be thermodynamically even more favorable, once the crucial PCET step between both sites is allowed.
We have computed the possibility to transfer the Fe–*O active species into Zn–*O to link the two paths in a bifunctional mechanism.51 The reaction can proceed through an O–Fe–O–Zn–OH substructure, where the H from the hydroxyl is transferred to the Fe–O moiety via effective proton-coupled electron transfer (PCET) between both metal centres.52 The barrier for such a process is only 0.33 eV. As suggested by the remaining electron density difference on the oxygen neighbours in the inset of Fig. 3a, the proton moves in the solution, assisted by a water molecule53 while the electron moves through the surface. Thus, the PCET step effectively moves the reaction site from Fe to Zn, regenerating the Fe–OH into its resting state, and generating a Zn–*O site, that offers a more thermodynamically favored pathway for the two remaining steps of the OER. In contrast, after the second oxidation towards the OER, an intermediate PCET process does not generate an analogous Ni–*O site. The most favoured pathway ends up in a non-oxyradical Ni = O configuration. This is demonstrated in Fig. 4 that shows how the residual charge resides either on the oxygen neighbour of Zn (a), or on the Ni center (b), leaving low radical character for the terminal oxygen in the latter case (see Fig. S10 and S11†). The results point out that the non-redox nature of the divalent dopant plays a major role in improving the electrocatalytic performance. The reason is that close-shell Zn2+ cannot accommodate/release any further electrons. Thus, the oxo M–*O structure has a more robust radical nature thus making the lifetime of the radical species longer and more likely to have a water nucleophilic attack. This aspect was overlooked in previous proposals of multiple-site mechanisms for the OER, where the dopant was improving the activity of the original atom.22,54,55 It is also worthy to mention that our DFT calculations confirm that Zn dopants preferentially sit on the surface even at high concentrations (see Fig. S8†), also supporting the different Ni vs. Zn doping effects. This agrees with the XRD analyses that showed how Ni-doping affects the crystal structure (Fig. S3†).
Experimental correlations with the DFT model
We gathered additional experimental evidences supporting a different OER mechanism for Ni- or Zn-doped materials. The corresponding XPS spectra before and after water electrolysis (Fig. S12–S20†) show identical features at all metallic edges (Ni, Zn or Fe). Recorded binding energy values are in agreement with the presence of Ni(II),3 Zn(II)56 and Fe(III)7 surrounded by oxygen atoms in the catalyst structures. Significant differences appeared in the O 1s XPS data. O 1s edge spectra of fresh catalysts show an intense band at 532 eV associated with the presence of hydroxo bridges (M(OH)x).3 After electrolysis tests, enhanced bands at lower binding energies appear, which are related to the presence of O–M bonds.3 Therefore, the catalyst surface gets oxidised during the electrocatalytic water oxidation process without affecting its catalytic performance.We correlated the XPS data for the O 1s signal in Fig. 4c with the electrocatalytic performance in Fig. 2. For the Ni-doped system, the current density increases when the area of the O 1s signal increases. The total area of the O 1s XPS signal can be directly related to oxygen coverage, as a good indicator of surface area. This observation concludes that a larger surface area enhances the electrocatalytic performance. However, the trend is the opposite for the Zn-doped system. The increased activity correlates with a decrease in the O 1s signal. A simple model for PCET using 2D random walk indicates that the probability for PCET decreases with the surface area, for a given number of exposed Zn (see the ESI† in Section 2D; random walk for PCET for the mathematical development and other details).
Discussion
The volcano plots47 for the doped hematites are presented in Fig. 5. Volcano activity plots appear as a consequence of the linear scaling relationships (LSR) between the energies of intermediates. In the OER, the key LSR exist between *OOH and *OH intermediates for all the systems considered (inset in Fig. 5 and Fig. S21† for better details) but differ depending on the nature of the dopant. The dependence found for the redox active centres agrees with that reported by Carter et al.,24i.e. with a slope of 1 and an offset of 3.2 eV, while the ideal case (no overpotential for the OER at an offset of 2.46 eV) is shown in the dashed grey line. The difference between 3.2 and 2.46 eV is assigned as responsible for the overpotential. Significantly, when the OER occurs on non-redox aliovalent dopants Zn and Mg (added for completeness) the *OOH vs. *OH points lie in a different group indicated in solid black. This line gets closer to the ideal dependence by 0.4 eV.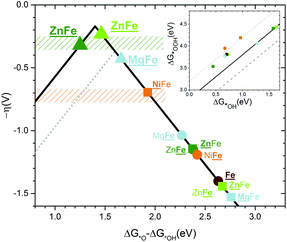 | ||
| Fig. 5 Volcano plot for the overpotential as a function of the energy difference ΔG*O − ΔG*OH computed without ZPE or entropic correction. The gray dotted line corresponds to the top volcano for redox doped hematite in agreement with the previous literature.24 The color code is the same as that in Fig. 1. The rectangle zones correspond to experimental measurements for Zn:Fe2O3 in green and Ni:Fe2O3 in orange. Underlined names correspond to the site where the OER occurs. A circle corresponds to a Fe site and a square to a dopant site. Both sites underlined or a triangle means PCET. The inset shows the linear scaling between the binding energies of *OOH as a function of *OH. The highest dotted line corresponds to the redox doped hematite and presents an offset of +3.2 eV. The solid line corresponds to an offset of +2.8 eV for the non-redox dopants. The lower dashed line corresponds to the ideal catalyst. All lines have a slope of 1. | ||
When the LSR are converted into the volcano plots (main Fig. 5), the overpotential (y-axis) is written in terms of the energy difference of *O and *OH intermediates (x-axis). Similar approaches combining experiments and theory have been reported for other systems in ref. 57–60. The redox dopants follow the dotted volcano, similar to that of Carter24 with Ni being the closest to the top. However, the non-redox volcano, shown by the continuous line, presents a higher top and thus a lower overpotential. When the *O–*OH energies of the combined Zn–Fe sites are considered (triangles in Fig. 5) the points are close to the top of the volcano with a value of 350 mV. Remarkably, the observed experimental values lie in the same range as the DFT prediction. The estimated binding energies also agree with the computed ones (Fig. S22†). Finally, as described before, the different doping-dependence observed, with a maximum for Ni (3%) and increasing from Zn, due to the ability of Zn to be accumulated on the surface while Ni subsurface positions are preferred at high loadings. Also Ferapontova et al. found better enhancement in photocatalysis at higher Zn dopant contents, showing that the onset of the photocatalytic phenomena might be linked to the active catalytic role in the OER.30
Conclusions
In summary, we have investigated OER electrocatalysis on Zn- and Ni-doped hematite. Our experimental and computational results for Ni-doped hematite show similar results to those in the literature, whereas Zn-doped hematite outperforms the state-of-the-art hematite-mediated OER electrocatalysis in alkaline solution, including nanostructured hematite electrodes.25 Indeed, our Zn-doped electrodes show superior performance to all published Fe-based OER catalysts in alkaline media as confirmed by current density data and turnover frequency (Table S9†).14,61–65The combination of experimental and theoretical investigations on the electrocatalytic performance, active surface area and morphology indicates that the improved OER catalytic properties of Zn-doped hematite should be linked to an alternative mechanistic pathway, including a thermodynamically favoured PCET process. The direct participation of the non-redox Zn centres as active sites during the O–O bond formation allows a higher top volcano to be reached for oxides that could not be achieved without it. This mechanism involving two sites is not suitable for redox-active dopants, like Ni, since the PCET does not activate a more favorable pathway, as Zn does. Until now, high-valent metal-oxo centres were exclusively regarded as the key to the high OER catalytic activity of metal oxides.66 Thus, this novel strategy opens interesting possibilities and could inspire new dopant strategies for enhancing the activity of other transition metal oxides for OER electrocatalysis, since Zn-doping has not been carefully studied in common binary/ternary metal oxides for OER electrocatalysis.67,68 Very recently, the positive effect of Zn-doping on OER activity in alkaline media has been independently reported for the case of NiFeOxHy.69 Of course, optimum doping levels and mechanistic considerations will depend on the structure and electronics of other host matrices. Such studies are in progress.
Experimental
Syntheses
All chemicals were commercially available (Sigma-Aldrich) and were used without further purification.Fe2O3 and doped Fe2O3 were obtained using the combustion method.31 A starting aqueous solution of 10 g of Fe(NO3)3·9H2O and 0.94 g of glycine in 150 mL of deionised water was prepared. This was followed by the addition of the dopants NiCl2·6H2O and ZnCl2 changing the doping concentration to 1.5%, 3%, 5%, 6.5% and 8%. After mixing the precursors with glycine, the solution was homogenised with a magnetic stirrer until total dissolution. Afterwards, the solution was heated up to 200 °C until the solvent was totally evaporated and glycine combusted. This flamy combustion process was accompanied by vigorous emission of gases (CO2, N2 and water vapor). The resulting porous dark solid was recovered and mechanically milled in an agate ball mill for 15 minutes at 25 Hz.
Electrode preparation
Catalysts were deposited on a nickel rotating disk electrode (Ni-RDE). The inks prepared contained 10 mg of catalyst and 10% of ionomer in weight (FAA-3 ionomer from FUMATEC®)70 and were made up to a final volume of 1 mL with a liquid mixture CH3CH2OH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O (3
H2O (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in volume). Then, 6 μL of ink were drop-cast on the clean surface of a nickel rotating disk electrode (Ni-RDE). The electrodes were dried at 60° to obtain a total loading of 0.84 mg catalyst per cm2.
1 in volume). Then, 6 μL of ink were drop-cast on the clean surface of a nickel rotating disk electrode (Ni-RDE). The electrodes were dried at 60° to obtain a total loading of 0.84 mg catalyst per cm2.
Electrochemical measurements
All electrochemical experiments were performed with a Biologic SP-150 potentiostat, an ALS Hg/HgO (1 M NaOH) reference electrode and a graphite rod counter electrode.A 877 Titrino Plus pH-probe (Metrohm) was used to measure the experimental pH for each measurement. The pH value was used to calculate the thermodynamic water oxidation potential 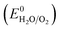 by employing the Nernst equation:
by employing the Nernst equation:
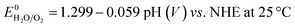 | (5) |
The overpotential (η) was calculated by subtracting the thermodynamic water oxidation potential from the applied experimental potential (Eapp).
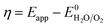 | (6) |
All potentials reported in this manuscript were converted to the NHE reference scale using E(NHE) = E(Hg/HgO) + 0.140 V. Unless otherwise stated, the solution electrolyte used for all electrochemical tests was 0.1 M KOH (pH 13). Before any electrochemical measurement, a current interrupt (0.5 mA) was applied to each electrode set-up, with a frequency of 0.2 s ten times to measure the Ohmic drop. An iR compensation of 80 ± 10 Ω was found to be the average for all electrodes, independent of the doping level. Before linear sweep voltammetry (LSV) experiments, a break-in protocol was also applied: N2 was bubbled through the electrolyte for 15–30 min to remove O2, and then inert gas was supplied above the electrolyte. The potential was cycled between 1.3 V vs. RHE and 1.7 V RHE at 75 mV s−1 until successive measurements were stable and reproducible. To collect LSV data, O2 was bubbled for 30 min (until OCP stabilisation). Then, LSV curves were measured at 1 mV s−1 starting from OCP to 1.7 V vs. RHE and back to 1.3 V vs. RHE. The LSV measurements were repeated until successive cycles showed good reproducibility (typically 2–3 cycles).
Characterization methods
Powder X-ray diffraction was carried out with a Bruker-AXS D8-Discover diffractometer, 40 kV and 40 mA. XPS data were collected at SSTTI University of Alicante. All spectra were collected using Al-Kα radiation (1486.6 eV), monochromatised with a twin crystal monochromator, yielding a focused X-ray spot with a diameter of 400 μm, at 3 mA × 12 kV. The alpha hemispherical analyser was operated in the constant energy mode with survey scan pass energies of 200 eV to measure the whole energy band and 50 eV in a narrow scan to selectively measure the particular elements. Charge compensation was achieved with a system flood gun that provides low energy electrons and low energy argon ions from a single source. ICP-OES was used to carry out elemental analysis with an Agilent 725-ES inductively coupled plasma optical emission spectrometer at the University of Valladolid. The basic solution after the electrochemical test was collected in a final volume of 50 mL. An aliquot of this basic solution was analysed by ICP-OES.Computational details
All DFT calculations were performed with Quantum Espresso 6.1 (ref. 35 and 36) for all the energetics using the Standard Solid State Pseudopotentials (doi.org/10.24435/materialscloud:2018.0001/v2). The kinetic energy cutoff for QE was ecutwfc = 40 Ry (544 eV) with ultrasoft pseudopotential and charge density cut-off and potential QE was ecutrho = 320.0 Ry (4353 eV). Bulk calculations were performed with 3 × 3 × 3 k-point sampling and slab calculations with 3 × 3 × 1. The PBE + U34 functional was used with the parameter U(Fe) = 4.2 eV. All input and output files can be accessed at the ioChem-BD database (DOI: 10.19061/iochem-bd-1-95). The computational SHE to calculate the Gibbs free energies, its derivation and other computational details can be found in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the European Union under the H2020 FET-PROACT A-LEAF project (Grant Agreement No. 732840). The authors thankfully acknowledge the computer resources at MareNostrum and the technical support provided by the Barcelona Supercomputing Center (QCM-2018-3-0012; theoretical studies on catalysis optimisation for an Artificial Leaf (A-LEAF)). We thank F. S. Hegner for critically reading the manuscript, and J. Lloret-Fillol for helpful discussion.Notes and references
- N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735 CrossRef CAS PubMed.
- N. S. Lewis, Nat. Nanotechnol., 2016, 11, 1010–1019 CrossRef CAS PubMed.
- L. Trotochaud, J. K. Ranney, K. N. Williams and S. W. Boettcher, J. Am. Chem. Soc., 2012, 134, 17253–17261 CrossRef CAS PubMed.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987 CrossRef CAS PubMed.
- R. D. L. Smith, M. S. Prevot, R. D. Fagan, S. Trudel and C. P. Berlinguette, J. Am. Chem. Soc., 2013, 135, 11580–11586 CrossRef CAS PubMed.
- J. B. Gerken, S. E. Shaner, R. C. Massé, N. J. Porubsky and S. S. Stahl, Energy Environ. Sci., 2014, 7, 2376–2382 RSC.
- L. Trotchaud, S. L. Young, J. K. Ranney and S. W. Boettcher, J. Am. Chem. Soc., 2014, 136, 6744–6753 CrossRef PubMed.
- C. C. L. McCrory, S. Jung, I. M. Ferrer, S. M. Chatman, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2015, 137, 4347–4357 CrossRef CAS PubMed.
- B. Gilbert, C. Frandsen, E. R. Maxey and D. M. Sherman, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 035108 CrossRef.
- K. Sivula, F. Le Formal and M. Gratzel, ChemSusChem, 2011, 4, 432–449 CrossRef CAS.
- M. S. Prevot and K. Sivula, J. Phys. Chem., 2013, 117, 17879–17893 CAS.
- C. Sanchez, K. D. Sieber and G. A. Somorjai, J. Electroanal. Chem. Interfacial Electrochem., 1988, 252, 269–290 CrossRef CAS.
- V. M. Aroutiounian, V. M. Arakelyan, G. E. Shahnazaryan, G. M. Stepanyan, J. A. Turner and O. Khaselev, Int. J. Hydrogen Energy, 2002, 27, 33–38 CrossRef CAS.
- Y. S. Hu, A. Kleiman-Shwarsctein, A. J. Forman, D. Hazen, J. N. Park and E. W. McFarland, Chem. Mater., 2008, 20, 3803–3805 CrossRef CAS.
- A. Kleiman-Shwarsctein, Y. S. Hu, A. J. Forman, G. D. Stucky and E. W. McFarland, J. Phys. Chem. C, 2008, 112, 15900–15907 CrossRef CAS.
- Y. Liu, Y. X. Yu and W. D. Zhang, Electrochim. Acta, 2012, 59, 121–127 CrossRef.
- H. Magnan, D. Stanescu, M. Rioult, E. Fonda and A. Barbier, Appl. Phys. Lett., 2012, 101, 133908 CrossRef.
- L. Guo, F. Chen, X. Fan, W. Cai and J. Zhang, Appl. Catal., B, 2010, 96, 162–168 CrossRef CAS.
- G. Carraro, D. Barreca, D. Bekermann, T. Montini, A. Gasparotto, V. Gombac, C. Monccato and P. Fornasiero, J. Nanosci. Nanotechnol., 2013, 13, 4962–4968 CrossRef CAS PubMed.
- G. K. Pradhan, N. Sahu and K. M. Parida, RSC Adv., 2013, 3, 7912–7920 RSC.
- C. Roy, B. Sebok, S. B. Scott, E. M. Fiordaliso, J. E. Sørensen, A. Bodin, D. B. Trimarco, C. D. Damsgaard, P. C. K. Vesborg, O. Hansen, I. E. L. Stephens, J. Kibsgaard and I. Chorkendorff, Nat. Catal., 2018, 1, 820–829 CrossRef CAS.
- B. Zhang, X. Zheng, O. Voznyy, R. Comin, M. Bajdich, M. Garcia-Melchor, L. Han, J. Xu, M. Liu, L. Zheng, F. P. Garcia de Arquer, C. T. Dinh, F. Fan, M. Yuan, E. Yassitepe, N. Chen, T. Regier, P. Liu, Y. Li, P. De Luna, A. Janmohamed, H. L. Xin, H. Yang, A. Vojvodic and E. H. Sargent, Science, 2016, 352, 333–337 CrossRef CAS PubMed.
- M. Rahman, N. Wadnerkar, N. J. English and J. M. D. MacElroy, Chem. Phys. Lett., 2014, 592, 242–246 CrossRef CAS.
- P. Liao, J. A. Keith and E. A. Carter, J. Am. Chem. Soc., 2012, 134, 13296–13309 CrossRef CAS PubMed.
- T. Odedairo, X. Yan, X. Yao, K. Ostrikov and Z. Zhu, Adv. Mater., 2017, 29, 1703792 CrossRef PubMed.
- Y. Chen, C. Kuo and Y. Hsu, J. Alloys Compd., 2018, 768, 810–816 CrossRef CAS.
- K. Sekizawa, K. Oh-ishi, K. Kataoka, T. M. Suzuki and T. Morikawa, J. Mater. Chem. A, 2017, 5, 6483–6493 RSC.
- A. Kay, D. A. Grave, D. S. Ellis, H. Dotan and A. Rothschild, ACS Energy Lett., 2016, 1, 827–833 CrossRef CAS.
- A. Tsyganok, D. Klotz, K. D. Malviya, A. Rothschild and D. A. Grave, ACS Catal., 2018, 8, 2754–2759 CrossRef CAS.
- N. Mirbagheri, D. Wang, C. Peng, J. Wang, Q. Huang, C. Fan and E. E. Ferapontova, ACS Catal., 2014, 4, 2006–2015 CrossRef CAS.
- J. Y. C. Chen, J. T. Miller, J. B. Gerken and S. S. Stahl, Energy Environ. Sci., 2014, 7, 1382–1386 RSC.
- M. Nikolic, M. Slankamenac, N. Nikolic, D. Sekulic, O. Aleksic, M. Mitric, T. Ivetic, V. Pavlovic and P. Nikolic, Sci. Sintering, 2012, 44, 307–321 CrossRef CAS.
- Z. Cao, M. Qin, Y. Gu, B. Jia, P. Chen and X. Qu, Mater. Res. Bull., 2016, 77, 41–47 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- P. Giannozzi, et al. , J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS.
- P. Giannozzi, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- M.-t. Nguyen, N. Seriani and R. Gebauer, J. Chem. Phys., 2013, 138, 194709 CrossRef PubMed.
- L. W. Finger and R. M. Hazen, J. Appl. Phys., 1980, 51, 5362–5367 CrossRef CAS.
- E. Krén, P. Szabó and G. Konczos, Phys. Lett., 1965, 19, 103–104 CrossRef.
- J. Lee and S. Han, Phys. Chem. Chem. Phys., 2013, 15, 18906–18914 RSC.
- R. Grau-Crespo, S. Hamad, C. R. A. Catlow and N. H. De Leeuw, J. Phys.: Condens. Matter, 2007, 19, 256201 CrossRef.
- M. J. Katz, S. C. Riha, N. C. Jeong, A. B. F. Martinson, O. K. Farha and J. T. Hupp, Coord. Chem. Rev., 2012, 256, 2521–2529 CrossRef CAS.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- Y.-H. Fang and Z.-P. Liu, J. Am. Chem. Soc., 2010, 132, 18214–18222 CrossRef CAS PubMed.
- M. García-Mota, A. Vojvodic, H. Metiu, I. C. Man, H.-Y. Su, J. Rossmeisl and J. K. Nørskov, ChemCatChem, 2011, 3, 1607–1611 CrossRef.
- N. Seriani, J. Phys.: Condens. Matter, 2017, 29, 463002 CrossRef PubMed.
- J. Rossmeisl, A. Logadottir and J. Nørskov, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- A. Hellman and R. G. S. Pala, J. Phys. Chem. C, 2011, 115, 12901–12907 CrossRef CAS.
- M. Busch, N. B. Halck, U. I. Kramm, S. Siahrostami, P. Krtil and J. Rossmeisl, Nano Energy, 2016, 29, 126–135 CrossRef CAS.
- R. I. Cukier, J. Phys. Chem. B, 2002, 106, 1746–1757 CrossRef CAS.
- N. J. English, M. Rahman, N. Wadnerkar and J. M. D. MacElroy, Phys. Chem. Chem. Phys., 2014, 16, 14445–14454 RSC.
- M. T. Koper, J. Electroanal. Chem., 2011, 660, 254–260 CrossRef CAS.
- X.-L. Wang, L.-Z. Dong, M. Qiao, Y.-J. Tang, J. Liu, Y. Li, S.-L. Li, J.-X. Su and Y.-Q. Lan, Angew. Chem., Int. Ed., 2018, 57, 9660–9664 CrossRef CAS PubMed.
- A. Sutka and K. A. Gross, Sens. Actuators, B, 2016, 256, 95–105 CrossRef.
- R. R. Rao, M. J. Kolb, N. B. Halck, A. F. Pedersen, A. Mehta, H. You, K. A. Stoerzinger, Z. Feng, H. A. Hansen, H. Zhou, L. Giordano, J. Rossmeisl, T. Vegge, I. Chorkendorff, I. E. L. Stephens and Y. Shao-Horn, Energy Environ. Sci., 2017, 10, 2626–2637 RSC.
- D.-Y. Kuo, J. K. Kawasaki, J. N. Nelson, J. Kloppenburg, G. Hautier, K. M. Shen, D. G. Schlom and J. Suntivich, J. Am. Chem. Soc., 2017, 139, 3473–3479 CrossRef CAS PubMed.
- S. Yang, A. Verdaguer-Casadevall, L. Arnarson, L. Silvioli, V. Čolić, R. Frydendal, J. Rossmeisl, I. Chorkendorff and I. E. L. Stephens, ACS Catal., 2018, 8, 4064–4081 CrossRef CAS.
- K. D. Jensen, J. Tymoczko, J. Rossmeisl, A. S. Bandarenka, I. Chorkendorff, M. Escudero-Escribano and I. E. L. Stephens, Angew. Chem., Int. Ed., 2018, 57, 2800–2805 CrossRef CAS PubMed.
- D. Xu, Y. Rui, Y. Li, Q. Zhang and H. Wang, Appl. Surf. Sci., 2015, 358, 436–442 CrossRef CAS.
- A. Tsyganok, D. Klotz, K. D. Malviya, A. Rothschild and D. A. Grave, ACS Catal., 2018, 8, 2754–2759 CrossRef CAS.
- Y. Yin, X. Zhang, L. Li, L. Spiccia and C. Sun, J. Phys. Chem. C, 2017, 121, 16059–16065 CrossRef CAS.
- N. T. Hahn and C. B. Mullins, Chem. Mater., 2010, 22, 6474–6482 CrossRef CAS.
- Y. Ling and Y. Li, Part. Part. Syst. Charact., 2014, 31, 1113–1121 CrossRef CAS.
- B. M. Hunter, H. B. Gray and A. M. Müller, Chem. Rev., 2016, 116, 14120–14136 CrossRef CAS PubMed.
- M. Gong and H. Dai, Nano Res., 2015, 8, 23–39 CrossRef CAS.
- B. You and Y. Sun, Acc. Chem. Res., 2018, 51, 1571–1580 CrossRef CAS PubMed.
- S. Y. Lim, S. Park, S. W. Im, H. Ha, H. Seo and K. T. Nam, ACS Catal., 2020, 10, 235–244 CrossRef CAS.
- M. Carmo, G. Doubek, R. Sekol, M. Linardi and A. D. Taylor, J. Power Sources, 2013, 230, 169–175 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc05669f |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2020 |